1. Introduction
Biofilms are dense accumulations of microbial cells on biotic or abiotic surfaces (called substrata) in aqueous environments. Once the microbial cells become sessile, they produce extracellular polymeric substances (EPS) that protect them against antibiotic attacks and mechanical washout [29]. Due to the sorption properties and enhanced mechanical stability of biofilms, they are beneficially used in wastewater treatment, soil remediation and groundwater protection [43]. On the other hand, biofilm formation and detachment can have very disadvantageous effects and lead to serious infections in the human body, biocorrosion of drinking water pipes or industrial facilities [11], contamination in food processing plants [27,30], etc. Biofilm formation is characterized by the balance of attachment, growth and detachment or dispersal processes [23,41]. Among these phenomena, there is a growing interest in the study of the latter, i.e. the release of microbial cells from the biofilm into the aqueous environment. Commonly, by detachment one refers to cell losses into the aqueous environment that are caused by external forces. Usually these external forces are shear forces due to bulk flow hydrodynamics [32]. These detachment losses can manifest themselves as sloughing or erosion of cells from the outer layers of the biofilm. By dispersal we refer to cell losses that can be internally triggered, e.g. by enzyme-mediated breakdown of the biofilm matrix [6], production of surfactants which loosen cells from the biofilm [8]; or externally triggered, e.g. by changes in nutrient availability [23], production of free radicals [4], or controlled by quorum sensing systems [34,37,45]. Dispersed cells can originate from inner layers of the biofilm and can contribute to downstream colonization, and thus eventually result in pipe obstruction, bacterial infection (biomedical implants), or increased microbial contamination in food processing plants [40].
Numerous mathematical models of biofilms have been proposed in the literature, focusing on different time and length scales and processes, and utilizing different mathematical concepts, from agent based to continuum mechanistic and from stochastic to deterministic. All dynamic models of biofilm formation include growth processes, including their dependence on nutrients. On the other hand, detachment and dispersal processes are often neglected, or treated in a rather qualitative manner, e.g. by coupling the detachment rate to biofilm thickness [12,43,44] or geometrical properties of the biofilm structure [46], without accounting for the processes that induce cell loss. No biofilm model is known that includes several or all known detachment and dispersal mechanisms. Rather each modeling study focuses on one particular trigger. A number of biofilm growth models have been proposed that include a physics based description of sloughing or erosion due to external forces, cf [1] for a simple one-dimensional model set in the Wanner-Gujer framework, and [31] for a 2D cellular automaton model. Only few papers have been published that use models of internally triggered biofilm dispersal: A cellular automaton model for nutrient limited dispersal was presented in [22,23], a cellular automaton model for detachment caused by enzymatic breakdown of the EPS matrix was presented in [47]. A partial differential equation based model for cell dispersal triggered by quorum sensing was presented in [18] and investigated there in first computer simulations. The question of well-posedness of the solutions of this model remained open. To give an answer to this question will be the focus of our current paper.
The model in [18] is an extension of a prototype biofilm growth model, which was originally introduced in [13] and did not include any detachment or dispersal processes. The biofilm is characterized in terms of the volume fraction that cells and EPS locally occupy. This is described by a highly non-linear diffusion-reaction equation for biomass, with two non-Fickian effects: (a) the diffusion operator degenerates like the porous medium equation for vanishing biomass densities and (b) it blows up if the local cell density approaches its maximum value. These effects ensure that the biofilm/water interface spreads at a finite speed and that the maximum biomass density is never exceeded. The biofilm expands spatially if the local cell density fills up the available volume while it does not spread notably if there is space locally available to accommodate new cells. In the prototype biofilm growth model, this biomass model is coupled with an additional non-degenerate diffusion-reaction equation for the nutrient that limits biomass growth. In [18] this model was extended to account also for the concentration of the quorum sensing molecules that trigger dispersal, and for an equation that describes the dispersed cells.
Previous extensions of this prototype biofilm growth model that included quorum sensing effects focused on the role of bulk hydrodynamics to facilitate non-local up-regulation due to advective transport [21], and on quorum sensing controlled EPS production [20] as a mechanism to switch from a colonization mode, in which resources are primarily invested in proliferation, to a protected mode of growth, in which EPS is produced, e.g. to mechanically stabilize the biofilm. In these models, down-and up-regulated cells are treated as two different cell fractions. For the model in [21] existence and uniqueness were derived in [38], whereby special features of the model assumptions could be used that do not hold in other, seemingly similar applications of the same biofilm modeling framework. In the current model, up-regulation is implicit. Rather than distinguishing between down-and up-regulated cells, we distinguish between cells that are sessile in the biofilm and motile ones, which after up-regulation disperse from the colony. The structure of the quorum sensing induced dispersal model is different from the previous multi-component biofilm models [10,24,38,40], in which one biomass type is described by a degenerate diffusion-reaction equation, and the other one by a semi-linear one.
To prove existence and uniqueness of solutions and continuous dependence of solutions on initial data we will use here ideas applied in [17] for the mono-species model and in [3] for a scalar degenerate reaction-diffusion equation of porous-medium type.
2. Mathematical model
We analyze the mathematical model of quorum sensing induced detachment in biofilms which was proposed in [18]. In this model we consider particulate biomass, i.e. biofilm bacteria, and suspended biomass, i.e. dispersed cells. As is common in many biofilm modeling studies, cf [44], we do not explicitly track EPS but subsume them in the biomass. The growth of both biomass fractions depends on a growth limiting nutrient. The bacterial cells have the ability to produce quorum sensing signal molecules which can trigger a switch from the sessile to the suspended mode of growth. The model is formulated for the dependent variables local density of particulate biomass (biofilm), ˜M, the concentration of dispersed cells, ˜N, the concentration of a nutrient, ˜C, and the quorum sensing molecule or autoinducer concentration ˜A. The independent variables are time ˜t and the spatial coordinate ˜x∈Ω⊂Rn,n=2,3; Ω is here the model domain that will be made more precise later. The model in dimensional form reads
|
∂˜t˜M=∇˜x⋅(˜DM(M)∇˜x˜M)+˜μ˜C˜k1+˜C˜M−˜k2˜M−˜η1(˜Am˜τm+˜Am)˜M,∂˜t˜N=˜d1Δ˜x˜N+˜μ˜C˜k1+˜C˜N−˜k2˜N+˜η1(˜Am˜τm+˜Am)˜M,∂˜t˜C=˜d2Δ˜x˜C−˜σ˜C˜k1+˜C(˜M+˜N),∂˜t˜A=˜d3Δ˜x˜A−˜λ˜A+[˜α+˜β˜Am˜τm+˜Am](˜M+˜N).
|
(1)
|
In model (1) we have intentionally omitted the re-attachment terms which were originally included in the model [18], because the simulations in [18] show that only a negligible amount of dispersed cells gets re-attached. Hence the inclusion or exclusion of the re-attachment terms will not make a significant difference from an application point of view, but it simplifies the mathematical analysis.
In the first equation of model (1), the diffusion term describes spatial expansion of the biofilm. This is a volume filling problem: as long as locally space is available to accommodate new cells the biofilm expands very slowly or not at all. When the maximum biomass density ˜M∞ that can be locally accommodated is nearly reached the biofilm starts to expand quickly. Following [13], this is described here by nonlinear, density dependent diffusion, with coefficient
|
˜DM(M)=˜dMa(1−M)b,wherea>1,b>1,˜d>0.
|
(2)
|
Here M:=˜M/˜M∞ is the volume fraction occupied by the biomass. This implies that we must have 0≤M<1. The diffusion coefficient ˜D(M) vanishes when the biomass density approaches zero and blows up when it tends to its maximum value. Note that the prototype biofilm growth model of [13] is a special case for this model in the absence of quorum sensing and/or dispersal effects, i.e. if ˜α=˜β=0 (and initially ˜A≡0≡˜N) or if ˜η1=0. The spatial expansion of the biofilm is thus driven by biomass accumulation. The polynomial degeneracy Ma, well known from the porous medium equation, guarantees that spatial spreading is negligible for low values of M and yields the separation of biofilm and liquid phase. For 0≪M≈1, the equation shows a super-diffusion effect, since the diffusion coefficient possesses a singularity at M=1 and blows up. In the prototype biofilm growth model of [13], this ensures the maximal bound for the biomass density which is a physical limitation as the number of cells that fits into a unit volume is bounded [16]. In particular, the blow up of the diffusion coefficient guarantees that M<1 if homogeneous Dirichlet conditions are specified for M on some parts of the boundary of the domain [16]. Since the production of biomass depends on the availability of nutrients, the upper bound on M cannot be guaranteed by the growth terms alone. The degeneracy Ma alone does not yield this maximum bound for the cell density, while the singularity (1−M)−b does not guarantee the separation of biofilm and liquid region by a sharp interface.
In model (1), diffusion of ˜N,˜C,˜A is Fickian with constant coefficients ˜d1,2,3. This is a simplification of [18], where it was assumed that the diffusion coefficients are smaller in the biofilm than in the aqueous phase, but well within one order of magnitude.
The reaction terms in (1) describe the following processes that are the same as in the model of [18]:
• Growth of sessile and dispersed cells ˜M and ˜N is controlled by the local availability of nutrients. This is described by standard Monod kinetics, cf [44], in the first and second equation of (1), where ˜k1 is the half saturation concentration and ˜μ1 is the maximum specific growth rate. The growth kinetics is assumed to be the same for both sessile and dispersed biomass.
• Natural cell death occurs at the same rate ˜k2 for ˜M and ˜N.
• Dispersal, i.e. the transition of bacteria from the sessile state ˜M into the suspended motile state ˜N, is controlled by the local concentration of the quorum sensing molecule ˜A. For small values of ˜A≪˜τ this transition is nearly zero (i.e. the biofilm is primarily down-regulated), but increases for large concentration values ˜A≫˜τ, and levels off at a maximum rate ˜η1 if ˜A is large (i.e. the biofilm is primarily up-regulated). This transition between both states is described by a Hill function, where ˜τ is the induction threshold and the exponent m>1.
• Consumption of nutrients is proportional to biomass growth, i.e. described by the same Monod kinetics. The maximum consumption rate is defined as ˜σ1=˜μ1/Y where Y is the yield coefficient.
• The signal molecules ˜A in the fourth equation of (1) are produced at a base rate ˜α if the local signal concentration is small, ˜A≪˜τ, and at the increased rate ˜α+˜β if it is large, ˜A≫˜τ. The transition between these two regimes is modeled by the same Hill function that was used to describe the triggering of dispersal, cf also [18]. According to [19] we assume ˜β=10˜α. Furthermore we have included an abiotic decay term, at rate ˜λ, for the signaling molecule, which was neglected in [18], but is included in many other quorum sensing models, e.g. [20,26,38,42].
To non-dimensionalize the model we express the biofilm biomass density ˜M by the volume fraction M as described above and further introduce the new dependent variables
|
N:=˜N˜M∞,C:=˜C˜C∞,,A:=˜A˜τ,
|
where ˜C∞ is the bulk substrate concentration that enters the model via boundary conditions (see below). The dimensionless independent variables are introduced as
where ˜L is a characteristic length scale of the domain, e.g. its length in case of rectangular Ω. In dimensionless form, the model becomes then
|
∂tM=∇⋅(DM(M)∇M)+Ck1+CM−k2M−η1 (Am1+Am)M,∂tN=d1ΔN+Ck1+CN−k2N+η1 (Am1+Am)M,∂tC=d2ΔC−σ Ck1+C(M+N),∂tA=d3ΔA−λA+[α+βAm1+Am](M+N).
|
(3)
|
Here the spatial derivative operators ∇ and Δ are now with respect to the dimensionless independent variable x. The parameters in (3) are di:=˜di˜μ˜L2,i=1,2,3, d:=˜d˜μ˜L2, DM(M):=d˜d˜D(˜M/˜M∞), k1:=˜k1˜C∞, α=˜α˜M∞˜τ˜μ, β=˜β˜M∞˜τ˜μ, η1=˜η1˜μ, σ=˜σ˜M∞˜μ˜τ and λ:=˜λ˜μ. The full list of the parameters and their values in dimensionless form that we use in our simulations later on is found in table 1.
Table 1. Parameters used in the numerical simulations.
| Parameter |
Description |
Value |
Source |
| k1 | half saturation concentration (growth) | 0.4 | [44] |
| k2 | lysis rate | 0.067 | assumed |
| σ | nutrient consumption rate | 793.65 | [19] |
| η1 | maximum dispersal rate | varied | [18] |
| λ | quorum sensing abiotic decay rate | 0.02218 | [39] |
| α | constitutive autoinducer production rate | varied | - |
| β | induced autoinducer production rate | 10×α | [19] |
| m | degree of polymerization | 2.5 | [19] |
| d1 | constant diffusion coefficients for N | 4.1667 | assumed |
| d2 | constant diffusion coefficients for C | 4.1667 | [15] |
| d3 | constant diffusion coefficients for A | 3.234 | [15] |
| d | biomass motility coefficient | 4.2×10−8 | [13] |
| a | biofilm diffusion exponent | 4.0 | [13] |
| b | biofilm diffusion exponent | 4.0 | [13] |
| L | system length | 1.0 | [15] |
| H | system height | 1.0 | assumed |
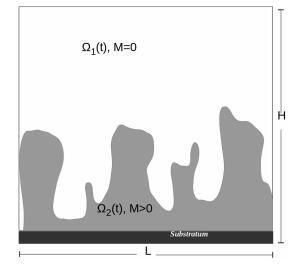
In this model, the actual biofilm is the region where sessile biomass is present, Ω2(t):={x∈Ω:M(t,x)>0}, whereas the surrounding aqueous phase corresponds to the region where sessile biomass is absent, Ω1(t):={x∈Ω:M(t,x)=0}, cf. Figure 1. Since M changes with time due to growth and dispersal, also these two regions change. They are separated by the biofilm/water interface, Γ(t):=∂Ω2(t)∖∂Ω. Neither Ω1(t) nor Ω2(t) need to be connected domains. In fact, Ω2(t) will in general consist of several colonies that are separated from each other by water-filled channels and voids. If a biofilm is contained in the inner region of Ω, away from its boundary, it is often called microbial floc (biofilm without substratum). This situation plays a major role in biological wastewater treatment.
It remains to specify initial and boundary values for the biomass fraction M and the concentrations of detached cells N, nutrient C and quorum sensing molecule A to complement the model. This will be made precise in the following section.
3. Analysis of the quorum sensing dispersal model
3.1. Preliminaries
For technical reasons we study the model in the auxiliary form
|
∂tM=∇⋅(DM(M)∇M)+Ck1+CM−k2M−η1 (|A|m1+|A|m)M⏟=g(M,N,C,A),∂tN=d1ΔN+Ck1+CN−k2N+η1 (|A|m1+|A|m)M⏟=f1(M,N,C,A),∂tC=d2ΔC−σ Ck1+C(M+N)⏟=f2(M,N,C,A),∂tA=d3ΔA−λ|A|+[α+β|A|m1+|A|m](M+N)⏟=f3(M,N,C,A),
|
(4)
|
with the initial and boundary conditions
|
M|∂Ω=0,N|∂Ω=0,C|∂Ω=C∞,A|∂Ω=0,M|t=0=M0,N|t=0=N0,C|t=0=C0,A|t=0=A0,
|
(5)
|
where C∞=1, and the functions M0,N0,C0,A0:Ω→R are non-negative and bounded. Moreover, we assume that
for some ρ∈(0,1), and M0,N0,C0 and A0 satisfy the compatibility conditions.
We point out that non-negative solutions of (3) solve (4) and vice versa, i.e. after the non-negativity is shown, the absolute value |.| can be removed from (4) to obtain the original model (3). Constant Dirichlet boundary conditions are imposed on the nutrient concentration C reflecting a constant unlimited nutrient supply at the boundary of the considered domain, while homogeneous Dirichlet boundary conditions are assumed for N and A enforcing the removal of dispersed cells and quorum sensing signal molecules. Similarly, homogeneous Dirichlet boundary conditions are assumed for the biomass fraction M. This describes the situation of a growing biofilm in the interior of the considered domain, away from the boundary. These specific boundary conditions are primarily chosen for convenience regarding the analysis, albeit boundary conditions of mixed type are often considered more appropriate in applications. Typically, Dirichlet boundary conditions are prescribed on some parts of the boundary while Neumann or Robin boundary conditions are specified on the other parts. In particular, the substratum on which the biofilm grows is impermeable for all dependent variables, which can be modelled by homogenous Neumann boundary conditions. An extension of our results for the Dirichlet problem to different boundary conditions can be achieved with the same strategy that was used in [17] for the prototype single-species/single-substrate biofilm model.
Here and in the sequel, we use the following notations, QT:=(0,T]×Ω for some T>0, Q=R+×Ω and
|
Φ(M):=∫M0DM(s)ds=∫M0dsa(1−s)bdsfor 0≤M<1.
|
(7)
|
Definition 3.1. We call (M,N,C,A) a solution of system (4) on [0,T] with the initial and boundary data (5), if the functions
|
M,N,C,A∈C([0,T];L1(Ω))∩L∞(QT)
|
and satisfy (4) in distributional sense.
More precisely, if M is a solution of system (4), then
|
∫Ω(Mφ)|s=t−∫ΩM0φ|s=0−∫Qt(M∂sφ+Φ(M)Δφ)=∫Qtg(M,N,C,A)φ,
|
(8)
|
for all t∈[0,T] and φ∈C2(¯QT) such that φ≥0 in QT and φ|∂Ω=0. Similarly, for C we have
|
∫Ω(Cφ)|s=t−∫ΩC0φ|s=0−∫Qt(C∂sφ+CΔφ)+∫t0∫∂ΩC∞∂νφ=∫Qtf2(M,N,C,A)φ,
|
(9)
|
for all t∈[0,T] and φ∈C2(¯QT) such that φ≥0 in QT and φ|∂Ω=0. As usual, ∂ν denotes the outward unit normal derivative at the boundary. The identities for N and A are accordingly.
3.2. Existence for smooth initial data
We consider smooth non-degenerate approximations for system (4) and show that their solutions converge to the solution of the degenerate problem (4). The ideas are based on the proof developed for scalar degenerate reaction-diffusion equations of porous medium type in [2], the solution theory in [17] for the single species biofilm model and the ideas applied in [10,24,38] and [39] for multi-species biofilm models.
For small ε>0, we define
|
Dε(M):={dεaif M<0,d(M+ε)a(1−M)bif 0≤M≤1−ε,d1εbifM≥1−ε,Φε(M):=∫M0Dε(s)ds,
|
(10)
|
and denote the solutions of the regular auxiliary systems
|
∂tMε=∇⋅(Dε(Mε)∇Mε)+g(Mε,Nε,Cε,Aε),∂tNε=d1ΔNε+f1(Mε,Nε,Cε,Aε),∂tCε=d2ΔCε+f2(Mε,Nε,Cε,Aε),∂tAε=d3ΔAε+f3(Mε,Nε,Cε,Aε).
|
(11)
|
where DM is replaced by Dε, by (Mε,Nε,Cε,Aε).
Lemma 3.2. Let the boundary and initial data be non-negative and smooth, M0, N0, A0∈C∞0(Ω), C0∈C∞(¯Ω) such that C0|∂Ω=1 and ‖M0‖L∞(Ω)<1−ρ for some ρ∈(0,1). Then, there exist unique solutions (Mε,Nε,Cε,Aε)∈C1,2(¯QT) of (4), that are non-negative and uniformly bounded w.r.t. ε>0.
Proof. By the classical theory for quasilinear parabolic equations there exist unique solutions (Mε,Nε,Cε,Aε)∈C1,2(¯QT) of (4) (cf. [25]). We use comparison theorems for quasilinear parabolic equations (e.g., see [2] or [5]) for each equation separately to show the non negativity and uniform boundedness of the solutions.
All components of the solution take non-negative values at the boundary, and the initial data are non-negative. Moreover, we observe that
|
g(0,N,C,A)=0=f2(M,N,0,A),
|
and, hence, zero is a subsolution for Mε and Cε. Since Mε is non-negative and
we conclude the non-negativity of Nε. Finally, we observe that
|
f3(M,N,C,0)≥0for M≥0,N≥0,
|
which implies that zero is a subsolution for Aε. Consequently, the parabolic comparison principle implies that Mε,Nε,Cε and Aε are non-negative.
To show the uniform boundedness of Mε we introduce the time-independent barrier function Mθ=1+θ, where θ is a solution of the elliptic problem
The maximum principle for elliptic equations [33] implies that θ≥0 in Ω, and
for some constant R1≥0. Moreover, we observe that
|
M0=Mε|t=0≤Mθ|t=0,0=Mε|∂Ω≤Mθ|∂Ω
|
and since Mθ is time-independent, it follows that
|
∂tMθ−∇⋅(Dε(Mθ)∇Mθ)−Cεk1+CεMθ+k2Mθ+η1(|Aε|n1+|Aε|n)Mθ=0+dεb−Cεk1+CεMθ+k2Mθ+η1(|Aε|n1+|Aε|n)Mθ≥dεb−Mθ+k2Mθ≥dεb−(1+R1)≥0=∂tMε−∇⋅(Dε(Mε)∇Mε)−g(Mε,Nε,Cε,Aε) ,
|
(13)
|
for all sufficiently small ε>0. Consequently, by the parabolic comparison principle there exists ε′0>0 such that the solutions Mε are uniformly bounded for all 0<ε≤ε′0.
Next, we show the uniform boundedness of the nutrient concentration Cε by defining Cmax:=max{||C0||L∞(Ω),1}. Then
|
∂tCmax−d2ΔCmax+σCmaxk1+Cmax(Mε+Nε)=σCmaxk1+Cmax(Mε+Nε)≥0,
|
(14)
|
where we used the non-negativity of the sessile biomass Mε and the dispersed cells Nε. This shows that Cmax is an upper solution, and hence, by the parabolic comparison principle Cε is bounded by Cmax. To prove the uniform boundedness of Nε we denote by ˆN the solution of the initial value problem
|
∂tˆN=d1ΔˆN+ˆN−k2ˆN+η1(1+R1),ˆN|∂Ω=0,ˆN|t=0=N0,
|
(15)
|
where 1+R1 is the upper bound for the sessile biomass fraction. We observe that ˆN is non-negative, it satisfies ˆN∈L∞(QT) and
|
∂tˆN−d1ΔˆN−Cεk1+CεˆN+k2ˆN−η1|Aε|m1+|Aε|mMε≥ ∂tˆN−d1ΔˆN−ˆN+k2ˆN−η1(1+R1)=0= ∂tNε−d1ΔNε−Cεk1+CεNε+k2Nε−η1|Aε|m1+|Aε|mMε.
|
(16)
|
Consequently, ˆN is an upper solution for the dispersed cells Nε.
Finally, we prove the uniform boundedness of the quorum sensing signal molecule concentration by showing that there exists a constant Amax≥‖A0‖L∞(Ω) which is an upper solution for Aε. It satisfies Amax|∂Ω≥0=Aε|∂Ω, Amax|t=0≥A0=Aε|t=0 and
|
∂tAmax−d3ΔAmax+λAmax−[α+β|Amax|m1+|Amax|m](Mε+Nε)=λAmax−[α+β|Amax|m1+|Amax|m](Mε+Nε)≥λAmax−(α+β)(|Mε|+|Nε|)≥λAmax−(α+β)(1+R1+ˆN)≥0,
|
(17)
|
where we use the boundedness of Mε and Nε, and |Amax|m1+|Amax|m≤1. This shows that if the constant Amax is sufficiently large, it is an upper solution, and by the parabolic comparison principle, it is a uniform upper bound for Aε.
In the following Lemma, we improve the upper bound on the sessile biomass density, in particular, we show that the singularity for M=1 is not attained.
Lemma 3.3. Under the hypothesis of Lemma 3.2, there exist δ>0 and ε0>0 such that Mε≤1−δ in QT for all 0<ε<ε0.
Proof. In order to improve the upper estimate on M we construct a suitable barrier function and consider the elliptic problem
The constants c1 and c2 are defined by
|
c1:=‖g(Mε,Nε,Cε,Aε)‖L∞(QT),c2:=‖Φε(M0)‖L∞(Ω),
|
(19)
|
for 0<ε<ε′0, where ε′0 was defined in the proof of Lemma 3.2, and
|
Φε(M0)=∫M00(s+ε)a(1−s)bdsfor 0≤M0<1−ε.
|
(20)
|
We remark that for sufficiently small ε1<ε′0, the constants c1 and c2 can be chosen uniform for all 0<ε<ε1. Moreover, the solution θ of (18) is bounded on Ω, and by the maximum principle for elliptic problems [33] it follows that θ≥c2 in Ω.
For 0<ε<ε1 we define Zε:=Φ−1ε(θ) and observe that
|
∂tZε−Δ(Φε(Zε))=c1=‖g(Mε,Nε,Cε,Aε)‖L∞(QT)≥∂tMε−Δ(Φε(Mε))
|
in QT. Moreover, the boundary conditions imply that
|
Zε|∂Ω=Φ−1ε(θ)|∂Ω=Φ−1ε(c2)≥Mε|∂Ω=0,
|
and the initial data satisfies
|
Zε|t=0=Φ−1ε(θ)|t=0≥Φ−1ε(c2)≥Φ−1ε(Φε(M0))=M0,
|
(21)
|
where we used the monotonicity of the function Φ−1ε. Consequently, the function Zε is an upper solution for the sessile biomass Mε. Using the fact that θ is bounded in Ω and that Φε(Mε)=dMεεb for Mε≥1−ε, we conclude by the parabolic comparison principle that there exist 0<ε0≤ε1 and δ∈(0,1) such that Mε≤Zε=Φ−1ε(θ)<1−δ for all 0<ε<ε0.
Lemma 3.4. Under the hypotheses of Lemma 3.2, the solutions Mε of (11) satisfy
|
∫QTDε(Mε)(∂tMε)2+supt∈[0,T]∫Ω|∇Φε(Mε)|2≤c, ∫QT(|∂tNε|2+|∂tCε|2+|∂tAε|2)+supt∈[0,T]∫Ω(|∇Nε|2+|∇Cε|2+|∇Aε|2)≤c,
|
(22)
|
for some constant c>0.
Proof. We first multiply the second equation in (11) by ∂sNε and integrate,
|
∫tτ∫Ω|∂sNε|2=−d12∫tτ∫Ω∂s|∇Nε|2+∫tτ∫Ω∂sNεf1(Mε,Nε,Cε,Aε),
|
(23)
|
where 0≤τ≤t≤T. Using Young's inequality leads to the estimate
|
∫tτ∫Ω|∂sNε|2+d12∫Ω|∇Nε|2|s=t=d12∫Ω|∇Nε|2|s=τ+∫tτ∫Ω∂sNεf1(Mε,Nε,Cε,Aε)≤d12∫Ω|∇Nε|2|s=τ+ξ∫tτ∫Ω|∂sNε|2+Cξ∫tτ∫Ω|f1(Mε,Nε,Cε,Aε)|2,
|
(24)
|
for small ξ>0, and some constant Cξ. Setting τ=0 we obtain
|
(1−ξ)∫Qt|∂sNε|2+d12∫Ω|∇Nε|2|s=t≤d12∫Ω|∇N0|2+Cξ∫Qt|f1(Mε,Nε,Cε,Aε)|2,
|
(25)
|
for small ξ>0, and some constant Cξ. Lemma 3.2 and the continuity of f1 now imply that
|
∫QT|∂tNε|2≤C′,supt∈[0,T]∫Ω|∇Nε|2≤C′,
|
(26)
|
for some constant C′≥0. The corresponding bounds for the solutions Cε and Aε can be obtained in the same way.
To derive the estimates for the biomass fraction Mε let
|
G(Mε,Nε,Cε,Aε):=∫Mε0Dε(ζ)g(ζ,Nε,Cε,Aε)dζ.
|
(27)
|
Multiplying the first equation of (11) by ∂s(Φε(Mε)) and integrating over Ω and from τ to t we obtain
|
∫tτ∫ΩDε(Mε)(∂sMε)2=∫tτ∫Ω∂s(Φε(Mε))∂sMε=∫tτ∫Ω∇⋅(Dε(Mε)∇Mε)∂s(Φε(Mε))+∫tτ∫Ω∂s(Φε(Mε))g(Mε,Nε,Cε,Aε)=−∫tτ∫ΩDε(Mε)∇Mε⋅∂s∇(Φε(Mε))+∫tτ∫Ω∂s(Φε(Mε))g(Mε,Nε,Cε,Aε)=−12∫tτ∫Ω∂s|Dε(Mε)∇Mε|2+∫tτ∫Ω∂s(Φε(Mε))g(Mε,Nε,Cε,Aε),
|
(28)
|
where we used integration by parts in the second step. Consequently, using the identity
|
∫ΩG(Mε,Nε,Cε,Aε)|s=t−∫ΩG(Mε,Nε,Cε,Aε)|s=τ=∫tτ∫Ω∂s(G(Mε,Nε,Cε,Aε))=∫tτ∫Ω∫Mε0Dε(ζ)∂s(g(ζ,Nε,Cε,Aε))+∫tτ∫Ω∂sMεDε(Mε)g(Mε,Nε,Cε,Aε)=∫tτ∫Ω∫Mε0Dε(ζ)(∂sN∂Ng(ζ,Nε,Cε,Aε)+∂sC∂Cg(ζ,Nε,Cε,Aε)+∂sA∂Ag(ζ,Nε,Cε,Aε))+∫tτ∫Ω∂s(Φε(Mε))g(Mε,Nε,Cε,Aε),
|
(29)
|
it follows that
|
∫tτ∫ΩDε(Mε)(∂tMε)2+12∫Ω|Dε(Mε)∇Mε|2|s=t=12∫Ω|Dε(Mε)∇Mε|2|s=τ+∫ΩG(Mε,Nε,Cε,Aε)|s=t−∫ΩG(Mε,Nε,Cε,Aε)|s=τ+∫tτ∫Ω∫Mε0Dε(ζ)(∂sN∂Ng(ζ,Nε,Cε,Aε)+∂sC∂Cg(ζ,Nε,Cε,Aε)+∂sA∂Ag(ζ,Nε,Cε,Aε)),
|
(30)
|
where ∂N,∂C,∂A denote the partial derivatives w.r.t. the variables N,C and A, respectively. Lemma 3.2 and Lemma 3.3 imply that there exists ε0>0 and δ∈(0,1) such that the approximate solutions Mε satisfy Mε<1−δ in QT for all 0<ε<ε0, where δ is independent of ε. Consequently, Dε(Mε) is positive and uniformly bounded from above by a constant, which is independent of ε,
|
dεa≤Dε(Mε(t,x))=d(Mε(t,x)+ε)a(1−Mε(t,x))b≤d(1−δ+ε)a(1−(1−δ))b≤dδb,(t,x)∈ QT,
|
for all 0<ε<ε1:=min{δ,ε0}. The last integral can therefore be estimated by
|
∫tτ∫Ω∫Mε0Dε(ζ)(∂sN∂2g(ζ,Nε,Cε,Aε)+∂sC∂3g(ζ,Nε,Cε,Aε)+∂sA∂4g(ζ,Nε,Cε,Aε))≤dδb∫tτ∫Ω((|∂sN|2+|∂sC|2+|∂sA|2)+∫Mε04∑i=2|∂ig(ζ,Nε,Cε,Aε)|2).
|
(31)
|
By the above estimates (26), Lemma 3.2, Lemma 3.3 and setting τ=0, we conclude that
|
∫QTDε(Mε)(∂tMε)2≤C′,supt∈[0,T]∫Ω|Dε(Mε)∇Mε|2≤C′,
|
for some constant C′≥0.
Lemma 3.5. Under the hypotheses of Lemma 3.2 the approximate solutions of (11) converge to a solution of the degenerate system (4) as ε>0 tends to zero.
Proof. By Lemma 3.3 the solutions Mε are uniformly bounded by 1−δ, and the following estimate for the diffusion coefficient was shown in the proof of Lemma 3.4,
|
dεa≤Dε(Mε(t,x))≤dδb,(t,x)∈ QT,
|
for all 0<ε<ε1. Moreover, if ε<ε1 we observe that
and consequently,
|
Φ(Mε(t,x))≤Φε(Mε(t,x))≤(1−δ)dδb,(t,x)∈ QT.
|
Lemma 3.3 and Lemma 3.4 further imply that
|
∫QT(∂t(Φ(Mε)))2=∫QT(DM(Mε)∂tMε)2≤∫QT(Dε(Mε)∂tMε)2≤‖Dε(Mε)‖L∞(QT)∫QTDε(Mε)(∂tMε)2≤cdδb,supt∈[0,T]∫Ω|∇Φ(Mε)|2=supt∈[0,T]∫Ω|DM(Mε)∇Mε|2≤supt∈[0,T]∫Ω|Dε(Mε)∇Mε|2≤c,
|
(32)
|
for some constant c≥0. This shows that the family Ψε:=Φ(Mε), 0<ε<ε1, is uniformly bounded in W={u∈L∞(0,T;H1(Ω))|∂tu∈L2(0,T;L2(Ω))}, which is compactly embedded into C([0,T];L2(Ω)) by Aubin-Lions' Lemma (e.g., see [7], Theorem Ⅱ.1.5). Consequently, there exists Ψ∈C([0,T];L2(Ω)) and a sequence εn tending to zero as n→∞ such that Ψεn→Ψ in C([0,T];L2(Ω)). This implies that Mεn=Φ−1(Ψεn)→M and Φ(Mεn)→Φ(M) in C([0,T];L2(Ω)).
Moreover, by Lemma 3.4 the approximate solutions Nε,Cε and Aε are uniformly bounded in W, which implies that there exist N,C,A∈C([0,T];L2(Ω)) and a sequence εn tending to zero as n→∞ such that
|
Nεn→N, Cεn→C, Aεn→AinC([0,T];L2(Ω)).
|
We can now pass to the limit ε→0 in the distributional formulation of the degenerate system (3) using the uniform boundedness of the approximate solutions and the continuous embedding C([0,T];L2(Ω))↪C([0,T];L1(Ω)), and conclude that the limits M,N,C,A are solutions of the degenerate problem.
3.3. Uniqueness and well-posedness for general initial data
Lemma 3.6. Let the hypotheses of Lemma 3.2 be satisfied. If (M,N,C,A) and (˜M,˜N,˜C,˜A) are two solutions corresponding to initial data (M0,N0,C0,A0) and (~M0,~N0,~C0,~A0), respectively, then
|
‖M(T)−˜M(T)‖L1(Ω)−‖M0−~M0‖L1(Ω)≤∫T0∫Ω|g0(t,x)|dxdt,‖N(T)−˜N(T)‖L1(Ω)−‖N0−~N0‖L1(Ω)≤∫T0∫Ω|h1(t,x)|dxdt,‖C(T)−˜C(T)‖L1(Ω)−‖C0−~C0‖L1(Ω)≤∫T0∫Ω|h2(t,x)|dxdt,‖A(T)−˜A(T)‖L1(Ω)−‖A0−~A0‖L1(Ω)≤∫T0∫Ω|h3(t,x)|dxdt,
|
(33)
|
where the functions g0 and hi are defined as
|
g0:=g(M,N,C,A)−g(˜M,˜N,˜C,˜A),hi:=fi(M,N,C,A)−fi(˜M,˜N,˜C,˜A),
|
(34)
|
for i=1,2,3.
Proof. The estimates immediately follow from Lemma 3.3 in [17].
Lemma 3.7. Let B be a bounded subset of R4+. Then for all (M,N,C,A) and (˜M,˜N,˜C,˜A)∈B we have
|
|g(M,N,C,A)−g(˜M,˜N,˜C,˜A)|+3∑i=1|fi(M,N,C,A)−fi(˜M,˜N,˜C,˜A)≤ c(|M−˜M|+|N−˜N|+|C−˜C|+|A−˜A|),
|
(35)
|
for some constant c≥0.
Proof. Let (M,N,C,A),(˜M,˜N,˜C,˜A)∈B. For the function f2 we obtain,
|
|f2(M,N,C,A)−f2(˜M,˜N,˜C,˜A)|=−σ|[(Ck1+C)(M+N)−(˜Ck1+˜C)(˜M+˜N)]|≤ r1(|M−˜M|+|N−˜N|),
|
(36)
|
for some constant r1≥0. To show that the functions f1,f3 and g satisfy (35) we observe, that
|
Am1X1−Am2X2=Am1(X1−X2)+X2(Am1−Am2)= Am1(X1−X2)+νX2(A1−A2)∫10(sA1+(1−s)A2)m−1ds,
|
(37)
|
which implies that |Am1X1−Am2X2|≤r|(X1−X2)+X2(A1−A2)| for some constants ν and r≥0 and (X1,A1),(X2,A2) in bounded subsets of R2+.
Applying this to f1, we obtain
|
|f1(M,N,C,A)−f1(˜M,˜N,˜C,˜A)|= |[(Ck1+C−k2)N+η1(Am1+Am)M] −[(˜Ck1+˜C−k2)˜N+η1(˜Am1+˜Am)˜M]|≤ |1−k2||N−˜N|+|η1|[|M−˜M|+|M(A−˜A)|]≤ r2(|N−˜N|+|M−˜M|+|A−˜A|)
|
(38)
|
for some constant r2≥0. Similarly, for f3 we obtain
|
|f3(M,N,C,A)−f3(˜M,˜N,˜C,˜A)|= |[−λA+[α+βAm1+Am](M+N)] −[−λ˜A+[α+β˜Am1+˜Am](˜M+˜N)]|≤ λ|A−˜A|+α[|M−˜M|+|N−˜N|] +β[|M−˜M|+|˜M||A−˜A|]+β[|N−˜N|+|˜N||A−˜A|]≤ r3(|A−˜A|+|M−˜M|+|N−˜N|)
|
(39)
|
for some constant r3≥0. Finally, for g we obtain
|
|g(M,N,C,A)−g(˜M,˜N,˜C,˜A)|= |[(Ck1+C−k2)M−η1(Am1+Am)M] −[(˜Ck1+˜C−k2)˜M−η1(˜Am1+˜Am)˜M]|≤ |1−k2||M−˜M|+η1[|M−˜M|+|˜M||A−˜A|]≤ r4|M−˜M|+r2|A−˜A|
|
(40)
|
for some constant r4≥0. Combining equations (36), (38), (39) and (40) gives
|
|g(M,N,C,A)−g(˜M,˜N,˜C,˜A)|+3∑i=1|fi(M,N,C,A)−fi(˜M,˜N,˜C,˜A)|≤ r′(|M−˜M|+|N−˜N|+|C−˜C|+|A−˜A|)
|
(41)
|
for some constant r′≥0.
Theorem 3.8. For every T>0 and initial data (M0,N0,C0,A0) in C(¯Ω) such that
|
M0≥0,‖M0‖L∞(Ω)<1−ρ,N0≥0,C0≥0,A0≥0,C0|∂Ω=1, M0|∂Ω=N0|∂Ω=A0|∂Ω=0,
|
for some ρ∈(0,1), there exists a unique solution (M,N,C,A) on [0,T] of model (4). The functions M,N,C and A are non-negative, belong to L∞(QT) and there exists δ∈(0,1) such that M satisfies ‖M‖L∞(QT)<1−δ.
Proof. We first assume the initial data are smooth and satisfy the hypotheses of Lemma 3.2.
If (M,N,C,A) and (˜M,˜N,˜C,˜A) are two solutions corresponding to initial data (M0,N0,C0,A0), and (˜M0,˜N0,˜C0,˜A0) respectively, then Lemma 3.6 and the estimate in Lemma 3.7 imply that
where
|
F(t):=‖M(t)−˜M(t)‖L1(Ω)+‖N(t)−˜N(t)‖L1(Ω)+‖C(t)−˜C(t)‖L1(Ω)+‖A(t)−˜A(t)‖L1(Ω).
|
(42)
|
By Gronwall's Lemma we conclude that
for some constant c≥0, which implies the uniqueness of solutions corresponding to smooth initial data. For general initial data, let Mn0,Nn0,Cn0,An0 be an approximating sequence satisfying the hypothesis of Lemma 3.2 such that
|
‖Mn0−M0‖L1(Ω)+‖Nn0−N0‖L1(Ω)+‖Cn0−C0‖L1(Ω)+‖An0−A0‖L1(Ω)→0
|
as n→∞. The Lipschitz continuity of solutions in L1(Ω) norm (43) implies that the corresponding solutions Mn,Nn,Cn,An satisfy
|
supt∈[0,T]{‖Mn(t)−Mk(t)‖L1(Ω)+‖Nn(t)−Nk(t)‖L1(Ω)+‖Cn(t)−Ck(t)‖L1(Ω)+‖An(t)−Ak(t)‖L1(Ω)}≤ CT(‖Mn0−Mk0‖L1(Ω)+‖Nn0−Nk0‖L1(Ω)+‖Cn0−Ck0‖L1(Ω)+‖An0−Ak0‖L1(Ω)).
|
(44)
|
for some constant CT≥0 and all n,k ∈ N. Consequently, Mn,Nn,Cn,An form a Cauchy sequence in C([0,T];L1(Ω)) and converge to the unique solution M,N,C,A of (4).
4. Numerical simulations
In the previous section we established the well-posedness of the quorum sensing induced biofilm detachment model, however, we are currently unable to describe the solutions of the model qualitatively based on rigorous analytical arguments. Hence, we illustrate the model behaviour in computer simulations.
For the numerical solution of the model we use a straightforward extension to the problem at hand of the numerical method for the prototype biofilm model that is described in detail in [14,36]. For space discretisation this uses a Finite Volume method on a uniform grid, which uses Finite Difference approximations for the diffusive fluxes across grid cell edges. We extended this method to account for the new dependent variables A and N which are treated in the same manner as C. A simple first order semi-implicit method is used for time-stepping. In every time step, this requires the solution of a sparse linear system for each dependent variable. By construction of the method, the system matrices are at least weakly diagonally dominant. These linear systems are solved with the stabilized biconjugate gradient method [35]. The linear solver is prepared for parallel execution on multi-core and shared memory multiprocessor architectures using OpenMP as described in [28]. Simulations are terminated when the biofilm (or the microbial floc) reaches a set target size, or when a set maximum simulation time is reached. The model parameters used in our simulations are summarised in Table 1.
In the numerical experiments, we investigate the model behaviour under different boundary conditions reflecting biofilms or microbial flocs with particular emphasis on the internal structure of the colonies. We define the following output parameters:
• Relative variation: This is the standard deviation of the sessile biomass density from its mean in the biofilm,
|
R(t):=[∫Ω2(M(t,x)−∫Ω2M(t,y)dy)2dx]12
|
(45)
|
• Relative biofilm (floc) size: This is the size of the biofilm relative to the domain size,
• Sessile biomass in the biofilm:
• Dispersed cells:
• Average signal molecule concentration in the biofilm:
|
Aave(t):=∫Ω2(t)A(t,x)dx∫Ω2(t)dx.
|
(49)
|
In these definitions, Ω is the fixed computational domain, and Ω2(t)⊂Ω is the biofilm subdomain where M>0, which evolves in time, as defined in Section 2.
4.1. Microbial floc
In the first simulation experiments, we consider a biofilm without substratum i.e. a microbial floc. We restrict ourselves to a two-dimensional setting with rectangular computational domain Ω=[0,1]×[0,1]. The boundary conditions used are the Dirichlet boundary conditions (5). One small circular floc is placed in the centre of the domain which at time t=0 contains only sessile cells of biomass density M0=0.1, while everywhere else in the domain M0≡0; this floc is circular and occupies 0.03% of the domain Ω.
Initially, no signal molecule A and no dispersed cells N are assumed to be in the system, thus A0≡0 and N0≡0. The nutrient concentration in the interior at time t=0 is everywhere at the same level as the concentration at the boundary, C0≡1.
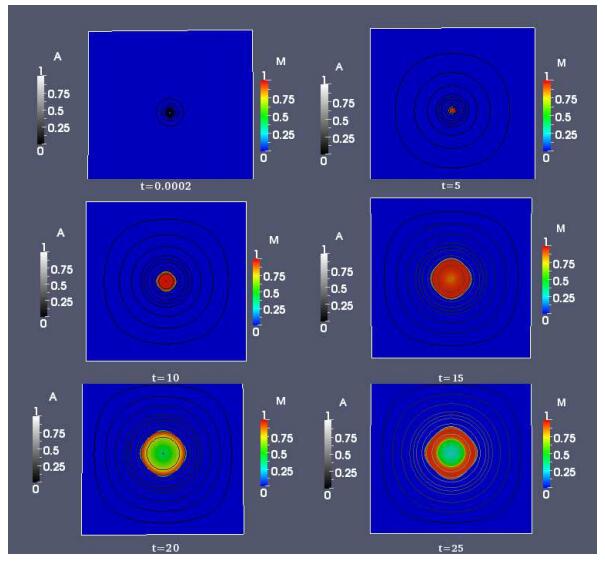
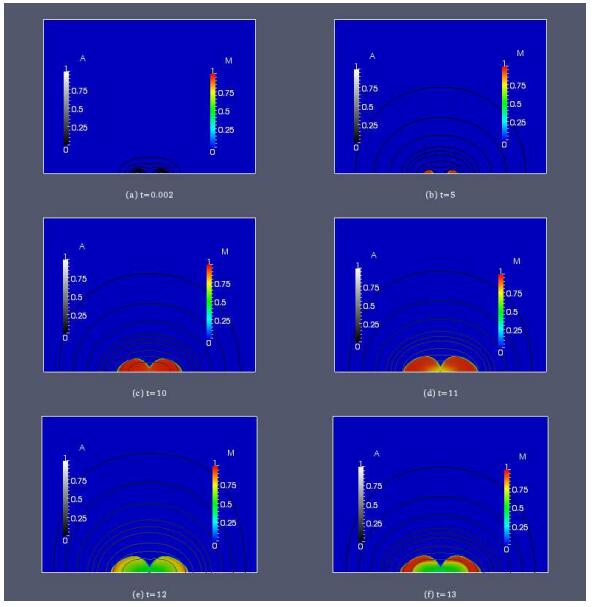
For the visualization presented in Figure 2, we used an autoinducer production rate α=30.7 and a maximum dispersal rate η1=0.6, every other parameter is as listed in Table 1. Immediately after the simulation starts, the floc is very small in size and the concentration of the signal molecule A is very low. At the snapshots t=5, t=10 and t=15, the original circular shape of the floc is still visible, the nutrient is not strongly growth limiting and the floc expands. As the floc grows within the rectangular domain, it looses its circular shape and expands faster toward the sides of the domain rather than towards the corners. This is a boundary condition effect that is prompted by the smaller diffusion length for substrates from the middle of the lateral sides than from the corners. Overall, however, the colony remains in a rather compact shape, in analogy with biofilms which have been found to grow in compact, homogenous layers when nutrients are nowhere severely limited. With the increase in biomass density in the system, the signal concentration also increases. The autoinducer concentration attains its highest values inside the floc and, due to diffusion and the parabolic maximum principle, decreases from there towards the floc/water interface and the boundary of the domain where the signal concentration is kept at A=0. At the next snapshot t=20, we observe a visible decrease in biomass density in the centre of the floc, thus creating a hollow in the floc due to conversion of sessile cells into dispersed cells and their subsequent diffusion out of the domain. The last snapshot taken at t=25 shows that the microbial floc has started growing again both internally and on the surface; and consequently the signal concentration has started rising.
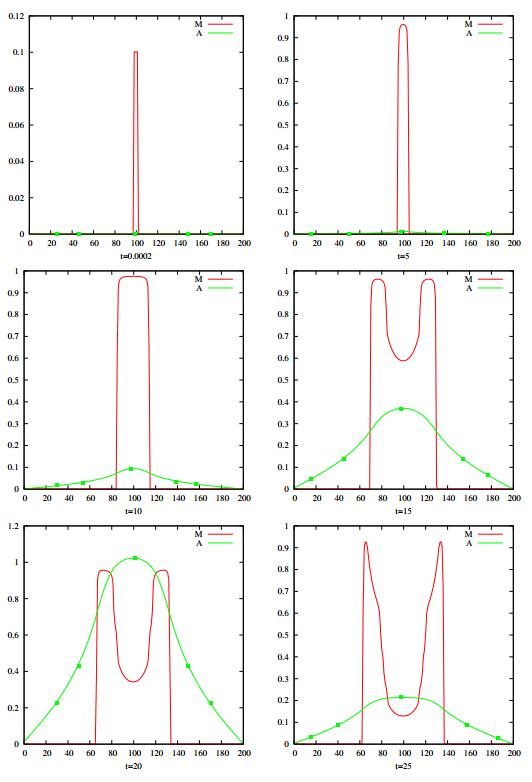
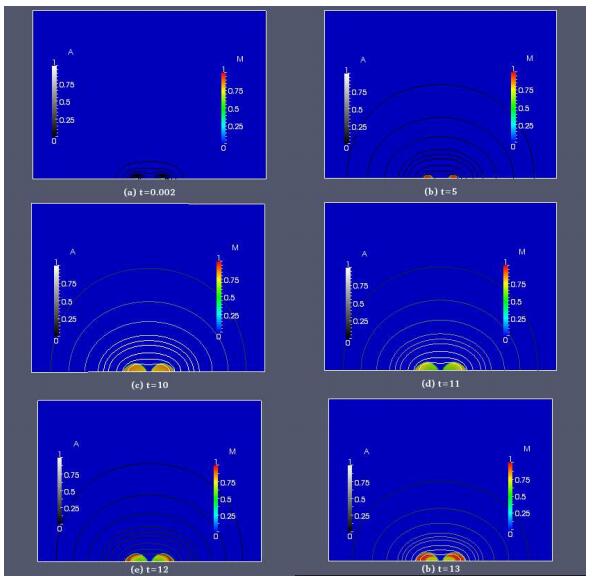
The 2-D structural representation of the biofilm shown in Figure 2 reveals that the bacterial cells leave from the inner core of the microfloc, but it does not illustrate the extent of the dispersal effect on the biofilm structure. Hence, we present a 1-D spatial representation of a typical biofilm dispersal event in Figure 3 whereby the biofilm is cut vertically to reveal the dispersal taking place in the inner core of the biofilm. The sessile biomass density and the concentration of the quorum sensing molecule are shown at selected times t=0.0002,5,10,15,20,25. From the top view of the microfloc, we observe that at times t=0.0002, t=5, and t=10 the microfloc is still in its initial growth phase, the sessile biomass density has increased leading to spatial spreading. The signal molecule concentration also rises until its level is high enough to induce cell dispersal, as seen at the next selected time t=15. The following two snapshots at times t=20 and t=25 show that the dispersal of cells from the microfloc creates voids in the floc and its depth increases over time (as seen from the top view).
Figures 2 and 3 illustrate that cell dispersal occurs from the inner core of the microfloc thereby creating hollowing structures, as reported in experimental studies, e.g. [9,22]. Furthermore, we will investigate the general extent of the hollow effect over a longer period of time through the lumped quantities Mtot,Ntot,Aave and R defined in equations (45)-(49).
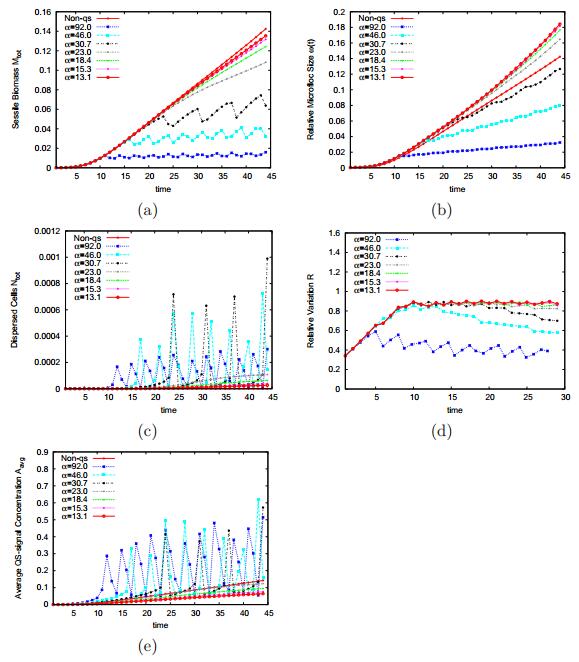
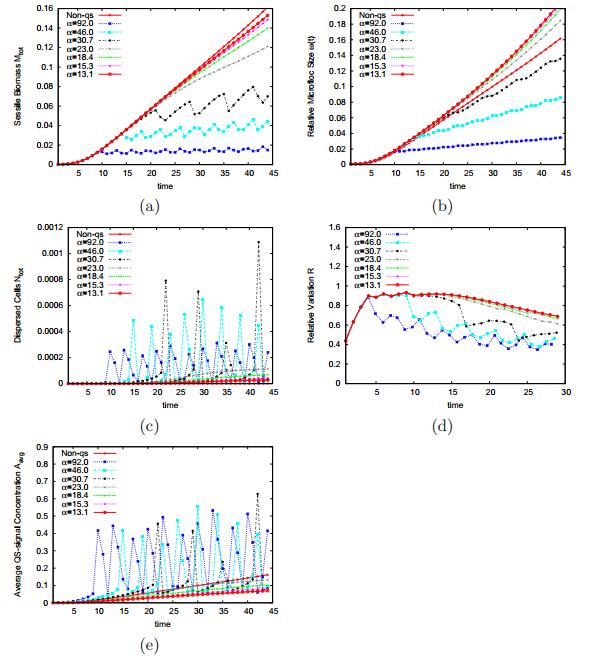
The temporal plots are shown in Figure 4 where the autoinducer production rate is varied as α=92.0,46.0,30.7,23.0,18.4,15.3,13.1. For α≥30.7, we observe a rapid removal of biomass and signal molecule (see Figure 4c, e) due to the Dirichlet conditions prescribed on the boundary. After the first dispersal event, the bacterial cells that are left behind in the floc are too few to maintain the signal concentration at a level high enough to sustain cell dispersal, so the biomass in the floc starts increasing. This also leads again to an increase in autoinducer concentration until the next dispersal event is triggered. This pattern continues, thus producing an almost periodic pattern of discrete dispersal events, cf. Figure 4. For α<30.7, the floc grows larger with higher levels of biomass density and autoinducer concentration before cell dispersal is induced. Here, the dispersal appears continuously and the biomass density in the floc reaches a plateau. The simulations in Figure 4 illustrate that cell dispersal is taking place, depending on the value of α in a continuous or periodic pattern. The relative size of the biofilm colony, however, does not reflect this as seen in Figure 4b. It indicates that most of the dispersed cells are from the inner core of the floc.
The relative variation of the biomass density defined in equation (45) is the standard deviation of the sessile biomass density from its mean in the microfloc. This is evaluated and plotted in Figure 4d. So far, we established that cell dispersal occurs in the inner core of the biofilm, it creates voids (hollows) whose depth increases over time when viewed from the top and the floc size does not shrink as a result of dispersal. The importance of the variable R is to investigate the spatiotemporal effect of cell dispersal, in order to analyze the extent of the voids over time. When the standard deviation is close to zero, the hollow in the floc is small (or narrow); on the other hand, if the standard deviation is large, the hollow is big (or wide). The plots in Figure 4d show that the size of the hollow decreases over time as the standard deviation from the mean decreases. This is more visible in smaller flocs (i.e. when α≥30.7). Hence, after the voids are created by cell dispersal, the floc grows both inside and outside. Loss of biomass occurs in the inner core even though the total floc size does not shrink. For bigger flocs (i.e. when α<30.7), the dispersal occurs rather continuously. The floc hardly grows, especially in the inner core, and hence the created hollow becomes constant, seen in Figure 4d as R approaches a plateau.
So far, we presented simulation experiments for a microfloc. We will compare this situation with a biofilm. Besides, we will investigate the effect of quorum sensing induced dispersal on merged colonies which has not been done in the previous study [18]. More specifically, we will analyze the behaviour of merging colonies in terms of biomass growth, cell dispersal and hollow structures.
4.2. Microbial biofilm
The simulated biofilm community consists of bacterial cells accumulating on a surface (substratum) surrounded by an aquatic region. The substratum is inoculated by two colonies of small pockets of sessile cells with biomass density M0=0.1 in each colony.
The substratum forms the bottom boundary of the domain Ω and is impermeable to biomass, substrate and signal molecule. This is described by homogeneous Neumann boundary conditions imposed on the dependent variables M,N,C,A. These can be understood as symmetry boundary conditions which enable us to view the small simulation section as a part of a much larger system. At the top boundary, we impose homogenous Dirichlet conditions for the dependent variables M, N and A by setting M=0, N=0 and A; this enforces a diffusion gradient from the biofilm in the interior of the domain to the boundary and mimics removal of quorum sensing molecule and dispersed cells into the surrounding bulk phase, where they are negligible due to instantaneous dilution. An inhomogeneous Dirichlet condition is imposed for C at the top boundary by setting C to the bulk concentration value (i.e. C=C∞=1); this reflects that the growth limiting substrate is added to the system through the top boundary. For the left and right boundaries, we impose homogeneous Neumann boundary conditions for all the dependent variables M,N,C,A which makes the left and right boundaries impermeable to biomass, substrate and signal molecules.
Initially, no dispersed cells and no autoinducers are in the system, and the concentration of nutrients is at bulk level, i.e. C0≡C∞=1,N0=A0≡0.
To investigate the effect of quorum sensing triggered dispersal on the spatial structure of the biofilm colony, we visualize the development, growth and cell dispersal of the biofilm in Figure 5. We used the autoinducer production rate α=30.7 and a maximum dispersal rate η1=0.6, which mimics the periodic dispersal events described in [18]. All other parameter values used are as listed in Table 1. We show the spatial distribution of the sessile biomass M and the iso-lines of the autoinducer concentration A within the first dispersal event (cycle); the selected time instances illustrate the biofilm growth and dispersal in response to autoinducer concentration.
After the simulation starts, the biomass M starts growing and colonies gradually expand as shown in the snapshots at t=0.002 and t=5, but due to the removal of signal molecules from three out of four boundary segments of the domain, accumulation of signal molecules is not strong enough to induce dispersal. Expansion starts locally when and where the biomass density M approaches its maximum value. As long as the nutrient substrate is not severely limited, the total biomass density M is close to 1 in the biofilm.
At the next shown time instance t=10, the biomass density M inside the colonies has increased. The colonies which were initially placed apart are now drawing close and then merge, albeit the biomass density inside the colonies still remains below the maximum biomass density. The autoinducer concentration has risen, though not strong enough to induce cell dispersal. Moreover, the merged colonies now act as one colony, whereby the iso-lines of the signal concentration are no longer separated. The autoinducer concentration in the middle of the merged colony has increased and few cells started dispersing as shown at the time instance t=11.
At the next snapshot t=12, we notice a huge biomass loss resulting in a significant decrease in the biomass density of the merged colony. An important observation is the void region of the colonies, seen at the centre of the merged colonies and not at the centre of the individual colonies as in the study [18]. At the snapshot t=13, the biomass density in the merged colony has started to increase again.
Furthermore, we investigate the behaviour of the biofilm if cell dispersal occurs before merging of the colonies. The simulation setup here is the same as in Figure 5 except that the autoinducer production rate is set to α=92.0 which relates to a small biofilm. Here, the biofilm grows less and merging of the colonies is delayed. Similar to the results in Figure 5, we notice that at the first two time instances t=0.002 and t=5, the colonies are still in the growth phase (see Figure 6). At the next two snapshots t=10 and t=11, we observe a significant biomass loss leading to hollow structures. After the dispersal event, the biofilm starts growing again albeit the colonies do not merge (see Figure 6f); the inability of the colonies to merge could be due to mass transfer. The signal concentration attains its highest values at the sides of the colony close to the neighbouring colonies, in accordance with the parabolic maximum principle, and hence more cells disperse from the sides which inhibits merging.
The extent of the hollow effect in the quorum sensing induced biofilm dispersal is investigated through the lumped quantities Mtot,Ntot,Aave,ω and R, shown in Figure 7, by varying the value of α as α=92.0,46.0,30.7,23.0,18.4,15.3,13.1. The time evolution profile presented in Figure 7 for the biofilm is similar to the one for the microbial floc in Figure 4. Small values of R indicate small hollows while large values of R indicate large deviation of the bacterial density from the mean, i.e. large hollows. The deviations in R show that the size of the hollows is not steady but rather decreases as new cells are produced during the biofilm intermittent growth phase. It is interesting that the size of the void in the biofilm changes as dispersal and growth takes place, which is not evident when dispersal happens continuously, whereby R attains a near constant value.
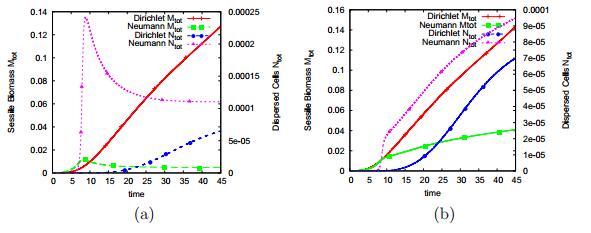
In the simulations discussed above, we prescribed homogeneous Dirichlet boundary conditions for the autoinducer A. We compare these results with the situation where homogeneous Neumann boundary conditions are imposed for the autoinducer. This assumption is made solely to isolate and emphasise the effect of accumulating QS molecules vs their removal from the system, and not thought of as a simulation of a realistic physical environment. The comparison is presented in Figure 8 where we used an autoinducer production rate α=18.4 and maximum dispersal rate η1=0.6; for the case of a microbial floc (see Figure 8a) with homogeneous Neumann boundary conditions imposed for M,N,C,A on all the boundaries, and for the microbial biofilm (see Figure 8b) with homogeneous Neumann conditions imposed for M,N,C,A on all boundaries except for the top boundary. The Neumann boundary condition models the case where the signal molecule cannot leave the domain and therefore accumulates faster. As a consequence, the onset of quorum sensing occurs much earlier than with Dirichlet boundary conditions. As a result of unhindered accumulation of signal molecules in the system, very high autoinducer concentrations are attained, hence quick up-regulation and cell dispersal occurs which reduces the density of sessile biomass in the floc. In the case of Dirichlet boundary conditions, the accumulation of the signal molecule is slower due to its early removal through the boundaries, hence causing a delay in up-regulation and cell dispersal.
5. Conclusion
In order to describe dispersal of cells from a biofilm colony into the aqueous environment, simple prototype biofilm growth models must be extended to include both the dispersing cells as well as the trigger that causes such detachment. In the case of quorum sensing induced dispersal these are autoinducer molecules that are produced in the biofilm colony. In total, this introduces two new dependent variables. The existence and uniqueness proofs for the underlying prototype model must be adapted and extended to account for this new complexity. Our particular model is based on a biofilm growth model that consists of a density-dependent diffusion-reaction equation for sessile biomass that is coupled with a semi-linear diffusion-reaction equation for nutrient, which are consumed in the biofilm. The extension of the model introduces additional semi-linear diffusion-reaction equations that describe quantities that are produced in the biofilm. Since the associated reaction terms have opposite signs than the nutrient terms, the approach to obtain estimates for the nutrient concentration does not carry over to the two new dependent variables and alternative arguments were developed. We formulated the analysis for the case of Dirichlet boundary conditions, but the results can be generalized to other situations with the same ideas that were used for the underlying prototype biofilm growth model. In numerical simulations we focus on the effect of quorum sensing controlled dispersal on the colony. The simulations suggest: (ⅰ) Depending on parameters, microflocs and biofilms do not shrink as a result of dispersal but hollow out, with lower biomass densities in the inner layers of the colonies. (ⅱ) After a rapid dispersal event the number of cells remaining in the colony drops which also leads to a drop in the amount of autoinducer molecules produced; if sufficient nutrients are available cells grow inside the colonies after the dispersal event, leading to increasing biomass there, i.e. a shrinkage of the inner hollow regions, until the next dispersal event. Thus, (ⅲ) quorum sensing induced hollowing of biofilm colonies is a dynamic feature, changing in size and depth over time.
Acknowledgments
We thank the referees for their careful reading of the manuscript and their helpful comments and remarks that greatly improved the writing of the paper. BOE acknowledges financial support received from the Ontario Ministry for Agriculture, Food and Rural Affairs through the HQP Scholarship program; HJE acknowledges financial support received from the Natural Science and Engineering Research Council of Canada through the Discovery Grant program.









 DownLoad:
DownLoad: