The extended gamma distribution with regression model and applications

1.   Introduction

In real-life problems, the analyzed data may consist of a mixed structure of more than one distribution. Especially, when data is heterogeneous structure model, using the mixture distribution will be an appropriate approach for data modeling. When the data has multimodality or unimodality, the mixture distributions are good choices to model the heterogeneous structure (Everitt and Hand ^[1]). However, mixture distributions have been used to model the heterogeneous data sets in many areas such as survival, biomedical, engineering, and social sciences (see, Chen et al. ^[2], Erisoglu et al. ^[3,4,5]).

Mixture distributions can be obtained by both mixtures of two identical distributions and a mixture of two non-identical distributions. Recently, many studies about the mixture of two identical distributions were made such as Ahmad and Rahman ^[6], Jiang and Murthy ^[7], Sultan et al. ^[8], Zakerzadeh and Dolati ^[9], Ateya ^[10], Abouammoh et al. ^[11], El-Bassiouny et al. ^[12] and Karakoca et al. ^[13]. On the other hand, the Lindley distribution, proposed by Lindley ^[14], is the first distribution that comes to mind about a mixture of two non-identical distributions. Its probability density function (pdf) can be written as

where $f_E \left({x; \theta } \right) = \theta e^{ - \theta x}$ (for $x > 0$ and $\theta > 0$) is the pdf of the exponential distribution with the scale parameter $\theta$, $f_G \left({x; \theta } \right) = \theta ^2 xe^{ - \theta x}$ (for $x > 0$ and $\theta > 0$) is the pdf of the gamma distribution with the shape parameter 2 and scale parameter $\theta$ and $p = \theta / \left(\theta+1\right)$ is the mixing proportion of distributions. Some mixture of two non-identical distributions has been also introduced in the literature, for example, the power Lindley distribution, denoted by $PL\left({\alpha, \theta } \right)$, introduced by Ghitany et al. ^[15] with pdf:

the gamma Lindley distribution, denoted by $GL\left({\alpha, \theta } \right)$, proposed by Nedjar and Zeghdoudi ^[16] with pdf:

and the xgamma distribution, denoted by $XG\left({\theta } \right)$, proposed by Sen et al. ^[17] with pdf:

Although gamma distribution is widely used in lifetime data modeling, it is not able to model different characteristics of the data sets such as the bathtub and upside-down failure rates. To remove the drawbacks of the gamma distribution, we propose a new extended gamma (NEG) distribution as a two-component mixture of xgamma and gamma distributions with suitable mixing proportions. The proposed distribution has several advantages over the well-known distributions. For instance, it has closed-form expressions for its mean, variance and skewness, and kurtosis measures and provides very flexible hazard rate shapes for lifetime data modeling. The statistical properties of the NEG distribution are derived. The regression model defined under the NEG density is proposed to model the right-skewed dependent variable.

Other parts of the study are as follows. In Section 2, the main properties of the NEG distribution are derived. In Section 3, the parameter estimation problem of the NEG distribution is discussed comprehensively. In Section 4, a simulation study is given to compare the estimation methods for the parameters of the NEG distribution. The new regression model is defined and studied in Section 5. The real data applications of the NEG distribution are presented in Section 6. The study is ended with the concluding remarks, given in Section 7.

2.   A new extended gamma distribution

The density of gamma distribution is

where $\Gamma\left(\cdot\right)$ is

and $\alpha > 0$ and $\theta > 0$ are the shape and scale parameters, respectively. In the recent years, several generalization of gamma distribution are introduced such as new generalized gamma distribution by Bourguignon et al. ^[18], reflected shifted-truncated gamma distribution by Waymyers et al. ^[19], Kumaraswamy generalized gamma distribution by Pascoa et al. ^[20] and among others. Now, we introduce the NEG distribution with following proposition.

Proposition 1. Let the random variable $X$ follows a NEG distribution if its pdf is given by

where $\alpha > 0$ and $\theta > 0$ are shape and scale parameters, respectively. Hereafter, the density (2.2) is denoted as $\mathit{\text{NEG}}\left(\alpha, \theta\right)$.

Proof. The NEG distribution is defined as follows

where $p = {{\left({\theta + 1} \right)} \mathord{\left/ {\vphantom {{\left({\theta + 1} \right)} {\left({\theta + 3} \right)}}} \right. } {\left({\theta + 3} \right)}}$, $f_{xgamma}\left({x; \theta } \right)$ and ${f_{gamma}}\left({x; \alpha, \theta } \right)$ are given in (1.2) and (2.1), respectively. Substituting (1.2) and (2.1) in (2.3), we have

The proof is completed.

The NEG distribution is a mixture distribution of $\text{xgamma}\left(\theta\right)$ and $\text{Gamma}\left(\alpha, \theta\right)$ distributions with mixing proportion $p = {{\left({\theta + 1} \right)} \mathord{\left/ {\vphantom {{\left({\theta + 1} \right)} {\left({\theta + 3} \right)}}} \right. } {\left({\theta + 3} \right)}}$. Therefore, statistical properties of NEG distribution can be derived using the properties of mixture distributions. The corresponding cumulative distribution function (cdf) to (2.2) is

where $\gamma\left(\alpha, \theta x \right)$ is

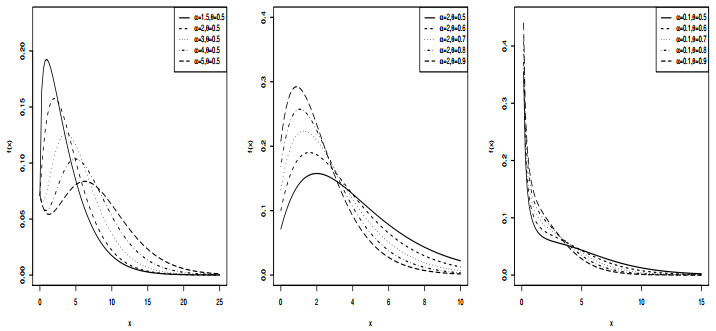
which is called as incomplete gamma function. The possible pdf shapes of NEG distribution are displayed in Figure 1. These figures reveal the flexibility of NEG distribution which can be used to model right-skewed and bi-modal data sets.

2.1.   Survival and mean residual life functions

The main reliability characteristics of NEG distribution are discussed via survival and mean residual life (MRL) functions The survival function (sf) represents the probability that a patient, device, or any object of interest survive after a specified time point. Therefore, sf has important application fields in reliability and survival analysis. The sf is defined as $S(t) = 1-F(t)$ which is given below for the NEG distribution

The mean residual life function of NEG distribution is

where $S\left(t\right)$ is given in (2.6) and

2.2.   Hazard rate function

The hazard rate function (hrf) is defined as $h(t) = f(t)/S(t)$ which is given below for the NEG distribution

The possible hrf shapes of NEG distribution are displayed in Figure 2. These plots reveal that NEG distribution is a very attractive distribution to model the different characteristics of the lifetime data sets with increasing, decreasing, bathtub, and upside-down shapes.

Further, Figure 3 indicates the possible shape regions of hrf of NEG distribution. They are bathtub, increasing, decreasing, uni-modal (upside-down) and N-shaped (increasing-decreasing-increasing) shapes.

2.3.   Lorenz curve

The Lorenz curve (LC), introduced by Lorenz ^[21], is widely used in economics to represent the distribution of income and inequality of wealth distribution. The LC of $X$ random variable is given by

which $f\left(\cdot \right)$ is the pdf of $X$ random variable. So, substituting pdf of NEG distribution, (2.2), in (2.10), the LC of NEG distribution is

It is obvious that (2.11) can be used in modeling the distribution of income by economists.

2.4.   Moments and related measures

Here, the mean, variance and related measures of the NEG distribution are derived.

Proposition 2. The $r\mathit{\text{th}}$ raw moments about the origin of $X$ are

Proof.

The proof is completed.

Using (2.12), the first (mean) and second raw moments of $X$ are given, respectively, by

The variance of $X$ is

Using the well-known relations, the skewness and kurtosis measures of NEG distribution are given, respectively, by

The skewness and kurtosis of the NEG distribution are displayed in Figure 4 for different values of the parameters $\alpha$ and $\theta$. From these figures, we conclude the following results: (ⅰ) when $\alpha$ increases, the skewness, and kurtosis both decrease; (ⅱ) when $\theta$ increases, the skewness, and kurtosis both increase.

Proposition 3. The moment generating function of $X$ is

Proof.

The proof is completed.

Substituting $t$ by $i t$ in (2.19), the characteristic function of NEG distribution is

2.5.   Generating random variables

Since the NEG distribution is a mixture distribution of $\text{xgamma}\left(\theta\right)$ and $\text{Gamma}\left(\alpha, \theta\right)$ distributions with mixing proportion $p = {{\left({\theta + 1} \right)} \mathord{\left/ {\vphantom {{\left({\theta + 1} \right)} {\left({\theta + 3} \right)}}} \right. } {\left({\theta + 3} \right)}}$, the below algorithm can be used for generating data from the NEG distribution.

1. Set the sample size $n$ and the parameter values $\alpha$ and $\theta$.

2. Generate $U_i \sim \text{uniform}\left(0, 1\right)$, $i = 1, 2, ..., n$.

3. Generate $V_i \sim \text{xgamma}\left(\theta \right)$, $i = 1, 2, ..., n$.

4. Generate $W_i \sim \text{Gamma}\left(\alpha, \theta \right)$, $i = 1, 2, ..., n$.

5. If $U_i \le {{\left({\theta + 1} \right)} \mathord{\left/ {\vphantom {{\left({\theta + 1} \right)} {\left({\theta + 3} \right)}}} \right. } {\left({\theta + 3} \right)}}$, $X_i = V_i$, otherwise, $X_i = W_i$.

3.   Estimation

In this section, three estimation methods are used to obtain unknown parameters of NEG distribution. These are maximum likelihood (ML), parametric bootstrap, and method of moments (MM) estimation methods. The rest of this section is devoted to inference on these estimation methods.

3.1.   Maximum likelihood

The log-likelihood function of $\text{NEG}\left(\alpha, \theta\right)$ is

Let $x_1, x_2, ..., x_n$ be a random sample following the distribution, $\text{NEG}\left(\alpha, \theta\right)$ and where $\bf\Phi = \left(\alpha, \theta \right)$ is the unknown parameter vector. Taking the partial derivatives of (3.1) with respect to $\alpha$ and $\theta$, the score vector components are obtained as

where $\psi\left(\alpha\right)$ is the digamma function which is defined as $\psi \left(\alpha \right) = {{\partial \ln \left({\Gamma \left(\alpha \right)} \right)} \mathord{\left/ {\vphantom {{\partial \ln \left({\Gamma \left(\alpha \right)} \right)} {\partial \alpha }}} \right. } {\partial \alpha }}$. The ML estimators of $\left(\alpha, \theta \right)$, say $\left(\hat \alpha, \hat \theta \right)$, can be obtained by simultaneous solutions of (3.2) and (3.3) against zero. However, it is not possible to obtain explicit forms of ML estimators of $\alpha$ and $\theta$ because of the non-linear functions in (3.2) and (3.3). Therefore, the direct maximization of (3.1) is needed to obtain the ML estimators of NEG distribution. Here, the optim function of R software is used to minimize minus of (3.1) which is equivalent to maximization of (3.1). The observed information matrix is given by

where ${I_{\alpha \alpha }} = {{{\partial ^2}\ell } \mathord{\left/ {\vphantom {{{\partial ^2}\ell } {\partial {\alpha ^2}}}} \right. } {\partial {\alpha ^2}}}$, ${I_{\alpha \theta }} = {I_{\theta \alpha }}{{ = {\partial ^2}\ell } \mathord{\left/ {\vphantom {{ = {\partial ^2}\ell } {\partial \alpha \partial \theta }}} \right. } {\partial \alpha \partial \theta }}$, ${I_{\theta \theta }} = {{{\partial ^2}\ell } \mathord{\left/ {\vphantom {{{\partial ^2}\ell } {\partial {\theta ^2}}}} \right. } {\partial {\theta ^2}}}$. The squared values of the diagonal elements of the inverse of above matrix give the standard errors of the estimated parameters. So, we have the following quantities for the confidence intervals of the parameters, $\alpha$ and $\theta$, respectively,

where ${Var({\widehat{\alpha}})}$ and ${Var({\widehat{\theta}})}$ are the square root of the diagonal elements of $I_F^{-1}\left(\bf\Phi\right)$ and $z_{p/2}$ is easily obtained by the quantile function of $\text{N}\left(0, 1\right)$.

3.2.   Parametric bootstrap

Parametric bootstrap method, introduced by Efron ^[22] can be used to obtain bias-corrected ML estimators of NEG distribution. The estimated bias of ${\bf{\hat\Phi}}$ is

where ${{ \pmb{\hat \Phi }}_j}$ is the MLE of ${\bf{\hat\Phi}}$ obtained from the $j$th bootstrap sample generated by assuming ${\bf{\hat\Phi}}$ is true and $B$ is the bootstrap replications (see, Mazucheli et al. ^[23,24]). So, the bootstrap bias-corrected (BBC) estimator of ${\bf{\hat\Phi}}$ is

3.3.   Method of moments

The MM is the simple and effective estimation method generally for large sample sizes. The idea of MM estimators is based on equating the theoretical moments to empirical ones. So, equating the first two theoretical moments of NEG distribution to their empirical counterparts, we have

where ${m_1} = {{\sum\limits_{i = 1}^n {{x_i}} } \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^n {{x_i}} } n}} \right. } n}$ and ${m_2} = {{\sum\limits_{i = 1}^n {x_i^2} } \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^n {x_i^2} } n}} \right. } n}$ are the first and second sample moments. The MM estimators of $\alpha$ and $\theta$, say $\hat \alpha_{MM}$ and $\hat \theta_{MM}$ are simultaneous solutions of (3.6) and (3.7).

3.4.   Least squares

Let $x_{1:n}$, $x_{2:n}$, $x_{3:n}, \cdots, \; x_{n:n}$ be an ordered sample of size $n$ from a probability distribution with cdf $F\left(\cdot\right)$. The mean and variance of $F\left(X_{j:n}\right)$ are, respectively,

The least squares estimators (LSEs) of $\alpha$ and $\theta$ are procured by means of the minimization of the following equation.

where $F\left({{Y_{j:n}}} \right)$ is in (2.5) and replacing it in (3.10), we have

The detailed information on the LSE can be found in Ding ^[25] and Ding et al. ^[26].

3.5.   Weighted least squares

The weighted LSEs (WLSEs) of $\alpha$ and $\theta$ are, respectively,

where

Replacing eqref{wj} and (2.5) with $w_j$ and $F\left(X_{j:n}\right)$, we have

The minimization of (3.14) give the WLSEs of the parameters, $\alpha$ and $\theta$.

4.   Simulation studies

The simulation studies are widely used to compare the finite sample performance of estimation methods (see, Zaka et al. ^[27] and Zaidi et al. ^[28]). Now, we give a simulation study to see the efficiencies of the presented estimation methods, in Section 3. The bootstrap replication $B$ is chosen $1,000$. The below steps are implemented.

1. Set the parameters $\alpha$, $\theta$ and the number of simulation replications, $N$,

2. Generate random variables from $\text{NEG}\left(\alpha, \theta\right)$,

3. Using the generated samples in step 2, estimated the parameters of $\text{NEG}\left(\alpha, \theta\right)$ by means of ML, BBC, LS and WLS estimation method

4. Estimate the biases, mean square errors (MSEs) and mean relative errors (MREs) for each parameters and estimation methods.

5. Repeat steps 2–4 $N$ times.

4.1.   Scenario I

In the first simulation scenario, the following settings are used: $N = 10,000$, $\alpha = 2$ and $\theta = 0.5$. The required formulations of biases, MSEs, and MREs can be found in Altun et al. ^[29]. We know that when $n \to \inf$, the estimated biases, and MSEs are near the zero and MREs are near the one. The statistical software, R, is used. The simulation results are graphically summarized in Figure 5. As seen from these plots, when the sample size increases, the estimated biases, and MSEs are near zero for all estimation methods. As expected, the estimated MSEs are also near the one for all estimation methods. However, we suggest the use of BBC estimation method for small samples since it approaches nominal values of the bias, MSE, and MRE faster than the other four estimation methods. One can obtain similar results for different simulation design.

4.2.   Scenario II

In the second scenario, the parameter values of the NEG distribution is changed. The used parameter values are $\alpha = 0.5$ and $\theta = 3$. The simulation results are summarized in Figure 6. The results are very similar to the results of the first scenario. All estimation methods work well based on the estimated values of the biases, MSEs, and MREs. However, the BBC method is better for small sample sizes.

5.   NEG regression model

The gamma regression model, proposed by Cepeda-Cuervo ^[30] and Cepeda and Gamerman ^[31], is widely used to model the right-skewed response variable (see, Bateson ^[32]). Recently, Altun ^[33,34] studied several models such as Lomax and weighted-exponential regression models to provide more accurate modeling of the skewed response variables. Let $Y \sim \text{Gamma}\left(\alpha, \theta\right)$. Using the transformation $\theta = \alpha / \mu$ in (2.1), we have

where $\mu > 0$, $\alpha > 0$ and $E\left(Y\right) = \mu$. Now, using the appropriate link function, we can link the covariates to mean of the random variable $Y$. In classical gamma regression model (with constant shape parameter), the mean structure is given by

where $\pmb \beta = {\left({{\beta _0}, {\beta _1}, ..., {\beta _k}} \right)^T}$ is the vector of unknown regression parameters $\left(k < n\right)$ and $\pmb x_i = {\left({{x _{i1}}, {x _{i2}}, ..., {x _{ik}}} \right)^T}$ is the vector of covariates. The link function, $g\left(\cdot \right):\left({0, \infty } \right) \mapsto \Re$ is the increasing and twice differentiable function (see, McCullagh and Nelder ^[35]).

Now, as in gamma regression model, we propose an alternative regression model to the gamma regression model by means of following proposition.

Proposition 4. Let $\theta = \left\{ {\sqrt {8\alpha \mu + 9{\mu ^2} + 6\mu + 1} - 3\mu + 1} \right\}{\left({2\mu } \right)^{ - 1}}$ be in (2.2). Under this re-parametrization, the pdf of NEG is

where $\mu > 0$, $\alpha > 0$ and $E\left(Y\right) = \mu$.

The reason of this re-parametrization is to make the mean equation of NEG simple for linking the covariates to mean of NEG random variable. The log-link function is used to link the covariates to mean of the random variable $Y$, as follows

5.1.   Estimation of the parameters of NEG regression model

We use the ML estimation method to obtain the unknown parameter of NEG regression model. The log-likelihood function of NEG regression model is

where $\pmb \tau = \left(\pmb \beta, \alpha \right)$, $\mu _i = \exp\left(\pmb x_i^T \pmb \beta\right)$. The ML estimators of $\pmb{\tau}$, say $\pmb{\hat \tau}$ is obtained by direct maximization of 5.5. To do this, optim function of R software is used. The well-known property of the MLE method is that the asymptotic distribution of $\widehat{\pmb{\tau}}-\pmb{\tau}$ is $N_{k+2}(0, K(\pmb{\tau})^{-1})$. Here, $K(\pmb{\tau})$ represents the expected information matrix which is approximated by observed information matrix. We calculate the observed information matrix evaluated at $\widehat{\pmb{\tau}}$ with the dimension $(k+2)\times (k+2)$ to obtain the standard errors of the estimated parameters. It can be obtained by hessian function of R software.

5.2.   Residuals analysis

The randomized quantile residuals (rqrs), introduced by Dunn and Smyth ^[36] is used to check the model accuracy on the fitted data set. The rqrs are defined by

where ${\hat u_i} = F\left(\left. {{y_i}} \right|{{ \pmb{\hat \beta} }}, \alpha \right)$. The rqrs are distributed $N\left(0, 1\right)$ if the fitted model is statistically valid.

6.   Empirical studies

In this section, NEG distribution is compared with competitive models to demonstrate its performance in real data modeling. Two real data sets are analyzed. The first application deals with the univariate data modeling. The second one is done for regression modeling.

6.1.   Myelogeneous leukaemia data

We compare the NEG distribution with several competitive models such as Lindley, xgamma, gamma, power Lindley and generalized Lindley distribution. The data represents the survival times of the patients having the acute Myelogeneous Leukaemia (see, Feigl and Zelen ^[37]). The data set was recently studied by Mead ^[38]. The selection of the best model for the data can be done with model selection criteria. In this study, we use three goodness-of-fit tests. These are Kolmogorov-Smirnov ($KS$), {Cramer-von-Mises}, ($W^{\ast }$) and Anderson-Darling ($A^{\ast }$). Additionally, two information criteria, Akaike Information Criteria (AIC) and Bayesian information criterion (BIC), is used to select the best model for the models passing the first step. The first step is the goodness-of-fit test. If the p-value of K-S test is larger than the critical value, $0.05$, it means that the distribution provides sufficient fit. In the second step, we use AIC, BIC, A* and W* statistics to select the model. In this case, the distribution with the lowest values of the AIC and BIC statistics is the best model for the data. Before starting the data analysis, it is very useful to have information about the empirical behavior of the hrf. The total time test (TTT) plot is used for this goal (see, Aarset ^[39]). According to the shape of the TTT plot, we decide the empirical shape of the hrf. If the TTT plot has a concave shape, the hrf is increasing, otherwise, the hrf is decreasing. If the TTT plot has a convex-concave shape, the hrf is a bathtub. The TTT plot of the used data is displayed in Figure 7 which indicates that the empirical hrf is the bathtub.

Table 1 contains the results for the fitted distributions. As mentioned above, we decide the best-fitted model in two steps. Based on the p-values of the KS test, NEG, power Lindley, generalized Lindley, and gamma distribution provide adequate fits. So, these distributions are passed the first step. Now, the distribution with the lowest values of the AIC, BIC, A* and W* statistics indicates the best model. According to Table 1, the NEG distribution has the lowest values of these statistics. Therefore, the proposed distribution is the best choice for the data used.

The fitted densities, empirical cdfs, and hrf plots of all model are sketched in Figure 8. Hence, we observe that the NEG fitting and successfully captures the empirical shape of the data set. Further, all estimated hrfs have not fitted as bathtub shaped except the NEG model. Hence, only the NEG model deals with Figure 7 for the data set.

6.2.   Homicide data

Now, we demonstrate the importance of the NEG regression model over the gamma regression model. The data source is the Better Life Index (BLI). The BLI is calculated for OECD countries as well as Brazil Russia and South Africa. These data set can be download from https://stats.oecd.org/index.aspx?DataSetCode=BLI2016. It consists of 11 indicators. These indicators have 24 variables. Here, we relate the homicide rate $\left(y_i \right)$ with long-term unemployment rate $\left(x_{i1} \right)$ and labour market insecurity $\left(x_{i2} \right)$. The NEG and gamma regression models are used to model below regression structure.

Table 2 lists the estimated parameters of gamma and NEG regression models and corresponding standard errors and p-values. As seen from these results, all estimated parameters are found statistically significant for both regression models. According to the estimated regression coefficients, we conclude that when the long-term unemployment rate increases, the homicide rate decreases surprisingly. On the other hand, when the labour market insecurity increases, the homicide rate also increases, as expected.

After fitting the regression models, we check the model accuracy with residual analysis. The rqs are obtained and plotted in Figure 9. Both regression model does not contain any possible outlier observation.

7.   Conclusions and future work

In this study, the two-parameter distribution is defined and studied comprehensively. The different estimation methods are investigated to estimate the unknown parameters of NEG distribution. Statistical properties of NEG distribution are derived. More importantly, a new regression model for the right-skewed response variable is introduced and is compared with the gamma regression model via an application to the actuarial data set. Empirical results show that NEG distribution could be a competitive model and can provide better modeling ability than its counterparts. The advanced residual analysis and influential diagnostics of the NEG regression model is a planned future work of this study. We believe that NEG distribution gains much attention from practitioners and increases its popularity soon.

Appendix

The derivations of the cdf and Lorenz curve are given below.

Conflict of interest

The authors declare there is no conflict of interest.