Application of Genetic Algorithm for Binary Optimization of Microstrip Antennas: A Review

Jeevani W. Jayasinghe; Jeevani W. Jayasinghe

doi:10.3934/electreng.2021016

AIMS Electronics and Electrical Engineering

2021, Volume 5, Issue 4: 315-333. doi: 10.3934/electreng.2021016

Previous Article Next Article

Review

Application of Genetic Algorithm for Binary Optimization of Microstrip Antennas: A Review

Jeevani W. Jayasinghe ^,

Department of Electronics, Wayamba University of Sri Lanka, Kuliyapitiya, Sri Lanka

Received: 23 September 2021 Accepted: 24 November 2021 Published: 02 December 2021

Researchers have proposed applying optimization techniques to improve performance of microstrip antennas (MSAs) in terms of bandwidth, radiation characteristics, polarization, directivity and size. The drawbacks of the conventional MSAs can be overcome by optimizing the antenna parameters while keeping a compact configuration. Applying a global optimizer is a better technique than using a local optimizer or a trial and error method for performance enhancement. This paper discusses genetic algorithm (GA) optimization of microstrip antennas presented by the antenna research community. The GA optimization procedure, antenna parameters optimized by using GA and the optimization objectives are presented by reviewing the literature. Further, evolution of GA in the field of MSAs and its significance are explored. Application of GA optimization to design broadband, multiband, high-directivity and miniature antennas is demonstrated with the support of several case studies giving an insight for further developments in the field.

Keywords:

Citation: Jeevani W. Jayasinghe. Application of Genetic Algorithm for Binary Optimization of Microstrip Antennas: A Review[J]. AIMS Electronics and Electrical Engineering, 2021, 5(4): 315-333. doi: 10.3934/electreng.2021016

Related Papers:

[1]	Aslı Alkan, Halil Anaç . The novel numerical solutions for time-fractional Fornberg-Whitham equation by using fractional natural transform decomposition method. AIMS Mathematics, 2024, 9(9): 25333-25359. doi: 10.3934/math.20241237
[2]	Musawa Yahya Almusawa, Hassan Almusawa . Numerical analysis of the fractional nonlinear waves of fifth-order KdV and Kawahara equations under Caputo operator. AIMS Mathematics, 2024, 9(11): 31898-31925. doi: 10.3934/math.20241533
[3]	Muath Awadalla, Abdul Hamid Ganie, Dowlath Fathima, Adnan Khan, Jihan Alahmadi . A mathematical fractional model of waves on Shallow water surfaces: The Korteweg-de Vries equation. AIMS Mathematics, 2024, 9(5): 10561-10579. doi: 10.3934/math.2024516
[4]	Khalid Khan, Amir Ali, Muhammad Irfan, Zareen A. Khan . Solitary wave solutions in time-fractional Korteweg-de Vries equations with power law kernel. AIMS Mathematics, 2023, 8(1): 792-814. doi: 10.3934/math.2023039
[5]	Hayman Thabet, Subhash Kendre, James Peters . Travelling wave solutions for fractional Korteweg-de Vries equations via an approximate-analytical method. AIMS Mathematics, 2019, 4(4): 1203-1222. doi: 10.3934/math.2019.4.1203
[6]	Ihsan Ullah, Aman Ullah, Shabir Ahmad, Hijaz Ahmad, Taher A. Nofal . A survey of KdV-CDG equations via nonsingular fractional operators. AIMS Mathematics, 2023, 8(8): 18964-18981. doi: 10.3934/math.2023966
[7]	Musong Gu, Chen Peng, Zhao Li . Traveling wave solution of (3+1)-dimensional negative-order KdV-Calogero-Bogoyavlenskii-Schiff equation. AIMS Mathematics, 2024, 9(3): 6699-6708. doi: 10.3934/math.2024326
[8]	M. Mossa Al-Sawalha, Rasool Shah, Adnan Khan, Osama Y. Ababneh, Thongchai Botmart . Fractional view analysis of Kersten-Krasil'shchik coupled KdV-mKdV systems with non-singular kernel derivatives. AIMS Mathematics, 2022, 7(10): 18334-18359. doi: 10.3934/math.20221010
[9]	Asif Khan, Tayyaba Akram, Arshad Khan, Shabir Ahmad, Kamsing Nonlaopon . Investigation of time fractional nonlinear KdV-Burgers equation under fractional operators with nonsingular kernels. AIMS Mathematics, 2023, 8(1): 1251-1268. doi: 10.3934/math.2023063
[10]	Yanhua Gu . High-order numerical method for the fractional Korteweg-de Vries equation using the discontinuous Galerkin method. AIMS Mathematics, 2025, 10(1): 1367-1383. doi: 10.3934/math.2025063

Abstract

1. Introduction

The general expansion of integer-order calculus to arbitrary order is fractional calculus (FC), which was developed at the end of the seventeenth century. One of FC's main advantages is that it can be used to describe memory and the inherited characteristics of many different phenomena. Additionally, classical calculus is a small subset of FC. The joint efforts of pioneers like Podlubny ^[1], Ross and Miller ^[2], Caputo ^[3], Riemann ^[4], Liouville ^[5], and many more created the foundation of fractional order derivative. The calculus of fractional order has been used in optics ^[6], electrodynamics ^[7], signal processing ^[8], chaos theory ^[9], and other fields ^[10,11]. It has also been connected to practical initiatives. The nature and behavior of nonlinear issues that emerge in daily life are largely described by the numerical and analytical solutions for differential equations of arbitrary order that arise in the events above ^[12,13].

The solutions of different kinds of nonlinear partial differential equations (NLPDEs) known as solitons exist as a specific form of solitary waves. These superb stable one-wave forms find extensive application in different areas because of their distinct properties. Dispersive waves dominate this system because they both disperse the waves inelastically and result in energy loss from radiation events. Thus, the solitary waves survive by keeping their shape and speed after completing a nonlinear connection. The soliton theory develops essential knowledge about the physical behavior and the meaning of nonlinear events. The theory of solitons attracts scientific exploration because it enables wide-ranging applications within transmission media along with design work, numerical materials study, mathematical physics, and various fields of nonlinear science. Research investigators today show greater interest in obtaining detailed calculations by using expert computation software to reduce complex mathematical operand complexity. Several advanced computational approaches described in the literature explore the characteristics of various types of solutions produced by nonlinear physical models as reported in ^[14,15,16].

Nonlinear systems research has identified fundamental complex dynamics that multiple scientific fields use. Studies in this domain focus on creating a unified model from the Korteweg-de Vries (KdV) equations and Schrödinger. The equartions contain vital elements of wave propagation and soliton processes that make them effective for studying different physical phenomena. When the nonlinear dispersive KdV combines with its quantum mechanical Schrödinger counterpart, it produces a coupled system that contains multi-dimensional linear and nonlinear dynamics processes ^[22,23,24]. The combined system delivers an expanded foundation for studying wave motion along with tools to analyze several remarkable effects created through the combined action of the equations. Scientists study the complete mathematical properties of coupled Schrödinger-KdV equations as a nonlinear system through research conducted from ^[25,26,27].

Analyses of numerous physical systems demand the study of nonlinear systems as a necessary method to understand their behavior. Such nonlinear systems give rise to the linked Schrödinger-KdV equations, which become an outstanding research problem because of their appealing nature. The system incorporates two essential parts containing the KdV equation used to explain nonlinear wave propagation alongside soliton characteristics and the Schrödinger equation dedicated to describing quantum mechanical properties. This combined equation system produces a new system that represents linear quantum phenomena with nonlinear dispersive dynamics, thus making it possible to explore different physical interactions ^[28].

The variational iteration technique was invented by He's ^{[29,30,31,32,33,34]} and has been successfully used in nonlinear poly crystalline solids, self-governing ordinary differential equations ^[34], and other fields. In one degree of freedom, an approximate solution to weakly nonlinear systems is constructed using an averaging technique, variational iteration method, method of variation of constants, and perturbation approach.

Liao Shijun introduced the homotopy analysis technique (HAM) in 1992 ^[35], utilizing homotopy, an essential term in differential geometry and topology. HAM has been successfully used to obtain approximate analytical solutions, free of linearization and perturbation, for issues that emerge in science and technology. Large amounts of computer memory and more time are required for the conventional approach (i.e., HAM). Therefore, combining this method with already-existing transform techniques is necessary to overcome these restrictions. Singh et al. ^[36] introduced the q-homotopy analysis transform method (q-HATM), a sophisticated combination of the Laplace transform and q-HAM. The series solution, which swiftly converges to the precise answer within a brief allowable zone, is managed and controlled by the future scheme. The ability of the suggested method to combine two powerful algorithms to solve linear and nonlinear fractional differential equations analytically and numerically is an improvement. The future approach is free from assumptions, discretization, and perturbation, and it has many robust qualities, such as nonlocal effect, simple solution process, and promising broad convergence region. The Laplace transform using semi-analytical methods takes less computation. It is time to calculate the solutions for complicated nonlinear models and phenomena that occur in research and industry, which is worth disclosing. The two auxiliary parameters, $\hbar$ and $n$ , that the q-HATM solution uses enable us to modify and regulate the solution's convergence. The suggested method can provide outcomes with greater efficiency while requiring less calculation time and effort than conventional methods. Many writers have recently used q-HATM to analyze various phenomena located in various locations. For example, the model of vibration equation of arbitrary order is studied by Srivastava et al. ^[37], the model of Lienard's equation is studied by Kumar et al. ^[40], many authors find the approximated analytical solution for nonlinear problems ^[41,42], Bulut and his coauthors analyze the arbitrary order model of the HIV infection ^[38], and Prakash and his coauthor find the approximated analytical solution for fractional multi-dimensional telegraph equation ^[39]. Many others find the approximated analytical solution for nonlinear problems ^[41,42].

The implementation of the q-HATM and the variational iteration transform method (VITM) to the fractional-order system of Schrödinger-KdV equations is examined in this paper. This study is innovative because it uses an extraordinary transformation known as the Mohand transformation (MT). The solutions to the provided issues demonstrate the efficacy of the proposed tactics. Tables and statistics are used to examine and illustrate the solutions of the recommended approaches.

2. Concepts of Mohand transform

Definition 2.1. Assume that $\mathbb{U}(\xi)$ is the function for which ^[43] defines the MT as:

$M[\mathbb{U}(\xi)] = R(s) = s^2\int_{0}^{\xi}\mathbb{U}(\xi)e^{-s\xi}d{\xi},\ \ {k}_{1}\leq s \leq{k}_{2}.$

A description of the Mohand inverse transform (MIT) appears in the following explanation:

$M^{-1}[R(s)] = \mathbb{U}(\xi).$

Definition 2.2 （^[44]). The fractional MT derivative is given as:

$M[\mathbb{U}^{\sigma}(\xi)] = s^{\sigma}R(s)-\sum\limits_{k = 0}^{n-1}\frac{\mathbb{U}^{k}(0)}{s^{k-(\sigma+1)}},\ 0 < \sigma\leq n.$

Definition 2.3. The following are a few of the features of the MT:

$(1)$ $M[\mathbb{U}'(\xi)] = sR(s)-s^{2}R(0)$ ,

$(2)$ $M[\mathbb{U}''(\xi)] = s^{2}R(s)-s^{3}R(0)-s^{2}R'(0)$ ,

$(3)$ $M[\mathbb{U}^{n}(\xi)] = s^{n}R(s)-s^{n+1}R(0)-s^{n}R'(0)-\cdots-s^{n}R^{n-1}(0)$ .

Lemma 2.1. Assume that $\mathbb{U}({{\eta}}, {\xi})$ is an exponentially ordered function. With $M[R(s)] = \mathbb{U}({{\eta}}, {{\xi}})$ , the MT is then characterized as:

$\begin{equation} M[D_{{{\xi}}}^{r{\sigma}}\mathbb{U}({{\eta}}, {{\xi}})] = {s}^{r{\sigma}}R(s)-\sum\limits_{j = 0}^{r-1}{s}^{{\sigma}(r-j)-1}D_{{{\xi}}}^{j{\sigma}}\mathbb{U}({{\eta}},0), 0 < {\sigma}\leq 1, \end{equation}$

(2.1)

where ${{\eta}} = ({{\eta}}_{1}, {{\eta}}_{2}, \cdots, {{\eta}}_{\sigma})\in \mathbb{R}^{\sigma}$ , $\sigma\in \mathbb{N}$ , and $D_{{{\xi}}}^{r{\sigma}} = D_{{{\xi}}}^{{\sigma}}.D_{{{\xi}}}^{{\sigma}}.\cdots.D_{{{\xi}}}^{{\sigma}}(r-times)$ .

Proof. The induction method demonstrates the truthfulness of Eq (2.1), while $r = 1$ allows solving the equation to obtain the following result:

$M[D_{{{\xi}}}^{2{\sigma}}\mathbb{U}({{\eta}}, {{\xi}})] = {s}^{2{\sigma}}R(s)-{s}^{2{\sigma}-1}\mathbb{U}({{\eta}},0)-{s}^{{\sigma}-1}D_{{{\xi}}}^{{\sigma}}\mathbb{U}({{\eta}},0).$

By Definition 2.2, Eq (2.1) is proven to be true for $r = 1$ . $r = 2$ is substituted in Eq (2.1) to obtain:

$\begin{equation} M[D_{r}^{2{\sigma}}\mathbb{U}({{\eta}}, {{\xi}})] = {s}^{2{\sigma}}R(s)-{s}^{2{\sigma}-1}\mathbb{U}({{\eta}},0)-{s}^{{\sigma}-1}D_{{{\xi}}}^{{\sigma}}\mathbb{U}({{\eta}},0). \end{equation}$

(2.2)

Take Eq (2.2) on the left-hand side:

$\begin{equation} L.H.S = M[D_{{{\xi}}}^{2{\sigma}}\mathbb{U}({{\eta}}, {{\xi}})]. \end{equation}$

(2.3)

Another approach to define Eq (2.3) is as follows:

$\begin{equation} L.H.S = M[D_{{{\xi}}}^{{\sigma}}D_{{{\xi}}}^{{\sigma}}\mathbb{U}({{\eta}}, {{\xi}})]. \end{equation}$

(2.4)

Assume

$\begin{equation} z({{\eta}}, {{\xi}}) = D_{{{\xi}}}^{{\sigma}}\mathbb{U}({{\eta}}, {{\xi}}). \end{equation}$

(2.5)

In Eq (2.4), put Eq (2.5) and then solve to get the following result:

$\begin{equation} L.H.S = M[D_{{{\xi}}}^{{\sigma}}z({{\eta}}, {{\xi}})]. \end{equation}$

(2.6)

In Eq (2.6), the Caputo derivative results in the following modifications:

$\begin{equation} L.H.S = M[J^{1-{\sigma}}z^{'}({{\eta}}, {{\xi}})]. \end{equation}$

(2.7)

The following is the solution of Riemann-Liouville (RL) integral modification to Eq (2.7):

$\begin{equation} L.H.S = \frac{M[z^{'}({{\eta}}, {{\xi}})]}{{s}^{1-{\sigma}}}. \end{equation}$

(2.8)

These results are achieved by using the MT derivative feature on Eq (2.8)

$\begin{equation} L.H.S = {s}^{{\sigma}}Z({{\eta}},{s})-\frac{z({{\eta}},0)}{{s}^{1-{\sigma}}}. \end{equation}$

(2.9)

The solution was achieved by applying Eq (2.5)

$Z({{\eta}},{s}) = {s}^{{\sigma}}R(s)-\frac{\mathbb{U}({{\eta}},0)}{{s}^{1-{\sigma}}}.$

As $M[z({{\xi}}, {{\eta}})] = Z({{\eta}}, {s})$ , consequently, Eq (2.9) may also be written as follows:

$\begin{equation} L.H.S = {s}^{2{\sigma}}R(s)-\frac{\mathbb{U}({{\eta}},0)}{{s}^{1-2{\sigma}}}-\frac{D_{{{\xi}}}^{{\sigma}}\mathbb{U}({{\eta}},0)}{{s}^{1-{\sigma}}}. \end{equation}$

(2.10)

Suppose that for $r = K$ , Eq (2.1) holds. Apply $r = K$ to Eq (2.1), then

$\begin{equation} M[D_{{{\xi}}}^{K{\sigma}}\mathbb{U}({{\eta}}, {{\xi}})] = {s}^{K{\sigma}}R(s)-\sum\limits_{j = 0}^{K-1}{s}^{{\sigma}(K-j)-1}D_{{{\xi}}}^{j{\sigma}}D_{{{\xi}}}^{j{\sigma}}\mathbb{U}({{\eta}},0),\ 0 < {\sigma}\leq1. \end{equation}$

(2.11)

Another step is to provide that Eq (2.1) holds for $r = K+1$ . Now, solve Eq (2.1), by replacing $r = K+1$ .

$\begin{equation} M[D_{{{\xi}}}^{(K+1){\sigma}}\mathbb{U}({{\eta}}, {{\xi}})] = {s}^{(K+1){\sigma}}R(s)-\sum\limits_{j = 0}^{K}{s}^{{\sigma}((K+1)-j)-1}D_{{{\xi}}}^{j{\sigma}}\mathbb{U}({{\eta}},0). \end{equation}$

(2.12)

Equation (2.12) may be used to deduce this result:

$\begin{equation} L.H.S = M[D_{{{\xi}}}^{K{\sigma}}(D_{{{\xi}}}^{K{\sigma}})]. \end{equation}$

(2.13)

Let

$D_{{{\xi}}}^{K{\sigma}} = g({{\eta}}, {{\xi}}).$

The following solution is achieved by applying Eq (2.13):

$\begin{equation} L.H.S = M[D_{{{\xi}}}^{{\sigma}}g({{\eta}}, {{\xi}})]. \end{equation}$

(2.14)

The Caputo's derivative and the RL integral are used to solve Eq (2.14)

$\begin{equation} L.H.S = {s}^{{\sigma}}M[D_{{{\xi}}}^{K{\sigma}}\mathbb{U}({{\eta}}, {{\xi}})]-\frac{g({{\eta}},0)}{{s}^{1-{\sigma}}}. \end{equation}$

(2.15)

Equation (2.11) may be used as a basis to develop Eq (2.15)

$\begin{equation} L.H.S = {s}^{r{\sigma}}R(s)-\sum\limits_{j = 0}^{r-1}{s}^{{\sigma}(r-j)-1}D_{{{\xi}}}^{j{\sigma}}\mathbb{U}({{\eta}},0). \end{equation}$

(2.16)

Here is another way to express Eq (2.16) as:

$L.H.S = M[D_{{{\xi}}}^{r{\sigma}}\mathbb{U}({{\eta}},0)].$

Equation (2.1) holds for $r = K+1$ , as mathematical induction demonstrates. It follows that for any positive integer, Eq (2.1) holds. □

Lemma 2.2. Suppose that the order of the function $\mathbb{U}({{\eta}}, {{\xi}})$ is exponential. $M[\mathbb{U}({{\eta}}, {{\xi}})] = R(s)$ shows the MT of $\mathbb{U}({{\eta}}, {{\xi}})$ . The MT contains the following statement about multiple fractional power series (MFPS):

$\begin{equation} R(s) = \sum\limits_{r = 0}^{\infty}\frac{\hbar_{r}({{\eta}})}{s^{r{\sigma}+1}}, s > 0, \end{equation}$

(2.17)

where ${{\eta}} = (\eta_{1}, {{\eta}}_{2}, \cdots, {{\eta}}_{\sigma})\in\mathbb{R}^{\sigma}, \ \sigma\in \mathbb{N}$ .

Proof. Consider the Taylor series:

$\begin{equation} \mathbb{U}({{\eta}}, {{\xi}}) = \hbar_{0}({{\eta}})+\hbar_{1}({{\eta}})\frac{{{\xi}}^{{\sigma}}}{\Gamma[{\sigma}+1]}++\hbar_{2}({{\eta}})\frac{{{\xi}}^{2{\sigma}}}{\Gamma[2{\sigma}+1]}+\cdots. \end{equation}$

(2.18)

We reach the following result by applying MT to Eq (2.18):

$M\left[\mathbb{U}({{\eta}}, {{\xi}})\right] = M\left[\hbar_{0}({{\eta}})\right]+M\left[\hbar_{1}({{\eta}})\frac{{{\xi}}^{{\sigma}}}{\Gamma[{\sigma}+1]}\right]+M\left[\hbar_{1}({{\eta}}) \frac{{{\xi}}^{2{\sigma}}}{\Gamma[2{\sigma}+1]}\right]+\cdots .$

To achieve the subsequent result, make use of MT's features

$M\left[\mathbb{U}({{\eta}}, {{\xi}})\right] = \hbar_{0}({{\eta}})\frac{1}{s}+\hbar_{1}({{\eta}})\frac{\Gamma[{\sigma}+1]}{\Gamma[{\sigma}+1]}\frac{1}{s^{{\sigma}+1}}+\hbar_{2}({{\eta}}) \frac{\Gamma[2{\sigma}+1]}{\Gamma[2{\sigma}+1]}\frac{1}{s^{2{\sigma}+1}}\cdots .$

This leads to an updated Taylor series. □

Lemma 2.3. In MFPS, the modified Taylor series takes this form when MT is symbolized as $M[\mathbb{U}(\eta, \xi)] = R(s)$

$\begin{equation} \hbar_{0}({{\eta}}) = \lim\limits_{s\rightarrow \infty}sR(s) = \mathbb{U}({{\eta}},0). \end{equation}$

(2.19)

Proof. Consider the Taylor series:

$\begin{equation} \hbar_{0}({{\eta}}) = sR(s)-\frac{\hbar_{1}({{\eta}})}{s^{{\sigma}}}-\frac{\hbar_{2}({{\eta}})}{s^{2{\sigma}}}-\cdots . \end{equation}$

(2.20)

The limit determined in Eq (2.19) is computed and simplified to provide Eq (2.20). □

Theorem 2.4. Let $M[\mathbb{U}({{\eta}}, {{\xi}})]$ denote a function. Then, $R(s)$ is expressed in the MFPS notation as follows:

$R(s) = \sum\limits_{r = 0}^{\infty}\frac{\hbar_{r}({{\eta}})}{{s}^{r{\sigma}+1}}, \ {s} > 0,$

where ${{\eta}} = ({{\eta}}_{1}, {{\eta}}_{2}, \cdots, {{\eta}}_{\sigma})\in\mathbb{R}^\sigma$ and $\sigma\in\mathbb{N}$ . Then, we have

$\hbar_{r}({{\eta}}) = D_{r}^{r{\sigma}}\mathbb{U}({{\eta}},0),$

where $D_{{{\xi}}}^{r{\sigma}} = D_{{{\xi}}}^{{\sigma}}.D_{{{\xi}}}^{{\sigma}}.\cdots.D_{{{\xi}}}^{{\sigma}}(r-times)$ .

Proof. Consider the Taylor series:

$\begin{equation} \hbar_{1}({{\eta}}) = {s}^{{\sigma}+1}R(s)-{s}^{{\sigma}}\hbar_{0}({{\eta}})-\frac{\hbar_{2}({{\eta}})}{{s}^{{\sigma}}}-\frac{\hbar_{3}({{\eta}})}{{s}^{2{\sigma}}}- \cdots. \end{equation}$

(2.21)

By applying limit to Eq (2.21), we obtain the subsequent result:

$\hbar_{1}({{\eta}}) = \lim\limits_{{s}\rightarrow \infty}({s}^{{\sigma}+1}R(s)-{s}^{{\sigma}}\hbar_{0}({{\eta}}))-\lim\limits_{{s}\rightarrow \infty}\frac{\hbar_{2}({{\eta}})}{{s}^{{\sigma}}} -\lim\limits_{{s}\rightarrow \infty}\frac{\hbar_{3}({{\eta}})}{{s}^{2{\sigma}}}- \cdots.$

Simplifying further, we get

$\begin{equation} \hbar_{1}({{\eta}}) = \lim\limits_{{s}\rightarrow \infty}({s}^{{\sigma}+1}R(s)-{s}^{{\sigma}}\hbar_{0}({{\eta}})). \end{equation}$

(2.22)

Using the basic ideas outlined in Lemma 2.1, we may construct the following variant of Eq (2.22):

$\begin{equation} \hbar_{1}({{\eta}}) = \lim\limits_{{s}\rightarrow \infty}({s}M[D_{{{\xi}}}^{{\sigma}}\mathbb{U}({{\eta}}, {{\xi}})]({s})). \end{equation}$

(2.23)

Equation (2.23) is derived using Lemma 2.2 as a foundation:

$\hbar_{1}({{\eta}}) = D_{{{\xi}}}^{{\sigma}}\mathbb{U}({{\eta}},0).$

The following result requires taking $\lim_{{s}\rightarrow \infty}$ once again and applying the Taylor series

$\hbar_{2}({{\eta}}) = {s}^{2{\sigma}+1}R(s)-{s}^{2{\sigma}}\hbar_{0}({{\eta}})-{s}^{{\sigma}}\hbar_{1}({{\eta}})-\frac{\hbar_{3}({{\eta}})}{{s}^{{\sigma}}}- \cdots .$

Using Lemma 2.2, the following results are obtained:

$\begin{equation} \hbar_2({{\eta}}) = \lim\limits_{{s}\rightarrow \infty}{s}({s}^{2{\sigma}}R(s)-{s}^{2{\sigma}-1}\hbar_{0}({{\eta}})-{s}^{{\sigma}-1}\hbar_{1}({{\eta}})). \end{equation}$

(2.24)

Lemmas 2.1 and 2.3 serve as the basis for modifying the Eq (2.24) in the following way:

$\hbar_{2}({{\eta}}) = D_{{{\xi}}}^{2{\sigma}}\mathbb{U}({{\eta}},0).$

By following the same process, we get:

$\hbar_{3}({{\eta}}) = \lim\limits_{{s}\rightarrow \infty}{s}(M[D_{{{\xi}}}^{2{\sigma}}\mathbb{U}({{\eta}},{\sigma})]({s})).$

This final solution is found using Lemma 2.3:

$\hbar_{3}({{\eta}}) = D_{{{\xi}}}^{3{\sigma}}\mathbb{U}({{\eta}},0).$

Generally,

$\hbar_{r}({{\eta}}) = D_{{{\xi}}}^{r{\sigma}}\mathbb{U}({{\eta}},0).$

□

The following theorem describes and explains the new form of Taylor's series convergence.

3. Methodology

3.1. q-homotopy Mohand transform method (q-HMTM)

Consider the following nonhomogeneous, nonlinear fractional order partial differential equation (PDE):

$\begin{equation} \begin{split} &D_{\xi}^{\sigma}{\mathbb{U}}(\eta,\xi)+\mathcal{R}{\mathbb{U}}(\eta,\xi)+\mathcal{N}{\mathbb{U}}(\eta,\xi) = {\mathbb{H}}(\eta,\xi),\ \ n-1 < \sigma\leq n. \end{split} \end{equation}$

(3.1)

$D_{\mathcal{R}}^{\sigma}{\mathbb{U}}(\eta, \xi)$ represents the Caputo derivative, whereas $\mathcal{N}$ and $\mathcal{R}$ represent the nonlinear and linear operators, respectively, and ${\mathbb{H}}(\eta, \xi)$ is the source.

Apply Mohand transform to Eq (3.1)

$\begin{equation} \begin{split} \mathcal{M}[{\mathbb{U}}(\eta,\xi)]-\frac{1}{s^{\sigma}}\sum\limits_{k = 0}^{n-1}s^{\sigma-k-1}{\mathbb{U}}^{k}(\eta,0)+\frac{1}{s^{\sigma}}[\mathcal{M}[\mathcal{R} {\mathbb{U}}(\eta,\xi)]+\mathcal{M}[\mathcal{N}{\mathbb{U}}(\eta,\xi)]-\mathcal{M}[{\mathbb{H}}(\eta,\xi)]] = 0. \end{split} \end{equation}$

(3.2)

The nonlinear function is given as:

$\begin{equation} \begin{split} {N}[{\varphi}(\eta,\xi;q)]& = \mathcal{M}[{\varphi}(\eta,\xi;q)]-\frac{1}{s^{\sigma}}\sum\limits_{k = 0}^{n-1}s^{\sigma-k-1}{\varphi}^{k}(\eta,\xi;q)(0^{+}) +\frac{1}{s^{\sigma}}[\mathcal{M}[\mathcal{R}{\varphi}(\eta,\xi;q)]\\&+\mathcal{M}[\mathcal{N}{\varphi}(\eta,\xi;q)]-\mathcal{M}[{\mathbb{H}}(\eta,\xi)]]. \end{split} \end{equation}$

(3.3)

Here, ${\varphi}(\eta, \xi; q))$ w.r.t $\eta$ , $\xi$ , and $q\in\Big[0, \frac{1}{n}\Big]$ are the real-value functions. A homotopy can be given as:

$\begin{equation} \begin{split} (1-nq)\mathcal{M}[{\varphi}(\eta,\xi;q)-{\mathbb{U}_{0}}(\eta,\xi)] = \hbar q\mathfrak{h}(\eta,\xi)\mathcal{N}[{\varphi}(\eta,\xi;q)]. \end{split} \end{equation}$

(3.4)

In the above expression, the initial condition is denoted by ${\mathbb{U}_{0}}$ , and the auxiliary parameter is denoted by $\hbar = 0$ .

The following result holds for both $0$ and $\frac{1}{n}$ :

$\begin{equation} \begin{split} {\varphi}(\eta,\xi;0) = {\mathbb{U}_{0}}(\eta,\xi),\ \ {\varphi}(\eta,\xi;\frac{1}{n}) = {\mathbb{U}}(\eta,\xi). \end{split} \end{equation}$

(3.5)

The strengthening of the $q$ parameter causes the solution ${\varphi}(\eta, \xi; q)$ to diverge from the initial predictive value ${\mathbb{U}_{0}}(\eta, \xi)$ to ${\mathbb{U}}(\eta, \xi)$ . The following expression results from applying Taylor's theorem to function ${\varphi}(\eta, \xi; q)$ when it depends on variable $q$ :

$\begin{equation} \begin{split} {\varphi}(\eta,\xi;q) = {\mathbb{U}_{0}}(\eta,\xi)+\sum\limits_{{m} = 1}^{\infty}{\mathbb{U}_{{m}}}(\eta,\xi)q^{{m}}, \end{split} \end{equation}$

(3.6)

where

$\begin{equation} \begin{split} {\mathbb{U}_{{m}}} = \frac{1}{{m}!}\frac{\partial^{m}{\varphi}(\eta,\xi;q)}{\partial q^{{m}}}|_{q = 0} \end{split}. \end{equation}$

(3.7)

The convergences series of (3.4) at $q = \frac{1}{n}$ for the appropriate values of ${\mathbb{U}_{0}}(\eta, \xi)$ , $n$ , and $\hbar$ . Consequently,

$\begin{equation} \begin{split} {\varphi}(\eta,\xi;q) = {\mathbb{U}_{0}}(\eta,\xi)+\sum\limits_{{m} = 1}^{\infty}{\mathbb{U}_{{m}}}(\eta,\xi)\Big(\frac{1}{n}\Big)^{{m}}. \end{split} \end{equation}$

(3.8)

The derivatives of Eq (3.4) and the parameter $q$ are} obtained by $q = 0$ , dividing by ${m}!$ , and calculating the derivative

$\begin{equation} \begin{split} \mathcal{M}[{\mathbb{U}_{{m}}}(\eta,\xi)-k_{{m}}{\mathbb{U}_{{m}-1}}(\eta,\xi)] = \hbar\mathfrak{h}(\eta,\xi) \mathcal{R}_{{m}}(\overrightarrow{{\mathbb{U}}}_{{m}-1}). \end{split} \end{equation}$

(3.9)

The auxiliary parameters $\hbar\neq0$ and the vectors are expressed as:

$\begin{equation} \begin{split} \overrightarrow{{\mathbb{U}}}_{{m}} = [{\mathbb{U}_{0}}(\eta,\xi),{\mathbb{U}_{1}}(\eta,\xi),\cdots,{\mathbb{U}_{{m}}}(\eta,\xi)]. \end{split} \end{equation}$

(3.10)

The outcome of applying the MIT to Eq (3.9) is as follows:

$\begin{equation} \begin{split} {\mathbb{U}_{{m}}}(\eta,\xi) = k_{{m}}{\mathbb{U}_{{m}-1}}(\eta,\xi)+\hbar\mathcal{M}^{-1}[\mathfrak{h}(\eta,\xi) \mathcal{R}_{{m}}(\overrightarrow{{\mathbb{U}}}_{{m}-1})], \end{split} \end{equation}$

(3.11)

$\begin{equation*} \begin{split} \mathcal{R}_{{m}}(\overrightarrow{{\mathbb{K}}}_{{m}-1}) = \frac{1}{({m}-1)!}\frac{\partial^{{m}-1}\mathcal{N}[{\varphi}(\eta,\xi;q)]}{\partial q^{{m}-1}}\mid_{q = 0}, \end{split} \end{equation*}$

$\begin{equation} \begin{split} k_{{m}} = \begin{cases}0\ \ \ if \ \ {m}\leq1,\\1\ \ \ if \ \ {m} > 1.\end{cases} \end{split} \end{equation}$

(3.12)

The elements of the q-HATM result are ultimately determined by solving Eq (3.11).

3.2. VITM

Consider the following nonhomogeneous, nonlinear fractional order PDE:

$\begin{equation} \begin{split} &D_{\xi}^{\sigma}{\mathbb{U}}(\eta,\xi) = \mathcal{R}{\mathbb{U}}(\eta,\xi)+\mathcal{N}{\mathbb{U}}(\eta,\xi)+{\mathbb{H}}(\eta,\xi),\ \ n-1 < \sigma\leq n. \end{split} \end{equation}$

(3.13)

Initial condition

$\begin{equation} \begin{split} {\mathbb{U}}(\eta,0) = {\mathbb{U}_{0}}(\eta). \end{split} \end{equation}$

(3.14)

Using the MT in Eq (3.13) is given as

$\begin{equation} \begin{split} &\mathcal{M}[D_{\xi}^{\sigma}{\mathbb{U}}(\eta,\xi)] = \mathcal{M}[\mathcal{R}{\mathbb{U}}(\eta,\xi)+\mathcal{N}{\mathbb{U}}(\eta,\xi) +{\mathbb{H}}(\eta,\xi)]. \end{split} \end{equation}$

(3.15)

The iteration property of transformation is defined as:

$\begin{equation} \begin{split} &\mathcal{M}[{\mathbb{U}}(\eta,\xi)]-\sum\limits_{{k} = 0}^{m-1}{s}^{\sigma-{k}-1}\frac{\partial^{{k}}{\mathbb{U}}(\eta,\xi)} {\partial\xi^{{k}}}|_{\xi = 0} = \mathcal{M}[\mathcal{R}{\mathbb{U}}(\eta,\xi)+\mathcal{N}{\mathbb{U}}(\eta,\xi)+{\mathbb{H}}(\eta,\xi)], \end{split} \end{equation}$

(3.16)

with the Lagrange multiplier of $(-\lambda({s}))$ ,

$\begin{equation} \begin{split} &\mathcal{M}[{\mathbb{U}_{n+1}}(\eta,\xi)] = \mathcal{M}[{\mathbb{U}_{n}}(\eta,\xi)] -\lambda({s})\Big[\mathcal{M}[{\mathbb{U}_{n}}(\eta,\xi)]-\sum\limits_{{k} = 0}^{m-1}{s}^{\sigma-{k}-1}\frac{\partial^{{k}}{\mathbb{U}} (\eta,0)}{\partial\xi^{{k}}}\Big], \end{split} \end{equation}$

(3.17)

where $\lambda({s}) = -\frac{1}{{s}^{\sigma}}$ , and substituting Eq (3.17) into Eq (3.16), we obtain

$\begin{equation} \begin{split} \mathcal{M}[{\mathbb{U}}_{n+1}(\eta,\xi)]& = \mathcal{M}[{\mathbb{U}_{n}}(\eta,\xi)] -\lambda({s})\Big[\mathcal{M}[{\mathbb{U}_{n}}(\eta,\xi)]-\sum\limits_{{k} = 0}^{m-1}{s}^{\sigma-{k}-1}\frac{\partial^{{k}}{\mathbb{U}} (\eta,0)}{\partial\xi^{{k}}}\\&+\mathcal{M}[\mathcal{R}{\mathbb{U}}(\eta,\xi)+\mathcal{N}{\mathbb{U}}(\eta,\xi) +{\mathbb{H}}(\eta,\xi)]\Big]. \end{split} \end{equation}$

(3.18)

The MIT in Eq (3.18) enables us to derive:

$\begin{equation} \begin{split} {\mathbb{U}}_{n+1}(\eta,\xi)& = {\mathbb{U}_{n}}(\eta,\xi) +\mathcal{M}^{-1}\Big[\frac{1}{{s}^{\sigma}}\sum\limits_{{k} = 0}^{m-1}{s}^{\sigma-{k}-1}\frac{\partial^{{k}}{\mathbb{U}} (\eta,0)}{\partial\xi^{{k}}}\\ &+\mathcal{M}[\mathcal{R}{\mathbb{U}}(\eta,\xi)+\mathcal{N}{\mathbb{U}}(\eta,\xi) +{\mathbb{H}}(\eta,\xi)]\Big]. \end{split} \end{equation}$

(3.19)

The starting constraints become:

$\begin{equation} \begin{split} &{\mathbb{U}}_{0}(\eta,\xi) = \mathcal{M}^{-1}\Big[\frac{1}{{s}^{\sigma}}\sum\limits_{{k} = 0}^{m-1}{s}^{\sigma-{k}-1}\frac{\partial^{{k}}{\mathbb{U}} (\eta,0)}{\partial\xi^{{k}}}\Big]. \end{split} \end{equation}$

(3.20)

The recursive system is followed as:

(3.21)

4. Problem 1

4.1. The implementation of q-HATM

Let's assume the system of Schrödinger-KdV equations of time-fractional order:

$\begin{equation} \begin{split} &D_{{{\xi}}}^{\sigma}\mathbb{U}(\eta ,\xi )-\frac{\partial ^2\mathbb{V}(\eta ,\xi )}{\partial \eta^2}-\mathbb{V}(\eta ,\xi )\mathbb{W}(\eta ,\xi ) = 0,\\ &D_{{{\xi}}}^{\sigma}\mathbb{V}(\eta ,\xi )+\frac{\partial ^2\mathbb{U}(\eta ,\xi )}{\partial \eta^2}+\mathbb{U}(\eta ,\xi )\mathbb{W}(\eta ,\xi ) = 0,\\ &D_{{{\xi}}}^{\sigma}\mathbb{W}(\eta ,\xi )+6\mathbb{W}(\eta ,\xi )\frac{\partial \mathbb{W}(\eta ,\xi )}{\partial \eta }+\frac{\partial ^3\mathbb{W}(\eta ,\xi )}{\partial \eta^3}-2\mathbb{U}(\eta ,\xi )\frac{\partial \mathbb{U}(\eta ,\xi )}{\partial \eta}-2\mathbb{V}(\eta ,\xi )\frac{\partial \mathbb{V}(\eta ,\xi )}{\partial \eta } = 0, \end{split} \end{equation}$

(4.1)

where $0 < \sigma \leq 1$ .

Initial conditions are given as:

$\begin{equation} \begin{split} &{\mathbb{U}}({{\eta}},0) = \cos (\eta ) \tanh (\eta ),\\ &{\mathbb{V}}({{\eta}},0) = \sin (\eta ) \tanh (\eta ),\\ &{\mathbb{W}}({{\eta}},0) = \frac{7}{8}-2 \tanh ^2(\eta ), \end{split} \end{equation}$

(4.2)

$\begin{equation} \begin{split} &\mathcal{M}[{\mathbb{U}}(\eta ,\xi )]+{s}\left(\cos (\eta ) \tanh (\eta )\right)+\frac{1}{s^{\sigma}}\mathcal{M}\Big[-\frac{\partial ^2\mathbb{V}(\eta ,\xi )}{\partial \eta^2}-\mathbb{V}(\eta ,\xi )\mathbb{W}(\eta ,\xi )\Big] = 0,\\ &\mathcal{M}[{\mathbb{V}}(\eta ,\xi )]+{s}\left(\sin (\eta ) \tanh (\eta )\right)+\frac{1}{s^{\sigma}}\mathcal{M}\Big[\frac{\partial ^2\mathbb{U}(\eta ,\xi )}{\partial \eta^2}+\mathbb{U}(\eta ,\xi )\mathbb{W}(\eta ,\xi )\Big] = 0,\\ &\mathcal{M}[{\mathbb{W}}(\eta ,\xi )]+{s}\left(\frac{7}{8}-2 \tanh ^2(\eta )\right)+\frac{1}{s^{\sigma}}\mathcal{M}\Big[6\mathbb{W}(\eta ,\xi )\frac{\partial \mathbb{W}(\eta ,\xi )}{\partial \eta }+\frac{\partial ^3\mathbb{W}(\eta ,\xi )}{\partial \eta^3}-2\mathbb{U}(\eta ,\xi )\frac{\partial \mathbb{U}(\eta ,\xi )}{\partial \eta}\\&-2\mathbb{V}(\eta ,\xi )\frac{\partial \mathbb{V}(\eta ,\xi )}{\partial \eta }\Big] = 0. \end{split} \end{equation}$

(4.3)

The definition} of nonlinear operators is given as follows:

$\begin{equation} \begin{split} \mathcal{N}^1[\varphi_1(\eta ,\xi;q),\varphi_2(\eta ,\xi;q),\varphi_3(\eta ,\xi;q)]& = \mathcal{M}[\varphi_1(\eta ,\xi;q)]+{s}\left(\cos (\eta ) \tanh (\eta )\right)\\&+\frac{1}{s^{\sigma}}\mathcal{M}\Big[-\frac{\partial ^2\varphi_2(\eta ,\xi;q)}{\partial \eta^2}-\varphi_2(\eta ,\xi;q)\varphi_3(\eta ,\xi;q)\Big],\\ \mathcal{N}^2[\varphi_1(\eta ,\xi;q),\varphi_2(\eta ,\xi;q),\varphi_3(\eta ,\xi;q)]& = \mathcal{M}[\varphi_2(\eta ,\xi;q)]+{s}\left(\sin (\eta ) \tanh (\eta )\right)\\&+\frac{1}{s^{\sigma}}\mathcal{M}\Big[\frac{\partial ^2\varphi_1(\eta ,\xi;q)}{\partial \eta^2}+\varphi_1(\eta ,\xi;q)\varphi_3(\eta ,\xi;q)\Big],\\ \mathcal{N}^3[\varphi_1(\eta ,\xi;q),\varphi_2(\eta ,\xi;q),\varphi_3(\eta ,\xi;q)]& = \mathcal{M}[\varphi_3(\eta ,\xi;q)]+{s}\left(\frac{7}{8}-2 \tanh ^2(\eta )\right)\\&+\frac{1}{s^{\sigma}}\mathcal{M}\Big[6\varphi_3(\eta ,\xi;q)\frac{\partial \varphi_3(\eta ,\xi;q)}{\partial \eta }+\frac{\partial ^3\varphi_3(\eta ,\xi;q)}{\partial \eta^3}\\&-2\varphi_1(\eta ,\xi;q)\frac{\partial \varphi_1(\eta ,\xi;q)}{\partial \eta}-2\varphi_2(\eta ,\xi;q)\frac{\partial \varphi_2(\eta ,\xi;q)}{\partial \eta }\Big]. \end{split} \end{equation}$

(4.4)

Also, the operators of the Mohand are given as:

$\begin{equation} \begin{split} &\mathcal{M}[{{\mathbb{U}}_{{m}}}(\eta,\xi)-k_{{m}}{{\mathbb{U}}_{{m}-1}}(\eta,\xi)] = \hbar\mathfrak{h}(\eta,\xi) {\mathcal{R}}_{{1,m}}[\overrightarrow{{\mathbb{U}}}_{{m}-1},\overrightarrow{{\mathbb{V}}}_{{m}-1},\overrightarrow{{\mathbb{W}}}_{{m}-1}],\\ &\mathcal{M}[{{\mathbb{V}}_{{m}}}(\eta,\xi)-k_{{m}}{{\mathbb{V}}_{{m}-1}}(\eta,\xi)] = \hbar\mathfrak{h}(\eta,\xi) {\mathcal{R}}_{{2,m}}[\overrightarrow{{\mathbb{U}}}_{{m}-1},\overrightarrow{{\mathbb{V}}}_{{m}-1},\overrightarrow{{\mathbb{W}}}_{{m}-1}],\\ &\mathcal{M}[{{\mathbb{W}}_{{m}}}(\eta,\xi)-k_{{m}}{{\mathbb{W}}_{{m}-1}}(\eta,\xi)] = \hbar\mathfrak{h}(\eta,\xi) {\mathcal{R}}_{{3,m}}[\overrightarrow{{\mathbb{U}}}_{{m}-1},\overrightarrow{{\mathbb{V}}}_{{m}-1},\overrightarrow{{\mathbb{W}}}_{{m}-1}]. \end{split} \end{equation}$

(4.5)

Here,

$\begin{equation} \begin{split} {\mathcal{R}}_{{1,m}}[\overrightarrow{{\mathbb{U}}}_{{m}-1},\overrightarrow{{\mathbb{V}}}_{{m}-1},\overrightarrow{{\mathbb{W}}}_{{m}-1}]& = \mathcal{M}[{\mathbb{U}_{m-1}}(\eta ,\xi )]+{s}\left(1-\frac{k_m}{n}\right)\left(\cos (\eta ) \tanh (\eta )\right)\\ &+\frac{1}{s^{\sigma}}\mathcal{M}\Big[-\frac{\partial ^2\mathbb{V}_{m-1}(\eta ,\xi )}{\partial \eta^2}-\sum\limits_{i}^{m-1}\mathbb{V}_{i}(\eta ,\xi )\mathbb{W}_{m-1-i}(\eta ,\xi )\Big],\\ {\mathcal{R}}_{{2,m}}[\overrightarrow{{\mathbb{U}}}_{{m}-1},\overrightarrow{{\mathbb{V}}}_{{m}-1},\overrightarrow{{\mathbb{W}}}_{{m}-1}]& = \mathcal{M}[{\mathbb{V}_{m-1}}(\eta ,\xi )]+{s}\left(1-\frac{k_m}{n}\right)\left(\sin (\eta ) \tanh (\eta )\right)\\&+\frac{1}{s^{\sigma}}\mathcal{M}\Big[\frac{\partial ^2\mathbb{U}_{m-1}(\eta ,\xi )}{\partial \eta^2}+\sum\limits_{i}^{m-1}\mathbb{U}_i(\eta ,\xi )\mathbb{W}_{m-1-i}(\eta ,\xi )\Big],\\ {\mathcal{R}}_{{3,m}}[\overrightarrow{{\mathbb{U}}}_{{m}-1},\overrightarrow{{\mathbb{V}}}_{{m}-1},\overrightarrow{{\mathbb{W}}}_{{m}-1}]& = \mathcal{M}[{\mathbb{W}_{m-1}}(\eta ,\xi )]+{s}\left(1-\frac{k_m}{n}\right)\left(\frac{7}{8}-2 \tanh ^2(\eta )\right)\\&+\frac{1}{s^{\sigma}}\mathcal{M}\Big[6\sum\limits_{i}^{m-1}\Big[\mathbb{W}_{i}(\eta ,\xi )\times\frac{\partial \mathbb{W}_{m-1-i}(\eta ,\xi )}{\partial \eta }\Big]+\frac{\partial ^3\mathbb{W}_{m-1}(\eta ,\xi )}{\partial \eta^3}\\&-2\sum\limits_{i}^{m-1}\mathbb{U}_i(\eta ,\xi )\frac{\partial \mathbb{U}_{m-1-i}(\eta ,\xi )}{\partial \eta}-2\mathbb{V}_i(\eta ,\xi )\frac{\partial \mathbb{V}_{m-1-i}(\eta ,\xi )}{\partial \eta }\Big], \end{split} \end{equation}$

(4.6)

$\begin{equation} \begin{split} &{\mathbb{U}_{{m}}}(\eta ,\xi) = k_{{m}}{\mathbb{U}_{{m}-1}}(\eta ,\xi)+\hbar\mathcal{M}^{-1}[\mathfrak{h}(\eta ,\xi) {\mathcal{R}}_{{1,m}}(\overrightarrow{{\mathbb{U}}}_{{m}-1},\overrightarrow{{\mathbb{V}}}_{{m}-1},\overrightarrow{{\mathbb{W}}}_{{m}-1}),\\ &{\mathbb{V}_{{m}}}(\eta ,\xi) = k_{{m}}{\mathbb{V}_{{m}-1}}(\eta ,\xi)+\hbar\mathcal{M}^{-1}[\mathfrak{h}(\eta ,\xi) {\mathcal{R}}_{{2,m}}(\overrightarrow{{\mathbb{U}}}_{{m}-1},\overrightarrow{{\mathbb{V}}}_{{m}-1},\overrightarrow{{\mathbb{W}}}_{{m}-1}),\\ &{\mathbb{W}_{{m}}}(\eta ,\xi) = k_{{m}}{\mathbb{W}_{{m}-1}}(\eta ,\xi)+\hbar\mathcal{M}^{-1}[\mathfrak{h}(\eta ,\xi) {\mathcal{R}}_{{3,m}}(\overrightarrow{{\mathbb{U}}}_{{m}-1},\overrightarrow{{\mathbb{V}}}_{{m}-1},\overrightarrow{{\mathbb{W}}}_{{m}-1}). \end{split} \end{equation}$

(4.7)

The initial condition in Eq (4.7) allows us to derive the following:

$\begin{equation} \begin{split} &{\mathbb{U}}_{1}(\eta,\xi) = -\frac{\hbar \xi^{\sigma } \left(16 \cos (\eta) \text{sech}^2(\eta)-17 \sin (\eta) \tanh (\eta)\right)}{8 \Gamma (\sigma +1)},\\ &{\mathbb{V}}_{1}(\eta,\xi) = -\frac{\hbar \xi^{\sigma } \left(17 \cos (\eta) \tanh (\eta)+16 \sin (\eta) \text{sech}^2(\eta)\right)}{8 \Gamma (\sigma +1)},\\ &{\mathbb{W}}_{1}(\eta,\xi) = \frac{9 \hbar \xi^{\sigma } \tanh (\eta) \text{sech}^2(\eta)}{\Gamma (\sigma +1)}, \end{split} \end{equation}$

(4.8)

$\begin{equation} \begin{split} {\mathbb{U}}_{2}(\eta,\xi)& = \frac{\hbar \xi^{\sigma }}{256}\Big(\frac{32 (n+\hbar ) \left(17 \sin (\eta) \tanh (\eta)-16 \cos (\eta) \text{sech}^2(\eta)\right)}{\Gamma (\sigma +1)}\\& -\frac{\hbar \xi^{\sigma } \text{sech}^3(\eta) (\cos (\eta) (2337 \sinh (\eta)+289 \sinh (3 \eta))+64 \sin (\eta) (19 \cosh (2 \eta)+15) \text{sech}(\eta))}{\Gamma (2 \sigma +1)}\Big),\\ {\mathbb{V}}_{2}(\eta,\xi)& = \frac{\hbar \xi^{\sigma }}{256}\Big(-\frac{32 (n+\hbar ) \left(17 \cos (\eta) \tanh (\eta)+16 \sin (\eta) \text{sech}^2(\eta)\right)}{\Gamma (\sigma +1)}\\&+\frac{\hbar \xi^{\sigma } \text{sech}^3(\eta) (64 \cos (\eta) (19 \cosh (2 \eta)+15) \text{sech}(\eta)-2 \sin (\eta) \sinh (\eta) (289 \cosh (2 \eta)+1313))}{\Gamma (2 \sigma +1)}\Big),\\ {\mathbb{W}}_{2}(\eta,\xi)& = \frac{1}{4} \hbar \xi^{\sigma } \text{sech}^4(\eta) \left(\frac{18 (n+\hbar ) \sinh (2 \eta)}{\Gamma (\sigma +1)}+\frac{83 \hbar \xi^{\sigma } (\cosh (2 \eta)-2)}{\Gamma (2 \sigma +1)}\right), \end{split} \end{equation}$

(4.9)

and so on.

Additionally, the other components may be identified in this manner. The q-HATM solution of Eq (4.1) is derived as follows:

$\begin{equation} \begin{split} &{\mathbb{U}}(\eta,\xi) = \mathbb{U}_{0}+\sum\limits_{{m} = 1}^{\infty}{\mathbb{U}}_{{m}}\left(\frac{1}{n}\right)^{{m}},\\ &{\mathbb{V}}(\eta,\xi) = \mathbb{V}_{0}+\sum\limits_{{m} = 1}^{\infty}{\mathbb{V}}_{{m}}\left(\frac{1}{n}\right)^{{m}},\\ &{\mathbb{W}}(\eta,\xi) = \mathbb{W}_{0}+\sum\limits_{{m} = 1}^{\infty}{\mathbb{W}}_{{m}}\left(\frac{1}{n}\right)^{{m}}. \end{split} \end{equation}$

(4.10)

For $\sigma = 1$ , $\hbar = -1$ , and $n = 1$ , solutions $\sum_{m = 1}^{N}{\mathbb{U}}_{{m}}\left(\frac{1}{n}\right)^{{m}}$ , $\sum_{m = 1}^{N}{\mathbb{V}}_{{m}}\left(\frac{1}{n}\right)^{{m}}$ , and $\sum_{m = 1}^{N}{\mathbb{W}}_{{m}}\left(\frac{1}{n}\right)^{{m}}$ converge to the exact solutions as $N\rightarrow \infty$ .

$\begin{equation} \begin{aligned} {\mathbb{U}}(\eta,\xi)& = \cos (\eta ) \tanh (\eta )-\frac{\hbar \xi^{\sigma } \left(16 \cos (\eta) \text{sech}^2(\eta)-17 \sin (\eta) \tanh (\eta)\right)}{8 \Gamma (\sigma +1)}\nonumber\\ &+\frac{\hbar \xi^{\sigma }}{256}\Big(\frac{32 (n+\hbar ) \left(17 \sin (\eta) \tanh (\eta)-16 \cos (\eta) \text{sech}^2(\eta)\right)}{\Gamma (\sigma +1)}\nonumber\\ & -\frac{\hbar \xi^{\sigma } \text{sech}^3(\eta) (\cos (\eta) (2337 \sinh (\eta)+289 \sinh (3 \eta))+64 \sin (\eta) (19 \cosh (2 \eta)+15) \text{sech}(\eta))}{\Gamma (2 \sigma +1)}\Big)\nonumber\\ &+\cdots,\nonumber \end{aligned} \end{equation}$

$\begin{align} {\mathbb{V}}(\eta,\xi)& = \sin (\eta ) \tanh (\eta )-\frac{\hbar \xi^{\sigma } \left(17 \cos (\eta) \tanh (\eta)+16 \sin (\eta) \text{sech}^2(\eta)\right)}{8 \Gamma (\sigma +1)}\\ &+\frac{\hbar \xi^{\sigma }}{256}\Big(-\frac{32 (n+\hbar ) \left(17 \cos (\eta) \tanh (\eta)+16 \sin (\eta) \text{sech}^2(\eta)\right)}{\Gamma (\sigma +1)}\\ &+\frac{\hbar \xi^{\sigma } \text{sech}^3(\eta) (64 \cos (\eta) (19 \cosh (2 \eta)+15) \text{sech}(\eta)-2 \sin (\eta) \sinh (\eta) (289 \cosh (2 \eta)+1313))}{\Gamma (2 \sigma +1)}\Big)\\ &+\cdots,\\ {\mathbb{W}}(\eta,\xi)& = \frac{7}{8}-2 \tanh ^2(\eta )+\frac{9 \hbar \xi^{\sigma } \tanh (\eta) \text{sech}^2(\eta)}{\Gamma (\sigma +1)}+\frac{1}{4} \hbar \xi^{\sigma } \text{sech}^4(\eta) \Big(\frac{18 (n+\hbar ) \sinh (2 \eta)}{\Gamma (\sigma +1)}\\ &+\frac{83 \hbar \xi^{\sigma } (\cosh (2 \eta)-2)}{\Gamma (2 \sigma +1)}\Big)\\ &+\cdots. \end{align}$

(4.11)

4.2. The implementation of VITM

Consider the time fractional order system of Schrödinger-KdV equations:

$\begin{equation} \begin{split} D_{{{\xi}}}^{\sigma}\mathbb{U}(\eta ,\xi )& = \frac{\partial ^2\mathbb{V}(\eta ,\xi )}{\partial \eta^2}+\mathbb{V}(\eta ,\xi )\mathbb{W}(\eta ,\xi ),\\ D_{{{\xi}}}^{\sigma}\mathbb{V}(\eta ,\xi )& = -\frac{\partial ^2\mathbb{U}(\eta ,\xi )}{\partial \eta^2}-\mathbb{U}(\eta ,\xi )\mathbb{W}(\eta ,\xi ),\\ D_{{{\xi}}}^{\sigma}\mathbb{W}(\eta ,\xi )& = -6\mathbb{W}(\eta ,\xi )\frac{\partial \mathbb{W}(\eta ,\xi )}{\partial \eta }-\frac{\partial ^3\mathbb{W}(\eta ,\xi )}{\partial \eta^3}+2\mathbb{U}(\eta ,\xi )\frac{\partial \mathbb{U}(\eta ,\xi )}{\partial \eta}\\ &+2\mathbb{V}(\eta ,\xi )\frac{\partial \mathbb{V}(\eta ,\xi )}{\partial \eta }, \end{split} \end{equation}$

(4.12)

where $0 < \sigma \leq 1$ .

Initial conditions are given as:

(4.13)

By employing the recursive formula defined by Eq (3.21), we can get

$\begin{align} {\mathbb{U}}_{n+1}(\eta ,\xi)& = {\mathbb{U}_{n}}(\eta ,\xi) +\mathcal{M}^{-1}\Big[\frac{1}{{s}^{\sigma}}\sum\limits_{{k} = 0}^{m-1}{s}^{\sigma-{k}-1}\frac{\partial^{{k}}{\mathbb{U}} (\eta,0)}{\partial\xi^{{k}}}+\mathcal{M}[\frac{\partial ^2\mathbb{V}_{n}(\eta ,\xi )}{\partial \eta^2}+\mathbb{V}_{n}(\eta ,\xi )\mathbb{W}_{n}(\eta ,\xi )]\Big], \\ {\mathbb{V}}_{n+1}(\eta ,\xi)& = {\mathbb{V}_{n}}(\eta ,\xi) +\mathcal{M}^{-1}\Big[\frac{1}{{s}^{\sigma}}\sum\limits_{{k} = 0}^{m-1}{s}^{\sigma-{k}-1}\frac{\partial^{{k}}{\mathbb{V}} (\eta,0)}{\partial\xi^{{k}}}+\mathcal{M}[-\frac{\partial ^2\mathbb{U}_{n}(\eta ,\xi )}{\partial \eta^2}-\mathbb{U}_{n}(\eta ,\xi )\mathbb{W}_{n}(\eta ,\xi )]\Big],\\ {\mathbb{W}}_{n+1}(\eta ,\xi)& = {\mathbb{W}_{n}}(\eta ,\xi) +\mathcal{M}^{-1}\Big[\frac{1}{{s}^{\sigma}}\sum\limits_{{k} = 0}^{m-1}{s}^{\sigma-{k}-1}\frac{\partial^{{k}}{\mathbb{W}} (\eta,0)}{\partial\xi^{{k}}}+\mathcal{M}[-6\mathbb{W}_{n}(\eta ,\xi )\frac{\partial \mathbb{W}_{n}(\eta ,\xi )}{\partial \eta }-\frac{\partial ^3\mathbb{W}_{n}(\eta ,\xi )}{\partial \eta^3}\\ &+2\mathbb{U}_{n}(\eta ,\xi )\frac{\partial \mathbb{U}_{n}(\eta ,\xi )}{\partial \eta}+2\mathbb{V}_{n}(\eta ,\xi )\frac{\partial \mathbb{V}_{n}(\eta ,\xi )}{\partial \eta }]\Big]. \end{align}$

(4.14)

The second approximation may be produced by inserting $n = 0$ , as shown in the expression below:

$\begin{equation} \begin{split} {\mathbb{U}}_{1}(\eta ,\xi)& = {\mathbb{U}_{0}}(\eta ,\xi) +\mathcal{M}^{-1}\Big[\frac{1}{{s}^{\sigma}}\sum\limits_{{k} = 0}^{m-1}{s}^{\sigma-{k}-1}\frac{\partial^{{k}}{\mathbb{U}} (\eta,0)}{\partial\xi^{{k}}}+\mathcal{M}[\frac{\partial ^2\mathbb{V}_{0}(\eta ,\xi )}{\partial \eta^2}+\mathbb{V}_{0}(\eta ,\xi )\mathbb{W}_{0}(\eta ,\xi )]\Big],\\ {\mathbb{V}}_{1}(\eta ,\xi)& = {\mathbb{V}_{0}}(\eta ,\xi) +\mathcal{M}^{-1}\Big[\frac{1}{{s}^{\sigma}}\sum\limits_{{k} = 0}^{m-1}{s}^{\sigma-{k}-1}\frac{\partial^{{k}}{\mathbb{V}} (\eta,0)}{\partial\xi^{{k}}}+\mathcal{M}[-\frac{\partial ^2\mathbb{U}_{0}(\eta ,\xi )}{\partial \eta^2}-\mathbb{U}_{0}(\eta ,\xi )\mathbb{W}_{0}(\eta ,\xi )]\Big],\\ {\mathbb{W}}_{1}(\eta ,\xi)& = {\mathbb{W}_{0}}(\eta ,\xi) +\mathcal{M}^{-1}\Big[\frac{1}{{s}^{\sigma}}\sum\limits_{{k} = 0}^{m-1}{s}^{\sigma-{k}-1}\frac{\partial^{{k}}{\mathbb{W}} (\eta,0)}{\partial\xi^{{k}}}+\mathcal{M}[-6\mathbb{W}_{0}(\eta ,\xi )\frac{\partial \mathbb{W}_{0}(\eta ,\xi )}{\partial \eta }-\frac{\partial ^3\mathbb{W}_{0}(\eta ,\xi )}{\partial \eta^3}\\&+2\mathbb{U}_{0}(\eta ,\xi )\frac{\partial \mathbb{U}_{0}(\eta ,\xi )}{\partial \eta}+2\mathbb{V}_{0}(\eta ,\xi )\frac{\partial \mathbb{V}_{0}(\eta ,\xi )}{\partial \eta }]\Big]. \end{split} \end{equation}$

(4.15)

By simplification, we get

$\begin{equation} \begin{split} &{\mathbb{U}}_{1}(\eta ,\xi) = \frac{\xi ^{\sigma} \left(16 \cos (\eta) \text{sech}^2(\eta)-17 \sin (\eta) \tanh (\eta)\right)}{8 \Gamma (\sigma +1)}+\cos (\eta) \tanh (\eta),\\ &{\mathbb{V}}_{1}(\eta ,\xi) = \frac{\xi^{\sigma} \left(17 \cos (\eta) \tanh (\eta)+16 \sin (\eta) \text{sech}^2(\eta)\right)}{8 \Gamma (\sigma +1)}+\sin (\eta) \tanh (\eta),\\ &{\mathbb{W}}_{1}(\eta ,\xi) = -\frac{9 \xi ^{\sigma} \tanh (\eta) \text{sech}^2(\eta)}{\Gamma (\sigma +1)}+2 \text{sech}^2(\eta)-\frac{9}{8}. \end{split} \end{equation}$

(4.16)

By taking $n = 1$ , we have

$\begin{equation} \begin{split} {\mathbb{U}}_{2}(\eta ,\xi)& = {\mathbb{U}_{1}}(\eta ,\xi) +\mathcal{M}^{-1}\Big[\frac{1}{{s}^{\sigma}}\sum\limits_{{k} = 0}^{m-1}{s}^{\sigma-{k}-1}\frac{\partial^{{k}}{\mathbb{U}} (\eta,0)}{\partial\xi^{{k}}}+\mathcal{M}[\frac{\partial ^2\mathbb{V}_{1}(\eta ,\xi )}{\partial \eta^2}+\mathbb{V}_{1}(\eta ,\xi )\mathbb{W}_{1}(\eta ,\xi )]\Big],\\ {\mathbb{V}}_{2}(\eta ,\xi)& = {\mathbb{V}_{1}}(\eta ,\xi) +\mathcal{M}^{-1}\Big[\frac{1}{{s}^{\sigma}}\sum\limits_{{k} = 0}^{m-1}{s}^{\sigma-{k}-1}\frac{\partial^{{k}}{\mathbb{V}} (\eta,0)}{\partial\xi^{{k}}}+\mathcal{M}[-\frac{\partial ^2\mathbb{U}_{1}(\eta ,\xi )}{\partial \eta^2}-\mathbb{U}_{1}(\eta ,\xi )\mathbb{W}_{1}(\eta ,\xi )]\Big],\\ {\mathbb{W}}_{2}(\eta ,\xi)& = {\mathbb{W}_{1}}(\eta ,\xi) +\mathcal{M}^{-1}\Big[\frac{1}{{s}^{\sigma}}\sum\limits_{{k} = 0}^{m-1}{s}^{\sigma-{k}-1}\frac{\partial^{{k}}{\mathbb{W}} (\eta,0)}{\partial\xi^{{k}}}+\mathcal{M}[-6\mathbb{W}_{1}(\eta ,\xi )\frac{\partial \mathbb{W}_{1}(\eta ,\xi )}{\partial \eta }-\frac{\partial ^3\mathbb{W}_{1}(\eta ,\xi )}{\partial \eta^3}\\&+2\mathbb{U}_{1}(\eta ,\xi )\frac{\partial \mathbb{U}_{1}(\eta ,\xi )}{\partial \eta}+2\mathbb{V}_{1}(\eta ,\xi )\frac{\partial \mathbb{V}_{1}(\eta ,\xi )}{\partial \eta }]\Big]. \end{split} \end{equation}$

(4.17)

As a result of simplifying the expression, we arrive at the following final result:

$\begin{align} {\mathbb{U}}_{2}(\eta ,\xi)& = \cos (\eta) \tanh (\eta)+\frac{\xi^{\sigma} \left(16 \cos (\eta) \text{sech}^2(\eta)-17 \sin (\eta) \tanh (\eta)\right)}{8 \Gamma (\sigma +1)}\\ &-\frac{9 \Gamma (2 \sigma +1) \xi^{3 \sigma} \tanh (\eta) \text{sech}^2(\eta) \left(17 \cos (\eta) \tanh (\eta)+16 \sin (\eta) \text{sech}^2(\eta)\right)}{8 \Gamma (\sigma +1)^2 \Gamma (3 \sigma +1)}\\ &-\frac{\xi^{2 \sigma } \left(289 \cos (\eta) \tanh (\eta)+32 \text{sech}^2(\eta) (17 \sin (\eta)+2 \tanh (\eta) (8 \cos (\eta)+\sin (\eta) \tanh (\eta)))\right)}{64 \Gamma (2 \sigma +1)},\\ {\mathbb{V}}_{2}(\eta ,\xi)& = \frac{1}{64}\Big(64 \sin (\eta) \tanh (\eta)+\frac{8 \xi^{\sigma } \left(17 \cos (\eta) \tanh (\eta)+16 \sin (\eta) \text{sech}^2(\eta)\right)}{\Gamma (\sigma +1)}\\ &+\frac{72 \Gamma (2 \sigma +1) t^{3 \sigma } \tanh (\eta) \text{sech}^2(\eta) \left(16 \cos (\eta) \text{sech}^2(\eta)-17 \sin (\eta) \tanh (\eta)\right)}{\Gamma (\sigma +1)^2 \Gamma (3 \sigma +1)}\\ &+\frac{\xi^{2 \sigma } \left(32 \text{sech}^2(\eta) (17 \cos (\eta)+2 \tanh (\eta) (\cos (\eta) \tanh (\eta)-8 \sin (\eta)))-289 \sin (\eta) \tanh (\eta)\right)}{\Gamma (2 \sigma +1)}\Big),\\ {\mathbb{W}}_{2}(\eta ,\xi)& = \frac{\text{sech}^2(\eta)}{512}\Big(\frac{10624 \xi^{2 \sigma } (\cosh (2 \eta)-2) \text{sech}^2(\eta)}{\Gamma (2 \sigma +1)}\\ &+32 \left(-\frac{144 \xi^{\sigma } \tanh (\eta)}{\Gamma (\sigma +1)}-9 \cosh (2 \eta)+23\right)\\ &+\frac{\Gamma (2 \sigma +1) \xi^{3 \sigma } (-623550 \sinh (\eta)+123235 \sinh (3 \eta)+289 \sinh (5 \eta)) \text{sech}^5(\eta)}{\Gamma (\sigma +1)^2 \Gamma (3 \sigma +1)}\Big). \end{align}$

(4.18)

5. Graphical and tables discussion

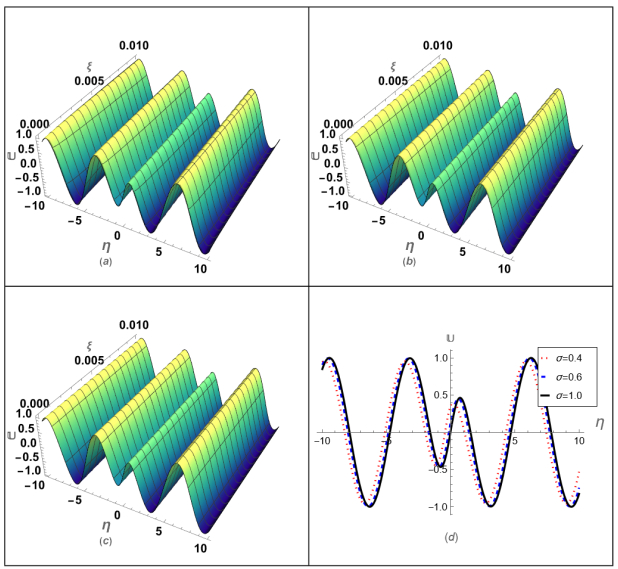
The research evaluates the graphical impact of fractional ordering effects on Schrödinger and KdV equation solutions by utilizing both VITM and q-HATM. represents how the solution ${\mathbb{U}}(\eta, \xi)$ reacts when fractional orders $\sigma$ increase. displays the solutions with corresponding fractional orders of 0.4, 0.6, and 1.0. Profile diagram analysis establishes that increasing the $\sigma$ value leads to significant changes in solution forms, which proves how fractional order fundamentally affects system dynamic behavior. shows solutions that illustrate transformations in system behavior across variable $\sigma$ values. The solutions of ${\mathbb{U}}(\eta, \xi)$ generated using q-HATM and VITM methods appear in . Examining the precision details of q-HATM and VITM through method comparison aids researchers to determine their applicability for fractional differential equation solutions. The analysis of ${\mathbb{U}}(\eta, \xi)$ for $\xi = 0.01$ appears in through q-HATM and VITM evaluation methods. The presented tabulated information permits an immediate comparison of accuracy and operational performance characteristics. demonstrates how the methods maintain their accuracy level in ${\mathbb{U}}(\eta, \xi)$ calculations when operating at $\xi = 0.01$ . The limited error ranges strengthen the reliability of both q-HATM and VITM for their capability to approximate solutions for fractional differential equations. presents the analysis of solution ${\mathbb{U}}(\eta, \xi)$ while varying fractional order parameters just like did. A unified comparison appears in while correspond respectively to the values $\sigma = 0.4$ , $\sigma = 0.6$ , and $\sigma = 1.0$ . The systematic variations confirm the high sensitivity of ${\mathbb{V}}(\eta, \xi)$ to modifications in $\sigma$ because FC impacts wave dynamics thoroughly. Such a figure depicts the q-HATM and VITM generated solutions of ${\mathbb{V}}(\eta, \xi)$ to demonstrate their match and mismatch points. Analytical methods in FC require such comparative assessments to validate their robustness. A thorough analysis of ${\mathbb{V}}(\eta, \xi)$ at the specific condition of $\xi = 0.01$ is presented in to display the results obtained from both methods to evaluate their performance characteristics. demonstrates the accuracy and reliability of employed methods to track fractional-order systems through absolute errors presented for ${\mathbb{V}}(\eta, \xi)$ evaluated at $\xi = 0.01$ . represents an examination of ${\mathbb{W}}(\eta, \xi)$ solutions by varying fractional order values. displays the solutions of the system when parameter $\sigma$ equals 0.4, 0.6, and 1.0. presents an overall comparison of the solutions. The graphical representations establish that the fractional parameter function is a primary influence that directs the solution's configuration. compares q-HATM and VITM solutions for ${\mathbb{W}}(\eta, \xi)$ , allowing assessment of method performance capabilities and constraints when used in fractional differential equations. showcases an extensive review of the ${\mathbb{W}}(\eta, \xi)$ solution at $\xi = 0.01$ through both methods to evaluate their operational capabilities and computational resource consumption. focuses on the absolute errors of ${\mathbb{W}}(\eta, \xi)$ , which strengthens the evidence regarding q-HATM and VITM as methods that produce accurate solutions for complex fractional systems with $\xi = 0.01$ . The tabular and graphical assessments demonstrate that q-HATM and VITM succeed efficiently in resolving fractional-order Schrödinger and KdV equations. These visualizations verify the fractional parameter sensitivities and show the accuracy and convergence of the proposed approaches that significantly benefit FC applications in mathematical physics and engineering.

Figure 1. Analysis of fractional-order and its effect on the approximate solution (a)

$\sigma = 0.4$ , (b)

$\sigma = 0.6$ , (c)

$\sigma = 1.0$ , and (d) comparison of various values of

$\sigma$ of the solution

${\mathbb{U}}(\eta, \xi)$ .

DownLoad: Full-Size Img PowerPoint

Figure 2. q-HMTM solution and MVIM solution comparison.

DownLoad: Full-Size Img PowerPoint

Table 1. Analysis of both methods for

$\mathbb{U}(\eta, \xi)$ at

$\xi = 0.01$ .

	$\mathbb{U}(\eta, \xi)$ for $\sigma=0.4$		$\mathbb{U}(\eta, \xi)$ for $\sigma=0.6$		$\mathbb{U}(\eta, \xi)$ for $\sigma=0.8$		$\mathbb{U}(\eta, \xi)$ for $\sigma=1.0$
$\eta$	q-HATM	VITM	q-HATM	VITM	q-HATM	VITM	q-HATM	VITM
0.5	0.36120935191	0.33861548115	0.44206697456	0.44097410128	0.42669166423	0.42664535753	0.41425805108	0.41425628931
1.0	0.07535823815	0.05590024405	0.32406890568	0.32312771582	0.38415640275	0.38411652310	0.40208860319	0.40208708594
1.5	-0.32972156568	-0.33284644536	-0.07709961858	-0.07725077008	0.01206320878	0.01205680426	0.04499401392	0.04499377026
2.0	-0.70578313652	-0.70388592079	-0.53169156256	-0.53159979358	-0.45236787232	-0.45236398393	-0.42032091350	-0.42032076556
2.5	-0.92543034468	-0.92376704004	-0.86907219111	-0.86899173649	-0.82382524949	-0.82382184051	-0.80321379853	-0.80321366884
3.0	-0.92017861851	-0.91938901088	-0.99124148703	-0.99120329343	-0.99167943639	-0.99167781807	-0.98805041295	-0.98805035138
3.5	-0.68816113531	-0.68788304269	-0.86729664860	-0.86728319717	-0.91298724593	-0.91298667597	-0.92716497971	-0.92716495802
4.0	-0.28644334453	-0.28637167633	-0.52912363819	-0.52912017157	-0.60860010156	-0.60859995468	-0.63700317136	-0.63700316578
4.5	0.18599199004	0.18600050937	-0.06065114716	-0.06065073508	-0.15431859025	-0.15431857279	-0.18993061663	-0.18993061597
5.0	0.61310384294	0.61309963502	0.42290082902	0.42290062548	0.33802542677	0.33802541815	0.30394877330	0.30394877298

| Show Table

DownLoad: CSV

Table 2. Comparison of absolute error of

$\mathbb{U}(\eta, \xi)$ at

$\xi = 0.01$ .

$\eta$	\| $q-HATM-VITM\|_{\sigma=0.4}$	\| $q-HATM-VITM\|_{\sigma=0.6}$	\| $q-HATM-VITM\|_{\sigma=0.8}$	\| $q-HATM-VITM\|_{\sigma=1.0}$
0.5	2.25939 $\times 10^{-2}$	1.09287 $\times 10^{-3}$	4.63067 $\times 10^{-5}$	1.76177 $\times 10^{-6}$
1.0	1.94580 $\times 10^{-2}$	9.41190 $\times 10^{-4}$	3.98796 $\times 10^{-5}$	1.51725 $\times 10^{-6}$
1.5	3.12488 $\times 10^{-3}$	1.51152 $\times 10^{-4}$	6.40452 $\times 10^{-6}$	2.43665 $\times 10^{-7}$
2.0	1.89722 $\times 10^{-3}$	9.17690 $\times 10^{-5}$	3.88839 $\times 10^{-6}$	1.47937 $\times 10^{-7}$
2.5	1.66330 $\times 10^{-3}$	8.04546 $\times 10^{-5}$	3.40898 $\times 10^{-6}$	1.29697 $\times 10^{-7}$
3.0	7.89608 $\times 10^{-4}$	3.81936 $\times 10^{-5}$	1.61832 $\times 10^{-6}$	6.15702 $\times 10^{-8}$
3.5	2.78093 $\times 10^{-4}$	1.34514 $\times 10^{-5}$	5.69958 $\times 10^{-7}$	2.16845 $\times 10^{-8}$
4.0	7.16682 $\times 10^{-5}$	3.46662 $\times 10^{-6}$	1.46886 $\times 10^{-7}$	5.58838 $\times 10^{-9}$
4.5	8.51933 $\times 10^{-6}$	4.12083 $\times 10^{-7}$	1.74606 $\times 10^{-8}$	6.64301 $\times 10^{-10}$
5.0	4.20793 $\times 10^{-6}$	2.03539 $\times 10^{-7}$	8.62425 $\times 10^{-9}$	3.28116 $\times 10^{-10}$

| Show Table

DownLoad: CSV

Figure 3. Analysis of fractional-order and its effect on the approximate solution (a)

$\sigma = 0.4$ , (b)

$\sigma = 0.6$ , (c)

$\sigma = 1.0$ , and (d) comparison of various values of

$\sigma$ of the solution

${\mathbb{V}}(\eta, \xi)$ .

DownLoad: Full-Size Img PowerPoint

Table 3. Analysis of both methods for

$\mathbb{V}(\eta, \xi)$ at

$\xi = 0.01$ .

	$\mathbb{V}(\eta, \xi)$ for $\sigma=0.4$		$\mathbb{V}(\eta, \xi)$ for $\sigma=0.6$		$\mathbb{V}(\eta, \xi)$ for $\sigma=0.8$		$\mathbb{V}(\eta, \xi)$ for $\sigma=1.0$
$\eta$	q-HATM	VITM	q-HATM	VITM	q-HATM	VITM	q-HATM	VITM
0.5	0.60780518968	0.62052294719	0.34873394344	0.34934910574	0.26672730729	0.26675337266	0.23789045679	0.23789144847
1.0	0.84275800769	0.83158438291	0.74172535549	0.74118488342	0.68218555413	0.68216265350	0.65652216132	0.65652129005
1.5	0.84963577507	0.83772282643	0.91892881087	0.91835257745	0.91395006747	0.91392565158	0.90758335221	0.90758242329
2.0	0.61966595118	0.61463070669	0.80836697215	0.80812341564	0.85497350506	0.85496318520	0.86911108695	0.86911069433
2.5	0.21537795275	0.21406841731	0.46328353857	0.46322019589	0.54469938306	0.54469669913	0.57383336205	0.57383325994
3.0	-0.25290584226	-0.25302592632	-0.00986821399	-0.00987402250	0.08371570260	0.08371545649	0.11947978154	0.11947977217
3.5	-0.66337152497	-0.66326844271	-0.48495767029	-0.48495268416	-0.40309544956	-0.40309523829	-0.36995510627	-0.36995509823
4.0	-0.91250404947	-0.91242128204	-0.84211744513	-0.84211344164	-0.79227766347	-0.79227749384	-0.77002506874	-0.77002506229
4.5	-0.93836059593	-0.93832117785	-0.99302480260	-0.99302289593	-0.98744366518	-0.98744358439	-0.98155603065	-0.98155602757
5.0	-0.73441447988	-0.73440024598	-0.90064889998	-0.90064821148	-0.94067965898	-0.94067962980	-0.95259683520	-0.95259683409

| Show Table

DownLoad: CSV

Table 4. Comparison of absolute error of

$\mathbb{V}(\eta, \xi)$ at

$\xi = 0.01$ .

$\eta$	\| $q-HATM-VITM\|_{\sigma=0.4}$	\| $q-HATM-VITM\|_{\sigma=0.6}$	\| $q-HATM-VITM\|_{\sigma=0.8}$	\| $q-HATM-VITM\|_{\sigma=1.0}$
0.5	1.27178 $\times 10^{-2}$	6.15162 $\times 10^{-4}$	2.60654 $\times 10^{-5}$	9.91676 $\times 10^{-7}$
1.0	1.11736 $\times 10^{-2}$	5.40472 $\times 10^{-4}$	2.29006 $\times 10^{-5}$	8.71271 $\times 10^{-7}$
1.5	1.19129 $\times 10^{-2}$	5.76233 $\times 10^{-4}$	2.44159 $\times 10^{-5}$	9.28921 $\times 10^{-7}$
2.0	5.03524 $\times 10^{-3}$	2.43557 $\times 10^{-4}$	1.03199 $\times 10^{-5}$	3.92627 $\times 10^{-7}$
2.5	1.30954 $\times 10^{-3}$	6.33427 $\times 10^{-5}$	2.68393 $\times 10^{-6}$	1.02112 $\times 10^{-7}$
3.0	1.20084 $\times 10^{-4}$	5.80851 $\times 10^{-6}$	2.46115 $\times 10^{-7}$	9.36364 $\times 10^{-9}$
3.5	1.03082 $\times 10^{-4}$	4.98612 $\times 10^{-6}$	2.11270 $\times 10^{-7}$	8.03791 $\times 10^{-9}$
4.0	8.27674 $\times 10^{-5}$	4.00349 $\times 10^{-6}$	1.69634 $\times 10^{-7}$	6.45385 $\times 10^{-9}$
4.5	3.94181 $\times 10^{-5}$	1.90667 $\times 10^{-6}$	8.07884 $\times 10^{-8}$	3.07365 $\times 10^{-9}$
5.0	1.42339 $\times 10^{-5}$	6.88499 $\times 10^{-7}$	2.91727 $\times 10^{-8}$	1.10990 $\times 10^{-9}$

| Show Table

DownLoad: CSV

Figure 4. q-HMTM solution and MVIM solution comparison.

DownLoad: Full-Size Img PowerPoint

Figure 5. Analysis of fractional-order and its effect on the approximate solution (a)

$\sigma = 0.4$ , (b)

$\sigma = 0.6$ , (c)

$\sigma = 1.0$ , and (d) comparison of various values of

$\sigma$ of the solution

${\mathbb{W}}(\eta, \xi)$ .

DownLoad: Full-Size Img PowerPoint

Figure 6. q-HMTM solution and MVIM solution comparison.

DownLoad: Full-Size Img PowerPoint

Table 5. Analysis of both methods for

$\mathbb{W}(\eta, \xi)$ at

$\xi = 0.01$ .

	$\mathbb{W}(\eta, \xi)$ for $\sigma=0.4$		$\mathbb{W}(\eta, \xi)$ for $\sigma=0.6$		$\mathbb{W}(\eta, \xi)$ for $\sigma=0.8$		$\mathbb{W}(\eta, \xi)$ for $\sigma=1.0$
$\eta$	q-HMTM	MVIM	q-HMTM	MVIM	q-HMTM	MVIM	q-HMTM	MVIM
0.5	-0.29452181924	-0.51342166394	0.19573362966	0.18514536901	0.35709374782	0.35664510709	0.41489347445	0.41487640557
1.0	-0.62532024144	-0.41562069162	-0.46502454994	-0.45488131071	-0.35984039106	-0.35941060656	-0.31351534831	-0.31349899683
1.5	-0.87911318876	-0.78529480710	-0.84778711073	-0.84324908340	-0.80087565389	-0.80068337076	-0.77803436109	-0.77802704554
2.0	-1.02249937462	-1.00232347897	-1.01751300066	-1.01653708566	-0.99907327449	-0.99903192349	-0.98969712693	-0.98969555370
2.5	-1.08541848196	-1.08166996825	-1.08466122354	-1.08447990665	-1.07771610556	-1.07770842288	-1.07412383315	-1.07412354085
3.0	-1.11017160848	-1.10940271801	-1.11004963325	-1.11001244175	-1.10747278314	-1.10747120728	-1.10613130885	-1.10613124890
3.5	-1.11950807646	-1.11931399352	-1.11948496307	-1.11947557521	-1.11853403114	-1.11853363336	-1.11803779954	-1.11803778440
4.0	-1.12297460963	-1.12291554550	-1.12296908001	-1.12296622306	-1.12261885089	-1.12261872984	-1.12243592637	-1.12243592177
4.5	-1.12425421872	-1.12423417578	-1.12425258832	-1.12425161883	-1.12412369198	-1.12412365090	-1.12405634751	-1.12405634595
5.0	-1.12472555004	-1.12471840557	-1.12472500497	-1.12472465939	-1.12467757932	-1.12467756467	-1.12465279786	-1.12465279730

| Show Table

DownLoad: CSV

Table 6. Comparison of absolute error of

$\mathbb{W}(\eta, \xi)$ at

$\xi = 0.01$ .

$\eta$	\| $q-HMTM-MVIM\|_{\sigma=0.4}$	\| $q-HMTM-MVIM\|_{\sigma=0.6}$	\| $q-HMTM-MVIM\|_{\sigma=0.8}$	\| $q-HMTM-MVIM\|_{\sigma=1.0}$
0.5	2.18900 $\times 10^{-1}$	1.05883 $\times 10^{-2}$	4.48641 $\times 10^{-4}$	1.70689 $\times 10^{-5}$
1.0	2.09700 $\times 10^{-1}$	1.01432 $\times 10^{-2}$	4.29784 $\times 10^{-4}$	1.63515 $\times 10^{-5}$
1.5	9.38184 $\times 10^{-2}$	4.53803 $\times 10^{-3}$	1.92283 $\times 10^{-4}$	7.31556 $\times 10^{-6}$
2.0	2.01759 $\times 10^{-2}$	9.75915 $\times 10^{-4}$	4.13510 $\times 10^{-5}$	1.57323 $\times 10^{-6}$
2.5	3.74851 $\times 10^{-3}$	1.81317 $\times 10^{-4}$	7.68267 $\times 10^{-6}$	2.92293 $\times 10^{-7}$
3.0	7.68890 $\times 10^{-4}$	3.71915 $\times 10^{-5}$	1.57586 $\times 10^{-6}$	5.99548 $\times 10^{-8}$
3.5	1.94083 $\times 10^{-4}$	9.38786 $\times 10^{-6}$	3.97778 $\times 10^{-7}$	1.51338 $\times 10^{-8}$
4.0	5.90641 $\times 10^{-5}$	2.85695 $\times 10^{-6}$	1.21053 $\times 10^{-7}$	4.60557 $\times 10^{-9}$
4.5	2.00429 $\times 10^{-5}$	9.69484 $\times 10^{-7}$	4.10785 $\times 10^{-8}$	1.56286 $\times 10^{-9}$
5.0	7.14447 $\times 10^{-6}$	3.45580 $\times 10^{-7}$	1.46428 $\times 10^{-8}$	5.57095 $\times 10^{-10}$

| Show Table

DownLoad: CSV

6. Conclusions

This research investigated the solution of Schrödinger and KdV equations using q-HATM and VITM under fractional-order differential equations. I changed nonlinear equations using Caputo fractional operator into efficient iterative algorithms for obtaining series solutions that showed rapid convergence. The two methods used for solving fractional differential equations showed ease of calculation while delivering precise results and confirmed the validity of obtained solutions through their established effectiveness. The utilized methods delivered powerful solutions for solving difficult wave oscillation and radiation problems. The research examined how fractional-order parameters shape nonlinear wave model dynamics, whereas FC proved essential for mathematical physics and engineering fields. The results highlighted the understanding of fractional-order parameters' influence on the dynamics of nonlinear wave models and deepened the appreciation of FC in mathematical physics and engineering. The proposed techniques that garnered attention from graphical illustrations increased confidence in numerically solving essential components of wave representation. These results can be further built upon by applying them to multidimensional and multi-order nonlinearity models, extending their reach across disciplines, including engineering and science.

Use of Generative-AI tools declaration

The author declares that he has not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The author declares that he has no conflict of interest.

References

[1]	Goudos SK, Kalialakis C, Mittra R (2016) Evolutionary algorithms applied to antennas and propagation: A review of state of the art. International Journal of Antennas and Propagation.
[2]	Hoorfar A (2007) Evolutionary programming in electromagnetic optimization: a review. IEEE T Antenn Propag 55: 523-537. doi: 10.1109/TAP.2007.891306
[3]	Rahmat-Samii Y, Kovitz JM, Rajagopalan H (2012) Nature-inspired optimization techniques in communication antenna designs. Proceedings of the IEEE 100: 2132-2144. doi: 10.1109/JPROC.2012.2188489
[4]	Johnson JM, Rahmat-Samii Y (1997) Genetic algorithms in engineering electromagnetic. IEEE Antenn Propag M 39: 7-21.
[5]	Weile DS, Michielssen E (1997) Genetic algorithm optimization applied to electromagnetics: A review. IEEE T Antenn Propag 45: 343-353. doi: 10.1109/8.558650
[6]	Haupt RL, Werner DH (2007) Genetic algorithms in electromagnetic. John Wiley & Sons.
[7]	Robinson J, Rahmat-Samii Y (2004) Particle swarm optimization in electromagnetic. IEEE T Antenn Propag 52: 397-407. doi: 10.1109/TAP.2004.823969
[8]	Karimkashi S, Kishk AA (2010) Invasive weed optimization and its features in electromagnetic. IEEE T Antenn Propag 58: 1269-1278. doi: 10.1109/TAP.2010.2041163
[9]	Rocca P, Oliveri G, Massa A (2011) Differential evolution as applied to electromagnetic. IEEE Antenn Propag M 53: 38-49. doi: 10.1109/MAP.2011.5773566
[10]	Villegas FJ, Cwik T, Rahmat-Samii Y, et al. (2004) A parallel electromagnetic genetic-algorithm optimization (EGO) application for patch antenna design. IEEE T Antenn Propag 52: 2424-2435. doi: 10.1109/TAP.2004.834071
[11]	Jayasinghe JM, Uduwawala D (2015) A Novel Multiband Miniature Planar Inverted F Antenna Design for Bluetooth and WLAN Applications. Int J Antenn Propag.
[12]	Sun SY (2009) Design of broadband microstrip antenna utilizing genetic algorithm. In International Symposium on Electromagnetic Compatibility.
[13]	John M, Ammann M (2006) Design of a wide-band printed antenna using a genetic algorithm on an array of overlapping sub-patches. IEEE Int Workshop on Antenna Technol.: Small Antennas and Novel Metamaterials (IWAT2006).
[14]	Mishra RG, Mishra R, Kuchhal P, et al. (2017) Optimization and analysis of high gain wideband microstrip patch antenna using genetic algorithm. International Journal of Engineering & Technology 7: 176-179.
[15]	Jayasinghe JW (2014) Optimization of the performance of microstrip patch antennas and arrays by using genetic algorithms. Ph.D. Thesis, University of Peradeniya.
[16]	Soontornpipit P, Furse CM, Chung YC (2005) Miniaturized biocompatible microstrip antenna using genetic algorithm. IEEE T Antenn Propag 53: 1939-1945. doi: 10.1109/TAP.2005.848461
[17]	Heidari AA, Dadgarnia A (2011) Design and optimization of a circularly polarized microstrip antenna for GPS applications using ANFIS and GA. General Assembly and Scientific Symposium, XXXth URSI, 1-4. IEEE.
[18]	Gupta R, Gurjar S, Kumar A (2013) Using genetic algorithms reduction of rectangular microstrip patches. International Journal of Advanced Research in Computer and Communication Engineering 2: 1643-1646.
[19]	Jayasinghe JW, Anguera J, Uduwawala DN (2012) A simple design of multi band microstrip patch antennas robust to fabrication tolerances for GSM, UMTS, LTE, and Bluetooth applications by using genetic algorithm optimization. Progress In Electromagnetics Research M 27: 255-269. doi: 10.2528/PIERM12102705
[20]	Jayasinghe JM, Anguera J, Uduwawala DN, et al. (2015) Nonuniform Overlapping Method in Designing Microstrip Patch Antennas Using Genetic Algorithm Optimization. Int J Antenn Propag.
[21]	Choo H, Hutani A, Trintinalia LC, et al. (2000) Shape optimisation of broadband microstrip antennas using genetic algorithm. Electron Lett 36: 2057-2058. doi: 10.1049/el:20001452
[22]	Griffiths LA, Furse C, Chung YC (2006) Broadband and multiband antenna design using the genetic algorithm to create amorphous shapes using ellipses. IEEE T Antenn Propag 54: 2776-2782. doi: 10.1109/TAP.2006.882154
[23]	Polivka M, Drahovzal M, Rohan J, et al. (2006) Multiband patch antenna with perturbation elements generated by genetic algorithm. In 2006 First European Conference on Antennas and Propagation, 1-4.
[24]	Xiao S, Wang BZ, Yang XS, et al. (2003) Reconfigurable microstrip antenna design based on genetic algorithm. IEEE Antennas and Propagatopm Society International Symposium 1: 407-410.
[25]	Wyant A, Venkataraman J (2008) Optimization of Reduced Size Microstrip Patch with slots using a Genetic Algorithm. Dept. of Electrical Engineering, Rochester Institute of Technology.
[26]	Alatan L, Aksun MI, Leblebicioglu K, et al. (1999) Use of computationally efficient method of moments in the optimization of printed antennas. IEEE T Antenn Propag 47: 725-732. doi: 10.1109/8.768813
[27]	Kerkhoff AJ, Rogers RL, Ling H (2004) Design and analysis of planar monopole antennas using a genetic algorithm approach. IEEE T Antenn Propag 52: 2709-2718. doi: 10.1109/TAP.2004.834429
[28]	Koziel S, Jayasinghe JW, Saraereh O, et al. (2017) Local Optimization of a Sierpinski Carpet Fractal Antenna, IEEE 12th International Conference on Industrial and Information Systems, 1-5.
[29]	Behera BR (2017) Sierpinski Bow-Tie antenna with genetic algorithm. Engineering Science and Technology 20: 775-782.
[30]	Adelpour Z, Mohajeri F, Sadeghi M (2010) Dual-frequency microstrip patch antenna with modified Koch fractal geometry based on genetic algorithm. 2010 Loughborough Antennas and Propagation Conference (LAPC), 401-404.
[31]	Spence TG, Werner DH (2004) Genetically optimized fractile microstrip patch antennas. In IEEE Antennas and Propagation Society International Symposium 4: 4424-4427.
[32]	Ozgun O, Mutlu S, Aksun MI, et al. (2003) Design of dual-frequency probe-fed microstrip antennas with genetic optimization algorithm. IEEE T Antenn Propag 51: 1947-1954. doi: 10.1109/TAP.2003.814732
[33]	Namkung J, Hines EL, Green RJ, et al. (2007) Probe‐fed microstrip antenna feed point optimization using a genetic algorithm and the method of moments. Microw Opt Techn Lett 49: 325-329. doi: 10.1002/mop.22120
[34]	Lu Q, Edward K, Sean D, et al. (2009) Optimum design of a probe fed dual frequency patch antenna using genetic algorithm. Proceedings of the ARMMS RF and Microwave Society.
[35]	Raychowdhury A, Gupta B, Bhattacharjee R (2000) Bandwidth improvement of microstrip antennas through a genetic‐algorithm‐based design of a feed network. Microw Opt Techn Lett 27: 273-275. doi: 10.1002/1098-2760(20001120)27:4<273::AID-MOP17>3.0.CO;2-8
[36]	Chattoraj N, Roy GS (2006) Application of Genetic Algorithm to the Optimization of Microstrip Antennas with and without Superstrate. Mikrotalasna revija, 32-35.
[37]	Aljibouri B, Lim EG, Evans H, et al. (2000) Multiobjective genetic algorithm approach for a dual-feed circular polarised patch antenna design. Electron Lett 36: 1005-1006. doi: 10.1049/el:20000766
[38]	Raychowdhury A, Gupta B, Bhattacharjee R (2000) Bandwidth improvement of microstrip antennas through a genetic‐algorithm‐based design of a feed network. Microw Opt Techn Lett 27: 273-275. doi: 10.1002/1098-2760(20001120)27:4<273::AID-MOP17>3.0.CO;2-8
[39]	Mukherjee P, Gupta B (2005) Genetic algorithm-based design optimisation of aperture-coupled rectangular microstrip antenna. Defence Sci J 55: 487. doi: 10.14429/dsj.55.2011
[40]	Ding M, Jin R, Geng J (2007) Optimal design of ultra wideband antennas using a mixed model of 2‐D genetic algorithm and finite‐difference time‐domain. Microw Opt Techn Lett 49: 3177-3180. doi: 10.1002/mop.22928
[41]	Silva CRM, Lins HWC, Martins SR, et al. (2012) A multiobjective optimization of a UWB antenna using a self organizing genetic algorithm. Microw opt Tech let 54: 1824-1828. doi: 10.1002/mop.26945
[42]	Kim J, Yoon T, Kim J, et al. (2005) Design of an ultra wide-band printed monopole antenna using FDTD and genetic algorithm. IEEE Microw Wirel Co 15: 395-397. doi: 10.1109/LMWC.2005.850468
[43]	Pourahmadazar J, Shirzad H, Ghobadi C, et al. (2010) Using a MAM and genetic algorithm to optimize UWB microstrip monopole antenna with FEM and HFSS. 5th International Symposium on Telecommunications (IST), 115-119.
[44]	John M, Ammann MJ (2007) Wideband printed monopole design using a genetic algorithm. IEEE Antenn Wirel Pr 6: 447-449. doi: 10.1109/LAWP.2007.891962
[45]	Sun S, Yinghua LV, Zhang J (2010) The application of genetic algorithm optimization in broadband microstrip antenna design. Antennas and Propagation Society International Symposium (APSURSI), 1-4.
[46]	Michael K, Kucharski AA (2006) Genetic algorithm optimization for broadband patch antenna design. International Conf. on Microwaves, Radar & Wireless Communications, 748-751.
[47]	Sun S, Yinghua LV, Zhang J (2010) The application of genetic algorithm optimization in broadband microstrip antenna design. Antennas and Propagation Society International Symposium (APSURSI), 1-4.
[48]	Deshmukh AA, Kumar G (2005) Compact broadband U‐slot‐loaded rectangular microstrip antennas. Microw Opt Techn Lett 46: 556-559. doi: 10.1002/mop.21049
[49]	Johnson JM, Rahmat-Samii Y (1999) Genetic algorithms and method of moments (GA/MOM) for the design of integrated antennas. IEEE T Antenn Propag 47: 1606-1614. doi: 10.1109/8.805906
[50]	Noor AOA (2015) An Automated Optimization Technique of a MSPA for Broadband Communication. Eng Tech J 33.
[51]	Lech M, Mitchell A, Waterhouse R (2000) Optimization of broadband microstrip patch antennas. Asia-Pacific Microwave Conference, 711-714.
[52]	Lotfi AA, Kashani FH (2004) Bandwidth optimization of the E-shaped microstrip antenna using the genetic algorithm based on fuzzy decision making. Antennas and Propagation Society International Symposium 3: 2333-2336. doi: 10.1109/APS.2004.1331839
[53]	Bulla G, de Salles AA, Vuong TP (2010) PIFA bandwidth optimization using genetic algorithm and capacitive feeding. IEEE International Conference on Wireless Information Technology and Systems (ICWITS), 1-4.
[54]	Nguyen TD, Duroc Y, Vuong TP (2011) Genetic algorithm for optimization of L-shaped PIFA antennas. Int J Microw Wirel T 3: 691-699. doi: 10.1017/S1759078711000985
[55]	Chandran PP, Viswasom S (2014) Gain and bandwidth optimization of a novel microstrip patch antenna. Fourth International Conference on Advances in Computing and Communications (ICACC), 315-318.
[56]	Tseng LY, Han TY (2010) An evolutionary design method using genetic local search algorithm to obtain broad/dual-band characteristics for circular polarization slot antennas. IEEE T Antenn Propag 58: 1449-1456. doi: 10.1109/TAP.2010.2044312
[57]	Spence TG, Werner DH, Groff RD (2004) Genetic algorithm optimization of some novel broadband and multiband microstrip antennas. Antennas and Propagation Society International Symposium 4: 4408-4411. doi: 10.1109/APS.2004.1330329
[58]	Jayasinghe JW, Anguera J, Uduwawala DN, et al. (2017) A multipurpose genetically engineered microstrip patch antennas: Bandwidth, gain, and polarization. Microw Opt Techn Lett 59: 941-949. doi: 10.1002/mop.30439
[59]	Choo H, Ling H (2003) Design of broadband and dual-band microstrip antennas on a high-dielectric substrate using a genetic algorithm. IEE Proceedings-Microwaves, Antennas and Propagation 150: 137-142. doi: 10.1049/ip-map:20030291
[60]	Fertas K, Kimouche H, Challal M, et al. (2015) Design and optimization of a CPW-fed tri-band patch antenna using genetic algorithms. ACES Journal 30: 754-759.
[61]	Wakrim L, Ibnyaich S, Hassani M (2016) Novel Miniaturized Multiband and Wideband PIFA Antenna for Wireless Applications. 3rd International Conference on Automation, Control, Engineering and Computer Science, 3-6.
[62]	Choo H, Ling H ((2002) Design of multiband microstrip antennas using a genetic algorithm. IEEE Microw Wirel Co 12: 345-347. doi: 10.1109/LMWC.2002.803144
[63]	Ohira M, Deguchi H, Tsuji M, et al. (2004) Multiband single-layer frequency selective surface designed by combination of genetic algorithm and geometry-refinement technique. IEEE T Antenn Propag 52: 2925-2931. doi: 10.1109/TAP.2004.835289
[64]	Sathi V, Taherizadeh S, Lotfi A, et al. (2010) Optimisation of multi-frequency microstrip antenna using genetic algorithm coupled with method of moments. IET Microw Antennas P 4: 477-483. doi: 10.1049/iet-map.2009.0020
[65]	Michael K, Kucharski AA (2006) Genetic algorithm optimization for Multiband patch antenna design. First European Conference on Antennas and Propagation, 1-4.
[66]	Werner DH, Werner PL, Church KH (2001) Genetically engineered multiband fractal antennas. Electron Lett 37: 1150-1151. doi: 10.1049/el:20010802
[67]	Ozgun O, Mutlu S, Aksun ML, et al. (2003) Design of dual-frequency probe-fed microstrip antennas with genetic optimization algorithm. IEEE T Antenn Propag 51: 1947-1954. doi: 10.1109/TAP.2003.814732
[68]	Griffiths L, Chung YC, Furse C (2005) Integrated dual band GSM microstrip monopole using GA and FDTD. Antennas and Propagation Society International Symposium 4: 48-51.
[69]	Lu Q, Korolkiewicz E, Danaher S, et al. (2009) Optimum design of a probe fed dual frequency patch antenna using genetic algorithm.
[70]	Villegas FJ, Cwik T, Rahmat-Samii Y, et al. (2002) Parallel genetic-algorithm optimization of a dual-band patch antenna for wireless communications. IEEE Antennas and Propagation Society International Symposium 1: 334-337. doi: 10.1109/APS.2002.1016316
[71]	Castellana F, Bilotti F, Vegni L (2001) Automated dual band patch antenna design by a genetic algorithm based numerical code. IEEE Antennas and Propagation Society International Symposium 4: 696-699.
[72]	Fertas K, Kimouche H, Challal M, et al. (2015) An optimized shaped antenna for multiband applications using Genetic Algorithm. 4th International Conference on Electrical Engineering (ICEE), 1-4.
[73]	Saxena NK, Khan MA, Pourush PKS, et al. (2011) GA optimization of cutoff frequency of magnetically biased microstrip circular patch antenna. AEU-Int J Electron C 65: 476-479. doi: 10.1016/j.aeue.2010.04.008
[74]	Herscovici N, Osorio MF, Peixeiro C (2002) Miniaturization of rectangular microstrip patches using genetic algorithms. IEEE Antenn Wirel Pr 1: 94-97. doi: 10.1109/LAWP.2002.805128
[75]	Lamsalli M, El Hamichi A, Boussouis M, et al. (2016) Genetic algorithm optimization for microstrip patch antenna miniaturization. Prog Electrom Res LE 60: 113-120. doi: 10.2528/PIERL16041907
[76]	Gupta VR, Gupta N (2006) Realization of a compact microstrip antenna: An optimization approach. Int J RF and Microw C E 16: 367-373. doi: 10.1002/mmce.20157
[77]	Chattoraj N, Roy JS (2007) Application of Genetic Algorithm to the Optimization of Gain of Magnetized Ferrite Microstrip Antenna. Eng let 14.
[78]	Kim D, Ju J, Choi J (2012) A mobile communication base station antenna using a genetic algorithm based Fabry-Perot resonance optimization. IEEE T Antenn Propag 60: 1053-1058. doi: 10.1109/TAP.2011.2173108
[79]	Jayasinghe JW, Anguera J, Uduwawala DN (2013) A high-directivity microstrip patch antenna design by using genetic algorithm optimization. Progress In Electromagnetics Research C 37: 131-144. doi: 10.2528/PIERC13010805
[80]	Chattoraj N, Roy JS (2006) The optimization of gain of patch antennas using Genetic Algorithm. ACTA TECHNICA CSAV 51: 279.
[81]	Zhu X, Shao W, Li JL, et al. (2012) Design and optimization of low RCS patch antennas based on a genetic algorithm. Progress In Electromagnetics Research 122: 327-339. doi: 10.2528/PIER11100703
[82]	Mittra R (1997) Genetic algorithm: the last word for solving all of your design problems. Antennas and Propagation Society International Symposium 3: 1672-1675.
[83]	Lu Q, Edward K, Sean D, et al. (2010) Optimum design of a probe fed dual frequency patch antenna using genetic algorithm. ARMMS RF and Microwave Society, 20-21.
[84]	Kim Y, Yun W, Yoon Y (1999) Dual-frequency and dual-polarisation wideband microstrip antenna. Electron Lett 35: 1399-1400. doi: 10.1049/el:19990995
[85]	Jayasinghe J, Anguera J, Uduwawala D (2015) On the behavior of several fitness functions for genetically optimized microstrip antennas. Int J Sci World 3: 53-58. doi: 10.14419/ijsw.v3i1.4132
[86]	Lee D, Lee S (2000) Design of a coaxially fed circularly polarized rectangular microstrip antenna using a genetic algorithm. Microw Opt Techn Lett 26: 288-291. doi: 10.1002/1098-2760(20000905)26:5<288::AID-MOP4>3.0.CO;2-U
[87]	See CH, Abd-Alhameed RA, Zhou D, et al. (2006) A new design of circularly-polarised conical-beam microstrip patch antennas using a genetic algorithm. First European Conference on Antennas and Propagation, 1-4.
[88]	Zentner R, Sipus Z, Bartolic J (2001) Optimization synthesis of broadband circularly polarized microstrip antennas by hybrid genetic algorithm. Microw Opt Tech Lett 31: 197-201. doi: 10.1002/mop.1397
[89]	Grimaccia F, Mussetta M, Pirinoli P, et al. (2006) Genetical swarm optimization (GSO): A class of population-based algorithms for antenna design. ICCE'06 First International Conference on Communications and Electronics, 467-471.
[90]	Günel T, Erer I (2002) Application of fuzzy genetic algorithm to the problem of synthesizing circular microstrip antenna elements with thick substrates. AEU-Int J Electron C 56: 215-217. doi: 10.1078/1434-8411-54100099
[91]	Zhang YJ, Gong SX, Wang X, et al. (2010) A hybrid genetic-algorithm space-mapping method for the optimization of broadband aperture-coupled asymmetrical U-shaped slot antennas. J Electromagnet Waves 24: 2139-2153. doi: 10.1163/156939310793699118
[92]	Pissoort D, Rogier H, Olyslager F, et al. (2003) Optimization of a microstrip antenna with a genetic algorithm for use as a ground penetrating radar. J Electromagnet Waves 17: 1197-1216. doi: 10.1163/156939303322519829
[93]	Akila M, Anusha P, Sindhu M, et al. (2017) Examination of PSO, GA-PSO and ACO algorithms for the design optimization of printed antennas. IEEE Applied Electromagnetics Conference, 1-2.
[94]	Mishra S, Chattopadyay S, Gangopadhyaya M (2015) A comparative study of DE, PSO and BFO for optimisation of Rectangular Microstrip Patch Antenna with inset feed parameter. International Conference and Workshop on Computing and Communication (IEMCON), 1-7.
[95]	Boada DFM, Sakomura ES, Nascimento DC (2021) Cavity model surrogate-based optimization for electrically thick circularly polarized rectangular microstrip antennas. AEU-Int J Electron C 131: 153597. doi: 10.1016/j.aeue.2020.153597
[96]	Koziel S, Bekasiewicz A (2016) Multi-objective design of antennas using surrogate models. World Scientific.
[97]	Lee W, Jung M, Kim TH, et al. (2020) Patch antenna design using the GA and the binary method for dual-band applications. J Electromagnet Waves 34: 1691-1704. doi: 10.1080/09205071.2020.1781697
[98]	Awan WA, Zaidi A, Hussain M, et al. (2021) The Design of a Wideband Antenna with Notching Characteristics for Small Devices Using a Genetic Algorithm. Mathematics 9: 2113. doi: 10.3390/math9172113

Reader Comments

Your name:*

Email:*
© 2021 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)