Effect of chitosan nanoparticles on quorum sensing-controlled virulence factors and expression of LasI and RhlI genes among Pseudomonas aeruginosa clinical isolates

1.   Introduction

The objective of combating climate change has forced governments and other agencies around the world to set plans to transform the conventional power system into low-carbon power systems ^[1]. This process presents a unique opportunity for the rapid development of renewable energy sources (RES) such as wind power. However, it also poses enormous technical challenges for power systems, especially from a viewpoint of frequency stability ^[2,3,4].

One of the reasons is that wind turbine generator (WTG) is connected by electronic devices. Most WTGs inherently provide either no inertial response or frequency regulation. In addition, the massive deployment of WTG is realized by displacement of large numbers of conventional generators. The deployment of WTGs would lead to further deterioration in both system frequency control and inertial response ^[5]. Therefore, to ensure a secure transition to future low-carbon electricity systems with high penetration of wind power, two requirements are established for power system frequency response. (i) Conventional generators should provide more flexible frequency regulation service for a wider frequency deviation ranges. (ii) The WTGs should undertake more responsibility for power system frequency response. Various frequency regulation control strategies for WTGs have been proposed to help WTGs operating like conventional power generators as in references ^[6,7,8,9,10]. Compared with conventional generators, the unpredictable and intermittent nature of wind power should be considered. Therefore, the participation of WTGs in power system frequency control needs to be further studied and new techniques required to be developed.

In our previous work ^[11], a variogram function is proved to be a useful tool to depict the variation characteristics of wind power, after which a three-parameter power-law model is established for estimating wind power variations. In ^[12], we use the three-parameter power-law model to predict the wind power variations in AGC control time-scale. An AGC feedforward control strategy for conventional generators is proposed. In ^[12], the AGC power set value can be advancingly adjusted before the wind power variation really occurs, based on the anticipated wind power variations. Then, the AGC units can respond in advance to match the imbalance between generation and load to improve system operational performance. However, the variation rates in generation are larger now with the increasing integration of wind power generation ^[13]. This leads to the fact that conventional AGC units may not be able to follow these variations as tightly as desired, which also results in the increase of system frequency deviations. As a result, the coordination feedforward control of both WTGs and conventional AGC units has a significant impact on system operational performance.

MPC is a new computer control algorithm proposed in the field of industrial process control in the 1970s. It is widely used in various fields because it is convenient for modeling with good dynamic performance and stability ^[14]. In recent years, stochastic MPC ^[15], centralized MPC ^[16], decentralized MPC ^[17], and distributed MPC ^[18] and other improved algorithms are used in frequency control of multi-area interconnected power systems. However, the above methods are mainly focused on the controlling of conventional generators, where wind farms are actively participating. In this paper, MPC is chosen as the control algorithm to realize the feedforward control for both WTGs and conventional AGC units. Two problems are mainly focused. The first one is to predicate the variations of wind power more accurately. The second one is to use the wind power prediction information to make wind power generators provide more stable and flexible frequency response capacities. To solve these problems, variations of wind power is predicted based on variogram function and used in MPC controller to improve system frequency response performance.

This paper is organized as follows. Section 2 presents the frequency response model of regional power system with wind power. Section 3 proposes a strategy of wind farm participating in AGC based on the characteristics of wind power variations. Section 4 presents simulations and the performance of the control strategy under different conditions. Conclusions are presented in Section 5.

2.   Frequency response model of regional power system with large-scale wind power integration

In this paper, the WTGs are considered participating in AGC system. Then, a multi-area frequency response model with large scale wind power is established.

2.1.   Frequency response model of the $i$-th area

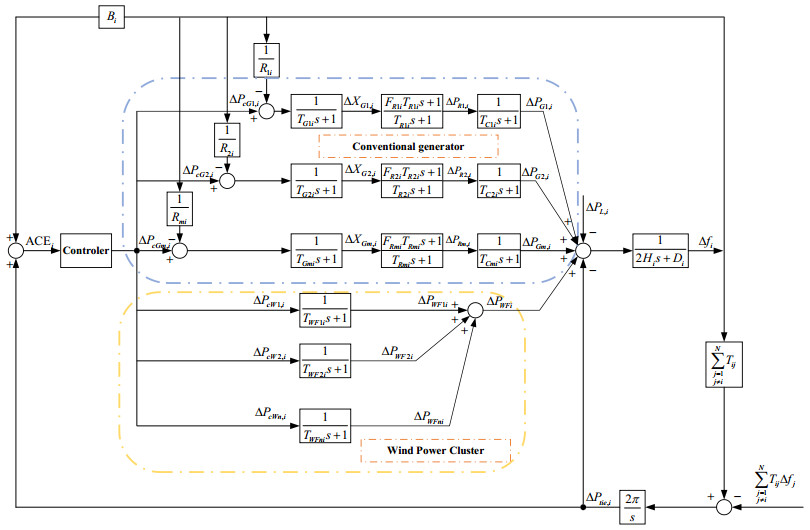
Consider that the interconnected power system is composed of $N$ areas. The frequency response model of area $i$ is shown in Figure 1 ^[19].

In this paper, the wind farm is considered as one equivalent wind farm in the AGC model since the control strategy is presented with respect to a wind-farm level. The detailed state equation of AGC system for area $i$ is as follows.

In this paper, $AC{E}_{i}$ is selected as the output of area $i$. The output equation can be obtained as follow:

where, ${\beta }_{i}$ is the area frequency deviation coefficient. $\varDelta {f}_{i}$ is the frequency deviation of area i. $\varDelta {P}_{tie, i}$ is the exchange power deviation of the tie-line. $\varDelta {X}_{Gk, i}$ is the variation of thermal generator governor position. $\varDelta {P}_{Rk, i}$ is power variation of re-heat turbine. ${\sum }_{k = 1}^{m}\varDelta {P}_{Gk, i}$ and ${\sum }_{l = 1}^{n}\varDelta {P}_{WFli}$ are the output power of thermal generators and wind farms respectively. $\varDelta {P}_{cGk, i}$ and $\varDelta {P}_{cWk, i}$ are active power control command signals respectively. $\varDelta {P}_{Li}$ is load fluctuations in the i-th area.

2.2.   State space model of regional interconnected power system

From the frequency response model in Fig.1, the state space model of area i can be obtained by (1)–(7).

where, ${x}_{i}, {u}_{i}, {w}_{i}, {y}_{i}$ is the state variable, control variable, disturbance variable and output variable respectively. ${A}_{i}, {B}_{i}, {F}_{i}, {C}_{i}$ is the corresponding state matrix, control matrix, disturbance matrix and output matrix of area i. ${A}_{ij}$ and ${B}_{ij}$ is the state interaction matrix and control interaction matrix respectively.

From the above analysis, the state variable ${x}_{i}$ consists of $\varDelta {f}_{i}$, $\varDelta {P}_{tie, i}$, $\varDelta {X}_{Gk, i}$, $\varDelta {P}_{Rk, i}$, $\varDelta {P}_{Gk, i}$ and $\varDelta {P}_{WFk, i}$:

The control variable of area $i$, ${u}_{i}$, is composed of all the power control signals that participating in AGC, namely:

The disturbance variable ${w}_{i}$ is defined as the load disturbance of area $i$, whose expression is ${w}_{i} = \varDelta {P}_{d, i}$; The output variable ${y}_{i}$ is considered as the regional deviation signal ACE, whose expression is ${y}_{i} = {\beta }_{i}\varDelta {f}_{i}+\varDelta {P}_{tie, i}$.

The state matrix of area $i$, ${A}_{i}$, can be obtained by (1)–(10):

The control matrix ${B}_{i}$ is

The disturbance matrix ${C}_{i}$ is

The output matrix ${C}_{i}$ is

It is noting that, only ${A}_{ij}\left(\mathrm{2, 1}\right) = -2\pi {\sum }_{j = 1, j\ne i}^{N}{T}_{ij}$, while other elements are 0 in ${A}_{ij}$. And that all the elements in ${B}_{ij}$ are 0.

With the state space model of area $i$, the state space model of inter-connected power system can be obtained as follows:

where, $x, u, w$ are the state variable, control variable and disturbance variable of the inter-connected power system.

The state matrix of the inter-connected power system is as follows:

where, ${A}_{ii} = {A}_{i}$ and ${B}_{ii} = {B}_{i}$.

3.   Strategy of AGC with wind power integration

In the latest Chinese national standard technical regulations (GB /t19963-2021) for wind farm integration, wind farms are supposed to participate in power system frequency regulation and peak load regulation. This section focuses on the strategy of wind farm participating in powers system AGC.

3.1.   Frequency control framework of wind farm participating in AGC based on MPC

Normally, the active power control command of the wind farm is set lower than its available power (maximum wind power that can be generated by wind turbine) to ensure the active power control capability. However, the above method is built on the assumptions that the actual power (the measured wind power) of the wind farm can track the power control command. In actual operation process, the available power of wind farm cannot reach the active power control command within a certain period due to the uncertainty and variability of wind power. At such time, the actual power generated by the wind farm would instead be the available power. The actual output curve of a wind farm in one day is shown in Figure 2.

In Figure 2, it is assumed that the active power control command of the wind farm is 35MW and remains unchanged. It can be seen that the available power of the wind farm is higher than the active power control command during the time period of 00:30–04:15, 04:40–05:25, 10:30–13:45 and 17:20–23:55. At these time periods, the actual generated power of the wind farm tracks the active power control command; In other periods, the available power of the wind farm is lower than the active power control command, and the actual output power of the wind farm is instead the real available power.

The above analysis shows that the wind farm output power should be regarded as an additional system disturbance when the available power of the wind farm is lower than the active power control command. Otherwise, the wind farm can participate in the system AGC when the available power of the wind farm is greater than the control command.

As a new computer control algorithm for industrial control process, MPC has the characteristics of high robustness, good control effect, strong adaptive ability and low requirement for model accuracy. In this paper, the AGC control strategy is proposed based on MPC controller. The overall control method is shown in Figure 3.

The core idea of this strategy is:

a) The total active power command of AGC system is calculated by MPC controller according to system frequency deviation and tie-line power flow;

b) The situation of each wind farm, i.e., whether they can participate in frequency regulation, is judged by wind power prediction;

c) Online rolling optimization is performed considering the output state of thermal generators and wind farms. After which, the active power control commands of wind farm and thermal generator are calculated.

3.2.   Wind power prediction model considering wind power variogram characteristics

It is noting that the control time step of AGC system is about 30s-1min, while the time-scale of ultra-short-term wind power prediction is 5–15 min ^[20]. The wind power prediction data of 5–15min scale could not be used as the control signal of AGC system. One of the solution is to generate a wind power prediction data with a time resolution of 1 min based on 5–15 minute wind power prediction data. The common algorithm is autoregressive integrated moving average model (ARIMA). However, the increasing wind power penetration leads to the fact that conventional AGC units may not be able to follow these variations as tightly as desired. Therefore, a more accurate and shorter time-scale prediction data may lead both the conventional units and wind farms to participate AGC system better. With the above analysis, it is necessary for the wind farm to provide wind power prediction data with a time scale of less than 1 min.

3.2.1.   Wind power variogram power law model in time domain

Based on the variation characteristics of wind power, this paper proposed a method to estimate the variations of wind power with a time scale of 5 s–1 min based on the 15 min wind power prediction data.

The variogram of the wind power output $P\left(t\right)$ during an interval $\left[t, t+\varDelta t\right]$ from $t$ to $t+\varDelta t$ with $\varDelta t$ duration is defined as ${P}_{\gamma }\left[t, \varDelta t\right]$

Let

where, ${\bar{P}}_{W}\left(t\right)$ is hourly average wind power with 15 min sampling interval; ${P}_{N}$ is the maximum power of wind farm. ${\bar{P}}_{W}^{*}\left(t\right)$ and ${P}_{\gamma }^{*}\left(t, \varDelta t\right)$ are per-unit values.

With the above definition, variation intensity ${I}_{\text{Var}}\left(t\right)$ is defined as follows:

${I}_{\text{Var}}\left(t\right)$ is an index to measure the change intensity of wind power.

By curve fitting, a three-power law model is presented as follows:

where $\alpha, \beta$ and $c$ are parameters of the power law model.

With (21) and (22), the variogram of wind power can be predicted when ${\bar{P}}_{W}\left(t\right)$ is obtained by real-time measurement.

3.2.2.   Wind power prediction based on variogram power law model

Suppose that the ${\bar{P}}_{W}\left(t\right)$ is available. Then the variance of wind power can be predicted using the following equation:

In (23), $\left|\varDelta {P}_{W}\left(t, \varDelta t\right)\right|$ represents the absolute value of wind power variance. The plus-minus sign of $\left|\varDelta {P}_{W}\left(t, \varDelta t\right)\right|$ is another important component, which can be obtained by

where ${P}_{ave}^{\left(t, t+\varDelta t\right)} = \left(\frac{1}{N}\right){\sum }_{i = 1}^{N}{P}_{W}\left({t}_{i}\right)$ is the wind power moving average in the time interval $\left[t, t+\varDelta t\right]$. $N$ is the total number of sampling points.

From (24), the predicted variation of wind farm output power can be expressed as

With (25), the prediction value of wind power at $t+\varDelta t$ is obtained

3.3.   Prediction model of MPC

From (25), the variation of wind power at $t+\varDelta t$ can be predicted by ${\bar{P}}_{W}^{*}\left(t\right)$. The predicted wind power variation sequence can be recorded as:

In Section 2, the state space model of (8) and (15) are continuous state space model. Using the zero-order holder discretization method, the discrete state space model of system (8) and (15) can be obtained as follows:

Where, ${x}_{i}\left(k\right)$, ${u}_{i}\left(k\right)$, ${w}_{i}\left(k\right)$, ${y}_{i}\left(k\right)$, $x\left(k\right)$, $u\left(k\right)$, $w\left(k\right)$ and $y\left(k\right)$ is the corresponding discrete variable respectively; ${A}_{d, i}$, ${B}_{d, i}$, ${C}_{d, i}$, ${F}_{d, i}$, ${A}_{d, ij}$, ${B}_{d, ij}$, ${A}_{d}$, ${B}_{d}$, ${C}_{d}$ and ${F}_{d}$ is the discrete matrix respectively.

Let ${N}_{p}$ be the prediction time domain, ${N}_{c}$ be the control time domain; ${x}_{i}\left(k+\tau \left|k\right.\right)$ and ${y}_{i}\left(k+\tau \left|k\right.\right)$ is set as the state vector and output vector of time $k+\tau$ predicted for time $k$; ${u}_{i}\left(k+\tau \left|k\right.\right)$ is set as the control vector of time $k+\tau$ predicted for time $k$.

3.4.   Optimization model

Based on the above analysis, the objective function of the interconnected power system is:

where, $J\left(k\right)$ is the objective function for time $k$; $Q$ and $R$ is the diagonal weighting matrix for output variable and control variable respectively.

System active power balance constraint is expressed as:

Active power output constraints of thermal generators is:

Climbing rate constraint of thermal generators is:

Tie-line power deviation constraint is:

3.5.   Feedback correction

Due to the error of wind power prediction, the prediction sequence of each wind farm is corrected after each optimization to compensate the error in real time.

The compensation strategy is as follows: The predicted wind power value at the next time interval is corrected according to the measured active power value of the wind farms.

For example, $\varDelta {P}_{WFk, i}\left(k+1|k\right)$ is considered as the prediction wind power for time $k+1$ predicted at time $k$. $\varDelta {P}_{WFk, i}^{*}\left(k+1|k\right)$ is the measured wind power at time $k+1$. The corrected wind power can be written as:

$\varDelta {P}_{WFk, i}^{corr}\left(k+1|k\right)$ is the corrected wind power for time $k+2$. The influence of wind power prediction error on control effect is reduced by this method.

4.   Simulation results

The control strategy proposed in Section 2 is studied by a three area inter-connected power system. It is assumed that the installed capacity and generator deployment of each region is consistent. Each area has thermal generators and wind farms, and the total installed capacity of each area is 3352 MW, where thermal AGC generator capacity is 1946 MW and wind power installed capacity 1406 MW. GRCs of different type AGC units are 1.5, 2 and 4 per minute, respectively. The control time step of MPC is set as 1 min, while the prediction time domain is ${N_p} = 15\min$ and the control time domain ${N_c} = 15\min$.

Load curve of each area is shown in Figure 4. Curves are drawn by actual measured data from 00:00 to 24:00. The load forecasting curve is obtained by 15-min average from actual load data. It is noting that, the load data of each area is assumed to be the same. The difference between each area is the control mode of AGC system.

The actual wind power curve and the forecasting wind power curve are shown in Figure 5. It is noting that, the forecasting wind power curve in Figure 5 is calculated based on the wind power variograms with a temporal lag of 30 s. The forecasting accuracy is much better than that of the 15 min wind power prediction.

In order to compare the performance of different AGC strategies, three control modes are proposed in this section for in-depth analysis. Different control modes are list as follows:

Control Mode I: MPC according to wind power prediction based on wind power variogram characteristics (MPC+VC);

Control Mode II: MPC according to ultra-short-term wind power prediction based on ARMIA (MPC+UST);

Control Mode III: Conventional PI control of AGC system;

The frequency deviation curves of three regions are shown in Figure 6. Figure 6(a) is the frequency deviation curve of area 1 with Control Mode I. Figure 6(b) is the frequency deviation curve of area 2 with Control Mode II and Figure 6(c) is the frequency deviation curve of area 3 with Control Mode III.

It can be seen from Figure 6 that each control mode can maintain the frequency deviation of each area at –0.1 ~ 0.1 Hz. With wind farms participate in AGC system, the frequency deviation is smaller than that of the conventional PI control of thermal generators. The control mode with prediction information based on wind power variogram characteristics has a better performance than the control mode with ultra-short-term wind power prediction information.

In order to verify that the wind power variogram characteristics based method can improve the accuracy of wind power prediction and make rational use of the reserve capacity of wind farms, comparative studies are performed. The simulation results of thermal generator output power by variogram characteristic based wind power prediction method and normal ultra-short-term wind power prediction method are selected. The results are shown in Figure 7.

In Figure 7, the output power curve of thermal generator by MPC + VC control mode is smoother than that of thermal generator by MPC + UST control mode. The active power control amplitude and control frequency of thermal power generators decreases when the wind farm participates in AGC. The participation of wind farm can well alleviate the frequency regulation pressure of thermal power generators.

5.   Discussion

This paper proposes an AGC control strategy with wind power participation based on wind power variogram characteristics. Through simulation verifications, the following conclusions are obtained:

1) Based on the wind power prediction data of AGC control time-scale, wind farm have more flexible reserves to enable the wind farm to participate in AGC system. The frequency stability of the power system with large-scale wind power is effectively improved.

2) With the three-parameter power-law model, the variation of wind power in future can be predicted and taken as the prediction model. The actual available power of wind farm is compared with the predicted wind power, and the prediction error of is corrected to reduce the impact on AGC system.

3) Simulation results show that with this new strategy, frequency deviations under wind power variations can be effectively decreased. The control strategy makes both conventional AGC generators and wind farms act in advance to race against time, and therefore reduce system frequency regulation pressure.

Conflict of interest

Authors declare no conflict of interest.