The analytical analysis of nonlinear fractional-order dynamical models

1.   Introduction

X-ray security screening is a preeminent protection for public safety in various venues such as airports, railway stations, undergrounds, post offices, and customs. To this end, X-ray scanning machines are deployed to detect and expose prohibited items concealed within the baggage, luggage, or cargo. Human operators play pivotal roles in threat screening^[1]. The expertise and proficiency of inspectors are indispensable for the accurate detection of threats; nevertheless, other factors, such as emotional fluctuation and physical fatigue, tend to divert their concentration. The necessity for a real-time, dependable, and automatic method for security screening is becoming increasingly pressing owing to the challenging conditions encountered during the checking process. Specifically, the random arrangement and extensive overlapping of content in luggage leads to highly occluded images, which significantly complicates the task of identifying prohibited items amidst cluttered backgrounds for inspectors ^[2].

Despite the growing interest in computer-assisted techniques to enhance the alertness and detection capabilities of screeners, research in this area has been understudied owing to the scarcity of extensive datasets and sophisticated deep-learning algorithms. Previous studies have primarily focused on conventional image analysis ^[3,4,5] and machine learning. Most recently, deep learning methods, especially convolutional neural networks (CNN), have demonstrated superior performance over conventional machine learning methods for threat object classification ^[6,7,8], detection ^[9,10] and segmentation ^[11,12]. Nevertheless, most methods merely achieve high accuracy and recovery rates on specific datasets.

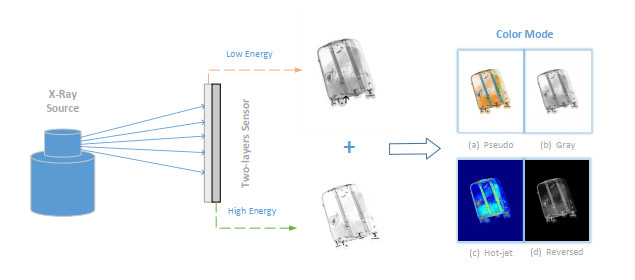
The principle underlying X-ray imaging is the penetration of an X-ray beam through a scanned object and its subsequent detection using a photoelectric sensor. The intensity of the X-ray signal is inversely proportional to the density of the object material, thereby enabling determination of the internal structure of the object. The formula for attenuation is $I_x = I_0 e^{ -\mu x }$, where $I_0$ is the initial density, $I_x$ is the attenuated density at x cm, and $\mu$ is the linear attenuation coefficient ^[13]. The formulation implies that $I_x$ is correlated with the object thickness x and the nature of its material. The influence of the object thickness is mitigated through the utilization of dual- or multi-energy imaging technology, which enables the determination of the object's density and properties, in particular, the effective atomic number $Z_{eff}$. Owing to the sensitivity of human perception to color, the density and effective atom number are converted to pseudo-color images or other color modes using lookup tables. The process of generating X-ray inspection images is depicted in Figure 1. In pseudo-color mode, different materials exhibit different colors during X-ray imaging. Conventionally, blue, orange, and green refer to the inorganic, organic, and mixed materials, respectively.

Figure 1.  Scenario of the X-ray image generation and the images can be displayed in four color modes: (a) pseudo, (b) gray, (c) hot-jet, and (d) reversed.

DownLoad: Full-Size Img PowerPoint

Data generation is an effective strategy for improving the performance of deep-learning methods, particularly in the context of prohibited object detection during X-ray security inspections. This is because the process of acquiring and annotating a large number of X-ray images in a real-world setting is both expensive and time-consuming. Nevertheless, in recent years, researchers have made tremendous efforts to create large-scale X-ray inspection datasets. Several commonly cited benchmarks include GDXray, UCL TIP, SIXray, and OPIXray ^{[14,15,16,17]}. With flourishing contemporary generative adversarial network (GAN) technology, its outstanding image-generation capacity has received wide attention. Various attempts have been made to synthesize X-ray images of prohibited items using GANs. For instance, Yang et al. ^[18] proposed a generative model based on improvements to WGAN-GP to generate ten classes of prohibited items using real images. Zhu et al. ^[19] attempted to synthesize images using SAGAN and CycleGAN to enrich the diversity of the threat image database, although the quality of the generated images could be improved. Liu et al. ^[20] developed a comprehensive framework based on GAN to synthesize X-ray inspection images for data enhancement.

Inspired by the concept of generative radiance fields (GRAF), we propose a stylized generative radiance fields (SGRF) that enables controllable synthesis of 3D-aware images. The framework of the model is shown in Figure 2, which will be described in detail in other sections. This model can generate images of prohibited items based on label prompts and serves as an implicit representation database, producing a large number of images with rich diversity in class, color mode, pose, etc. More specifically, we make the following contributions.

Figure 2.  The framework of the stylized generative radiance fields (SGRF).

DownLoad: Full-Size Img PowerPoint

● We implemented a stylized generative radiance field to learn the implicit representation of multiple objects with different color styles using a single multilayer perceptron (MLP).

● We attained explicit control over the generation of 3D-aware images by entangling and disentangling class and style labels into/from random latent codes.

● We utilized the model to significantly augment the X-ray inspection datasets and effectively increase the generalization ability of state-of-the-art detection algorithms in security screening.

The rest of this paper is organized as follows. Section 2 presents a literature review of the 2D and 3D image synthesis methods. Section 3 describes stylized generative radiance field methodology. Section 4 describes the experimental setup and details. Section 5 presents the experimental results for the proposed model. Section 6 concludes the paper and provides recommendations for future research.

2.   Related works

GAN: In 2014, Goodfellow et al. ^[21] introduced GANs, which are deep generative models inspired by the game theory. During the training process, generator G and discriminator D compete to reach a Nash equilibrium state. The principle of G is to generate as much fake data as possible to fit the potential distribution of the real data, whereas the principle of D is to correctly distinguish real data from fake data. The input of G is a random noise vector $z$ (usually a uniform or normal distribution). The noise was mapped to a new data space via G to obtain a fake sample G($z$), which is a multidimensional vector. The discriminator D is a binary classifier that takes both the real sample from the dataset and the fake sample generated by G as the input, and the output of D represents the probability that the sample is real rather than fake. The architecture of GAN is illustrated in Figure 3.

Figure 3.  The GAN comprises a generator (G) and a discriminator (D), where $z$ is the input noise, X is the real image, and G($z$) is the fake image.

DownLoad: Full-Size Img PowerPoint

Following this principle, various GANs were developed for image generation and translation ^[22,23]. Initially, GAN adopted a fully connected MLP as the generator and discriminator. Taking advantage of a CNN, Radford et al. ^[24] proposed a deep convolutional generative adversarial network (DCGAN) that achieved superior performance in image generation. Owing to the use of random latent vectors as inputs, unrestricted variables may result in collapse of the training process. To address this issue, conditional GANs, such as CGAN, ACGAN, and InfoGAN ^[25,26,27] have incorporated conditional variables (including labels, text, or other relevant data) into both the generator and discriminator of the model. These modifications result in a more robust training process and the ability to generate images based on specific conditions. Moreover, considerable effort has been devoted to optimizing the objective function for stabilizing Gan's training. For example, Arjovsky et al. ^[28] proposed a Wasserstein generative adversarial network (WGAN). They first showed theoretically that the Earth-Mover (EM) distance produces better gradient behaviors than other distance metrics. Gulrajani et al. ^[29] presented a gradient penalty named WGAN-GP to enforce the Lipschitz constraint, which performs better than the original WGAN. Petzka et al. ^[30] introduced a new penalty term known as the WGAN-LP to enforce the Lipschitz constraint.

Image translation, or converting images from one domain to another, is another primary task of GANs. Isola et al. ^[31] utilized a pix-to-pix GAN to perform image adaptation between pairs of images. Subsequently, the HD pix-to-pix GAN ^[32] enhanced the quality and resolution of the generated images up to 2048 × 1024 pixels. Owing to the difficulties in obtaining paired data in real-world scenarios, CycleGAN, DiscoGAN, and DualGAN ^[33,34,35] employed a term of cyclic consistency to train the model using unpaired data. Choi et al. ^[36] proposed StarGAN, which accomplished image translation across multiple domains by using a single model.

To date, contemporary GAN technology has achieved outstanding performance in synthesizing high-resolution photo-realistic 2D images; however, GAN cannot synthesize novel views of objects, and the generated images unable to maintain 3D consistency.

NERF: Neural radiance fields ^[37] are powerful for learning 3D scene implicit representations, where the scene is represented as a continuous field and stored in a neural network. The neural radiation field can render high-fidelity images from any perspective by training on a set of posed images. The implicit rendering process is illustrated in Figure 4. The inputs are the position $o$, direction $d(\theta, \phi)$, and the corresponding coordinates $(x, y, z)$ of the emitted light from a certain perspective, which are fed into the neural radiation field to obtain the volume density $\sigma$ and color $(r, g, b)$ and obtain the final image through volume rendering. To obtain clear images, positional encoding optimizes the networks by mapping a 5D input to a high-dimensional space to represent the high-resolution geometry and appearance. Additionally, a coarse-to-fine strategy was adopted for hierarchical volume sampling to increase rendering efficiency.

Figure 4.  Implicit rendering process of NERFs, where, $\textbf{x}(x, y, z)$ refers to the 3D location of the point, $\textbf{o}$, $\textbf{d}(\theta, \phi)$ refers to the origin, direction of the ray, and $\textbf{c}(r, g, b)$/$\sigma$ refers to the color/density of the rendering point, respectively.

DownLoad: Full-Size Img PowerPoint

NERF has achieved impressive success in view synthesis, image processing, controllable editing, digital human body, and multimodal applications. The limitations of NERF are its slow training and rendering, restriction to static scenes, lack of generalization, and the requirement of a large number of perspectives. To address these issues, Garbin et al. ^[38] proposed FastNeRF that can render high-fidelity and realistic images at 200 Hz on high-end consumer GPUs. Li et al. ^[39] presented the neural scene flow fields to expand it to dynamic scenes by learning implicit representation of scenes from monocular videos. Because the NERF requires retraining for a new scene and cannot be extended to unseen scenes, academic research on this topic comprises pixelNeRF and IBRNet ^[40,41]. Moreover, NERF stores one scene in one fully connected multilayer network (MLP), which restricts the representation of multiple scenes in a single model.

GRAF: Taking advantage of GAN and NERF, GRAF ^[42] designed a generative model of NERF by integrating a neural field into a GAN generator. The model can generate 3D-aware images from the latent code (noise) and can be trained using a set of unposed images. In addition to changing the perspective, GRAF also allows the modification of the shape and appearance of the generated objects. Although GRAF has demonstrated remarkable capabilities in generating high-resolution images with 3D consistency, its performance in more complex real-world settings is limited, owing to its inability to effectively handle multi-object scenes. GIRAFFE ^[43] aims to represent scenes as synthetic neural feature fields that can control the camera's pose, position, and angle of objects placed in the scene as well as the shape and appearance of objects. GIRAFFE is a combination of multiple MLP networks, each of which representing a scene or an object. Our goal was to utilize a single MLP to store various objects or scenes. Inspired by previous studies, we designed stylized generative radiance fields to accomplish this objective. Using this model, we exercised explicit control over the generation of objects based on the class and style labels.

3.   Methods

GAN is a generative model primarily utilized for image generation and translation tasks, but the synthesized images are unable to maintain multi-view consistency. By contrast, NERFs enable the generation of 3D-aware images owing to the inherent nature of the radiance field. GRAF is a combination of GAN and NERF, and has been proven successful for novel view synthesis from a random latent code, which also allows modification of the shape and appearance of the generated object based on latent code. However, the shapes and appearances of the objects are randomly generated without explicit control. Moreover, the GRAF prototype employs an MLP to learn the implicit representation of one object or scene, leading to high memory consumption in multiple-scene cases. Therefore, we argue for representing multiple scenes using a single MLP and generating objects with explicit control through the SGRF, which has evolved from GRAF. In the following section, we briefly review the NERF and GRAF models, which form the basis of our model.

3.1.   Neural radiance fields

Neural radiance fields ^[37] provide the foundation for various NERF-derived models. Its contributions include implicit representation of 3D geometry and differentiable volume rendering.

Implicit representation: Radiance fields provide implicit representations of 3D geometry. The radiance field is a continuous function with the input of the 3D location x = $(x, y, z)$, viewing direction d = $(\theta, \phi)$, output of the emitted color c = $(r, g, b)$, and volume density values $\sigma$. The mapping of the function from input to output is implemented using an MLP network $F_{\Theta}:(\textbf{x}, \textbf{d}) \rightarrow (\textbf{c}, \sigma)$ and its weights are optimized to map each input 5D coordinate to its corresponding volume density and directional emitted color. The network $F_{\Theta}$ directly operated on 5D input coordinates performs poorly at representing high-frequency variations in color and geometry because deep networks are biased toward learning low-frequency functions. Positional encoding was used to map a 3D location x$\in\mathbb{R}^3$ and viewing direction d $\in\mathbb{S}^2$ into a higher-dimensional space to enable the MLP to more easily approximate a higher-frequency function. Formally, the positional encoding function is defined in Eq (3.1) ^[37].

This function $\gamma$(·) is applied separately to each of the three coordinate values in x and the three components of the Cartesian viewing-direction unit vector d. In the experiments, $L$ = 10 for $\gamma$(x) and $L$ = 4 for $\gamma$(d). In Eq (3.2) ^[37], an MLP network $f_{\Theta}$(·) is applied to map the resulting features to a color value $\textbf{c}\in\mathbb{R}^3$ and volume density $\sigma\in\mathbb{R}^{+}$.

Volume rending: To render a 2D image from the radiance field $f_{\Theta}$(·), the volume density $\sigma$(x) can be interpreted as the differential probability of a ray terminating at an infinitesimal particle at the location x. The expected color C(r) of the camera ray r($t$) = o + $t$d with near and far bounds $t_n$ and $t_f$ is calculated using Eq (3.3) ^[37].

Rendering a view from a continuous NERF requires estimating integral C(r) for a camera ray traced through each pixel of the camera. This continuous integral of C(r) is numerically estimated using deterministic quadrature, which limits the resolution of the representation, because the MLP would only be queried at a fixed discrete set of locations. Instead, a stratified sampling approach was used to partition [$t_n$, $t_f$] into N evenly spaced bins and draw one sample uniformly at random from each bin. This approximation approach estimates the integral value from a discrete set of samples. In Eq (3.4) ^[37], let ${(c_r^i, \sigma_r^i)}_{i = 1}^{N}$ denote the color and volume density values of N random samples along camera ray $r$. The rendering function $\pi$(·) maps these values onto the color value $c_r$. The color value, $c_r$, was calculated using Eq (3.5) ^[37].

where $T_r^i$ and $\alpha_r^i$ denote the transmittance and alpha value of sample point $i$ along ray $r$ and $\delta_r^i = \|x_r^{i+1}-x_r^{i}\|_2$ is the distance between neighboring sample points. Network $F_{\Theta}$ is trained with a set of posed images by minimizing the reconstruction loss between observations and predictions. In addition, a hierarchical volume sampling strategy was applied to improve the rending efficiency.

3.2.   Generative radiance fields

The GRAF ^[42] comprises a radiance field-based generator and a multi-scale patch discriminator. It differs from NERF in that it attempts to learn a model using unposed images rather than posed images.

3.2.1.   Generator

The generator takes the camera intrinsic matrix K, camera pose $\xi$, 2D sampling pattern $\nu$, and shape/appearance codes $z_s/z_a$ as inputs, and predicts the image patches $P^{'}$. The camera poses $\xi = [R|t]$ sampled from a pose distribution $p_\xi$ and $\nu(\textbf{u, s})$ determines the center $u \in R^2$ and scale $s \in R^+$ of the virtual $K\times K$ patch drawn from a uniform distribution. The shape and appearance variables $z_s$ and $z_a$ are obtained from the shape and appearance distributions $p_s$ and $p_a$, respectively.

Ray sampling: $K \times K$ patch $P(\textbf{u}, s)$ is determined by a set of 2D image coordinates that describe the location of every pixel of the patch in the image domain $\Omega$. In Eq (3.6) ^[42], the corresponding 3D rays are uniquely determined by $P(\textbf{u}, s)$, the camera pose $\xi$, and the intrinsic matrix K.

3D point sampling: As with the NERF, stratified sampling was used to sample N points $\{\textbf{x}^i_r\}^N_{i = 1}$ along each ray $r$ for the numerical integration of the radiance field.

Conditional radiance fields: The radiance field was implemented using a fully connected neural network with parameter $\theta$. In addition to a regular radiance field, it is conditional on two latent codes: shape code $z_s$ and appearance code $z_a$, which determine the object's shape and appearance. As shown in Figure 5, the shape encoding $h$ is derived from the positional encoding of $\gamma(\textbf{x})$ and shape code $z_s$ and then transformed to the volume density $\sigma$ by density head $\sigma_\theta$. The volume density is computed independently without using viewpoint $\textbf{d}$ and appearance code $z_a$ to disentangle the shape from the appearance during the inference. To predict the color $\textbf{c}$, the concatenating vector of the shape encoding $h$, positional encoding of $\gamma(\textbf{d})$, and appearance code $z_a$ are passed to the color head $c_\theta$.

Figure 5.  A conditional radiance fields $g_\theta$, with shape encoding $h_\theta$, color head $c_\theta$, and density head $\sigma_\theta$. Here, $z_s$/$z_a$ refers to shape/appearance code.

DownLoad: Full-Size Img PowerPoint

Volume rendering: Given the color and volume density ${(c_r^i, \sigma_r^i)}_{i = 1}^{N}$ of N points along a ray, the color $\textbf{c}_r\in\mathbb{R}^3$ of the pixel corresponding to the ray is obtained using the volume rendering operator $\pi$. The predicted patch $P^{'}$ is generated by combining the results of all sampling rays.

3.2.2.   Discriminator

The discriminator was implemented as a convolutional neural network with leaky ReLU activation. To accelerate training and inference, the discriminator compares the synthesized patch $P^{'}$ with a patch $P$ extracted from a real image $I$ drawn from the data distribution $p_D$. To extract a $K \times K$ patch from a real image, the real patch $P$ is sampled by querying a real image at 2D image coordinates P(u, s) using a bilinear interpolation operation, which is referred to as $\Gamma(I, \nu)$. It was proven that the discriminator with shared weights was sufficient for all patches even though they were sampled at random locations with different scales. As the scale determines the receptive field of the patch, starting with patches of larger receptive fields to capture the global context, patches with smaller receptive fields are progressively sampled to refine the local details.

3.2.3.   Train and inference

During adversarial training, the goal of generator $G(\theta)$ is to minimize the objective function, and that of discriminator $D(\phi)$ is to maximize the objective function. The non-saturating objective function $V(\theta, \phi)$ with R1-regularization is defined in Eq (3.7) ^[42].

where $f(t) = -\log(1 + \exp(-t))$, $I$ denotes an image from the data distribution $p_D$, $p_\nu$ denotes the distribution over random patches, and $\lambda$ controls the strength of regularization. Spectral and instance normalization were used for the discriminator. RMSprop was used as an optimizer with a batch size of 8 and learning rates of 0.0005 and 0.0001 for the generator and discriminator, respectively.

3.3.   Stylized generative radiance fields

GRAF can synthesize novel views of an object from latent code, although the generation of the shape and appearance of an object is random and lacks explicit control. To address this issue, we propose the use of SGRF that enable the implicit representation of multiple 3D objects using a single MLP, providing precise control over 3D-aware image synthesis according text prompts (labels).

3.3.1.   Generator

In the generator, the label codes of the class and style are entangled with a latent vector as the input of the conditional radiance field. This encourages the generator to use label-embedding latent vectors to synthesize objects with explicit control in terms of class and style. The schema of label embedding is illustrated in Figure 6.

Figure 6.  The schema for embedding label codes into latent vectors by multiplication (X).

DownLoad: Full-Size Img PowerPoint

Input: The random latent code $z\in\mathcal{N}$(0 $\backsim$ 1) is split into shape code $z_{s}$ and appearance code $z_{a}$. The class and style labels are embedded into the embedding layers, and the label-embedded codes $z^{'}_{s}$ and $z^{'}_{a}$ are produced by multiplying the shape code $z_{s}$ and appearance code $z_{a}$ with the label codes.

Output: In contrast to GRAF, which employs a single value of $\sigma$ and $c$, the conditional radiance field $g(\theta)$ in our model produces a volume density array $[\sigma(i)]^{N-1}_{i = 0}$ and color array $[c(j)]^{M-1}_{j = 0}$, both indexed by numerical labels. In practice, the number of classes was set to $N$ = 5 and the number of styles at $M$ = 4.

Conditional radiance field: The network structure of conditional radiance fields $g(\theta)$ is illustrated in Figure 7. The mechanism of prediction for volume density $\sigma$ and color $c$ is the similar to that of GRAF. However, the input and output of $g(\theta)$ are manipulated for entangling and disentangling label codes accordingly. In practice, a total of 1024 rays are sampled for one image with parameters $P(\textbf{u}, s)$, camera pose $\xi$ and intrinsic K, then 64 points are sampled along each ray $r$. Here, $\gamma(\textbf{x})$, and $\gamma(\textbf{d})$ are the positional encoding of the 3D coordinates $\textbf{x}$ and ray direction $\textbf{d}$ of the point. $z^{'}_{s}$ and $z^{'}_{a}$ are the latent codes associated with class and style, respectively.

Figure 7.  The structure of conditional radiance fields $g(\theta)$ with inputs of $z^{'}_{s}, z^{'}_{a}$, $\gamma(x)$ and $\gamma(d)$, and outputs of volume density array $[\sigma(i)]^{4}_{i = 0}$ and color array $[c(j)]^{3}_{j = 0}$.

DownLoad: Full-Size Img PowerPoint

3.3.2.   Discriminator

In addition to using a regular discriminator $D(\phi)$ to compare the synthesized patch $P^{'}$ with a real patch $P$, another auxiliary classifier $D_{vgg}$ based on VGG16 is added to distinguish the class and style of an object or scene. VGG16 ^[44] is a classical deep CNN that is typically used for multi-classification tasks owing to its superior generalization ability. Initially, the discriminator $D_{vgg}$ is trained using the annotated images $I^{'}$, which are downsampled from real image $I$.

3.3.3.   Train and inference

In the training phase, the loss function guides network optimization. The discriminator $D(\phi)$ is trained using a real patch $P$ and a synthesized patch $P^{'}$ with labels. The discriminator $D_{vgg}$ was trained using a rescaled real image $I^{'}$. The loss function of $G(\theta)$ is expressed by Eq (3.8).

where $L_{adv}$ is the adversarial loss of $P$ and $P^{'}$, $L_{cls}$ and $L_{sty}$ denote the classification and style loss of the generator, respectively, and $\lambda_{1}$ and $\lambda_{2}$ are weights for $L_{cls}$ and $L_{sty}$. In this experiment, MSE and RMSprop were used as the adversarial loss function and optimizer, respectively, with parameters $\lambda_{1}$ = 2.0 and $\lambda_{2}$ = 3.0 and a batch size of 8. During the inference phase, class and style labels are embedded into latent codes $z_{s}$ and $z_{a}$, respectively, for controllable synthesis of 3D-aware images.

4.   Experiments

4.1.   Datasets

Owing to the difficulty in obtaining X-ray data in a real scene, we trained the model on a synthetic dataset. In a 3D editing software, such as Blender, an object was set at the origin and the camera was on the surface of the upper hemisphere facing toward the origin of the coordinate system. By manipulating the camera's pose, we can capture natural images of an object from a variable perspective. Subsequently, the captured images were binarized and converted into a semantic map as an input to an HD pix-to-pix GAN. The four types of semantic maps correspond to the four display styles individually. The image translator is a pretrained HD pix-to-pix GAN that is responsible for the style transfer of the captured images. The dataset comprises five classes of images of prohibited items, such as guns, forks, pliers, knives, and scissors, and each class is displayed in four color modes: grey, pseudo, hot jet, and reversed. The image synthesis pipeline is illustrated in Figure 8.

Figure 8.  The pipeline of the synthesis of training dataset from 3D models.

DownLoad: Full-Size Img PowerPoint

4.2.   Baselines

We trained the model on the synthesized dataset prepared in Section 4.1 and compared its results with those of the NERF, GRAF, and GIRAFFE models, respectively. NERF learns 3D geometry from posed images and synthesizes novel views using differentiable volumetric rendering. GRAF generates high-quality 3D-aware images from latent codes of shape and appearance without requiring posed images. GIRAFFE is a combination of multiple MLP networks that represent multiple objects in a given scene.

4.3.   Evaluation metrics

Frechet inception distance (FID) scores have been extensively adopted to evaluate the quality and diversity of generated images. We calculate the FID scores using Eq (4.1) ^[45].

where pair ($m_r$, $C_r$) corresponds to real images, pair ($m_g$, $C_g$) corresponds to generated images, and m and C are the mean and covariance, respectively. We also introduce kernel inception distance (KID) ^[46], which does not require a normal distribution hypothesis such as FID and is an unbiased estimate. In addition, average precision (AP) and mean average precision (mAP) are the most popular metrics used to evaluate object detection performance.

5.   Results

5.1.   Synthesis of X-ray images of prohibited items

The model was trained on a synthetic dataset (Section 4.1). We employed an RMSprop optimizer with learning rates of 0.0001 and 0.0005 for the discriminator and the generator, respectively. During the inference phase, the inputs of the MLP are label-embedded latent codes $z^{'}_{s}$ and $z{'}_{a}$ and view direction d$(\theta, \phi)$. The average inference time was 0.7723 s for each image with a size of 128. In Figures 9 and 10, some X-ray images were predicted based on the class and style labels after 50,000 iterations. In Figure 11, novel views of prohibited items are synthesized by altering the pose of the virtual camera. Here, $\theta, \phi$ are the pitch and yaw angles of the camera in a spherical coordinate system.

Figure 9.  Samples of the synthesized X-ray images of prohibited items with class labels (i = 0, 1, 2, 3, 4), style labels (j = 0), and view direction d$(\theta, \phi)$.

DownLoad: Full-Size Img PowerPoint

Figure 10.  Samples of the synthesized X-ray images of prohibited items with class label (i = 0), style labels (j = 0, 1, 2, 3), and view direction d$(\theta, \phi)$.

DownLoad: Full-Size Img PowerPoint

Figure 11.  Novel view synthesis of prohibited items by manipulating camera pose. Here, $\theta, \phi$ are the pitch and yaw angles of the camera, respectively.

DownLoad: Full-Size Img PowerPoint

The FID score indicates the differences between the real and generated images; the lower the FID score, the better the generative model's performance. As shown in Figure 12, the 'guns' and 'pliers' presented superior quality and diversity compared to other category because they have more complex details in the internal structures than other categories.

Figure 12.  FID scores of prohibited items grouped by category and color mode.

DownLoad: Full-Size Img PowerPoint

5.2.   Ablation studies

Our model was derived from the GRAF model by modifying the inputs and outputs of the MLP in the prototype. Therefore, we performed ablation studies by comparing the results of our model with those of its counterparts. In Table 1, we quantitatively compared the FID and KID scores of GRAF with our model under the pseudo-color mode, indicating no significant variance between the two models.

Table 1.  FID and KID Comparison for each model in the pseudo-color mode.

Class		Gun	Fork	Knife	Pliers	Scissor
GRAF	($FID$)	$43.55$	$45.25$	$80.14$	$46.92$	$55.35$
/without	($KID$)	$0.038$	$0.029$	$0.084$	$0.042$	$0.048$
Ours	($FID$)	$47.74$	$51.81$	$78.43$	$48.27$	$54.52$
/with	($KID$)	$0.042$	$0.032$	$0.079$	$0.039$	$0.050$

---

 | Show Table

DownLoad: CSV

5.3.   Synthesis of x-ray inspection images

By fusing the prohibited item image with a benign background image, we synthesized X-ray inspection images using pixel-by-pixel alpha-blending algorithms ^[20]. A schematic of the synthesis of X-ray inspection images is shown in Figure 13. Some samples of the synthesized images are shown in Figure 14. The prohibited objects were located within red bounding boxes.

Figure 13.  Schema of synthesis of X-ray inspection images based on the pix-by-pix alpha-blending algorithm.

DownLoad: Full-Size Img PowerPoint

Figure 14.  Samples of the synthesized X-ray inspection images in the pseudo-color mode. Each image comprises (Ⅰ) one prohibited item (Ⅱ), two prohibited items, or (Ⅲ) two or more overlapping prohibited items.

DownLoad: Full-Size Img PowerPoint

In the experiment, we first prepared two datasets: Dataset A, which included 2000 images selected from the real dataset, and Dataset B, which included 1000 images from the real dataset and 1000 synthesized images. Each dataset comprises five classes of prohibited items: guns, forks, knives, pliers, and scissors. The two datasets were then split into training and validation sets in a ratio of 4:1. For validation, we employed YOLOv8 ^[47] as the object detection paradigm. The model was trained on Datasets A and B separately. The training curves demonstrated that the model trained on Dataset B outperformed the model trained on Dataset A, achieving improvements of approximately 4.4$\%$ in mAP$_{0.5}$ and 11.9$\%$ in mAP$_{0.5:0.95}$.

During the inference phase, Model A was the pretrained model on Dataset A and Model B was the pretrained model on Dataset B. Both models were tested on the same test set, which comprised 500 real images from an available dataset. By evaluating the mAP values of both models in Table 2, Model B achieves superior performance over Model A, demonstrating that augmented Dataset B effectively improves the detection accuracy and generalization ability of the deep learning algorithms. We expect to further enhance the detection performance by adding additional synthesized X-ray inspection images to the training set.

Table 2.  The evaluation metrics of pretrained Models A and B on the test set.

Model	Class	P	R	mAP (0.5)	mAP (0.5:0.95)
	Gun	$0.79$	$0.81$	$0.85$	$0.56$
	Fork	$0.77$	$0.63$	$0.71$	$0.34$
Model	Knife	$0.62$	$0.52$	$0.54$	$0.30$
(A)	Pliers	$0.72$	$0.68$	$0.73\quad$	$0.47$
	Scissor	$0.71$	$0.46$	$0.60\quad$	$0.42\quad$
	$\textbf{Mean}$	$\textbf{0.72}$	$\textbf{0.62}$	$\textbf{0.68}$	$\textbf{0.42}$
	Gun	$0.93$	$0.91$	$0.92$	$0.67$
	Fork	$0.78$	$0.55$	$0.61$	$0.37$
Model	Knife	$0.65$	$0.43$	$0.56$	$0.38$
(B)	Pliers	$0.82$	$0.65$	$0.83\quad$	$0.51$
	Scissor	$0.74$	$0.51$	$0.62\quad$	$0.44\quad$
	$\textbf{Mean}$	$\textbf{0.78}$	$\textbf{0.61}$	$\textbf{0.71}\uparrow$	$\textbf{0.47}\uparrow$

---

 | Show Table

DownLoad: CSV

6.   Conclusions

In this study, we propose a novel stylized generative radiance field for the controllable synthesis of 3D-aware images. By manipulating the input and output of the conditional radiance field (MLP) and incorporating a new discriminator (VGG16), we enabled the entanglement and disentanglement of class and style labels into and from random latent vectors, thereby achieving explicit control over the generation of prohibited items. Moreover, our model can generate nonexistent images in the training set using transfer learning. The main advantages of this model are that it can learn multiple objects using a single MLP and synthesize novel views according to class and style labels. The experimental results reveal that our image generation model significantly increases the quantity and diversity of the images of prohibited items, and the augmented dataset effectively promotes the accuracy and generalization of object detection algorithms. Furthermore, our proposed model has the potential to be extended to other fields such as medial image generation. In the future, we plan to add more subclasses to a class, such as different types of guns in a gun class, enriching the diversity in the 3D geometry of prohibited items within one category.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work has been supported by Henan Province Program for Science and Technology Development under Grant No. 162102210009.

Conflict of interest

The authors declare there are no conflicts of interest.