New generalizations for Gronwall type inequalities involving a $\psi$-fractional operator and their applications

1.   Background and preliminaries

The fractional calculus is nowadays considered as an important branch of mathematics, with a positive impact on several applied sciences; see, for example, the classical monograph by Samko et al. ^[1] and Kilbas et al. ^[2]. In ^[3], Kiryakova proposed a theory of a generalized fractional calculus (generalizations of fractional integrals and derivatives) and their applications. One of the proposed generalizations of the fractional calculus operators which has wide applications is the $\psi$-fractional operator. This notion is referred to as the fractional derivative and integral of a function with respect to another function $\psi$. Several properties of this operator could be found in ^{[1,2,4,5,6,7]}. For some new developments on this topic; see ^{[8,9,10,11,12]} and references therein.

Inequalities play a vital role in both pure and applied mathematics. In particular, inequalities involving the derivative and integral of functions are very captivating for researchers ^[13]. Integral inequalities have many applications in the theory of differential equations, theory of approximations, transform theory, probability, and statistical problems and many others. Therefore, in the literature we found several extensions and significant developments for the forms of classical integral inequalities. Furthermore, the study of qualitative and quantitative properties of solution of fractional differential and integral equations requires the use of various types of integral inequalities.

As our concern is Gronwall's inequality, we state its classical form as follows.

Theorem 1.1. ^[14] Let $u\left(t\right), g\left(t\right)$ be nonnegative functions for any $t\in \left[a, T\right]$ and $\ a, T$ and $v$ be nonnegative constants such that

then

We review some recent results for the sake of comparison. In ^[15], Bellman generalized Theorem 1.1 by letting $v$ be a nonnegative and nondecreasing function, which is stated in many references such as ^[13,16]. In ^[17], Pachpatte also established the following inequality

In ^[18], Kender et al. proved the following further generalizations of inequality (1.3) by replacing the linear term of the unknown function $u$ by the nonlinear term $u^{p}$ in both sides of the inequality and obtain the following

In ^[19], Jiang and Meng discussed the following integral inequality

under the same initial condition. For further detail on Gronwall-type inequalities involving the Riemann-Liouville fractional integrals ^[20,21], for the Hadamard fractional integrals ^[22,23] and for the Katugampola fractional integrals ^[24,25], where other formulations of the Gronwall's inequality can be found via fractional integrals ^[26,27].

As one of the objectives of this article is to propose a generalized Gronwall's inequality, we state the inequality of Gronwall which was first introduced in fractional settings in ^[28]

where $u\left(t\right), v\left(t\right)$ are nonnegative functions and $g\left(t\right)$ is a nonnegative and nondecreasing function for $t\in \left[0, T\right].$ In ^[12], the Gronwall's inequality (1.6) was generalized as under

where $\psi \in \mathcal{C}^{1}[a, T]$ is an increasing function such that $\psi ^{\prime }\left(t\right) \neq 0$, $\forall \; t\in \lbrack a, T]$. Further in ^[29], Willett discussed the linear inequality

The following generalizations of the Gronwall type inequality were given in ^[30,31]

and

Oriented by above discussion, some other generalizations for the inequalities (1.1) and (1.6) have been elaborated. For relevant results; see ^{[32,33,34,35,36,37]} and the references cited therein.

The main objective of this paper is to extend Theorem 1.1, Gronwall-type inequalities (1.6), (1.7), (1.9) and (1.10) to the general case by the implementation of $\psi$-fractional operator. We claim that the results of this paper are obtained within a general platform that includes all previous forms as particular cases. As applications, we prove the existence and uniqueness of solutions for $\psi$ -fractional initial value problem and study the Ulam-Hyers stability of solutions for $\psi$-fractional differential equations. Particular examples are given to confirm the proposed results.

We continue with the definitions and properties of the fractional derivative and integral of a function $u$ with respect to given function $\psi$. These definitions are referred to as $\psi$-fractional operators.

The standard Riemann-Liouville fractional integral of order $\alpha > 0$, namely

The left-sided factional integrals and fractional derivatives of a function $u$ with respect to another function $\psi$ in the sense of Riemann-Liouville are defined as follows ^[2]

and

respectively, where $n = [\alpha]+1\ $ and $u, \psi \in \mathcal{C}^{n}[a, T]$ are two functions such that $\psi$ is increasing and $\psi^{\prime }(t)\neq 0$, for all $t\in \lbrack a, T]$.

We propose the remarkable paper ^[38] in which some generalizations using $\psi$-fractional integrals and derivatives are described. In particular, we have

where $J_{a+, t}^{\alpha }$, $^{H}J_{a+, t}^{\alpha }$ and $^{\rho }J_{a+, t}^{\alpha }$ are the classical Riemann-Liouville, Hadamard and Katugampola fractional operators, respectively.

Lemma 1.1. ^[2] Let $\alpha, \beta > 0$. Then, we have the following

and

where

Lemma 1.2. ^[6,11] Given a function $u\in C^{n}[a, T]$ and $\alpha \in (0, 1)$. Then, we have

For $\alpha, \beta > 0$, the following properties are valid

and

The next result is helpful for the investigation obtained subsequently.

Lemma 1.3. (Young's Inequality) [39, page 622] For any $A, B > 0$ and $1 < p, q < +\infty, 1/p+1/q = 1, \varepsilon > 0$, we get

where

Definition 1.1. ^[40] The Mittag-Leffler function is given by the series

where ${Re}\left(\alpha \right) > 0$ and $\Gamma \left(z\right)$ is a Gamma function. In particular

where ${erf}\left(z\right)$ error function.

We outline the structure of the paper as follows: Section $2$ is devoted to the new generalizations for the $\psi$-Gronwall-type inequality. Meanwhile, two remarks are addressed to show that the obtained forms of Gronwall-type inequality include other results as particular cases. Section $3$ provides applications for the proposed results. Firstly, we demonstrate that the new inequalities can be used as handy tools in the study of existence and uniqueness of solutions of $\psi$-fractional initial value problem. Secondly, we use the the new inequalities to investigate the Ulam-Hyers stability of $\psi$-fractional differential equations. We also give some interesting examples to illustrate the effectiveness of our main results in Section $4$. At last, the paper is concluded in Section $5$.

2.   New generalized $\psi$-Gronwall's inequality

By the same arguments of [30, Lemma 2.1], we can easily obtain the following result, which plays a very important role in proving the main results.

Lemma 2.1. For any $t\in \left[a, T\right)$,

where all functions are continuous. The constants $\alpha _{i} > 0$. $g_{i}$ $(i = 0, 1, \ldots, n)$ are bounded, nonnegative, and monotonic increasing functions on $\left[a, T\right)$, then $U\left(t\right) \geq 0$, $t\in \left[a, T\right)$.

Proof. Clearly, $U\left(a\right) \geq 0$. If the proposition is false, that is

where $\phi$ is an empty set, then there exists a point $t_{0}$ on $\left[a, T\right)$ which satisfies $\left. U\right \vert _{\left[a, t_{0} \right] }\geq 0, \ U\left(t_{0}\right) = 0$. The function $U$ is a strictly monotonic decreasing function on $\left(t_{0}, t_{0}+\varepsilon \right) \subset \left[a, T\right)$. Let $\varepsilon > 0$. Hence, for each $t\in \left(t_{0}, t_{0}+\varepsilon \right),$ we have $U\left(t\right) < 0$ and

which implies that

Let $t\longrightarrow t_{0}$, then we have a contradiction, that is, $0\geq 1$. The proof of Lemma 2.1 is completed.

In light of the approach introduced in ^[30], we generalize Gronwall's inequality as follows.

Theorem 2.1. Let $\psi \in \mathcal{C}^{1}[a, T]$ be an increasing function such that $\psi^{\prime }\left(t\right) \neq 0$, $\forall \; t\in \lbrack a, T]$. Assume that

● $(H_1)$ $u(t)$ and $v(t)$ are nonnegative functions locally integrable on $[a, T)$;

$(H_2)$ The functions $\left(g_{i}\right)_{i = 1, \ldots, n}\ $ are the bounded and monotonic increasing functions on $[a, T);$

$(H_3)$ The constants $\alpha _{i} > 0, \, \left(i = 1, 2, \ldots, n\right).$

If

then

Proof. Suppose that

By Dirichlet's formula and using the definition of Beta function, the following equality is given

From the fact that $g_{i}$ $(i = 0, 1, \ldots, n)$ are monotonic increasing functions on $\left[a, T\right)$ and $g_{i^{\prime }}\left(s\right) \leq g_{i^{\prime }}\left(t\right)$, for all $s\leq t$, we obtain

By using (2.5), the inequality (2.6) can be rewritten as

Let $j = \left(k+1\right) ^{\prime }$ then, from (2.7), we have

which implies that

Let $U\left(t\right) = w\left(t\right) -u\left(t\right)$, then we have

According to Lemma 2.1, $U\left(t\right) \geq 0$. That is, $u\left(t\right) \leq w\left(t\right)$ and $t\in \left[a, T\right)$. The proof of Theorem 2.1 is completed.

Corollary 2.1. Under the hypotheses of Theorem 2.1, assume further that $u\left(t\right)$ is a nondecreasing function for $t\in \left[a, T\right)$, then

where $E_{\alpha _{i}}$ is the Mittag-Leffler function.

Proof. From (2.4) and $v\left(t\right)$ is a nondecreasing function for $t\in \left[a, T\right),$ we have

Then, with the help of (1.12) and Lemma 1.1, it follows that

The proof is completed.

Remark 2.1. From Theorem 2.1, we have the following particular cases as follows:

● ● If $n = 1$, then Theorem 2.1 reduces to inequality (1.7) which itself contains, as a special case, the inequalities (1.1) and (1.6).

● If $n = 2$, then Theorem 2.1 reduces to the inequality given by [28,Theorem 2].

Remark 2.2. From Theorem 2.1, we have the following particular cases in the general forms of Gronwall's inequality as follows:

● ● If $\psi(t) = t$, then the inequality given by [30,Theorem 1.4] reduces to the Gronwall's inequality for Riemann-Liouville fractional integral operator.

● If $\psi (t) = \ln t$, then the inequality given by [30,Theorem 1.5] reduces to the Gronwall's inequality for Hadamard fractional integral operator.

● If $\psi (t) = t^{\rho }$, then the inequality given by [24,Theorem 2.1. with $n = 1$] reduces to the Gronwall's inequality for Katugampola fractional integral operator.

With the help of this Theorem 2.1, we have the following results.

Theorem 2.2. Let $\psi \in \mathcal{C}^{1}[a, T]$ be an increasing function such that $\psi ^{\prime }\left(t\right) \neq 0$, $\forall \; t\in \lbrack a, T]$. Assume that $(H_1)$ holds and

● $(H_4)$ The functions $\left(g_{i}\right)_{i = 1, \ldots, n}$ and $\left(c_{i}\right)_{i = 1, \ldots, n}$ are the bounded and monotonic increasing functions on $[a, T);$

$(H_5)$ The constants $0 < \alpha _{1} < \alpha _{2} < \cdots < \alpha _{n}\leq 1$ and $0 < \lambda _{i} < 1, \, \left(i = 1, 2, \ldots, n\right)$.

If

then

where

and

Here $\varepsilon$ is an arbitrary given positive number.

By Young's inequality (Lemma 1.3), we have

which implies that, for any $t\in \left[a, T\right]$

Hence, we have

Consequently,

The proof is completed.

Corollary 2. Let $\psi \in \mathcal{C}^{1}[a, T]$ be an increasing function such that $\psi ^{\prime }\left(t\right) \neq 0$, $\forall \; t\in \lbrack a, T]$. Assume that $(H_1)$, $(H_4)$ hold and

● $(H_6)$ The constants $0 < \alpha _{1} = \alpha _{2} = \alpha _{n} = 1$ and $0 < \lambda_{i} < 1\, \left(i = 1, 2, \ldots, n\right)$.

If

then

where

and $\tilde{g}_{i^{\prime }}\left(t\right) = \varepsilon g_{i}\left(t\right)$ is defined by $(2.12)$ for $i = 1, \ldots, n$.

Remark 2.3. From Theorem 2.2, we have the following particular cases:

● ● If $n = 1$, then Theorem 2.2 reduces to one of the well-known Gronwall's inequality.

● If $\lambda _{i} = 1$ or $\lambda _{i} = 0$ $\left(i = 1, \ldots, n\right)$, then it reduces to one of the well-known Gronwall's inequality.

● If $\psi (t) = t^{\rho }$, then

● If $\rho \to 1$, then the inequality given by [31,Theorem 4.] and [36,Theorem 2.1] reduces to the Gronwall's inequality for Riemann-Liouville fractional integral operator.

● If $\rho \to 0^{+}$, then the inequality given by [31,Theorem 5] reduces to the Gronwall's inequality for Hadamard fractional integral operator.

We conclude that Theorem 2.2 is more general than [31,Theorem 4 or Theorem 5].

3.   Some applications

In this section, we present some applications of Theorem 2.1 and Theorem 2.2 to obtain the existence and uniqueness of the solution for $\psi$-fractional initial value problem. Further, we apply the main results of this work to study the stability of the $\psi$-fractional differential equations.

3.1.   Existence and uniqueness

Consider the initial value problems with the $\psi$-fractional derivative

where $0 < \alpha _{1} < \alpha _{2} < \cdots < \alpha _{n} < 1$, $D_{a+, t}^{\alpha _{i}, \psi }$, $J_{a+, t}^{\alpha _{i}, \psi }$ denote the left-sided of fractional derivative and fractional integral operators of a function $u$ with respect to another function $\psi$ in the sense of Riemann-Liouville, $f\in \mathcal{C}([a, T]\times \mathbb{R}, \mathbb{R})$ and $\delta \in \mathbb{R}$.

The following lemma presents the uniqueness of solution for the initial value problem (3.1). For simplicity of presentation, we set $f_{u}\equiv f\left(t, u\left(t\right) \right).$

Lemma 3.1. For each $t\in \left[a, T\right)$, suppose that $\gamma \left(t\right) \geq 0$ is a bounded and monotonic increasing function and

If the initial value problem $(3.1)$ has a solution, then the solution is unique.

Proof. The proof will be given in two claims.

Claim 1. Since $0 < \alpha _{1} < \alpha _{2} < \ldots < \alpha_{n} < 1$, then according to Lemma 1.2, we get

where $c_{i}$, $(i = 1, 2, \ldots, n)$ are some real numbers. By (3.3) and (1.15) we also have

Applying the fractional integral operator $\left(J_{a+, t}^{1-\alpha _{n}, \psi }\right)$ to both sides of (3.4), we get

Hence, we have

We obtain

By (3.5), we have

Since

Claim 2. Let $u_{1}$ and $u_{2}$ be two solutions of (3.1). Then from (3.6) and (3.2), we get

which yields

Therefore, we can conclude that

Then the initial value problem (3.1) has at most one solution. The proof is completed.

Consider the following fractional system with the $\psi$-fractional derivative

where $0 < \alpha _{1} < \alpha _{2} < \cdots < \alpha _{n} < 1$, $D_{a+, t}^{\alpha _{i}, \psi }$, $J_{a+, t}^{\alpha _{i}, \psi }$ denote the left-sided of fractional derivative and fractional integral operators of a function $u$ with respect to another function $\psi$ in the sense of Riemann-Liouville, $f, g\in \mathcal{C}([a, T]\times \mathbb{R}, \mathbb{R})$ and $\delta _{1}, \delta _{2}\in \mathbb{R}$.

We have the following lemma.

Lemma 3.2. Let $f, g:\left[a, T\right] \times \mathbb{R}\to \mathbb{R}$ be two continuous functions and let $u, v$ be solutions of the two systems (3.9). Assume that the following assumptions hold:

● $(A_1)$ There exists a positive constant $c$ such that

$(A_2)$ There exists a continuous function $\chi :\left[a, T\right] \to \mathbb{R}_{0}^{+}$ such that

Then, for all $t\in \left[a, T\right]$, we have the following inequality:

where the function $w:\left[a, T\right] \to \mathbb{R}$ is defined by

Proof. With the help of ($A_{1}$) and ($A_{2}$), it follows that

Setting

By applying Theorem 2.1 to (3.12), the desired inequality (3.10) is obtained. This completes the proof.

Remark 3.1. In particular, when $f = g$ then $\chi \left(t\right) \equiv 0,$ we obtain a simpler formula (3.10) with

In view of inequality (3.10) with (3.14), we see that the solution of system (3.9) is unique.

Consider the following fractional system

where all functions are continuous. Moreover, $h_{i}\left(t\right) > 0$ and the constants $\lambda_{i}$, $\alpha _{i} > 0$ ($i = 1, 2, \ldots, n$). Consider $\lambda _{0} > 0$, $\delta \in \mathbb{R}$ and $\max \left \{ \alpha _{i}:i = 1, 2, \ldots, n\right \} < \alpha _{n+1} < 1.$

By applying similar arguments to the technique used in Lin ^[31], we can conclude the following result.

Lemma 3.3.. Suppose that

● $(A_3)$ The function $h_{n+1}\left(t\right) > 0$ is continuous and the constant $\lambda_{n+1}\in \left(0, 1\right)$, such that

for any $t\in \left[a, T\right]$ and for all $u_{1}, u_{2}\in \mathbb{R}$.

(i) If $\max \left \{ \lambda _{i}:i = 1, 2, \ldots, n+1\right \} < \lambda _{0}$, then for any solution $u\left(t\right)$ of the problem (3.15), we get

where

and

(ii) If $\min \left \{ \lambda _{i}:i = 1, 2, \ldots, n+1\right \} \geq \lambda _{0}$, then the continuous solution of problem (3.15) is unique.

(i) Since $\max \left \{ \alpha _{i}:i = 1, 2, \ldots, n\right \} < \alpha _{n+1} < 1,$ by using Lemma 1.1 and Lemma 1.2, we obtain

It follows from (3.16) and (1.15) that

which, together with (1.15) and (1.20), imply that

From Lemma 1.2, we have

From (3.19), we have

From the condition (3.15) and (3.20), we have

and

Let $w\left(t\right) = u^{\lambda _{0}}\left(t\right)$ and applying (3.16) and (3.21), given the fact that

obtains the following

Rearranging the terms of (3.22), and by using condition (3.16), we obtain

which gives

If $\max \left \{ \lambda _{i}:i = 1, 2, \ldots, n+1\right \} < \lambda _{0}$, then, for any $\left(i = 1, 2, \ldots, n+1\right),$ $\frac{\lambda _{i}}{ \lambda _{0}} < 1$. Setting, for any $t\in \left[a, T\right]$,

By virtue of Theorem 2.2, we obtain

where the expression of $\tilde{v}\left(t\right)$ is shown in (3.18). Hence, the conclusion of (i) is derived.

(ii) We assume that problem (3.15) has two continuous solutions $u_{1}$ and $u_{2}$. Combining with the fact that $h_{i}\left(t\right) \in \mathcal{ C}([a, T], \mathbb{R})$ for any $i = 1, \ldots, n+1$ and the boundedness of the continuous function on a closed interval, there exists a finite number $M$ which satisfies that, for any $t\in \left[a, T\right],$

Cauchy's mean value theorem provides the following inequality

where $\xi _{i},$ $i = 1, \ldots, n+1,$ are the numbers between $u_{1}\left(t\right)$and $u_{2}\left(t\right)$. The following estimation is deduced by applying (3.23) and the hypothesis of $\lambda _{0}\leq \min \left \{ \lambda _{i}:i = 1, 2, \ldots, n+1\right \}$ in (ii)

holds for any $t\in \left[a, T\right] \ $and $i = 1, \ldots, n+1$. Therefore, (3.21), (3.23), and (3.24) give

According to Theorem 2.2, we have

which means that $u_{2}^{\lambda _{0}}\left(t\right) = u_{1}^{\lambda _{0}}\left(t\right).$ This completes the proof of (ii).

3.2.   Ulam-Hyers stability

In this subsection, we study the Ulam-Hyers stability of the initial value problem (3.1).

Remark 3.2. For every $\epsilon > 0,$ a function $u_{\varepsilon }\in \mathcal{C}([a, T], \mathbb{R})$ is a solution of the inequality

if and only if there exists a function $h\in \mathcal{C}([a, T], \mathbb{R})$, (which depends on $u_{\varepsilon }$) such that

(i) $\left \vert h\left(t\right) \right \vert \leq \epsilon, \ \forall t\in \left[a, T\right].$

(ii) $\sum_{i = 1}^{n}\left(D_{a+, t}^{\alpha _{i}, \psi }\right) \left[u\right] = f\left(t, u\left(t\right) \right) +h\left(t\right).$

Lemma 3.4.. Assume that $f_{u_{\varepsilon }}$ is a continuous function that satisfies (3.2). The Eq (3.1) is Ulam-Hyers stable with respect to $\psi \ $if there exists a real number $C_{\epsilon } > 0$ such that for each $\epsilon > 0$ and for each solution $u_{\varepsilon }\in \mathcal{C}^{1}\left(\left[a, T\right], \mathbb{R}\right)$ of the inequality (3.25)$, \ $there exists a solution $u^{\ast }\in \mathcal{C} ^{1}\left(\left[a, T\right], \mathbb{R}\right)$ of (3.1) with

Proof. If $u_{\varepsilon }$ is a solution to (3.25), then $u_{\varepsilon }$ is a solution to the problem

For each $t\in \left[a, T\right]$, one has

Then, it follows that

In virtue of (2.3), one has

where

Setting

By using Corollary 2.1, we obtain

Therefore

This shows that (3.26) holds. The proof is completed.

4.   Particular examples

In this section, we provide some particular examples that validate and confirm the proposed theorems.

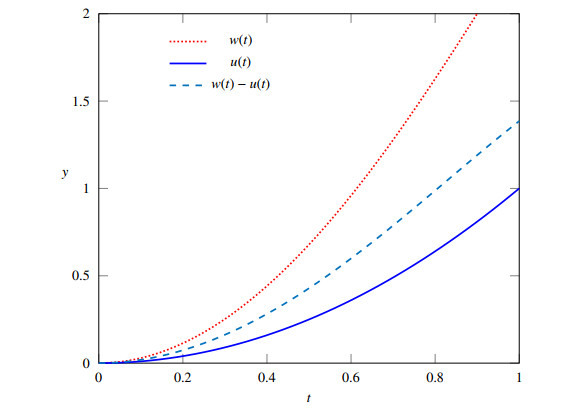
Example 4.1. we consider the linear inequality as follows

Here $n = 3$, $\alpha _{1} = 1/2$, $\alpha _{2} = 1$, $\alpha _{3} = 2$, $\psi (t) = t$, $g_{i}\left(t\right) = 1/2\Gamma \left(\alpha _{i}\right)$, $i = 1, 2, 3$ and

By equality (4.2), we derive that $v\left(t\right)$ is nonnegative and increasing on $[0, 1]$. According to Corollary 2.1, we have

it can be seen that the values of exact solution the linear integral equation

is $u\left(t\right) = t^{2}$. In Figure 1, we plot the graphs of estimated bound of $w\left(t\right)$, $u\left(t\right)$ and $w\left(t\right)-u\left(t\right)$ for $t\in \left[0, 1\right)$.

Example 4.2. Consider the following initial value problems with the $\psi$-fractional derivative of the form:

Here $n = 3$, $\alpha _{1} = 1/8$, $\alpha _{2} = 1/4$, $\alpha _{3} = 1/2$ with $0 < \alpha _{1} < \alpha _{2} < \alpha _{3} < 1$, $\psi (t) = t$, $\delta = 0$, and

It follows that the inequality

From (3.2) with the above inequality, we get the function $\gamma (t) = t/2$ is a bounded and monotonic increasing on $t\in \lbrack 0, 1]$. It is easy to see that the function $u(t) = t^{2}$ is a solution of the initial value problem (4.5). Since all assumptions of Lemma $3.1$ are satisfied, then the problem (4.5) has a unique solution on $[0, 1]$. Furthermore, we can also compute that the real number

Therefore, by Lemma $3.4$, the problem (4.5) is Ulam-Hyers stable with respect to $\psi$ on $[0.1]$.

Example 4.3. Consider the following fractional system with the $\psi$-fractional derivative of the form:

Here $n = 1$, $\alpha _{1} = 1/2$ with $\psi (t) = t$, $\delta _{1} = 1/2$, $\delta _{2} = 1/3$ and for $t\in \lbrack 0, 1]$,

It follows that the inequalities

The assumption $(A_{1})$-$(A_{2})$ of Lemma $3.2$ are satisfied with the positive constant $c = 1/4 > 0$ and the continuous function $\chi (t) = t^{2}/4$. Then, for all $t\in \lbrack 0, 1]$, we have the following inequality

where $w\left(t\right) = 1/(6\sqrt{t\pi })+(4t^{5/2})/(15\sqrt{\pi })$.

Example 4.4. Consider the following fractional system of the form:

Here $n = 2$, $\alpha _{1} = 1/2$, $\alpha _{2} = 2/3$, $\alpha _{3} = 3/4$, $\psi (t) = e^{t}$, $\delta = 0$, $h_{i}(t) = (e^{t}+i-1)^{1-2\lambda _{i}}$, for $i = 1, 2$ and

For $u_{1}$, $u_{2}\in \mathbb{R}$, we have

The assumption $(A_{3})$ of Lemma $3.3$ is satisfied with the continuous function $h_{3}(t) = (1/6)(e^{t}+2)^{\left(1-2\lambda _{3}\right) } > 0$ for $t\in \lbrack 0, 1]$ and the constant $\lambda _{3} = 1/6\in (0, 1)$.

(i) If we set $\lambda _{0} = 1/2$, $\lambda _{1} = 1/3$ and $\lambda _{2} = 1/4$, we get that $\max \{ \lambda _{1}, \lambda _{2}, \lambda _{3}\} < \lambda _{0}$. Then, for any solution $u(t)$ of the problem (4.8), we can estimate that

where

and

Since $v\left(t\right)$ is nonnegative and increasing, $\tilde{v}\left(t\right)$ is also nonnegative and increasing, where

and

and

In Figure 2, we plotted the graph of $\tilde{v}\left(t\right) = \tilde{v}\left(t, \varepsilon \right) \ $for $t\in \left[0, 1\right)$ with $\varepsilon = 10^{-3}, 10^{-2}, 10^{-1}, 1, 10$ and $10^{2}$.

(ii) If we set $\lambda _{0} = 1/2$, $\lambda _{1} = 1/2$ and $\lambda _{2} = 3/4$, we get that $\min \{ \lambda _{1}, \lambda _{2}, \lambda _{3}\} \geq \lambda _{0}$. Then the continuous solution of problem (4.8) is unique.

5.   Conclusions

In this paper, we introduced new generalizations for Gronwall's inequality within the $\psi$-fractional integral operators. The results of this paper provide general forms of Gronwall's inequality that include the forms obtained in ^[12,30,31]. Furthermore, Gronwall's inequalities involving fractional integrals of Riemann-Liouville, Hadamard and Katugampola types as well as fractional integrals of a function with respect to another function are recovered for particular cases of function $\psi$.

To examine the validity and applicability of our results, we discussed the existence and uniqueness of solutions of $\psi$-fractional initial and boundary value problems which are an important and useful contributions to the existing theory. On the other hand, the stability of $\psi$-fractional differential equations was studied via the obtained generalized $\psi$ -Gronwall's inequality. Interesting examples are discussed at the end for the sake of confirming the results.

Reported results in this paper can be considered as a promising contribution to the theory of fractional integral inequalities. These results can be used to study and develop further quantitative and qualitative properties of generalized fractional differential equations.

Acknowledgement

J. Alzabut would like to thank Prince Sultan University for supporting and fundingthis work.

Conflict of interest

The authors declare that they have no competing interests.

Author's contributions

All authors contributed equally and significantly to this paper. All authors have read and approved the final version of the manuscript.