Progression and transmission of HIV (PATH 4.0)-A new agent-based evolving network simulation for modeling HIV transmission clusters

1.   Introduction

In this paper, we consider the infectious disease transmission models. Denoted by $S(t)$, $I(t)$, and $R(t)$, the numbers of susceptible, infective, and recovered or removed individuals at time $t$, respectively. The classical susceptible-infective-recovered-susceptible (SIRS) model has the form

where $b > 0$ and $d > 0$ represent the recruitment rate and the natural death rate of population respectively, $\mu > 0$ expresses the natural recovery rate of the infective individuals, and $\delta > 0$ denotes the rate at which recovered individuals lose immunity and return to the susceptible class. $g(I)S$ is the incidence rate, and $g(I)$ measures the infection force of a disease.

In most epidemic models, the incidence rate adopts the form of mass action with bilinear interactions, namely $g(I)S = k IS$, where the constant $k$ is the probability of transmission per contact and $g(I) = k I$ is unbounded when $I\geq0$. The model (1.1) with $g(I) = k I$ usually has at most one endemic equilibrium and has no period orbit. The disease will die out if the basic reproduction number is less than one and will persist otherwise (see Hethcote ^[4]). Recently, different types of nonlinear incidence rates have been applied in the study of epidemic diseases. For example, Liu et al. ^[5] proposed a general nonlinear incidence rate defined by

where $k I^p$ measures the infection force of the disease, $1/(1+\alpha I^q)$ describes the inhibition effect from the behavioral change of the susceptible individuals when the number of infectious individuals increases (see Capasso and Serio ^[6]). $\alpha\geq 0$ measures the psychological or inhibitory effect, $p, \, k, \, q$ are real constants with $p > 0, \, \, k > 0, \, \, q\geq 0$. Note that $g(I)S = kSI$ in (1.2) if $\alpha = 0$ and $p = 1$.

For general $p$ and $q$, Hu et al. in ^[1] studied the SIRS model (1.1) with (1.2). For simplicity, they considered the reduced system

By calculation, $E(I^*, R^*)$ is a positive equilibrium of system (1.3) if and only if $I^* > 0$ satisfies

where

It was shown in ^[1] that the model (1.3) can have very rich and complex dynamical behaviors. More precisely, system (1.3) can have multiple endemic equilibria and different types of bifurcations, including Hopf and Bogdanov-Takens bifurcations. Note that the expressions of the positive equilibria cannot be explicitly expressed for general $p$ and $q$. They only gave the calculation formula of the first Lyapunov constant of the unique positive equilibrium (if it is linearly a center), which can be found in many books. In addition, the first Lyapunov constant is a very complex function of $I^*$. In other words, the exact codimension of Hopf bifurcation remains unknown. Furthermore, the conditions for determining the codimension of Bogdanov-Takens bifurcation are complex functions of $I^*$. Thus, they can not determine the maximum codimension of Bogdanov-Takens bifurcation.

In the paper ^[3], the nonlinear function $g(I)$ is classified into the three types: unbounded incidence function with $p > q$, saturated incidence function with $p = q$, and nonmonotone incidence function $p < q$. The results on the dynamics of system (1.1) can be found in ^{[2,3,6,7,8,9,10,11]} and reference therein.

For saturated incidence function with $p = q$, as early as $1991$, Hethcote and van den Driessche ^[7] showed that Hopf bifurcation can occur in system (1.1) with saturated incidence rate (1.2) (when $q = p$). For similar reasons as in ^[1], they did not determine the exact codimension of Hopf bifurcation. For the special case of $q = p = 1$, Gomes et al. ^[12] showed the existence of backward bifurcations, oscillations, and Bogdanov-Takens points in SIR and SIS models. For the special case of $q = p = 2$, system (1.1) with (1.2) was analysed by Ruan and Wang in ^[2]. It was shown that it can undergo Bogdanov-Takens bifurcation of codimension two and Hopf bifurcation of codimension one. Later, Tang et al. in ^[3] calculated the higher order Lyapunov constants of the weak focus and proved that the maximal order of the weak focus is two. They also obtained the coexistence of a limit cycle and a homoclinic loop. Recently, Lu et al. ^[13] considered a more general model and proved that the codimension of Bogdanov-Takens bifurcation is at most two. These results indicate that the case $q = p > 1$ may be very complicated and deserves further investigation.

Although a lot of work on SIRS models have been obtained, there are still a lot of open problem for it. In order to understand the dynamical behavior of system (1.1) and also motivated by the works in ^[1], ^[2], ^[3], ^[7] and ^[13], we focused on the model (1.1) with a general saturated incidence rate $k I^p/(1+\alpha I^p)$, i.e., the case $q = p$ in (1.2). Based on the results of ^[1], the model with $p\leq 1$ has the simple dynamics. Hence, we study the SIRS epidemic model (1.1) with $q = p > 1$ in this paper, i.e., the system defined as

where $S(0)\geq 0$, $I(0)\geq 0$, $R(0)\geq 0$ and $k, \alpha, b, d, \mu, \delta > 0, p > 1$.

For general $p > 1$, to study the model (1.5), one of the difficulties is that the coordinate of positive equilibria cannot be explicitly expressed for $p$. The second difficulty is that the model of this type is often not a polynomial differential system or can not transformed into a polynomial differential system. Finally, another difficulty is the lack of the methods to determine the order of a weak focus. In this paper, we will provide some available methods and techniques to overcome these difficulties, and perform qualitative and bifurcation analysis of system (1.5). We find that system (1.5) have the complicated dynamical behaviors and bifurcation phenomena like the special case of $p = 2$. It is shown that the codimension of Bogdanov-Takens bifurcation is at most two, which coincides with the corresponding results for $p = 2$ in ^[13]. In addition, This also improves the results for $p = 2$ in ^[2] and ^[3]. Moreover, our results on Hopf bifurcation coincides with the ones for $p = 2$ in ^[3] and ^[13], and also can be seen as a complement of the results for $p = 2$ obtained in ^[1] and ^[2]. Furthermore, there exist some critical values $\alpha = \alpha_0$ (i.e., $b = b_0$ or $\delta = \delta_0$) and $\delta = \delta_2$ such that: (i) if $\alpha > \alpha_0$ (i.e., $b < b_0$, or $\delta < \delta_0$), the disease will die out; (ii) if $\alpha = \alpha_0$ (i.e., $b = b_0$, or $\delta = \delta_0$) and $\delta\leq \delta_2$, the disease will die out for almost all positive initial populations; (iii) if $\alpha = \alpha_0$ (i.e., $b = b_0$, or $\delta = \delta_0$) and $\delta > \delta_2$, the disease will persist in the form of a positive coexistent steady state for some positive initial populations; and (iv) if $\alpha < \alpha_0$, the disease will persist in the form of multiple positive periodic coexistent oscillations and coexistent steady states for some positive initial populations.

Though the SIRS epidemic models with nonlinear incidence rates have been extensively studied, to the best of our knowledge, this is the first time that the exact codimension of Hopf bifurcation and Bogdanov-Takens bifurcation have been determined in epidemic model for general parameter. It is worth mentioning that the difficulties of study of system (1.5), as mentioned above, are not only a common problem of other infectious disease models, but also a common problem of chemical molecular reaction models, physical systems, etc. The methods and techniques developed in this paper can be applied to study most of the complex dynamical systems.

The rest of this paper is organized as follows. In Section $2$, we give some preliminary results. Section $3$ is devoted to study saddle-node bifurcation, Bogdanov-Takens bifurcation and Hopf bifurcation, and illustrate these results by simulation.

2.   Preliminary results

In this section, we are going to provide some preliminary results, which are the basis for proving the main results.

2.1.   Model reduction

To simplify the system (1.5), we first give the following lemma.

Lemma 2.1. System $(1.5)$ has the invariant manifold defined by $S(t)+I(t)+R(t) = b/d$, which is attracting in the first quadrant.

Proof. Let $N(t) = S(t)+I(t)+R(t)$. It follows from (1.5) that

Obviously, $N(t) = b/d$ is a stable equilibrium of the above equation, which implies the conclusion.

It follows from Lemma 2.1 that the plane $S(t)+I(t)+R(t) = b/d$ is a limit set of system (1.5) and all important dynamical behaviors of (1.5) are on this plane. Thus, in the rest of this paper we consider the following limit system in the first quadrant

Denote

Obviously $\mathcal{D}$ is a positive invariant set of system (2.1).

Take the scalings

to get

where we rewrite $\tau$ into $t$, and

which give

The positively invariant set $\mathcal{D}$ becomes

The dynamics generated by system (2.2) and (2.1) in $\mathcal{D}$ are topological equivalent. Hence we only need to study system (2.2) in the region $\mathcal{D}$ with parameters satisfying the conditions (2.4).

Remark 2.2. In the rest of this paper, we study system $(2.2)$ in $\mathcal{D}$ with the assumption that the inequlities in $(2.4)$ hold.

2.2.   Analysis of equilibria of system (2.2)

$E_0(0, 0)$ is always an equilibrium of system (2.2). The Jacobian matrix of system (2.2) at $E_0$ is

which has two negative eigenvalues $-m$ and $-1$. Thus, $E_0(0, 0)$ is a stable hyperbolic node.

Denote by $E(\bar{x}, \bar{y})$ a positive equilibrium of system (2.2). Then

in the interval $(0, A/(n+1))$, or

where

A direct computation shows that

where

It is obvious that $h'(x)$ has a unique positive root at $x = x_{*}$. Therefore, $h(x)$ has no positive zero if $h(x_{*}) > 0$, or has a unique positive zero at $x = x_{*}$ if $h(x_{*}) = 0$, or has two positive zeros at $x = x_1$, $x_2$ with $0 < x_1 < x_{*} < x_2$ if $h(x_{*}) < 0$. Notice that $h(A/(n+1)) > 0$, which means $x_2 < A/(n+1)$. By calculation, $h(x_*) < 0$ is equivalent to $A > A_{*}$, i.e., $\beta < \beta_{*}$, or $n < n_{*}$, where

Theorem 2.3. Let $x_{*}$, $A_{*}$, $\beta_{*}$ and $n_{*}$ are given by $(2.8)$ and $(2.9)$. System $(2.2)$ always has a disease-free equilibrium $E_0(0, 0)$. Moreover, for system $(2.2)$,

(I) if $A < A_{*}$ (i.e., $\beta > \beta_{*}$, or $n > n_{*}$), then there is no positive equilibrium;

(II) if $A = A_{*}$ (i.e., $\beta = \beta_{*}$ or $n = n_{*}$), then there is a unique positive equilibrium at $E_*(x_{*}, y_{*})$;

(III) if $A > A_{*}$ (i.e., $\beta < \beta_{*}$, or $n < n_{*}$), then there are two positive equilibria at $E_1(x_1, y_1)$ and $E_2(x_2, y_2)$, where $0 < x_1 < x_{*} < x_2 < 2x_{*}$.

Notice that $E_0(0, 0)$ is a stable node. According to the index theory, since $\mathcal{D}$ is positively invariant, system (2.2) has no limit cycle in $\mathcal{D}$ if it has no equilibrium. By Theorem 2.3(I), we have the following result.

Theorem 2.4. The disease-free equilibrium $E_0(0, 0)$ of system $(2.2)$ is globally asymptotical stable in $\mathcal{D}$ if $A < A_{*}$ (i.e., $\beta > \beta_{*}$, or $n > n_{*}$).

By Theorem 2.4, we get the following corollary.

Corollary 2.5. The disease-free equilibrium $(b/d, 0, 0)$ of system $(1.5)$ is globally asymptotical stable in the interior $\mathbb{R}^3_+$ and the disease will die out if $A < A_{*}$ (i.e., $\beta > \beta_{*}$, or $n > n_{*}$).

Remark 2.6. From $(2.3)$ and Theorem 2.4, we obtain that $A < A_{*}$ is equivalent to $\alpha > \alpha_0$ or $b < b_0$ or $\delta < \delta_0$ by calculation, where

Therefore, the disease will die out if either $\alpha > \alpha_0$, or $b < b_0$, or $\delta < \delta_0$.

Remark 2.7. When $p = 2$, it follows from Remark 2.6 that

which coincides with the $\alpha_0$ in Remark 2.1 of ^[13] when $\beta = 0$.

Next consider the positive equilibrium $E(\bar{x}, \bar{y})$ of system (2.2), whose coordinate satisfies

The Jacobian matrix of system (2.2) at $E(\bar{x}, \bar{y})$ is

where

which gives

and its sign is determined by $h'(\bar{x})$, where $h'(x)$ is defined in (2.7).

The trace of $J(E)$ is

where

To study the positive equilibria, let

Note that $p > p_{1}$ if and only if $n_{1} > 0$.

Theorem 2.8. If $A = A_{*}$, then system $(2.2)$ has a unique equilibrium at $E_{*}(x_{*}, y_{*})$ in $\mathcal{D}$.

(I) If (i) $1 < p\leq p_{1}$, or (ii) $p > p_{1}$, $n\neq n_{1}$, then $E_{*}$ is a saddle-node.

(II) If $p > p_{1}$ and $n = n_{1}$, then $E_{*}$ is a cusp of codimension two.

Proof. If $A = A_*$, it follows from Theorem 2.3 that system (2.2) has a unique positive equilibrium $E_{*}(x_{*}, y_{*})$, where $x_{*}$ is given by (2.8) satisfying $h(x_{*}) = h'(x_{*}) = 0$, and $y_{*} = nx_{*}$. This implies $\text{Det}\left(J(E_{*})\right) = 0$. It follows from $h(x_{*}) = 0$ and (2.8) that

Substituting it into $S_T(x_{*})$, we get

If $mp-m-1\leq 0$, i.e., $1 < p\leq p_{1}$, then $S_T(x_{*}) < 0$. Assume that $mp-m-1 > 0$, i.e., $p > p_{1}$, then $S_T(x_{*}) < 0$ if and only if $n < n_{1}$, $S_T(x_{*}) > 0$ if and only if $n > n_{1}$ and $S_T(x_{*}) = 0$ if and only if $n = n_{1}$, respectively.

(I) Suppose either $1 < p\leq p_{1}$, or $p > p_{1}$ and $n\neq n_{1}$. Then $\text{Tr}\left(J(E_*)\right)\not = 0$ and $\text{Det}\left(J(E_*)\right) = 0$, which imply that $0$ and $J_{11}(E_*)-1 = \text{Tr}(J(E_*))\not = 0$ are eigenvalues of the matrix $J(E_*)$. Taking the changes $X = x-x_{*}, \, \, Y = y-y_{*}$ and $\bar X = -n X+J_{11}(E_*)Y, \, \, \bar Y = -n X+Y, \, \, \tau = \text{Tr}\left(J(E_*)\right)t$, system $(2.3)$ is written as (for simplicity, still denote $\bar X, \, \bar Y, \, \tau$ by $x, \, y, \, t$, respectively)

where $\eta_2, \eta_3, \eta_4$ are real numbers, and it follows from (2.11) that

Solving the equation $y+Q_2(x, y) = 0$, we get that $y(x) = -\eta_1x^2+\cdots$, which implies that $P_2(x, y(x)) = \eta_1x^2+\cdots$. By Theorem 7.1 of Chapter 2 in ^[14], the origin is a saddle-node of system (2.12). This proves the assertion (I).

(II) Suppose that $A = A_{*}$ and $n = n_{1}$. Let $X = x-x_{*}, \, Y = y-y_{*}$. Then system (2.2) takes the form (rewrite $X$, $Y$ into $x, y$, respectively)

where

Let $X = x$, $Y = x-y/n_1$ to get (rewrite $X$, $Y$ into $x, y$, respectively)

Taking the change $z = y+ (a_2+a_3 n_1) x^2-a_3 n_1 xy+o(\mid(x, y)^2\mid), t = (1+ a_3n_1 x)\tau$, system $(2.14)$ is reduced to the following system in the small neighborhood of $(0, 0)$

Let $Y = z(1+a_3n_1 x)$ and rewrite $Y$ as $y$. We have

where

Since $n_1-\beta = (1+\beta+m\beta)/(mp-m-1)\neq 0$, we have $a_2+a_3 n_1\neq 0$ and $2 a_2+a_3 n_1\neq 0$. By the results in ^[15], $E_{*}(x_{*}, y_{*})$ is a cusp of codimension two.

Theorem 2.9. If $A > A_{*}$ (i.e., $\beta < \beta_{*}$ or $n < n_{*}$), system $(2.2)$ has two positive equilibria $E_1(x_1, y_1)$ and $E_2(x_2, y_2)$, where $0 < x_1 < x_{*} < x_2 < 2x_{*}$. Moreover, $E_1$ is always a saddle point, and $E_2$ is

(I) a stable focus (or node) if $S_T(x_2) < 0$; or

(II) a weak focus (or a center) if $S_T(x_2) = 0$; or

(III) an unstable focus (or node) if $S_T(x_2) > 0$, where $S_T$ is given in $(2.10)$.

Proof. The first half of the theorem holds by Theorem 2.3. To determine the types of $E_1$ and $E_2$, consider the signs of $h'(x_1)$, $h'(x_2)$, $S_T(x_1)$ and $S_T(x_2)$, where $h'(x)$, $S_T(x)$ are given in $(2.7)$ and $(2.10)$, respectively. Noting $0 < x_1 < x_* < x_2$ (cf. Theorem 2.3), we have $h'(x_1) < 0 < h'(x_2)$. This follows that the Jacobian determinants at $E_1$ and $E_2$ satisfy $\text{Det}\left(J(E_1)\right) < 0$ and $\text{Det}\left(J(E_2)\right) > 0$, respectively. Hence we obtain the types of $E_1$ and $E_2$.

3.   Bifurcation analysis

We are going to investigate various bifurcations in system $(2.2)$ in this section.

3.1.   Saddle-node bifurcation

From Theorem 2.8, we know that the surface

is the saddle-node bifurcation surface under the assumption (2.4). On one side of this surface there is no equilibrium and on the other side there are two equilibria.

3.2.   Bogdanov-Takens bifurcation

In this subsection, we study the Bogdanov-Takens bifurcation of codimension two for system (2.2).

Theorem 3.1. If $A = A_{*}$, $n = n_1$, $p > p_1$ and conditions $(2.4)$ hold, then the unique positive equilibrium $E_*(x_*, y_*)$ is a cusp of codimension two (i.e., Bogdanov-Takens singularity), and system $(2.2)$ undergoes Bogdanov-Takens bifurcation of codimension two in a small neighborhood of $E_*(x_*, y_*)$ when we choose $A$ and $n$ as bifurcation parameters. Hence, there are different parameter values such that system $(2.2)$ has an unstable limit cycle or an unstable homoclinic loop.

Proof. Consider the system

in a small neighborhood of the equilibrium $E_*(x_*, y_*)$, where $\lambda_1$ and $\lambda_2$ are small parameters. To convenience, in below the functions $P_1(x, y, \lambda_1, \lambda_2)$ and $Q_i(x, y, \lambda_1, \lambda_2), \, \, i = 1, 2, 3, 4$, are $C^\infty$ functions at least of third order with respect to $(x, y)$, whose coefficients depend smoothly on $\lambda_1$ and $\lambda_2$, .

Taking the changes $X = x-x_*$, $Y = y-y_*$, system (3.1) is rewritten as (we still denote $X$, $Y$ by $x$, $y$, respectively)

where

Let

System (3.2) takes the form (we rewrite $X$, $Y$ as $x$, $y$, respectively)

with

Next let $dt = (1-c_6 x)d \tau$. System (3.3) takes the form (still denote $\tau$ by $t$)

Let $X = x$, $Y = y(1-c_6 x)$, and rewrite $X$, $Y$ as $x$, $y$ respectively. System (3.4) becomes

where

If $\lambda_1 = \lambda_2 = 0$, then by direct computation and the proof of Theorem 2.8, we get

Further, let $X = x+d_2/(2d_4), \, \, Y = y$. System (3.5) becomes (we rewrite $X$, $Y$ as $x$, $y$, respectively)

where

Finally, taking the changes

one obtains (we rewrite $X$, $Y$ as $x$, $y$, respectively)

where

We can express $\mu_1$ and $\mu_2$ in terms of $\lambda_1$ and $\lambda_2$ as follows:

where

Since

for $p > p_1$ (i.e., $mp-m-1 > 0$), $n_1-\beta\neq 0$, $p > 1$, $m > n_1 > 0$, $\beta > 0$, the change (3.8) is a homeomorphism in a small neighborhood of $(0, 0)$. According to the results in ^[16,17,18], system (3.7) (i.e., (3.1) or (2.2)) undergoes Bogdanov-Takens bifurcation if $(\lambda_1, \lambda_2)$ changes in a small neighborhood of the origin.

By the results in ^[19], we obtain the local representation of the bifurcation curves as follows:

(i) The saddle-node bifurcation curve is

(ii) The Hopf bifurcation curve is

(iii) The homoclinic bifurcation curve is

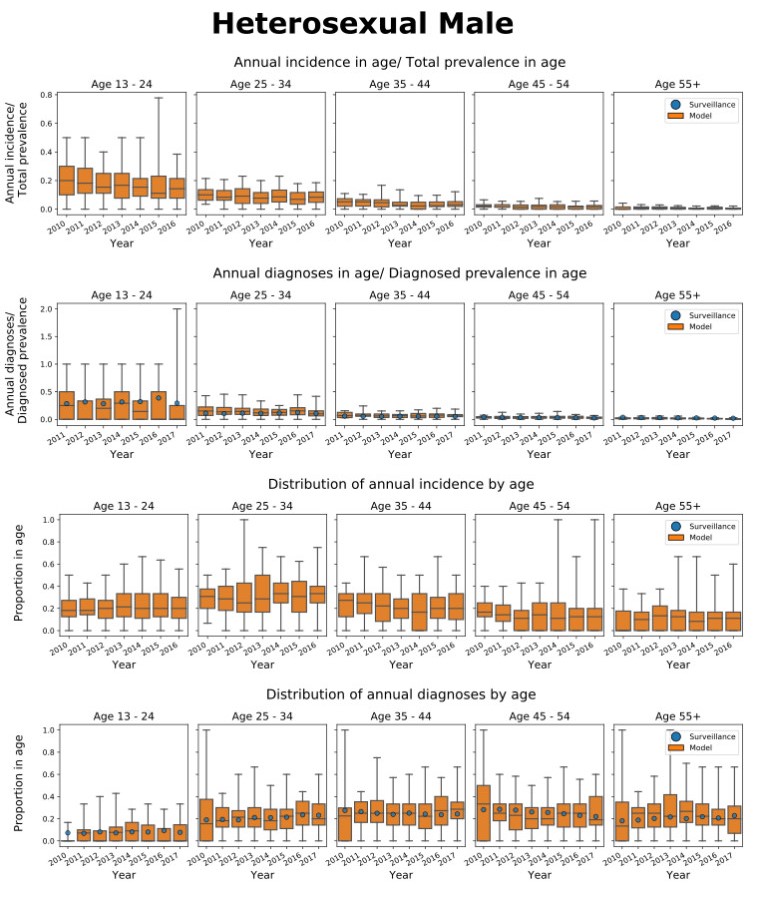
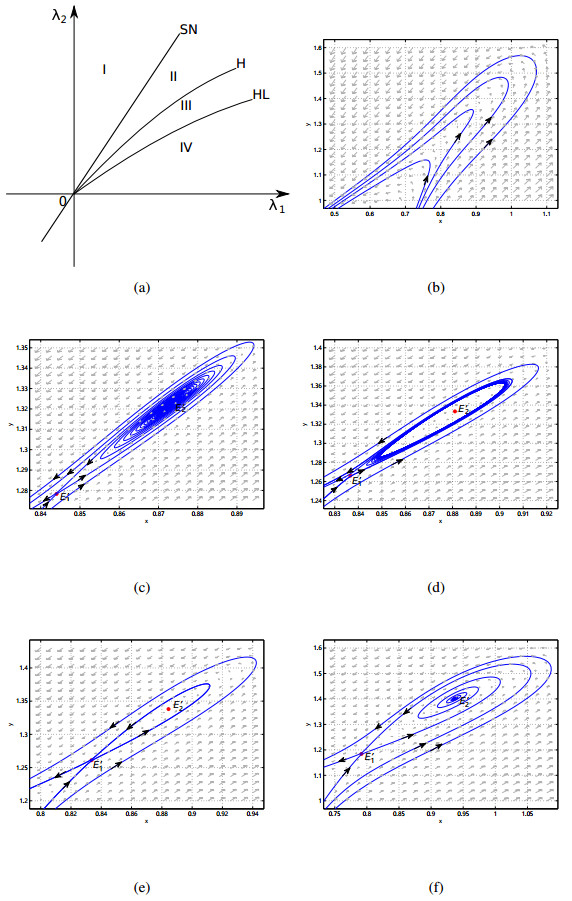
The Bogdanov-Takens bifurcation diagram and the phase portraits of system $(3.1)$ are shown in Figure 1. The small neighborhood of the origin in the parameter $(\lambda_1, \lambda_2)$-plane are divided into four regions (see Figure 1(a)) by bifurcation curves $H$, $HL$, and $SN$.

(a) The unique positive equilibrium is a cusp of codimension two if $(\lambda_1, \lambda_2) = (0, 0)$.

(b) There are no equilibria if $(\lambda_1, \lambda_2)\in I$ (see Figure 1(b)), implying the diseases die out.

(c) The unique positive equilibrium $E_*$ is a saddle-node if $(\lambda_1, \lambda_2)$ lies on $SN$.

(d) If the parameters $\lambda_1, \lambda_2$ cross $SN$ into the region II, the saddle-node bifurcation occurs, and there are two positive equilibria $E_1$ and $E_2$ which are saddle and unstable focus respectively (see Figure 1(c)).

(e) If the parameters $\lambda_1, \lambda_2$ cross $H$ into III, an unstable limit cycle will appear through the subcritical Hopf bifurcation around $E_2$ (see Figure 1(d)). The focus $E_2$ is stable in region III, whereas it is an unstable weak focus of order one on $H$.

(f) If $(\lambda_1, \lambda_2)\in HL$, an unstable homoclinic orbit will occur through the homoclinic bifurcation around $E_1$ (see Figure 1(e)).

(g) If the parameters $\lambda_1, \lambda_2$ cross the $HL$ curve into IV, the relative location of one stable and one unstable manifold of the saddle $E_1$ will be reversed (compare Figure 1(c), (f)).

3.3.   Hopf bifurcation

We study Hopf bifurcation around the equilibrium $E_2(x_2, y_2)$ in this subsection. Let

To simplify the computation, we follow our previous techniques in ^[20,21] and take the changes

under which system (2.2) is reduced to (we rewrite $\tau$ as $t$)

Setting

and dropping the bars, system (3.10) becomes

Since the equilibrium $E_2(x_2, y_2)$ of system (2.2) becomes the equilibrium $(1, 1)$ of system (3.12), we have

Note that the positive equilibrium $E(x, y)$ of system (3.12) satisfies that $y = x$ and $h(x) = 0$, where $h(x)$ is given by (2.6). From the discussion of $h(x)$ in Section $2$, we have $h'(1) > 0$ since $1$ is the bigger positive root of $h(x)$. By (2.7) and (3.13), one gets

Thus, we have the following condition

This yields that the condition (2.4) becomes

Next letting $dt = (1+ \beta x^p)d\tau$ and substituting (3.13) into (3.12), one obtains (still denote $\tau$ by $t$)

where $\beta, A, m, n, a$ satisfy (3.15). Since $1+ \beta x^p > 0$ holds in $\mathbb{R}^+_2 = \{(x, y) | x\geq 0, \ y\geq0\}$, the topological structure of (3.16) is the same as (3.12).

In what follows we study the Hopf bifurcation around $\tilde{E}_2(1, 1)$ in system (3.16), instead of $E_2(x_2, y_2)$ in system (2.2). We always assume that the conditions in (3.15) hold for (3.16).

Theorem 3.2. System $(3.16)$ has an equilibrium at $\tilde{E}_2(1, 1)$. Moreover, it is

(I) an unstable node or focus if $a < a_{*}$;

(II) a stable node or focus if $a > a_{*}$;

(III) a weak focus or a center if $a = a_{*}$.

Proof. The Jacobian matrix of system (3.16) at $\tilde{E}_2(1, 1)$ is

Then

By(3.14), $\text{Det}(J(\tilde{E}_2)) > 0$. The trace of $J(\tilde{E}_2)$ is

By conditions (3.15), we have that $\text{Tr}(J(\tilde{E}_2)) = 0$ ($> 0$ or $< 0$) if $a = a_{*}$ ($a < a_{*}$ or $a > a_{*}$). This completes the proof.

Next we study Hopf bifurcation around $\tilde{E}_2(1, 1)$ in system (3.16). By Theorem 3.2, if Hopf bifurcation occurs, then

Firstly the following inequality shows the transversality condition holds:

We are going to calculate the first Lyapunov constant for $\tilde{E}_2(1, 1)$. Take the changes $X = x-1$, $Y = x-1$, and let $a = a_{*}$. System (3.16) becomes (we rewrite $X, Y$ as $x, y$, respectively)

where

By the formula in ^[14], one gets the first Lyapunov coefficient with the aid of Maple-17 as follows

where

The program for the computation of Lyapunov coefficient is available for noncommercial purpose via email to: gnsydyf@126.com.

By conditions in (3.17), the sign of $V_3$ is the same as that of

Now we investigate whether there exist some parameters such that $\varphi_1 = 0$ (i.e., $V_3 = 0$) under the conditions (3.17).

Lemma 3.3. If conditions in $(3.17)$ hold, then we have $c_1 > 0$.

Proof. We will show that $c_1(p) > 0$ for all $p > 1$. A straightforward calculation shows that

Then $c_1'(p) > c_1'(1) = (\beta-1)^2\geq 0$ for all $p > 1$. This implies that $c_1(p)$ is strictly monotonically increasing on $(1, +\infty)$. Note that

Thus, $c_1(p) > c_1(1) > 0$ for all $p > 1$. This completes the proof.

Denote

Note that $c_0 > 0$ if and only if either (i) $\beta\geq 1$, or (ii) $\beta < 1$ and $p\leq p_{*}$. Furthermore, we have $c_0 = 0$ if and only if $\beta < 1$ and $p = p_{*}$, $c_0 < 0$ if and only if $\beta < 1$ and $p > p_{*}$, respectively. By the above discussions, one obtains the following theorem.

Theorem 3.4. If conditions in $(3.17)$ hold, then the following statements hold.

(I) If either (i) $\beta\geq 1$, or (ii) $\beta < 1$ and $p\leq p_{*}$ (i.e., $\varphi_1 > 0$ or $V_3 > 0$), then $\tilde{E}_2(1, 1)$ is an unstable weak focus of order one.

(II) If $\beta < 1$ and $p > p_{*}$ and

(II.1) $m > \tilde{m}$ (i.e., $\varphi_1 > 0$ or $V_3 > 0$), then $\tilde{E}_2(1, 1)$ is an unstable weak focus of order one;

(II.2) $m < \tilde{m}$ (i.e., $\varphi_1 < 0$ or $V_3 < 0$), then $\tilde{E}_2(1, 1)$ is a stable weak focus of order one;

(II.3) $m = \tilde{m}$ (i.e., $\varphi_1 = 0$ or $V_3 = 0$), then $\tilde{E}_2(1, 1)$ is a center or a weak focus of order at least two.

Define two hypersurfaces

By Theorems 3.2 and 3.4, we know that $\tilde{E}_2(1, 1)$ is an unstable focus (resp. a stable focus) when $\varphi_1 > 0$ and $a\leq a_{*}$ (resp. $\varphi_1 < 0$ and $a\geq a_{*}$), while $\tilde{E}_2(1, 1)$ is a stable focus (resp. an unstable focus) as $\varphi_1 > 0$ and $a > a_{*}$ (resp. $\varphi_1 < 0$ and $a < a_{*}$). Hence, if parameters pass from one side of the surface $H_1$ (resp. $H_2$) to the other side, system (3.16) can undergo a subcritical (resp.supercritical) Hopf bifurcation. An unstable limit cycle (resp. a stable limit cycle) can bifurcate from the small neighborhood of $\tilde{E}_2(1, 1)$. The hypersurface $H_1$ (resp. $H_2$) is called the subcritical (resp. supercritical) Hopf bifurcation hypersurface of system.

In Figure 2, we give the limit cycles arising from Hopf bifurcation around $\tilde{E}_2(1, 1)$ of system (3.16). In Figure 2(a), we fix $p = 2$, $\beta = 0.2$, $m = 1.4$ and $n = 10$, and get $a = 0.1$ from $\text{tr}(J(\tilde{E}_2)) = 0$, then we obtain $V_3 = -1.62280702$. Next perturb $a$ such that $a$ decreases to $0.099$. So $\tilde{E}_2(1, 1)$ becomes an unstable hyperbolic focus, yielding to a stable limit cycle to appear around $\tilde{E}_2(1, 1)$. In Figure 2(b), we fix $p = 2$, $\beta = 0.2$, $m = 2$ and $n = 3$. Using the same arguments as above, we obtain an unstable limit cycle around $\tilde{E}_2(1, 1)$.

3.4.   Degenerate Hopf bifurcation of codimension two

By (II.3) of Theorem 3.4, $V_3 = 0$ if $m = m_{*}$. Using the formal series method in ^[14] and Maple-17, one gets the second Lyapunov constant

where $c_1$ is given by (3.19) and

Lemma 3.5. If $(3.17)$ and the condition (II.3) of Theorem 3.4 hold, then $V_5 > 0$.

Proof. From the condition (II.3) of Theorem 3.4, we have $\beta < 1$ and $p\beta-p+\beta+1 > 0$. This follows that $p \beta-2p+\beta+1 < 0$. Thus, $\varphi_2 < 0$, which implies $V_5 > 0$.

Theorem 3.6. The equilibrium $E_2(x_2, y_2)$ of system $(2.2)$ is an unstable weak focus of order at most two. System $(2.2)$ can undergo degenerate Hopf bifurcation of codimension two in the small neibourhoof of $E_2(x_2, y_2)$.

Proof. Since the equilibrium $\tilde{E}_2(1, 1)$ in system (3.16) corresponds to $E_2(x_2, y_2)$ in system (2.2), we are going to focus on $\tilde{E}_2(1, 1)$ of system (3.16) in this proof, instead of $E_2$ in system (2.2).

For convenience, denote $V_{1} = \text{tr}(J(\tilde{E}_2))$. By Theorem 3.4 and Lemma 3.5, for any given parameters $(p_1, \beta_1, n_1, a_1, m_1)$ satisfying (3.17) and the condition (III.3) of Theorem 3.4, i.e.,

we have $V_{1}(p_1, \beta_1, a_1, m_1) = V_{3}(p_1, \beta_1, n_1, m_1) = 0$ and $V_{5}(p_1, \beta_1, n_1) > 0$. Therefore, $\tilde{E}_2(1, 1)$ in system (3.16) is a weak focus of order at most $2$.

Now we show that two limit cycles can bifurcate from $\tilde{E}_2(1, 1)$, which means that the Hopf cyclicity for the equilibrium $\tilde{E}_2(1, 1)$ is $2$. We first perturb $m$ near $m_1$ such that $V_3V_5 < 0$ and adjust $a$ such that $V_1 = 0$. Then the first limit cycle appears. The second limit cycle is obtained by perturbing $a$ such that $V_1V_3 < 0$, see Figure 3. Therefore, system (3.16) can undergo degenerate Hopf bifurcation of codimension two near $\tilde{E}_2(1, 1)$.

In the end of this section we give a numerical simulation in Figure 3 to show the coexistence of two limit cycles. Choosing $p = 2.4$, $\beta = 0.2$ and $m = 1$, we deduce that $n = 5.8$, $a = 1/6$ by $V_3 = 0$ and $tr(J(\tilde{E}_2)) = 0$, respectively, and $V_5 = 115.8683452$, i.e., $\tilde{E}_2(1, 1)$ is an unstable weak focus of order two. Then we perturb $m$ and $a$ such that $m$ and $a$ decreases to $1-0.005$ and $1/6-0.002$, respectively. An unstable limit cycle and a stable limit cycle occur around $\tilde{E}_2(1, 1)$, see Figure 3.

Acknowledgments

This work is supported by the NNSF of China (No.11971495) and Guangdong-Hong Kong-Macau Applied Math Center (No.2020B1515310014).

Conflict of interest

The authors declare there is no conflict of interest.