Corporate social responsibility in agri-food firms: the relationship between CSR actions and firm's performance

1.   Introduction

The attitude stabilization problem has attracted extensive attention in recent years for its significant applications in spacecraft navigation, satellite formation flying and the recycling of space debris. To achieve satisfactory tracking performance, system uncertainties and other nonlinear dynamics of the controlled spacecraft should be handled effectively. A wide range of control techniques have been proposed to address these issues, including adaptive control ^[1], output feedback control ^[2] and robust control ^[3]. What is more, spacecraft systems commonly experience actuator constraints such as saturation and degradation, which would severely undermine their practicality and reliability. To deal with these actuator nonlinearity problems, several methods have been developed in ^[4,5,6]. However, the majority of above-mentioned strategies can only realize asymptotic stabilization of the system, implying that the convergence time of tracking errors is infinite and cannot be determined by users, which is contrary to the requirement that some real-time space missions require a rapid convergence.

To improve the convergence rate of the aforementioned strategies, the concept of finite-time control was initially proposed in ^[7] and continuously applied to a variety of nonlinear systems^[8,9,10]. However, the convergence time cannot be predefined as desired, and its upper bound is an infinite function of original states. This deficiency was addressed by developing a fixed-time controller ^[11], which has the appealing merit that its time is independent of initial configurations. Sliding mode methods are widely employed to realize control performance. In ^[12], a nonsingular terminal sliding mode surface (NTSMS) is designed by using a piecewise continuous function. And based on the NTSMS, an adaptive controller is proposed for spacecraft formation, allowing for fixed-time coordinated attitude tracking. In ^[13], a robust fixed-time attitude controller is established through the use of a faster fixed-time sliding mode surface and a fixed-time observer is designed for lumped uncertainty. In addition to sliding mode control, a backstepping technique can also be used in the construction of fixed-time controllers. In ^[14], a fixed-time backstepping controller is constructed by virtue of a command filter for a class of nonstrict-feedback nonlinear systems, and the fuzzy logic system is introduced to approximate uncertainties, input saturation and dead zones. In ^[15], a fixed-time control protocol is proposed for hyper sonic vehicles by using a tracking differentiator for the calculation of the derivatives of virtual control law. In ^[16], a command filter based backstepping control scheme is introduced to avoid the computational complexity of the derivative of virtual control law in conventional backstepping schemes. In ^[17], the backstepping control technique is combined with a dynamic surface method to light the computational burden. Notwithstanding, no explicit functions between tunable parameters and settling time can be obtained via the above-mentioned methods.

Recently, the stabilization of systems with predefined-time convergence has become a hotpot and many meaningful studies have been conducted on this topic because of its enhanced property as compared to fixed/finite-time control schemes when it comes to rendering states into the origin with the settling time that is explicitly equal to a user-tuning parameter. The sliding mode control and backstepping are two of the most commonly used methods for designing predefined-time controllers, and some representative work of predefined-time control of spacecraft systems has been reported in ^{[18,19,20,21]}. However, the estimate of the convergence time bound in these works is somewhat conservative, resulting in the actual settling time being several times shorter than the estimate.

Another important control goal of designed controllers is to achieve desirable transient performance. To this end, prescribed performance control (PPC) protocol was first developed in ^[22] and heavily implemented in spacecraft systems^[23,24,25] in recent years. In ^[25], combining PPC and NTSMS, a fixed-time sliding mode attitude controller is designed for flexible spacecraft systems. Unlike the conventional exponential convergence prescribed performance function (PPF), a novel predefined-time PPF is designed in ^[26], and it has the more appealing property that the convergence time is prescribed by users. Chen et al. ^[27] utilized a polynomial function to design the PPF with predefined time convergence; it can mitigate the chattering problem caused by an exponential function. Bu et al. ^[28] constructed a finite-time prescribed performance controller for waverider vehicles, and no fuzzy/neural systems are required to estimate the unknown dynamics. In ^[29] and ^[30], two brand-new types of finite-time PPFs are explored for the purpose of minimizing the overshoot and overcoming the fragility problem caused by actuator saturation. Notwithstanding, the condition that the PPFs should be larger than the tracking errors at the incipient stage needs to be satisfied for the execution of most of the above PPF-based controllers.

To the best of the authors' knowledge, developing a predefined-time controller for spacecraft systems with inertia perturbation, space-environment disturbances and actuator faults is an open topic. Inspired by the existing work, we have designed a radial basis function neural network (RBFNN)-based controller with prescribed performance and appointed-time convergence which ensures that the tracking error will converge to a prescribed small region in the vicinity of the origin within the predefined time. The main contributions can be summarized as follows.

$1)$ By employing the proposed PPC control scheme, both the convergence time and tracking accuracy can be arbitrarily predefined by users. The designed controller presents great robustness against input saturation, actuator misalignment and unexpected disturbance.

$2)$ By applying a novel shifting function to conventional PPC, we release the constraints for the initial tracking errors to be smaller than the initial PPF values. Additionally, the shifting function also allows for an improved handling of input saturation.

$3)$ Following the representative backstepping design methodology, we propose an attitude controller with prescribed performance and appointed-time convergence for spacecraft systems. The singularity problem associated with virtual control law is avoided via the design of a piecewise continuous function.

$4)$ RBFNN and minimum learning parameter (MLP) techniques are combined to estimate the system uncertainty and the derivative of virtual control law. Moreover, the fixed-time convergence of the learning parameter is ensured by constructing the adaptive law.

2.   Preliminaries and problem formulation

2.1.   Lemmas

Lemma 1. ^[11] Considering a nonlinear system

suppose that there exists a positive-definite Lyapunov function $V$ and scalars $\gamma_{1} > 0$, $\gamma_{2} > 0$, $p > 1$, $0 < q < 1$ and $\Delta > 0$ such that the following property holds:

Then, the equilibrium of (2.1) is practically fixed-time stable with the settling time $T_{f} \le \frac{1}{\gamma_{1}\kappa(1-p)}+\frac{1}{\gamma_{2}\kappa(q-1)}$, where $0 < \kappa < 1$. The solution of (2.1) will converge to a residual set that is given as

Lemma 2. ^[31] For $x, y\in {\mathfrak{R}}$, the following relationship holds:

where $m > 0$, $n > 0$ and $c > 0$.

Lemma 3. ^[32] For $y > x$ and $l > 0$, we have

Lemma 4. ^[33] For the variables ${x_1}, {x_2}, \ldots {x_n} > 0$, $0 < y_{1}\leq1$ and $y_{2} > 1$, the following inequalities hold:

Notation 1. In this paper, ${\rm{si}}{{\rm{g}}^\alpha }\left({\boldsymbol \beta} \right) = \left[{{\left| {{\xi _1}} \right|}^\alpha }{\rm{sgn}}({\beta _1}), {{\left| {{\beta _2}} \right|} ^\alpha } \notag {\rm{sgn}}({\beta _2}), \ldots, {{\left| {{\beta _n}} \right|}^\alpha }{\rm{sgn}}({\beta _n})\right]^T$, where ${\boldsymbol \beta} = {\left[{{\beta _1}, {\beta _2}, \ldots, {\beta _n}} \right]^T}$; $\rm sgn(\cdot)$ denotes the sign function. The definition of the skew-symmetric matrix is given by ${\boldsymbol \beta}^{\times } = \left[0, - \beta_{3}, \beta_{2}; \beta_{3}, 0, - \beta_{1};- \beta_{2}, \beta_{1}, 0\right]$, when $n = 3$.

2.2.   Problem statement

The kinematic equation and dynamics of a spacecraft can be presented as

where ${\boldsymbol q} = \left[{{q_0}, q_{1}, q_{2}, q_{3}}\right]^T = {\left[{{q_0}, {{\boldsymbol q}_v}} \right]^T}\in {\boldsymbol {\mathfrak{R}}}^{4}$ denotes the unit quaternion vector which is used to parameterize the orientation of spacecraft satisfying the identity $q_0^2 + {\boldsymbol q}_v^T{{\boldsymbol q}_v} = 1$; ${\boldsymbol \omega } \in {\boldsymbol {\mathfrak{R}}}^{3}$ represents the angular velocity of spacecraft; ${\boldsymbol d} \in {\boldsymbol {\mathfrak{R}}}^{3}$ denotes the unknown environment disturbance torque; ${\boldsymbol {J}} = {\boldsymbol J_0} + {{\rm \Delta}{\boldsymbol J}} \in {\boldsymbol{\mathfrak{ R}}}^{3\times 3}$ denotes the inertia matrix of the spacecraft system, with ${\boldsymbol J_0}$ and ${{\rm \Delta} {\boldsymbol J}}$ being the nominal and perturbed components, respectively; ${ \boldsymbol \tau} \in {\boldsymbol {\mathfrak{R}}}^{3}$ is the control torque acting on spacecraft.

The relationship between the actual control torque and the command input can be given by ^[34]:

where ${\boldsymbol u}_c = {\left[{{u_{c1}}, {u_{c2}}, {u_{c3}}} \right]^T} \in {\boldsymbol{\mathfrak{ R}}}^{3}$ is the command torque generated by controllers; ${\boldsymbol E} = {\rm{diag}}\left\{ {{e_1}(t), {e_2}(t), {e_3}(t)} \right\} \in {\boldsymbol{\mathfrak{ R}}}^{3\times 3}$ represents the failure coefficient matrix indicating the effectiveness condition of the actuator with $0 \le {e_i}\left(t \right) \le 1$; ${\boldsymbol \sigma} = {\left[{{ \sigma}_1}, {{\sigma}_2}, {{\sigma}_3} \right]^T}\in {\boldsymbol{\mathfrak{ R}}}^{3}$ is the bias faults vector. The saturation characteristic of an actuator ^[35] can be formulated as ${\rm sat} (u_{ci}) = {\rm sgn} (u_{ci}) \cdot \min\{\left| u_{ci}\right|, u_{maxi}\}$, where $u_{maxi}$ denotes the maximum permissible torque generated by actuators.

Define ${\boldsymbol {q}_d} = \left[{{q_{d0}}, {q_{d1}}, {q_{d2}}, {q_{d3}}} \right]^T = \left[{{q_{d0}}, {\boldsymbol q}_{dv}} \right]^T \in {\boldsymbol {\mathfrak{R}^{4}}}$ as the expected attitude vector. The attitude error described in unit quaternion format ^[36] is given by ${\boldsymbol {q}_e} = \left[{{q_{e0}}, {q_{e1}}, {q_{e2}}, {q_{e3}}} \right]^T = \left[{{q_{e0}}, {\boldsymbol q}_{ev}} \right]^T$, ${{\boldsymbol q}_{ev}} = {{ q}_{d0}}{ {\boldsymbol q}_v} - {\boldsymbol q}_{dv}^ \times {{\boldsymbol q}_v} - {q_0}{\boldsymbol {q}_{dv}}$, ${{ q}_{e0}} = {\boldsymbol q}_{dv}^ \times {{\boldsymbol q}_v} + {q_0}{{q}_{d0}}$ and $q_{e0}^2 + {\boldsymbol q}_{ev}^T{{\boldsymbol q}_{ev}} = 1$. Considering the rest-to-rest attitude maneuvering case, we have that ${\boldsymbol \omega}_e = {\boldsymbol \omega}$ in this paper.

The attitude error dynamics of the spacecraft systems is given by

where ${\boldsymbol M} = - { {{\boldsymbol \omega} _e} ^ \times }{\boldsymbol J}_{0} {\boldsymbol \omega} _e$ and ${\boldsymbol N} = - {\rm \Delta} {\boldsymbol J}{\dot {\boldsymbol \omega}}_{e} - {\boldsymbol {\omega} _e} ^ \times {\rm \Delta} {\boldsymbol J}{{\boldsymbol \omega} _e}$.

Define ${\boldsymbol x}_{1} = {\boldsymbol q}_{ev}$ and ${\boldsymbol x}_{2} = \dot {\boldsymbol q}_{ev}$; (2.11) and (2.12) can be reconstructed as

where ${\boldsymbol G} = {\dot {\boldsymbol F}(\boldsymbol{q}_{ev})}{\boldsymbol {\omega} _e} + {\boldsymbol F(\boldsymbol {q}_{ev})}{\boldsymbol J_{0}}^{-1}{\boldsymbol M}$, ${\boldsymbol \Pi} = {\boldsymbol F(\boldsymbol {q}_{ev})}{\boldsymbol J_{0}}^{-1} {\boldsymbol N}+{\boldsymbol F(\boldsymbol {q}_{ev})}{\boldsymbol J_{0}}^{-1}\left({\boldsymbol E}-{\boldsymbol I}_{3}\right)u_{c}+ {\boldsymbol F(\boldsymbol {q}_{ev})}{\boldsymbol J_{0}}^{-1} {\boldsymbol \sigma}+{\boldsymbol F(\boldsymbol {q}_{ev})}{\boldsymbol J_{0}}^{-1} \left({\boldsymbol E}\left(\rm {sat}\left({\boldsymbol u}_{c}\right)-{\boldsymbol u}_{c}\right)\right)$, ${\boldsymbol d}_{2} = {\boldsymbol F(q_{ev})}{\boldsymbol J_{0}}^{-1} {\boldsymbol d}$ and $\boldsymbol F\left({{\boldsymbol q_{ev}}} \right) = \frac{1}{2}\left({\boldsymbol q_{ev}^ \times + {{ {q}}_{e0}}{\boldsymbol{I}_3}} \right)$.

Assumption 1. The perturbed part of the inertia matrix, the external disturbance and the faulty torque are unknown but bounded. The lumped disturbance is bounded and satisfies $\| {\boldsymbol d}_{2}\| \le \bar{d}$, where $\bar{d}$ is a positive constant.

The primary objective is to design an adaptive controller for spacecraft systems in the presence of actuator fault so as to achieve the prespecified tracking accuracy within a predefined time and satisfy the prescribed performance boundaries throughout the entire process, as well as to ensure the fixed-time boundedness of other closed-loop signals. Both the settling time and tracking precision can be defined according to the specific requirements of users, irrespective of the initial conditions.

3.   Prescribed performance control

To guarantee that attitude trajectory of the spacecraft remains within the prescribed boundaries with desirable transient and static performance, the following constraints are constructed first:

where ${\overline \delta_i}, {\underline \delta_i} > 0$, $(i = 1, 2, 3)$ are two adjustable parameters and $\rho _{i}(t)$ is the PPF.

3.1.   Predefined-time PPF

In this paper, we propose a novel predefined-time PPF as

where $\rho_{i0} > \rho_{i\infty} > 0$ are constants, $T_{c} > 0$ is the predefined maximum allowable convergence time that can be arbitrarily defined by users and $a_{i} > 0$ represents a preset constant that can adjust the convergence rate. $\rho_{i}(t)$ is a monotonically decreasing smooth function that can converge from $\rho_{i0}$ to $\rho_{i\infty}$ within $T_{c}$.

3.2.   Shifting function

The traditional PPC method requires that the initial tracking errors satisfy the condition (3.1). Based on this constraint, the values of ${\overline \delta_i}$, ${\underline \delta_i}$ and even $\rho_{i}$ need to be reassigned when the original tracking error exceeds the initial value of the PPF, which is challenging considering that the initial configurations are unavailable. To overcome this weakness, we introduce a shifting function to map the value of the initial tracking error into the interval $\left[-\underline \delta_i \rho_{i0}, \overline \delta_i \rho_{i0} \right]$ as

where $k_{i} = \left\{ \begin{aligned} \overline \delta_i \rho_{i0} &, & q_{evi} \ge 0, \\ \underline \delta_i \rho_{i0} &, & q_{evi} < 0.\\ \end{aligned} \right.$. Note that we set $\overline \delta_{i} = \underline \delta_i = 1$ in the following paper for the simplicity of analysis.

Remark 1. From (3.3), it can be seen that $\mathop {\lim }\limits_{{q_{evi}} \to - \infty } \eta_{i} = - \rho_{i0}$, $\mathop {\lim }\limits_{{q_{evi}} \to + \infty } \eta_{i} = \rho_{i0}$, which indicates that, regardless of the largeness of the attitude errors, they will not violate the prescribed boundary requirements defined in (3.1) at the outset. Moreover, when $\mathop {\lim }\limits_{t \to T_{c}} {\eta _i} = 0$, we can obtain $\mathop {\lim }\limits_{t \to T_{c}} {q_{evi}} = 0$, meaning that the predefined-time attitude maneuvering can be achieved by rendering $\eta_{i}$ to zero within a prescribed interval.

Since $\eta_{i}$ satisfies the boundary conditions, we have

From (3.3), the prescribed boundary for the attitude error $q_{evi}$ is shifted into

where $h_{i}(t) = \tan\left(\frac{\pi}{2k_{i}}\rho_{i}(t)\right), (i = 1, 2, 3)$. $h_{i}(t)$ is a monotonically decreasing function with $\mathop {\lim }\limits_{t \to T_{c}} {h _i} = \tan\left(\frac{\pi}{2k_{i}}\rho_{i}(\infty)\right)$.

3.3.   Transformation function

To convert the constraint on $q_{evi}$ into its unconstrained counterpart, the transformation function is defined as

Obviously, ${T}({\varepsilon _i})$ is a monotonically increasing function with the following properties: (1) ${ -1 < T\left({{\varepsilon _i}} \right) < 1}$; (2) ${\mathop {\lim }\limits_{{\varepsilon _i} \to + \infty } T\left({{\varepsilon _i}} \right) = 1}$; (3) ${\mathop {\lim }\limits_{{\varepsilon _i} \to - \infty } T\left({{\varepsilon _i}} \right) = -1}$; (4) $T(0) = 0$.

In what follows, we define

Therefore, the transformed error $\varepsilon_{i}$ is introduced as

where $\xi_{i} = \frac{\eta_i}{\rho_{i}}$ is the normalized error.

During the period of actuator saturation, the attitude errors may grow to exceed the prescribed envelopes, which can result in the transformed error $\varepsilon_{i}$ approaching infinity. Consequently, the actuator will be kept saturated, compromising the stability and reliability of the system. To this end, we redesign the coefficient of our proposed shifting function as follows:

where $0 < s_{i} < \frac{\pi}{2}$ is a positive constant.

Remark 2. According to the properties of ${T}({\varepsilon _i})$, it is obvious that the desired performance for the shifted attitude errors $\eta_{i}$ prescribed in (3.4) can be achieved when the boundedness of ${\varepsilon _i}$ is ensured. In this respect, the problem of (3.4) is converted into its equivalent of stabilizing the transformed state $\varepsilon_{i}$ by designing the controller.

Remark 3. Unlike the previous finite-time PPFs proposed in ^{[26,27,28,37]}, the settling of $\rho_{i0}$ is independent of $q_{evi}(0)$. With the assistance of the shifting function provided in (3.3), the PPF defined in (3.2) does not require prior knowledge of initial errors to design the parameters. The removal of restrictions on initial conditions simplifies the design process and contributes to the reliability and practicality of the proposed PPC scheme.

Remark 4. When there is input saturation, the shifting function ensures that the shifted error $\eta_{i}$ remains within the appointed boundary $\left[- \rho_{i}, \rho_{i} \right].$ With a smaller $\eta_{i}$, the value of the normalized error $\xi_{i}$ will be reduced, resulting in a smaller transformed error $\varepsilon_{i}$ and a decline in the control input. When the actuator exits its saturation zone, the coefficient of the shifting function changes to $s_{i}$. Compared with the existing strategies^[37,38,39], this method can reduce the control output by minimizing the absolute value of the normalized error $\eta_{i}$. (The proof can be seen in Appendix.)

4.   Adaptive controller design and stability analysis

4.1.   Controller design

To facilitate the implementation of backstepping methods, we can define

From (2.13), the time derivative of $\boldsymbol z_{1}$ is

To remove the initial value constraints, we impose the following shifted function on $z_{1}$ and obtain the shifted error signals:

Define the first normalized tracking error $\xi_{1i} = \frac{\eta_{1i}}{\rho_{1i}}$, and using the transformation function defined in (3.6), we can obtain

The time derivative of $\varepsilon_{1i}$ is

where $\psi_{1i} = \frac{\pi}{2 \rho_{1i}} \sec\left(\frac{\pi}{2} \xi_{1i}\right)^{2}$, $g_{1i} = \frac{2k_{1i}}{\pi\sqrt{1+z_{1i}^2}}$ and $f_{1i} = \frac{\eta_{1i}\dot \rho_{1}}{\rho_{1i}}$.

We can rewrite $\varepsilon_{1i}$ in vector form as

where $\boldsymbol{\psi}_{1} = \rm {diag}\left\{\psi_{1i}\right\}$, $\boldsymbol{g}_{1} = \rm {diag}\left\{g_{1i}\right\}$ and $\boldsymbol{f}_{1} = \left[f_{11}, f_{12}, f_{13}\right]^{T}$.

Then, the virtual control law $\boldsymbol{\alpha}_{2} = \left[\alpha_{21}, \alpha_{22}, \alpha_{23}\right]^{T}$ can be established as

where $k_{1} > 0$, $k_{2} > 0$, $p > 1$ and $\boldsymbol{\phi}_{1} = [\phi_{11}, \phi_{12}, \phi_{13}]^{T}$ is a piecewise continuous function designed as

where $0 < q < 1$, $l_{1} = 0.5q^{2}-2.5q+3$, $l_{2} = -q^{2}+4q-3$, $l_{3} = 0.5q^{2}-1.5q +1$ and $\mu$ is a tiny positive constant.

Remark 5. If ${\boldsymbol \alpha}_{2}$ is designed as ${\boldsymbol \alpha}_{2} = -(\boldsymbol{g}_{1})^{-1}(\boldsymbol{\psi}_{1})^{-1}\left(k_{1}{\rm sig}^{p}(\boldsymbol{\varepsilon}_{1})+k_{2}{\rm sig}^{q}(\boldsymbol{\varepsilon}_{1})-\boldsymbol{\psi}_{1}\boldsymbol{f}_{1}\right)$, then its derivative will be $\boldsymbol {\dot{ \alpha}}_{2} = -(\boldsymbol{g}_{1})^{-1}(\boldsymbol{\psi}_{1})^{-1}\left(k_{1} {\boldsymbol{\dot \varepsilon}_{1}}{\rm sig}^{p-1}(\boldsymbol{\varepsilon}_{1})+k_{2} {\boldsymbol{\dot \varepsilon}_{1}}{\rm sig}^{q-1}(\boldsymbol{\varepsilon}_{1})-\boldsymbol{\psi}_{1} {\boldsymbol{\dot f}}_{1}\right)$. The singularity problem may happen in $\dot {\boldsymbol \alpha}_{2}$ because of $0 < q < 1$ when $\varepsilon_{1i} = 0$ and $\dot \varepsilon_{1i} \neq 0$. To avoid the problem, we design the above piecewise function at the switching point $\mu$. The values of $l_{1}$, $l_{2}$ and $l_{3}$ are selected to ensure the continuity of $\phi_{1i}$ and its first and second derivative.

The candidate of the first Lyapunov function is defined as

Differentiating ${V}_{1}$ yields

Substituting (4.7) into (4.10), when $\left| \varepsilon_{1i}\right| > \mu$, we have

When $\left| \varepsilon_{1i}\right| \le \mu$, we can obtain

Note that, when $\left| \varepsilon_{1i}\right| \le \mu$, there is only a bounded term $6k_{2}(\mu^2)^{\frac{q+1}{2}}$ added to the structure of (4.11).

Taking the derivative of $\boldsymbol{z}_{2}$, we can obtain

Similarly, we can relax the feasibility condition by introducing the shifting function to ${\boldsymbol z}_{2}$ and obtain the shifted error signals:

Define the second normalized tracking error $\xi_{2i} = \frac{\eta_{2i}}{\rho_{2i}}$, and the $i$th component of the transformed error vector can be defined as

The time derivative of $\varepsilon_{2i}$ is

where $\psi_{2i} = \frac{\pi}{2 \rho_{2i}} \sec\left(\frac{\pi}{2} \xi_{2i}\right)^{2}$, $g_{2i} = \frac{2k_{2i}}{\pi\sqrt{1+z_{2i}^2}}$ and $f_{2i} = \frac{\eta_{2i}\dot \rho_{2i}}{\rho_{2i}}$.

The vector form can be rewritten as

where $\boldsymbol{\psi}_{2} = {\rm diag}\left\{\psi_{2i}\right\}$, $\boldsymbol{g}_{2} = {\rm diag}\left\{g_{2i}\right\}$ and $\boldsymbol{f}_{2} = \left[f_{21}, f_{22}, f_{23}\right]^{T}$.

Substituting (4.13) into (4.17), we have

Choose the second Lyapunov function candidate as

Differentiating ${V}_{2}$ with respect of time yields

where ${\boldsymbol D} = {\boldsymbol \psi}_{2}{\boldsymbol g}_{2}({\boldsymbol \Pi}-\dot {\boldsymbol \alpha}_{2}) = [D_{1}, D_{2}, D_{3}]^{T}$ is the lumped disturbance which can be approximated with the aid of the following RBFNN:

where ${\boldsymbol W} \in \mathfrak{R}^{n\times 3}$ denotes the optimal weight matrix, $n$ represents the number of network neurons, ${\boldsymbol Z} = [{\boldsymbol q}_{ev}, {\boldsymbol \omega}_{e}, {\boldsymbol \varepsilon}_{1}]^{T}$ is the input vector, ${\boldsymbol \zeta}\in \mathfrak{R}^{3}$ is the approximation error vector with $\Vert {\boldsymbol \zeta} \Vert \le \zeta_{m}$ and ${\boldsymbol S}({\boldsymbol Z}) = \frac{\left[{ S}_{1}({\boldsymbol Z}), { S}_{2}({\boldsymbol Z}), ..., { S}_{n}({\boldsymbol Z})\right]^{T}}{\sum\limits_{i = 1}^n{ {\boldsymbol S}_{i}({\boldsymbol Z)}}} \in \mathfrak{R}^{n}$ is the basis function vector with

where $\beta_{i}$ and $H$ are the receptive field center and width of the neural cell, respectively.

By defining $\theta = \Vert \boldsymbol W \Vert^{2}$, we use the MLP technique. In this way, we regulate the norm of the ideal weight matrix rather than its elements and only one learning parameter is required to be updated for the execution of the neural network. Therefore, the computational burden and the complexity of the propounded strategy can be significantly reduced.

The RBFNN-based adaptive controller can be designed as

where $r_{1} > 0$, $r_{2} > 0$, $r_{3} > R+\frac{1}{2}$ and $R = \|{\boldsymbol \psi}_{2}\|^{2}\|{\boldsymbol g}_{2}\|^{2}$. The adaptive law of the learning parameter $\theta$ is developed as

where $w_{1} > 0$, $w_{2} > 0$, $\lambda > 0$ and $h > 0$.

Substituting (4.23) into (4.20), we have

With the help of Young's inequality and the property that $0\le {\boldsymbol S}^{T}{\boldsymbol S}\le 1$, we have

4.2.   Stability analysis

Theorem 1. Considering the spacecraft system (2.13), the controller (4.23) and the adaptive law (4.24), one can ensure the practical fixed-time boundedness of all of the closed-loop signals. Besides, for any constants $\nu$ and $T$, if the PPF (3.2) parameters are respectively set as $\rho_{1i\infty} = \frac{2s_{ 1i}}{\pi}\arctan\left(\nu\right)$ and $T_{c} = T$, the tracking error will converge into the predefined region $\left | {q}_{evi}\right| \le \nu$ within the predefined time $T$, irrespective of the initial conditions.

Proof. Choose the third Lyapunov function for the whole system:

where $\tilde \theta = \theta - \hat \theta$.

Differentiating ${V}_{3}$ yields

Together with (4.11), (4.12), (4.24), (4.25), (4.26) and (4.27), one has

With the help of Young's inequality, the following inequality is true.

By invoking (4.31), (4.30) can be rewritten as

where $\Delta_{1} = 6k_{2}(\mu^2)^{\frac{q+1}{2}}+\frac{{ \bar {d}}^{2}}{2}+\frac{h^{2}}{2}+ \frac{3 {\zeta}_{m}^{2}}{2}$.

Applying Lemma 2 and selecting $x = \frac{w_{1}}{2\lambda}\tilde{\theta}^2$, $y = 1$, $m = \frac{1+p}{2}$, $n = \frac{1-p}{2}$ and $c = \frac{2}{p+1}$ yields

In view of Lemma 3, one has

Hence, substituting (4.33) and (4.34) into (4.32), we can obtain

where $a_{1} = k_{1}2^{\frac{p+1}{2}}$, $b_{1} = k_{1}2^{\frac{q+1}{2}} 3^{\frac{1-q}{2}}$, $a_{2} = r_{1}2^{\frac{p+1}{2}}$, $b_{2} = r_{2}2^{\frac{q+1}{2}} 3^{\frac{1-q}{2}}$, $a_{3} = w_{1}^{\frac{p+1}{2}}$, $b_{3} = \frac{2^{{\frac{q+1}{2}}}w_{2}q\lambda^{\frac{q+1}{2}}}{\lambda(1+q)}$, $\gamma_{1} = \min\left\{a_{1}, a_{2}, a_{3}\right\}$, $\gamma_{2} = \min\left\{3^{\frac{1-q}{2}}b_{1}, 3^{\frac{1-q}{2}}b_{2}, 3^{\frac{1-q}{2}}b_{3}\right\}$ and $\Delta = \frac{w_{1}}{2\lambda}{\theta}^{2}+\frac{1-p}{2}\left(\frac{2}{p+1}\right)^{-\frac{1+p}{1-p}}+\frac{w_{2}q}{\lambda(1+q)}\theta^{q+1}+\Delta_{1}.$

(1) In light of Lemma 1, $V_{3}$ will converge to the region ${\rm {\Omega}} _v = \min \left\{ {{{\left({\frac{\Delta}{\gamma_{1}(1-\kappa)}} \right)}^{\frac{2}{p+1}}}}, {{{\left({\frac{\Delta}{\gamma_{2}(1-\kappa)}} \right)}^{\frac{2}{q+1}}}}\right\}$ within the fixed time $T_{f}$. The settling time is bounded by $T_{f} \le T_{max} = \frac{2}{\gamma_{1}\kappa(1-p)}+\frac{2}{\gamma_{2}\kappa(q-1)}$.

Apparently, $\varepsilon_{1i}$ and $\varepsilon_{2i}$ will converge to the following regions, respectively:

Based on (4.4) and (4.15), we can further obtain the residual sets that $\eta_{1i}$ and $\eta_{2i}$ will respectively converge to ${\rm \Omega }_{\eta_{1i}}$ and ${\rm \Omega }_{\eta_{2i}}$ within $T_{f}$.

(2) In view of (3.4) and the property of $\rho_{1i}(t)$, the inequality $- \rho_{1i}(\infty) < {\eta_{1i}} < \rho_{1i}(\infty)$ is satisfied when $t \ge T$. By designing $\rho_{1i}(\infty) = \rho_{1i\infty } = \frac{2s_{1i }}{\pi}\arctan\left(\nu\right)$ and $T_{c} = T$, we have

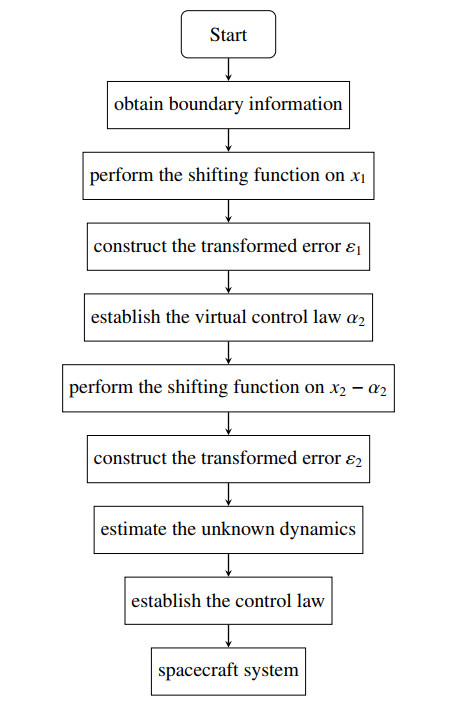
Therefore, the attitude error can converge to a prescribed region ${\rm \Omega } = \left\{ { q}_{evi} \mid \left| { q}_{evi}\right| \le \nu \right\}$ within the predefined time $T$. The flowchart that manifests the process for generating the proposed control action is shown in Figure 1.

Remark 6. The tracking accuracy and convergence time can be explicitly and arbitrarily settled in advance, irrespective of the initial conditions, by tuning $\nu$ and $T$ respectively. A smaller $\nu$ and $T$ contribute to improved precision, as well as a shorter convergence period. However, it is noted that the setting of the parameters $\nu$ and $T$ is exactly based on a trade-off between ambitious aims and allowable practices.

Remark 7. The control parameters $p$, $q$, $r_{1}$, $r_{2}$, $k_{1}$ and $k_{2}$ can be selected by trial-and-error methods to ensure that all other closed-loop signals are fixed-time bounded. The setting of these parameters does not necessarily require taking the values of $\nu$ and $T$ into consideration.

5.   Simulation

The nominal component of the inertia matrix is defined as

The uncertain part of the inertia matrix is

The external disturbance is set to be

The actuator misalignment takes the form of

The desired attitude is ${\boldsymbol q}_{d} = \left[1, 0, 0, 0\right]^{T}$. We consider two groups of different initial values to perform the simulation. Case 1: ${\boldsymbol q}\left(0 \right) = \left[{\rm{ 0.6698}}, {\rm{-0.5158}}, {\rm{0.4716}}, {\rm{0.2508}} \right]^T$; Case 2: ${\boldsymbol q}\left(0 \right) = \left[{\rm{0.1737}}, {\rm{-0.2632}}, {\rm{0.7896}}, {\rm{-0.5264}} \right]^T$. The maximum control torque is considered to be $u_{maxi} = 7.5$ N $\cdot$ m.

For the virtual control law (4.7) and the actual control law (4.23), the parameters are selected as $k_{1} = 1$, $k_{2} = 2$, $p = 1.2$, $q = 0.8$, $r_{1} = 10$, $r_{2} = 5$ and $\mu = 0.01$. The parameters of the update law (4.24) are chosen as $w_{1} = 2$, $w_{2} = 1$, $\lambda = 10$ and $h = 1$. The shifting function parameters are given as $s_{1i} = s_{2i} = 0.4$. The initial PPFs are set as $\rho_{1i0} = \rho_{2i0} = 0.4$. It is noteworthy that the initial condition has been violated since the initial errors $q_{e2}(0)$ and $q_{e3}(0)$ in Case 1 and $q_{e2} (0)$ and $q_{e3}(0)$ in Case 2 are bigger than $\rho_{1i0}$.

5.1.   Simulation one

In this section, Cases 1 and 2 are considered to demonstrate the efficacy of our proposed approach when it comes to handling attitude tracking problems with a predefined convergence time independent of the original states. The predefined-time PPF parameters are given as $\nu = 0.01$, $T = 10$, $\rho_{1i\infty} = \frac{2s_{1i}}{\pi}\arctan\left(\nu\right) = 0.0025$, $\rho_{2i\infty} = 0.1$ and $a_{1i} = a_{2i} = 1.2$.

The simulation results are shown in Figures 2–7. Figures 2 and 3 show that the proposed controller performs fairly well under different initial conditions, and that the actual settling time is $7.5$ s, which is shorter than the predefined one. With the implementation of the shifting function, the proposed controller is able to maintain attitude errors within prescribed envelopes despite the tracking errors exceeding the PPFs at the beginning. As shown in Figure 4, different control torques are required under different initial conditions to provide the desired performance. It can be seen in Figures 5 and 6 that the transformed errors $\varepsilon_{1i}$ and $\varepsilon_{2i}$ are fixed-time bounded. The boundedness of the adaptive parameter is shown in Figure 7.

5.2.   Simulation two

To further illustrate that the attitude maneuvering performance of spacecraft systems can be prescribed with our proposed method in terms of convergence time, we present the results of the simulation with two different convergence times $T = 10$ and $T = 15$. Case 1 is considered for the initial attitude value. Other parameters of the PPFs and the proposed controller remain unchanged from Simulation one.

The corresponding results are shown in Figures 8–10. It is observed in Figure 8 that the proposed controller will render attitude error into the predefined region $\left| q_{evi} \right| \le 0.01$ within $T$. Figures 8 and 9 also show that the convergence time of attitude errors with our proposed methods can be directly and arbitrarily set by selecting different values of $T$. In general, a smaller $T$ indicates a shorter stabilization period but a greater control burden as shown in Figure 10.

5.3.   Simulation three

To demonstrate that the tracking performance of spacecraft systems can be prescribed with our propounded controller in terms of control accuracy, we present the simulation with $\nu$ as $\nu = 0.01$ and $\nu = 0.001$ and the same value of prescribed settling time $T = 5$. Hence, $\rho_{1i\infty}$ values are set as $\rho_{1\infty i} = 0.0025$ and $\rho_{1\infty i} = 2.5 \times 10^{-4}$, while other adjustable parameters remain the same as those in Simulation one. We consider the example in Case 2 as the initial value of the quaternion.

The results are depicted in Figures 11 and 12. It is shown in Figure 11 that the attitude error is stabilized into the prescribed region $\left| q_{evi } \right| \le \nu$ within $T$ no matter whether the initial values of the quaternion violate the prescribed constraints. Generally, a smaller $\nu$ contributes to improved precision in attitude maneuvering at the expense of a heavier burden on the controller, as shown in Figure 12.

5.4.   Simulation four

To illustrate the advantage of our propounded controller, the fault-tolerant fast fixed-time convergent attitude control (FTFFTCAC) proposed in ^[38] is considered to perform the comparative study. The preset convergence time and prescribed accuracy are respectively given as $T = 10$, $v = 0.01$. Other control parameters remain unchanged. We select Case 2 for the initial tracking errors.

For the following modified prescribed performance function (MPPF) developed in ^[38], the MPPF parameters are chosen as $k = 0.4$, $T_{m} = 10$, $\rho_{0} = 1$ and $\rho_{\infty} = 0.01$. Other control parameters are chosen as ^[38].

It can be seen in Figures 13 and 14 that our proposed control scheme exhibits better tracking performance than the FTFFTCAC scheme, with faster convergence and higher accuracy. Figure 15 shows that the control consumption of the designed controller is significantly less than that of FTFFTCAC, and that the control action is smoother.

5.5.   Simulation five

To demonstrate the robustness of our proposed control scheme, an additional disturbance is imposed on the spacecraft during the period of $13–18$ s with the term ${\boldsymbol d}_{sud} = \left[{\begin{array}{*{20}{c}} 2+0.5\sin(0.2t)\\ 2+0.5\sin(0.2t)\\ 2+0.5\sin(0.2t) \end{array}} \right] \rm{N\cdot m}$.

Figure 16 shows that the proposed controller can guarantee the tracking errors with performance in terms of convergence time and steady-state precision in the presence of an unexpected disturbance. The shifted errors are always kept within the constraints, which verifies the robustness of our proposed controller. It is depicted in Figure 17 that the control torque is bounded and not chattering when a sudden change in disturbance occurs. As shown in Figure 18, the attitude error $q_{e1}$ reaches the guaranteed performance boundary at around $t = 14$ s, resulting in a loss of efficacy for the FTFFTCAC controller.

6.   Conclusions

In this article, a novel adaptive predefined-time prescribed performance controller is presented for spacecraft systems. By employing a predefined-time PPF, we guarantee that the attitude errors will satisfy the prescribed tracking accuracy within a predefined time. By introducing a novel shifting function, we eliminate the constraints on initial errors, enabling the proposed method to be implemented even if the attitude errors violate the prescribed boundaries initially. RBFNN and MLP techniques have been introduced to approximate the lumped uncertain dynamics, and the adaptive law has been designed to ensure the fixed-time convergence of the learning parameter. Our proposed method has the notable merit of allowing the settling time and the tracking precision to be directly prespecified by setting two adjustable parameters. The proposed control scheme exhibits excellent performance against input saturation, actuator misalignment and unexpected disturbances.

Acknowledgments

This research was supported by the National Natural Science Foundation (NNSF) of China under Grants 61333008, 61603320, 61733017 and 61673327 and Xiamen Key Laboratory Of Big Data Intelligent Analysis and Decision.

Conflict of interest

The authors declare that there is no conflict of interest.

Appendix

To achieve $\left | e \right| \le v$, the PPF parameter should be designed as $\rho_{\infty } = v$ according to previous PPC schemes ^[37,38,39].

The PPF defined in (3.2) and in ^[37,38,39] can be rewritten in a general form as follows:

where $0 \le r \le 1$ refers to the monotonically decreasing component of the PPFs. For a given time, $r$ is a constant.

For our proposed PPC control strategy, according to Theorem 4.1, we need to design $\rho_{\infty} = \frac{{2s}}{\pi}\arctan\left(\nu\right)$ to guarantee that the tracking error converges to the region $\left |e \right| \le v$. Therefore, the PPF defined in (3.2) can be rewritten as

where $0 < k = \frac{{2s}}{\pi} < 1$.

The traditional formulation of normalized error in ^[37,38,39] can be written as

In our proposed scheme, the new normalized error is defined as

Letting $f(e) = \left|\xi_{2}\right|-\left|\xi_{1} \right| = \xi_{2}\left(\left|e\right|\right)-\xi_{1}\left(\left|e\right|\right)$ yields

Define $g(\left|e\right|) = k\arctan(\left|e\right|)\left(r\rho_{0}+(1-r)v\right)-\left|e\right|\left(r\rho_{0}+(1-r)k\arctan(v)\right)$. Differentiating $g$ with respect to $e$, we can obtain

When $v \to 0$, we have $\arctan (v) = v$. Thus, $\dot g$ can be rewritten as

Given that $0 < k < 1$, when $e < 0$, it is obvious that $\dot g > 0$. Similarly, when $e > 0$, we can obtain $\dot g < 0$. Therefore, we have that $f(e) \le f(0) = 0$ for any $e \in \mathfrak{R}$. From this perspective, the absolute value of normalized error is reduced by our method. In addition, due to the property that the transformed function is monotonically increasing, a decrease in the transformed error and the control torque output can be achieved with the same error $e$.