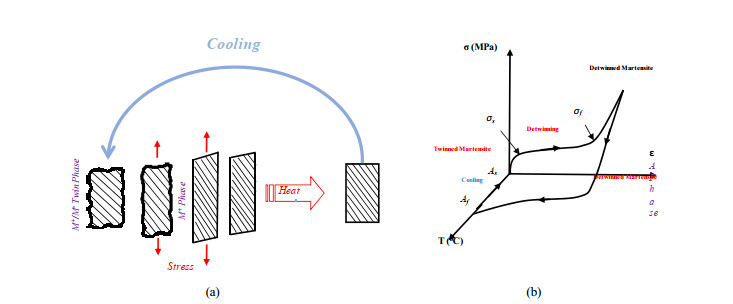
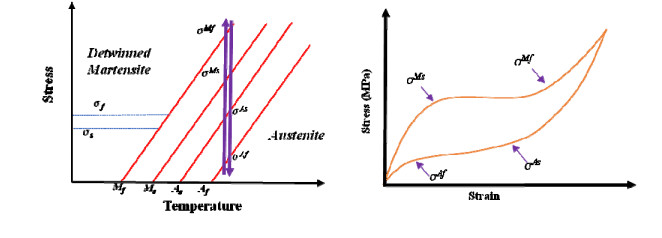
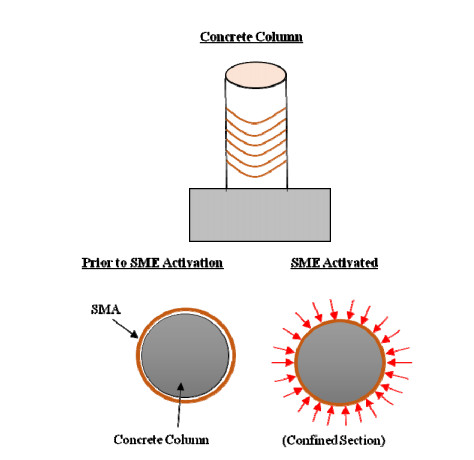
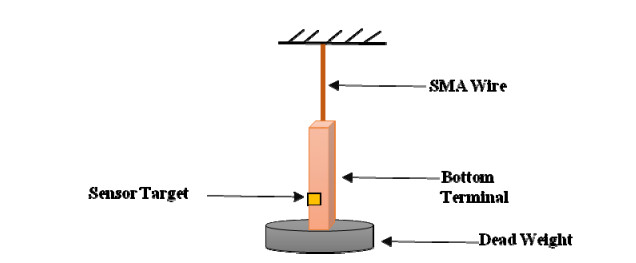
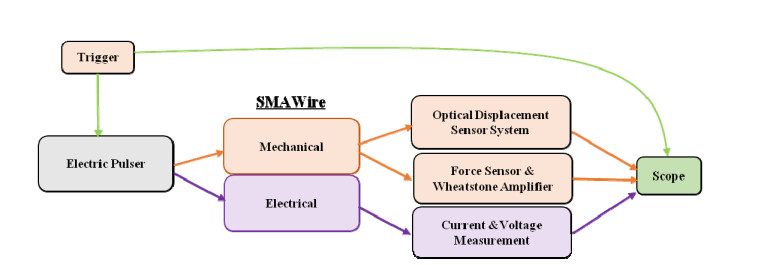
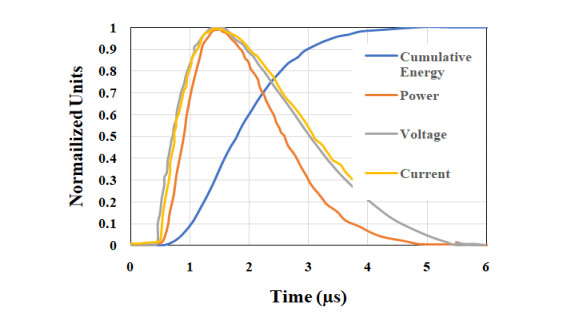
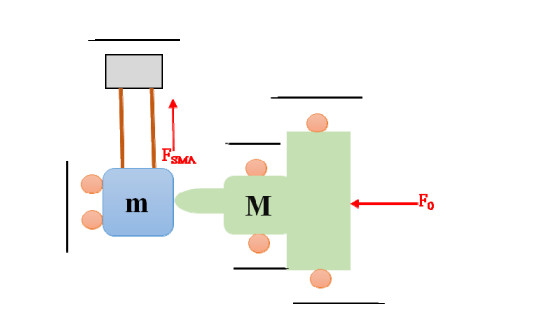
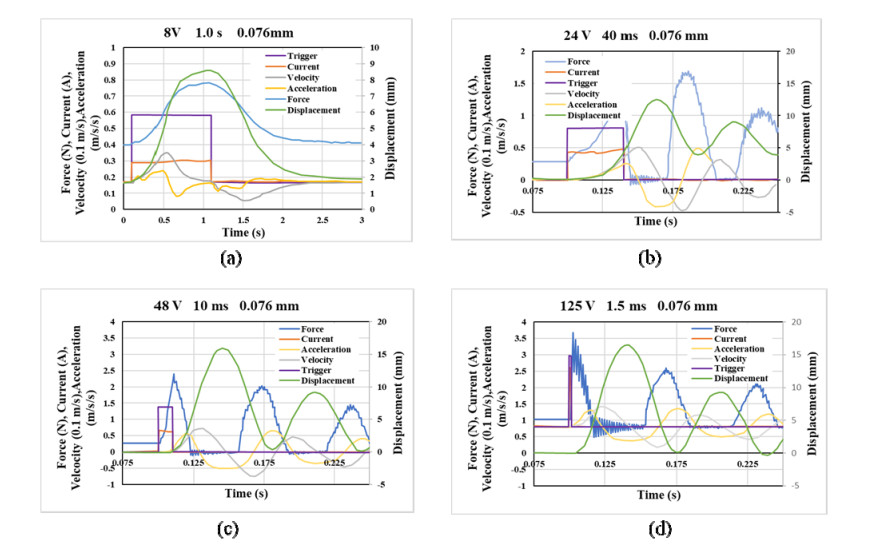
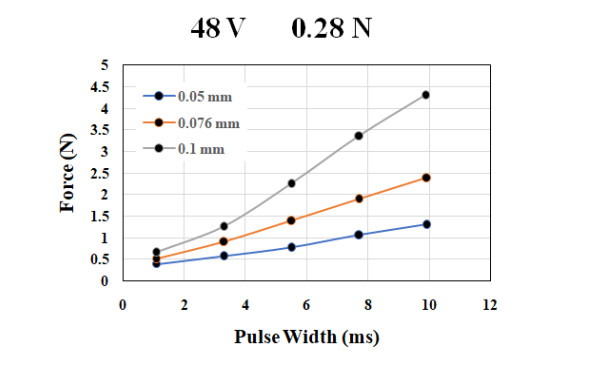
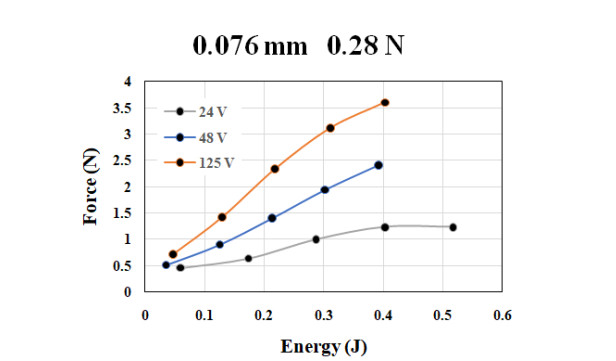
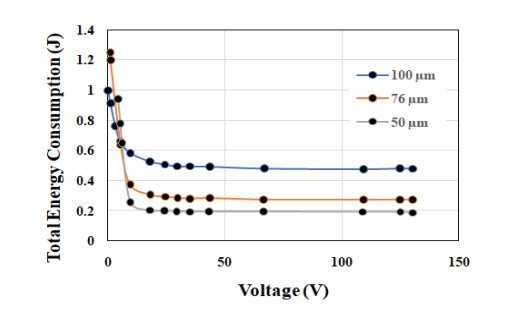
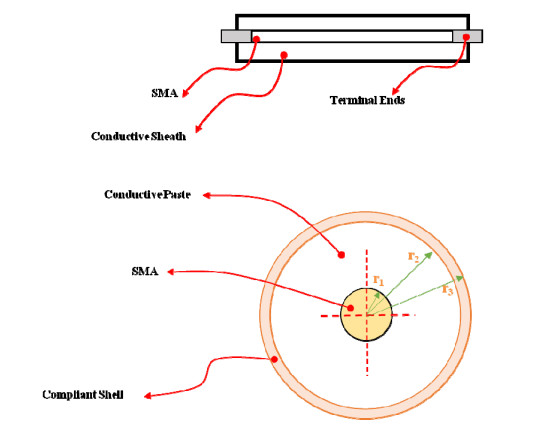
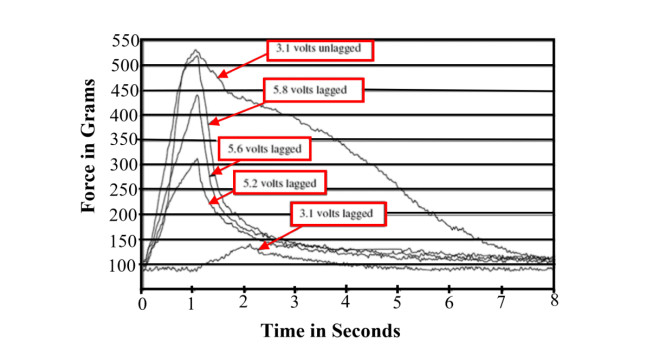
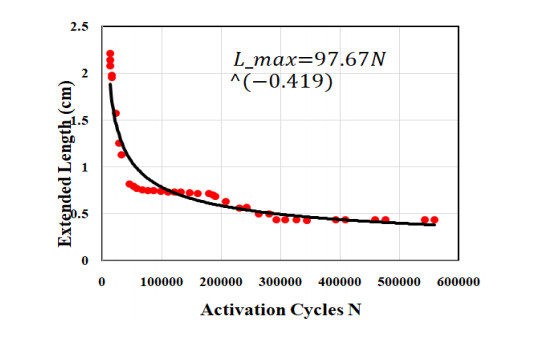
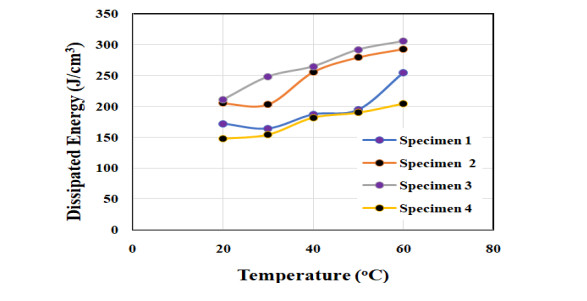
The use of shape memory alloys (SMAs) in civil structures attracted the attention of researchers worldwide. This interest is due the unique properties of SMAs, the shape memory effect (SME) and pseudoelasticity. Other desirable attributes for SMA include biocompatibility, high specific strength, wear resistance, anti-fatigue characteristics, and high yield strength. These beneficial qualities allow for a wide range of applications ranging from aerospace field to the medical and civil engineering fields. To intelligently utilize shape memory alloys and widen their application potential, certain characteristics including the heat activation and heat transfer mechanisms must be thoroughly understood. Such understanding would allow the development and optimization of systems utilizing SMA. Hence, this paper presents a state-of-the-art review about shape memory alloys with specific focus on the heat activation mechanisms and the heat transfer modes.
1.
Introduction
A coupled system of two Kirchhoff plate equations is considered:
where Ω is a bounded domain of R2 with a smooth boundary Γ=∂Ω=Γ0∪Γ1, such that ¯Γ0∩¯Γ1=∅, the initial data y0, y1, z0 and z1 lie in appropriate Hilbert space.
The symbols yt and ytt refer, respectively, to first order and second order derivatives (with respect to t) of y, while Δ and Δ2 are the Laplacian and Bilaplacian operators. The functions hi and fi (for i=1,2) verify some assumptions that will be given in the next section. ρ is a positive constant, x=(x1,x2) is the space variable, and the operators B1 and B2 are defined by
and
where the constant 0<μ<12 is the Poisson coefficient. Here, ∂ν stands for normal derivative, ν=(ν1,ν2) is the unit outer normal vector to Γ and τ=(−ν2,ν1) is a unit tangent vector.
Model (1.1) describes the interaction of two viscoelastic Kirchhoff plates with rotational forces, which possess a rigid surface and whose interiors are somehow permissive to slight deformations, such that the material densities vary according to the velocity [1]. Each one of these two plates is clamped along Γ0, and without bending and twisting moments on Γ1. The analysis of stability issues for plate models is more challenging due to free boundary conditions and the presence of rotational forces, etc. [2]. Moreover, in our case the source term competes with the dissipation induced by the viscoelastic term only. Therefore, it will be interesting to study this interaction [3].
We start off by reviewing some works related to quasi-linear wave equation and plate equation. Cavalcanti et al. [1] considered the following equation
and proved the global existence of weak solutions and a uniform decay rates of the energy in the presence of a strong damping, of the form −γΔut acting in the domain and assuming that the relaxation function decays exponentially. Messaoudi and Tatar [3] studied (1.2) but without a strong damping (γ=0). They showed that the memory term is enough to stabilize the solution. The global existence and uniform decay for solutions of (1.2), provided that the initial data are in some stable set, are obtained in [4] with the presence of a source term and with γ=0. Later, in [5], for γ=0, the authors investigated the general decay result of the energy of (1.2) with nonlinear damping. In [6], the author investigated (1.2) with weakly nonlinear time-dependent dissipation and source terms, and he established an explicit and general energy decay rate results without imposing any restrictive growth assumption on the damping term at the origin. For other related results for quasi-linear wave equations, we refer the reader to [7,8,9,10]. For quasi-linear plate equations, we mention the work of Al-Gharabli et al. [11] where the authors studied the well-posedness and asymptotic stability for a quasi-linear viscoelastic plate equation with a logarithmic nonlinearity. Recently, Al-Mahdi [12] studied the same problem as in Al-Gharabli et al. [11], but with infinite memory. With the imposition of a minimal condition on the relaxation function, he obtained an explicit and general decay rate result for the energy. Very recently, in [13], the authors considered a plate equation with infinite memory, nonlinear damping, and logarithmic source. They proved explicit and general decay rate of the solution.
The stability of coupled quasi-linear systems has been discussed by many authors. Liu [14] considered two coupled quasi-linear viscoelastic wave equations. He showed that the viscoelastic terms' dissipations guarantee that the solutions decay exponentially and polynomially. Later on, with more general relaxation functions and specific initial data, He [15] extended the result of Liu [14]. Recently, Mustafa and Kafini [16] considered the same problem and improved earlier results for a wider class of relaxation functions. In [17], the authors studied the same problem, but with nonlinear damping, and showed a general decay rate estimates of energy of solutions. Very recently, Pişkin and Ekinci [18] generalized and improved earlier results by considering a degenerate damping. Finally, let's mention the recent works of Fang et al.[19] and Zhu et al.[20] that relate to our problem.
As I know, there is no work regarding quasi-linear plate equations. This paper seems to be the first that deals with this problem.
The structure of this paper is shown as follows: In Section 2, we present some presumptions that are necessary for the proof of essential results. The third section provides the proof of well-posedness of our system. The general energy decay result is stated and established in Section 4. The fifth section provides two examples that illustrate explicit formulas for the energy decay rates. A concluding section is given at the end.
2.
Preliminaries
This part is devoted to give some necessary materials and assumptions for the proof of our key results. We define
and
Denoting dx=dx1dx2, we define the bilinear form b:V×V→R by:
Firstly, we must recall Green's formula (see [2]):
and a weaker version of it (see Theorem 5.6 in [21]) in the following form:
We need the following lemma.
Lemma 2.1. ([22]) For any y∈C1(0,T;H2(Ω)), we get
where
In this paper, we suppose that:
(A1): The two non-increasing C1 functions hi:[0,+∞)→(0,+∞) (for i=1,2) such that
(A2): There are a positive C1 functions Gi:(0,+∞)→(0,+∞), that are linear or strictly increasing and strictly convex C2 on (0,r],(r<1), with Gi(0)=G′i(0)=0, satisfying for all t≥0
where ξ1 and ξ2 are positive non-increasing differentiable functions.
(A3): fi:R2→R (for i=1,2) are C1 functions and there exists a positive function F, such that
and
for some constant d>0 and βij≥1 for i,j=1,2.
Remark 2.1. 1.The condition (A1) guarantees the hyperbolicity of the first two equations in the system (1.1).
2. By (2.6) and the mean value theorem, we have for some positive constant d1
and
for all (x1,x2),(u1,u2)∈R2 and i=1,2.
The energy functional is defined by
Here,
represent, respectively, the kinetic and the elastic potential energy of the model.
We have the following dissipation identity:
Proposition 2.1.
Proof. Multiplying (1.1)1 by yt and (1.1)2 by zt, summing the resultant equations and integrating over Ω to get
Inserting (2.3) in (2.11), we get the desired result.
Throughout this paper, c denotes a generic positive constant, and not necessarily the same at different occurrences.
3.
Global existence
We begin this part by defining a weak solution of the system (1.1).
Definition 3.1. A couple of functions (y,z) defined on [0,T] is a weak solution of the problem (1.1) if y∈C([0,T],V)∩C1([0,T],W),z∈C([0,T],V)∩C1([0,T],W), and satisfies
and
for a.e. t∈[0,T] and all test functions u,v∈V.
Theorem 3.1. Let (y0,y1),(z0,z1)∈V×W. Assume that assumptions (A1)–(A3) are true. Then, the system (1.1) has at least a local weak solution. Moreover, this solution is global and bounded.
Proof. With the help of the Faedo-Galerkin approach, the existence is demonstrated. In order to achieve this, let {wj}∞j=1 be a basis of V. Define Em=span{w1,w2,...,wm}. On the finite dimensional subspaces Em, the initial data are projected as follows:
such that
Considering the following solution
which satisfies the following approximate problem in Em:
This leads to a system of ordinary differential equations (ODEs) for unknown functions pk and qk. Hence, from the standard theory of system of ODEs, a solution (ym,zm) of (3.2) exists, for all m≥1, on [0,tm), with 0<tm≤T,∀m≥1.
A priori estimate 1: Let w=ymt in (3.2)1 and w=zmt in (3.2)2. Combining the resultant equations and integrating on Ω to obtain
where
Noting, by (3.1), that
Then, by integrating (3.3) over (0,t),0<t<tm, we get a constant M1>0 that doesn't depend on t and m, satisfying
Hence, tm can be replaced by some T>0, for all m≥1.
A priori estimate 2: Let w=ymtt in (3.2)1 and w=zmtt in (3.2)2, adding the resultant equations, integrating on Ω, and using Young's inequality to obtain for all η>0
Using Hölder's inequality, Sobolev's embedding, (2.7) and (3.4), one has for some M2>0,
Similarly, we obtain that
From (3.5)–(3.7), we infer that
Integrating (3.8) on (0,T), and using (3.4) gives us
Choosing η small enough, such that
and so that
Consequently, (3.9) becomes
Then, we have
for some constant M3>0.
From (3.4) and (3.10), we conclude that
and
Hence, we can extract subsequence of (ym) and (zm), still denoted by (ym) and (zm) respectively, such that
and
Analysis of the non-linear terms:
1. Term fi(ym,zm): We have that (ym) and (zm) are bounded in L∞(0,T;V). This shows, by the use of the embedding of V⊂L∞(Ω)(Ω⊂R2), the boundedness of (ym) and (zm) in L2(Ω×(0,T)). Likewise, (ymt) and (zmt) are bounded in L2(Ω×(0,T)). Hence, by the use of the Aubin-Lions Theorem, we get, up to a subsequence, that
Then,
and, therefore, from (A3),
On the other hand, we have (ym) and (zm) that are bounded in L∞(0,T;L2(Ω)), then, by using (2.7) and (3.4), we get that fi(ym,zm) is bounded in L∞(0,T;L2(Ω)). This fact and (3.17) leads to
2. Terms |ymt|ρymt and |zmt|ρzmt: We recall that (ymt) and (zmt) are bounded in L∞(0,T;W), which gives that (ymt) and (zmt) are bounded in L∞(Ω×(0,T)), and so in L2(Ω×(0,T)). By the same, we deduce that (ymtt) and (zmtt) are bounded in L2(Ω×(0,T)). Now, using Aubin-Lions theorem, we conclude, up to a subsequence, that
and
Using (3.4), we see that
and similarly
where C∗ is a positive constant satisfying ‖u‖2≤C∗‖∇u‖2, for all u∈W.
Then, the sequences (|ymt|ρymt) and (|zmt|ρzmt) are bounded in L2(Ω×(0,T)). Combining (3.18), (3.19) and (3.20) and using Lion's lemma [23], one derives
Next, by integrating (3.2) on (0,t), one obtains
Letting m→+∞, the aforementioned convergence results give that
for all w∈V.
Since the terms in the right hand side of (3.23)1 and (3.23)2 are absolutely continuous, then (3.23) is differentiable for a.e. t≥0, and, therefore, one has for all w∈V
Regarding the initial conditions, we recall that
Consequently, the use of Lion's Lemma [23] leads to
Hence, ym(x,0) and zm(x,0) make sense and ym(x,0)→y(x,0), zm(x,0)→z(x,0) in L2(Ω). Recalling that
we obtain that
Besides, multiplying (3.2) by ϕ∈C∞0(0,T) [24] and integrating on (0,T), to get
and
As m→+∞, we have for any w∈V and any ϕ∈C∞0(0,T)
and
This means that (see [24])
Since yt and zt∈L2(0,T;L2(Ω)), we deduce that yt and zt∈C(0,T;V).
So, ymt(x,0) and zmt(x,0) make sense and
But
Hence,
Consequently, the proof of local existence of weak solutions is complete. Besides, it is easy to see that
which gives the globalness and boundedness of the solution of problem (1.1).
4.
General decay
We denote by ξ(t)=min and G(t) = \min\{G_1(t), G_2(t)\} .
Theorem 4.1. Let (u_0, u_1), (v_0, v_1)\in V\times W . Suppose that (A1)–(A3) hold. Thus, the energy E(t) satisfies
for some positive constants \beta_1 and \beta_2 .
Remark 4.1. ([16])
1. We recall the Jensen's inequality: Assume F is a concave function on [a, b], \; f:\Omega \to [a, b] and g are in L^1(\Omega) , with g(x)\geq 0 and \int_\Omega g(x)\; dx = m > 0 , then
2. From (A2), one has \lim_{t\rightarrow +\infty}h_i(t) = 0 . Hence, \exists\; t_1\geq0 is large enough, verifying
One can easily check, for i = 1, 2 , that
for some constants a_i > 0 and b_i > 0 . This implies that
Proof of Theorem (4.1): The proof is divided into three steps.
Step 1: In this step, we give estimates for the derivatives (with respect to t ) of the functionals \varphi(t) and \psi(t) defined below by:
with
and
with
Lemma 4.1. If (A1)–(A3) hold. The functional \varphi(t) defined in (4.4) verifies, along the solution of (1.1),
Proof. We have \varphi'(t) = \varphi^{'}_1(t)+\varphi^{'}_2(t) . By using (1.1), we obtain
Since \int_0^t h_1(s)ds\leq \int_0^{+\infty} h_1(s)ds = 1-l_1 , then, by the use of Cauchy-Schwarz's inequality and Young's inequality, we derive
Inserting (4.9) in (4.8), we get that
Similarly, we infer that
Summing the last two inequalities, we get the desired inequality (4.7).
Lemma 4.2. If (A1)–(A3) hold. The functional defined in (4.6) verifies, for any 0 < \delta < 1 and for all t\geq t_1 , along the solution of (1.1),
Here h_0 = \min\Big\{ \int_0^t h_1(s) ds, \int_0^t h_2(s) ds\Big\} .
Proof. Differentiating \psi_1(t) with respect to t and using (1.1)_1 , we get
Now, we estimate the terms in the right-hand side of (4.11) as follows:
\bullet Estimation of the term \int_0^t h_1(t-s) b\left(y, y(t)-y(s)\right)ds.
Cauchy Schwarz's inequality and Young's inequality are used to get, for any \delta > 0 ,
\bullet Estimation of the term - \int_0^t h_1(t-\zeta) \int_0^t h_1(t-s)b\left(y(s), y(t)-y(\zeta)\right)ds\; d\zeta.
We have
\bullet Estimation of the term - \int_{\Omega} {{\boldsymbol{\nabla y_t}}} \int_0^t h'_1(t-s)(y(t)-y(s))ds dx.
One has
\bullet Estimation of the term \int_\Omega f_1(y, z) \int_0^t h_1(t-s)(y(t)-y(s))ds\; dx.
By using (2.7) and (3.27), we derive that
\bullet Estimation of the term -\frac{1}{\rho+1} \int_{\Omega} \vert y_t\vert^{\rho}y_t \int_0^t h'_1(t-s)(y(t)-y(s))ds\; dx.
Using (3.27) again, we infer that
By combining (4.12)–(4.16), using the fact that - \left(\int_0^t h_1(s)ds\right)\leq -h_0 for all t\geq t_1 and choosing \delta_1 small enough, we derive the estimate (4.10).
Repeating the calculations above with \psi_2(t) yields
Combining (4.10) and (4.17), we obtain the following result.
Corollary 4.1. Assume that (A1)–(A3) hold. Then, the functional \psi satisfies, along the solution, the estimate
for any 0 < \delta < 1 .
Step 2: The aim of this step is to establish the inequality (4.26).
Let's define the functional
where N > 0 . For N sufficiently large, one has that F\sim E , i. e.
for some c_1, c_2 > 0.
Let l = \min\left\{l_1, l_2\right\} . By using (2.10), (4.7), (4.18), and taking \delta = \frac{lh_0}{16c} , we get for any t\geq t_1
Taking N , such that
to obtain that
By the virtue of (2.10) and (4.3), we infer that for any t\geq t_1 ,
and similarly
Hence, (4.21) becomes
where \alpha > 0 . Define \mathcal{H}(t) = F(t)+cE(t) . It is easy to see that \mathcal{H}(t)\sim E(t) . Using (4.22), we get
The following two situations are then distinguished.
First Case: G_1(t) and G_2(t) are linear.
By multiplying (4.23) by \xi(t) and using (A2) and (2.10) to obtain
Since \xi is non-increasing, then by using (4.24), the functional \mathcal {F}(t) = \xi(t)\mathcal{H}(t)+cE(t) satisfies for any t\geq t_1 ,
It is obvious that \mathcal{F} \sim E , and then we get the existence of some positive constant m_1 , such that
By applying Gronwall's Lemma, there exists a constant m_2 > 0 , such that
and then we have
where m_3 > 0 .
Second Case: G_1(t) or G_2(t) is nonlinear. Defining J_1 and J_2 by
and
Since b(y(t), y(t))+b(y(t-s), y(t-s))\leq \frac{2}{l}\left(E(t)+E(t-s)\right)\leq \frac{4}{l}E(0) , for all 0 < s < t , we infer that
and similarly
By taking 0 < \lambda < 1 sufficiently small, we get, for all t > 0 ,
Now, defining K_1(t) and K_2(t) by
and
One can easily check that K_i(t)\leq-c E'(t) , for i = 1, 2 .
Given that G_1(0) = 0 and the strict convexity of G_1 on (0, r] , one has then G_1(\kappa x)\leq \kappa G_1(x), \; \forall\; 0\leq\kappa\leq 1 and x\in(0, r] . Now, using (A1), (4.25) and Jensen's inequality, we obtain
Note that \overline{G}_1 is an extension of G_1 , satisfying \overline{G}_1 as strictly convex and strictly increasing on (0, +\infty) . Thus, we have
Similarly, we have
where \overline{G}_2 is an extension of G_2 .
We infer from (4.23) that
Step 3: Here, we shall prove the desired inequality (4.1).
We set G = \min\{\overline{G}_1, \overline{G}_2\} . For \varepsilon_0 < r , using (4.26) and since E'\leq0 , \overline{G}_i^{'} > 0 , \overline{G}_i^{''} > 0 , i = 1, 2 , we claim that the functional {\mathcal{G}} , defined by
is equivalent to E(t) and satisfies
The convex conjugate of G in the Young's sense (see [25]) is denoted by G^{*} and satisfies
The following inequality holds true:
with A = G'\left(\varepsilon_0\frac{E(t)}{E(0)}\right) and B_i = \overline{G}_{i}^{-1}\left(\frac{\lambda K_i(t)}{\xi_i(t)}\right), \; i = 1, 2.
Using (4.27), (4.28) and (4.29), we obtain
Since K_i(t)\leq -cE'(t) (for i = 1, 2) , we infer that
Consequently, letting \mathcal{G}_1 = \xi \mathcal{G}+cE , we have: \alpha_1\mathcal{G}_1(t)\leq E(t)\leq\alpha_2\mathcal{G}_1(t), for some \alpha_1, \alpha_2 > 0 .
Thus, we get
where \beta_1 > 0 and \mathcal{G}_2(t) = tG'(\varepsilon_0t) . Since \mathcal{G}_2'(t) = G'(\varepsilon_0t)+\varepsilon_0tG''(\varepsilon_0t) , then using the strict convexity of G_{i} (i = 1, 2) on (0, r] , we have \mathcal{G}_2'(t), \mathcal{G}_2(t) > 0 on (0, 1] . Since \mathcal{G}_1\sim E and using (4.31), one derives that
and
with \beta_2 > 0 . Integrating the last inequality over (t_1, t) yields
Now, the function G_0 defined by G_0(t) = \int^r_t\frac{1}{sG'(s)}ds, is strictly decreasing on (0, r] and satisfies \lim\limits_{t\rightarrow0}G_0(t) = +\infty . Thus, we deduce that
This inequality together with (4.32) yields to (4.1). This ends the proof of Theorem (4.1). □
5.
Examples
In this section, we give two examples that illustrate explicit formulas for the decay rates of the energy.
1. Let h_1(t) = h_2(t) = pe^{-k(1+t)^q}, \; t\geq0 , where p > 0 , 0 < q\leq1 and p > 0 is chosen so that h_i satisfies (2.4). We can see, for i = 1, 2 , that
where \xi_i(t) = qk(1+t)^{q-1} and G_i(t) = t . From (4.1), it holds that
2. Let h_i(t) = \frac{p_i}{(1+t)^{q_i}}, \; i = 1, 2 , where q_i > 0 and p_i > 0 is chosen such that, (2.4) holds true. One has, for i = 1, 2 ,
where \xi_i(t) = \frac{q_i}{p_i^{\frac{1}{q_i}}} and G_i(t) = t^{\frac{q_i+1}{q_i}}.
Putting q_3 = \min\{q_1, q_2\} . Therefore, it follows from (4.1) that
6.
Conclusions
This paper focuses on the existence and the asymptotic stability of solutions for a system of two coupled quasi-linear Kirchhoff plate equations in a bounded domain of \mathbb{R}^2 , subject only to viscoelasticity dissipative terms and with the presence of rotational forces and source terms. Each one of these two equations describes the motion of a plate, which is clamped along one portion of its boundary and has free vibrations on the other portion of the boundary. This work is motivated by previous results concerning coupled quasi-linear wave equations [14,15,16] and single quasi-linear plate equation [12,13].
As future works, we can change the type of damping by considering, for example, weak damping (of the form y_t ), Balakrishnan-Taylor damping (of the form (\nabla y, \nabla y_t) \Delta y ) or strong damping (of the form \Delta^2 y_t) .
Acknowledgments
This work is supported by Researchers Supporting Project number (RSPD2023R736), King Saud University, Riyadh, Saudi Arabia.
Conflict of interest
The author declares that there are no conflicts of interest.












 DownLoad:
DownLoad: