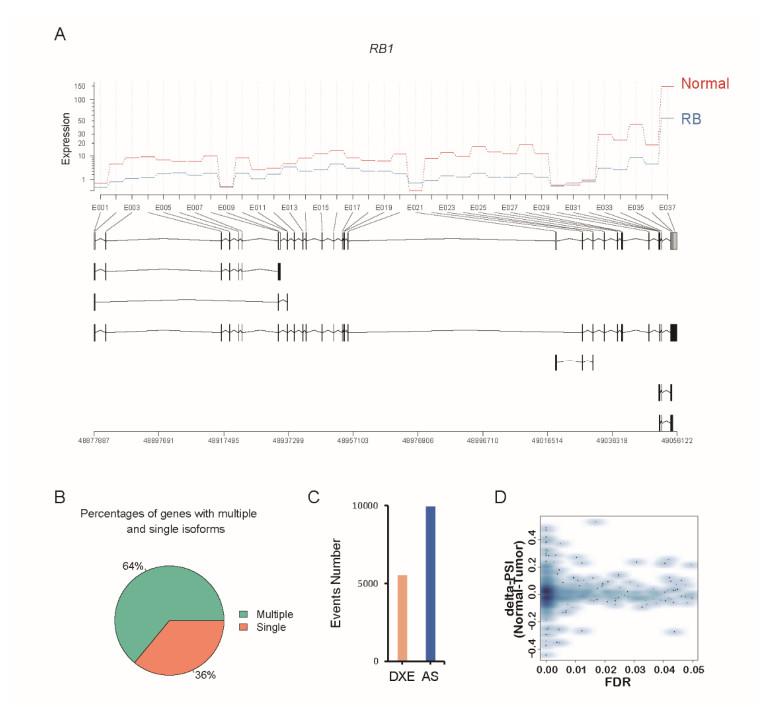
Retinoblastoma (RB) is one of the most common cancer in children. However, the specific mechanism about RB tumorigenesis has not been fully understood. In this study, to comprehensively characterize the splicing alterations in the tumorigenesis of RB, we analyzed the differential alternative splicing events in RB. Specifically, the isoforms of RB1 were downregulated in the RB samples, and a large proportion of differentially expressed genes had multiple differentially expressed transcripts (64%). We identified 1453 genes with differential alternative splicing, among which, SE accounted for the majority, followed by MXE, RI, A3SS, and A5SS. Furthermore, the biological function related to the normal function of eyes, and E2F family TFs were significantly enriched by the genes with differential alternative splicing. Among the genes associated with visual sense, ABCA4 was found to have two mutually exclusive exons, resulting in two isoforms with different functionalities. Notably, DAZAP1 was identified as one of the critical splicing factors in RB, which was potentially involved in E2F and RB pathways. Functionally, differential binding sites in DAZAP1 protein were significantly observed between RB and normal samples. Based on the comprehensive analysis of the differential alternative splicing events and splicing factors, we identified some driver genes with differential alternative splicing and critical splicing factors involved in RB, which would greatly improve our understanding of the alternative splicing process in the tumorigenesis of RB.
1.
Introduction
Right (resp., left, null) quasi-Frobenius extensions of rings were first introduced by Müller [1] as a generalization of quasi-Frobenius rings and Frobenius extensions. They are closely related with separable extensions and group rings [1,2]. For instance, K. Hirata [2] established that a central projective separable extension equivalently characterized as a quasi-Frobenius extension. Extensive research has focused on the invariant properties of rings under right (resp., null) quasi-Frobenius extensions. Notably, key homological invariants such as the dominant dimension, injectivity, and related properties are preserved under quasi-Frobenius extensions, as demonstrated in [1,3].
In the 1960s, Auslander and Bridge [4] initially introduced the concept of finitely generated modules having Gorenstein dimension zero over a Noetherian ring; these modules are now widely termed Gorenstein projective (see [4,5] for further details). A number of studies, including [6,7,8,9,10], have explored the invariance of Gorenstein projective modules under various ring extensions such as excellent extensions, Frobenius extensions, trivial ring extensions, and separable equivalences.
It is known that the Gorenstein algebra, the Cohen-Macaulay finite algebra (CM-finite algebra, for short), and the Cohen-Macaulay finite algebra (CM-free algebra, for short) are characterized in terms of Gorenstein projective modules [3,11]. Recall that a ring Λ is called a Gorenstein ring, if the injective dimension of ΛΛ and that of ΛΛ are finite. Let Γ≥Λ be a quasi-Frobenius extension of Λ with ΓΛ a generator for Λ-modules. It follows from [3, Proposition 7] that Λ is a Gorenstein ring when Γ is so. Note that a generator for Λ-modules is completely faithful, but a completely faithful module is not a generator in general (see [12, P234], for detail). In this study, we shall develop their arguments and apply obtained results to right quasi-Frobenius extensions ultimately establishing the following theorem.
Theorem A. Let Γ be a right quasi-Frobenius extension of a two-sided Noetherian ring Λ.
(1) Suppose that Γ is a completely faithful left Λ-module. Then, Λ is a Gorenstein ring, when Γ is so.
(2) Suppose that Γ is a separable extension of Λ. Then, Γ is a Gorenstein ring, when Λ is so.
In [10], Zhao proved that CM-free (resp., CM-finite) properties are invariant under separable Frobenius extensions of commutative Artin rings. It is shown by Huang et al. [7] that CM-free (resp., CM-finite) properties are invariant under the strongly separable quasi-Frobenius extensions. In this paper, we shall improve them and prove the same results for right quasi-Frobenius extensions of Artin algebras.
Theorem B. Let Γ be a separable right quasi-Frobenius extension of an Artin algebra Λ.
(1) If Λ is CM-free, then so is Γ. Furthermore, if Γ is a generator for Λ-modules, the converse also holds.
(2) If Λ is CM-finite, then so is Γ. Furthermore, if M is a relative generator for FG(Γ), where FG(Γ) is the category formed by all finitely generated Gorenstein projective left Λ-modules, then EndΛM is a right quasi-Frobenius extension of EndΓM.
Essential definitions and results frequently employed in this work are given in Section 2. Theorems A and B are proved in Section 3.
2.
Preliminaries
In this study, unless otherwise specified, all rings are assumed to be two-sided Noetherian rings, and all modules are finitely generated left modules. Given a ring Λ, the category composed of all finitely generated left Λ-modules is denoted by modΛ.
Definition 2.1. ([1, Definition 1.1]) Let Λ be a subring of Γ containing the identity of Γ. Then Γ is said to be a ring extension of Λ, represented as Γ≥Λ. Such an extension Γ≥Λ is said to be a right quasi-Frobenius extension (right QF-extension, for short), if
(1) ΓΛ is projective;
(2) ΛΓΓ∈addΛ(HomΛ(ΓΓΛ,ΛΛΛ)Γ, where addΛ(HomΛ(ΓΓΛ,ΛΛΛ)Γ denotes the category formed by direct summands of finite copies of ΛHomΛ(ΓΓΛ,ΛΛΛ)Γ.
The definition of a left quasi-Frobenius extension follows analogously. When a right QF-extension Γ≥Λ additionally satisfies the criteria for a left QF-extension, it is termed a quasi-Frobenius extension (QF-extension, for short). Moreover, a QF-extension Γ≥Λ is called a Frobenius extension if there is a bimodule isomorphism ΛΓΓ≅ΛHomΛ(ΓΓΛ,ΛΛΛ)Γ; see [13, Theorem 1.2] for detail.
The following remark is easy, which is important for our arguments.
Remark 2.2. Let Γ≥Λ be a right QF-extension, then
(1) ΓHomΛ(ΛΓΓ,ΛΛ)Λ∈addΓΓΛ.
(2) ΛΓ is projective.
Recall from [13, Section 2.4] that a ring extension Γ≥Λ is said to be a separable extension, if the map
is a split epimorphism of the Γ-bimodule. By the definition of separable extensions, we have the following lemma.
Lemma 2.3. Let Γ≥Λ be a separable extension and N∈modΓ. Then, we have ΓN∈addΓ(Γ⊗ΛN).
Proof. By the definition of separable extensions, there exist a Γ-bimodule Y and a Γ-bimodule isomorphism ΓΓΓ⊕ΓYΓ≅Γ(Γ⊗ΛΓ)Γ. Then, for a Γ-module N, one gets Γ-module isomorphisms
Thus, we have ΓN∈addΓ(Γ⊗ΛN). □
For a module M∈modΛ with the projective presentation,
Following [4], the transpose of M, denoted by TrM, is defined as the cokernel of the dualized map of f∗, where (−)∗=HomΛ(−,Λ).
Lemma 2.4. ([6, Lemma 3.1]) Suppose that Γ≥Λ is a ring extension.
(1) For any M∈modΛ, there exist projective right Γ-modules Q1,Q2 and a right Γ-module isomorphism Tr(Γ⊗ΛM)Γ⊕Q1≅(TrM⊗ΛΓ)Γ⊕Q2.
(2) If ΓΛ is projective and N∈modΓ, then there exist projective right Λ-modules P1,P2 and a right Λ-module isomorphism (TrN)Λ⊕P1≅TrN⊗ΓHomΛ(ΛΓΓ,ΛΛ)Λ⊕P2.
Recall from [4, Proposition 3.8] that M is said to have Gorenstein dimension zero, denoted by GpdΛM=0, if Ext≥1Λ(ΛM,Λ)=0=Ext≥1Λo((TrM)Λ,Λ). These modules are now often termed Gorenstein projective (see [5, Definition 10.2.1] for detail). The full subcategory of modΛ comprising all finitely generated Gorenstein projective modules is denoted by FG(Λ). The Gorenstein projective dimension (or Gorenstein dimension) of M, denoted by GpdΛM, is defined as the minimal integer n≥1 for which there exists an exact sequence in modΛ: 0→Dn→⋯→D1→D0→M→0 with each Di∈FG(Λ) (see [4,14] for detail). If no such finite sequence exists, GpdΛM is defined to be infinite. The finitistic dimension of Λ, denoted fin.dimΛ, is defined as the supremum of projective dimensions across all modules M in modΛ having finite projective dimensions.
Lemma 2.5. [6, Lemma 2.5] For a two-sided Noetherian ring Λ, fin.dimΛ=sup{GpdM∣M∈modΛ and GpdM<∞}.
Let B be a Λ-module. From [15, P87], we know that its character module B+ is the right Λ-module HomZ(B,Q/Z). Recall from [12, P233] that B is called completely faithful, provided that for every homomorphism f, f⊗ΛB=0 implies f=0. Recall that B is a generator (resp., cogenerator) for Λ-modules if each Λ-module is a quotient (resp., submodule) of direct sums (resp., products) of B. Clearly, every generator is completely faithful, but the converse is not true in general.
Lemma 2.6. ([12, P234]) The equivalence of the following statements holds for a projective Λ-module Q.
(1) Q is a completely faithful module.
(2) Let V be a right Λ-module. Then, V⊗ΛQ=0 implies V=0,
(3) The character module Q+ is a cogenerator in modΛop.
Lemma 2.7. Let Λ and Γ be Noetherian rings.
(1) [15, Corollary 10.65] In the situation (ΛA,ΓBΛ,ΓC), assume that BΛ is projective. Then, for any n≥1, there is an isomorphism
(2) [5, Theorem 3.2.15] In the situation (ΛA,ΓBΛ,ΓC), assume that ΛA is projective. Then, for any n≥1, there is an isomorphism
3.
Main results
Lemma 3.1. Let Γ≥Λ be a right QF-extension, and X∈modΛ. Then, for any i≥1, we have the following isomorphisms
(1) ExtiΓ(Γ⊗ΛX,Γ)≅ExtiΛ(X,Λ)⊗ΛΓ;
(2) ExtiΓ(Γ⊗ΛX,Γ)≅ExtiΛ(ΛX,ΛΓ).
Proof. Noting that ΛΓ and ΓΛ are projective by assumption and by Remark 2.2(2), the assertion follows directly from Lemma 2.7. □
Lemma 3.2. Suppose that Γ≥Λ is a right QF-extension with ΛΓ completely faithful. Then,
(1) HomΛ(ΛΓ,ΛΛΛ) is a completely faithful right Λ-module.
(2) ΓΛ is completely faithful.
Proof. (1) It suffices to prove that the character module HomΛ(ΛΓ,ΛΛΛ)+Λ is a cogenerator by Lemma 2.6(3), because HomΛ(ΛΓ,ΛΛΛ)Λ is projective by Remark 2.2(1).
Let X be a finitely generated right Λ-module satisfying HomΛ(X,HomΛ(ΛΓΓ,ΛΛΛ)+)=0. Since ΛΓ is projective, by [14, P78,Theorem 3.2.11], there are isomorphisms
So, HomΛ(ΛX,Λ+)=0 by the completely faithful property of ΛΓ. Since Λ+ is also a cogenerator, X=0, which implies that HomΛ(ΛΓ,ΛΛ)+ is a cogenerator. Thus, we obtain our claim by Lemma 2.6(3).
(2) Since HomΛ(ΛΓΓ,Λ)Λ∈addΓΛ by Remark 2.2(1), Γ is a completely faithful right Λ-module as desired.
□
Remark 3.3. (1) Let Γ≥Λ be a right QF-extension such that Γ is a completely faithful right Λ-module. It is not known that Γ is completely faithful as a left Λ-module.
(2) Let Γ≥Λ be a right QF-extension with ΛΓ a generator for Λ-modules, then ΓΛ is completely faithful by Lemma 3.2. For example, if Γ is an excellent extension of Λ. It follows from [6, Proposition 4.3] that Γ is a right QF-extension of Λ. By the definition of excellent extensions, Γ is a free Λ-module. It follows from Lemma 3.2 that Γ is a completely faithful right Λ-module.
Proposition 3.4. Let Γ≥Λ be a right QF-extension, and let M∈modΛ. If ΛM is Gorenstein projective, so is Γ(Γ⊗ΛM). Furthermore, if ΛΓ is a completely faithful Λ-module, then the converse holds.
Proof. By assumption, for any i≥1, we have ExtiΛ(M,Λ)=0=ExtiΛ((TrM)Λ,Λ). Since Γ≥Λ is a right QF-extension, one obtains that ΛΓ is projective by Remark 2.2(2). By Lemma 3.1(1), one has ExtiΓ(Γ⊗ΛM,Γ)≅ExtiΛ(M,Λ)⊗ΛΓ=0 for any i≥1. On the other hand, since both ΛΓ and ΓΛ are projective, by Lemma 2.4 and Lemma 3.1(2), for any i≥1, there are isomorphisms
This implies that Γ⊗ΛM∈FG(Γ).
Conversely, assume that ΛΓ is completely faithful and Γ⊗ΛM∈FG(Γ). Then, ExtiΓ(Γ⊗ΛM,Γ)=0=ExtiΓ(Tr(Γ⊗ΛM),Γ) for any i≥1.
By Lemma 3.1(1), one gets 0=ExtiΓ(Γ⊗ΛM,Γ)≅ExtiΛ(M,Λ)⊗ΛΓ for any i≥1. Since ΛΓ is completely faithful, by Lemma 2.6(2), ExtiΛ(M,Λ)=0 for each i≥1.
It remains to show Ext≥1Λ(TrM,Λ)=0. Since ΛΓ is projective by Remark 2.2(2), for i≥1, we have
Note that Γ is a completely faithful right Λ-module by Lemma 3.2(2), then Ext≥1Λ((TrM)Λ,ΛΛ) = 0. □
Corollary 3.5. Let Γ≥Λ be a right QF-extension with ΛΓ completely faithful, and let M∈modΛ. Then
Proof. Since ΓΛ is projective, by [6, Proposition 3.2], one obtains GpdΓ(Γ⊗ΛM)≤GpdΛM.
On the other hand, without loss of generality, let GpdΓ(Γ⊗ΛM)=n<∞. Taking an exact sequence in modΛ,
with each Gi∈FG(Λ). Applying the exact functor Γ⊗Λ− to the above sequence yields an exact sequence in modΓ
By the first part of Proposition 3.4, one gets Γ⊗ΛGi∈FG(Γ) for all 0≤i≤n−1. So, Γ⊗ΛKn∈FG(Γ) by assumption and by [16, Theorem 2.20]. It follows from the second part of Proposition 3.4 that Kn∈FG(Λ). This implies GpdΛM≤n by [16, Corollary 2.21]. □
Corollary 3.6. Suppose that Γ≥Λ is a right QF-extension of Λ and M∈modΛ. If M is Gorenstein projective as a Λ-module, then so is HomΛ(ΛΓΓ,M) as a Γ-module.
Proof. Since Γ≥Λ is a right QF-extension, from Remark 2.2 one has HomΛ(ΛΓΓ,M)≅HomΛ(ΛΓΓ,Λ)⊗ΛM ∈addΓ(Γ⊗ΛM). By Proposition 3.4, Γ⊗ΛM is Gorenstein projective. The assertion follows from [16, Theorem 2.5]. □
Proposition 3.7. Let Γ be a right QF-extension of Λ and N∈modΓ. Suppose that N is Gorenstein projective as a Γ-module, then so is the underlying module N as a Λ-module. Furthermore, the converse holds when Γ≥Λ is separable.
Proof. By assumption, for any i≥1, one has ExtiΓ(N,Γ)=0=ExtiΓ((TrN)Γ,Γ). Hence, for each i≥1, ExtiΓ(ΓN,HomΛ(ΛΓΓ, Λ))=0, because ΓHomΛ(ΛΓΓ,Λ) is projective by Remark 2.2(1). By Lemma 2.7(1), for any positive integer i, we have
On the other hand, since ΛΓ is projective by Remark 2.2(2), for any positive integer i, we have
This means ΛN∈FG(Λ) as desired.
Conversely, assume that N∈FG(Λ). By the first part of Proposition 3.4, Γ⊗ΛN∈FG(Γ). Noting that Γ≥Λ is separable, then, by Lemma 2.3, we obtain ΓN∈addΓ(Γ⊗ΛN). Thus, by [16, Theorem 2.5], one gets N∈FG(Γ). □
Proposition 3.8. Let Γ≥Λ be a right QF-extension, and let N∈modΓ. Then, GpdΛN≤GpdΓN. Moreover, the equality holds true when Γ≥Λ is separable.
Proof. We may assume, without loss of generality, that GpdΓN=m, then we have the following exact sequence in modΓ:
in modΓ, where each ΓDi lies in FG(Γ). Clearly, the above sequence remains exact in modΛ. Also, by the first part of Proposition 3.7, we have ΛDi∈FG(Λ), for each 0≤i≤m. This implies GpdΛN≤m.
Let Γ≥Λ be a separable right QF-extension, and we have ΓN∈addΓ(Γ⊗ΛN), by Lemma 2.3. So, one has GpdΓN≤GpdΓ(Γ⊗ΛN)≤GpdΛN by ([6, Proposition 3.2]. □
Theorem 3.9. If Γ≥Λ is a separable right QF-extension with ΛΓ completely faithful, then
Proof. This assertion follows immediately from Lemma 2.5, Corollary 3.5, and the second part of Proposition 3.8. □
Theorem 3.10. Let Γ and Λ be two Artin algebras.
(1) Let Γ≥Λ be a right QF-extension with ΛΓ completely faithful. If Γ is Gorenstein, then so is Λ.
(2) Let Γ≥Λ be a separable right QF-extension. If Λ is Gorenstein, then so is Γ.
Proof. According to [17, Theorem 1.1], an Artin algebra is Gorenstein precisely when every finitely generated left module has finite Gorenstein projective dimension. (1) follows directly from Corollary 3.5, while (2) is an immediate consequence of the first part of Proposition 3.8. □
Let Λ be an Artin algebra over a commutative Artin ring R. Recall from [18, Section 1] that a Λ-module M is termed semi-Gorenstein projective, provided Ext≥1Λ(M,Λ)=0. We write ⊥Λ={X∈modΛ|Ext≥1Λ(X,Λ)=0}. Λ is termed left weakly Gorenstein, if GP(Λ)=⊥Λ. The notion of left weakly Gorenstein algebras is a generalization of that of Gorenstein algebras. Hence, Λ is left weakly Gorenstein if, and only if, every semi-Gorenstein projective Λ-module is Gorenstein projective.
Theorem 3.11. Let Γ and Λ be two Artin R-algebras.
(1) Let Γ≥Λ be a right QF-extension with ΛΓ completely faithful. If Γ is left weakly Gorenstein, then so is Λ.
(2) Let Γ≥Λ be a separable right QF-extension. If Λ is left weakly Gorenstein, then so is Γ.
Proof. (1) Let M be a semi-Gorenstein projective Λ-module. Then, one has Ext≥1Λ(M,Λ)=0. By assumption and by Remark 2.2(2), both ΛΓ and ΓΛ are projective. Then, by Lemma 2.7(1), for any i≥1, we have ExtiΓ(Γ⊗ΛM,Γ)≅ExtiΛ(M,Γ)=0, which implies that Γ⊗ΛM is semi-Gorenstein projective. So, Γ⊗ΛM∈FG(Γ) by assumption. It follows from the second part of Proposition 3.4 that M∈FG(Λ). Hence, Λ is a left weakly Gorenstein algebra.
(2) suppose that Λ is left weakly Gorenstein. Given a semi-Gorenstein Γ-module N, by Lemma 2.7(1) and by [6, Proposition 3.2], there are isomorphisms ExtiΛ(N,Λ)≅ExtiΛ(Γ⊗ΓN,Λ)≅ExtiΓ(ΓN,HomΛ(ΛΓΓ,Λ)) = 0 for any i≥1, because ΓHomΛ(ΛΓΓ, Λ) is projective by Remark 2.2(1). It implies that N is also a semi-Gorenstein Λ-module, and, hence, one obtains N∈FG(Λ) by assumption. Therefore, N∈FG(Γ) by the second part of Proposition 3.7. Thus, we complete this proof. □
The following lemma is due to Y. Kitamura in [19].
Lemma 3.12. [19, Theorem 1.2] Let Γ≥Λ be a right QF-extension and N∈modΓ. If ΓΓ⊗ΛN∈addΓN, then EndΛN≥EndΓN also is a right QF-extension.
Let Λ be an Artin R-algebra. By D(−), we denote the standard duality HomR(−,E(R/rad(R))), where E(R/rad(R)) is the injective envelope of R/rad(R). Following [11, Section 1], Λ is termed Cohen-Macaulay free, or simply, CM-free, provided FG(Λ)=P(Λ) (where P(Λ) is the category of finitely generated projective Λ-modules). Additionally, Λ is called Cohen-Macaulay finite[20, Section 8], or simply, CM-finite, if there exists a Gorenstein projective Λ-module G such that FG(Λ)=addΛG, and G is called a relative generator for FG(Λ). Clearly, a Cohen-Macaulay free algebra is Cohen-Macaulay finite.
Theorem 3.13. Suppose Γ is a separable right QF-extension of an Artin R-algebra Λ. Then,
That is,
(1) If Λ is CM-free, then so is Γ. Moreover, the converse holds when Γ is a generator for modΛ.
(2) If Λ is CM-finite, then so is Γ. Moreover, if M is a relative generator for FG(Γ), then the ring homomorphism ρ:EndΓM→EndΛM is a right QF-extension.
Proof. (1) For N∈FG(Γ), one has N∈FG(Λ) by the first part of Proposition 3.7. Hence, by assumption, one obtains ΛN∈P(Λ). So, Γ⊗ΛN∈P(Γ). Noting that Γ≥Λ is separable, ΓN∈addΓ(Γ⊗ΛN) by Lemma 2.3. Then, ΓN is projective. Thus, Γ is a CM-free algebra.
Conversely, assume that ΛΓ is a generator, and Γ is CM-free. Let M∈FG(Λ). By Corollary 3.6, we have HomΛ(ΛΓΓ,M)∈FG(Γ), which is projective by assumption. Hence, D(HomΛ(ΛΓΓ,M)) is an injective right Γ-module. By [15, Lemma 3.60], there is an isomorphism D(HomΛ(ΛΓΓ,M))≅DM⊗ΛΓ. Hence, DM is injective by [3, Proposition 7], which implies that M is projective. Therefore, Λ is CM-free.
(2) Assume that Λ is Cohen-Macaulay finite, with G being a relative generator for FG(Λ). By Proposition 3.4, we have Γ⊗ΛG∈FG(Γ). For any X∈FG(Γ), one gets ΛX∈FG(Λ) by Proposition 3.7. So, ΛX∈addΛG and, hence, one gets Γ(Γ⊗ΛX)∈addΓ(Γ⊗ΛG). On the other hand, noting that the ring extension Γ≥Λ is separable, we have ΓX∈addΓ(Γ⊗ΛX). It follows that ΓX∈addΓ(Γ⊗ΛG), which means that Γ is CM-finite.
By assumption and by the above discussion, one obtains that Γ is Cohen-Maulay finite. If M is a relative generator for FG(Γ), then we have that M∈FG(Λ) by Proposition 3.7. It follows from the first part of Proposition 3.4 that Γ(Γ⊗ΛM)∈FG(Γ). So, Γ(Γ⊗ΛM)∈addΓM by assumption and by Proposition 3.4, which satisfies the condition of Lemma 3.12. Therefore, EndΛM≥EndΓM is a right QF-extension as a direct consequence of Lemma 3.12. □
Recall that a separable extension Γ≥Λ is said to be strongly separable, if M∈addΛ(Γ⊗ΛM) for any Λ-module M. Under this condition, ΛΓ is a generator for Λ-modules. Due to Theorems 3.10 and 3.13, we re-obtain results in [7].
Corollary 3.14. Let Γ be a strongly separable quasi-Frobenius extension of Λ. Then
(1) ([7, Corollary 3.9]) Λ is Gorenstein if, and only if, Γ is Gorenstein.
(2) ([7, Corollary 3.10]) Λ is CM-free if, and only if, Γ is CM-free.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This work was financially supported by NSFC 12061026 and Foundation for University Key Teacher by Henan Province 2019GGJS204.
Conflict of interest
The authors declare there are no conflicts of interest.

















 DownLoad:
DownLoad: