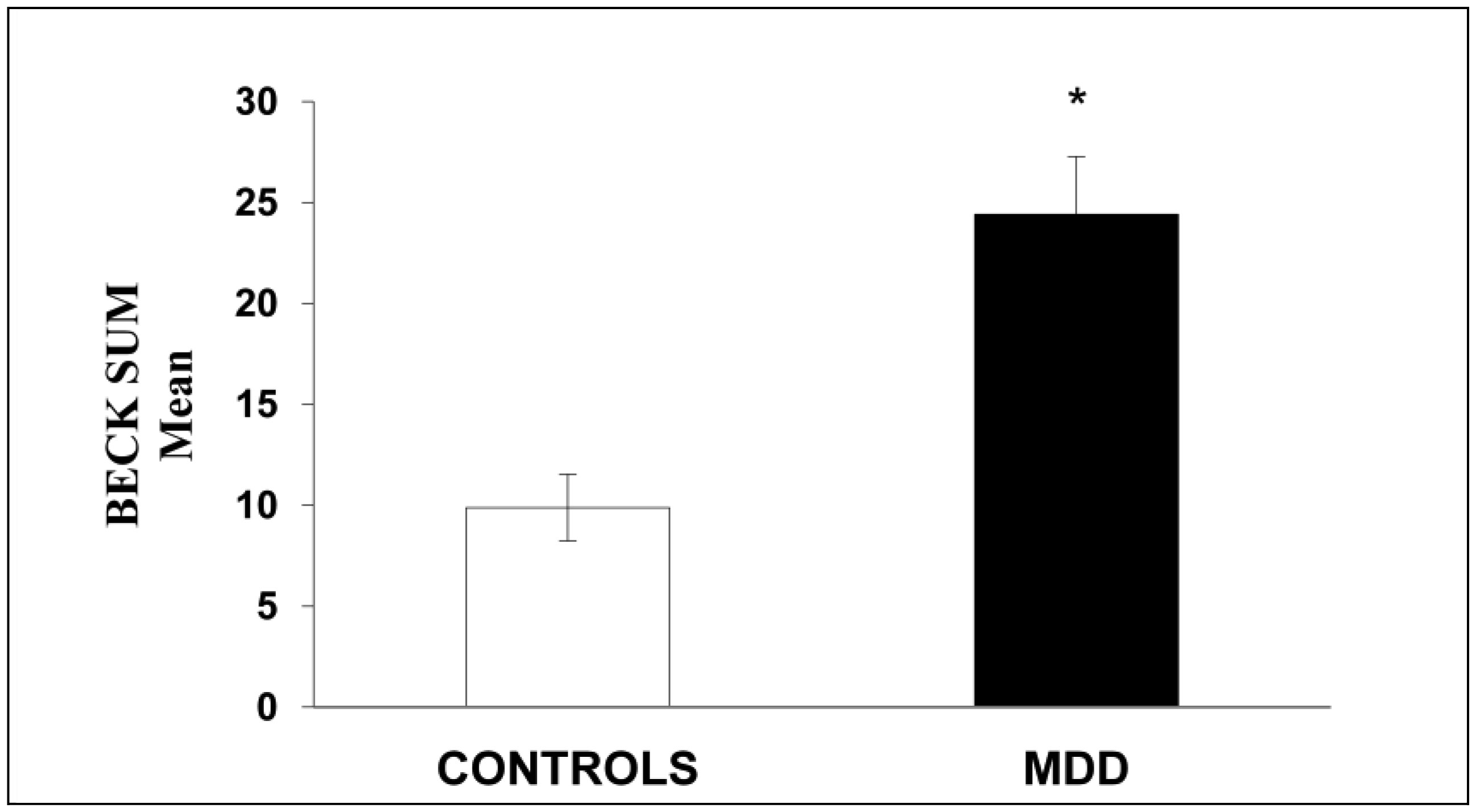
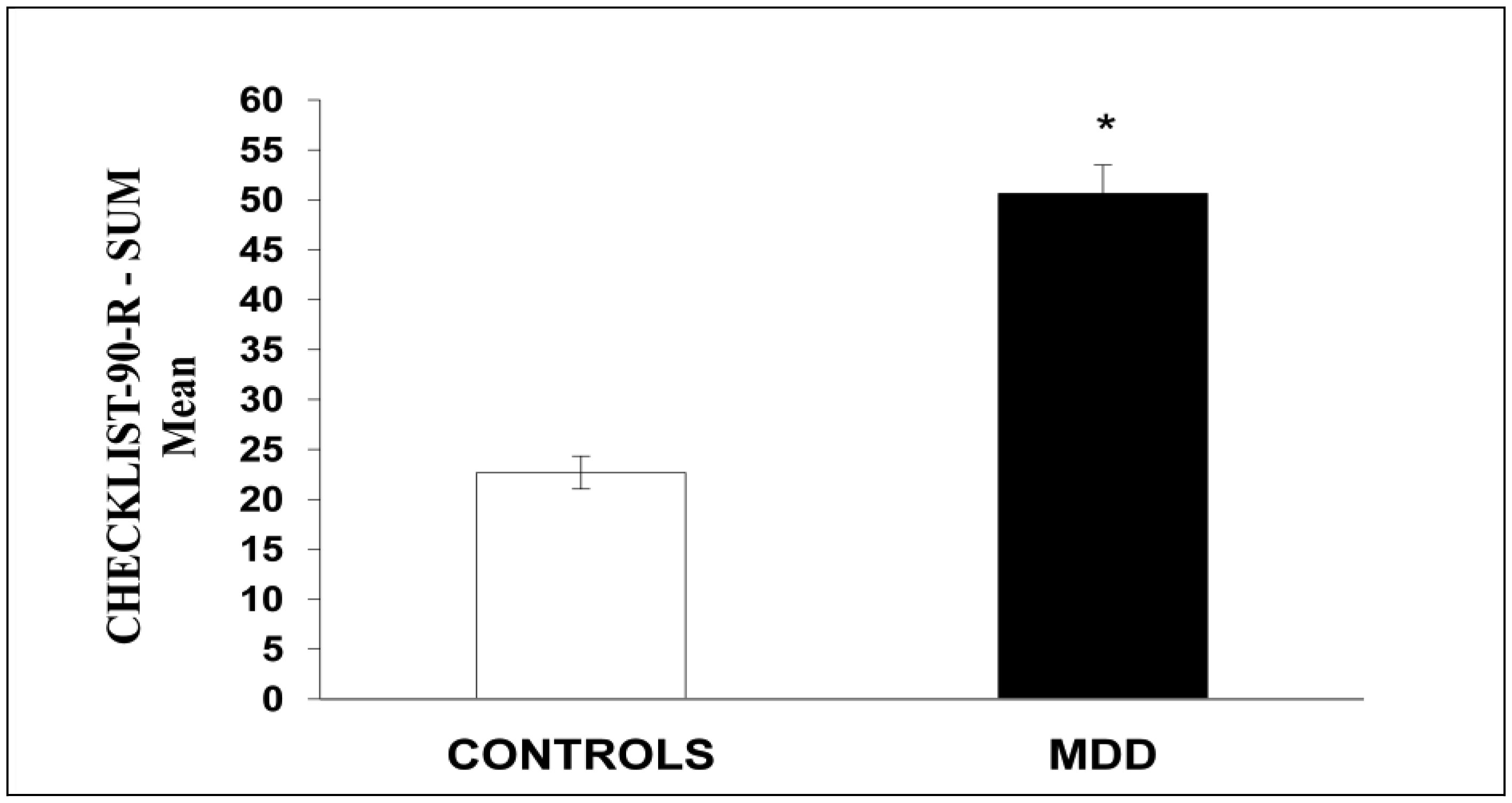
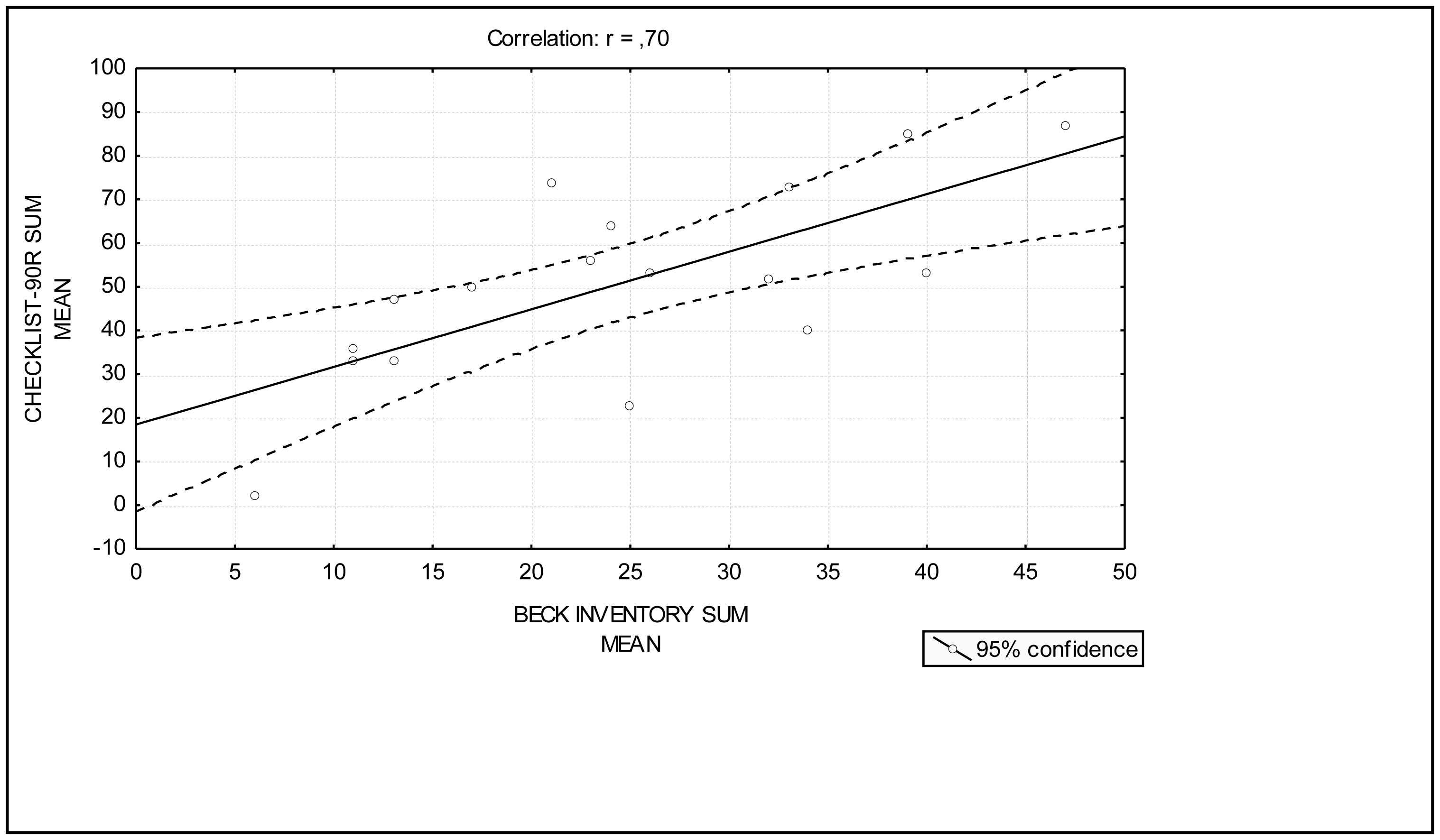
Major depressive disorder (MDD) is one of the disorders that most causes disability and affects about 265 million people worldwide, according to the World Health Organization (WHO). Chronic stress is one of the most prevalent factors that trigger MDD. Among the most relevant biological mechanisms that mediate stress and MDD are changes in the hypothalamic-pituitary-adrenal (HPA) axis function. Hypercortisolism is one of the relevant mechanisms involved in response to stress and is present in many people with MDD and in animals subjected to stress in the laboratory. This study aimed to investigate the levels of stress and cortisol in individuals diagnosed with MDD from the Basic Health Unit (BHU) in a small city in the western region of Santa Catarina, Brazil. Depression scores were assessed using Beck's inventory. For the investigation of stress, an adaptation with twenty-four questions of the Checklist-90-R manual was performed. The analysis of the cortisol levels in the individuals' serum was by the chemiluminescence method. Depression and stress scores were significantly higher in individuals with MDD than in control subjects (p < 0.001). Cortisol levels were also significantly higher in individuals with MDD (p < 0.05). Besides, depression scores were positively correlated with stress scores in individuals with MDD (Pearson's “r” = 0.70). Conclusion: Individuals with MDD had higher stress levels and cortisol than control subjects. The positive correlation between the levels of stress and depression in MDD individuals suggests that these conditions are related to a dysregulation of the HPA axis function.
1.
Introduction
Nematic liquid crystals are aggregates of molecules which possess same orientational order and are made of elongated, rod-like molecules. Hence, in the study of nematic liquid crystals, one approach is to consider the behavior of the director field d in the absence of the velocity fields. Unfortunately, the flow velocity does disturb the alignment of the molecules. More importantly, the converse is also true, that is, a change in the alignment will induce velocity. This velocity will in turn affect the time evolution of the director field. In this process, we cannot assume that the velocity field will remain small even when we start with zero velocity field.
In the 1960's, Ericksen [3,4] and Leslie [10,11] developed the hydrodynamic theory of liquid crystals. The Ericksen-Leslie system consists of the following equations [12]:
where (1.1)1, (1.1)2 and (1.1)3, represent the conservation of mass, linear momentum and angular momentum respectively. Besides, ρ denotes the fluid density, u=(u1,u2,u3) is the velocity vector and d=(d1,d2,d3) the direction vector,
where Fi is the external body force, Gi denotes the external director body force and β, γ come from the restriction of the direction vector |d|=1. The following relations also hold:
and
where
On the basis of the second law of thermodynamics and Onsager reciprocal relation, one obtain
The nonlinear constraint |d|=1 can also be relaxed by using the Ginzburg-Landau approximation, that is, instead of the restriction |d|=1, we add the term 1ε2(|d|2−1)2 in ρF. In addition, to further simplify the calculation, one take ρ1=0, βj=0, γ=0, Fi=0 and ρF=|∇d|2+1ε2(|d|2−1)2, choose the domain Ω=R3, obtain the simplified model of nematic liquid crystals:
with the following initial conditions
and
for any integer N≥3 with a fixed vector ω0∈S2, that is, |ω0|=1. In this paper, we assume that f(d)=1ε2(|d|2−1)d (ε>0) is the Ginzburg-Landau approximation and the pressure p=p(ρ) is a smooth function in a neighborhood of ˉρ with p′(ˉρ)>0 for ˉρ>0. Moreover, μ and λ are the shear viscosity and the bulk viscosity coefficients of the fluid, respectively. As usual, the following inequalities hold:
The study of liquid crystals can be traced back to Ericksen [3,4] and Leslie [10,11] in the 1960s. Since then, there is a huge amount of literature on this topic. For the incompressible case, we refer the author to [2,6,12,13,20] and the reference therein. There are also many papers related to the compressible case, see for instance, [1,5,7,8,17,19] and the reference cited therein.
In [19], the authors rewrote system (1.5) in the perturbation form as
where ϱ=ρ−ˉρ, ˉμ=μˉρ, ˉλ=λˉρ, γ=p′(ˉρ)¯ρ2 and the nonlinear functions of ϱ are defined by
We remark that the functions h(ϱ), g(ϱ) and ϕ(ϱ) satisfy (see [19])
Wei, Li and Yao [19] obtained the small initial data global well-posedness provided that ‖ϱ0‖H3+‖u0‖H3+‖d0−ω0‖H4 is sufficiently small. Moreover, the authors also showed the optimal decay rates of higher order spatial derivatives of of strong solutions provided that (ϱ0,u0,∇d0)∈˙H−s for some s∈[0,12].
Next, we introduce the main results in [19]:
Lemma 1.1. (Small initial data global well-posedness [19]) Assume that N≥3 and (ϱ0,u0,d0−ω0)∈HN(R3)×HN(R3)×HN+1(R3). Then for a unit vector ω0, there exists a positive constant δ0 such that if
then problem (1.8) has a unique global solution (ϱ(t),u(t),d(t)) satisfying that for all t≥0,
Lemma 1.2. (Decay estimates [19]) Assume that all the assumptions of Lemma 1.1 hold. Then, if (ϱ0,u0,∇d0)∈˙H−s for some s∈[0,12], we have
and
The main purpose of this paper is to improve the decay results in [19]. First, we give a remark on the symbol stipulations of this paper.
Remark 1.3. In this paper, we use Hk(R3) (k∈R), to denote the usual Sobolev spaces with norm ‖⋅‖Hs, and Lp(R3) (1≤p≤∞) to denote the usual Lp spaces with norm ‖⋅‖Lp. We also introduce the homogeneous negative index Sobolev space ˙H−s(R3):
endowed with the norm ‖f‖˙H−s:=‖|ξ|−sˆf(ξ)‖L2. The symbol ∇l with an integer l≥0 stands for the usual spatial derivatives of order l. For instance, we define
If l<0 or l is not a positive integer, ∇l stands for Λl defined by
where ˆf is the Fourier transform of f. Besides, C and Ci (i=0,1,2,⋯) will represent generic positive constants that may change from line to line even if in the same inequality. The notation A≲B means that A≤CB for a universal constant C>0 that only depends on the parameters coming from the problem.
It is worth pointing out that in [19], the authors consider problem (1.5) in 3D case, the negative Sobolev norms were shown to be preserved along time evolution and enhance the decay rates. However, because the Ginzburg-Landau approximation term is difficulty to control, only s∈[0,12] were considered in [19]. In this paper, we ovcome the difficult caused by Ginzburg-Landau approximation, assume that s∈[0,32), obtain the optimal decay rates of higher order spatial derivatives of strong solutions for problem (1.5). Our main results are stated in the following theorem.
Theorem 1.4. Assume that all the assumptions of Lemma 1.1 hold. Then, if (ϱ0,u0,∇d0)∈˙H−s for some s∈[0,32), we have
and
Note that the Hardy-Littlewood-Sobolev theorem implies that for p∈(1,2], Lp(R3)⊂˙H−s(R3) with s=3(1p−12)∈[0,32). Then, on the basis of Lemma 1.2 and Theorem 1.4, we obtain the optimal decay estimates for system (1.8).
Corollary 1.5. Under the assumptions of Lemma 1.2 and Theorem 1.4, if we replace the ˙H−s(R3) assumption by
then for l=0,1,⋯,N−1, , the following decay estimate holds:
Remark 1.6. Lemma 1.1 shows the global well-posedness of strong solutions for system (1.5) provided that the smallness assumption (1.10) holds. One can use the energy method to obtain the higher order energy estimates for the solution to prove this lemma (see [19]). We remark that the negative Sobolev norm estimates did not appear in the proving process of Lemma 1.1, it is only used in the decay estimates. Hence, the value of s in Lemma 1.2 and Theorem 1.4 do not affect the energy estimates (1.10) and (1.11). And those two estimates hold for both Lemma 1.2 and Theorem 1.4.
Remark 1.7. The main purpose of this paper is to prove Theorem 1.4 and Corollary 1.5 on the asymptotic behavior of strong solutions for a compressible Ericksen-Leslie system. We remark that the global well-posedness and asymptotic behavior of solutions are important for the study of nematic liquid crystals system. Thanks to the above properties of solutions, one can understand the model more profoundly. Our results maybe useful for the study of nematic liquid crystals.
The structure of this paper is organized as follows. In Section 2, we introduce some preliminary results. The proof of Theorem 1.4 is postponed in Section 3.
2.
Preliminaries
We first show a useful Sobolev embedding theorem in the following Lemma 2.1:
Lemma 2.1. ([15]) If 0≤s<32, one have
In [14], the author proved the following Gagliardo-Nirenberg inequality:
Lemma 2.2. ([14]) Let 0≤m,α≤l, then we have
where θ∈[0,1] and α satisfies
Here, when p=∞, we require that 0<θ<1.
One also introduce the Kato-Ponce inequality which is of great importance in our paper.
Lemma 2.3. ([9]) Let 1<p<∞, s>0. There exists a positive constant C such that
where p2,q2∈(1,∞) satisfying 1p=1p1+1p2=1q1+1q2.
The Hardy-Littlewood-Sobolev theorem implies the following Lp type inequality:
Lemma 2.4. ([16]) Let 0≤s<32, 1<p≤2 and 12+s3=1p, then
In the end, we introduce the special Sobolev interpolation lemma, which will be used in the proof of Theorem 1.4.
Lemma 2.5. ([18]) Let s≥0 and l≥0, then
3.
Proof of Theorem 1.4
Equation (1.8)3 can be rewritten as
In [19], the authors proved the L2-norm estimate of d−ω0 provided that the assumptions of Lemma 1.1 hold.
Lemma 3.1. ([19]) Assume that all the assumptions of Lemma 1.1 hold. Then, the solution of (3.1) satisfies
In the following, we prove the decay estimates of strong solutions for system (1.8). The case s∈[0,12] was shown in Lemma 1.2, one only need to consider the case s∈(12,32). We first derive the evolution of the negative Sobolev norms of the solution.
Lemma 3.2. Under the assumptions of Lemma 1.1, if s∈(12,32), we have
Proof. Applying Λ−s to (1.8)1, (1.8)2, Λ−s∇ to (1.8)3, multiplying the resulting identities by γΛ−sϱ, Λ−su and Λ−s∇d respectively, summing up and integrating over R3 by parts, we arrive at
Note that s∈(12,32), it is easy to see that 12+s3<1 and 3s∈(2,6). For the terms K1, by using Lemmas 2.2 and 2.4, Hölder's inequality, Young's inequality together with the estimates established in Lemma 1.1, we deduce that
similarly, for K2–K6, we have
and
where we have used the fact (1.9) in (3.8)–(3.10). Next, by using Lemmas 2.2–2.4, Hölder's inequality, Young's inequality together with Lemma 1.1 on the energy estimates of the solutions, it yields that
For K8, we first consider s∈(12,1). Thanks to Lemma 2.2, one easily obtain
Then, by Hölder's inequality, Young's inequality, the facts |d|<1, |ω0|=1 together with Lemmas 1.1, 2.2 and 2.3, we derive that
Moreover, if s∈(1,32), the following inequality holds:
Combining (3.4)–(3.12) together, we obtain (3.3) and complete the proof.
Now, we give the proof of our main results.
Proof of Theorem 1.4. First of all, the sketch of proof for the decay estimate with s∈[0,12] will be derived in the following. Note that this part follows more or less the lines of [19], so that we do note claim originality here. Then, by using this proved estimate, one can obtain the decay results for s∈(12,32).
Now, consider the decay for s∈[0,12]. We first establish the negative Sobolev norm estimates for the strong solutions, obtain one important inequality:
Then, define
we deduce from (3.2) and (3.3) that for s∈[0,12],
which implies (1.12) for s∈[0,12], i.e.,
Moreover, if l=1,2,⋯,N−1, we may use Lemma 2.4 to have
Then, by (3.14) and (3.15), it yields that
Hence, for l=1,2,⋯,N−1,
Thus, we deduce from (1.11) the following inequality
Solving this inequality directly gives
Then, by (3.14), (3.17) and the interpolation, we obtain the following inequality holds for s∈[0,12]:
Second, we consider the decay estimate for s∈(12,32). Notice that the arguments for s∈[0,12] can not be applied to this case. However, observing that we have ϱ0,u0,∇d0∈˙H−12 hold since ˙H−s⋂L2⊂˙H−s′ for any s′∈[0,s], we can deduce from (3.18) for (1.10) and (1.11) with s=12 that the following estimate holds:
Therefore, we deduce from (3.3) and (3.2) that for s∈(12,32),
which implies that (1.12) holds for s∈(12,32), i.e.,
Moreover, thanks to (1.11) and (3.16), we can also obtain the following inequality for s∈(12,32):
which implies
Next, using (3.21), (3.22), and Lemma 2.5, we easily obtain
It then follows from (3.22) and (3.23) that
Hence, we obtain (1.15) for s∈(12,32) and complete the proof.
4.
Conclusions
In this paper, we consider the optimal decay estimates for the higher order derivatives of strong solutions for three-dimensional nematic liquid crystal system. We use the pure energy method, negative Sobolev norm estimates together with the classical Kato-Ponce inequality, Gagliardo-Nirenberg inequality, overcome the difficulties caused by the Ginzburg-Landau approximation and the coupling between the compressible Navier-Stokes equations and the direction equations, obtain the decay estimates. Since the result (1.16) is same to the decay of the heat equation, it is optimal. We remark that our results may attract the attentions of the researchers in the nematic liquid crystals filed.
Acknowledgments
The author would like to thank the anonymous referees and Dr. Xiaopeng Zhao for their helpful suggestions. This paper was supported by the Fundamental Research Funds of Heilongjiang Province (grant No. 145109131).
Conflict of interest
The author declares no conflict of interest.














 DownLoad:
DownLoad: