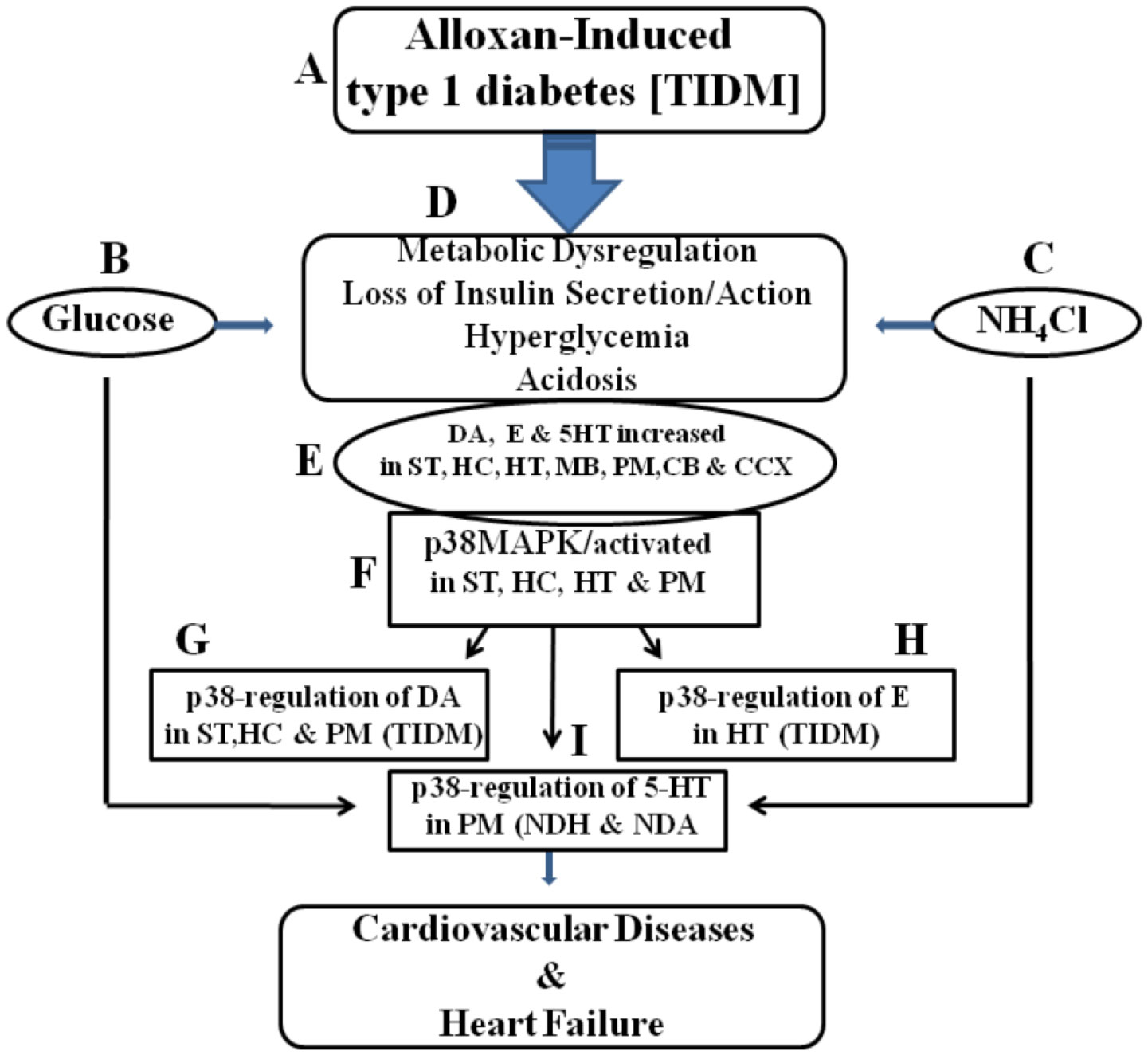
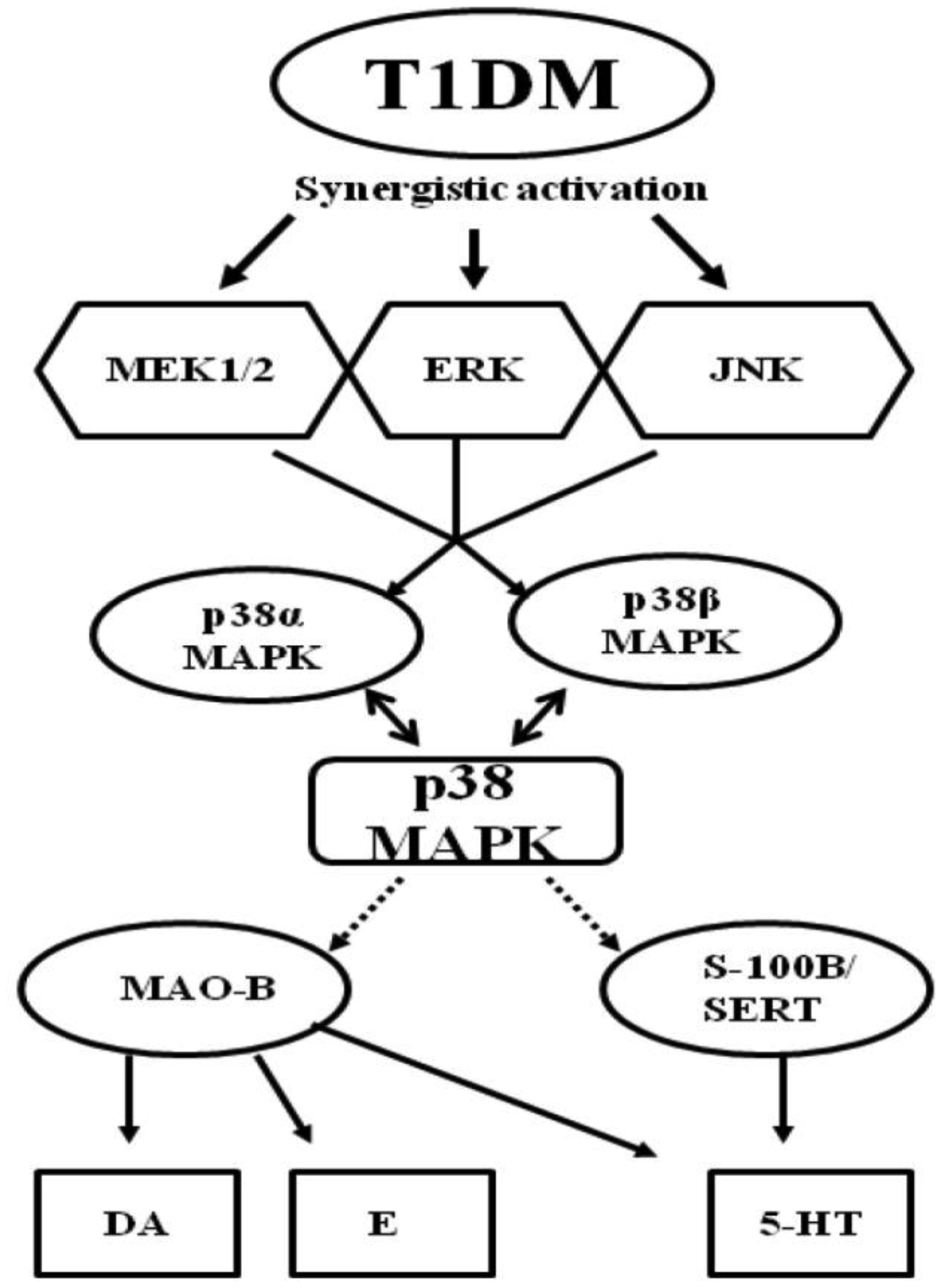
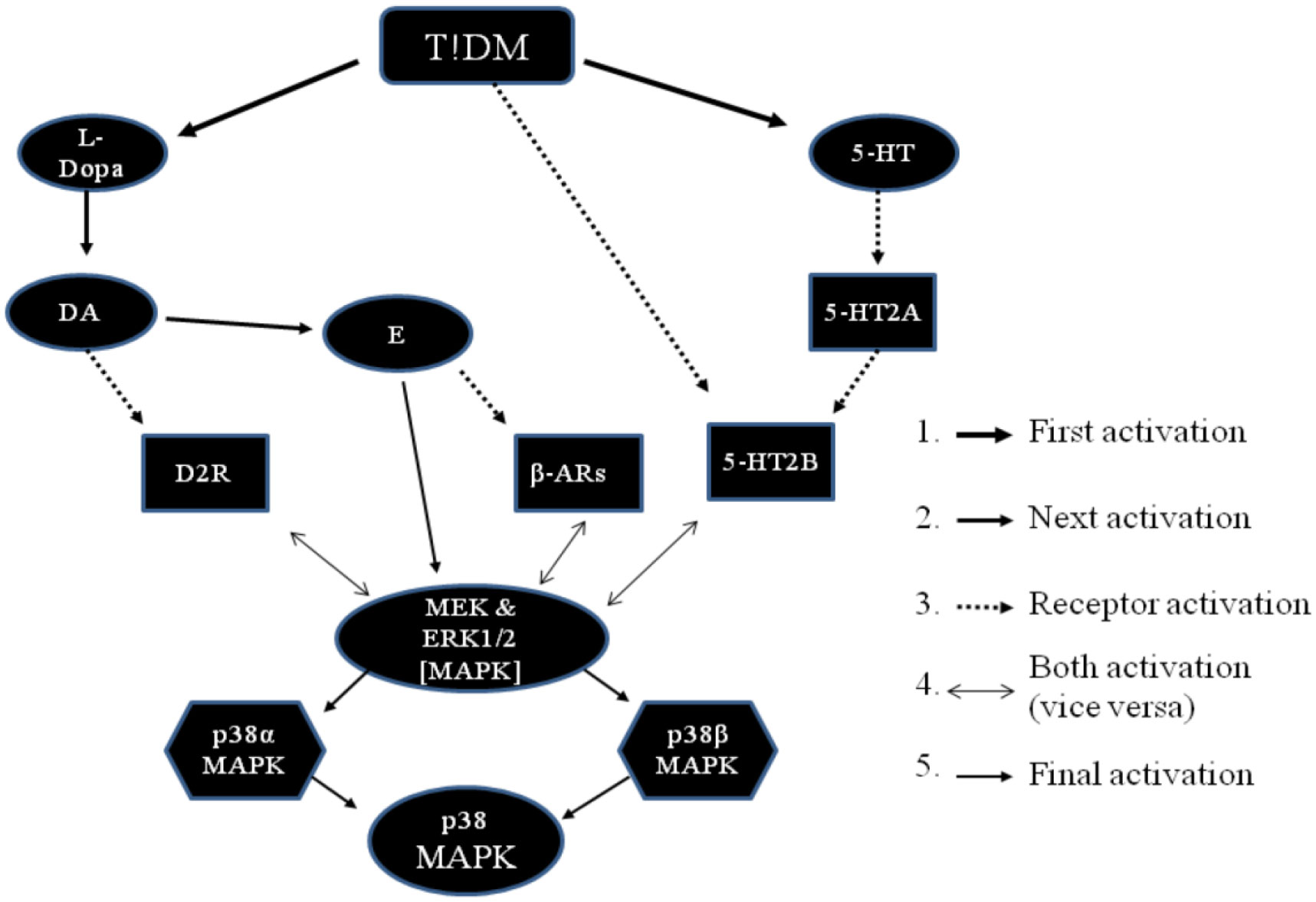
Serotonin or 5-HT, DA and E, all monoamine neurotransmitters, work also as hormones, plays crucial role in the brain and body. This 5-HT, DA and E increased significantly, and regulated by activated p38 MAPK in type I diabetes mellitus (T1DM), and that has been shown to involve in metabolic disorders as well as cardiovascular diseases, leading to heart failure. Even though these molecules are being considered for clinical trials in the treatments of various cardiovascular diseases, the synergistic-pathophysiological mechanisms of these p38 MAPK and neurotransmitters on target molecules, cells and tissues in heart failure are not completely understood in T1DM. However, T1DM results in metabolic dysregulation, impairment/loss of insulin secretion, hyperglycemia and acidosis. These changes are widely reported to be involved in abnormal functions of receptors, which provide binding site for signaling molecules. We are constantly focusing on the mechanisms of alloxan-induced-diabetes, glucose-induced-hyperglycemia and ammonium chloride-induced-acidosis (non-diabetic hyperglycemia (NDH) and non-diabetic acidosis (NDA), respectively) on the levels and functions of neurotransmitters and p38 MAPK. Here, in this review, we are proposing the mechanisms of insulin and/or some of the pharmacological agents on the level and functions of p38 MAPK and neurotransmitters in various areas of rat brain under diabetic or its associated conditions, which leads to cardiovascular dysfunctions. Targeting these molecules/pathways may be useful in the treatment of cardiovascular diseases and diabetes mediated heart failure.
1.
Introduction
Issues related to water, production and universal access to energy as well as food production and their frequent lack are contemporary problems of the population occurring in many countries of the world. Water, energy and food (WEF) are fundamental resources for basic functioning and improvement of living conditions and sustainable development. These three resources: water, energy and food are therefore important for maintaining life on earth, important for human well-being and economic activity. Due to a number of variables such as population growth, urbanization, rising incomes and the resulting changes in consumption patterns and climate change, the situation in these three sectors is systematically changing. Consequently, the demand for research in these three sectors, which are essential for economic and social progress, on the path of sustainable development, is also constantly increasing [1,2]. Because there are significant interrelationships between these three sectors and climate changes, the word "nexus" between food energy and water is used to indicate significant importance for the joint management of these elements [1,3]. The issue of nexus of water energy food can be considered from the global, international as well as local point of view. Climate change, global warming is a global phenomenon, but its effects affect the situation of individual countries. Some phenomena affect a geographic region with several countries. For example, heavy rainfall in Ethiopia, where the source of the Nile is located, affects agriculture in Egypt as well. Therefore, sometimes it's difficult to separate local, international or global scale. Integrated WEF systems, helps understand synergies and trade-offs across the water, energy, and food sectors. Thus is a critical initial step toward integrated idea of WEF nexus modeling and management [4]. Since the Bonn conference in 2011, special attention has been paid to the linkages and feedbacks between the water, energy and food sectors. They suggested that global population, economic growth and climate change would lead to a rising demand for energy, food and water [5,6]. To add to the complexity, water, energy and food are interconnected resources forming what we referred to as water-energy-food nexus. For example, to produce food, we need energy in the form of fertilizers or electricity and water for irrigation. To produce clean water, we need energy for cleaning, and to produce energy we need water for cooling, and food if we were to use biofuels [7]. Therefore, a system approach is needed involving interdisciplinary and transdisciplinary research teams to meet the complex challenges arising from these connections [8,9]. The interdisciplinary dimension focus on the complexity of linkages among WEF resources, systems, and sectors by highlighting the trade-offs and synergies between these components. The transdisciplinary dimension enhances cooperation with diverse groups of stakeholders and improves governance across sectors by using systems thinking by government policy-making processes. Thus, the key challenge for the policy of the state and main decision makers is the integration and sustainable planning and management of resources, balancing different user goals and interests in order to reduce negative impact between individual sectors [10,11,12]. The most important assumption is that each sector should be treated equally [13] and any planned changes in any sector should only be implemented after considering the impact on other sectors [14]. In the near future, there will be acceleration in the creation of new cooperation between many disciplines and organizations that will integrate knowledge from physical and biological sciences, social and mathematical sciences and engineering to create comprehensive and integrated thinking on water-energy-food interfaces [9]. The importance of the relationship between water, energy and food is growing steadily as the demand for each of these resources increases [15]. The relationship between water, energy and food, as well as climate change and possible problems occurring in one of the links in this chain and the transfer of this problem to other links constituted the essence of the completed research [3,16].
2.
Materials and methods
Descriptive methods based on desk research analysis as well as interviews and observations were used in the present study [17]. The presented article will indicate and describe the achieved results of research carried out in this field. A considerable amount of cross-sector data such as the amount of water used to generate energy, energy used to produce water, and water and energy used to produce food, etc. may be the subject of further research concerning linkage quantitative models. The main methods used in this study were primary research (observations, interviews) and secondary research [17]. As part of secondary research, an external desk study was used, which includes research carried out outside and gathering relevant information (i.a. WEF, renewable energy, sustainability development). These external resources were implemented as Online Desk Research. The text analysis as a secondary study was based on Polish and English language literature, as well as on reports and articles published in the specialist press (energy, agriculture and climate). As part of the source study, content analysis, analysis of existing statistical data, as well as historical and comparative analysis were carried out. An analysis of the data contained in the annual reports of energy companies, agriculture and climate institutes as well as reports of EU institutions and the governmental (Government Published Data) was carried out, as well as an analysis of data from other literature and specialist journals. As part of the primary study, arable, urban and rural areas were observed, and farmers were interviewed. In-depth interviews on site in the villages were carried out with 10 farmers owning farms in the vicinity of Warsaw, who specialize in breeding dairy cows and producing milk as well as cultivating potatoes, corn and grain. Due to the family farms structure in Poland the interviews were realized with farmers in age from 25 to 70 years old, often father/mother, son/daughter, grandson/granddaughter. Questions were posed according to the basic scheme: the size of the farm, the number of cattle (if it is on the farm), the financial/economic amount of input, the number of yields (achieved results), and financial results.
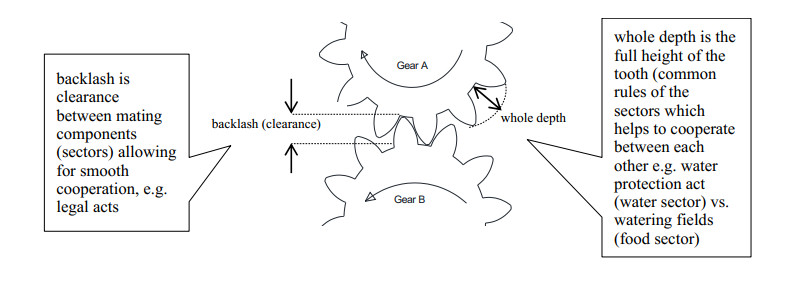
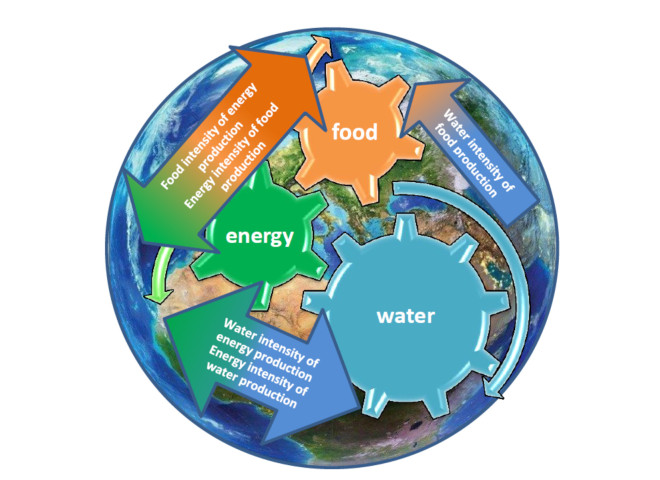
All research materials concerned the existing links between individual sectors, i.e. water, energy, food. Research model which is shown at the Figure 1, consist with three sectors and the resources which create those sectors. Energy sector means energy companies that produce energy based on natural resources (coal, renewable sources, including water, wind and the sun). In this study, the main focus is on the sources on which the energy sector is based. Water sector means all water resources (rivers, lakes, seas, storage reservoirs) used by man for his livelihood (mainly food production and industrial activities). The food sector is primarily natural resources needed to produce food of plant and animal origin (including cereals, vegetables, fruits, meat and milk). The idea of the connections and relationships that exist between these sectors are presented in the form of gear teeth, while the proper functioning of these sectors in a balanced and sustainable way are presented by arrows indicating the proper functioning of the entire WEF nexus.
To understand the idea of a research model schematically represented as a gear mechanism shown against the backdrop of the globe at the Figure 1, the more detailed scheme is presented at the Figure 2. It should be noted that the magnitude of interaction between the teeth (sectors) is critical to their cooperation and durability. Illustratively, interdependency WEF sectors can be shown by press fit and clearance in gear mechanism. Too loose linkages cause too much freedom that negatively affects the entire mechanism (e.g liberalization of the rules for logging trees in forests in order to enhance crop sites can negatively affect climate change), and too much fit will generate high friction and lead to rapid failure of the mechanism (e.g. milk quotas limiting milk production in European Union introduced in 1984. Ultimately in 2015 milk quotas were removed in the name of a more open and competitive European and global market).
As shown in the research model presented in Figure 1, there is an overlapping (meshing together), called as inter-sectoral relationship between the individual sectors. Moreover, the resources that constitute the sector are limited (they are found on the globe) and depend on the surrounding, changeable, difficult to predict climate and atmospheric phenomena and they also interact with each other. Resources are a system of interconnected vessels, there is a balance between resources and increased exploitation of one of them will negatively affect the functioning of the others. There are relationships between water, energy and food, e.g. and some research questions should be asked. How much water can be used for arable irrigation, how much water can be absorbed (used) by humans, how much energy needs to be put in to produce food, how much food can be used for energy purposes (e.g. corn) that the price of food will not increase and that there would be no food shortages. There are many such questions related to WEF, and similar to the aim of contemporary research carried out in many academic institutions of the world, the main goal of this research is to find answers and try to find the balance. The availability of water is critical to the effectiveness and efficiency of energy production technologies, while energy is ultimately essential to supply the water supply of all food production (agricultural activity), energy and water supply to industry and households [13,18].
3.
Discussion
There are important key links between WEF sectors and, in addition, external influences such as population size or climate change can be observed. Population growth affects the consumption of water, energy and food, and climate change affects all sectors at the same time. There are dependencies between sectors that interact with each other.
3.1. Water for food vs population
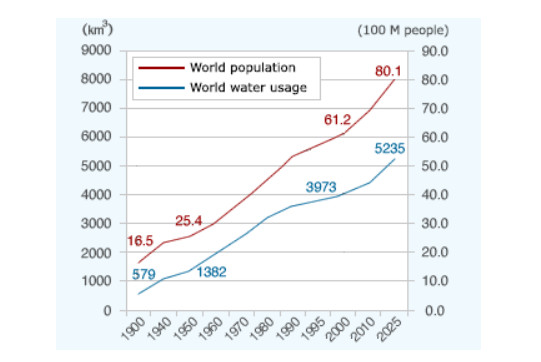
The world population growth and industry driven economic development has tight influence on the available natural resources which have to meet the growing demand for water, energy and food [18]. Population growth means an increase in direct water consumption but at the same time an increase in food production and consumption (indirect water consumption). In the perception of water management, we should take into account the fact that the world is developing extremely dynamically, the world's population is steadily increasing, and thus the amount of water consumption also increases, while the amount of water per capita is constantly decreasing [19,20]. The forecasts for population growth and water consumption increase until 2025 are presented in Figure 3.
Currently, water shortage affects more than 40% of the world's population, and forecasts until 2050 foresee even greater restrictions on access to water. These threats include a growing world population, which is projected to rise to 9.1 billion by 2050 [22]. Expected climate change should also be taken into account, which has a significant impact on water resources, and often harmful human activities (global climate change, land degradation, land scarcity and deforestation) must be considered [13,23]. Already, human activities have destroyed 50% of forests [22]. Increased deforestation in areas of agammaessive human activity (large-scale deforestation) is causing local climate warming. And the scale of warming increases with the rate of disappearance of the forest covers [24]. Temperature differences between areas affected by deforestation and areas with preserved natural tree stands are the greatest in the driest months of the year. In the most deforested areas, temperature increases of up to 1.5 ℃ are recorded [25,26]. Due to climate change, drought phenomenon (metrological, hydrological and agricultural) is becoming more common in countries that seemed to be rich in water. Severe droughts and violent floods reduce crops, which translates into rising food prices. Water shortages also have a negative impact on the energy sector, including hydropower.
3.2. Water vs climate situation in Poland
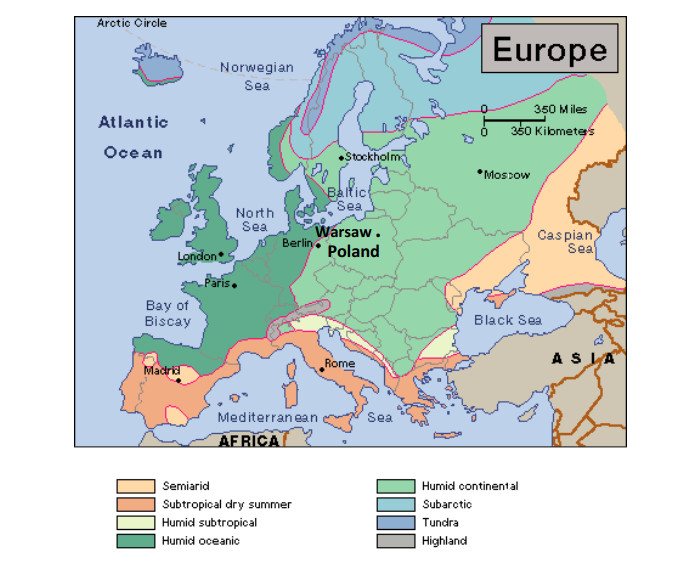
In Poland, the clash of continental and oceanic influences causes high seasonal variability and rainfall unpredictability. The location of the country relative to the ocean also affects the amount of rainfall that decreases in Europe as it moves from the ocean deeper into the continent, from west to east, and shapes the climate in Europe from humid oceanic through humid continental to semiarid (semi-dry). Rapid weather changes, violent storms and atmospheric phenomena (hail, hurricanes and whirlwinds) in our region will have negative impact but also they can have positive impact. On the one hand they will lead to local sudden inundation and flooding, but on the other hand they can help to avoid the prolonged drought experienced which is predicted in southern European countries. Types of climate occurring in Europe are shown in Figure 4.
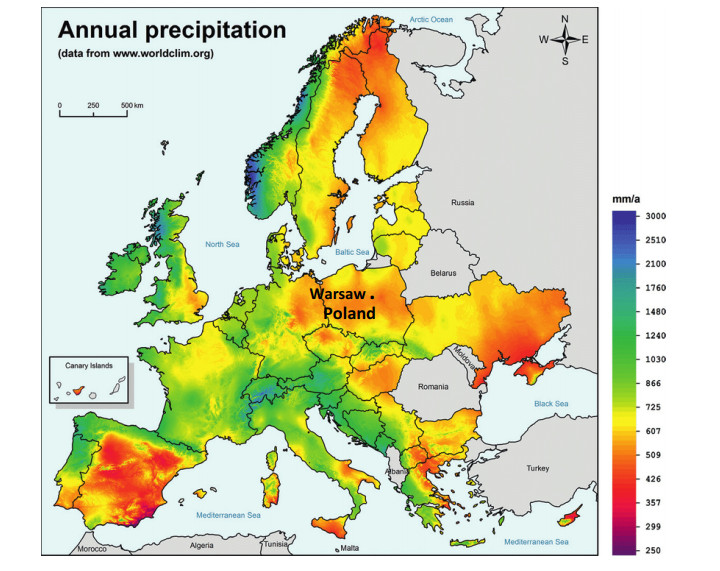
Increased intensity and frequency of precipitation in many regions of Europe will mean frequent and serious floods. However, in other parts of Europe, including southern Europe, higher temperatures and less precipitation will mean that many areas can be affected by drought. The amount of precipitation is shown in Figure 5.
As shown in the presented Figure 5, rainfall in Poland is lower than in most countries located in the western part of Europe. In addition, there are significant changes in the form of precipitation, e.g. snowfall is less frequent in winter, but rainfall is more frequent. In turn, in spring, both the amount of solid (snow) and mixed (sleet) precipitation decreases. Analyzing the annual availability of clean water for Europe, it can also be seen that areas of Central and Eastern Europe, including Poland in the east and areas of the Iberian Peninsula mainly Spain in the west of the continent, have on average less than 200 mm of fresh water available each year, while demand for water is 3-10 times higher.
Poland is a country with one of the lowest rates of drinking water per capita in the European Union [29]. An additional problem is the snowless winters that have been frequent in recent years, during which the lack of snow and water stored in it, supplying surface and underground waters, adversely affect the country's water resources. There is more and more talk about falling water levels in rivers and lakes or the drying up of wetlands, which is deadly for the flora and fauna living there. The forecast for the coming years is rather pessimistic not only for Poland, but also for the whole world [30,31]. Climate change will continue, which will result in even more severe droughts. Another problem is the sunny, cloudless aura, which translates into high evaporation of moisture from the soil and from plants (with low rainfall at the same time), which causes drought. This problem is observed both in water resources accumulated in soil and in shallow aquifers. Water resources in Poland are characterized by high seasonal variability and uneven territorial distribution [32]. Retention reservoirs have a small capacity and can stop only 6% of the annual outflow of water in the country, which does not provide sufficient protection against periodic excess or deficits of water.
Taking into consideration hydrological conditions and the geographical location of Poland within the range of a moderate transitional climate, water resources are relatively small [32]. They are also characterized by significant spatial diversity, which is a consequence of the meaningful variability of environmental conditions that shape the hydrological cycle. The regional differentiation of individual elements of the water balance-atmospheric precipitation, field evaporation and outflow (surface and underground) results from the heterogeneity of factors such as climate, land cover, terrain, including mountain ranges as orographic barriers, geological structure and soil type. Flowing waters in Poland are fed with both surface runoff of rainwater and meltwater, as well as groundwater [33]. Half of the average runoff from the river to the Baltic Sea in the north of the country comes from groundwater supply. This is due to the presence of porous rock formations in the ground, ensuring, thanks to its high permeability, an almost continuous inflow of groundwater to the rivers [34].
In the modern world, broadly understood water management is one of the key sectors of the economy of each country [35]. As in many regions of the world, concerns about water deficit and water scarcity are also growing in Europe, given the increased risk of drought due to climate change. About 80% of the fresh water consumed in Europe (for drinking and other uses) comes from rivers and groundwater, making these sources extremely vulnerable to risks associated with over-exploitation, pollution and climate variability. Water management should be considered in terms of its objectives, water resources, water infrastructure, management system and national and international legal regulations such The Water Law Act [36,37], The Law of International Resources [38], Water Framework Directives [39].
3.3. Urbanization and water
Many people who thought that climate change, lack of energy security problems and food shortages are issues pertaining to some distant countries have recently had reasons to verify their opinion on this matter. It is already clear that the climate is changing [40]. The climate changes that have occurred in recent years are the result of not only natural processes, but also the result of human activity (greenhouse gas emissions, deforestation, changes in the surface of the earth, land development, urban development) [18,23]. As cities expand, changes are taking place in rural areas just outside these cities. Large-scale urbanization and industrial development have created serious environmental challenges. Both energy and water are considered key to the sustainable development of urban areas [7,41]. In Poland the development of built-up and urbanized land takes place mainly at the expense of arable land. The meaningful scale of changes in land use that took place in rural areas mainly concerned two ownership groups, namely: natural persons1 and the State Treasury Lands2. An example of urbanization of agricultural land near Warsaw is shown in Figure 6.
1 In jurisprudence, a natural person is a person (in legal meaning, i.e., one who has its own legal personality) that is an individual human being.
2 State Treasury Lands are types of state and other public lands resources.
Urban agglomerations are characterized by a strongly transformed environment. The consequence of the progressing urbanization processes is the phenomenon of urban "heat island", air pollution, reduction of biodiversity as well as pollution and degradation of the surface and underground water resources. Replacing biologically active surfaces that have absorbent properties with buildings, roads, pavements, parking lots with a noteworthy proportion of sealed surfaces causes, that the volume and speed of surface runoff is increasing, in particular in torrential rainfall, as well as the degree of their pollution. Overloaded drainage systems in urban areas during heavy rainfall are unable to absorb such amount of water in such a short time. There is local flooding and even flood.
3.4. Climate, water and food
These transformations regarding human activities and climate change pose serious problems for agriculture. Any climate change causes disturbance in agriculture, forcing us to seek new solutions and production methods. The challenge in achieving food security will be the development, evaluation and implementation of technologies, crops and varieties that will sustainably increase food production per unit area, while minimizing excessive water consumption [22,32]. The availability of water is critical to the effectiveness and efficiency of energy production technologies, while energy is ultimately essential to supply the water supply of all food production (agricultural activity), energy and water supply to industry and households [13,18].
One of the important issues in agriculture is the development of new technologies and methods in crop growth. The effects of climate change affect agricultural production, such as changes in farming practices and technology [42]. A good sample of new technology can be deep placement fertilizer applicator permits to increase labor-saving, raise crop yields and the quality thereof, by reducing the amount of fertilizer used. In addition, this technology decreases environmental damage to the atmosphere and water [43].
Next of the methods used can be a system of dynamically integrated (sustainable) agricultural production, which enables the implementation of economic and ecological goals through the conscious use of modern production techniques, systematic improvement of management and implementation of various forms of progress, mainly biological. In a dynamically integrated system, decisions are made at the most appropriate moment using the best available knowledge. With the transition from intensive conventional management to an integrated system, it is possible to reduce the consumption of industrial inputs, which has a positive effect on the environment and crop quality [44]. Cooling or warming periods change the ranges of individual crops, deadlines for field work, yielding, cropping methods, etc. This indicates the significant role of research in crop development, crop systems and agricultural and breeding practices that increase the efficiency of water and nutrient use [22,32]. Therefore, the problem of adaptation to the observed climate changes is becoming one of the major challenges for modern agriculture.
Poland is a country very seriously exposed to floods and droughts. It is worth recalling the catastrophic floods in 1997 and 2010, and the droughts of 2019 and 2020, which exposed the country not only to multi-billion Euro economic losses, but significant social and ecological losses. According to the estimates of the Institute of Environmental Protection (Poland), every year extreme phenomena such as floods, inundations, storms and droughts cause a decrease in Polish GDP by up to 0.4% that is about 0.5-0.6 billion Euro. In some years it may be as much as 1% of GDP. In recent years (2001-2016), negative climate changes have caused losses of over 17.5-18 billion Euro [45].
Extreme weather phenomena have been haunting Poland for several years. Floods and droughts (meteorological and hydrological) appear at short intervals. Therefore, a long-term increase in water scarcity as a result of climate change is to be expected, as well as short-term water abundance in the form of floods. As it can be seen in the Figure 8, the difference in levels between the extreme conditions on the Vistula River was about 7.5 meters from the state of 34 cm during drought to the state of 780 cm during a flood wave. Heavy rainfall also negatively affects agricultural crops. On the Figure 10, we can see a field with maize with a place where the water causes the lack of yields corn.
In Poland, the danger of severe drought has appeared in recent years. Meteorological and hydrological droughts have become an increasingly frequent phenomenon in Poland but also agricultural droughts become a real threat. In the years 1951-1981 they occurred on average every five years, while in the period 1982-2012 on average every three years, while since 2013 droughts of varying duration and range have already occurred every year [46]. The last dry years and snowless winters have contributed to the increase in soil moisture deficiency. Despite the heavy downpours, there is still a significant shortage of water in the soil. Water shortages mean that agricultural drought occurs more and more often in agricultural areas, e.g. in areas where cereals (wheat, oats, or corn), vegetables and fruit shrubs are grown. Changes in average temperature and precipitation, as well as extreme weather and climate conditions, are already affecting livestock yield and productivity [40]. These phenomena have a serious negative impact on the volume of agricultural production. Drought causes the destruction of plant crops and reduction of water resources for living and communal needs. Plants that require significant amounts of water will be particularly vulnerable to climate change [45,46,47]. The phenomenon of drought affects the increased likelihood of fires, erosion, dust storms, etc. Meteorological conditions therefore have a major impact on the yield in Poland, of cereals, fruits and vegetables, as well as on the quantity and quality of feed for farm animals. Even a small water deficit causes a decrease in a yield from a few to several percent. As a result of agricultural drought as well as meteorological one, there is less roughage and they are of lower quality, have more fungi and contain higher concentrations of plant protection products, and less protein. Due to those negative factors, it's predicted that food prices will rise sharply. Economic losses will be a consequence of hurricanes, storms and floods, storms, drought and crop failure, the spread of pests and outbreaks of various epidemics [48]. This year (2020), however, the impact of drought and floods on price increases will be partly mitigated by the oversupply on the meat or milk market that appeared due to restaurant closures and logistical difficulties due to COVID-19.
Agriculture will be one of the largest water consumers in the coming years, thus increasing the water deficit in Europe. The agricultural sector is already the largest user of water resources, accounting for around 70% of all freshwater abstractions in the world [22]. This is because more and more agricultural land needs to be irrigated, especially in southern European countries. Irrigation costs are expected to increase in the coming years if predictions of lower rainfall and longer growing season come true due to climate change. The vegetation periods of some crops have extended, and it is expected that this trend will continue with the expansion of thermophilic crops in higher latitudes. Overall, climate change can make it difficult to grow and cultivated plants and raise animals in the same way and in the same places as was done in the past [42]. Climate change has consequences for agriculture worldwide, with clear differences between regions [49]. However in many regions, the yield for some crops is expected to decrease due to heat and drought. That is why it is important to systematically implement innovative solutions such as efficient irrigation techniques and to develop and implement varieties that are more efficient in terms of water consumption, which can have a significant impact on reducing water demand, especially in rural areas. There are many options for adapting to the changing climate:
● breeding new breeds of animals with increased resistance to heat stress and more frequent pressure changes,
● breeding of new crop varieties resistant to summer drought and snowless winters,
● winter crops,
● not leaving unsupported fields,
● planting mid-field woodland strips, collecting water from roofs and paved yards for irrigation,
● creating water retention systems.
These innovative solutions to improve agriculture can be implemented through existing programs promoting improved land use practices in agriculture. However, where these practices involve costs or other burdens for the farmer, their use may be low unless some form of incentive is provided [50]. It is also important to understand farmers' behavior and to know their decision-making processes [51].
3.6. Food (agriculture) and energy
Energy has a significant share in agricultural production inputs. The growing prices of energy carriers and the requirements of sustainable development make it necessary to take measures to improve the efficiency of agricultural inputs. The functioning of modern farms is closely related to the need to cover the growing demand for energy, especially for electricity. On a farm, energy issues relate to farm distribution systems, electric motors, lighting, heating, lightning protection of livestock, buildings and fences, problems with stray voltage and alarm systems [52]. Farmers should undertake rational energy management and look for alternative sources of supply. Modern agriculture is predominantly based on energy supplies obtained mainly from fossil fuels. However, the available amount of fossil fuel is not infinite, and climate change makes it critical to limit their use [53]. Searching for alternative solutions to fossil energy sources is the best option to limit the adverse impact on the environment and at the same time to mitigate the effects of the energy crisis [54,55]. Electricity from renewable sources should be seen on the farm as part of a more general transformation that will require the significant transformation and adaptation of the current agricultural process to create truly sustainable agriculture [53]. The shift to a low carbon and zero-emissions economy implies a growing importance for renewable energy in the energy system. Limiting the negative impact on the surrounding environment and society [56] while adhering and maintaining the principles of sustainable development has influences the construction of new and innovation development strategies and new market model [57]. However, the question is how a shift from fossil fuel-based energy sources to renewable energy sources will help reduce climate change and what effect it will have on the environment [58]. There are relationships between energy produced from renewable sources and CO2 reduction as well as country development. The conducted research presented in the Table 1 has shown that carbon dioxide emissions are lower in countries with a high consumption of renewable energy and at the same time with a lower degree of country development.
Based on the results presented in Figure 9, one more important relationship can be analyzed. This is an important issue worth noting, i.e. the relationship between renewable energy consumption and the increase in depletion of natural resources (depletion of minerals, water, energy, forests and air). Sarkodi, Owusu [58] and Taghizadeh-Hesary [61] drew attention to a similar problem regarding the relationship between renewable energy, fossil fuel energy and food prices. Otherwise, there is one issue more called as six energy paradoxes. The most famous, but very often forgot, is Jevons Paradox, which consists that people, when things get more efficient and cheaper consume more and in this way causes increased of used those things [62]. The higher the energy efficiency, the lower the results in terms of reducing energy and resource consumption [63,64]. There is therefore the so-called reinforcement loop Another paradox can be called as NIMBY what signifies that people want renewable or zero emission energy (wind, nuclear) but Not In My BackYard [62,65].
The energy efficiency of the Polish economy is lower than the most developed European countries. In the world ranking, Germany is 1st, Italy is 2nd and Poland is 14th. Therefore, Poland has scope for energy saving. In agriculture, energy is used to drive tractors and agricultural machinery, prepare hot water for production purposes and illuminate barns and other farm buildings.
3.7. Energy from the water
Basically, all people deal with the energy sector as final energy consumers and recently quite often as active consumers and producers (prosumers). The key issue for the end customer is the continuity of supply and acceptable energy costs [66]. Many countries use hydropower on a large scale. Energy can be obtained from the proper use of water drops. Water can be a renewable energy source that is cheaper than conventional sources and does not cause climate change [67]. The largest percentage of energy with the participation of hydro energy is produced by countries with favorable conditions-i.e. mountainous countries. In Poland, there are not very good natural conditions that would favor the development of hydropower, in particular the construction of industrial hydropower plants. This is due to the lowland nature of our country, a slight decrease in rivers, moderate rainfall and geological structure (a meaningful share of permeable rocks in the land cover). The hydropower potential of Poland is small in relation to the country's area. Poland is one of the countries with poor water resources. The average annual surface water outflow, including inflows from abroad, in the years 1980-2010 amounted to 62.3 km3, and from the country area 54.4 km3. Calculated per capita, this gives an annual water supply of about 1.6 dam3 (cubic decameter it is the volume of a cube of side length one decameter 10 m. 1 dam3 = 1000 m3), while in European countries these resources are estimated at 4.6 dam3 [68]. In Poland, potential of hydropower resources are used only in 12%; for comparison, Germany uses them in 80%, in Norway-84%, and in France-almost 100% [67]. In the 1950s, there were over 2700 mills and water power plants operating in Poland, while currently there are only over 760 hydropower plants. However, there are some reserves for the development of this branch of energy and especially small hydropower plants (SHP). The total installed capacity in Polish hydropower plants was 988.38 MW, of which 294.75 MW was for SHP [69]. The development of small hydropower is strongly recommended in Poland. Small hydropower plants allow to generate energy and allow for small retention in steppe Poland [67]. Small-scale hydropower is one of the technological options for generating and supplying electricity to networks and applications in rural areas with almost zero emissions [70]. Small hydro power plants produce electricity mainly for local needs. Small hydropower projects and small hydropower plants are helpful in decentralized electricity generation and micro networks [71]. Thanks to growing consumer awareness and implementing technological, economic, organizational and social innovations future of energy market is going to active consumer (prosumer) direction [57]. With increasing energy prices, SHP can be a solution that helps in the electrification of rural areas, and SHP do not consume or degrade water by turbine (the water is not polluted and flows back into the river or reservoir). The advantage of this technology is its extremely robust, and the systems can work 50 years or more with little maintenance [72]. Hydroelectric power plants of this type, due to the scale of their occurrence, can be important for improving the devastated environment, because due to the construction of locks and ponds they retain a lot of water and as a result they can improve the hydrological and hydrobiological balance of the country. In the event of drought, hydropower becomes a limited source of energy production. Droughts clearly reduce water flows in rivers and thus reduce energy production. For owners of hydroelectric power plants, just like for many other entrepreneurs using natural water resources, extending the duration of drought can be a significant problem [73]. If dams were built, this would prevent some drought effects, but would also enable the development of small hydro power.
In large-scale energy, a significant amount of water is required in the production, purification and distribution processes [74]. Water is necessary for the power industry, as it is used for cooling in power plants using fossil fuels. Power plants require cooling with water from rivers or other reservoirs in so-called open circuit. There are still five power plants in Poland that draw water directly from rivers. This means that heat, no rainfall and low water levels may lead to the need to shut down some blocks. In Poland, significant limitation of energy production by hydropower plants due to drought occurred in 2015. Some hydropower plants did not work at the time because of the lack of water, and many others worked with less power. Due to the hydrological drought prevailing in practically the entire country, there is a great threat of limiting the capacity of the industrial power plants in summer.
4.
Short case study showing the application of theory in practice
It is necessary to promote rational use of water, energy and food not only by residents, but above all by industry, which is responsible for over 70% of water consumption in Poland [28,75]. Similar to the global trends concerning the idea of the water-energy-food nexus [76], various projects devoted to this issue are also carried out in Poland. There are some projects in Poland to promote nexus water energy food. For example: Building capacity for integrated governance at the Food-Water-Energy nexus in cities. The aim of this project is to develop and test technological solutions that will help local authorities manage water, food and energy more sustainably [77]. Another project is dedicated to water-food nexus. In this project the water footprint was calculated. Water footprint, which is an indicator of the water consumption necessary to produce a given product: the water footprint of 1 kg of cucumbers is 353 liters, 250 ml of tea is 27 liters, 1 kg of cheese is 3178 liters, and 1 kg of chocolate and beef is 17, 196 and 15, 415 liters, respectively. That is why it is worth buying only what we need, in the right quantities, and if possible, choose first of all those articles whose production was the most neutral for the environment. Food production places a burden on the environment, including through inputs of water and energy that are wasted with food thrown away. Throwing 1 kg of pork into the garbage is associated with the waste of approx. 6 thousand liters of water used to produce it, and 1 kg of discarded bread is 1.6 thousand liters of water [78].
The industry uses energy to purify water, while transporting water is one of the basic media without which industrial enterprises could not function. The applications of water in industry are very diverse-most often it is used in technological processes as a raw material, thinner, as a coolant or cleaning agent. The way to reduce the deepening water deficit in industrial districts and the need to reduce the load of pollutants discharged into the environment is a challenge facing many companies. Pollution reduction can be carried out using the method of water renewal, i.e. technological water recovery from wastewater and re-use mainly for industrial purposes, but also for consumption and economic purposes. Below there are some applications to reduce water and energy consumption. Below are presented some examples used in industry and agriculture to reduce water and energy consumption.
4.1. Pharmaceutical plant
An example of saving water in industry can be actions taken by the company's management to reduction in water consumption at a water-based drug production facility. Raw water used in the plant has a dual role: it is a raw material from which purified water is produced, and in the next stage water for injection is used without any treatment for sanitary purposes. Therefore, the factory uses different types of water. In general installations in the factory, mainly raw water is used, while for production purposes water is used, which is subjected to treatment, i.e. softened, highly purified water. Reduction of water consumption for social purposes was made by introducing new equipment, i.e. replacing old restroom and kitchen faucets with faucets equipped with water automatic touchless sensor and auto shut-off. Water consumption for social purposes by employees was about 25 m3/day. The introduction of new devices and the improvement of employees' awareness contributed to savings of 2 m3/day. This means savings of around 730 m3 throughout the year. Reduction of water consumption for medical purposes consisted in implementing changes in the technological process. The filter rinsing time was shortened, and their frequency changed. Changes in the technological process and the reduction of the filter rinsing time as well as the change in the frequency of rinsing them contributed to the reduction of the amount of water used by about 3 m3 per day, i.e. 1096 m3 per year. The greatest benefits have been achieved by modernizing equipment and optimizing processes. This most important stage of modernization allowed to reduce the annual consumption of raw water by 2736 m3, softened water by 1248 m3, highly purified water (HPW) by 1068 m3 and water for injection (WFI) by 276 m3. The total reduction in water consumption at the plant was 730 m3 + 2736 m3 + 1248 m3 + 1068 m3 + 276 m3 = 6058 m3
4.2. Fish farming plant
Another example of water saving can be the implementation of innovative solutions used in aquaculture. The system of intensive or extensive or ecological production with the re-use of purified water in closed tanks. The management team of examined the enterprise introduced the RAS system (Recirculating Aquaculture System). This is an innovative way of breeding and growing fish more and more often combined with the closed system RAS, equipped with its own water treatment plant which allows recirculation, water return. More than 90% of the pollutants can be filtered and separated by microsieves, which means a phosphorus reduction of over 80% and a biochemical oxygen demand BOD reduction of about 80%. All organic waste is collected for beneficial uses and they can be used as fertilizer on agricultural farming land or as a basis for biogas production. A closed RAS system generates much less wastewater than a regular flow system. Recirculation is a modern way in fish farms, in halls or in the open air. The implementation of a closed recirculation system allows you to increase fish production (even 300%) and increase quality while reducing water consumption. Innovative RAS systems allow you to increase the financial results while saving water and having a positive impact on environmental protection. [79,80]. The use of closed flow systems in a fish farm reduces water consumption on an industrial scale [81]. A big advantage of such kind of the system, are small losses associated with water intake. Strategies for water reuse lead to drinking water savings, reduction of eutrophication and GHG emissions, and can reduce energy consumption [82].
Based on the Table 2 we can conclude that system RAS is very effective. Comparison of degree of recirculation at different intensities showed that system super intensive RAS used ten times less water than system flow-through. From an environmental point of view, reducing the amount of water used in recirculation is of course very beneficial, as water has become a limited resource in many regions of the world. Recirculation aquaculture can therefore be considered a most environmentally friendly way of producing fish at a commercially viable level.
4.3. Farm
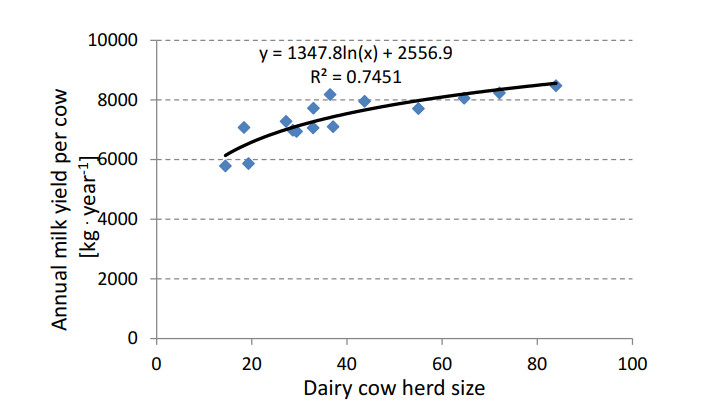
In agriculture, however, one form of obtaining energy cost reduction is self-generated electricity. It can be achieved by using photovoltaic modules or combustion of biogas from manure anaerobic digestion [84]. It can be realized by the possibility of using digestate from a biogas plant cooperating with a sewage treatment plant. A farm may adopt a treatment system to improve the efficiency of waste management based on its own energy production [54]. Technologies for converting waste into energy, in particular direct incineration and anaerobic digestion systems, are an alternative to reassessing this waste as a source energy while reducing their environmental impact [40]. Organic waste from the food industry is a suitable substrate for anaerobic digestion [85]. Another way to reduce water and energy consumption on a farm is to modernize the cowshed with captive posts for a free-standing barn. This allows you to move away from the wired milking machine, which results in high energy consumption for the "fishbone" milking machine, which improves milking and reduces energy consumption during milking. After milking, the milk will be cooled in coolers with heat recovery, which will then be used to heat the technical water [86]. Modernization and improvement of conditions increases the milk yield of cows [87]. According to many studies, the annual milk yield is systematically increasing. On the farm belonging to the Warsaw University of Life Sciences, milk production efficiency increased from 6, 280 l/cow before modernization to 10, 270 l/cow [86,88]. In addition, the yield increases as the herd grows. Therefore, the conducted modernizations are aimed not only at improving the conditions of use and environmental impact, but also allow to increase the size of the herd. It is important in terms of financial results for farmers. In recent years (1984-2015), there was a quota limitation in milk production by farms, which caused some perturbations among farmers. Since 2015, the limits imposed by the EU have been abolished and milk production takes place on a free market basis [89].
As shown at the Figure 11 the annual milk yield per cow increases with the increase in the herd size. It is therefore another argument for modernizing or building new barns, allowing the increase of the herd size.
5.
Conclusion, recommendation and limitation
Research has shown the importance of connections between WEF sectors and directions of activities in which cooperation in the field of water, energy and food should develop. The importance of climate and its changes, which directly and indirectly affect the said WEF chain, was also shown. Climate change forces the use of new, innovative solutions in agriculture (including new plant varieties, new forms of cultivation and breeding) to meet the demand for food. Drought, which is the result of climate change, also affects the energy sector. Rising energy consumption in hot spells, falling water levels, and the difficulty of producing energy are challenging the global economy. When analyzing the links between the elements of the water, energy, food chain, and attention should be paid to economic and social compromises in the planning of these sectors, as the importance of the relationship between water, energy and food (WEF) increases.
The conducted research has shown that in industry it is possible to reduce the amount of water used, e.g. in a pharmaceutical plant, thanks to which it makes a positive contribution to environmental protection. In a farm producing fish, water can be reduced and at the same time, thanks to innovative technologies, influencing the increase in production. In agriculture, modernization can reduce the amount of energy consumed by using agricultural biogas. This reduces the negative impact on the environment. In addition, modernization may increase the efficiency of cows (milk yield increases), which has a positive effect on the food sector.
As there are few articles that discuss the WEF nexus in Poland so it is worth conducting further research in this area and disseminating the idea in scientific articles. As the next stage of research, it is worth making detailed quantitative calculations for Poland related to water consumption for economic (industrial) and energy purposes. Perform a simulation of the shift away from the coal-based economy towards RES. It is also worth preparing scenarios taking into account climate change. Increasing drought periods as a negative factor, and extending vegetation seasons as a positive factor.
Primary research on water and energy consumption was carried out by author in two production plants, while research related to the use of energy in food production was carried out on one farm. Therefore, it would be worth extending primary research to a larger group of companies. Primary research about climate and food production was realized on the group of 10 farmers, so it also would be value extended this kind of research to a more numerous group of respondents.
Acknowledgment
Mrs M. Goździewska for help in compiling data on water savings.
Conflict of interest
Author declares no conflicts of interest in this paper.









 DownLoad:
DownLoad: