Sewage sludge is a very harmful waste when improperly discharged into the environment because of its inherent abundant pathogens, organic pollutants, and heavy metal constituents. The pyrolysis of sewage sludge is viewed not only to reduce pollutants associated with it but also one of the viable alternative sources for renewable energy or biofuel production. In this study, the effect of catalyst and temperature on the yield and composition of bio-oil obtained from the catalytic and non-catalytic pyrolysis of desludging sewage samples (DSS) was investigated. Modified pyrolysis reactor was used to pyrolyze the DSS at temperature ranges of 300–400,400–500,500–600 and 600–700 ℃ with and without the use of zeolite-Y catalyst. The 'heterogeneous' catalysis reaction yielded 20.9 wt% bio-oil, while the reaction without catalyst yielded 18.2 wt% bio-oil. Pyrolysis of the DSS favored char yield of between 55.4 and 76.6 wt%. The X-ray Fluorescence (XRF) analysis showed high silica (46 and 56.1 wt%), calcium (20.9 and 15.50 wt%), and low organic matter (12 and 12.87 wt%) contents present in the desludging feedstock before and after pyrolysis respectively. The gas chromatography–mass spectrometry (GCMS) analysis indicated the presence of nitrogen-containing compounds (between 20 and 50 wt%), mono-aromatics (18 and 28 wt%) and oxygenated compounds, in the form of carboxylic acids, aliphatics, ketones, ethers, esters and aldehydes in the bio-oils. Pyrolysis process development is, therefore, essential to clean the environment of pollutants from sewage sludge, by its conversion to more useful chemicals. In contrast, sewage sludge with high silica content may be tailored to the production of building materials.
1.
Introduction
Today, the modern man can hardly function without energy in some form or the other [1]. Energy has dramatically improved man's standard of living as its usefulness transcends all human spheres [2]. And in all these, man has turned to the world's abundant natural endowment, the nonrenewable and rapidly depleting natural fossil fuels [3,4]. The unsustainable nature of fossil fuels, which has led to the rapid increase in cost and its negative impact on the environment, has significantly prompted further research into alternative sources of energy and chemical feedstock [5]. Statistics from the International Energy Agency [6] claim 81% of the world's energy supply comes from fossil fuels. The use of these fossil fuels is slowly contributing to global warming as they give off a considerable amount of carbon dioxide (CO2) when burnt, which is one of the greenhouse gases [7].
Biomass has been of considerable interest due to its several advantages, such as sustainable abundance and availability, CO2 neutrality, or ecosystem friendliness compared to fossil fuels [8]. Biomass and waste buildups like sludge [9] are known to be among the most sustainable power sources that can give carbon and hydrogen. Sludge biomass could be very harmful when improperly discharged to the environment because of its abundance of pathogens, organic pollutants, and heavy metals constituents [10]. It becomes a very troublesome waste to oversee not just because of its large quantity but also its high convergence of substantial metals and disease-causing micro-organisms, which adversely affect the environment and human health [11,12]. Although the challenge posed by sewage sludge is global one, in Malaysia alone, the volume of sewage sludge, on a wet basis, has been estimated to ascend to 7 million m3 by the year 2020 [13]. Bio-solid waste is one that would not cease to increase as long as human activities proceed on earth [14]. The issue is that most times these bio-solids are dropped directly on the land surface and into the water bodies without proper treatment [15]. The land application allows the sludge to penetrate the ground surface and even into the groundwater sources thereby, exposing the environment to disease-causing organisms and increasing the greenhouse gas emissions [16]. Although landfilling could be advantageous as it increases soil nutrient and thus enhances plant development [17]. Land application is the most prominent method recognized around the globe and is being considered to stand out amongst the most reasonable ways to deal with sludge disposal [18]. Burning i.e. incineration, is a viable method to diminish the sewage sludge volume and neutralize the sludge material content [19]. When joined with cogeneration, burning procedures can adequately recoup energy. Although, the air given off as a result of burning is unwanted [20].
Sustainable assets such as solar, wind, water, and organic matter have been considered as solid choices to supplant fossil assets because of their endless accessibility and their natural decreasing carbon dioxide emanation ability [21,22]. Biomass and bio-solids are, as of now, making new waves as the sustainable power source to substitute fossil assets for fluid power creation [23]. Hence processing them by treatment methods that empower them to get chemically valuable items like fuels and other fine chemicals is worthwhile. Biomass has an impartial dropping impact of discharging the same amount of CO2 as it uses up during its formulation and synthesis reaction [24].
Pyrolysis is a promising bioconversion procedure for energy recovery, waste management, and conversion of biomass into valuable items [25]. And it has pulled in significant consideration amid the previous decade, [26,27]. Pyrolysis technology can produce biofuel from biomass, which is abundant in our environment [28]. Sewage sludge is a highly unwanted waste in the environment. It is composed of numerous materials such as fat, food waste, grease [29], and other volatile substances that can be converted to useful materials [30,31] under the appropriate conditions. The solidified component of sludge is said to comprise about 60–80% biomass, which is made up of 20–30% crude protein, 6–35% fats, and 8–15% carbohydrates [18,28]. Even with this knowledge of the vast minerals and nutrients contained in sludge, it is most generally disregarded as it has been widely accepted as waste [20]. These materials are problematic wastes that are sometimes difficult to dispose of. And considering the current sewage sludge disposal methods employed in urban and industrial setups, the need for intensive study and investigation into safer and more advantageous methods becomes necessary if domestic and industrial water is going to be kept clean [31]. Aside from the traditional strategies utilized for sludge disposal (fertilizer, burning and landfilling), of late there is expanded enthusiasm for its pyrolysis or thermal processing [32,33] into bio-oil, biochar, and pyrolysis gases [33,34]. Pyrolysis is defined as a decomposition reaction in the absence of oxygen with some likely side reactions or oxidation taking place [35,36]. Pyrolysis of a natural material produces bio-gas and bio-oil that can be utilized as an energy source and also a carbon-rich product in the solidified state known as char [37]. The process constitutes a complicated chain of chemical reactions [38], that break down natural matters or biomass residues into bioproducts, [39,40,41,42]. The resulting products of sludge pyrolysis include oils, gases, and char [20]. While the material used is usually the main factor in determining temperatures for optimum oil yield [43] the distribution of the three products is greatly determined by temperature [20]. The gas component formed is essentially carbon monoxide, hydrogen gas, carbon dioxide, and some lightweight sub-atomic hydrocarbons [44,45]. The solid component is a carbonaceous material called char highly concentrated with components such as Na and Mg, which would then be able to be utilized as fertilizer or an adsorbent [46,47]. Pyrolysis is used for volume reduction and energy recovery, and as such, it is significantly more acceptable for bio-solids waste management [17]. It is increasingly being considered because of the recuperation of oil with reduced emanations of NOx and SOx. Also, it maintains a strategic distance from the development of harmful substances, for example, dioxins, with low working expenses, when contrasted with incineration [20].
Zeolite-Y is the catalyst of choice in the catalytic pyrolysis process because of its broad spectrum of chemical conversions, their high thermal stability, and their ability to exchange cations during catalysis. Zeolites are nanoporous heterogeneous catalysts; they have very high surface areas that include compact active sites that are directly involved in the pyrolysis reaction at a molecular level [48]. They can also be readily regenerated for re-use whenever they tend to lose reactivity, and the production technology is not complicated when compared to other catalysts.
In this study, a sewage sludge sample, collected from a sewage sludge drying bed, was prepared, analysed and subjected to non-catalytic and catalytic pyrolysis processes respectively, and at over a wide experimental temperature range of between 300–700 ℃. Beginning at a temperature of 300 ℃ and at an interval of 100°, four different bio-oil samples were collected from each of the pyrolytic processes, which were analysed to obtain their chemical compositions using a GC–MS machine.
2.
Materials and method
2.1. Materials
The desludging sewage sample (DSS) was obtained from a sludge drying bed at the sewage treatment plant, while the Zeolite Y catalyst was obtained from the zeolite production pilot plant, both located in Covenant University, Ota, Nigeria.
2.1.1. Equipment/apparatus
Jacketed pyrolysis reactor equipped with 1.5 kW heating coil, k-type thermocouple, two pipes, one serving as the inlet for inert gas (optional), and the other used as the outlet for pyrolysis vapors, condensers, electronic weighing balance (Ohaus, Model: Scout Pro S/N: SPU2001), drying oven (Genlab, UK Model: MIN075 S/N: 12F147), Muffle furnace, (Carbolite, Model: HTF1700), gas chromatography–mass spectroscopy (GC–MS, AGILENT 7890B GC/5977 MS), X-ray fluorescence machine (Rigaku 3064, Model 3065), beakers (250 mL, J-Sil Borosilicate), mortar and pestle (Porcelain), sample bottles, crucibles (Silica), Liebig condensers (J-Sil Borosilicate) and cocks.
2.1.2. X-ray fluorescence machine
A trained analyst used the X-ray Fluorescence (XRF) analyzer—a Rigaku 3064 sequential spectrometer with a Model 3065 and 108 position sample changer. It is a closed x-ray system. The x-ray tube is protected by an interlock switch that prevents turn-on of high voltage, and thus x-rays, If the tube is not in the machine. This instrument is equipped with a fail-safe x-ray warning light, shutter open indicator light, and power applied indicator.
2.1.3. Experimental setup
The equipment set up consisted of the pyrolysis reactor connected to a temperature control panel, the mains, and a condenser system. A gasket was placed in between the reactor and the top cover to ensure that the reactor was airtight. A total of 9 screws were then firmly installed across the reactor top, gasket, and the reactor cover to seal it up during the reaction. The reactor had 2 pipes with two valves, respectively attached to its top cover with one outlet for pyrolysis vapors and the other inlet for inert gas (optional). The inlet pipe into the reactor was slightly lowered than the outlet pipe. The outlet pipe connected to 3 condensers in series, was mounted close to a water source, with a collecting/receiving flask positioned at the end of the condenser. The reactor regulator had a control OFF/ON switch for the 1.5 KW heating element, and it allowed the regulation of the reaction temperature on a small display screen, which had several buttons where the desired set point temperature was programmed. The schematic diagram of the reactor is shown in Figure 1.
2.2. Procedure—determination of proximate analysis
2.2.1. Moisture content
5 g of the pulverized DSS was weighed and put into an already weighed crucible (W1). The crucible was then weighed with the sludge sample inside to give (W2). Weight obtained was recorded. The sample was dried in a conventional oven at 105 ℃ till constant weight was obtained. The dried sample was cooled in a desiccator and re-weighed (W3) to obtain the loss in moisture. The % moisture content was then calculated by using Eq 1.
2.2.2. Ash content
The ash content was determined by using the standard test method ASTM D-1102. 1 g of the moisture-free sample was measured and put into a crucible of already known weight. The crucible with the sample inside was weighed and put in the muffle furnace at 550–600 ℃ for 4 h. After that, the sample was cooled down and then weighed. The process was then repeated until a constant weight was obtained. The ash content of the sample was obtained using Eq 2.
2.2.3. Volatile matter
The volatile content was derived using the ASTM E-872 standard test method, where 1 g of the moisture-free sample was placed in a crucible, covered, and put into a muffle furnace at a temperature of 950 ℃ for just 7 min. The resulting loss of mass was expressed as the volatile matter in the sample using Eq 3.
where: A = weight of sample used, g and B = weight of the sample after heating, g.
While the % volatile matter of the sample was calculated using Eq 4.
where: W = % weight loss and M = % moisture content.
2.2.4. Fixed carbon
The fixed carbon content of the sample was determined using Eq 5.
2.2.5. Gas chromatography–mass spectroscopy analysis
The temperature programmer of the GC was maintained at an initial temperature of 40 ℃ and held for 1 min, followed by gradual increase to 300 ℃ at 10 ℃/min for 8 min. 1 mL of each sample was injected in the split mode with a split ratio of 1:10. The IUPAC nomenclature of identified components was based on retention time on the capillary column and matching of the GC mass spectra with the National Institute of Standards and Technology (NIST) library.
2.2.6. Reaction without catalyst
150 g of pulverized DSS was weighed and poured into the reactor and closed up securely, and the reactor switched on, and the temperature gauge set at 400 ℃ using the temperature control panel. During the heating process, the outlet pipe connected to the condensers allows the flow of gases out of the reactor. This indicated the start of the pyrolysis reaction. The gases then passed through the condensers and began to condense and flow down into the receiving beaker along with the non-condensable gases. The reactor temperature regulated and maintained at this temperature. All the oil in the system (reactor and condensers) was allowed to drain into the receiving flask and stored in an appropriately labelled sample bottle.
The reactor was again switched on, and the above process repeated for higher temperatures of 500 and 600 ℃ to obtain other bio-oil samples. The reactor was put off and left to cool down to a temperature below 100 ℃ and opened up to get the sample residue, which was then in the form of char. The char sample was collected and weighed to aid material balance.
2.2.7. Reaction with catalyst
Here the catalyst was mixed directly with the pulverized DSS feedstock in the ratio 0.3 g catalyst to 1 g of feedstock. As such, 45 g of zeolite Y catalyst was weighed and thoroughly mixed with 150 g of the sewage sludge. The resulting mixture was then vigorously stirred to achieve uniform distribution. The new mass of 195 g of feedstock (DSS + catalyst) was then poured into the reactor, and the entire procedure repeated, as stated in section 2.2.6.
3.
Results
Tables 1–12 and Figures 2–5 presented below give the results of the proximate analysis and the pyrolysis of DSS at the stated experimental conditions. Proximate analysis, XRF and GC–MS machines were respectively used to generate the various results presented.
4.
Discussion
4.1. Proximate analysis of desludging sewage sample (DSS)
Table 1 shows the proximate analysis of the DSS. The percentage moisture content was 5.44%, which confirmed that the DSS was appreciably dry before the pyrolysis process commenced compared to sewage sludge that could naturally contain up to 70% by weight of moisture [44]. This value allowed for easier material handling and enhanced bio-oil quality. The volatile percentage matter and the ash content of the sewage sludge were 44.85% and 48.89%, respectively, which were similar to the results previously obtained by other researchers [43,49]. Volatile matter is the most important aspect of proximate analysis that directly affects bio-oil yield. The higher the volatile matter in the feedstock, the higher the yield of the bio-oil and vice versa. Volatile matter constitutes hydrocarbons (which form bio-oils) and some gases such as carbon monoxide, carbon dioxide, sulfur dioxide, and nitrogen (which would later constitute the non-condensable gases). However, 44.85% of the volatile matter obtained was not very high, considering bio-oil as the main product obtained from this sludge sample.
The ash content (48.89%) obtained was high in comparison with what other researchers obtained [43,49], which implies a high concentration of inorganic matter. The preceding inference will not apply when the ash is, however, concentrated with some specific compounds such as silica, which was the case with the sewage feedstock used in this work (Table 4) since silica does not take part in pyrolysis reactions. Fixed carbon is the amount of solid material left after the pyrolysis of the organic matter to form bio-oil. The low fixed carbon (6.2%) obtained was advantageous as it indicated the production of more bio-oil. The amount of fixed carbon affects the quantity of char produced after pyrolysis, and bio-char activation and production become a viable plan when the organic content in the char is high. The XRF analysis of sewage sludge before and after the reaction revealed the total organic contents were respectively 12% and 12.9%, while the total inorganic contents were 86% and 86.9%, respectively. The very high inorganic content gives an indication that the sludge could be processed and used for the production of building materials, while the low organic content of the sludge sample indicates the possible low bio-oil yield from it.
4.2. Effect of pyrolysis with or without catalyst on product distribution
Table 2 shows the product distribution obtained after pyrolysis of the sewage sludge with and without catalysis. The reaction without catalyst showed that pyrolysis of the sewage sludge under the applied conditions favored the solid char yield of 76.6, bio-oil yield 18.2, and the non-condensable gases of 5.2 wt%. The use of catalysts was seen from Table 2 to increase the bio-oil yield during the heterogeneous catalysis slightly. The char, bio-oil, and non-condensable gases obtained from the heterogeneous catalysis were 62, 20.9, and 17.1 wt%, respectively. Relatively, the bio-oil yield was rather very low compared to the results of other researchers such as [49,50,51], that obtained higher than 50% bio-oil from similar investigations. The reason for the huge difference may be attributed to the very high inorganic content such as silica in the DSS, which could not be pyrolyzed.
4.3. Effect of temperature on bio-oil yield
The bio-oil yield was also investigated at several temperature intervals, as shown in Table 3. The aim was to determine the optimum temperature range for the bio-oil yield. The reaction only started to yield a product in the form of a dirty whitish gas from the reactor outlet into the condenser at exactly 300 ℃. This observation showed that the DSS was a recalcitrant pyrolysis material compared to other organic materials that normally begin to experience pyrolysis product at a temperature of 200 ℃. The gas obtained was mainly non-condensable gases at this first interval. Condensation started to occur at 346 ℃ and increased until almost all the product coming out of the condenser was only bio-oil at 460 ℃. And this only happened for a short period. Maximum bio-oil yield recorded (40.29%) from the pyrolysis without the use of a catalyst in the temperature interval of 400–500 ℃, which corresponds to an average temperature of 450 ℃ recorded in the literature for sewage sludge pyrolysis. Whereas the maximum bio-oil (30.87%) obtained from the heterogeneous catalysis of the sewage sample pyrolysis took place within 300–400 ℃ temperature range. From this point, bio-oil yield steadily decreased with increasing temperature intervals for the heterogeneous catalysis, while for the pyrolysis with no catalyst, the bio-oil yield got to a maximum within the temperature interval of 400–500 ℃ [52,53] and then began to decrease with increasing temperature as shown in Table 3. More of non-condensable gases were observed at the 500–600 ℃ intervals while little or no bio-oil was observed at temperatures above 650 ℃.
4.4. Effect of pyrolysis on the composition of the DSS before and after pyrolysis
XRF analysis result, as displayed in Table 4, gives the composition of the desludging sewage sample (DSS) used before and after pyrolysis (which is the residue). The DSS was mainly composed of silica and calcium oxide at 46% and 20.9%, respectively, with low organic matter content of only 12%. The amount of organic matter is the major determinant of bio-oil yield as pyrolysis is the decomposition of organic matter in the absence of air. The low organic matter explains the relatively low product—bio-oil and non-condensable gases obtained from this work. The result, however, is not binding on sewage sludge samples from other sources because sewage sludge is a variable material with very unpredictable composition depending on where and how it is obtained. The sample used in this study was collected from the sludge drying bed some weeks after the septic tank was cleared for routine maintenance.
The pyrolysis reaction had only very little impact on the material composition of the residue obtained after the pyrolysis in comparison to the DSS. Increased silica content (from 46% to 56.1%) and minimal organic content (from 12% to 12.87%) were observed, while most of the oxides were observed to have decreased. The chemical composition of the char or residue remained relatively the same in composition as with the DSS before pyrolysis. The residue can be a useful by-product in certain applications depending on its composition. High silica and calcium oxide contents suggest application in building and construction materials because they are both cement strengthening materials.
4.5. Effect of catalyst and temperature on the bio-oil chemical composition
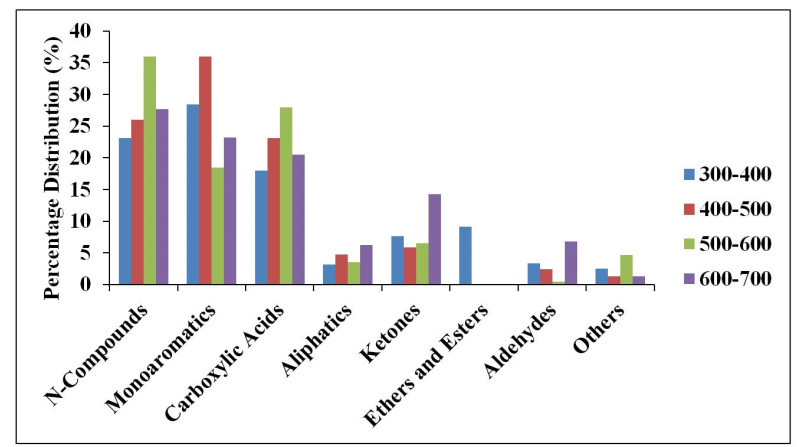
Some of the major chemical compounds obtained from the GCMS are presented in Tables 5–12 and they illustrate the varied and abundant chemical compounds inherent in the condensed and collected bio-oil samples, which were also observed by other researchers [54,55]. The retention time (RT) shows the various times at which the various compounds were eluted, while the area percentage measured of the abundance or the amount of each compound contained in the bio-oil sample. Phenol was identified as the compound with the highest area percentage and it occurred in all the bio-oil samples, as shown in all the Tables 5–12 (at retention times of 4.9–5.3). The bio-oil collected at a temperature interval of 300–400 ℃ (Table 9) recorded the highest phenol composition of 15.43%.
The different compounds were classified using their functional groups. And they include the N–compounds, which are the nitrogen-containing compounds such as the amides (R–CONH2), amines (R–NH2), and nitriles (R–CN). Others include the mono-aromatic compounds, carboxylic acids (R–COOH), aliphatic compounds, ketones (R–COR), esters (R–COOR), ethers (R–OR), aldehydes (R–COH). However, a few more compounds did not fit into any of the above-classified groups. They are all shown in Figures 2 and 3. N–compounds that occurred include famotidine, nicotinamide, guanidine, hydrazine, and pyrazine. The monoaromatic compounds were essentially alcohol (R–OH) containing compounds like phenol, cresol, hexanol, and the likes. The next class was the carboxylic acid group, where compounds such as propanoic acid, acetic acid, and oxalic acid occurred. Aliphatic compounds were the pure hydrocarbons, which were the first three functional groups; alkanes, alkenes, and alkynes. The arenes (family of benzene) were also a member of this group. Other groups highlighted were the ketones, esters, and the ethers group and the aldehydes. Others, which were the last group, included inorganic compounds containing silicon and phosphorous, which could not be classified under any of the other groups.
It was observed that the same group of compounds that occurred for both the catalyzed pyrolysis and the non-catalyzed pyrolysis of DSS at the different temperature intervals considered. The use of heterogeneous catalysis favored the production of more of the N–compounds giving a minimum of 39% compared to the maximum of 35% of N–compounds obtained when no catalyst was used. In all, the N–group of compounds was more in the bio-oils produced in comparison to other groups. This finding corresponds to the work of other researchers [56,57] who also observed that nitrogenated compounds were essential part of bio-oils.
Tables 5–12 show the list of the major compounds identified by GCMS at the various pyrolysis conditions. Apart from phenol, it was observed that different chemical compounds were produced from the DSS and were dependent on the various prevailing pyrolysis conditions. Phenol was a typical and more abundant constituent displayed in each of the Tables 5–12. Other very pronounced constituents include the nitrogen-containing compounds of either the amide, amine, or nitrile group attached to them. They contained about 20–40% of nitrogen-containing groups. The only exceptions were the first oils collected at 300–400 ℃ and 400–500 ℃ during the run without a catalyst, which was more concentrated with monoaromatics. The use of catalysts was seen to enhance the production of nitrogen-containing compounds. Monoaromatic compounds were the next most predominant group. Carboxylic acids were present in considerable quantities also. Aliphatic compounds, ketones, esters, ethers, aldehydes occurred in little amounts. For the mono-aromatic compounds, catalysis favored their production except at the 400–500 ℃ temperature intervals when pyrolysis without the use of catalyst favored their production. The use of the heterogeneous catalysis did not improve the percentage fractions of the carboxylic acids, aliphatic, ketone, and other compounds in the bio-oil samples.
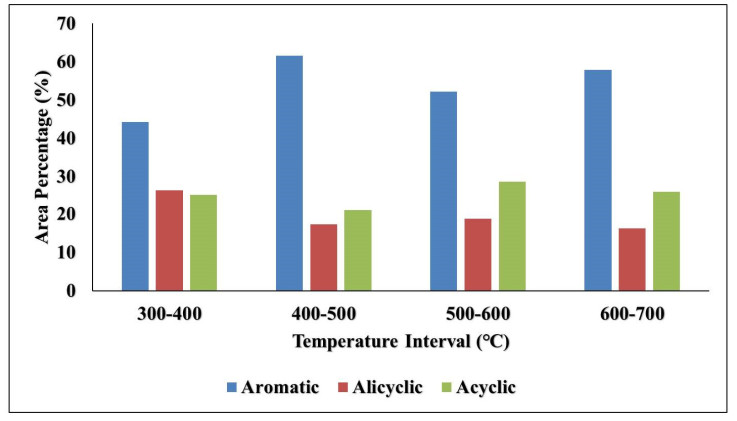
The compounds were also classified based on structure into aromatic, alicyclic, and aliphatic, as shown in Figures 4 and 5 above. Aromatic compounds are compounds in the benzene family that have a cyclic double bond. Alicyclic compounds are single bonded cyclic compounds, while acyclic compounds are purely straight-chained compounds, whether branched or unbranched. Figures 4 and 5 showed that most (40–70%) of the compounds identified were aromatic. The highest aromatic yield (61.5% and 66.3%) was identified respectively for pyrolysis without and with a catalyst between 400–500 ℃ for both processes. It was observed that the use of catalyst slightly favored the formation of aromatic compounds in comparison with the alicyclic and aliphatic.
The percentage composition of the alicyclic and aliphatic compounds decreased during the heterogeneous catalysis at the different temperature ranges investigated. This phenomenon may be explained thus: as the pyrolysis vapors rise through the catalyst bed, catalytic reforming processes such as cracking, polymerization, isomerization, and dehydrogenation take place, which is what accounts for the decrease in the alicyclic and aliphatic composition in favor of the aromatic compounds. Alicyclic compounds were generally the least represented.
5.
Conclusions
The use of catalyst increases the yield of bio-oil, but it does not appreciably affect the chemical composition of the bio-oil obtained. In the non-catalytic pyrolysis of the DSS, the bio-oil yield got to a maximum at a temperature interval of 400–500 ℃ but began to decrease steadily as the temperature interval was increased. For heterogeneous catalysis, the optimum bio-oil yield was obtained at a temperature interval of 300–400 ℃ but, after that, decreased steadily as the pyrolysis temperature increased steadily. Catalysis only prompted product redistribution at the various temperature intervals studied; no new pyrolysis product was formed. The composition of the pyrolysis residue did not reveal any considerable difference from the DSS before pyrolysis.
Acknowledgements
The authors gratefully acknowledge the financial support of the Management of Covenant University, Ota Ogun State, to publish this article.
Conflict of interests
All authors declare no conflicts of interest in this paper.
Author contributions
Vincent E. Efeovbokhan: conceptualization, methodology, supervision, writing-reviewing, and editing. Augustine A. Ayeni: supervision, writing-reviewing and editing. Osuvwe P. Eduvie: investigation, data curation, writing, original draft preparation. James A. Omoleye: writing-reviewing, and editing. Oladotun Bolade: validation, writing-reviewing and editing. Ajibola T. Ogunbiyi: supervision, reviewing, and editing. Victoria N. Anyakora: conceptualization, methodology, reviewing, and editing.










 DownLoad:
DownLoad: