1.
Introduction
Injection molding, as one of the significant manufacturing techniques for plastic processing, fabricates at least 30% of the plastic parts worldwide. After long-term development, this technology has been greatly matured with highly standardized process characteristics and mold components. In many aspects, injection molding has shown evident advantages than 3D printing of plastic parts [1,2], e.g. cheap price, high productivity, stable quality, etc. Generally, feeding and plasticizing, injection, holding, cooling, and demolding, altogether make a complete injection molding process. These process procedures are briefly illustrated below:
1) Feeding and plasticizing. Add plastic powders or particles to the barrel of the injection molding machine and heat them to viscous flowable state. At this stage, the distribution of composition, density, viscosity, and temperature of the melted plastic is relatively uniform, which ensures qualified fluidity for the next-stage injection.
2) Injection. The high pressure from the screw pushes the plastic melt to rapidly enter the mold cavity through the nozzle.
3) Holding. The screw moves forward slowly and slightly to pressurize and compact the melt so that the density of plastics will be increased through material compensation.
4) Cooling. The plastic part is gradually cooled down to increase the stiffness and strength so that they could be successfully demolded.
5) Demolding. Remove the plastic part from mold cavity through demolding mechanisms.
Even though five stages are involved, cooling occupies the largest proportion of an injection molding cycle, generally between 70 and 80%. Experiments show that 95% of the heat is transferred to the mold during cooling and is taken away by the coolant in the cooling system. Therefore, cooling has a significant impact on product quality and production efficiency. Design of the cooling system has drawn the attention from both academia and industry, and extensive research efforts have been put on investigating novel ideas and design methods for the cooling system. The ultimate goal is to achieve uniform surface temperature of the part, reduced warpage and deformation, and shorten the cooling cycle time. At early stages, parametric design optimization of the straight-line cooling channels was focused. Numerical simulation plus the surrogate modeling-based optimization were widely explored to find the optimal set of design variables. However, the design space of straight-line cooling channels is limited due to the geometric restriction. Given the increasingly complex engineering structures [3], counting on straight-line cooling channels is infeasible. Later, the conformal cooling concept was developed. The conformal cooling channels have curved cooling circuit that closely follows the mold cavity shape, so that the thermal conduction distances between the part and the cooling channels tend to be uniform. In addition, the average thermal conduction distance is much shorter. Therefore, conformal cooling channels can significantly reduce the warpage defect and shorten the cooling cycle time compared with the traditional straight-line cooling circuits [4,5]. Owning to the rapid development of computational design techniques and additive manufacturing technology [6], design and manufacturing methods for conformal cooling circuits have been greatly developed. For example, topology optimization, as a freeform computational design methodology [7,8], has been intensively employed for conformal cooling channels [9,10]. To guarantee the organic structure being manufacturable, manufacturing-oriented topology optimization has been widely targeted [11,12,13,14]. Hence, to fully disclose the advantages of conformal cooling, the underlying physics, geometric forms, computational design methods, and advanced manufacturing techniques of conformal cooling are carefully investigated in this paper. A comprehensive review is developed to summarize the state-of-the-art of conformal cooling system design, and the future perspectives are discussed as well.
2.
Physical model of conformal cooling simulation
In continuous injection-molding operations, the cycle-averaged temperature reaches a steady state in which the conservation of energy requires that the heat transferred into the system equals to the heat transferred out [15], namely:
in which QP is the heat carried in by the molten plastic, J; QC is the heat carried out by the coolant, J; QE is the heat dissipated to the surrounding environment, J.
An injection-molded product cools down and solidifies in the in-mold cooling stage [16]. The governing equation for analyzing the mold cycle-average temperature distribution is formulated as:
where k is the thermal conductivity, W/(m∙K); T is the temperature, K; and x, y, z are the coordinates, m. By this equation, the steady cycle-averaged temperature field can be calculated to represent the overall cooling behavior via the cooling system considering a fully transient analysis is computationally expensive.
The cooling process is very complicated in a physical sense and is affected by many factors. To be specific, the conformal cooling channel design is a complex heat transfer problem with transient and 3D design conditions. The experimental results show that 95% [17,18] of the heat in the injection process is taken away by the cooling system through convective heat transfer. The heat transferred by convection can be calculated by Newton's law of cooling:
where A is the heat transfer area, m2; h is the convective heat transfer coefficient, W/(m2∙K); TW is the wall temperature, K; Tf is the temperature of the fluid, K. In practice, h is a function controlled by many factors:
in which u is the cooling fluid velocity, m/s; ρ is the density, kg/m3; c is the specific heat capacity, J/(kg∙K); v is the kinematic viscosity, m2/s; L is the characteristic length, m; Ψ is a factor affected by geometric features of the heat transfer surface, such as shapes and relative positions, etc.
In view of the heat exchange characteristics of injection molding industry, the physical model of cooling needs to be simplified in order to establish a mathematical model for calculation and analysis. Some typical assumptions are as follows:
1). The coolant is a continuous Newtonian fluid.
2). The physical properties of the coolant are constant.
3). There is no heat generation in the fluid, and the heat dissipation caused by viscous dissipation and heat radiation are neglected.
4). Only the heat transfer in the holding and cooling stages is considered because the filling time is very short.
3.
Development of conformal cooling systems
Since Professor Sachs [19,20] from Massachusetts Institute of Technology put forward the conformal cooling technology for injection molds, a number of studies have demonstrated the superior characteristics of conformal cooling channels in terms of reduced warpage, shortened cooling time, and improved temperature uniformity [21] compared with the conventional straight-line cooling channels. The cooling efficiency was also proved to be higher than baffle cooling channels [22]. Mazur et al. [23] further verified through both numerical simulation and physical experiments that lower cooling temperature and better temperature uniformity could be achieved in conformal cooling comparing with baffle cooling. About the different layouts of conformal cooling, Khan et al. [24] performed a comparative study on the series conformal cooling channels, parallel conformal cooling channels, and the conformal cooling channels with additive cooling lines, wherein the last option led to the most uniform temperature distribution of the part. The cross-section shape of the channels obviously affects the cooling effect. The square section [25] and milled grooved square shape [26,27] have been investigated, wherein improved warpage reduction and cooling time reduction were observed. However, the application to injection molding parts with complex geometric features is questionable that should be further verified. Kamarudin et al. [28] added sub grooves to the square cross-section. It was found that the application of sub-grooves increased the contact area leading to enhanced thermal convection effect and disturbed the coolant flow to make it turbulent. Better heat transfer rate and cooling effect were observed than the milled grooved square shape. It was also discovered that the improper design of cross-section shape and cooling channel locations [29] may lead to degraded cooling performance even with conformal cooling channel distribution.
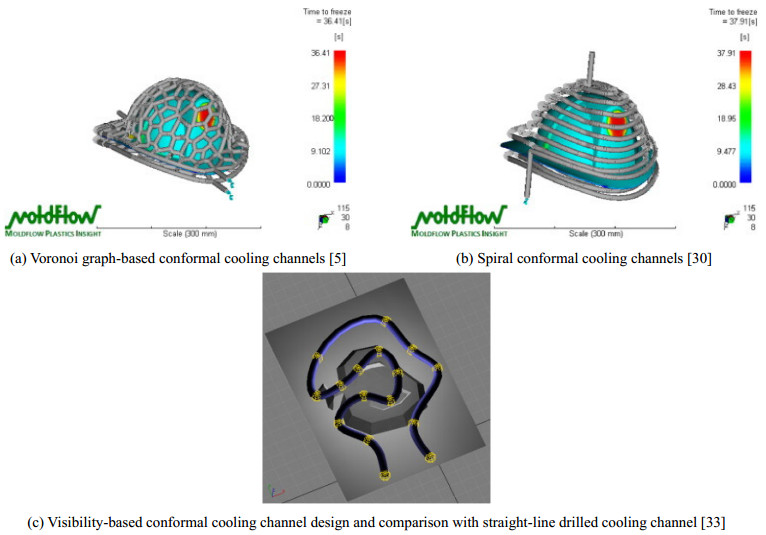
In the above works, the conformability was emphasized but the geometric complexity of the cooling channels was relatively low. To further dig out the potential of conformal cooling, many complex geometric patterns of conformal cooling channels have been proposed (referring to Figure 1). Wang et al. [5] proposed a Voronoi graph-based conformal cooling channel network that reduced the cooling time by 26% compared with the straight-line water channels. However, the flow rate and temperature distribution inside the cooling circuit are highly non-uniform, leading to a degraded performance of cooling uniformity and unnecessarily increased pumping power requirement. At the same time, it is technically non-trivial and expensive to manufacture the cooling circuit with such complex channel connectivity. To address this problem, the same authors [30] put forward the spiral conformal cooling channels, leading to a further reduced cooling time by 11% and also evidently reduced the part temperature. The spiral channels that fully accounted for the parts’ geometric characteristics have been used in automotive injection molds [31]. In addition, a twin-spiral conformal cooling system was proposed in [32] for barrel-shaped parts such as syringes. Both the velocity and temperature of the coolant were analyzed to comprehensively demonstrate the advantages of conformal cooling. Au et al. [33] also proposed a visibility-based design automation method to automatically generate conformal cooling channels, which significantly improved the cooling performance with reduced temperature difference and in-cavity residual stress. Later, Au and Yu [34] proposed a distance adjustment method to alter the distance between the part surface and the conformal cooling surface, and has achieved even better cooling uniformity than the visibility-based conformal cooling channels.
Multi-material option was another idea of enhancing conformal cooling systems. Saifullah et al. [35] employed the copper tube for cooling channels and carried out thermo-fluid analysis of the conformal cooling. In the reported work, the significantly reduced cooling time and improved fatigue life of cooling channels were summarized as the benefits. However, damages to the mechanical properties of the mold are noteworthy. Zink et al. [36] also studied the effect of altering cooling channel materials on the cooling efficiency. They verified the benefits of enhanced cooling performance of conformal cooling channels plus materials of high thermal conductivities such as copper.
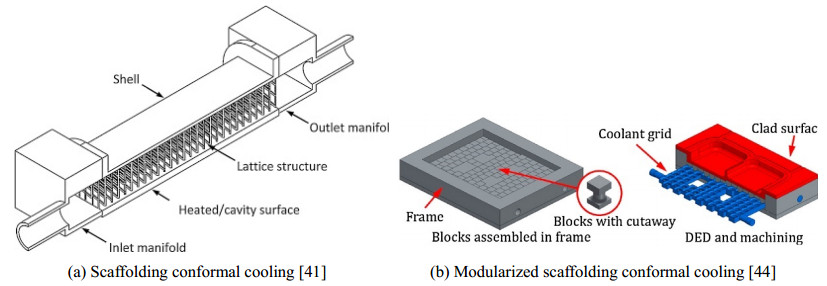
The increased geometric complexity raises a new problem that it is non-trivial to have the conformal cooling channels being manufactured and increasingly more attempts have been made to investigate the additive manufacturing-based conformal cooling system. Eiamsa-ard and Wannissorn [37] designed the conformal bubbler cooling channels and had the design fabricated with metal deposition process. The idea is novel and interesting, but this method is not suitable for complex structures. Au and Yu [38] proposed the scaffolding structure-based conformal cooling system. This idea was followed in some later researches and the ideas of multi-connected cooling water channels [39] and the conformably deformed scaffolds [40] were explored as well, which achieved better uniform cooling effects and slightly better cooling rate. Similarly, Brooks and Brigden [41] employed self-supporting gird cells to build the scaffolding cooling channels. Felipe et al. [42] proposed a hybrid design which combined the parallel and series conformal cooling channels with the scaffolding waterways. The enhanced coolant flow turbulence improved both the cooling efficiency and cooling uniformity compared with the conventional series conformal cooling channels. A limitation of the scaffolding cooling system lies in the often-encountered dead zones that degrades the cooling effect. Generally speaking, the mold including scaffolding cooling channels can only be manufactured with additive manufacturing and one manufacturing example can be found in [43]. In [44], the scaffolding cooling system was modularized by discretizing the scaffolding grid cells which were separately fabricated with DED (Direction Energy Deposition) additive manufacturing. An outstanding feature is that the mold can be manufactured with hybrid additive-subtractive manufacturing which can reduce the manufacturing cost to the lowest level as possible. Some of the scaffolding conformal cooling concepts are reported in Figure 2.
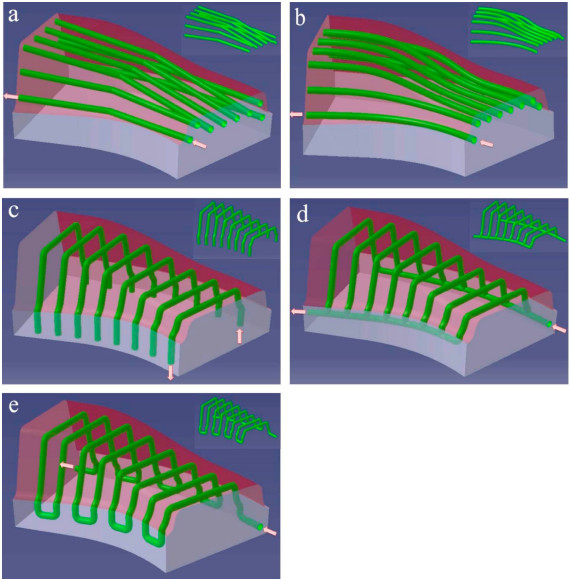
Ding and Yamazaki [45] simulated the optimality of branching systems in nature to design cooling channels. And the idea was inherited by Choi et al. [46] to develop the conformal cooling system based on the binary branching law, which reduced the temperature deviation by 30%. Hu et al. [47] studied the performance of straight-hole, longitudinal conformal cooling channels, lateral conformal cooling channels, parallel conformal cooling channels, and serpentine conformal cooling channels through a full factorial design (see Figure 3). They drew the conclusion that the serpentine conformal cooling channel was the best under low Reynolds number and the longitudinal conformal cooling channel was the best under high Reynolds number. For the reason, when the Reynolds number is small, serpentine conformal cooling channel has the greatest coolant turbulence and the highest coolant velocity, both of which intensify the heat transfer effect. When the Reynolds number is high, the coolant flows are all turbulent. The longitudinal conformal cooling channel’s cooling performance is better because of the larger cooling area and the more uniform distances between the cooling channels and the part surface.
This section mainly introduces the spatial structure and geometric characteristics of the conformal cooling channel, and the methods to generate the conformal cooling channel including Voronoi graph-based method, helix, binary branching law, variable pitch method and Scaffolding or lattice structure. The common purposes of these methods are:
1). Realize the violent turbulence of the coolant to enhance the heat exchange efficiency within the mold.
2). Increase the heat exchange area between cooling water pipe and parts.
3). Uniform cooling and reduction of warpage and residual internal stress can be achieved by keeping the distance from the channel to all details of the part surface consistent.
Designers can choose the method suitable for their own parts' geometric characteristics, and rapidly design and build the conformal cooling channel.
4.
Optimization of the conformal cooling systems
4.1. Parametric optimization
Parametric design optimization of conformal cooling channels has been widely explored for its simplicity in implementation, since the tedious sensitivity analysis is not involved. Some of the representative works are briefly summarized below.
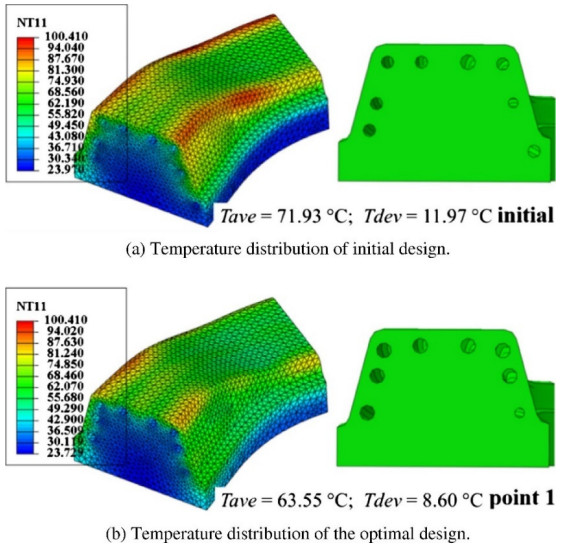
Jahan et al. [48,49] employed a DOE (Design of Experiment) [50] approach to perform the optimal design of conformal cooling channels. The parameters of channel diameter, pitch distance, and channel centerline and mold wall distance were assigned as the design parameters for numerical experiment design. An optimal set of design parameters were derived through DOE-based optimization. Furthermore, five cross section shapes were studied and the rectangular cross section was observed to generate the best cooling effect. The reason lies in the fact that the long side of the rectangular cross section gets close to the part, so as to enforce the convective heat transfer with an enlarged convection surface. The DOE-based conformal cooling system optimization was similarly performed in [51], wherein the radius of cooling channels, the distance from channel center to tool work surface, and the ratio of each channel center were defined as the design parameters, the average temperature and temperature deviation at the working surface were employed as the objective function, and response surface modeling was adopted to build the surrogate model for design optimization. The new design adjusted the layout and sizes of cooling channel to effectively utilize the coolant. The optimized longitudinal conformal cooling channel reduces the average temperature and temperature deviation of the tool surface (referring to Figure 4 for the optimization effect). Venkatesh [52] used the taguchi orthogonal experiment to create an L27 (33) orthogonal table to study the effects of cross section shape, channel path type, and center line distance on the maximum part surface temperature, and it was found that the channel path type and center line distance had the greatest impact on the cooling effect. Interestingly, a different observation on the effect of the cross section shape was derived from [48,49], wherein circle was identified as the best cross sectional shape to reduce the maximum part surface temperature when combined with the spiral channel path, while rectangular was identified as the best when combined with the spiral square path type. Not enough data was provided to analyze the above phenomenon, but at least, it indicates that the cross-section shape is not a dominating factor influencing the cooling performance. Hazwan et al. [53,54,55,56,57] obtained the empirical relationship between the part warpage and design parameters including the coolant temperature, the melting temperature, the injection pressure, and the cooling time. Then, the part warpage was minimized through response surface modeling combined with genetic algorithm and glowworm swarm optimization. Dang and Park [58] built the analytical model for 2D heat transfer analysis through combined DOE approach and numerical simulation. Then, for any 3D conformal cooling system design, the analytical model was employed to quickly find a near-to-optimal design solution of the cooling channel configuration since the analytical model was only a few mathematical formulas and its analysis accuracy was moderate. Finally, the optimization with detailed 3D numerical simulation was performed to fine-tune the rough optimal solution, while the effort of 3D heat transfer analysis was greatly saved due to the pre-optimization with the analytical model. Kitayama et al. [59] employed the radial basis function for surrogate modeling and performed the sequential approximation optimization to finalize the pareto-frontier of the multi-objective optimization problem. A balanced design effect between the cycle time and warpage was achieved.
Mercado-Colmenero et al. [60] proposed a lattice-based conformal cooling modeling method and applied genetic algorithm to optimize the parameters of the size, shape, and layout of the lattices. However, the time consumed for optimization was not reported. Actually, the huge computational scale can be anticipated since genetic algorithm takes a large number of iterations to converge while the injection molding simulation is time-consuming. Later, Mercado-Colmenero et al. [61] developed an automated cooling system design method by discretizing the topological structure of the part, detecting the planes, grooves, thick walls, and other features that are difficult to cool, and accordingly, initializing the layout of cooling channels. Then, the channel diameter, channel separation, and other parameters were optimized through genetic algorithm to improve the cooling uniformity. Even though the straight cooling channels were used, the cooling effect was claimed compatible to conformal cooling.
In summary, the aforementioned parametric design optimization approaches have achieved the effect of design improvement. The general work flow is to pick up a few design or process parameters that may have a significant influence on the cooling effect as the variables, for example, the channel diameter, pitch distance, channel centerline to mold wall distance, cross section shape, channel path type, and many others. Then, DOE is performed referring to standard methods including Taguchi method, Central composite design, Box-Behnken design, etc. Regression analysis is performed in a following step to build the response surface model (polynomials) or the radial basis model, so that an empirical model can be constructed bridging up the objective function (maximum part surface temperature, maximum part warpage, part surface temperature uniformity, etc.) and the design variables. Finally, gradient-based methods (e.g. steepest descent method or sequential approximation methods for constrained problems) or the global search methods (genetic algorithm, particle swarm method, and others) are adopted to find the optimum. However, they share a common limitation that a prototype design has to be established as a premier and only a few of the geometric parameters can be assigned as design variables. Otherwise, a large number of numerical experiments have to be conducted, which leads to a high computational expense [9,58].
4.2. Sensitivity-driven design optimization
Sensitivity-based design optimization was recently widely employed for conformal cooling channel optimization, since with the appropriately calculated sensitivity information, the computational scale would not change with the increased number of design variables [7,9]. Hence, the design space can be greatly extended without influencing the computational cost. More importantly, a preliminarily established conformal cooling system design is not mandatory for the sensitivity-based design optimization [9].
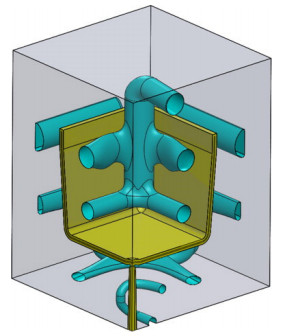
Agazzi et al. [62,63] proposed a novel method based on the morphological surface concept. A cooling surface was established, and the cooling channel distribution inside the cooling surface was optimized through a conjugate gradient algorithm to maximize the cooling efficiency and temperature uniformity. Finally, a post-treatment was performed to determine the location, number, and shape of the conformal cooling channels. An example is illustrated in Figure 5.
Li et al. [9] proposed a topology optimization method for conformal cooling channel design. Boundary element method was employed to simulate the cooling process. An idea similar to the conventional ground structure method for truss structure optimization was proposed, i.e., build a dense cooling channel network and then gradually eliminate the less-effective cooling channels. One optimization result is shown in Figure 6 which demonstrates that both cooling efficiency and uniformity have been improved compared with the baffle channels. Besides, this method was still initial guess dependent, but since an arbitrary initial guess could be adopted, the initial guess dependency was greatly weakened. Wu and Tovar [10] developed a thermal-fluid topology optimization algorithm for conformal cooling system design. However, restricted by the computational scale, the underlying physics was simplified, and the derived topological design was geometrically simple.
Variable-density lattice topology optimization was popular recently [64,65,66,67] and its application has been extended to design scaffolding conformal cooling systems. Wu and Tovar [68] presented a topology optimization approach for lattice structures subjected to thermal and mechanical loads. The optimal injection molds were characterized by a quasi-periodic distribution of lattice unit cells of varying densities. The numerical model of the optimized mold shows that with respect to a traditional solid mold design, a mass reduction of over 30% can be achieved with a small increase in nodal displacements (under 5 microns) and no difference in nodal temperatures. Jahan et al. [69] optimized the mechanical structure of the entire injection cavity using a topology optimization method, through which the lattice unit size and cooling channel parameters were concurrently optimized to enhance both the mechanical and heat transfer properties of the injection mold.
4.3. Manufacturability considerations of the conformal cooling system optimization
Additive manufacturing techniques has prompted the development of conformal cooling. However, the accessible cases that include full details of the experiments are limited. There are still many issues that are non-disclosed about the additively manufactured metallic injection molds. The main issue lies in the manufacturing accuracy. As widely known, additive manufacturing was often criticized for the low surface roughness; however, how much the poor surface roughness will influence the flow and cooling performances is currently unknown. Besides, the residual distortion of metallic additive manufacturing is un-ignorable [70] since it evidently deviates the layout of the cooling channels from the original design. Therefore, it is necessary to control the manufacturing process to minimize the deviation [71] or consider the distortion during the design optimization to make compensations. The employment of hybrid additive-subtractive manufacturing provides a fundamental approach to address the issues of low manufacturing accuracy [72]. The frequent switches of additive and subtractive operations lead to a modularized manufacturing strategy that has each volume to be accurately manufactured given both surface roughness and sizing/shape accuracy [73]. Subsequently, both additive- and subtractive-manufacturing oriented constraints should be addressed when designing the conformal cooling channels. For example, the self-support constraint for additive manufacturing [74,75,76,77] and the uniform-diameter cooling channel related cutter accessibility [78,79,80,81,82,83] and length scale [84,85,86] constraints. Another difficulty of employing the hybrid manufacturing scheme is the immature process planning technique. So far, automatic process planning for hybrid manufacturing was only developed to some form-feature based product designs [87,88] that have low geometric complexity. Hence, completing the process planning technique is an urgent job at this time point. Other than the manufacturing accuracy issue, the high cost of metallic manufacturing is another issue that deserves the attention. It is widely acknowledged that the manufacturing of injection mold through SLM (Selective Laser Melting) [89] or hybrid manufacturing [72,87] is costly. The high expenses will hold back potential users of injection molds including conformal cooling. Hence, lowering the costs of additively manufactured metallic injection molds through process amendment or cost-constrained design optimization [89] is an important topic to investigate.
5.
Conclusion and future perspectives
Effective cooling performance enhancement of conformal cooling systems has been proved by numerous studies. Diversified geometric forms of conformal cooling channels have been proposed which all demonstrate the fast and uniform cooling capability. To further dig the potentials, computational design methods have been developed to modify the embodiment details to extremely enhance the cooling performance. At the same time, the utilization of additive manufacturing technology to fabricate the as-design conformal cooling circuits has been widely employed and demonstrated the success.
Even though extensively investigated, the development of conformal cooling concept is far from maturity. There are still many design and manufacturing issues to conquer and a few major future perspectives are summarized below.
1). Orthogonal experiments and response surface analysis are widely used to perform the surrogate model-based parametric design optimization. However, a prototype design has to be established as a premier, and only a few of the geometric parameters can be assigned as the design variables. This goes against the freeform characteristic of conformal cooling and can only lead to limited cooling performance improvement due to the restricted design space. Hence, computational design skills were concentrated in recent years wherein the physical equations were accounted to calculate the physics-based adjoint sensitivity information that provides the directions for design update. A large number of design variables can be involved with the sensitivity-based design update for which the computational scale would not be evidently influenced.
2). Computational design methods are superior in freeform cooling channel design given the design efficiency and the extremely large design space. However, as disclosed in Section 4.2, the development of sensitivity-based computational design methods is limited. A main reason lies in the difficulties of sensitivity analysis. As widely acknowledged, injection molding simulation involves the transient thermo-fluid analysis with turbulence models. Performing the sensitivity analysis on the turbulence terms is technically non-trivial. Even if the sensitivity is obtained, the computing scale of solving the governing physical problem and the adjoint problem will be larger, which makes it unsuitable to be adopted by the iterative computational design methodology [90,91]. Hence, a general situation is to simplify the underlying physics into a static thermal-mechanical problem without turbulence [92,93,94,95,96]. This scheme has demonstrated the effectiveness [10], but how much of the cooling design effect has been compromised is not clear, which deserves careful investigations. More importantly, developing the sensitivity model of the complete physical equations-based optimization problem is necessary and the employment of high-performance computing to shorten the computing time is foreseen as a perspective future direction [97,98].
3). Scaffolding conformal cooling channels were recently developed and manufactured. The effectiveness has been proved but the majority of existing designs come from the artificial works. There is a lack of numerical optimization algorithms for design optimization since extremely fine mesh is required to model the scaffolding lattices and the computational cost is not affordable. Then, if multi-scale simulation was used, the homogenization of the heat transfer and fluid flow properties would be non-trivial. Regarding this issue, some efforts were made recently as reported in [99]. The effective properties of the fluid flow were derived from the Darcy–Forchheimer law and the flow was analyzed based on the Brinkman–Forchheimer equation. The fluid cooling effect was obviously enhanced through variable-density lattice topology optimization, but there are still observable numerical simulation errors, which needs to be improved.
Acknowledgement
The authors would like to acknowledge the support from Shandong Research Institute of Industrial Technology; Shandong Province Higher Educational Science and Technology, China (J15LG04); and Key Laboratory of High-efficiency and Clean Mechanical Manufacture at Shandong University, Ministry of Education.
Conflict of interests
The authors declare that there are no conflicts of interest regarding the publication of this paper.









 DownLoad:
DownLoad: