The number of rational points of certain quartic diagonal hypersurfaces over finite fields

1.   Introduction 

In the integrated pest management, chemical control is one of the main control tactics, and the pesticides and other chemicals for the pest management are employed in reality ^[1,2,3,4]. The emergence of chemical synthetic insecticides has made great contributions to the control of some vector insects, agricultural pests and infectious diseases spread by them. At the same time, chemical pesticides are easy to operate and can control pests quickly and effectively. Therefore, in a long time at present and in the future, it is still a favorable weapon to fight vector insects and agricultural pests in rural areas. However, due to the high frequency and large-scale use of pesticides all over the world, long term accumulation leads to the occurrence and development of resistance and serious environmental pollution, which results in the decrease of the sensitivity of pests to pesticides, so they are not inhibited or poisoned by pesticides^[5,6,7,8].

Therefore, how to reduce or delay the resistance of pests to pesticides, how to make the pesticides play their role to the maximum extent, and how to reduce the impact of pesticides on the ecological environment are issues of agricultural administrative departments. The purpose of resistance management is to find appropriate ways to slow down and prevent the occurrence and development of pest resistance to pesticide, or restore resistant pest to a sensitive state. The key of resistance management is to reduce the selection pressure of pesticides on pests^[9,10,11]. The development of pest resistance to pesticide is divided two types: external induced resistance and genetic resistance. The external induced resistance is that the pest developed the resistance to pesticide due to the large dosage and high frequency of pesticide spraying. Genetic resistance refers to the resistance generated by genetic inheritance of the resistance of the previous generation of pests to pesticides ^[12]. Since most of the pests that are sensitive to pesticides are killed during the use of pesticides, the surviving pests with pesticide resistance will pass on the resistance genes to the next generation. Therefore, with the change of generations, the proportion of pests carrying resistance genes becomes higher and higher, and the effect of pesticides gradually decreases, which seriously affects the success or failure of pest and disease control. In order to restrain the resistance of pest to pesticide, some principles have been proposed including rotation or switching between different types of pesticides, using biological control techniques, delaying the emergence of resistance, restoring the sensitivity of pests to pesticides and so on ^{[13,14,15,16,17]}.

Recently, pest management models with pest resistance to pesticide have been widely studied. Dobson and May combining population dynamics and genetics modelled the development of pest resistance to pesticide ^[18]. Liang et al. developed a continuous pest population growth model with both evolution of pesticide resistance and instantaneous pesticide applications, and studied the optimal time for switching between different kinds of pesticides under three different threshold levels ^[10]. Considering the growth of most pest population is not continuous, the novel discrete pest population models with the evolution of pest resistance to pesticide have been proposed and analyzed by Liang et al, who studied the effects of complex dynamical behaviour of pest population on pesticide switching strategies^[11]. The genetic resistance was ignored and they only considered the external induced resistance in all of those studies.

An interesting question is how to describe impulsive control strategies implemented within each generation when pests have non-overlapping generations, including impulsive release of natural enemies and spraying of pesticides. In order to solve this problem, some interesting modeling methods have been proposed recently. Tang et al. simplified hypothesis control strategy which is implemented at the beginning or the end of each generation ^[19]. Wang et al. first proposed a single population model with multiple impulsive pesticides applications within each generation, and then studied the existence and stability of the unique positive equilibrium^[20]. Liang et al. proposed an analysis method of extended discrete model based on continuous logistic model under impulse perturbation to model the effects of single pesticide applications within each generation on populations growth^[21].

Once the pest resistance to pesticide is genetic, the questions are how to model the external induced resistance and genetic resistance in pest control model, and how to management the pest resistance to pesticide to achieve the purpose of pest control to solve those problems, according to the genetic laws and pesticide spraying, we modeled a pest resistance to pesticide model combine the external induced resistance and genetic resistance. Then we introduce the pest resistance to pesticide model into pest control models, the threshold conditions of pest eradication were discussed. For resistance management, we discussed the pesticide switching strategy, and the optimal switching time was investigated under the control strategy of one times pest control within each pest generation and multiple pest control within each pest generation. Moreover, the effects of the death rate of susceptible pests, the spraying times of pesticide within each generation, the dominance of resistance allele on the pesticide switching generations were studied.

2.   The evolution of pesticide resistance and pest control model 

As described in the first part of the introduction, the development of pests' resistance on pesticide has a significant impact on pest control. To address those effects, we first investigate the evolution of pests' resistance, i.e.. we will analyze the development of pests' resistance from the perspective of gene inheritance and establish the development equation of pests' resistance. Moreover, the evolution of pests' resistance has been combined into the pest growth model.

2.1.   Simple genetic model with pesticide resistance 

We assume that the pesticide resistance is determined by a single gene with two alleles $R$ and $S$. $R$ denotes the resistance allele which represents the ability to survive on pesticide spraying. $S$ denotes the susceptibility allele which represents the ability to survive with no resistance to the pesticide. According to Mendelian genetic law, we divide the pest population into three different types: homozygote resistant individuals $RR$, homozygote susceptibles $SS$ and heterozygotes $RS$. In the presence of an application of pesticide, we denote $W_{RR}$, $W_{RS}$, $W_{SS}$ are the fitness of $RR$ type pest, the fitness of $RS$ type pest and the fitness of $SS$ type pest, respectively. Note that the fitness of an individual is independent of its genotype frequency ^[22], and we assume that pest individual is mated randomly. According to the hardy-weinberg principle ^[23], if the frequence of resistance allele is $p_n$ and the frequence of susceptible allele is $q_n$ in generation $n$ (with $p_n+q_n = 1$), then the genotype frequencies in pests after selection are given by the following equations

where $\overline{W}_n$ is the mean fitnesses with

The averages fitnesses of the resistance allele $R$ at generation $n$ is

Consequently, the frequence of the resistance allele $R$ in generation $n+1$ becomes

Submitting $q_n = 1-p_n$, we have the evolution of pesticide resistance

Note that this genetic model has been widely used in different fields ^{[14,24,25,26,27,28]}.

2.2.   The effects of frequency of pesticide spraying on evolution of resistance 

From Eq (2.1), it is obvious to see that $p_n$ depends on the relative values of $W_{RR}$, $W_{RS}$ and $W_{SS}$. Now we focus on deriving equations that represent the fitness of the three different genotypes: $RR$, $RS$, and $SS$. We know that the death rate of pests strictly depends on the dosage of pesticide spraying. For simplification, we assume that the same dosage of pesticide is sprayed at each control event, and without loss of generality, we assume that one unit dose of pesticide is sprayed at each control event. Naturally, the homozygote susceptibles $SS$ are assumed to die with a higher death rate $d_1$ $(0\leq d_1\leq1)$ when a single pest control is carried out with one unit dose of pesticide is sprayed (Note that the different pesticides have different $d_1$, for convenience, we use $d_1$ as death rate in the whole study. For the specific pesticide, we only need to give specific value of $d_1$ in the following results). However, death rate is reduced by the level of dominance of pesticide resistance allele $h$ $(0\leq h\leq 1)$ in $RS$ individuals, thus, the death rate of heterozygous individuals is $(1-h)d_1$ after one unit of sprayed pesticide. And the death rate of resistant individuals $RR$ is $d_2$, for simplicity, we assume that the death rate of resistant individuals $RR$ extremely low, that is $d_2\approx 0$. Consequently, the fitness of each genotype after pesticide is applied once within each generation is

In reality, farmers usually spray pesticides multiple times within each pest generation. In order to investigate the evolution of pests' resistance in this case, we assume that the pesticide is sprayed $M$ times ($M \geq 1$) within each generation, and the fitness of each genotype after $m-$times pesticide spraying in each generation is $W_{RR}^{(m)}$, $W_{RS}^{(m)}$, $W_{SS}^{(m)}$, ($m = 1, 2, ...M$). We know that the fitness of homozygote sensitives $W_{SS}$ is $W_{SS}^{(1)} = 1-d_1$ for once pesticide spraying, $W_{SS}^{(2)} = (1-d_1)^2$ for $2-$times pesticide spraying, $\cdots$, and the fitness of heterozygotes $W_{RS}$ is $W_{RS}^{(1)} = 1-(1-h)d_1$ for once pesticide spraying, $W_{RS}^{(2)} = (1-(1-h)d_1)^2$ for $2-$times pesticide spraying$\cdots$. Thus, the fitness of each genotype after spraying pesticide $m$ times within each generation can be expressed as

Thus, the frequence of genotypes after $m$ times pesticide spraying in the $n$th generation are given by the following equations

where $\overline W_{n, m}$ is the mean fitness of the pest population after $m$ times pesticide spraying in the $n$th generation, which is given by

And the averages fitnesses of the resistance allele $R$ after $m$ times pesticide spraying in the $n$th generation is

Thus, the frequency of the resistance allele $R$ in pests from $n$th generation, to $n+1$th generation is

If the pesticide have completely kill rate to the homozygote sensitives (i.e., $d_1 = 1$ and $W_{SS}^{(M)} = 0$), then

Solving equation Eq (2.3) with initial gene frequency $p_0$, we have

where $\beta = \frac{W_{RS}^{(M)}}{2W_{RS}^{(M)}-W_{RR}^{(M)}}$.

In the next section, calculating the $n$ is important to investigate the optimal generation for switching pesticide. From Eq (2.4), we can get

Now we consider the general case (i.e., $W_{SS}^{(M)}\neq0$). In order to obtain $p_n$ or $n$, we calculate the amount of change in gene frequency per generation by using Haldance' method ^[29], i.e..

We further assume that gene frequency is very low ^[30], its rate of change per generation could be given by

In order to calculate $n$, we divide it into three cases:

Case 1: $R$ is completely dominant gene in $RS$, i.e., $h = 1$ ^[31].

Integrating Eq (2.7) with the initial condition $p_0$, we have

Case 2: $R$ is completely recessive gene in $RS$, i.e., $h = 0$ ^[31].

Integrating Eq (2.7) with the initial condition $p_0$, we can get

Case 3: $R$ is incomplete dominant or incomplete recessive gene in $RS$, i.e., $0 < h < 1$.

Integrating Eq (2.7) with the initial condition $p_0$, we can get

where ${D} = \frac{W_{SS}^{(M)}}{W_{RS}^{(M)}-W_{SS}^{(M)}}$, ${E} = -\frac{1}{1-W_{RS}^{(M)}}$, ${F} = \frac{{W_{RS}^{(M)}}^2-W_{SS}^{(M)}}{(1-W_{RS}^{(M)})(W_{RS}^{(M)}-W_{SS}^{(M)})}$ and ${G}_n = (1-2W_{RS}^{(M)}+W_{SS}^{(M)})p_n+W_{RS}^{(M)}-W_{SS}^{(M)}$. $[a]$ denotes the greatest integer no larger than $a$.

Next, we investigate the effects of death rate of pesticide for homozygote susceptibles ($d_1$) and the spraying times ($M$) on the frequence of resistance ($p_n$). Because of the highly nonlinearity of Eq (2.10), we only focus on the effects in case 1 and case 2 theoretically, and for case 3, we just carry out some numerical simulations.

For case 1, i.e.. $R$ is completely dominant gene in $RS$, differentiating Eq (2.8) with respect to $d_1$ and $M$ respectively, we have

For case 2, i.e.. $R$ is completely recessive gene in $RS$, differentiating Eq $(2.9)$ with respect to $d_1$ and $M$ respectively, we have

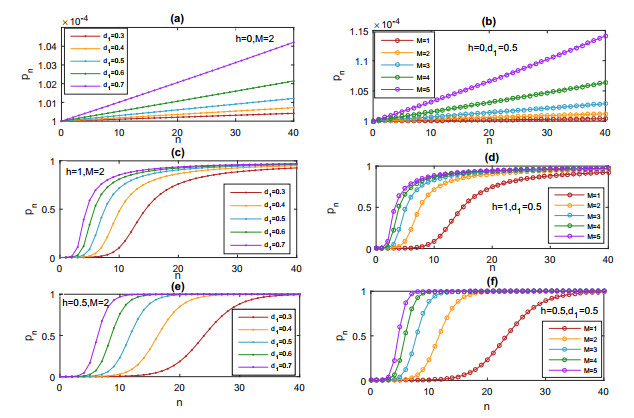
From the above formulas, we can see that $p_n$ is an increasing function with respect to $d_1$ and $M$ in both case 1 and case 2. That is, decreasing the death rate of susceptible pests or decreasing the spraying times of pesticide in each generation can decrease the values $p_n$. In order to show in more detail how the level of dominance of pesticide resistance allele $h$, the mortality rate $d_1$ and $M$ affect evolution of pesticide resistance, we analyze those by numerically simulation in Figure 1. From Figure 1 (a) and (c), we can see that the higher the efficiency of the pesticides (i.e. the higher mortality rate), the faster the resistance development is. From Figure 1 (b) and (d), we can see that the more times of the pesticide spraying in one generation, the faster the resistance development is.

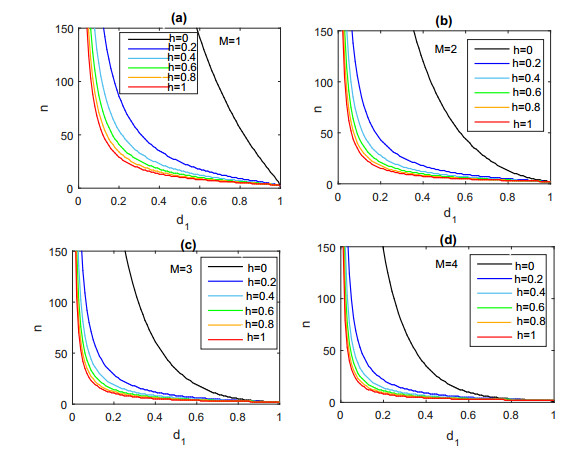
If we fix the frequence of resistance, then we want to know how the death rate ($d_1$), spraying times ($M$) and the level of dominance of pesticide resistance ($h$) on generation ($n$) which reach to fixed resistance level. For this purpose, we carry out the sensitivity analysis of $n$ in Figure 2. In Figure 2, we fix $p_n = 50\%$, and we can see that the higher the efficiency of the pesticides is (i.e., the higher mortality rate), the faster of the pest population reaches the fixed resistance level; The more times of the pesticide sprayed in one generation, the faster of the pest population reaches the fixed resistance level; The higher the level of dominance of pesticide resistance, the faster of the pest population reaches the fixed resistance level.

2.3.   Pest growth model with pesticide resistance 

Throughout this study, the pest population is assumed to grow logistically within each generation $[n, n+1]$,

where $x(t)$ is the density of the pest population at time $t$, $r$ denotes the intrinsic growth rate and $K$ represents the carrying capacity.

In reality, people usually spray pesticide within a fairly short period, so it's reasonable to assume that the density of pests can be reduced instantaneously once the chemical control tactics are applied. Therefore, the impulsive hybrid model based on Eq $(2.11)$ can be employed to depict this control measure.

If the pesticides is applied at time $n+\tau_m$ ($0\leq \tau_m \leq1$) with an instantaneous killing rate $D_{n, m}$, then we have

From the former section, we have

with

and

It is clear that the instantaneous killing rate $D_{n, m}$ decreases as pesticide resistance develops.

3.   Switching strategy for spraying once pesticide within each generation 

In this section, we assume that once control is implemented within each pest generation. We then investigate how to switch pesticides and manage the development of genetic resistance such that the pest population can be eventually eliminated or maintained at a density below EIL. In order to investigate those questions, we propose two different switching strategies, and investigate the optimal switching times under once control within each generation.

3.1.   Switching pesticide with threshold condition of pest eradication as a guide 

We assume that pesticide was used once within each generation at time $n+\tau_1$ ($0\leq\tau_1\leq1$) in $n$th generation. The model Eq $(2.12)$ becomes

where $D_{n} = D_{n, 1}$. Solving Eq $(3.1)$ within $[n, n+1]$, we have

Thus, we have

and

Denote $x(n) = x_n$, then we have the following iteration equation from $n$th generation to $n+1$th generation

which is a non-autonomous Beverton-Holt difference equation, i.e. the so-called extended Beverton-Holt model. For more details of extended Beverton-Holt model, please see the references ^{[32,33,34,35,36,37]}.

According to the properties of the extended Beverton-Holt model, we have that if $e^r(1-D_{n}) < 1$, then the zero solution of Eq $(3.3)$ is globally asymptotically stable. Consequently, we can define the threshold value $R_n$ as

where $D_{n}$ can be calculated by Eq $(2.13)$. Thus, the pest population will be eradicated if $R_n < 1$ for all $n = 0, 1, 2, \cdots$.

Note that $R_n$ is dynamic and depends on $D_{n}$. We can see that $D_{n}$ is a monotonic decreasing function of $n$. Therefore, as the pest generations increases, the threshold value $R_n$ increases and exceeds one, resulting in pest resurgence and outbreaks.

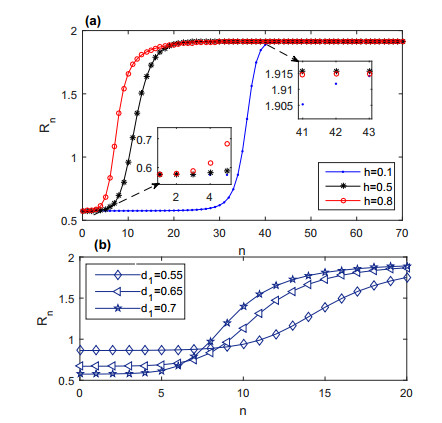
In Figure 3, we simulate the threshold $R_n$ with different level of dominance of pesticide resistance allele in $RS$ ($h$) and the mortality rate ($d_1$), which reveal that $R_n$ is an increasing function with respect to $n$, and will exceed 1 after several pesticide pesticide applications. From Figure 3 (a), we can see that the greater of $h$ is, the faster growth of $R_n$ is. This is because that the higher of the level of dominance of pesticide resistance allele in $RS$ is, the faster development of the pests' resistance is. All those confirm that the pest population will be resurgence and outbreaks as the pesticide resistance evolution. From Figure 3 (b), it is obvious that the effects of mortality rates $d_1$ on $R_n$ are more complicated with the development of time $n$. The bigger $d_1$ is, the smaller $R_n$ is, when $n$ is small. And with the increase of n, the effects of mortality rates $d_1$ on $R_n$ is changed, the bigger $d_1$ is, the smaller $R_n$ is. This is due to that in the early stages of the pest control, the more dosage of pesticide is sprayed, the higher of the mortality rate is, and the pest population is more easy to control with the high efficiency of pesticide. With the increasing of $n$, the pest control times is increasing, and the pest's resistance is developed, which the results is the decline in efficiency of pesticide, and the pests' outbreak.

In order to prevent pest population outbreaks and restrain the development of pesticide resistance, farmers usually switch some different type pesticide. And what is the optimal switching time with the aim of eradication of pest population. For this aim, we only need the threshold $R_n$ below one for all $n = 0, 1, 2, \cdots$. Therefore, farmers need to switch the pesticide before the threshold value $R_n$ goes to one. Without loss of generality, we assume that the threshold value $R_n$ will increase and exceed the unit after $n_1$th generation i.e

and the optimal switching time is $n_1$, or the maximum number of one type of pesticide spraying is $n_1+1$ (note that the first pesticide application is at time $n = 0$). That is, after $n_1+1$ times pesticide spraying, farmers should switching another type of pesticide.

In order to determine $n_1$ analytically, we let $R_n = 1$, then

From Eq $(2.13)$, we can get

That is

In order to solve Eq (3.6), we define the function $f(x)$ as follows

where

and

The Eq (3.6) becomes to $f(p_n) = 0$. Now we solve this equation with respect to $p_{n}$, and substituting $p_{n} = p_{n_1}$ into Eq $(2.5)$ or Eqs $(3.10)$–$(2.10)$, we can obtain the optimal switching time $n_1$ under different cases.

The $p_{n_1}$ can be defined as follows:

The detailed calculation of the $p_{n_1}$ is provided in Appendix A.

Now we turn our attention to the effect of the timing of pesticide applications $\tau_1$ on the density of pest population $x_n$. From Eq $(3.3)$ we have the following iteration equation

where

and

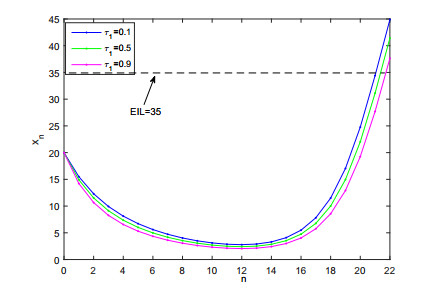
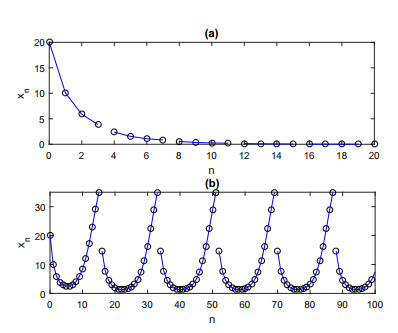
It's easy to see that $x_n$ is a decreasing function with respect to $\tau_1$, this means that the later of pest control is, the smaller of pest population density is, and more benefit to pest control. In Figure 4, we simulate the development of $x_n$ with respect to $n$ under different $\tau_1$. From Figure 4, we can see that the later insecticide spraying time is, the smaller the population density is, and we also see that the density of pest population $x_n$ is decreasing at the beginning of pest control, and then the density of pest population $x_n$ is increasing after some pesticide applications. The reason is that with the increasing of number of pesticide sprayings, the pesticide resistance is developed, and consequently, the density of pest population can not decrease any more, instead, it increases rapidly, even exceeds the EIL.

3.2.   Switching pesticide with EIL as a guide 

As mentioned in the introduction, the pre-set goal of the pest management is to control the density of the pest below the EIL. However, the pest population will exceed the EIL eventually if only one type of pesticide is used (i.e. do not switch pesticides), see Figure 4. Thus, in order to successfully control the density of pest population below the EIL, farmers should switch another kind of pesticide before the density of pest population reach to EIL. In this subsection, we will investigate the optimal switching time with EIL as switching guide.

In there, we assume that the pest population density exceeds EIL for the first time in the $n_2+1$th generation.This indicates that $x_{n_2}\leq EIL$ and $x_{n_2+1} > EIL$, that is the optimal switching generation is $n_2+1$.

From Eq $(3.3)$, we have

and we can get

It follows from $x_{n_2}\leq EIL$ that

then

where $E_1 = \frac{(e^r-1)(K-EIL)}{e^r(K-EIL)+EIL e^{r\tau_1}}$. It is easy to see that $E_1$ is decreasing as $\tau_1\rightarrow1$. This implies that $n_2$ is increasing as $\tau_1\rightarrow1$, in other words, under the EIL guided switching strategy, the number of the same pesticide used increases with the increasing of $\tau_1$.

Substituting Eq $(3.8)$ into Eq $(3.10)$, we have

thus

where $Z_{n_2} = (K-EIL)N_{n_2+1}-EIL\sum_{i = 1}^{n_2}\left(e^{r(i+\tau_1)}D_i\prod_{j = 0}^{i-1}(1-D_j)\right)$.

Therefore,

In order to understand these two different switching strategies more intuitively, we draw some numerical simulations in the Figure 5. From Figure 5 (a) we can see that under the $R_n$ guided switching strategy the pest population will be eradicated completely after several pesticide switches, where $n_1 = 3$. That is after four pesticide applications of one kind of pesticide (note that the first pesticide application is at time $n = 0$), the farmers must switch to another kind of pesticide to eradicate the pest quickly. From Figure 5 (b) we can see that under the EIL guided switching strategy pest control will tends to periodic control after a certain number of pesticide switches. This is due to the development of resistance of pest on the same type pesticide, the density of pest population will exceed EIL after some numbers of the same type pesticide spraying, under the EIL guided switching strategy pest control, farmers should switching another type of pesticide at the last number of pesticide spraying before the density of pest population reach to EIL (we assume that the pest population has the same development of pesticide resistance on different type of pesticide), due to the same process of pesticide resistant evolution and pest control period, the pest control will tends to periodic control under this switching strategy.

4.   Multiple control actions applied within each generation 

In reality, the pesticide is sprayed for multiple times in each generation to control pest. Therefore, in this section, we developed an extended discrete single population model with multiple impulsive chemical control within each generation, and then investigate the optimal generation for switching pesticides.

4.1.   Switching pesticide with threshold condition as a guide 

We assume that the pesticides are applied $M$ times within each generation, that is to see, there exist $\tau_m (m = 1, 2\cdots, M)$ with $n\leq n+\tau_1\leq n+\tau_2\leq\cdots\leq n+\tau_M\leq n+1$, such that the pesticides have been applied at $n+\tau_m$ with a proportion $D_{n, m}$ of the pest being killed. We have

For convenience, we denote $D_{n, 0} = 0$. Therefore, by employing the same methods proposed before, we have the following extended discrete single population model with multiple impulsive chemical control within each generation

In particular, if $M = 1$ then we have $\sum_{m = 1}^{M}(e^{r\tau_m}D_{n, m}\prod_{j = 1}^{m}(1-D_{n, j-1})) = e^{r\tau_1}D_{n}$.

For simplicity, we assume that the pesticides are sprayed periodically within each generation, which satisfies $\tau_{m+1}-\tau_{m} = T$ for m = 1, 2..., M and $0 < T\leq\frac{1-\tau_1}{M-1}$, thus we can get

with $\lambda_n = e^r\prod_{m = 1}^{M}(1-D_{n, m})$ and $\mu_n = \sum_{m = 1}^{M}(e^{r(\tau_1+(m-1)T)}D_{n, m}\prod_{i = 1}^{m}(1-D_{n, i-1}))$. Note that this is the extended Beverton-Holt model, and if $e^r\prod_{m = 1}^{M}(1-D_{n, m}) < 1$, the population size is gradually reduced and becomes extinct eventually. We can define the dynamic threshold value $R_n^M$ as follows:

that is, if $R_n^M < 1$, the population size is gradually reduced and becomes extinct eventually.

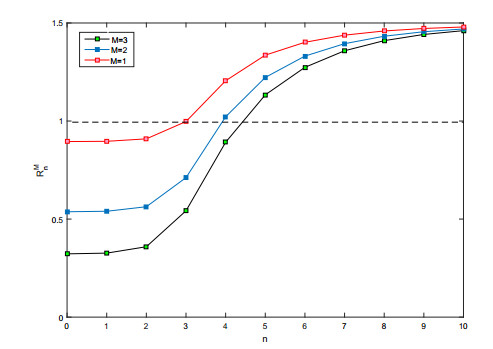
In order to analyse the effects of the spraying times $M$ of pesticides in each generation on the threshold value $R_n^M$, we simulate the threshold value $R_n^M$ with different spraying times $M$ in Figure 6. From Figure 6, we can see that $R_n^M$ is a decreasing function with respect to $M$, that is, the more spraying times in each generation is, the later of the density of pest population reaching to $R_n^M$ is.

From Figure 6, we can also see that the density of pest population will reach to the threshold after several times of spraying pesticide, due to the development of pesticide resistance. Therefore, in order to eradicate pest population, the alternative choice is to switch another pesticide after the using of one pesticide for several times. In the following, we will discuss the optimal switching time.

Note that, in order to eradicate the pests population, the threshold value $R_n^M$ should below one for all $n = 0, 1, 2, \cdots$. Therefore, it's necessary to switch the pesticides before the threshold value $R_n^M$ reach to one. Here, we assume that the threshold value reach or exceed to 1 firstly after pest control in $n_3$th generation, i.e..

and the optimal generation for switching pesticides is $n_3$. In order to determine $n_3$ analytically, we let $R_n^M = 1$, that is

or

From Eq $(2.13)$, we have

submitting the former Eq (4.4), we get

Letting

with

where $\mathbb{C}_{M+1}^i = \frac{(M+1)!}{i!(M+1-i)!}$ is combinatorial number, and

Then Eq $(4.5)$ becomes $g(p_n) = 0$. Solving $g(p_n) = 0$ with respect to $p_n$ we can obtain $p_{n_3}$, with

The detailed calculation of the $p_{n_3}$ is provided in Appendix B. We substitute $p_{n_3}$ into Eq $(2.5)$ or Eqs $(3.10)$–$(2.10)$, and we can obtain the optimal switching time $n_3$ under different cases.

In the following, we address how the $x_{n}$ varies as the parameters $\tau_1$ and $T$ change, which are quite important for pesticide applications. Firstly, by induction, we can get the recursion formula for $x_{n}$ of Eq $(4.3)$ as follows:

where

with

From Eq $(4.7)$ we can see that $x_n$ is a decreasing function with respect to $\tau_1$ and $T$, which means that the longer of period or the later of pesticide spraying is, the more benefit to pest control.

4.2.   Switching pesticide with EIL as a guide 

In this subsection, we focus on the control tactics of $EIL$. That is farmers should control pest when the density of pest population reach to $EIL$. As the former states, because of the resistance of pesticide, spraying one type of pesticide could not maintain the density of pest population below the $EIL$. Thus after some times of one type of pesticide spraying, farmers should switch another type of pesticides.

We assume that after the $n_4$th generation, farmers should switch another type of pesticide, which means that $x_{n_4}\leq EIL$ and $x_{n_4+1} > EIL$, that is, the optimal switching generation is $n_4+1$. In order to find the $n_4$, we let $x_{n_4+1} > EIL$. From Eq $(4.3)$, we have

then we can get

Due to $x_{n_4}\leq EIL$, from Eq (4.9), we can get

From Eq $(2.13)$, we can get

and $\mu_{n_4}$ can be calculated as follows

with

thus Eq $(4.10)$ can be rewritten as follows

where

This indicates that $p_{n_4}$ should be satisfied

where $\widehat{A}_{h, d_1}^M = H_1-(K- EIL)a_1^{(1)}$, $\widehat{B}_{h, d_1}^M = H_2-(K- EIL)b_1^{(1)}$ and $\widehat{C}_{d_1}^M = (K- EIL)c_1^{(1)}-H_3.$

Substituting Eq $(4.7)$ into Eq $(4.9)$ gives

with $Y_{n_4} = (K-EIL)N_{n_4+1}^M-EIL\delta_{n_4+1}$. Thus, we have

5.   Conclusions 

There are many factors to cause the resistance of pest to pesticide. The main factors are the external factor (i.e. the high frequency and large doses spraying of pesticides) and the genetic factors. Consider the above two factors, we set up the evolution equations of pesticide resistance under one times spraying pesticide in one generation or multiple spraying pesticide in one generation, and introduce the equation into pest control models.

Due to the development of pesticide resistance, the long-term use of the same kind of pesticides to control pests, farmers cannot reach the aim of pest control, however, the pest population should be outbreak again. In order to control pest population, farmers usually need to switch pesticides in some kind of pesticides. In this work, we study the threshold condition to eradicate pest population under one times spraying pesticide in one generation, analyze the relationship of the threshold condition and evolution of pesticide resistance. Moreover, we get the maximum number of one type of pesticide sprayings, and optimal switching time of pesticide. In the aim of controlling pest population below the EIL, we also analyze the optimal switching time of pesticide under the case of one times spraying pesticide in one generation. Farmers usually control pest population many times in one generation, under this case, we research the optimal switching time of pesticide with the aim of eradicating pest population and controlling pest population below the EIL, respectively.

6.   Discussions 

In this study, by assuming that the pest resistance to pesticide is determined by a single gene with two alleles $R$ and $S$ and according to the genetic laws, we developed a novel model for pest resistance to pesticide with external induced resistance and genetic resistance describing the dynamics of the development of the pesticide resistance. With this model, we investigated the impact of the death rate of susceptible pests and the spraying times of pesticide in each generation on the frequency of the resistance allele. We showed that when $R$ is completely recessive gene or completely dominant gene, decreasing the death rate of susceptible pests and the spraying times of pesticide in each generation can help to decrease the frequency of the resistance allele.

In practice, pest control, including spraying pesticide and releasing the natural enemies are usually implemented impulsively. Therefore, many mathematical models with impulsive chemical control by spraying the pesticide and natural enemies have been proposed and deeply studied ^{[38,39,40,41,42,43,44,45]}. In theses studies, they usually assumed that the chemical and biological control were implemented at the beginning at the end of one generation. However, pests usually have non-overlapping generations, which indicates that control methods should be taken within each generation. In this study, we incorporate the impulsive control within each generation into a discrete population model. Through the analytical methods, we then drived a novel model based on the continuous Logistic model with both single pesticide applications and the evolution of pest resistance to pesticide. Based on these models, we investigated the effects of the timing of pesticide application on the density of pest population by calculating iteration equation. Our theoretical analyses reveal that the later the pesticide was spraying, the smaller the density of the pests is. Further, we extended a discrete pest population growth model by including both the multiple instantaneous pesticide applications within each generation and the evolution of pest resistance to pesticide. Finally, we provided a threshold condition for pest eradication, and based on the threshold condition we discussed the optimal generation when different types of pesticides were used with a switching regime. With the aim of controlling the density of the pest population below EIL, we provided a switching strategy guided by EIL, where the optimal generation for switching another pesticides was investigated.

Note that, biological control by releasing the natural enemies, as an important component of the IPM, helps to decrease the pest and slow down the development of the pesticide resistance. It remains challenging how to combine the biological to chemical control aiming at fighting against the development of pesticide resistance, and what the optimal releasing rate of the natural enemies should be. This was left for our future works.

Acknowledgments 

This work was supported by the National Natural Science Foundation of China (NSFCs 11871319, 11631012).

Appendix A.   calculating the $p_{n_1}$ 

Note that,

due to $a_1^{(1)}+b_1^{(1)}+c_1^{(1)} = 1$ and $a^{(1)}+b^{(1)}+c^{(1)} = 0$.

In order to solve equation $f(p_n) = 0$, we analyze the equation $f(x) = 0$ from the following cases:

Case ($A_1$): ${C}_{d_1} > 0$ (i.e. $0 < d_1 < 1-e^{-r}$).

In this case, we can easy to see that $f(0) > 0$.

If $A_{h, d_1} > 0$, then $f(x) > 0$ for all $0\leq x\leq1$.

If $A_{h, d_1}\leq0$, we can easily see that ${B}_{h, d_1} > 0$ (due to ${C}_{d_1} > 0$), then $f(x) > 0$ for all $0\leq x\leq1$.

thus, $f(p_n) > 0$ ($0 < p_n \leq 1$).

Case ($A_2$): ${C}_{d_1} < 0$ and ${A}_{h, d_1}\neq0$.

For this case, $f(0) = {C}_{d_1} < 0$ (i.e $1-e^{-r} < d_1 < 1$), the equation $f(p_n) = 0$ has solution $p_{n_1} = \frac{-{B}_{h, d_1}+\sqrt{{B}_{h, d_1}^2-4{A}_{h, d_1}{C}_{d_1}}}{2{A}_{h, d_1}}$

Case ($A_3$): ${C}_{d_1} < 0$ and ${A}_{h, d_1} = 0$.

For this case, the equation $f(x) = 0$ turns to $f(x) = {B}_{h, d_1} x+{C}_{d_1} = 0$. Due to $f(1) > 0$ and $f(0) < 0$, then the equation $f(p_n) = 0$ has solution $p_{n_1} = \frac{-{C}_{d_1}}{{B}_{h, d_1}}$.

Case ($A_4$): ${C}_{d_1} = 0$ (i.e. $d_1 = 1$ or $d_1 = 1-e^{-r}$).

If $d_1 = 1$, then

If $h\geq e^{-r}$, then $B_{h, d_1}\geq0$, we can easy to see that $f(p_n) > 0$ for all $0 < p_n\leq 1$; If $h < e^{-r}$, then $B_{h, d_1} < 0$ and $A_{h, d_1} > 0$, then then the equation $f(p_n) = 0$ has solution $p_{n_1} = \frac{-{B}_{h, d_1}}{{A}_{h, d_1}}$.

If $d_1 = 1-e^{-r}$, then

for this case, we can easy to see that $f(p_n) > 0$ for all $0 < p_n\leq 1$.

Appendix B.   calculating the $p_{n_3}$ 

Note that,

due to $a_1^{(M+1)}+b_1^{(M+1)}+c_1^{(M+)} = a_1^{(1)}+b_1^{(1)}+c_1^{(1)} = 1.$

Using the same methods as in the proof of Appendix A, we analyze the equation $g(x) = 0$ from the following cases:

Case ($B_1$): ${C}^M_{d_1} > 0$ (i.e. $0 < d_1 < 1-e^{\frac{-r}{M}}$).

In this case, we can easy to see that ${B}^M_{h, d_1} > 0$ due to $(M+1)(1-d_1)^M-e^{-r} > 0$ for all $0 < d_1 < 1-e^{\frac{-r}{M}}$ and $\sum_{i = 2}^{M+1}\left(2(hd_1)^i\mathbb{C}_{M+1}^i(1-d_1)^{M+1-i}\right) > 0$. Thus, $g(x) > 0$ ($0\leq x \leq 1$) for all $0 < d_1 < 1-e^{\frac{-r}{M}}$.

Case ($B_2$): ${C}^M_{d_1} < 0$ and ${A}^M_{h, d_1}\neq0$.

For this case, $g(0) = {C}^M_{d_1} < 0$ (i.e $1-e^{\frac{-r}{M}} < d_1 < 1$), the equation $g(x) = 0$ has solution $p_{n_3} = \frac{-{B}^M_{h, d_1}+\sqrt{{{B}^M_{h, d_1}}^2-4{A}^M_{h, d_1}{C}^M_{d_1}}}{2{A}^M_{h, d_1}}.$

Case ($B_3$): ${C}^M_{d_1} < 0$ and ${A}^M_{h, d_1} = 0$.

For this case, the equation $g(x) = 0$ turns to $g(x) = {B}^M_{h, d_1} x+{C}^M_{d_1} = 0$. Due to $g(1) > 0$ and $g(0) < 0$, then the equation $g(p_n) = 0$ has solution $p_{n_3} = \frac{-{C}^M_{d_1}}{{B}^M_{h, d_1}}$.

Case ($B_4$): ${C}^M_{d_1} = 0$ (i.e. $d_1 = 1$ or $d_1 = 1-e^{\frac{-r}{M}}$).

In this case, if $d_1 = 1$, then ${A}^M_{h, 1} = -2h^{M+1}+2he^{-r}+1-e^{-r}$ and ${B}^M_{h, 1} = 2h(h^M-e^{-r})$. It is easy to know that ${A}^M_{h, 1}+{B}^M_{h, 1} > 0$. If $h\geq e^{\frac{-r}{M}}$, then ${B}^M_{h, 1}\geq0$, we can easily know that $g(x) > 0$; If $h < e^{\frac{-r}{M}}$, then ${B}^M_{h, 1} < 0$ and ${A}^M_{h, 1} > 0$, thus, we have $g(p_{n_3}) = 0$ with $p_{n_3} = \frac{-{B}^M_{h, d_1}}{{A}^M_{h, d_1}}$.

If $d_1 = 1-e^{\frac{-r}{M}}$, then

for this case, we can easy to see that $g(p_n) > 0$ for all $0 < p_n\leq 1$.