1. Introduction
Most of the recent advances in nanoscience and nanotechnology are based on the relevant achievements reached in the synthesis of materials with desirable dimensions, morphology and composition, as well as in their subsequent use as building blocks in many fields of technological research. In this way, a precise control of the synthesis process is required in order to exploit the capabilities of low dimensional materials, for which many synthesis approaches have been followed so far. Among the most challenging and promising morphologies, tubular micro- and nanostructures are attracting increasing attention due to their characteristic geometry which confers them improved performances. In particular, apart from the widely investigated carbon nanotubes [1], some other tubular micro and nanostructures of different materials are facing challenging performance in energy storage, environmental applications, sensing and optoelectronics [2,3,4]. Despite the growing interest on the applicability of tubular structures, their fabrication is not an easy task and several synthesis methods are being employed, as for instance electrospinning, hydrothermal, or template-based methods [5,6,7], being the latter the most commonly used. However, the tubes synthesized by these procedures are usually polycrystalline and mesoporous, instead of highly crystalline materials. In order to optimize the fabrication of these characteristic hollow structures, their growth mechanisms in different materials still require to be further understood and controlled.
In this work we report on the synthesis of micro and nanotubes of different transparent conductive oxides (TCO), such as SnO2, TiO2, ZnO and In2O3, by a vapor-solid (VS) method which avoids the use of catalyst or templates [8,9,10]. Some other growth methods, such as vapor-liquid-solid (VLS) [11], or solid-liquid-solid (SLS) [12] require the use of a catalyst, usually Au, in form of drops or a thin film, which governs the anisotropic growth of elongated nanostructuresachieving ordered arrays of the nanostructures on a substrate. However, the presence of the catalyst in the as-grown structures is hardly avoided, and usually nanowires decorated with Au or with Au at the tip are obtained by these methods, which could be detrimental for some applications. Besides, usually wires, but not tubes, are grown by VLS and SLS methods. The VS method avoids the use of catalysts and leads to the growth of structures with a wide variety of morphologies, including tubes, which confers higher versatility to this method. On the other hand, contrary to the VLS method, a wide dispersion of sizes is usually obtained by the VS method as the control of the dimensions of the as grown micro- and nanostructures is not easy in this case. The VS method employed in this work results in large concentrations of high crystalline quality materials in form of tubes and also in other forms such as wires, arrows, rods, or complex structures. In particular, the tubes are good candidates to be used in optoelectronics, as well as in sensors and bio-chemical molecular detection and environmental applications, as recently reported by different authors [13,14,15]. As an example, the optical response of ZnO microtubes can be modulated when filled with a fluid [16]. Moreover, Sn filled ZnO nanorods have been recently proposed to be used as thermal nanosensors, soldering and electrical nanocomponents [17], whereas ZnO microtubes have shown good properties as optical resonators [18].
In this work also the doping of the tubes with different elements of technological interest, such as Cr, Er, or Li in the case of SnO2 microtubes, Cr for TiO2, and Zn or Sn for the In2O3 samples, has been investigated. Energy Dispersive X-ray spectroscopy (EDS) has been used to study and quantify the presence of dopants in the samples. The effects caused by doping on the optical properties of the tubes are analyzed by cathodoluminescence (CL). Mechanisms involved in the formation of the tubes, such as screw-dislocation driven growth, are also discussed.
2. Materials and Method
The synthesis method employed by our group for the growth of the tubes is based in a catalysis-free vapor-solid process [8]. The precursor powder is pressed into pellets and placed in a furnace. Afterwards, thermal treatments are carried out under a controlled argon flow at different temperatures (600-1400 ºC) as a function of the precursor. For the growth of the doped tubes, the initial powder is mixed with a dopant-based material in a controlled weight ratio. In this work, undoped SnO2 microtubes have been grown using SnO2 powder as precursor, while Cr, Er or Li doped SnO2 microtubes have been fabricated by using an initial mixture of SnO2 and Cr2O3 (5% wt.), Er2O3 (5% wt.) or Li2CO3 (5% wt.), respectively. Cr doped rutile TiO2 microtubes have been fabricated using either TiN mixed with Cr2O3 (10% wt.) or Cr doped TiO2 nanoparticles (Cr 10% cat.) as precursors. ZnO tubes have been grown using metallic Zn as initial powder. In the case of In2O3, rods with nanopipes in the core were synthesized using either InN or In2S3 as precursors. Sn or Zn doped In2O3 rods and microstructures showing pipes have been fabricated by adding SnO2 (10% wt.) or ZnO (5% wt.), respectively to the initial powders.
The micro and nanotubes were characterized by using different techniques. X-ray Diffraction (XRD) measurements were performed in a Philips X'Pert Pro diffractometer using Cu Ka radiation. In the study of the morphology, a Leica 440 Steroscan and a Fei Inspect Scanning Electron Microscopes (SEM) were used. Transmission Electron Microscopy (TEM) characterization was carried out using a Philips CM30 TEM operated at 300 kV. Cathodoluminescence (CL) spectra were acquired in a Hitachi S2500 SEM using a Hamamatsu PMA-11 charge-coupled device camera. A Bruker AXS Quantax system was used for the Energy Dispersive X-Ray Spectroscopy (EDS) measurements and a Bruker e-FlashHR+ electron backscattered diffraction (EBSD) system was employed for the structural analysis of the microtubes.
3. Results and Discussion
3.1. Rutile microtubes (SnO2, TiO2)
Figure 1a shows a SEM image where a high amount of SnO2 microtubes, grown by thermal treatments at 1400 ºC during 10 hours, can be observed. These tubes have been grown on the surface of the pellet, which in this case acts as source of material and substrate, and they show lengths up to hundreds of microns and widths between a few and tens of microns. These tubes, with widths ranging from hundreds of nm to few microns, show square or rectangular sections [8]. The microtubes can be easily detached from the surface of the pellet and manipulated in order to complete their study and to be used as building blocks in optoelectronic devices. XRD and EBSD measurements, not shown here, show that the lateral faces of the tubes correspond to the {110} planes of rutile SnO2 and that the tubes grow along the [001] direction, as schemed in the inset of Figure 1a. By modifying the composition of the initial powders, doped SnO2 tubes can be also achieved. As an example, Cr doped SnO2 microtubes are fabricated at 1400 ºC by mixing SnO2 and Cr2O3 (5% wt.) in the precursor powder. The dimensions of the tubes are similar to the undoped ones, but in this case the lateral faces are smoother and thinner, and occasionally tubes with peaked endings are observed, as shown in Figure 1b. These tubes exhibit new optical properties as compared with the undoped ones. In particular, the Cr doped SnO2 tubes are purplish, as observed in the optical image in the inset of Figure 1b, while the undoped SnO2 microtubes are transparent in the visible range. If Er2O3 (5%wt.) is added to the initial mixture, Er doped SnO2 microtubes can be grown at 1400 ºC [19], as shown in Figure 1c. In this case the surfaces of the tubes are more irregular, as shown in the inset of Figure 1c, and appear usually with cracks. In addition, the resistivity of these tubes increases due to the Er doping, as denoted by charge effects during SEM observation. Also Li doped SnO2 microtubes have been fabricated at 1400 ºC by adding Li2CO3 (5% wt.) in the initial powders, as shown in Figure 1d. In that case, the tubes show a smoother appearance and higher dimensions, as compared with undoped ones. However, in some cases, the Li doped tubes exhibit a high irregular ending formed by complicated microstructures, as observed in the inset of Figure 1d. The doped tubes also grow along the [001] direction and are formed by {110} surfaces, as demonstrated by XRD and EBSD measurements (not shown here). These surfaces are reported to be the more stable for rutile materials such as SnO2 and TiO2 [20,21]. Beltran et al. [22] calculated the stability conditions and energetic cost of the different SnO2 stoichiometric surfaces. Their calculations indicate that the (110) surface is the most stable which is in agreement with the results obtained by EBSD of the rutile tubes. The (001) and (201) planes have a relative higher surface energy, which may lead to a growth along these directions in agreement with the [001] assignment for the growth direction of the rutile tubes, based on Raman polarized measurements.
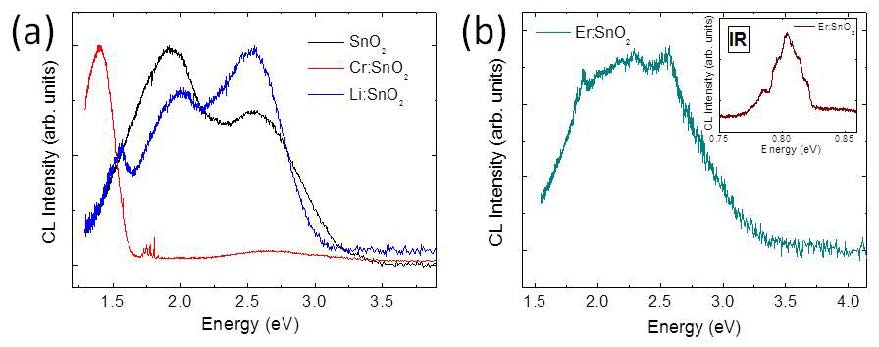
In order to investigate the effects of the dopants on the optical properties of the SnO2 tubes, CL of the undoped and doped tubes has been investigated. Figure 2 shows the CL spectra of the undoped and the Cr and Li doped SnO2 microtubes. The presence of dopants clearly modifies the luminescence of the tubes, as observed in the CL spectra shown in Figure 2, acquired at 18 kV and room temperature.
The wide bandgap of SnO2 (3.6 eV) provides luminescence in a wide spectral range. In particular, CL emission from undoped SnO2 mainly consists of three emissions centered around 1.94 eV, 2.25 eV and 2.58 eV, known as orange, green and blue bands respectively [23]. The orange band is associated with oxygen vacancies related defects and, although the origin of the green band is still under discussion, most works also associate this emission with oxygen deficiency [8,24,25]. The blue band is usually related to transitions involving surface defects. The presence of dopants alters the concentration of these defects, which modifies the CL signal. Moreover, new emissions associated with the dopants can be also generated. Cr doping drastically alters the luminescence of SnO2 (Figure 2a). The characteristic visible emission of SnO2 is quenched due to the Cr doping and a new emission around 1.4 eV dominates the corresponding CL spectrum, as shown in Figure 2a. Narrow emission lines can be also observed at 1.8 eV which are related to Cr3+ intraionic transitions [26]. Doping with Li also modifies the luminescence of SnO2, but in this case the CL spectrum is more similar to the undoped SnO2. Apart from the orange, green and blue bands, the relative intensities of which change with respect to undoped SnO2, a new emission appears at around 1.6 eV, which is associated with the Li doping. When doping with Er, in addition to the characteristic emissions of SnO2, narrow weak emissions appear at 1.87 eV and 2.23 eV. These emissions are associated with Er3+ 4f intraionic transitions [19], in particular to 4F9/2 -4I15/2 (1.87 eV) and 4S3/2-4I5/2 (2.23 eV). Moreover, an infrared emission at 0.8 eV appears (Figure 2b), related to 4I3/2-4I15/2 Er3+ intraionic transitions due to Er3+ substituting Sn4+ in the SnO2 lattice [19]. Some of these emissions allow to extend the applicability of SnO2 in optoelectronic devices. As an example the 0.8 eV emission related to Er doping lies at the region of minimum losses for silica-based waveguides, mainly used in optical communications. The vapor solid method used for the growth of the tubes allows homogeneous doping and low doping content ranging from 0.5-3 at.%, as measured by EDS.
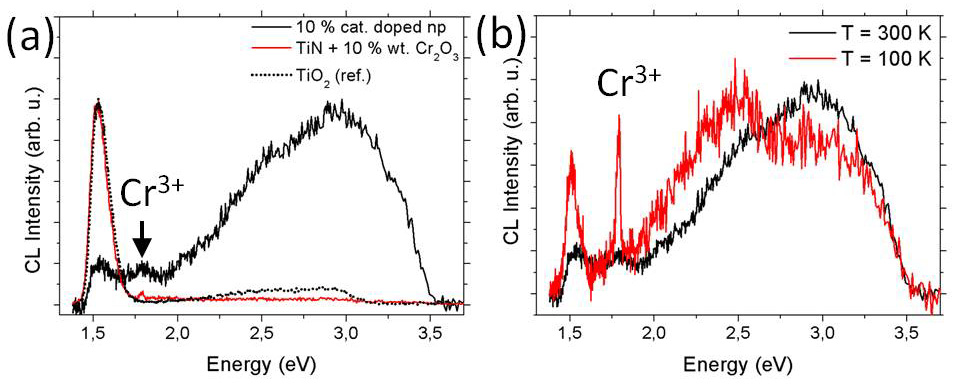
Cr doped TiO2 microtubes have been also fabricated by the vapor-solid method at 1250-1300 ºC either using Cr doped TiO2 nanoparticles, or TiN mixed with Cr2O3 as initial powders (5-10% cat. Cr) [9]. The tubes show rectangular or squared sections, as the SnO2 tubes, but in this case the dimensions are lower, of about 5 µm lateral size and tens of micrometers length, as shown in Figures 3a and 3b, corresponding to SEM images of Cr doped microtubes grown from Ti0.9Cr0.1O2
nanoparticles and TiN mixed with 10% wt. Cr2O3, respectively. The maximum Cr content observed in the microtubes by EDS analysis is 3% cationic fraction. The Cr is homogeneously distributed along the microtubes, as observed in the EDS elemental mapping for Ti and Cr shown in Figure 3c. The Chromium concentration can be controlled by the amount of Cr in the precursor powders, as well as by the temperature and duration of the thermal treatments. Combined Raman-EBSD measurements [9] show that the rutile TiO2 tubes grow along the [001] direction and the lateral faces are formed by {110} surfaces independently of the precursor, in agreement with the results on SnO2 microtubes. The morphological and crystallographic similarities observed between SnO2 and TiO2 microtubes could be due to similar growth mechanisms, since both materials shares the rutile crystalline structure. However, contrary to SnO2, for which undoped microtubes can be also grown, in the case of rutile TiO2 the presence of Cr clearly benefits the growth of microtubes which rarely appears for undoped TiO2. The CL study reveals changes in the luminescent response of the tubes as a function of the final morphology and the employed precursor. Figure 4a shows the normalized CL spectra acquired at room temperature (300 K) from microtubes grown using Cr doped TiO2 nanoparticles (10% cat.) and TiN mixed with 10% wt. Cr2O3. CL spectrum of undoped TiO2 has been also included as a reference. The characteristic CL spectrum of undoped rutile TiO2 is dominated by a relatively intense IR band located at 1.52 eV, which is frequently attributed to radiative recombinations related to reduced Ti3+ ions induced by oxygen deficiency at the TiO2 surface [9,27], and a broad and weaker band extended from the visible (VIS) to UV region centered at approximately 2.5 eV, attributed to shallow traps related to oxygen vacancies and other oxygen related defects as F-centers or adsorbed oxygen [9]. For the microtubes grown from the mixture of TiN and Cr2O3 powders the IR band is slightly red-shifted but still dominates the CL spectrum, whereas the VIS-UV region shows a decreased relative intensity. In addition, a small narrow band appear at 1.8 eV (marked with an arrow in Figure 4a) associated with intraionic 2E-4A transition in Cr3+ in octahedral coordination [26], which confirms the incorporation of Cr within the rutile lattice. The opposite behavior can be observed for microtubes grown from Cr doped TiO2 nanoparticles, as shown in Figure 4a. In that case, the relative intensity of the IR band decreases with respect to the VIS-UV band, which dominates the CL spectrum. Moreover, the VIS-UV band is centered at about 3 eV, which can be due to an increase of near band-edge defects induced by Cr ions. In this case the band at 1.8 eV is not well defined and appears as a weak band. However, reducing the thermal broadening and phonon contribution, by decreasing the temperature down to 100 K (Figure 4b), this band is well defined at 1.8 eV, confirming the presence of Cr3+ ions in the rutile lattice.
3.2. Hexagonal ZnO micro and nanotubes
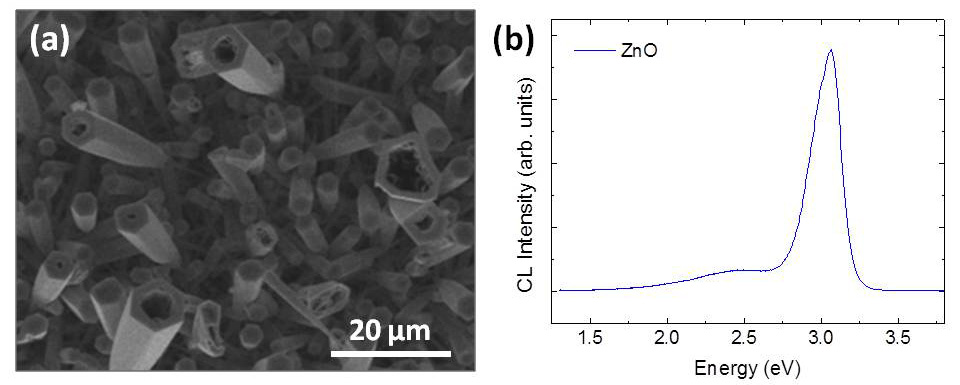
In addition to the rutile SnO2 and TiO2, microtubes of hexagonal wurtzite ZnO have been grown by this method. ZnO microtubes were fabricated by a vapor solid process using metallic Zn as precursor and thermal treatments at 700 ºC for 2-4 hours. In that case, the microtubes, with lengths of tens of microns and widths of a few microns (Figure 5a), show hexagonal sections. ZnO presents three fast growth directions along [0001], [10-10]. [2-1-10]. Among them the [0001] direction exhibits the maximal growth rate whereas the (2-1-10) are the most stable surfaces [18], which is in agreement with the hexagonal appearance of the ZnO tubes presented here. The ZnO tubes usually appear partially filled, which in some cases results in narrow cavities. CL spectra from the ZnO tubes, shown in Figure 5b, are dominated by an intense emission around 3.2 eV and a broad band with a low relative intensity at 2.4 eV. The former is associated to near bandgap emission, while the green band at 2.4 eV is commonly associated to Zn interstitials and oxygen vacancies defects in ZnO [28]. Most of the works which report the growth of ZnO tubes are based on hydrothermal or wet chemical methods, usually leading to amorphous or polycrystalline materials. Fewer authors referred the growth of single-crystalline ZnO microtubes [18,29], similar to those analyzed in the present work. In those cases, an oxidation-sublimation process without using catalysts or carrier gases is proposed for the growth of the tubes, which also exhibit hexagonal cross sections. In that process a Zn/Zn suboxide nanostructure is formed at the beginning. The initial nuclei rod reacts continuously with oxygen to form an outer shell ZnO by surface oxidation, acting graphite as reducing agent. The remaining Zn core inside the rods is finally sublimated, due to the high temperature employed in the process which reachs 1000 ºC. In our case, a similar process is proposed, although an argon flow is employed throughout the vapor-solid process leading to the growth of ZnO microtubes, and no reducing agent is needed. Moreover, this vapor-solid process occurs at lower temperatures, avoiding the sublimation of Zn.
3.3. Hollow elongated structures in cubic materials (In2O3 nanopipes)
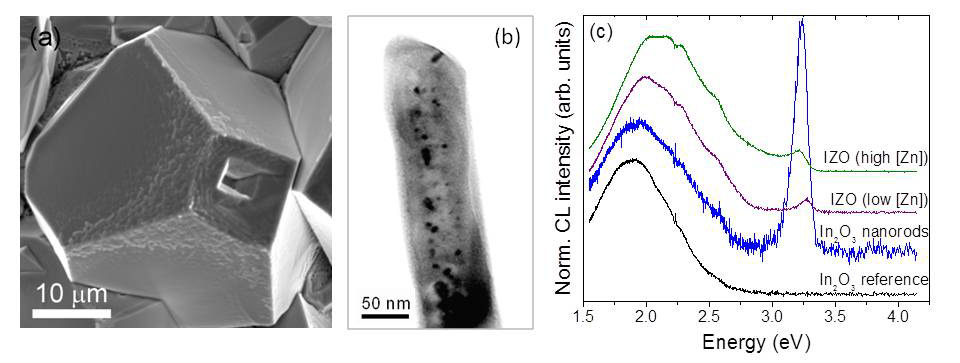
In this work, either InN or In2S3 have been used as precursors to fabricate In2O3 elongated micro and nanostructures with a hollow core. When using InN as precursor, tubular micro and nanostructures of bixbyite In2O3 were obtained by thermal treatments at 650-750 ºC for 5-10 hours. These treatments lead to the formation of In2O3 micro and nanoarrows and rods of tens of microns length and hundreds of nanometers width [30]. TEM measurements demonstrate the presence of a hollow core, named as nanopipe [10], as shown in Figure 6a. These nanopipes, with a width of around 20 nm, independently of the cross section of the structure, extend along the core of the arrows and rods. Vapour-Solid growth has been commonly used as fabrication technique of In2O3 elongated structures, however, the driven force behind the VS process for these 1-dimensional cubic In2O3 structures is still unclear. Some authors have proposed a supersaturation driven process, where low supersaturation conditions would lead to a 3D growth mode, whereas high supersaturation would induce an anisotropic 1D growth [31]. An autocatalytic process has also been used to explain the 1D growth, arguing that the formation of liquid indium droplets during the growth could support this growth mode as in a Vapor-Liquid-Solid process [32]. In the case of the tubular structures analyzed in the present work, the uniformity in the inner channel section, independent of the section of the structure, is an evidence of the relaxation mechanism induced by screw dislocations with giant Burgers vectors, as proposed by Frank [33]. Therefore, the presence of the pipes can be associated with a dislocation-driven growth mechanism which governs the formation of the In2O3 elongated structures [10]. This method, firstly proposed first by Sears [34] to explain the rapid growth of Hg whiskers, has been recently applied to explain the growth of PbS nanotrees [35] and nanoplates of different materials. The dislocation related steps at the surface are preferential points for the adsorption of new molecules, promoting the growth of 1D structures.
Evidences of this mechanism driving the growth of other hollow and compact indium oxide structures have been observed in samples grown using In2S3 instead of InN as precursor, and thermal treatments at 950 ºC for 10 hours. Figures 6b-d show respectively the images of a In2O3 microcrystal grown at the substrate, and two different microrods with cuboctahedral microcrystals at their apex. Both kinds of microcrystals (either grown at the substrate or at the tip of the rods) are formed by a combination of (111) and (100) surfaces and present facetted pinholes at the centre of their faces. The shape of the pinholes depends on the specific crystalline plane of the microcrystal faces, being triangular for (111) faces, and squared for (100) faces. Pyramidal and octahedral growth of In2O3 exhibiting {111} lateral faces has been reported, which correspond to the equilibrium shape of cubic-lattice crystallites determined by a higher growth rate in the [100] direction [36]. Meanwhile cubic shaped indium oxide crystals have been described to grow along the [111] direction exhibiting {100} family plane facets [37,38]. A competition between both processes is produced depending mainly on the supersaturation and temperature of the growth atmosphere and the growth direction and therefore the shape of the crystals will depend on the ratio between the growth rate along the [100] and [111] directions. Pinholes have been previously associated with the emergence of dislocations at the surface [29,39,40]. CL images obtained from these structures (Figure 6e) show a typical bright and dark contrast usually associated to the presence of dislocations.
Doping In2O3 with Zn or Sn leads to the formation of, respectively, hollow truncated micropyramids presenting a large pinhole at the surface [41], as it can be observed in Figure 7a, and tubular nanoarrows filled with a core decorated with metallic Sn [42], as shown in Figure 7b, among other structures. Zn-doped In2O3 structures were grown using a mixture of InN and ZnO (5% wt.) powders as precursors and thermal treatments at 900 ºC for 10 h, while for Sn-doped In2O3 structures a mixture of InN and SnO2 (10% wt.) was used and thermal treatments at 650 ºC. CL spectra of indium oxide elongated structures (Figure 7c) show a characteristic band centered at around 1.9 eV, which sometimes presents a broadening in the high energy tail at around 2.9 eV. The origin of the high-energy emission band is related to the presence of oxygen vacancies, as established by several works [43,44]. The origin of the 1.9 eV characteristic band, on the other hand, is still unclear. Some authors have attributed it to the presence of oxygen vacancies, however, the results from some works are in clear contradiction to this hypothesis [30,45]. Some other works have related this band to a good crystalline quality [46]. For Zn content below 2% at., Zn-doped indium oxide structures show a luminescence spectrum which is identical to that of undoped indium oxide. However, for a Zn concentration above 2% at., the CL spectra show a broad and complex band peaked at 2.1 eV, with a long tail at the high energy range covering the whole optical range up to the band edge emission at 3.2 eV. The band edge emission, which is not present in the undoped structures, can be resolved as a single peak the energy of which decreases with increasing Zn content [41]. The 2.1 eV band, on the other hand, does not show an energy shift, but its overall intensity increases with Zn content The emissions from the high energy tail increases faster than the 2.1 eV peak. The different behaviours observed for Zn contents below and above 2% at. have been related to the formation of indium zinc oxide (IZO) ternary compounds with the general chemical formula In2ZnkO(k+3).
4. Conclusion
To summarize, different tubular micro- and nanostructures have been fabricated by a vapor-solid method, which avoids the use of templates or catalysts. The growth of SnO2, TiO2, ZnO or In2O3 elongated hollow structures has been achieved using different precursor powders and thermal treatments. Following this procedure, rutile (SnO2, Cr doped TiO2) well-facetted microtubes with rectangular sections are obtained, as well as ZnO microtubes with hexagonal sections and variable diameter of the inner channel. Moreover, In2O3 elongated structures showing a hollow core, named as nanopipe, have been fabricated by this method. The morphology and optical properties of these tubes vary when doping with different elements (Cr, Er, Li, Sn, Zn). Dopant contents about 0.5-3% at. have been achieved by this method. CL analysis shows that variations in the luminescence can be associated directly with the dopants (as the 1.79 eV and 0.8 eV emissions related to Cr3+ and Er3+, respectively), or to a modification in the defects caused by doping. Different growth mechanisms are proposed for the anisotropic growth leading to the tubes fabricated by the VS process. Despite the fact that diverse mechanisms, such as anisotropic growth, self-catalytic growth, defect-induced growth and oxide assisted growth, have been usually considered to be involved in the VS process, the microscopic nature of the growth mechanisms as well as the driving forces leading to the growth of elongated micro- and nanostructures are not completely understood so far. Parameters such as vapor pressure, supersaturation ratios and surface energies are involved in the VS anisotropic growth, therefore variation of these parameters due to the thermal treatments or the doping process should be considered in the study of the growth of elongated structures by VS. The intrinsic anisotropic character associated with the rutile (SnO2, TiO2) and wurtzite (ZnO) lattices can partially explain the growth of elongated structures by the VS process, while for cubic In2O3, defects, such as dislocations, should be also involved in the growth of elongated microstructures. Actually, the presence of pipes in the In2O3 elongated structures can be explained attending to a dislocation-driven growth mechanism. Moreover the surface energy associated to the different faces forming the tubes should be also considered. The characteristic morphology of these tubular structures, as well as the capability of being filled, can widen their applicability in diverse fields of research, for which a deeper understanding of their properties and growth mechanisms is required. Recent works report on the use of micro- and nanotubes as sensors in environmental applications, optoelectronics, nanosolders and nanothermometers.
Acknowledgments
This work was supported by UCM-Banco Santander, program GR3/14 and MINECO (Project Nos. MAT 2012-31959, MAT 2015-65274-R and Consolider Ingenio CSD 2009-00013).
Conflict of Interest
The authors declare no conflict of interest.










 DownLoad:
DownLoad: