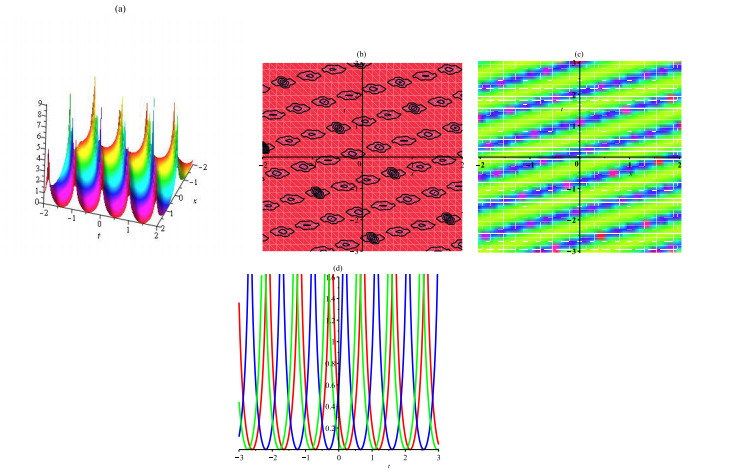
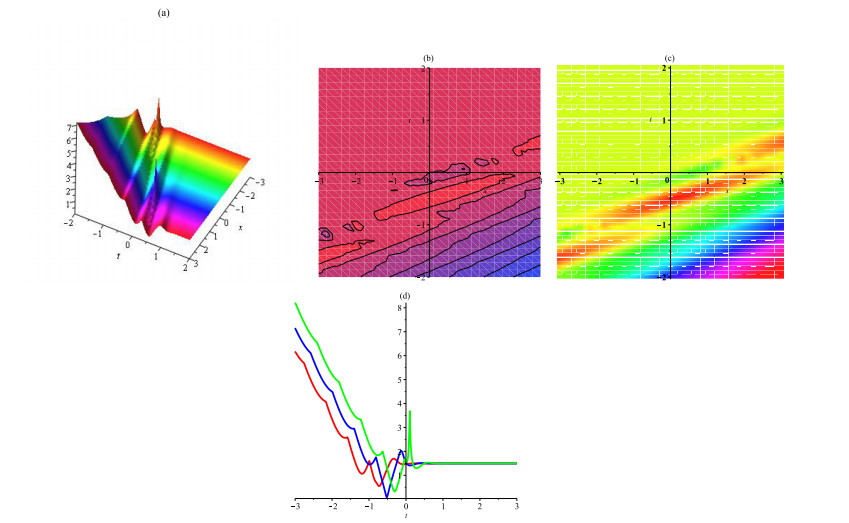
In this article, the mathematical modeling of DNA vibration dynamics has been considered that describes the nonlinear interaction between adjacent displacements along with the Hydrogen bonds with utilizing five techniques, namely, the improved tan(φ/2)-expansion method (ITEM), the exp(-Ω(η))-expansion method (EEM), the improved exp(-Ω(η))-expansion method (IEEM), the generalized (G'/G)-expansion method (GGM), and the exp-function method (EFM) to get the new exact solutions. This model of the equation is analyzed using the aforementioned schemes. The different kinds of traveling wave solutions: solitary, topological, periodic and rational, are fall out as a by-product of these schemes. Finally, the existence of the solutions for the constraint conditions is also shown.
1.
Introduction
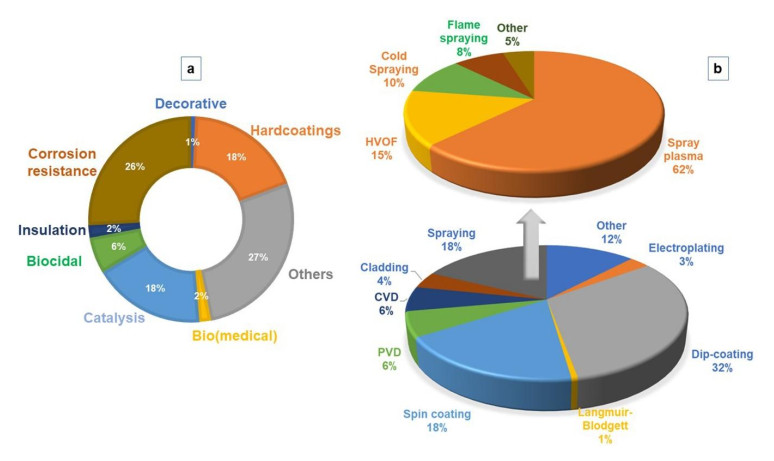
Coatings represent complex structural interfaces, nowadays with practically unlimited possibilities of chemical speciation and structural architecture and with a wide application palette, ranging in any proportion between purely decorative to functional, between nanoscale and macroscale level [1,2]. An insight into the application field of inorganic, organic and hybrid coatings obtained through complex criterial analysis of the information provided by the Web of Science platform (Clarivate Analytics, December 2018) has revealed that most of the research from the year 1975 up to date is focused on obtaining coatings with improved tribomechanical properties and corrosion resistance [3,4,5] (Figure 1a), followed closely by the catalytic applications (which include various aspects of synthesis, energy storage, photocatalysis, etc.) [6,7,8], biocidal (i.e., antibacterial and antibiotic character) [9,10], bio(medical), thermal, radiation, electromagnetic-insulative applications [11,12], and so forth.
For coatings of inorganic nature (which account for nearly 53% from the total, without considering composite-hybrid ones, based on the research data available from the Web of Science platform) several (electro)chemical or physical fabrication methods are available (Figure 1b) [13,14,15,16,17,18].
Among the physical fabrication methods, thermal spraying (with its technological variants) has been traditionally employed since the 1920's for achieving corrosion resistant hard coatings [19,20], reconditioning of worn metallic parts and tools [21], and more lately, to manufacture functional coating materials (thermal barriers [22,23], enhanced electrochemical response anodes [24], optically-active materials [25], semiconductors [26], biomaterials [27], solid fuel cells [28], and so forth).
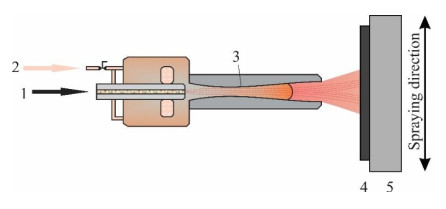
All technological variants of this technique imply spraying a combustion flame- or plasma-heated feedstock material (which may be in the form of powder, wire, rod, liquid, etc.) onto a desired substrate (usually metal or ceramic) [29,30]. The melted or partly-melted feedstock (colloquially called "splat") is projected on the substrate with a high velocity, being deformed (spread) onto the substrate surface on impact, generating a characteristic lamellar-layered coating upon its solidification [31]. Traditionally, coatings with thickness varying from 10 μm to a few mm can be obtained, but with the help of the high velocity oxy-fuel (HVOF) and plasma spraying techniques, the limit being lowered to 200–500 nm [32,33]. If the coatings are not nanometric, then nanopatterns can be exhibited on the surface in a highly reproducible manner [31,32].
This paper is focused on reviewing the current trends in photocatalytic coatings achievement through different thermal spraying techniques. Photocatalytic coatings represent the state-of-the-art in advanced oxidation processes for environmental and medical applications, in designing self-cleaning smart materials, converting raw materials into new useful products, in energy generating applications and so forth [30,34]. Traditionally, physical (PVD) and chemical (CVD) vapor deposition, along with the sol-gel (SG) process have been usually employed for most of the studies involving photocatalytic coatings achievement [35]. PVD and CVD have the advantage of obtaining photocatalytic coatings with tunable (and constant) chemical composition and thickness, avoiding the oxidation/chemical modification of the feedstock material during the deposition [30,36]. However, these are both energy-intensive and expensive processes, not currently upscalable to deposit coatings on large substrates. Sol-gel processes are instead more cost-effective, but also more time-consuming. Also, the chemical composition, morphology and the thickness of the SG coating is very difficult to be maintained, especially for large parts with complex geometry. Another issue that makes sol-gel processes less useful when considering upscaling to pilot or industrial-level applications is represented by the coatings low wear resistance, hardness and adhesion to the substrate. Also, as a trendline, there are comparatively fewer studies dealing with the obtaining of photocatalytic coatings on metal substrates (more relevant when considering the processes on a larger scale) with any of these techniques (PVD, CVD, SG), in comparison with ceramics, glass and organic substrates [37,38].
Even if thermal spraying can be currently considered as complete technique, it has all the requirements of being a successful candidate for photocatalytic coatings achievement: low equipment maintenance cost, lower environmental footprint (compared to CVD or PVD), versatility regarding the physical state and chemical composition of feedstock material (liquid precursors could be also sprayed, generating the photocatalytic coating on the substrate through the precursor decomposition; both metallic and high-refractory ceramic particles can be flame or HVOF-sprayed; even polymers can be successfully sprayed or employed as substrates for coatings with cold spraying technique), the possibility of application to large surfaces with complex geometry, the possibility of nanopatterning the surface, and so forth [38,39,40,41]. The disadvantages of thermal spraying reside mainly in unwanted oxidation of the feedstock material during spraying, which lowers the mechanical properties of the coatings and their adherence to the substrate which can be diminished by the adequate use of inert protection gases), and a more difficult control in the thermal sprayed coating thickness, which could be overcome by a careful controlling of the process operational parameters [42,43]. Another drawback could be constituted by higher deposition temperature (in flame spraying and plasma spraying technique) which affects the photocatalytic yield of the coating, due to allotrope/polymorph transformations of the material (e.g., in the case of TiO2, high temperatures promote the anatase to rutile transformation) [44,45,46].
There are currently relatively few researches involved in photocatalytic coatings achievement through thermal spraying, this application being at present time under continuous development. New sub techniques, such as liquid precursor spraying or powder composite-agammaegate spraying have permitted the achievement of coatings with improved nanopatterned structure and photocatalytic response. Based on the data from the Clarivate Analytics Web of Science platform, it can be concluded that roughly 74% of the coatings applied in photocatalysis are TiO2-based. Narrowing the domain of interest to photocatalytic coatings obtained by thermal spraying, TiO2 coatings account for 84% of the total research. Based on criterial topic search algorithms, the majority of the thermally-sprayed photocatalyst coatings were deposited on glass and ceramic substrates.
The current state-of-the-art (mini-review) is focused on presenting several important developments and trends in the photocatalytic coatings developing through thermal spraying and could serve as a starting point for crystalizing new ideas in this broad research domain.
2.
Methods of obtaining photocatalytic coatings
2.1. Flame spraying
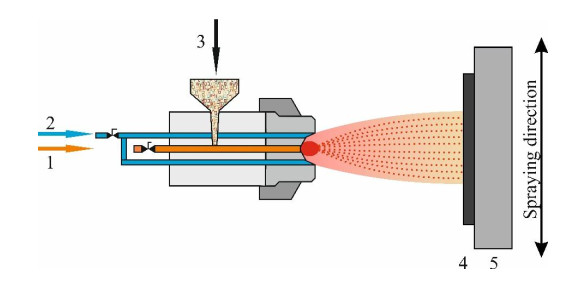
Flame spraying represents the oldest thermal spraying technique. It implies the combustion of a fuel gas (typically acetylene) with oxygen to melt a feedstock material which is propelled on a substrate [47], as shown schematically in Figure 2.
Flame spraying has been frequently used to generate high-quality wear- and corrosion-resistant coatings, or for reconditioning various metal parts, but to a lesser extent in the fabrication of photocatalytically-active coatings [30]. Flame spraying technique generates the second highest processing temperatures (typically in the range of 2500–3400 ℃) after plasma spraying [49]. With this thermal spraying technique, the oxidation of feedstock is to a considerable extent almost inevitable [50]. The so called "time of flight", i.e., the time required for the feedstock to travel from the thermal spray nozzle to the substrate is a crucial parameter in the flame spraying technique. It needs to be carefully chosen, by tuning the distance between spraying gun and substrate material [30,50,51].
Usually the feedstock is in powder form (metal or ceramic), but suspensions have also been recently used with high velocity suspension flame spraying (HVSFS) variant. In the HVSFS technique, the conventional gas-fueled torch is modified in order to process liquid feedstock. Moreover, with this technique, organic solvents (i.e., aliphatic alcohols) injected into the HVOF flame undergo an exothermic combustion reaction, increasing the heat input conferred to the particles. The resulting combustion gasses add a supplementary drag to the particles exiting the spraying gun determining a more efficient packing of the sprayed material, i.e., higher density of the coating [52,53].
Various processes have been developed to obtain micro and nanoparticulate photocatalysts, employing the use of metal-organic precursors, or custom liquid fuels (aliphatic alcohols) instead of gaseous hydrocarbons [54,55] but photocatalytic coatings obtained by flame spraying have been relatively sparingly studied.
Kavitha et al. have obtained titania films on silica substrates by flame spraying of a stabilized hydrous titanium oxide (Ti(OH)4) sol. The band gap of obtained films ranged from 3.11 to 3.16 eV. Remazol brilliant blue dye was successfully degraded by the films under UV light irradiation [56]. Similarly, Yang et al. have obtained rutile-rich nanostructured coatings starting from butyl titanate. They have proposed a mechanism for the nucleation of the rutile phase, starting from the surface of the initial anatase, resulting in a hybrid surface with a rutile outer layer and an anatase core [57].
Liquid flame spraying could be considered a simple method to obtain doped photocatalyst coatings. Yang et al. have obtained Ag+-doped-nanostructured TiO2 photocatalytic coatings by using this approach. The phase structure of coatings was not significantly influenced by the silver ion doping, but the photocatalytic activity of doped coatings was higher than that of the reference TiO2 coating, regardless of the dopant concentration [58]. In another study, the same group obtained Cu2+-doped TiO2 coatings. The enhancement of photocatalytic activity when adding the dopant could be attributed to the adsorption ability of oxygen and other reactants on the surface of the TiO2 coatings [59].
Ctibor et al. have used a commercially-available anatase-rich TiO2 powder, a pre-reduced TiOx powder and a powder agglomerated from nanometric particles as feedstock for obtaining porous coatings photocatalytically-active in the UV domain, using acetone as degradation model compound. They have found that through flame spraying, the anatase phase is preserved in a higher amount in comparison with plasma spraying [60].
Huang et al. have obtained nanocomposite titania-hydroxyapatite-reduced graphene oxide coatings by liquid flame spray deposition. An aqueous suspension containing submicron particles of the components has been used as feedstock for spraying on stainless steel. Two variants of nanopatterned coatings have been obtained: with thickness of 120–150 μm and 20–30 μm. A maximum BET surface area of 0.8 m2/g was responsible for a good photocatalytic response regarding the UV degradation of methylene blue dye [61].
Roata et al. have used a different approach in designing thick photocatalytically-active coatings on copper substrates. They have employed an aluminum bronze powder (containing also small amounts of iron) as feedstock material and a conventional flame spraying torch. The photocatalytic response of the coatings was generated by the copper and iron oxides developed during the spraying of the metal powder. By varying the distance between the flame spraying torch and the substrate between 150 and 200 mm, coatings with different oxide contents and photocatalytic activities could be obtained. Moreover, the attained oxides present a nanopatterned texture, and the metal (mainly Al) acts as charge carrier separation means, contributing to the overall efficiency of the coatings for the UV-driven methylene blue degradation [30].
Navidpour et al. have obtained hematite coatings through plasma and flame spraying techniques on 316 stainless steel plates, starting from pure hematite as the initial feedstock powder. The average size of the particles was around 5 μm. The thermal spraying distance greatly influences the hematite/magnetite ratio. In this respect, the weight percent of the hematite was decreased by increasing the distance of the spraying torch from the substrate, consequently with the visible light-mediated photodegradation efficiency against methylene blue aqueous solutions [62]. Flame-sprayed coatings were more photocatalytically efficient than plasma-sprayed coatings, due to their higher active surface and α-Fe2O3 content.
2.2. HVOF thermal spraying
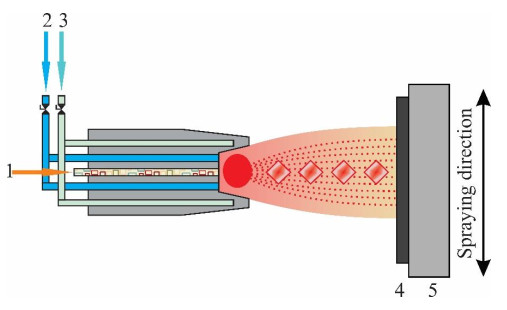
In the high velocity oxy-fuel (HVOF) variant of thermal spraying, the feedstock material is accelerated at supersonic velocity through a converging or converging/diverging nozzle by means of the rapidly expanding gases evolved in the chemical reactions between hydrogen and oxygen, or gaseous hydrocarbons and oxygen (Figure 3) [63,64]. This allows for lower temperatures (hence lower oxidation degrees and chemical degradation of the coated material) and better mechanical bonding of the coating with the substrate than in the case of conventional thermal spraying [65].
Up to date, there are only a few studies, regarding the application of HVOF to obtain TiO2 thick and hydrophilic coatings in order to remove organic pollutants in gaseous phase. Titania represents probably one of the most widely employed photocatalysts [66], due to the ability to function as a photocatalyst under UV irradiation and to easily tunable photocatalytic response through doping or mixing with species that facilitate charge carriers separation. High anatase/rutile ratios can be generally obtained through HVOF, with increased surface areas which is beneficial for photocatalysis [67,68].
Toma et al. have obtained 5–20 μm thick photocatalytic TiO2 coatings through HVOF spraying for photodegradation of NO and NOx nitrogen oxides [69]. The feedstock material comprised of anatase-rich and anatase-10 wt% Al micro-sized powders, or micro-agglomerated TiO2 (92% anatase) powders. It has been observed that after the HVOF process, anatase converts into the rutile polymorph, which presents a lower photocatalytic efficiency than anatase (the anatase content was only ~12% after spraying). The Al provides a more efficient charge carrier separation during UV-light irradiation, leading to improved efficiencies. The values of the conversion ratio ranged between 30 and 32% for NO and 16–18% for NOx [70]. In another study, Toma et al. have obtained HVOF-sprayed coatings starting from aqueous suspensions containing 40 wt% rutile and anatase phases, using ethylene as fuel gas. The parameters of spraying process were chosen to obtain mechanically stable coatings and to preserve a high content of the initial crystalline phases of the powders [71].
Colmenares-Angulo et al. have performed a comparison between the photocatalytic activities of HVOF and plasma-sprayed TiO2 coatings. Partially reduced oxidic species were registered in all coatings, such as Ti8O15, which are detrimental for photocatalysis applications. As-prepared samples showed limited photocatalytic activity towards methylene blue degradation, but with the HVOF-generated coating being more efficient than the plasma-sprayed one. In contrast, post-deposition oxidation of the samples in air resulted in significantly improved catalytic performance of the coatings, due to the increase of the anatase content [72]. Detailed structural studies performed by Yang et al. have indicated that the rutile phase in plasma-sprayed TiO2 presents a more significant preferential orientation along the (101) atomic plane than the same material deposited through HVOF, due to the tensile stresses concentrated in the individual splats. The (101) diffraction planes may change their orientations parallel to the coating surface under tensile stress at high temperature during splat cooling. This preferential orientation has a negative influence on the efficiency of the photocatalysis process [73,74].
The comparative study on the microstructure and photocatalytic properties of titanium dioxide coatings obtained by different thermal spray methods: atmospheric plasma spraying, suspension plasma spraying, and HVOF using agglomerated and nonagglomerated TiO2 nanopowders as feedstock materials led by Toma et al. has indicated that the coatings elaborated by suspension plasma spraying presented a specific structure that depended on the nature of the solvent used in the preparation of the suspensions. The coatings obtained starting from aqueous suspensions were able to preserve a higher ratio of anatase than in the case of alcoholic feedstock powder suspensions, therefore showing remarkable photocatalytic efficiency that in some conditions was higher than that of the corresponding anatase powder [75].
Similarly, Ctibor et al. obtained rutile-rich TiO2 coatings through HVOF, with band gap energies ranging from 2.17 to 3.15 eV, efficient for UV photodegradation of acetone [76]. Different researchers have obtained TiO2 coatings with higher anatase contents (35 to 55%) through modifying the geometry of the thermal spray nozzle, allowing lower temperatures, below that corresponding to the anatase-rutile polymorph transition at ~600 ℃ [77] Bozorgtabar et al. have obtained a coating containing 80% anatase by volume at 120 mL/min low fuel flow rates. The results show that the as-sprayed TiO2 HVOF coatings were highly photocatalytically reactive for the degradation of ethanol [78].
Studies led by Pala [79] have indicated that nanopatterned and anatase-rich (20.45–69.14%) coatings can be obtained by suspension high velocity oxy-fuel spraying approach (principle scheme shown in Figure 4), with potential photocatalytic and/or sonophotocatalytic applications. In their study they have used anatase nanoparticles (with diameters between 50 and 180 nm) 20 wt% suspensions in water, which they have directly injected into the center of the HVOF combustion chamber.
Higher heat powers lead to the achievement of surfaces with higher roughness as well as to the presence of micro- and nanopatterned formations that could be beneficial for catalytic applications.
2.3. Plasma spraying
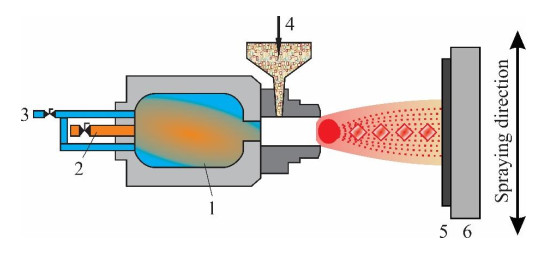
This variant of thermal spraying uses DC- or RF-generated plasma as a spraying heat source. Owing to high temperatures of the plasma, a wide range of refractory ceramics and alloys could be successfully sprayed at velocities of 200–300 m/s. With this thermal spraying technique, powders as well as liquid precursors and particle suspensions could be used as feedstock materials (Figure 5).
As a general trendline, plasma spray ceramic coatings present an inherent connected-pores structure, which is beneficial for photocatalytic activity. Considering that usually splat size of micrometer scale into account, the surface area is not so high as other type of coatings (e.g., obtained by flame spraying) [80,81,82].
In some cases where the high temperature of the plasma spray process promotes undesirable changes in the coating structure, it has been found that spraying with suspensions and liquid precursors is more benefic in obtaining a higher photocatalytic yield of the coating [83]. During suspension/precursor droplets spraying, the liquid dispersing media/solvent is evaporated, resulting submicron-agglomerated particles, which are melted and accelerated to the substrate.
Dosta et al. have obtained highly stable TiO2 coatings with a wide range of structural characteristics for their application as photoanodes, starting from conventional rutile and anatase powder aqueous suspensions as spraying materials. The solar-irradiated photoelectrocatalytic performance for degrading Acid Orange 7 dye was 70% [84]. An aqueous suspension of Degussa P25 TiO2 has been employed by Vu et al. to obtain UV-photocatalytic coatings by plasma spraying. They have found that the heating of the Degussa Powder at temperatures of 800 ℃ generates pure rutile of about 200 nm crystallite size in the coating [85].
Solonenko et al. obtained titania coatings on stainless steel by plasma spraying of an ethanolic solution of titanium tetra iso-butoxide precursor, which decomposes thermally into TiO2. The novelty of the study consisted in using a specially-designed cascade plasma torch operating on argon-helium mixture which owed for an increased anatase content in the sprayed coatings. Good mineralization of the model dye compound has been achieved after 6 hours of UV-light irradiation [86]. Regarding TiO2 coatings, it has been found that a minimum 15–20% anatase content is required for efficient photocatalysis. Another issue related to spraying TiO2 is that fully-oxidized coatings are rarely obtained, with several other undesired phases being developed, such as Ti2O3 and TiO. A post-deposition heat treatment (650 ℃, 48 hours) ensures the complete oxidation of titanium to TiIV+, subsequent with the anatase to rutile transformation [87].
Ctibor et al. have proven that the initial morphology of the feedstock powder has a low influence on the microstructure of the plasma-sprayed coatings of titanium dioxide. This influence is more significant when discussing the photochemical response and respectively phase composition and crystallite size [76,88]. Since UV light generating is energy-intensive and it accounts for only ~5% of the solar spectrum, intensive research has been focused on obtaining photocatalytic coatings that are able to harvest light in the visible domain of electromagnetic radiation [89]. In this respect, suspension plasma spraying has been applied by Zai et al. for obtaining composite Ti2O3–TiO2 coatings with reduced band gap (2.71 eV). The sprayed aqueous suspension contained Degussa P25 TiO2 nanoparticles and surfactant polymers. The coatings present fine nanometric and submicrometric grains, have a gray color, thus being more efficient in light absorption. The coatings present an efficiency of 89% for degradation of aqueous methylene blue dye [90].
In another study, Ctibor et al. have used gas-stabilized (GSP) and water-stabilized (WSP) plasma guns to obtain TiO2–Fe2O3 composite powders by atmospheric plasma spraying (APS). The novelty was to use a phase-controlling Na2SiO3 additive suitable for feeding into the plasma jet. The GSP coating has the best photocatalytic activity under both UV and VIS light irradiation. The coatings produced with the Na2SiO3 additive were dominatingly amorphous and more active in the UV domain [91].
Through the solution precursor plasma-spray route (SPPS), ZnO films with nanostructured surface morphologies have been obtained by Yu et al. [92,93]. Zinc acetate has been chosen as precursor, being dissolved in a water-ethanol mixture at concentrations ranging from 0.2 to 0.4 mol/L. Needle and bud-like nanopatterns were formed on the surface of the coatings, which were responsible for degradation of Orange II dye in under 100 minutes, under UV irradiation conditions. The assemblies presented bandgap values of 3.02 eV. Zinc oxide coatings could be obtained also through traditional plasma-spray routes. For example, Navidpour et al. have obtained coatings with specific surface areas of 25–45 m2/g starting from ZnO powder with an average diameter of 2 μm, with moderate efficiency in photodegrading methylene blue dye [94]. Through the same technique, Chen et al. have obtained highly porous titania surfaces using titanium isopropoxide in aqueous phase as precursor. The amount of anatase and rutile phases in the as-sprayed coatings can be adjusted by simply changing the plasma power. With the increase of plasma power, the coating anatase content decreases and the rutile content increases [95].
Coatings with a wide palette of chemical compositions can be obtained with plasma spraying technique. Doping the main photocatalytic-active feedstock material is facile, by mixing the appropriate amount of dopant with the liquid precursor, or through mixing powders with different chemistry in the desired ratios. For example, composite coatings have been obtained by Zeng et al. by powder plasma spraying of TiO2 and ZnFe2O4 powders under various mixing ratios. The maximum methylene blue decomposition efficiency was ~75% under UV (365 nm) irradiation [96,97]. Platinum-doped TiO2 coatings have been obtained by powder plasma spraying. The obtained coatings present ~70% photo-efficiency under light irradiation combined with a 15 V potential bias [98].
Composite TiO2–Fe3O4 coatings have been obtained by co-spraying powder mixtures with various compositions, namely TiO2–5 wt% Fe3O4, TiO2–10 wt% Fe3O4, TiO2–12.7 wt% Fe3O4, TiO2–22.5 wt% Fe3O4 and TiO2–32.6 wt% Fe3O4 powders. The coatings were able to completely degrade gaseous acetaldehyde in about 120 min [99].
Dom et al. have obtained ~25 μm-thick photocatalytic composite coatings starting from aqueous and organic (ethylene glycol) precursor solutions Zn2+ and Fe2+, complexed with citric acid. Preparation of a stable precursor by metal–citrate complexation has been found to inhibit the oxidation of individual metallic species during film deposition. The chemistry of the coatings was mainly ZnFe2O4. This phase exhibited a band gap of 1.9 eV. The highly porous nature of the film favored its photocatalytic performance as indicated by methylene blue discoloration under solar radiation (~30% degradation efficiency) [100].
Liu et al. have reported for the first time a hierarchical-nanostructured coating comprising of aluminum zinc oxide (AZO), deposited on a glass substrate through atmospheric plasma spraying. The coatings were of 60 μm thickness and porosity of 24%. The Eg value of the coating sample was 3.24 eV. Related to the photodegradation efficiency of these coatings a decrease of 36% in methylene blue concentration has been observed after 72 hours of UV irradiation [101].
Recently, a new technique has been developed by Sulzer Metco AG (Switzerland), which combines the physical vapor deposition (PVD) method with the low-pressure plasma spraying (LPPS) or vacuum plasma spraying (VPS) variant of thermal spraying. The advantage of this technique is that it can deposit coatings out of the vapor phase. This process uses a high energy plasma gun operated at a reduced work pressure of 0.1 kPa (1 mbar) which accelerates and projects the vaporized feedstock material that impacts the cooled substrate, thus resulting unique coating microstructures [102]. Up to date it has been used only for obtaining ceramic thermal barriers and hard coatings, but its extension to the obtaining of photocatalytic surfaces would be very promising [103].
2.4. Cold spraying
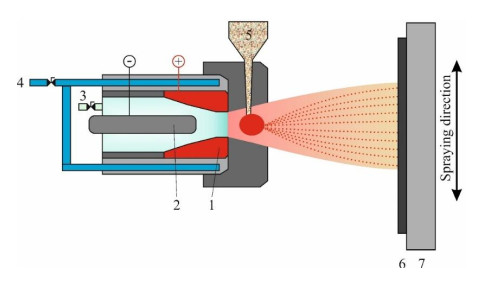
This variant of thermal spraying has been implemented already for obtaining corrosion- and wear-resistant coatings or for electromagnetic interference shielding [18,104,105]. In cold spraying (CS) (also named cold gas spraying), the feedstock particles are accelerated to supersonic velocities, like in the HVOF variant, but in CS they are being maintained at temperatures significantly lower than their melting point for their entire time of flight. Inert carrier gasses can be used to minimize oxidation (Figure 6). Depending on the process parameters, the impact velocity with the substrate is in the 200–1500 m/s range. Interparticle or particle/substrate bonding is facilitated mainly by plastic deformation [106,107,108,109].
Regarding photocatalytic coatings, most cold spraying applications resume to titania. Yang et al. have used TiO2 anatase powders (10–45 μm) to obtain nanopatterned coatings on stainless steel by cold gas spraying, using nitrogen as a driving/carrier gas with an inlet pressure of 2.0 MPa and temperature of 300 ℃. Higher anatase contents have been reported by comparing to the typical values obtained through plasma or HVOF spraying, owing to the lower deposition temperatures. The photocatalytic response of the coatings was evaluated against gaseous acetaldehyde under UV irradiation. Almost complete removal of this model pollutant as achieved after 30 minutes of irradiation [110].
Yamada et al. have concluded that cold spraying is an ideal process for fabricating anatase-rich TiO2 photocatalyst coating. The anatase structure could be preserved by carefully controlling the spraying parameters, mainly the processing gas temperatures (200–400 ℃), which are below the anatase to rutile transition temperature. The nature of the gas (nitrogen or helium) does not seem to have a significant influence on the performance of the coatings [111]. Cold spray was employed by Yang et al. for obtaining TiO2 photocatalytic films with thickness of ~15 μm. The photocatalytic performance was examined through acetaldehyde degradation under ultraviolet illumination. Results showed that no phase and particle size changes occurred to TiO2 during deposition, and the coating was efficient towards degradation of acetaldehyde [112]. The low deposition temperatures of the cold gas spraying process allow for deposition on polymer or glass substrates, otherwise unfeasible by traditional flame and plasma spraying methods [113]. Robotti et al. have obtained 200–400 μm-thick nanopatterned titania coatings on polymer substrates with good photodegradation yield against NOx (~20–80%) under UV irradiation [114]. Composite coatings with various surface chemistry have been obtained by Park et al. starting from ATO (Sb2O5:SnO2, 15:85 wt%, 13–22 nm) and titania (15 nm) nanopowders using FTO glass as substrate. The complete photocatalytic decolorization of methylene blue in an aqueous solution under UV light irradiation has been achieved after 6 hours [115].
A relatively new variant approach of this thermal spraying method is represented by vacuum cold spraying. Through this technique an optimum balance can be achieved between a high photocatalytic activity (fine structure and large surface area) and a good adhesion between coating and substrate surface [116]. For example, Yao et al. have demonstrated by molecular dynamic simulation that nano-scale feedstock powders are subjected to an increased localized plastic deformation during collision at low velocities, while at high velocities the intensive deformation promotes the nanoparticles adhesion rather than rebounding off [117].
Yao et al. prepared a composite nano-TiO2/polyethyleneglycol (PEG) powder as feedstock material for vacuum cold spraying and the photocatalytic activity of the coatings was assessed through photodegradation of phenol in water. Results showed that post-deposition annealing of the coating between 450 and 500 ℃ yielded both higher activity and increased adhesion to the substrate. The TiO2 coating, resulting from the composite powder/PEG feedstock presented much higher activity than that deposited with the primary nanopowders, which can be attributed to its high porosity, which facilitates the contact of the reactant with the photocatalyst phases [118].
3.
Conclusion
The mechanisms underlying the photocatalytic response of thermal sprayed coatings reside in both the surface chemistry of the feedstock material or the in-situ generated material (i.e., its optical band gap) and the specific surface area of the coating. The latter is mainly influenced by the roughness and nanopatterning of the surface (obtaining of nano-agammaegates). Thermal spraying offers the means to fine tune both the chemical composition of the coating (through choosing the appropriate feedstock material, spraying distance, gasses involved in combustion/transport, etc.) as well as the roughness and the degree of clustering of the agammaegates on the surface of the material.
Most of the research involving thermal spraying applied to photocatalytic coatings achievement deal with TiO2 powders, powder suspensions or organic precursors which can generate the titania in-situ (in the flame or plasma). These coatings are mainly active in the UV-part of the electromagnetic radiation domain. Composite coatings bearing titania or doped titania can also be obtained with the plasma and HVOF spraying techniques, which present moderate photocatalytic activity in the visible domain. The second most frequent system employed in thermal spraying is based on ZnO, which possesses a lower band gap than TiO2 and can harvest visible light more efficiently.
High velocity oxy-fuel spraying and cold spraying have been generally found to be up to 25–35% more efficient in the photodegradation of organic compounds compared with flame spraying or plasma spraying. For the latter techniques, polymorph structural conversions affect the photocatalytic yield, with unwanted material oxidation, substrate overheating and delamination from the substrate. Flame spraying, with its suspension flame spraying technological variant is a relatively simple method and the operational cost is significantly less than the other techniques, needing a careful choosing of the feedstock material and operational parameters.
Acknowledgments
We would like to thank the structural funds project PRO-DD (POS-CCE, O.2.2.1, ID 123, SMIS 2637, ctr. No 11/2009) for partly providing the means for accessing the international research-indexing databases used in this work.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: