Discrete-time population dynamics on the state space of measures

1.   Introduction

H.265/HEVC stands for high efficiency video coding. It is a new generation of video compression coding standards officially released by the ITU-T | ISO/IEC Joint Collaboration Team on Video Coding (JCT-VC). A more efficient video coding algorithm saves 50% of the bit rate compared to the previous generation coding standard H.264/AVC, which greatly increases the video data transmission speed and supports higher-definition video coding ^[1]. The encryption and decryption operations of video data require a large number of ciphers, which are the same as the requirements of the 'one-time pads' encryption technology proposed by Shannon ^[2]. For any piece of plain text information, a cipher with the same volume as the plain text information must be generated, and a bit XOR operation obtains ciphertext information of equal volume. Chaos is the externally complex performance of nonlinear deterministic systems due to inherent randomness. In the material world, chaos can be seen everywhere, as large as the entire universe, as small as a single elementary particle, everything is subject to chaos theory. The introduction of chaos theory into cryptography was first proposed by British scholar R. Matthews in 1989 ^[3], therefore chaotic systems have received great attention in the field of cryptography and information security, especially in the aspect of rapid processing of a large quantity of video data, which makes the chaotic cryptography algorithm a promising cryptographic algorithm ^[4].

As an increasing number of chaotic stream cipher algorithms have been proposed, the security and efficiency issues of applying chaotic map to stream cipher algorithms have also received attention. Chaotic systems used in cryptographic algorithms can be divided into two categories: one-dimensional chaos and high-dimensional chaos. The advantage of a one-dimensional chaotic system is its simple structure and ease of implementation, such as Logistic map and Tent map, but a one-dimensional chaotic system has some inherent defects in cryptography, such as uneven orbit distribution, a small key space, and a low Lyapunov exponent. High-dimensional chaotic systems have the advantages of a large key space and strong randomness, but the calculation process of high-dimensional maps is complicated, and the efficiency in the computer realization process is insufficient, which hinders the practical application of high-dimensional chaotic cryptographic algorithms. The coupled map lattice (CML) model is introduced to ensure that the one-dimensional chaotic system has a high-dimensional chaotic map, and simultaneously reduces the calculation process complexity ^[5]. Wang et al. proposed using the segmented Logistic map as a local chaotic map and introduced it into the two-dimensional coupled map lattice model to construct a chaotic model with complex dynamics ^[6]. By introducing the state value offset, the state value probability of the model was solved. Considering the problem of uneven density distribution, analysis of the Lyapunov exponent, bifurcation, ergodic interval and probability density distribution of the parameter settings in the model shows that the proposed model has good performance. Zhang et al proposed a new image encryption algorithm based on spatiotemporal nonadjacent coupled graphs ^[7]. Compared with the logical map or the coupled map lattice, the nonadjacent coupled map lattice system has a better encryption function in terms of dynamics. In the encryption of the image, a bit-level pixel replacement method is used to make the bit planes of the pixels replace each other without any additional storage space. However, obtaining data directly on the chaotic trajectory and directly outputting it exposes certain characteristics of the chaotic map, making it possible to predict the trend of the chaotic trajectory, which in turn leads to its weak security. Lv proposed a pseudorandom number generator based on time-varying coupled map lattice ^[8]. The calculation of the next value of the current grid is not only related to the current value of the model, but also uses a similar Chebyshev map to determine the time delay t, and couples the grid at the current time with the grid before time t, which increases the chaos of the system degree, making its orbit in phase space more complicated. However, the probability density of the core components used in the system is not uniform. In the process of designing cryptographic algorithms, choosing core components with uniform probability density helps increase the difficulty of the attacker attacking the algorithm. Yang proposed an improper fractional-order laser chaos system and applied it to image encryption ^[9]. The experimental results show that the key space, correlation coefficient, information entropy, histogram, differential attack and robustness of the encryption scheme are good. The improper fractional-order laser chaotic system not only has rich dynamic characteristics, but also is used in image encryption algorithms. It has better safety at the time. However, this system is a high-dimensional chaotic system, and its computational complexity is not superior to that of a lower-dimensional system.

The selective encryption algorithm usually selects some important syntax elements for encryption during the encoding process, while the encrypted video can maintain format compatibility and ensure that it can be decoded by the HEVC standard decoder. The encrypted and decoded video produces distortion, and unauthorized access users cannot obtain effective information from it. Saleh et al. proposed a scheme to encrypt moving targets in HEVC ^[10]. This solution selectively encrypts the moving objects in the video content, selects the vertical data with a motion vector difference, and uses the AES algorithm for encryption. This solution only protects the moving objects in the video sequence and skips the static objects. If the moving objects in the video to be encrypted are not closely related in the time domain and the spatial domain, the encryption effect is greatly reduced. If the encrypted data are very small, such as only the sign bit of the motion vector difference or the sign of the transform coefficient, the encrypted data are vulnerable to brute force attacks. However, the solution performs well in terms of calculation cost, time consumption, format compatibility and bit increase, and it can be used for videos of different resolutions. Chen et al. proposed a HEVC-aware encryption scheme based on the RC4 algorithm ^[11]. This scheme constructs a key stream generation method based on RC4, which can adjust the ratio of "1" and "0" in the key stream. The four syntax elements of the sign of the motion vector difference, the magnitude of the motion vector difference, the sign of the luminance residual coefficient, and the sign of the chrominance residual coefficient are encrypted by the selected key stream. This solution has the advantages of large encryption space, low calculation cost, no increase in bit rate, and format compatibility. However, when the encryption ratio is not high, the video encryption effect is not good. Long et al. proposed a separable and reversible data hiding and encryption scheme for HEVC ^[12]. In the encoding stage, the RC4 key stream is used to encrypt the symbols of the motion vector difference and the remaining coefficients, and hide the data in the nonzero AC remaining coefficients. The encryption scheme has good perceived security and sufficient encryption space, which can effectively resist brute force attacks on video content. While ensuring that the video content is protected, data embedding can also be completed, and format compatibility can be ensured. However, it is necessary to complete data encryption and embedding, and the calculation cost is moderate. Yang et al. proposed an efficient format-compatible encryption scheme ^[13]. This solution selects the most important syntax elements in video reconstruction for encryption, and ensures that the encrypted bit stream is compatible with the HEVC standard. The suffix of the absolute value of the motion vector difference, the remaining coefficients, the motion vector difference, and the suffix of the absolute value of the difference between the coding unit quantization parameter and the predicted value in the prediction unit are encrypted using AES. The encryption scheme does not need to modify the structure of the HEVC standard decoder, and can ensure format compatibility after encryption. However, there is a trade-off between security and computational complexity. When security is the primary consideration, the computational cost increases accordingly. Zhang et al. proposed a selective encryption scheme based on hyperchaotic Lorenz system for HEVC ^[14]. First, the hyperchaotic Lorenz system is discretized, and the generated chaotic state value is converted into a chaotic pseudo-random sequence for encryption. The experimental results show that the encrypted video is highly disturbed and the video information cannot be identified. The analysis of the objective index results shows that the scheme is both efficient and safe. But it also has the disadvantage of high computational complexity, which is not conducive to video data with the characteristics of large data volume and strong real-time performance. The paper will propose a one-dimensional chaotic system, and will focus on solving the problems that exist when high-dimensional chaotic systems are applied to encryption. In the choice of syntax elements to be encrypted, reference ^[14] is selected as the comparison algorithm.

2.   The proposed scheme

2.1.   A new one-dimensional chaotic system based on coupled map lattice

Chaotic systems can produce complex nonlinear behaviors in both time and space domains. Spatiotemporal chaos is a kind of nonlinear dynamic system with chaotic characteristics in both dimensions of time and space. CMLs are a classic spatiotemporal chaotic system. CML has more complex dynamic characteristics and a larger key space, so they are widely used in the construction of cryptographic systems ^[15,16,17]. The definition of CML under discrete time n can be described as Eq (1):

A typical feature of chaotic systems is that they have a positive Lyapunov value, and the calculation equation of Lyapunov is defined as:

where $\varepsilon$ is coupled constant, $i$ is the lattice position, and $f(x)$ is the dynamic chaotic function. The CML diffusion process is the adjacent coupled process produced by the same map equation, so it is also called self-coupled. Wang proposed in ^[6] that the maximum Lyapunov exponent of the coupled map lattice model represented by Eq (1) is determined by $f(x)$.

Han et al. proposed an iterative chaotic map with infinite collapses (ICMIC) ^[18]. Equation (3) is the function of ICMIC, and the value range of a is $a \in (0, \infty)$.

Compared with the existing chaotic maps that fold infinitely in a limited space, ICMIC has good chaotic characteristics, which are manifested in stronger sensitivity to the initial value of the iteration and a larger Lyapunov exponent value. Therefore, after combining with a logistic map, a new one-dimensional chaotic system L-ICMIC (Logistic-ICMIC) is proposed. The equation is defined as Eq (4), and the value range of a is also $a \in (0, \infty)$, where the initial value ${x}_{0}\ne 0, \frac{a\pi }{{x}_{n}-{x}_{n}{}^{2}}\ne \frac{k\pi }{2}\iff {x}_{n}\ne \frac{1}{2}\pm \sqrt{\frac{1}{4}-\frac{2a}{k}}(k = 1, 2, \mathrm{3...})$. The scope of the chaotic map is $\left(0, 1\right]$.

The following analyzes the performance indicators of the L-ICMIC chaotic map, mainly analyzing and comparing its chaotic performance from the bifurcation graph, ergodicity, and Lyapunov exponent.

(1) The bifurcation diagram of the chaotic map can intuitively reflect the bifurcation of the period-doubling of the chaotic map, indicating the change in the characteristics of the chaotic system when the system parameters change.

It can be clearly seen in Figure 1. that L-ICMIC enters a completely chaotic state earlier than ICMIC, and the corresponding control parameters a have a larger value range when the system is in a chaotic state. This means that the key space when L-ICMIC is utilized as an encryption algorithm is larger than that of ICMIC.

Figure 1.  Bifurcation of ICMIC and L-ICMIC chaotic dynamical systems.

DownLoad: Full-Size Img PowerPoint

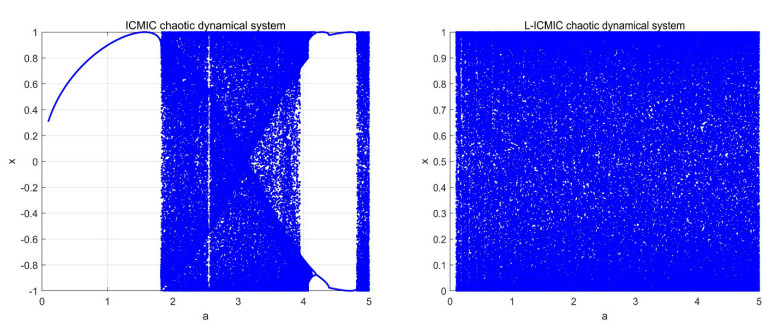
(2) The ergodicity of the chaotic map describes the distribution of state values in the phase space of the system. When the stronger ergodicity of a chaotic map is utilized for encryption, the stronger the violent anti-attack capability, and encryption, the better the performance.

Figure 2 shows the distribution of state values of ICMIC and L-LCMIC chaotic maps as a function of control parameter a. When the L-ICMIC chaotic map state value occupies the entire phase space, the control parameter has a larger value range. It also confirms the change in bifurcation. Therefore, when both L-ICMIC and ICMIC meet the ergodicity requirements, L-ICMIC has a larger parameter value range.

Figure 2.  Ergodicity of ICMIC and L-ICMIC chaotic dynamical systems.

DownLoad: Full-Size Img PowerPoint

(3) The definition and expression of the Lyapunov exponent were given earlier, and the Lyapunov exponent is an important indicator to measure whether a dynamic system is a chaotic system. The higher the value of the Lyapunov exponent is, the better the degree of chaos of the dynamic system.

Figure 3 shows that compared to ICMIC, L-ICMIC has a wide continuous range of chaotic parameters and stable dynamic characteristics. It is a robust nonlinear dynamic system that meets the requirements of cryptographic security properties.

Figure 3.  Lyapunov exponent of ICMIC and L-ICMIC chaotic dynamical systems.

DownLoad: Full-Size Img PowerPoint

It can be seen in ^[5,6,7,8,9] that CML has better chaotic characteristics. Now the proposed L-ICMIC is applied to the CML model to obtain a chaotic system with better performance in various aspects, and a pseudorandom sequence is generated for encryption. Next is the analysis of the new model system. Wang proposed in ^[6] that the largest Lyapunov exponent of the model has nothing to do with the size L and coupling strength $\varepsilon$ of the model. The L-ICMIC-CML equation set after the introduction of CML can be expressed as Eq (5):

n represents the time after discretization, i represents the lattice space coordinates, f(x) is the local chaotic map L-ICMIC, $\varepsilon$ is the coupling strength; L is the number of lattices.

The following analyzes the performance indicators of the L-ICMIC-CML chaotic system, mainly comparing its chaotic performance from the bifurcation diagram, Lyapunov exponent, dynamic characteristics of the system model, and Kolmogorov-Sinai entropy density analysis.

(1) For M-dimensional spatiotemporal chaotic systems, the Lyapunov exponent can be defined by calculating the Jacobian matrix of the coupled lattice. The Jacobian matrix of spatiotemporal chaos is defined as Eq (6):

Substitute a set of chaotic state values $\overrightarrow {{x_i}} (i = 0, 1, 2 \ldots n)$ into Eq (6) and perform the product operation to obtain R_M:

By calculating the M eigenvalues of the matrix R_M, the M Lyapunov exponents of the spatiotemporal chaotic system are obtained:

Figure 4 shows the bifurcation and Lyapunov exponent of the L-ICMIC-CML system. After using the coupled map lattice, compared to the one-dimensional chaotic system L-ICMIC, the value of a has a larger range, which indicates that the system can enter the chaotic state faster.

Figure 4.  Bifurcation and Lyapunov exponent of L-ICMIC-CML system.

DownLoad: Full-Size Img PowerPoint

(2) The spatiotemporal chaos model will show different states depending on the setting of the number of lattices, coupling parameters and other factors. When the CML system enters a fully developed chaotic state, the entire phase space orbit of the CML will be completely covered by the chaotic state. It can be seen from Figure 5 that the L-ICMIC-CML system is completely chaotic in time and space.

Figure 5.  The chaotic state of L-ICMIC-CML system.

DownLoad: Full-Size Img PowerPoint

(3) Kolmogorov-Sinai entropy is used to describe the rate of increase of the amount of information in a dynamic system over time. The higher the entropy value, the better its nonlinearity and randomness. For M-dimensional spatiotemporal chaotic systems, the Kolmogorov-Sinai entropy value is proportional to the system size M. In order to eliminate the influence of the number of spatial lattices on the entropy value and make the test results have general meaning, the Kolmogorov-Sinai entropy density is used to measure the degree of chaos, it can be expressed as Eq (9):

${D_{KS}}$ represents the average chaotic performance of the overall system, and ${D_L}$ represents the proportion of the number of lattices in the chaotic state to the total lattice, which represents the chaotic behavior within different lattices. $\sum\limits_{i = 1}^L {{\lambda ^ + }(i)}$ represents the sum of positive Lyapunov in all L lattices, ${D_{KS}} > 0$ represents the system is in a chaotic state, and $\sum\limits_{i = 1}^L {{L^ + }(i)}$ represents the total number of lattices in a chaotic state.

It can be clearly seen from the left side of Figure 6 that the L-ICMIC-CML system is in a chaotic state in the entire parameter space range. From the right side of Figure 6 it can be seen that all lattices of the L-ICMIC-CML are in a chaotic state.

Figure 6.  The Kolmogorov-Sinai entropy density of L-ICMIC-CML.

DownLoad: Full-Size Img PowerPoint

Therefore, the proposed system has stable chaotic characteristics and can be utilized to generate pseudorandom key streams. The steps of the binary stream cipher generator based on L-ICMIC-CML are as follows:

Step 1: Choose the 256-bit initial key S and divide it into 32 groups, each with 8 bits.

Step 2: Use S as the initial value of each lattice and enter it into the L-ICMIC-CML system. Removing the first 100 iterations of the output can effectively avoid the degradation of chaotic performance caused by transients and perform the following operations $\psi$ on the P generated by each lattice.

n represents the number of iterations $(n \geqslant 101)$, i represents the position of the lattice, and the floor function represents the rounding down operation.

Step 3: Pn(i) is a real number in the interval (0, 1), which is operated on $\vartheta$ to form a byte integer Kn(i).

Step 4: After performing operation $\nu$ on the results generated by each lattice, combine them to generate the final pseudorandom sequence k.

In this way, a binary key stream k is generated from the hyperchaotic Lorenz system.

2.2.   Screening encrypted syntax elements based on HEVC

The most secure encryption method is to directly encrypt the binary data of the video file using a cryptographic algorithm. However, this complete encryption algorithm destroys the syntax and semantic format of the video, making the encrypted video file unable to be played, and destroys the real-time attributes of the video, so this encryption algorithm has a narrow application range. Selective encryption is an improvement to complete encryption. The purpose of protecting video content is achieved by encrypting some key syntax elements, and a video encryption method that combines the encryption process with video compression coding.

In the process of HEVC encoding, context-based adaptive binary arithmetic coding (CABAC) is an entropy coding method for most syntax elements, and entropy coding is utilized for lossless data compression. As shown in Figure 7, in the CABAC encoding process, both binarization and context modeling will constantly update the context model, which is not conducive to encryption. Therefore, the syntax elements of the bypass mode are selected for encryption during the binary arithmetic encoding process. In addition to the conditions for entropy coding through the bypass mode, the conditions that should be met are binarized syntax elements through fixed-length coding or k-order Exp-Golomb coding ^[19]. Satisfying the above conditions can ensure the compatibility of the code stream and the constant compression rate in HEVC. Therefore, the syntax element of encryption is selected as follows: MVD sign and value, DCT transform coefficient sign and suffix, QP sign and suffix. Next, the pseudorandom cipher stream generated in the previous section is used to encrypt these syntax elements, and the specific encryption scheme and flowchart are shown in Eq (3) and Figure 8.

Figure 7.  The block diagram of CABAC.

DownLoad: Full-Size Img PowerPoint

Figure 8.  Encryption scheme flow diagram.

DownLoad: Full-Size Img PowerPoint

Where ep represents the encrypted syntax element and k represents the chaotic pseudorandom key stream.

3.   Experimental results and analysis

Experiments were performed by laptop computer with an Intel (R) Core (TM) i7-9750H CPU @ 2.60 GHz, 16 GB memory, Windows 10, Microsoft Visual Studio 2017, MATLAB 2017b. The reference software model HM 16.20 is implemented for the proposed scheme. The profile used in HM 16.20 is encoder_lowdelay_main, and group of pictures (GOP) is 4. QP is set to 22. Table 1 shows 5 video sequences with different resolutions selected in this experiment. These video test sequences reflect video attributes such as resolution, quantization parameters, motion, color, texture, contrast, foreground and background transformations, and can cover most of the video features. Another scheme that utilizes a hyperchaotic system to generate a key stream is given for comparison ^[22]. Except for the generation of pseudorandom key streams, the syntax elements of selective encryption are the same.

Table 1.  Video test sequence.

Test sequence	Resolution	Frame rate
PeopleOnStreet	2560ⅹ1600	60
BQTerrace	1920ⅹ1080	50
FourPeople	1280ⅹ720	60
ChinaSpeed	832ⅹ480	30
RaceHorses	416ⅹ240	30

---

 | Show Table

DownLoad: CSV

3.1.   Security analysis of encryption

3.1.1.   Analysis of pseudorandom characteristics of chaotic sequences

In this part, the NIST SP800-22 test standard is utilized to test the randomness of the generated pseudorandom sequence. The test item produces Pvalue, which represents the probability that, given a nonrandom evaluation test, the sequence generated by a perfect random number generator is less random than the sequence being tested. If Pvalue > 0.01, then the sequence under test is considered to be uniformly distributed. SP800-22 Revla suggests that the length of the bit sequence to be tested is 103 to 107, and this algorithm utilizes the test sequence with a length of 106 bits. Table 2 shows the test results. In Table 2, we can conclude that the cipher generated by the L-ICMIC-CML is random.

Table 2.  SP800-22 Revla test result of cipher.

Method	P-value	Result
The Frequency Test	0.8842	Pass
Frequency Test within a Block	0.7984	Pass
The Runs Test	0.6874	Pass
Tests for the Longest-Run-of-Ones in a Block	0.2269	Pass
The Binary Matrix Rank Test	0.1731	Pass
The Discrete Fourier Transform Test	0.8011	Pass
The Non-overlapping Template Matching Test	0.4687	Pass
The Overlapping Template Matching Test	0.5523	Pass
Maurer's "Universal Statistical" Test	0.6812	Pass
The Linear Complexity Test	0.5947	Pass
The Serial Test	0.7298	Pass
The Approximate Entropy Test	0.1695	Pass
The Cumulative Sums Test	0.6321	Pass
The Random Excursions Test
x = −4	0.3574	Pass
x = −3	0.7045	Pass
x = −2	0.3708	Pass
x = −1	0.8654	Pass
x = 1	0.4967	Pass
x = 2	0.8953	Pass
x = 3	0.6701	Pass
x = 4	0.9567	Pass
The Random Excursions Variant Test
x = −9	0.6983	Pass
x = −8	0.2087	Pass
x = −7	0.7762	Pass
x = −6	0.8539	Pass
x = −5	0.9064	Pass
x = −4	0.8871	Pass
x = −3	0.6007	Pass
x = −2	0.4235	Pass
x = −1	0.5748	Pass
x = 1	0.9335	Pass
x = 2	0.6446	Pass
x = 3	0.3754	Pass
x = 4	0.3328	Pass
x = 5	0.2649	Pass
x = 6	0.3687	Pass
x = 7	0.4773	Pass
x = 8	0.4510	Pass
x = 9	0.3308	Pass

---

 | Show Table

DownLoad: CSV

3.1.2.   Analysis of PSNR and SSIM

The peak signal-to-noise ratio (PSNR) ^[20] and structural similarity index metric (SSIM) ^[21] are reference image quality evaluation indexes that are utilized to analyze the image quality of the video before and after encryption from an objective perspective. Table 4-6 lists the average PSNR values of the first 100 frames of the eight test video sequences.

Table 3.  PSNR for original and encrypted videos sequences.

Sequence	PSNR (dB)
	Original	Hyperchaotic system	L-ICMIC-CML system
PeopleOnStreet	42.31	13.95	13.23
BQTerrace	40.57	12.81	11.42
FourPeople	42.43	14.55	12.49
BasketballDrillText	40.69	9.09	10.23
RaceHorses	39.94	11.91	11.54

---

 | Show Table

DownLoad: CSV

Table 4.  SSIM for original and encrypted videos sequences.

Sequence	SSIM
	Original	Hyperchaotic system	L-ICMIC-CML system
PeopleOnStreet	0.944	0.4636	0.3824
BQTerrace	0.973	0.5430	0.5056
FourPeople	0.965	0.6263	0.5741
BasketballDrillText	0.921	0.2710	0.3029
RaceHorses	0.958	0.2355	0.1986

---

 | Show Table

DownLoad: CSV

Table 5.  Encoding time and video data size of original video and encrypted video.

Sequence	Encoding time(s)		Video data size(byte)
	Original	Encrypted	Original	Encrypted
PeopleOnStreet	9488.33	9578.47	15089138	15203211
BQTerrace	5172.34	5217.33	10367701	10414977
FourPeople	1297.69	1317.15	492159	495801
ChinaSpeed	1929.41	1883.10	2213147	2227377
RaceHorses	325.74	331.60	618658	624615

---

 | Show Table

DownLoad: CSV

Table 6.  The EDR of encrypted sequences.

Sequence	Original	Encrypted
PeopleOnStreet	0.189	0.947
BQTerrace	0.148	0.922
FourPeople	0.137	0.934
ChinaSpeed	0.163	0.911
RaceHorses	0.144	0.933

---

 | Show Table

DownLoad: CSV

It can be seen from Tables 3 and 4 that the PSNR and SSIM values of the encrypted images have significantly decreased, and L-ICMIC-CML is more advantageous than hyperchaotic system.

3.1.3.   Analysis of key space

The key space is the value range of the seed key, and it is another important factor that determines the security of the password. The key space must be large enough to resist brute force attacks. It is generally believed that the key space must be at least greater than 2¹²⁸. The length of the algorithm seed key proposed in this paper is 256 bits, indicating that the key space can reach at least 2²⁵⁶, which fully meets the conditions of resistance to brute force cracking.

3.2.   Subjective quality analysis of encryption

3.2.1.   Analysis of the visual disturbance effect

Through the previous analysis of PSNR and SSIM, the image quality of video frames decreases significantly after encryption. Figures 9−13 reflect the effect of subjective visual disturbance. The left side of each figure is the original video frame, the middle is the encrypted video frame of hyperchaotic system ^[14], and the right side is the encrypted video frame of the proposed scheme. It can be clearly seen in the comparison figure that the encrypted video frames have a significant subjective disturbance effect and are almost unrecognizable. The visual disturbance effect of the proposed scheme is better than that of the hyperchaotic system.

Figure 9.  Encrypted frame of PeopleOnStreet.

DownLoad: Full-Size Img PowerPoint

Figure 10.  Encrypted frame of BQTerrace.

DownLoad: Full-Size Img PowerPoint

Figure 11.  Encrypted frame of FourPeople.

DownLoad: Full-Size Img PowerPoint

Figure 12.  Encrypted frame of ChinaSpeed.

DownLoad: Full-Size Img PowerPoint

Figure 13.  Encrypted frame of RaceHorses.

DownLoad: Full-Size Img PowerPoint

3.2.2.   Analysis of encoding time and video data size

The selective encryption algorithm must strictly control the encryption speed, and cannot cause a significant increase in video encoding time. Additionally, the encryption operation cannot affect the original video compression performance, resulting in a significant increase in bit rate. Table 5 shows the encoding time and video file size of 5 video sequences.

From the data in Table 5, it can be concluded that the video compression encoding time of the selective encryption algorithm has no significant change compared with the unencrypted encoding time. The encoding time of videos with strong motion attributes is only slightly increased, and the encoding time of videos with more complex textures is slightly reduced after the encryption operation. This is caused by the encryption operation that flattens the complex textures. The size of the video file does not change greatly before and after encryption. The video with strong motion attributes has a large motion vector difference. The encryption process changes the original motion compensation mode, which makes the encrypted file slightly larger. In summary, the selective encryption algorithm based on L-ICMIC-CML has no negative impact on the video encoding time and compression efficiency.

3.2.3.   Analysis of key sensitivity

The key sensitivity in video encryption refers to using a value close to the correct key to decrypt the video file. If the wrong key is extremely similar to the correct key, valuable video plaintext information cannot be recovered. The video encryption algorithm has high key sensitivity, otherwise the key sensitivity is not strong, and the security is low. In Figure14, the RaceHorses video sequence is taken as an example, and the original image is on the left. Keeping the initial key S unchanged, the video image decrypted by it is shown in the middle, and the wrong decryption key is modified by 1 bit, and the corresponding decrypted video image is shown on the right. Obviously, it can be seen that although only a very slight modification of the key has been made, the video image decrypted by the wrong key is still completely confused and unrecognizable.

Figure 14.  Test of key sensitivity for RaceHorses.

DownLoad: Full-Size Img PowerPoint

3.2.4.   Analysis of edge detection attack

The edge is the boundary of the region where the gray level changes sharply in the image. Therefore, the edge detection first converts the color image to the gray image, and then detects the edge information in the image according to a certain detection algorithm, and finds the coordinates where the gray value changes sharply. Is the edge of the image. The edge detection attack is to perform gray-scale processing on the ciphertext image of the video, and then detect the residual edge information in it, and draw the edge detection map. If the video encryption effect is not good, some edge information will be detected in the ciphertext, thereby revealing the contour and texture characteristics of the plaintext. In order to analyze the video encryption algorithm's resistance to edge detection attacks from a quantitative perspective, this paper uses Sobel operator to perform edge detection on the image. The edge difference ratio (EDR) is calculated to measure the ability to resist edge detection attacks. The calculation method of EDR is shown in Eq (21).

where $P(m, n)$ is the edge pixel value of the original video frame and $\overline P (m, n)$ is the edge pixel value of the encrypted video frame. The closer the EDR is to 1, the stronger the encryption of the algorithm on the edge structure is, and the closer the EDR is to 0, the more similar the edge structure of the two images is. Table 6 shows the EDR of 5 video sequences, all of which are above 0.9. This means that the algorithm can resist edge detection attack well. In addition, Figure 15 shows the edge detection images before and after encryption of the football video.

Figure 15.  Edge detection of BQTerrace.

DownLoad: Full-Size Img PowerPoint

4.   Conclusions

This paper proposes a new chaotic system L-ICMIC-CML based on coupled map lattice. The chaotic dynamic characteristics of the system are analyzed in terms of Lyapunov exponent, bifurcation and ergodicity, and the results show that all indicators are significantly better than traditional chaotic systems. The obtained pseudo-random chaotic sequence perfectly passed the key sensitivity test, key space analysis, linear complexity test, differential attack test, periodic analysis, correlation analysis, spatial distribution test and other security and randomness evaluations, the test results It shows that the binary sequence generated by this method has the characteristics of security, stability, and high efficiency, and is suitable for use as a stream cipher, thereby solving the security and efficiency problems of constructing a stream cipher with a low-dimensional nonlinear system. Through the analysis of the HEVC coding structure, a more suitable encryption scheme is proposed to perform encryption operations on the syntax elements of MVD sign and value, DCT transform coefficient sign and suffix, QP sign and suffix. The test results show that the selective video encryption algorithm solves the problems of security, real-time and bit rate retention while maintaining the video format. Chaos theory research has been carried out for many years, and there have been relatively mature systems and results. However, the research of chaotic cipher basically draws on classical cipher theory and numerical simulation technology, and there is no complete chaotic cipher theory system. Therefore, the construction of chaotic cryptanalysis theory is worthy of further study.

Acknowledgments

This work was supported by the National Natural Science Foundation of China under Grant No. 61672531. And the authors would like to acknowledge the Department of Information Security for providing assistance.

Conflict of interest

The authors declare that they have no conflicts of interest.