Conditionally stable unique continuation and applications to thermoacoustic tomography

1.   Introduction

Let $\Omega\subset {\bf R}^n$ be a bounded domain with a smooth boundary. The purpose of this note is to formulate geometric conditions for conditionally stable unique continuation of solutions of wave type of equations from Cauchy data on a part $S$ of ${\bf R}\times \partial \Omega$ into some subset (which we call $Q_ \varepsilon$ below) of ${\bf R}\times \Omega$. We want to emphasize that the stability is of Hölder type, local, and conditional. Such type of stability holds even for elliptic second order equations; while in classical sense, that problem is unstable, of course. On the other hand, unique continuation is not conditionally Hölder stable in general: One has weak logarithmic stability only ^[2,3]. The behavior of the geodesic flow plays a critical role. The subdomain $Q_ \varepsilon$ of ${\bf R}\times \Omega$ where the conditional estimate holds is smaller that the domain of influence where we have unique continuation, and in particular has the property that every zero bicharacteristic (projected to the base) through it hits $S$. It remains an open question if that characterizes the optimal $Q_ \varepsilon$. The proof is based on an estimate of Carleman type established in ^[7,10].

We consider the case where a subdomain of $\Omega$ can be foliated by strictly convex hypersurfaces covering in particular a part $\Gamma$ of $\partial \Omega$, see Figure 1. This is connected to the existence of a strictly convex function $\rho$ as shown in ^[13]. Such assumptions have been found to be useful in Control Theory, see, e.g., ^[26] but they become more important with the recent progress in the local inversion of the geodesic X-ray transform in dimensions $n\ge3$ ^[20,27] and the boundary and the lens rigidity problems ^[18,19]. We choose a suitable pseudo-convex function in ${\bf R}\times\Omega$ related to $\rho$ which would allow us to apply the results in ^[7,10].

We present an application to multiwave tomography proving conditional local Hölder stability from partial measurements in Section 4.

2.   Elliptic equations

We start with a short review of the elliptic case. Let $\Delta_g$ be the Laplacian associated with a smooth Riemannian metric $g$ in $\bar\Omega$. Let $\Gamma\subset \partial \Omega$ be a relatively open subset of the boundary. We are interested in the stability of the following boundary value problem

where $\nu$ is the unit (in the metric) external normal. Note that (1) may not be solvable with any prescribed $f$, $h_0$ and $h_1$, even if $f = 0$. On the other hand, the possible solution is unique in $\Omega$, by classical unique continuation, which also follows from the theorem below.

Then we have the following conditional stability theorem.

Theorem 2.1. [10,Theorem 3.3.1] For every domain $\Omega_0$ with $\bar\Omega_0 \subset \Omega\cup \Gamma$, there exists $\kappa\in(0, 1)$, $C > 0$, so that for any solution $u\in H^1(\Omega)$ of (1) satisfies

with

This theorem implies unique continuation in particular: If $f$, $h_0$ and $h_1$ all vanish, then $u = 0$. It also implies conditional stability in the following sense: If $u$ is a priori bounded in $H^1(\Omega)$, and when $F$ is uniformly bounded (the real interest in (3) is when $F\ll1$), then

where $C$ depend on those a priori bounds. The result holds if we add lower order terms to $\Delta_g$ with real coefficients. Note that the geometry of $g$ does not play an apparent role.

The estimate is obtained with Carleman estimates and the existence of a positive constant $\kappa$ comes from an optimization of the large parameter in the Carleman estimate and gets small, as $\Omega_0$ gets closer to $\Omega$. This means decreased stability.

Such an estimate may look unexpected since the Cauchy problem for elliptic equations is a classical example of a unstable problem. The reason it holds is the a priori assumption that $u$ is bounded in the larger $\Omega$ where $u$ can grow even more. The following example illustrates this fact.

Example 1. Let $\Omega = (0, \pi)\times (0, 1)$ and consider the following family of harmonic functions

with $m = 1, 2, \dots$. Let $\Gamma$ be the lower side of the square. Then $u$ vanishes on $\Gamma$ (and on the lateral sides of the square) and $h_1 : = u_y|_{y = 0} = m \sin(mx)$. Therefore, $h_0 = 0$, $\|h_1\|_{L^\infty(\Gamma)} = m$. It is straightforward to show that $\|u\|_{H^1(\Omega)}\ge C e^{m}$, therefore,

and there is no stability since $m$ can be arbitrary large. It is also clear that even if we use different Sobolev norms, the conclusion would be the same.

On the other hand, if $\Omega_ \varepsilon = (0, \pi)\times (0, 1- \varepsilon)$ with $0 < \varepsilon < 1$, then it is easy to see that $\|u\|_{H^1(\Omega_ \varepsilon)}\sim Ce^{(1- \varepsilon)m}$, as $m\to\infty$. Then in (2),

Therefore, (2) holds for $\Omega_0 = \Omega_ \varepsilon$ with $0 < \kappa\le \varepsilon$ and $C = C(\varepsilon)$.

Similar result holds for analytic continuation as well (analytic functions solve the elliptic $\bar\partial$ equation). Even though analytic continuation is unstable, there is a a conditional stability in the complex plane, for example by the Hadamard three-circle theorem. In other words, there is conditional stability from one domain to another, bounded one, if there is an a priori estimate in a third even larger one but that third has to be complex.

3.   Conditional stability for the wave equation

Let $g$ be a Riemannian metric in ${\bf R}^n$. Consider the wave equation

where $P = \partial_t^2-L$, and $L = \Delta_g+a^j\partial_{x^j}+q$ is a first order perturbation of $\Delta_g$ with smooth coefficients, and $T > 0$ is fixed. Let $\Gamma\subset \partial \Omega$ be a relatively open subset. In time-space, the underlying metric is the Lorentzian one $- \mathrm{d} t^2+g$.

3.1.   Review of unique continuation

Let $f = 0$ for now. Then the Cauchy data of $u$ on $[0, T]\times \Gamma$ determine $u$ uniquely in the domain of influence:

by Tataru's uniqueness continuation theorem ^[23,24], see also ^[15,16] for a formulation in this setting. This argument does not prove Hölder type of stability, even a conditional one but there are weaker logarithmic estimates ^[2,3]. Indeed, if there are unit speed geodesics $\gamma(t)$ so that $(t, \gamma(t))$ is contained in $Q_{\Gamma, T}$ but does not hit $[0, T]\times\Gamma$ (and this is possible for some $\Gamma$'s), one can concentrate solutions having singularities that do not reach the observation domain, see, e.g., ^[14] and then those singularities of $u$ would be invisible. On the other hand, if that cannot happen, the singularities of $u$ over $Q_{\gamma, T}$ (they are on the light cone) would be stably recoverable. That argument alone however does not imply that $u$ restricted to $Q_{\gamma, T}$ or any subcompact set is stably recoverable. If we knew that $u$ were supported in $Q_{\gamma, T}$ then one could apply the argument that a priori uniqueness and stable recovery of singularities implies actual Lipschitz stability ^[14]. On the other hand if $u$ has such a support it would be zero by unique continuation. Note that for those arguments, $u$ needs to solve the wave equation in $Q_{\Gamma, T}$ only, up to its lateral boundary $[0, T]\times \partial \Omega$.

3.2.   (Strong) pseudo-convexity and convexity

We recall the basic notions pseudo-convexity related to Carleman estimates and also recall the link between them and geometric convexity w.r.t. the geodesic flow. For the definitions below, see, e.g., ^[7]. Let $P$ be a differential operator $P$ with real principal symbol $p(x, \xi)$. The oriented level hypersurface $\Sigma = \{\psi = 0\}$ of a smooth function $\psi$ with $\mathrm{d}\psi\not = 0$ is called pseudo-convex w.r.t. $P$ if $H_p^2\psi > 0$ whenever $\psi = p = H_p\psi = 0$, $\xi\not = 0$, where $H_p$ is the Hamiltonian vector field of $p$. This definition is independent of the choice of $\psi$ defining $\Sigma$. In our case, $p = -\tau^2+|\xi|^2$, where $|\xi|$ is again the norm of the covector $\xi$ in the metric $g$. In geometric terms, those conditions say that $\Sigma$ is strictly convex w.r.t. the lightlike geodesics of $- \mathrm{d} t^2+g$.

The smooth function $\psi$ is pseudo-convex w.r.t. $P$ if $H_p^2\psi > 0$ on $p = 0$, $\xi\not = 0$. The function $\psi$ is strongly pseudo-convex if it is pseudo-convex and $\{\Re p_\psi, \Im p_\psi\} > 0$ for $p_\psi = 0$, $\xi\not = 0$, $\tau > 0$, where $p_\psi = p(x, \xi+ \mathrm{i}\tau\nabla\psi)$. The level hypersurface $\Sigma = \{\psi = 0\}$ of a smooth function $\psi$ with $\mathrm{d}\psi\not = 0$ is called strongly pseudo-convex w.r.t. $P$ if it is pseudo-convex and $\{\Re p_\psi, \Im p_\psi\} > 0$ for $p_\psi = \{p_\psi, \psi\} = 0$, $\xi\not = 0$, $\tau > 0$.

For second order operators $P$, strong pseudo-convexity of non-characteristic hypersurfaces is equivalent to pseudo-convexity.

Given such a defining function $\psi$ of a (strongly) pseudo-convex hypersurface, the function $\phi = \exp(\lambda\psi)-1$ is a (strongly) pseudo-convex for $\lambda\gg1$, see, e.g., ^[7,25]; and $\Sigma = \{\phi = 0\}$, moreover, $\{\phi > 0\} = \{\psi > 0\}$.

If $g$ is a Riemannian or a Lorentzian metric, $\psi$ is called strictly convex if the Hessian ${\rm Hess}(\psi) = \nabla\nabla \psi$, where $\nabla$ is the covariant derivative, is positive as a quadratic form, i.e.,

We recall a conditional stability theorem proven in ^[7,10]. The version below is as in [7,Theorem 3.3], see also ^[6,17]. Given a smooth domain $Q$ and a smooth function $\phi$, set

In particular, $Q_0 = Q_ \varepsilon$ with $\varepsilon = 0$.

In [10,Theorem 3.4.1], a Hölder type conditional stability estimate for the wave, and for more general hyperbolic problems, see also ^[7], similar to (2) is proven assuming existence of a suitable pseudo-convex function. The goal of the next theorem is to connect the foliation condition of a subdomain of $\Omega$ with the existence of a pseudo-convex function and as a result to get conditional stability.

Theorem 3.1. ^[7,10] Let $Q$ be a bounded domain with ${\bf R}^{1+n}$ with $C^1$ boundary $\partial Q$. Let $S\subset \partial Q$ be relatively open. Assume that $\phi\in C^\infty$ is pseudo-convex w.r.t. $P$ on $\bar Q$ and that $\phi < 0$ on $\partial Q\setminus S$. Then there exists $\kappa\in(0, 1)$, so that for any solution $u\in H^1(Q)$ of $Pu = f$ in $Q$ with

satisfies, for $0 < \varepsilon\ll1$,

where

The theorem actually holds for second order real principal type of operators with $C^1$ coefficients in the real part and locally $L^\infty$ lower order coefficients.

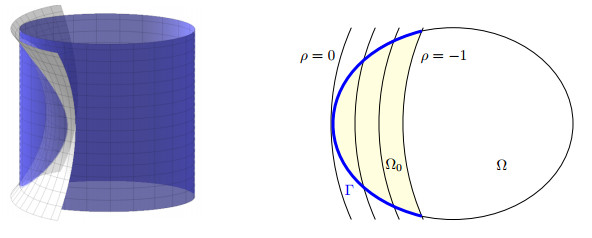
We say that $\Omega_0\subset \Omega$ is foliated by strictly convex hypersurfaces if there exists $c > 0$ and a smooth $\rho:M\to [-c, 0]$ so that $\mathrm{d}\rho\not = 0$ on $M$, the level sets of $\rho = C$ are strictly convex and $\Omega_0\subset \rho^{-1}([-c, 0])$ when viewed from $\rho\ge C$. The strict convexity property is equivalent to $G^2\rho > 0$ when $\rho = c$ and $G\rho = 0$, where $G$ is the generator of the geodesic flow. In applications, it is also required $\rho^{-1}(0)\cup \Omega_0 = \rho^{-1}(0)\cup \partial \Omega_0$. It was shown in ^[13] that the existence of a strictly convex foliation is equivalent to the existence of a strictly convex function (of the kind $\phi(\rho)$ with some $\phi$) if $\Omega_0$ is connected at least.

Set

see also the definition of $\kappa$ in ^[26].

Corollary 3.1. Let $\rho\in C^\infty({\bf R}^n)$ be such that $\rho\le0$ in $\bar\Omega$, and $| \mathrm{d}\rho| > 0$, ${\rm Hess}(\rho)\ge 2c_H > 0$ when $-c\le\rho\le 0$. Let

Let $\phi = c+\rho-\alpha t^2$ with $0 < \alpha < \min(c_H, c_d)$. Then for $0 < \varepsilon\ll1$, there exists $\kappa\in(0, 1)$, $C(\varepsilon) > 0$, so that for any solution $u\in H^1(Q)$, with $Q = (0, T)\times \Omega$, of (4) satisfying (7) we have (8).

Proof. Clearly, $\phi > 0$ implies $\rho > \alpha t^2-c\ge -c$. On the other hand, $\phi\le c$ in ${\bf R}\times\bar\Omega$, see also Figure 1. Therefore, $\phi$ takes values in $[0, c]$ in $Q_0$. We show first that the levels $\phi = C\in [0, c]$ are timelike when $\phi > 0$, and in particular, non-characteristic. We have

Since $\mathrm{d}\phi = (-2\alpha t, \mathrm{d}\rho)$, this proves the claim.

We will show that $\phi$ is pseudo-convex when $\phi \in[0, c]$. It is enough to do this in the tangent instead of the cotangent bundle, see, e.g., ^[17]. The generator of the lightlike geodesics of $- \mathrm{d} t^2+g$ is proportional to $\partial_t\pm G$. We have $(\partial_t\pm G)^2\phi = -2\alpha+G^2\rho$. Since $G^2\rho = {\rm Hess}(\rho)(v, v)\ge 2c_H$, we get $(\partial_t \pm G)^2\phi\ge 2c_H-2\alpha > 0$. Note that at this point of the proof we needed $G^2\rho > 0$ not just along directions tangent to the level sets of $\rho$. Therefore, $\phi$ is pseudo-convex. We can take $\psi = e^{\lambda\phi}-1$ with $\lambda\gg1$ to get a strongly pseudo-convex function $\psi$ with $\{\phi > 0\} = \{\psi > 0\}$. Then we apply Theorem 3.1.

To estimate the largest $|t|$ on $S\cap \{\phi > 0\}$, we write $c+\rho-\alpha t^2 > 0$; therefore $|t| < \sqrt{(c+\rho)/\alpha}$ and since the maximal value of $\rho$ in $\bar\Omega$ is $0$, we get $|t| < \sqrt{c/\alpha}$. Since $\alpha < \min(c_H, c_d)$, taking $\alpha$ closer and closer to its upper bound, we get that the supremum of $|t|$ for such $\alpha$ and $\varepsilon > 0$ is $T_0$.

3.3.   Relation to propagation of singularities

The conditional estimate (8) would not hold if there is a lightlike geodesic in $Q_ \varepsilon$ which does not hit $S$. We can see directly that this does not happen. Indeed, for every lighlike geodesic $\gamma(t)$, since $0 < \alpha < c_H$,

as long as $\phi$ is pseudo-convex. Indeed, for every vector $v = (v^0, v')\in {\bf R} \times {\bf R}^n$, we have ${\rm Hess}(\phi)(v, v) = -2\alpha |v^0|^2 +{\rm Hess}(\rho)(v', v')$, and if $v$ is lightlike, then $|v^0|^2 = |v'|^2$, therefore, ${\rm Hess}(\phi)(v, v)\ge (2c_H-2\alpha)|v'|^2 > 0$. Therefore, $\phi\circ\gamma(t)$ is a strictly convex function and as such, it increases either strictly for $t > 0$ or for $t < 0$ in negative direction. Then $\gamma(t)$ hits ${\bf R}\times \partial \Omega$ in $\{\phi > 0\}$ which is contained in $S$ where we have "measurements". The singularities of $u$ are lightlike only; and regarded as vectors (rather than covectors), they are lightlike as well and occupy entire lightlike geodesics $(\gamma, \dot\gamma)$. Therefore, all singularities of $u$ are "measured".

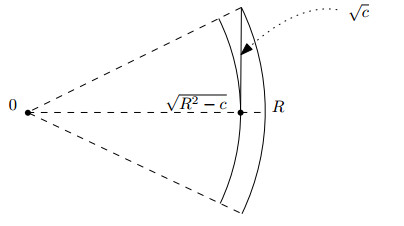
It is interesting to estimate how optimal the set $\{\phi > 0\}\subset S$ is w.r.t. the requirement that each singular bicharacteristic of $u$ reaches $S$. Let $g$ be Euclidean and let $\Omega = B(0, R)$ with $R > 1$. One can take $\rho = |x|^2-R^2$. Then $-c < \rho < 0$ defines the annuls $\Omega_0: = \{\sqrt{R^2-c} < |x| < R\}$, and we assume $c < R^2$. We have ${\rm Hess}(\rho)(v, v) = 2|v|^2$ and $\phi = c+|x|^2-R^2-\alpha t^2$. Then $c_H = 1$ and $| \mathrm{d}\rho| = 2|x|$; therefore,

Thus $c_d\ge1$. Then the condition for $\alpha$ reduces to $0 < \alpha < 1$ and $T_0 = \sqrt{c}$.

On the timelike geodesics $\gamma(t) = (t_0+t/\sqrt\alpha, x_0+t\theta)$, $|\theta| = 1$, (11) vanishes. This characterizes $\{\phi = 0\}$ as the union of all such spacelike geodesics tangent to that hypersurface at some point (for uniqueness, one can take points on $t = 0$). For each fixed $t$, those are the geodesics starting from some $x\in\bar\Omega$ with $\phi(t, x)\ge0$ maximizing the escape time (with speed $\sqrt\alpha$) to the boundary. Taking $\alpha < 1$ closer and closer to $1$, we see that $Q_0$ is, asymptotically, the smallest domain for which there would be no lightlike geodesics through it not hitting $S\cap\{\phi\ge0\}$. Therefore, at least in this case, $Q_ \varepsilon$ is a sharp domain.

Let us say that we are interested in $u|_{t = 0}: = f$ as in the next section. Note that to have unique continuation of $f$ on some subdomain $\Omega_0$ in $\bar\Omega$ from $(-T, T)\times\Gamma$ with $\Gamma\subset \partial \Omega$, we need $T$ such that every point $x$ there can be reached from $\Gamma$ at time $T$ or less, see (5). This is a condition on the shortest geodesic from $x$ (assuming convexity). In contrast, the conditional stability requires $T$ to exceed the length of the longest escape time from every such $x$ and every direction; and it is sharp at least in the special case above. To be more precise, denote by $\gamma_{x, v}(\tau)$ the unit speed geodesic starting from $(x, v)\in S\Omega$. Set

where $\tau(x, v)$ is the shortest time $\tau$ when $\gamma_{x, v}(\tau)$ hits $\Gamma$, if it does; if it does not, we set $\tau(x, v) = \infty$. Then we need $T > T_{\rm esc}$. In the Euclidean example above, $T_{\rm esc}$ is maximized when $|x|^2 = R^2-c$ and $v$ is tangent to that ball; then $T_{\rm esc}\to T_0$ as $\alpha\to1-$, see Figure 2.

4.   Applications to photo and thermo-acoustic tomography

Consider the multiwave tomography model in a closed domain modeling waves reflecting from the boundary, see ^{[4,9,11,12,22]} and the UCL photoacoustic imaging group experimental setup in ^[5]. In thermo- and photo-acoustic imaging, one sends a short microwave/optical impulse into a tissue which triggers heat expansion and generates ultrasound waves by the thermo-acoustic or the photo-acoustic effect. Those waves are measured on the boundary, very often just a subset of the whole boundary. The goal is to recover the acoustic source which would tell us more about the properties of the tissue. The model with reflecting waves is described below, following ^[22].

Let $\Omega\subset {\bf R}^n$ be a bounded smooth domain and fix $T > 0$. The acoustic pressure $u$ solves the problem

where $c(x) > 0$ is a smooth wave speed in $\bar\Omega$, and $\nu$ is the unit outward normal. One can replace $\Delta$ by the Laplace-Beltrami operator related to a fixed Riemannian metric, see ^[21]. The measurements operator $\Lambda$ is given by

The energy

is preserved. The natural space for $f$ is the Dirichlet one with the norm $\|f\|_{H_D(\Omega)} = \|\nabla f\|_{L^2(\Omega)}$, which is really a norm on functions in $H_0^1(\Omega)$ and equivalent to the norm in the latter space by the Poincaré inequality. We also assume that ${\rm supp}~ f\in K$ with some smooth compact set $K\Subset\Omega$; then $f\in H_D(K)$ and that $\partial \Omega$ is convex w.r.t. the metric $c^{-2} \mathrm{d} x$. Then all singularities of $f$ hit $\partial \Omega$ transversely and $\Lambda: H_0^1(K)\to H^1((0, T)\times \partial \Omega)$ is continuous. Next, the zero initial condition for $u_t$ at $t = 0$ implies that the even extension of $u$ in the $t$ variable solves the wave equation as well and we may assume that $\Lambda$ is given on $(-T, T)\times \partial \Omega$.

Assume that we know $\Lambda f$ on $(0, T)\times\Gamma$, where $\Gamma\subset \partial \Omega$ as before. The following sharp uniqueness theorem follows directly from unique continuation, see ^[22].

Theorem 4.1. ^[22] $\Lambda f|_{(0, T)\times\Gamma}$ determines uniquely $f$ in the set

and $f$ restricted to $\Omega\setminus\bar\Omega_T$ can be arbitrary.

In ^[15], we also showed that one can get recover all visible singularities in a stable way (by time reversal, which is an FIO of order zero associated with a canonical graph). The point $(x, \xi)\in T^*\Omega\setminus 0$ is called visible singularity for this problem if either the geodesic issued from $(x, \xi/|\xi|)$ or that issued from $(x, -\xi/|\xi|)$ reaches $\partial \Omega$ for time $< T$. Here, $|\xi|$ is the norm of the covector $\xi$ at $x$ in the metric, identified with a vector by the metric. Note that the there might be singularities over $\Omega_T$ that are invisible.

Even when $T^*\bar\Omega_0\setminus 0$ contains visible singularities only (then $\Omega_0\subset \Omega_T$), one cannot prove stability of recovery of $f$ in a set $\Omega_0$ based on the uniqueness theorem above and combined with the microlocal stability statement because the latter only applies under the a priori assumption that ${\rm supp}~ f\subset\Omega_0$ as in ^[15]. Using the methods above, we get the following.

Theorem 4.2. Let $\rho$ and $T_0$ be as in Corollary 3.1 and let $\Omega_ \varepsilon = \Omega\cap \rho^{-1}(-c+ \varepsilon, 0)$, $\varepsilon\ge0$. Let $\Gamma = \partial \Omega \cap \rho^{-1}[-c, 0]$. Then, if $T > T_0$, for every $\varepsilon\in (0, 1)$ we have

with some $C > 0$, $\kappa\in(0, 1)$ depending on $\Omega_ \varepsilon$.

Proof. We apply Corollary 3.1. Set $Q = [-T, T]\times\Omega$ with $T > 0$ large enough so that $\bar Q\supset \bar Q_0$, with $Q_ \varepsilon$ defined in (6). Even though $Q$ does not have smooth boundary, one can always make it smooth if needed by a small modification and this would not affect Corollary 3.1. Note that $\Omega_ \varepsilon = Q_ \varepsilon\cap \{t = 0\}$. Then

To estimate the $u$-term on the right, write

We also have $\|\Lambda f\|_{H^1(S)}\le C\|f\|_{H^1}$. Those arguments show that the r.h.s. of (15) can be estimated as in (14).

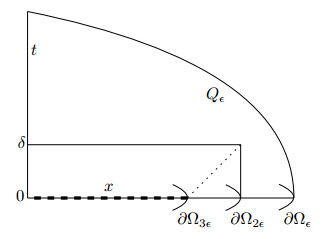
To estimate the l.h.s. of (15) from below, notice first that for $0 < \delta\ll1$, $[-\delta, \delta]\times \Omega_{2 \varepsilon}\subset Q_ \varepsilon$, see also Figure 3.

Therefore,

By standard energy estimates used to prove for domain of influence/domain of influence results, $E_{\Omega_{2 \varepsilon}}(t, u)\ge E_{\Omega_{3 \varepsilon}}(0, u)$ when $\delta\ll1$, therefore,

One the other hand,

by the trace theorem. Those two estimates allow is to estimate the l.h.s. of (15) by $\|f\|_{H^1(\Omega_{3 \varepsilon})}$.

Therefore, we proved (14) with $\Omega_0$ replaced by $\Omega_{3 \varepsilon}$. We can extend $\rho$ a bit so that it has the same properties as before on $-1-3 \varepsilon\le \rho\le0$ for $0 < \varepsilon\ll1$ and then apply what we proved above.

If $\Gamma$ has the property that every geodesic of $c^{-2} \mathrm{d} x^2$ through $K$, reflecting from the boundary according to the law of geometric optics eventually intersects $\Gamma$ either for positive and negative time $\pm T$, then one has even a Lipshitz non-conditional estimate on $f$ in the whole $K$, as it follows form control theory, see ^[1,22], also ^[26]. On the other hand, in Theorem 4.2, $\Gamma$ does not need to satisfy that condition and even of it does, one needs $T$ to be larger in general that what we require. Also, on the rest of the boundary one can impose diferent boundary conditions, even absorbing ones, as long as the boundary value problem is well posed. One can have an infinite $\partial \Omega$ with an infinite $\Gamma$ as well (with $\partial \Omega$ not closed in particular) and by finite speed of propagation, $\Lambda f$ would be supported on a compact set depending on $T$.

One can also apply those arguments to the classical model where the waves propagate into the whole space but measurements are still taken on $(0, T)\times \partial \Omega$. For that, one needs to recover, in a Hölder stable way, the normal derivative $\partial_\nu$ on $(-T, T)\times\Gamma$ from the knowledge of $u$ there. This is a non-trivial step and uniqueness was first proved in ^[8] when $c = 1$ and in ^[15] for a variable $c$. First that we can extend the data to $t\in (-T, -T)$ as an even function as noted above. Then we recover the Neumann data on a part of $\Lambda f|_{(-T, T)\times\Gamma}$ first, then we use unique continuation to recover $f$ near $\Gamma$ only; that allows us to recover the Neumann (and therefore, the Cauchy) data on a large part of $\Lambda f|_{(0, T)\times\Gamma}$; and in finitely many step, we recover $f$ in $\Omega_T$. We will not pursue this further.

Acknowledgments

The author thanks Lauri Oksanen for his remarks which helped improve the exposition. The work was partly supported by NSF Grant DMS-1600327.

Conflict of interest

The author declares that there is no conflict of interest in this manuscript.