Classification and simulation of chaotic behaviour of the solutions of a mixed nonlinear Schrödinger system

1.   Brief highlights

In the last recent decades, interests have been directed towards PDE systems. Theoretical and numerical developments as well as practical studies have shown that these systems are better descriptors of several physical and natural phenomena than modelling with a single equation. Among these models nonlinear Schrödinger's systems of equations have taken a crucial role. Such types are applied in several fields such as optics, plasma, fluid mechanics, solitons' physics, chaos, fractals, ... etc.

However, we have noticed that most of the nonlinear Schrödinger system models developed revolve around cubic nonlinearities for both single and mixed nonlinearities composed of two or more terms. Few works have dealt with mixed terms with non-cubic parts. This may be due to the fact that in the cubic nonlinear Schrodinger equation the general form of the solution is the well known soliton type

where $a$, $c$, $\theta$, $\varphi$ and $\phi$ are some appropriate constants. It consists in fact of a soliton-type disturbance which travels with the speed $c$.

In our work we consider a mixed nonlinear term composed of two parts, a super-linear part and a cubic part. It may be understood as a perturbation of the cubic system. We propose to develop a classification of solutions, their behaviour, existence and uniqueness. We also noticed during this study that some chaotic behaviour can take place. Consequently, we have considered some types of dynamical systems from the Schrödinger system and we have carried out some numerical simulations of the chaotic behaviour of these systems. The chaotic behaviour in our knowledge is not yet investigated. This may be due to the perturbation of the cubic system.

2.   Introduction

Schrödinger equation since its discovery constitutes a challenging concept in physics as it models many phenomena in optics, plasma, fluid mechanics, etc. Enormous studies have investigated such an equation and the exact determination of solutions remains a complex task in the nonlinear case. In such a case even if we know some solutions, the linear combination may not be one also. Many types of solutions have been discovered in the nonlinear case such as solitons.

Recently, studies have been focused on the extension of such single equation to the case of a system of coupled equations of Schrödinger type and proved that such systems may describe better many phenomena in different fields such as simultaneous solitons, interaction of solitons, etc.

The present paper is subscribed in this last case and focuses on a special type of nonlinear coupled Schrödinger equations in one dimension space. We study a couple of NLS equations characterized by mixed nonlinearities involving convex and concave parts such as cubic, super-linear and sub-cubic power laws. Classification of the solutions as well as existence and uniqueness of the steady state solutions have been investigated. Numerical simulations illustrating the effects of the problem parameters on the solution are provided. We stress here on the fact that, in our knowledge, no previous study has investigated the present mixed case, but instead the majority of studies dealing with mixed nonlinearities have been conducted for the cubic-cubic special case.

The paper is devoted to the study of some nonlinear systems of PDEs of the form

where $u = u(x,t)$, $v = v(x,t)$ on $\mathbb{R}\times(t_0,+\infty)$, $t_0\in\mathbb{R}$ with suitable initial and boundary conditions. The operators $\mathcal{L}_1$ and $\mathcal{L}_2$ are linear Schrödinger-type operators of the form

leading to a nonlinear Schrödinger system. $u_{xx}$ is the second order partial derivative relatively to $x$, $u_t$ is the first order partial derivative in time, $\sigma_i$, $i = 1,2$ are constant real positive parameters. $f_1$ and $f_2$ are nonlinear continuous functions of two variables.

Remark that for $\sigma_1 = \sigma_2 = 1$, $u = v = \varphi$ and $f_1 = f_2 = f$, we come back to the original Schrödinger equation

On the other hand, this last equation itself may lead to a system of PDEs of real valued functions satisfying a Heat system. Indeed, assume that $u = v$ and let $\varphi = u+iv = (1+i)u$, we get a system of coupled Heat ones

where $f_1$ and $f_2$ are issued from the real and imaginary parts of $f(\varphi)$.

Return again to the system (1) in the simple case $\sigma_i = 1$ and denote $\varphi = u+iv$ and $f(\varphi) = f_1(u,v)+if_2(u,v)$, we come back to the classical NLS equation where $u$ and $v$ may be seen as real and imaginary parts of the solution $\varphi$ of an equation of the form (2).

As related to many physical/natural phenomena such as plasma, optics, condensed matter physics, etc, nonlinear Schrödinger systems have attracted the interest of researchers in different fields such as pure and applied mathematics, pure and applied physics, quantum mechanics, mathematical physics, and continue to attract researchers nowadays with the discovery of nano-physics, fractal domains, planets understanding, etc. For instance, in hydrodynamics, the NLS system may be a good model to describe the propagation of packets of waves according to some directions where a phenomenon of overlapping group velocity projection may occur [16]. In optics also, the propagation of short pulses has been investigated via a system of NLS equations [25]. See also [33].

The most known solutions in the case of NLS equation are the so-called solitons. These are special wave functions characterized by a self-reinforcing wave packet and maintaining their shape along their propagation direction while their velocity is maintained constant. However, a rigorous and complete definition is no longer determined. Therefore, researches are always growing up to approach such waves. For example, it is well known in particle physics that solitons may interact to yield other forms of solitons as well as other physical particles. In [14] interactions of multi-soliton solutions have been studied with an asymptotic expansion. In [19] soliton type solutions are discovered for a couple of NLS equations in the framework of intensity redistribution leading to particles' collision. In [25] solitons solutions have been investigated in the case of propagation of short pulses in birefringent single-mode fibers governed by an NLS model. More about soliton solutions for single as well as coupled nonlinear Schrödinger equations may be found in [27,32,36,37].

In single NLS equation, studies have been well developed from both theoretical and numerical aspects. Recently, a mixed model has been developed in [4,5,6,7,8,9,10,15,20,21,24,26,34,35] with a general form

which coincides for $u = v$ with the two variable extending interesting model

In the literature, few works are done on the general model (5). The major studies have focused on the mixed cubic-cubic ($p = q = 3$)

For example, in [36], (2+1)-dimensional coupled NLS equations have been studied based on symbolic computation and Hirota method via the cubic-cubic nonlinear system

where $\alpha$ and $\sigma$ are real parameters. The same system has been also studied by many authors such as [1,14,18,19,27,32]. In [37], the following more general system has been investigated for the asymptotic time behavior of the solutions,

See also [17]. In [13] the following $p$-Laplacian stationary system has been discussed for necessary and sufficient conditions for the existence of the solutions

where $\Delta_pu = div(|\nabla u|^{p-2}\nabla u)$ is the $p$-Laplacian $(1<p<N)$. In [11], solutions of the type

where $u$ is a real function known as standing wave or steady state and $w\in\mathbb{R}$ has been investigated leading to the time-independent problem

See also [33]. Already with the familiar cubic-cubic case, numerical solutions have been developed in [38] for the one-dimensional system

on $\mathbb{R}$, where $u$ and $v$ stand for the wave amplitude considered in two polarizations. The parameter $\beta$ is related to phase modulation. $u_0$ and $v_0$ are fixed functions assumed to be sufficiently regular.

Coupled NLS system has been analyzed for symmetries and exact solutions in [23]. The problem studied is related to atmospheric gravity waves governed by the following general coupled NLS system.

It is noticed that such a problem may be transformed to the well known Boussinesq equation.

In [2] novel effective approach for systems of coupled NLS equations has been developed for the model problem

where $f$ and $g$ are smooth nonlinear real-valued functions depending on $(|u|^2,|v|^2)$ and $\sigma_1$, $\sigma_2$ are real parameters. In [29] the following nonlinear cubic-quintic and coupling quintic system of NLS equations has been examined,

where $u$ and $v$ describe the complex envelopes of an electric field in a co-moving frame. $\alpha$ and $\gamma$ are potentials. $\beta$ and $\delta$ are amplifications. The functions $f_j$ and $g_j$, $j = 1,2,3,4$ describe the cubic, quintic and coupling quintic nonlinearities coefficients, respectively. $m_1$ and $m_2$ stand for the dispersion parameters.

In [22] existence of ground state solutions has been studied for the NLS system

$x\in\mathbb{R}$, $t>0$, $j = 1,2$.

In [30] a multi-nonlinearities coupled focusing NLS system has been studied for existence of ground state solutions and global existence and finite-time blow-up solutions. The authors considered precisely the coupled system

where $u_j:\mathbb{R}^N \times \mathbb{R}\rightarrow\mathbb{C}$, $j = 1,2,\dots,m$ and the $a_{jk}$'s are positive real numbers with $a_{jk} = a_{kj}$.

In the present work, we focus on the nonlinear mixed super-linear cubic defocusing model

with $\lambda>0$ and $1<p\not = 3$. We consider the evolutive nonlinear Schrödinger system on $\mathbb{R}\times(0,+\infty)$,

Focuses will be on the steady state solutions according to their initial values. We propose precisely to develop a classification of the steady state solutions of problem (18) provided with the existence and uniqueness problems. We will consider specifically the case where the two waves $u$ and $v$ have the same frequency or the same pulsation $\omega$. In this case, the steady state solution of problem (18) is any solution of the form

$\omega>0$. Substituting $W$ in problem (18), we immediately obtain a solution $(u,v)$ of the system

We will see that classifying the solutions of problem (19) depends strongly on the positive/negative/null zones of the nonlinear function model

which in turns varies according to the parameters $p$, $\lambda$ and $\omega$. Denote

and

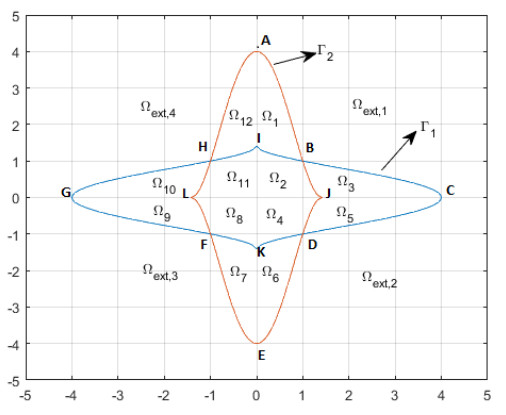
It is noticeable that such curves are more and more smooth whenever the parameter $p$ increases. To illustrate this fact, we provided in Appendix 8.2 a brief overview for some cases of $\Gamma_1$, $\Gamma_2$ and $\Lambda$. See Figures 1 and 2.

Note here that $\Lambda$ does not depend in fact on $\omega$, and that the problem is symmetric in $(u,v)$. However, if the two waves have different pulsations $\omega_1$ and $\omega_2$ we get a non-symmetric problem and new difficulties appear.

The paper is organized as follows. The next section is concerned with the development of our main results on the classification, existence and uniqueness of a coupled mixed cubic, superlinear sub-cubic Schrödinger system. Numerical simulations are also developed to illustrate graphically the theoretical findings. Section 3 is concerned to the development of the special cases regarding the initial value. Section 4 is devoted to some numerical simulations where a possible chaotic behavior of some dynamical systems issued from the original system is described. Such simulations make more deeper studies to be necessary for future directions to study associated chaotic dynamical systems. Concluding and future directions are next raised in section 5. Section 6 is devoted to some discussions of some special cases issued from the present study such as the case $w = 0$ which corresponds also to the asymptotic problem where $t$ goes to infinity. We also discussed in a second part the possible extensions of our results on the half-space and on the finite interval. Section 7 is the general conclusion of our work in which we raised possible extensions for other forms of coupled systems similar to the one studied here and the p[possibility to benefit from the calculus applied here. An appendix is developed in section 8 to illustrate the effects of the parameters of the problem on the classification of the solutions. We notice that the problem may be completely changing according to these parameters regarding the behavior of the solutions, existence of positive solutions, sign-changing. In some cases such as $p<0$ we may lose the Lipschitz characteristic of the problem and thus any study will necessitate different and more advanced techniques. For example, for some values of $p$ and $\omega$ the region $\Lambda\cap[-1,1]$ is not contained in $\Omega_{2}\cup\Omega_{4}\cup\Omega_{8}\cup\Omega_{11}$ as in our case. The second appendix concerns indeed the validity of Lipschitz theory in our case to guarantee the existence and uniqueness of the solutions.

3.   Main results

As it is noticed in the introduction, the behavior of the solutions depends strongly on the parameters of the problem, especially those affecting the sign of the function $g_{\omega}$. It holds in fact that some of these parameters may be relaxed to

which simplifies the computations needed later. Indeed, denote

The functions $\widetilde{u}$ and $\widetilde{v}$ satisfy immediately the system

Moreover, consider the scaling modifications

where $K_1$, $K_2$, $\alpha$ and $\beta$ are constants to be fixed. The functions $\overline{u}$ and $\overline{v}$ satisfy the system

The constants $K_1$, $K_2$, $\alpha$ and $\beta$ satisfy

which in turns yields that

and

where

and

Given these facts, we will consider in the rest of the paper the problem (20) with the initial conditions

where $a,b\in\mathbb{R}$. Denote also $\omega_{s} = \omega^{\frac{1}{s-1}}$, for $s\in\mathbb{R}$, $s\not = 1$. Figure 1 illustrates the partition of the plane $\mathbb{R}^2$ according to the curves $\Gamma_1$ and $\Gamma_2$. Figure 2 illustrates the partition of the plane $\mathbb{R}^2$ according to all the curves $\Gamma_1$, $\Gamma_2$ and $\Lambda$.

We now start developing our main results. For this aim, we assume in the rest of the paper that

It is straightforward that $\omega_{p}>\omega_{3}$. Moreover, the closed curves $\Gamma_1$ and $\Gamma_2$ intersect at four points $B$, $D$, $F$ and $H$ as it is shown in Figure 1. Notice also that the curves $\Gamma_1$ and $\Gamma_2$ split the plane $(u,v)$ into twelve regions, $\Omega_i$, $i = 1,2,...,12$ and an external region $\Omega_{ext} = \bigcup\limits_{1\leq i\leq4}\Omega_{ext,i}$. Such regions are in the heart of the classification of the solutions of problem (20)-(22). Notice also from the symmetry of the function $g_\omega$ that the points $B$ and $F$ satisfy the Cartesian equation $u = v$ and the points $D$ and $H$ satisfy $u = -v$. Furthermore the polygon $BDFH$ is a square. We may notice that the coordinates of the main points are $A(0,\omega_{p})$, $I(0,\omega_{3})$, $B(u_B,u_B)$ where $u_B$ is the unique positive root of $u^{p-1}+u^2-\omega = 0$. The points $C$, $D$, $E$, $F$, $G$, $H$, $J$, $K$ and $L$ may be deduced from $A$, $B$ and $I$ by symmetries.

The symmetry also shows easily that whenever $(u,v)$ is a pair of solutions of the system (20), the pairs $(-u,v)$, $(u,-v)$ and $(-u,-v)$ are also solutions. Consequently, in the rest of the paper we will focus only on the case where $u(0) = a\geq0$ and $v(0) = b\geq0$. The remaining cases may be deduced by symmetry. As the function $f(u,v)$ is locally Lipschitz continuous, the existence and uniqueness of the solution are guaranteed by means of the famous Cauchy-Lipschitz theory. This will be proved in the Appendix later.

Theorem 3.1. Whenever the initial data $(u(0),v(0)) = (a,b)\in\Omega_1$, the problem (20)-(22) has a unique $(u,v)$ satisfying

$\bf i.$ $u$ and $v$ are oscillating,

$\bf ii.$ $u$ is infinitely sign-changing and $v$ is positive,

$\bf iii.$ $(u,v)$ lies in $\Omega_1\cup\Omega_{12}\cup\Omega_{ext,1}\cup\Omega_{ext,4}$.

Proof. Writing problem (20) at $x = 0$ yields that

Hence, there exists $\delta>0$ small enough such that

Consequently, $u'$ is nonincreasing on $(0,\delta)$ and $v'$ is nondecreasing on $(0,\delta)$. Next, as $u'(0) = v'(0) = 0$, it therefore follows that $u$ is nonincreasing on $(0,\delta)$ and that $v$ is nondecreasing on the same small interval. We claim that $u$ and $v$ do not remain with the same monotony on the $(0,\infty)$ as at the origin. Indeed, assume for example that $v$ remains nondecreasing on $(0,\infty)$. Then, it has a limit $l_v$ as $x$ goes to infinity. Because of the energy functional $E$ associated to problem (20) and defined by

and which is constant as a function of $x$, the limit $l_v$ is finite and positive. Consequently, $u^2$ has also a limit $L_u$ at infinity such that $l_v^{p-1}+L_u-\omega = 0$. Moreover, $|u|$ goes to $l_u = \sqrt{L_u}$. Henceforth,

Assume now that $l_u = 0$. In this case, the solution $(u,v)$ lies in the region $\Omega_{1}$ with its limit being equals to the point $A$ and such that $u$ is nonincreasing and $v$ is nondecreasing on the whole interval $(0,\infty)$. We get

On the other hand

So, consider for $b$ fixed the function

We immediately get

as $[0,a]\times\{b\}\subset\overline{\Omega_{1}}$. Consequently,

Now consider the function

On the interval $(b,\omega_{p})$ it is a nondecreasing function. As a result,

We get a contradiction with the fact that $E(u,v)(x)$ is constant. As a result, $l_u\not = 0$. We conclude that

This yields that $(l_u,l_v)\in\{B,D,F,H\}$ which is contradictory with the eventual monotony assumed for $(u,v)$. We thus conclude that $u$ and $v$ do not remain with the same monotony as in the origin on the whole domain $(0,\infty)$. Let $r_1$ and $r_2$ be the first critical points of $u$ and $v$ respectively. Without loss of the generality we may suppose that $r_1\leq r_2$. Denote next $M_i = (u,v)(r_i)$, $i = 1,2$. We claim that $M(r_1)\in\Omega_{12}\cup\Omega_{ext,4}$. Indeed, assume by the contrary that the turning point $M_1\notin\Omega_{12}\cup\Omega_{ext,4}$. Relatively to the position of the initial point $M_0 = (u,v)(0) = (a,b)$ there are many cases for $M_1$.

Case 1. ${M_1\in\overline{\Omega_{1}}.}$ Multiplying the first equation in (20) by $v$ and integrating on $(0,r_1)$ we get

which is contradictory.

Case 2. $b\leq\omega_{3}$ and $M_1\in\Omega_{2}:$ In this situation we notice firstly that $v(r_1)\geq y_B$. Let $t_0>0$ be the first point in which the curve $(u,v)$ crosses the curve $(B,I)$. We immediately obtain

This is a contradiction as the left-hand and the right-hand quantities have different signs.

Remark 1. $\bullet$ One may prove that for $(a,b)\in\Omega_1$ there exists $\widetilde{b}>0$ depending on $a,b,p,\omega$ such that the solution $(u,v)\in(x_H,x_B)\times(y_B,\omega_p+\widetilde{b})$. A good question is to express $\widetilde{b}$ by means of $\omega$, $p$, $a$ and $b$.

$\bullet$ For $r_1$ and $r_2$ defined above, is it true that $\Bigl(r_1\leq r_2\;\Longleftrightarrow\;\; a\leq b\Bigr)$?

Figures 3, 4, 5, 6 and 7 illustrate some cases of the theoretical result proved in Theorem 3.1. In all these figures we fixed the parameters $p = 1.5$ and $\omega = 2$. In Figure 3 we fixed the initial values $(a,b) = (0.25,2.75)$. It yields that $g_{\omega}(a,b) = 13.3317$ and $g_{\omega}(b,a) = -0.4587$ which confirms that $(a,b)\in\Omega_{1}$. In Figure 4 the initial values are fixed to $(a,b) = (1,\omega_3-0.1)$ which gives $g_\omega(a,b) = 0.6938$ and $g_\omega(b,a) = -0.2830$ which confirms here also that $(a,b)\in\Omega_{1}$. We notice clearly from these figures the compatibility with the result in Theorem 3.1. Moreover we provided in Figure 5 a sketching graph of both $u$ and $v$ starting inside of $\Omega_{1}$. The oscillating behavior of both $u$ and $v$ is clearly illustrated. Furthermore, to confirm again the oscillating behavior we provided in Figures 6 and 7 the phase plane portraits of $u$ and $v$ respectively. The figures show clearly the oscillating behavior.

The next result deals with the behavior of the solution when starting from an initial data $(a,b)\in\Omega_{2}$. We will see that the result depends technically on the position of the initial value in the four sub-regions $\Omega_{2}^1$, $\Omega_{2}^2$, $\Omega_{2}^3$, $\Omega_{2}^4$ shown in Figure 8. In fact we have

and

and where $G_{\omega}(a,b) = g_{\omega}(a,b)-g_{\omega}(a,b)$. The region $\Omega_{2}^1$ will be the union

where $\Gamma_{P_1P_2}$ is the curve joining the points $P_1$ and $P_2$ including them, $\Gamma_{P_2P_3}$ is the curve joining the points $P_2$ and $P_3$ including them. $[O,P_2]$ is the closed segment joining the point $O$ to $P_2$ and finally $[P_2,B]$ is the closed segment joining the point $P_2$ to $B$. In the sequel we will also use the following sets.

● $\overset{\circ}{\Gamma}_{P_1P_2}$ to designate the curve $\Gamma_{P_1P_2}$ without the extremities $P_1$ and $P_2$.

● $\overset{\circ}{\Gamma}_{P_2P_3}$ is the curve $\Gamma_{P_2P_3}$ without the extremities $P_2$ and $P_3$.

● $]O,P_2[$ is the open segment joining the point $O$ to $P_2$.

● $]P_2,B[$ is the open segment joining the point $P_2$ to $B$.

Theorem 3.2. Whenever the initial data $(u(0),v(0)) = (a,b)\in\Omega_2$, the problem (20)-(22) has a unique solution $(u,v)$ where $u$ and $v$ are oscillating and may be both infinitely sign-changing.

Proof. We will develop the proof for the case $(u(0),v(0)) = (a,b)\in\Omega_2^1$. The remaining cases may be checked by similar techniques with necessary modifications and by using the invariance of the domain $\Omega_2$ and problem (20) relatively to the axial symmetry $u = v$.

Whenever $(u(0),v(0)) = (a,b)\in\Omega_2^1$ we may check by similar techniques as in the proof of Theorem 3.1 that

$\bullet$ $u$ and $v$ are nondecreasing on $(0,\delta)$ for some $\delta>0$ small enough.

$\bullet$ $u$ and $v$ are oscillating on the whole interval $(0,\infty)$.

So, let as previously $r_1$ and $r_2$ be the first positive critical points of $u$ and $v$, respectively and assume without loss of the generality that $r_1\leq r_2$. We claim that $M_1 = (u(r_1),v(r_1))\in\Omega_{1}\cup\Omega_{ext,1}$. Indeed, assume that it is not true.

Case 1. Assume that $M_0\in\overline{\Omega_2^1}$. By multiplying the first equation in problem (20) by $v$ and integrating on $(0,r_1)$ we obtain

which is contradictory.

Case 2. $M_1\in\Omega_2^4$. Let $M_1 = (u(x_1),v(x_1)), x_1< r_1$ be the point where the curve $(u,v)$ intersects $[P_2,B]$. On $[x_1,r_1]$ we get

which is impossible as the left and the right terms have opposite signs.

Case 3. $M_1\in\Omega_3$. Let $x_2$ be such that $(u(x_2),v(x_2))$ is the intersection point of the curve $(u,v)$ with the curved line $(B,J)$. Integrating the first equation in problem (20) multiplied by $v$ on the interval $(x_2,r_1)$ we get a contradiction as in case 1.

As a consequence of these cases we conclude that the point $M_1\in\Omega_{1}$ and thus the solution $(u,v)$ crosses at the curved line $(I,B)$. Now, Theorem 3.1 yields the behavior of the solution.

Now similarly to the previous case we provide in Figures 9, 10 and 11 some graphical illustrations of the theoretical result proved in Theorem 3.2. We fixed here also for all these graphs $p = 1.5$ and $\omega = 2$ as previously to be adequate with the previous case. The Figures show clearly the oscillating behavior of the solutions and show further the compatibility with the result in Theorem 3.2.

Theorem 3.3. Whenever the initial data $(u(0),v(0)) = (a,b)\in\Omega_{ext,1}$, the problem (20)-(22) has a unique solution $(u,v)$ where

$\bf i.$ $u$ and $v$ are oscillating and may be both infinitely sign-changing.

$\bf ii.$ The first turning point of $(u,v)$ belongs to $\Omega_{ext,3}\cup\Omega_{ext,4}$.

Proof. It is easy to see that $u$ and $v$ are nonincreasing at the origin. Assume that they remain with the same monotony on the whole domain $(0,\infty)$. They will have therefore finite limits $l_u$ and $l_v$ respectively. We claim that $l_ul_v\not = 0$. Indeed, assume in the contrary that $l_ul_v = 0$.

Case 1. $l_u = l_v = 0$. In this case, the pair of solution $(u,v)$ behaves at infinity like the solution of the problem

for which the energy $E(u,v)$ satisfies at infinity

where $\omega_0 = \sqrt{\omega}$, which is contradictory.

Case 2. $l_u = 0$, $l_v\not = 0$. In this case, $u$ behaves at infinity like the solution of the problem

which is oscillatory. We get a contradiction.

Case 3. $l_u\not = 0$, $l_v = 0$ is similar to the previous one. We thus conclude from all these cases that $(u,v)$ behaves at infinity like the solution of the problem

So, they are both oscillatory, which is also contradictory. We conclude that $u$ and $v$ cannot remain with the same monotony on the whole interval $(0,\infty)$. Furthermore, they cannot have finite limits simultaneously. It remains the possibility that $u$ is nonincreasiing with limit 0 and $v$ is oscillating infinitely. In this case, $u\sim Ce^{-\omega_0 x}$ at infinity which in turns yields from the first equation in problem (20) that $v^2$ goes to 0 at infinity, which is contradictory. So as Assertion i is proved. Assertion ii may be proved by similar techniques as in the previous theorems. In Figures 13 and 14 some numerical simulations are presented to illustrate the result of Theorem 3.3.

Besides, Figures 15 and 16 illustrate clearly the oscillating behaviour of the solution $(u,v)$ whenever the initial values $(a,b)\in\Omega_{ext,1}$.

4.   Study of the special cases

In this section we will consider the problem (20)-(22) when the initial value $(a,b)$ lies on the frontiers of the region $\Omega_i$. An obvious case is when $(u,v)(0) = (a,b)\in\{O,A,B,C,D,E,F,G,H,I,J,K,L\}$. In this case the solution is always constant equals to its initial value $(a,b)$ due to the Lipschitz theory. As a consequence we will consider in the rest of this section the non trivial cases. Here also because of the symmetries of the problem we will consider only the case $0\leq a\leq b$.

4.1.   Case 1: $(a,b)\in)A,B($.

As usual $u$ starts by decreasing on a small interval $(0,\delta)$, for some $\delta>0$ small enough. Now at $x = 0$ we have

Even though we claim that $v$ can not remain constant on any interval $(0,\delta)$, $\delta>0$. Indeed, if this occurs on some interval $(0,\delta)$, we get immediately

So, $|u|$ is also constant ($\equiv a$) on $(0,\delta)$. Therefore, we get

This means that

which contradicts the fact that $|u|$ is constant, except if $K_1 = 0$. However, in this case we again get $a = 0$, which is contradictory. So as the claim. Consequently, two situations may occur. $(i)$ the pair solution $(u,v)$ remains on the edge $)A,B($ and being non constant. $(ii)$ the pair solution $(u,v)$ bifurcates toward $\Omega_{1}$. Whenever the situation (i) occurs we immediately conclude that $v$ is constant, which is a contradictory with the previous claim. Consequently, the situation (ii) occurs only. Next, as in the previous cases, $u$ cannot remain nonincreasing on $(0,\infty)$. So, let $r_0>0$ be the first positive critical point of $u$. That is, $u'(r_0) = 0$ and $u'(x)<0$ for all $x$ such that $0<x<r_0$. By applying similar techniques as previously we deduce that the turning point $M_0 = (u(r_0),v(r_0))\in\Omega_{12}\cup \Omega_{ext,4}$ and thus the solution $(u,v)$ joins the class described in Theorem 3.1 and the symmetric behavior of the one described in Theorem 3.3 relatively to the y-axis.

Figures 17, 18, 19 and 20 illustrate graphically the theoretical results above. Notice here that the initial values $a$ and $b$ are related by $g_\omega(b,a) = 0$ which is equivalent to $a = \sqrt{\omega-|b|^{p-1}}$. We fixed here $p = 1.5$ and $\omega = 2$.

4.2.   Case 2: $(a,b)\in\{0\}\times(0,\infty)\setminus\{A,I\}$.

In this section we assume that the initial value $(u,v)(0) = (0,b)\in]0,\omega_p[\setminus\{\omega_3\}$. Using the well known Lipschitz theory we immediately observe that $u\equiv0$ and thus the problem (20)-(22) becomes

where $w_3<b<w_p$. Denote

Denote also

Consider firstly the case where $b\in(0,\omega_p)\setminus\{\omega_3\}$. In this case, we have $v_p<w_p<\tilde{v}_p$. Notice that the function $g$ is even and is nondecreasing on $(0,\infty)$. Moreover $g(\omega_p) = 0$ and $g$ is positive on $(\omega_p,\infty)$. Now, at the origin $x = 0$, $v$ starts by increasing. Whenever it continues with the same monotony on $(0,\infty)$ it has the unique finite limit $l_v = \omega_p>b$. However in this case, $v$ behaves at infinity as the solution $z$ of

which is oscillatory which in turns contradicts the its monotony. As a consequence $v$ is oscillatory on $(0,\infty)$ infinitely. Let $\zeta_0 = <\zeta_1<\zeta_2<\dots<\zeta_{2k}<\zeta_{2k+1}\dots$, $k\in\mathbb{N}$ be the sequence of successive critical points of $v$ such that $\zeta_{2k}$, $k\in\mathbb{N}$ are the maximums and $\zeta_{2k+1}$, $k\in\mathbb{N}$ are the minimums. We claim that

Indeed, for $k = 0$ for example, we have

Whenever $v(\zeta_1)< w_p$ we get from (24)

which is contradictory. Similarly for the rest (By recurrence on $k$). As a result we proved the following result.

Theorem 4.1. For all $b\in]-\omega_p,\omega_p[\setminus\{0\}$ the problem (24) has a unique solution which is oscillatory around $\pm\omega_p$ infinitely. Furthermore, there exists $(\xi_k)_k$ and $(\zeta_k)_k$ satisfying $v(\xi_k) = -\omega_p$ for all $k$) or ($v(\xi_k) = \omega_p$ for all $k$), $v'(\zeta_k) = 0$ and the alternance

Consider now the case where $b>\omega_p$. As in the previous cases, the solution $v$ is not monotone on its whole domain $(0,\infty)$. Indeed, $v$ is nonincreasing at the origin. If it continues with the same monotony it has two possible limits at infinity, $l_v = 0$ or $l_v = \pm\omega_{p}$. Consider the energy functional associated

which is obviously constant as a function of $x$. So, whenever $l_v = 0$ and $b\not = \widetilde{v}_p$ we obtain

which is contradictory. Now, whenever $l_v = 0$ and $b = \widetilde{v}_p$ we obtain $E(v)(x) = 0$ for all $x$. Consequently, $v'(x) = -\sqrt{-2F(v)(x)}$ for all $x$. Integrating on $(0,\infty)$ we get

which is impossible. Now, if the limit is $\pm\omega_{p}$ the solution $v$ behaves at infinity as the solution $z$ of the problem

which is oscillating. So, we get a contradiction also. We thus conclude that $v$ cannot be monotone on $(0,\infty)$. Let next $x_0$ be the first critical point of $v$. We claim that $0<v(x_0)<\omega_{p}$. If not, we have one of the following cases.

$\bf i.$ $v(x_0)\geq\omega_{p}$.

$\bf ii.$ $v(x_0) = 0$.

$\bf iii.$ $-\widetilde{v}_p\leq v(x_0)<0$.

$\bf iv.$ $v(x_0)<-\widetilde{v}_p$.

In the case (i.) we obtain

which is contradictory.

In the case (ii.) we obtain for $\eta/0$ small enough

which leads to a contradiction.

For the case (iii.) let $\zeta_0>0$ be the zero of $v$ on $(0,x_0)$. We obtain in one hand $E(v)(\zeta_0) = \dfrac{1}{2}v'(\zeta_0)^2>0$. On the other hand, $E(v)(x_0) = F(v(x_0))<0$. This is contradictory as the energy $E(v)$ is constant.

For the case (iv.) let $\zeta_1\in(0,x_0)$ be such that $v(\zeta_1) = -\widetilde{v}_p$. It holds immediately that $F(v(x))>0$ on $(\zeta_1,x_0)$. Now observing that $v'(x)^2 = -2F(v(x))$ on $(\zeta_1,x_0)$ we get here also a contradiction.

From all these cases we conclude that $0<v(x_0)<\omega_{p}$. Applying next the same techniques we obtain the following result.

Theorem 4.2. For all $b\in]\omega_p,\infty[$ the problem (24) has a unique solution which is oscillatory around $\omega_p$ infinitely. Furthermore, there exists $(\xi_k)_k$ and $(\zeta_k)_k$ satisfying $v(\xi_k) = \omega_p$ for all $k$, $v'(\zeta_k) = 0$ and the alternance

4.3.   Case 3: $(a,b)\in)I,B($.

This section is resembles somehow to the one where the initial value $(a,b)$ belongs to the curved arc $)A,B($ as the problem is symmetric in $(u,v)$. In fact we observe that $\Gamma_{1}$ and $\Gamma_{2}$ are symmetric by means of the axial symmetry $x = y$. Moreover the curve $\Lambda$ is invariant via the same symmetry. This permits to deduce the result in the present case easily.

Figures 21, 22 and 23 illustrate graphically the behavior of the solution for $(a,b)\in )I,B($. Recall that in this case the initial values $a$ and $b$ are related by $g_\omega(a,b) = 0$ which is equivalent to $b = \sqrt{\omega-|a|^{p-1}}$. We fixed as usual $p = 1.5$ and $\omega = 2$.

4.4.   Case 4: $a=b\in(0,\infty)$.

In this section we propose to study the case where the functions $u$ and $v$ start from the same origin point $u(0) = v(0)$. It is straightforward that $u\equiv v$ on the whole domain $(0,\infty)$. Consequently we obtain the single problem

The situation here is similar to subsection 4.2. Indeed, denote

Denote also $\underline{u}_{p,\omega}$, ${u}_{p,\omega}$ and $\overline{u}_{p,\omega}$ the positive unique zeros of $g$, $f'$ and $F$ respectively. In other words, $\underline{u}_{p,\omega}$ is the unique positive real number such that

Similarly, ${u}_{p,\omega}$ is the unique positive real number satisfying

Finally, $\overline{u}_{p,\omega}$ is the unique positive real number for which

We may check easily that

Consequently, by applying similar arguments as in subsection 4.2 we get the following results.

Theorem 4.3. For all $a\in]-{u}_{p,\omega},{u}_{p,\omega}[\setminus\{0\}$ the problem (27) has a unique solution which is oscillatory around $\pm{u}_{p,\omega}$ infinitely. Furthermore, there exists $(\xi_k)_k$ and $(\zeta_k)_k$ satisfying $v(\xi_k) = -{u}_{p,\omega}$ for all $k$) or ($v(\xi_k) = {u}_{p,\omega}$ for all $k$), $v'(\zeta_k) = 0$ and the alternance

Theorem 4.4. For all $a\in]{u}_{p,\omega},\infty[$ the problem (27) has a unique solution which is oscillatory around ${u}_{p,\omega}$ infinitely. Furthermore, there exists $(\xi_k)_k$ and $(\zeta_k)_k$ satisfying $v(\xi_k) = {u}_{p,\omega}$ for all $k$, $v'(\zeta_k) = 0$ and the alternance

5.   Some possible chaotic behavior

We provide in the present section some numerical simulations where an eventual chaotic behaviour of the solution is clearly recorded. Figure 24 concerns the dynamical system

Figure 25 is simulated for the dynamical system

For Figure 26 we considered the dynamical system

For Figure 27 we considered the dynamical system

6.   Further discussions

6.1.   Steady state solution with $w=0$

In investigating NLS equation as well as system, steady state solutions constituted a large set of studies. These solutions may be obtained as waves propagating with some positive frequency as dealt in the previous sections. Another way to obtain a different class of steady state solutions is to let the time $t$ approximate $\infty$ which is also equivalent to relax the frequency to $w = 0$. In this case the problem (20)-(22) becomes

Notice here that the nonlinear function model is

which is a positive function. So, the case here resembles in some sense to the cases where the initial value $(a,b)\in\Omega_{ext}$ investigated in the previous sections. Indeed, the curves $\Gamma_1$ and $\Gamma_2$ are reduced to

and thus the whole plane $\mathbb{R}^2$ will be splitted into regions according to $\Lambda$ as in Figure 28. The energy functional associated to (34) is written as

As in the previous sections, this energy is constant and positive and satisfies precisely

This guarantees that the solution $(u,v)$ is bounded and oscillating infinitely without limit. Table 1 and Figures 29, 30, 31 and 32 illustrate the behavior of the solution $(u,v)$ of problem (34) for some cases,

To illustrate more clearly this behavior, we provided in Figure 33 the phase plane portrait $(u',u)$ for $p = 1.5$, $w = 0$ and $(a,b) = (0.25,0.5538)\in\Lambda$ corresponding to Figure 29. Figure 34 illustrates the phase plane portrait $(v',v)$ for $p = 1.5$, $w = 0$ and $(a,b) = (0.25,0.35)\in R_2$ corresponding to Figure 30. Figure 35 illustrates the behaviors of $u$ and $v$ separately for $p = 1.5$, $w = 0$ and $(a,b) = (0.5,1)\in R_1$ corresponding to Figure 31. We notice easily from all these figures the oscillating behavior of the solution $(u,v)$. Finally, Figure 36 represents the energy $E(u,v)(x)$ for $w = 0$ at the top and $w = 2$ at the bottom. We notice easily that the energy is constant as a function of $x$, which is already confirmed theoretically.

6.2.   Steady state solutions on the half-space and the interval

Remark that in our study for reasons of symmetry (parity properties of the nonlinear part) problems (18) and (19) or the simplified form (20) are invariant under the transformation $u(x)\rightarrow u(-x)$. This is also applicable for the last special case (34). Notice that all these problems are also autonomous (relatively to the space variable $x$). All these reasons make it possible to extend the results on all the real line.

However, on a finite interval such that $[0,1]$ this needs a deep study as we notice clearly that the constants $\sigma_1$, $\sigma_2$ and $\lambda$ could not be relaxed simultaneously as in the present case. This will allow to loss many symmetry characteristics of the problem, the subdivision of the plane $\mathbb{R}^2$ into regions according to $\Gamma_1$, $\Gamma_2$ and $\Lambda$. This will induce careful modifications in the study. Nonetheless, we may adapt the techniques developed here to a finite interval such as $(0,1)$ in a special case where the first zeros of $u$ and $v$ coincide, but for a slightly modified (by scaling laws) problem. Indeed, denote $x_0$ the first common zero for $u$ and $v$ and consider the scaling versions

The pair $(\widetilde{u},\widetilde{v})$ satisfies the re-scaled version of problem (19) on $(0,1)$ as follows

This means that relaxing all the parameters simultaneously as in the case of the whole line such as the case investigated in our present work could not be applied. Many ideas have been investigated especially in the single case of NLS equation such as the so-called shooting parameter method and also the well-known Emden-Fowler transformation. These are motivating ideas to re-consider the extension of the present study on finite intervals.

The shooting parameter method consists in fixing the value of the solution at the last extremity of the interval (for example $x = 1$ when considering the interval $(0,1]$) and studying its behavior at the origin. The Emden-Fowler approach consists in transforming the problem on $(0,\infty)$ to the interval $(0,1)$ and vice-versa, and next deducing the behavior of the solution of the original problem from the one of the transformed version. See for instance [3,12,6,7,9,28,31].

7.   Conclusion

In the present work, 1D problem of coupled NLS equations has been investigated for the classification of the steady state solutions in the presence of mixed nonlinearities, a first odd cubic term added with a second odd superlinear subcubic one. Classification of the solutions as well as existence and uniqueness of the steady state solutions have been investigated. Numerical simulations have been provided illustrating graphically the behavior of the solutions such as oscillating and phase plane portraits.

Inspired from the present work, some analogue studies may be of interest such as the radial problem in higher dimensional cases where for the example no conservative energy could occur.

We may also consider cases where assumption (23) does not hold. For example, for $p<0$ the Lipschitz characteristic of the problem is not satisfied which necessitates different and more advanced techniques for the study. For some values of $p$ and $\omega$ the region $\Lambda\cap[-1,1]$ is not contained in $\Omega_{2}\cup\Omega_{4}\cup\Omega_{8}\cup\Omega_{11}$ which induces more and more difficulties and different behaviors for the solutions.

Moreover, we may be interested in coupled problems such as

● The Heat operator

leading to a nonlinear Heat system.

● The mixed Schrödinger-Heat operator

leading to a nonlinear coupled system of Schrödinger-Heat type.

Finally, as discussed above, considering similar study on finite interval is also of great interest. A forthcoming study in the case of higher dimensional space $\mathbb{R}^N$, $N\geq2$ is at the mid of being achieved.

8.   Appendix

8.1.   Appendix A

Recall that in the previous sections, we applied for many times the well-known Cauchy Lipschitz theorem on the existence and uniqueness of solutions. In this section and for convenience, we will show that the generator function used is already locally Lipschitz continuous.

Denote $\varphi = u'$ and $\psi = v'$. The system (20)-(22) becomes

Denoting $X = (u,v,\varphi,\psi)^T$, where $^T$ stands for the transpose, we get

where $F$ is the function defined by

Lemma 8.1. $F$ is locally Lipschitz continuous on $\mathbb{R}^4$.

Proof. Let $\delta>0$ be small enough and $X^0 = (x_1^0,x_2^0,x_3^0,x_4^0)\in\mathbb{R}^4$ be fixed. For all $X,Y$ in the ball $B(X^0,\delta)$ we have

We shall now evaluate the quantity $(g(x_1,x_3)x_1-g(y_1,y_3)y_1)^2$. Similar techniques will lead to $(g(x_3,x_1)x_3-g(y_3,y_1)y_3)^2$. We have

where $C_1(p,X_0,\delta)>0$ is a constant depending only on $p$, $X_0$ and $\delta$. $C_2(X_0,\delta)>0$ is a constant depending only on $X_0$ and $\delta$. $C(p,X_0,\delta,\lambda)>0$ is a constant depending only on $p$, $X_0$, $\delta$ and $\lambda$. Therefore,

Similarly,

with some constant $\widetilde{C}(p,X_0,\delta,\lambda)>0$ analogue to ${C}(p,X_0,\delta,\lambda)$. Combining all these inequalities, we obtain

8.2.   Appendix B

In this part, we investigate the dependence of the different regions $\Omega_i$, $i = 1,\dots,12$, $\Omega_{ext,i}$, $i = 1,\dots,4$ and the different curves $\Gamma_1$, $\Gamma_2$ and $\Lambda$ on the parameters $p$ and $\omega$. So denote $\Lambda^* = \Lambda\setminus\{(u,v)\in\mathbb{R}^2;\;|u|\not = |v|\}$. Denote also $\Omega_{int} = \bigcup\limits_{i = 1}^{12}\Omega_i$ and $\mathcal{A}_p$ the interior area countered by the curve $\Lambda^*$.

Lemma 8.2. The area $\mathcal{A}_p\subset[-1,1]^2$.

Indeed, denote for $(u,v)\in\mathcal{A}_p$

It is straightforward that $r$ is maximum whenever $(u,v)$ is on the frontier $\Lambda_{p}^*$, which may be then governed by the polar equation

Otherwise,

Straightforward calculus yield that whenever $0<p<3$, the radius $r$ is extremum for $\theta\in\{0,\pm\frac{\pi}{2},\pi\}$, which gives the vertices $(\pm1,0)$, $(0,\pm1)$. In fact $r(\theta)$ may be extended at $\theta = \{\pm\frac{\pi}{4},\pm\frac{3\pi}{4}\}$. However, these points yield immediately $|u| = |v|$, which is the trivial (unbounded) part of $\Lambda$.

As a result of Lemma 8.2, we immediately deduce that whenever $0<\omega\leq1$ and $1<p<3$ the inclusion $\Omega_{int}\subset\mathcal{A}_p$. However, for $\omega\geq1$ and $1<p<3$, the area $\mathcal{A}_p$ is contained in the curved octagonal shape $IBJDKFLH$.

Acknowledgment

The authors would like to thank the editor and the handling editor of ERA as well as the anonymous referees for the time they have spent to evaluate our work. Their comments have been of great importance and have improved the present work well.