A generalized mathematical model for a class of mechanical systems with lumped and distributed parameters

1.   Introduction

Application of the Hamiltonian variation principle for constructing dynamic equations for mechanical systems with lumped and distributed parameters, in particular, for the systems of rigid bodies mounted on a beam (or a rod) with the aid of springs, implies consideration of hybrid systems of differential equations (HSDEs) ^[1]. Until recently, any investigations of HSDEs have remained beyond the scope of interest of many researchers.

HSDE is understood as a system of differential equations, comprised by ordinary differential equations and partial differential equations together. In particular, HSDEs are constructed in the process of investigations of mechanical vibrations of elements of various constructions, parts and mechanisms, for which the schemes to be computed are represented by rigid bodies or by systems of interconnected rigid bodies attached to some beams by elastic joints.

In papers ^{[2,3,4,5,6,7,8,9,10,11,12,13]}, considered were mathematical models for the investigation of free vibrations of mechanical systems, which, in each of the cases, represented a system of rigid bodies mounted on an Euler-Bernoulli beam with the aid of springs. These systems were called either beam-mass systems or two-degree-of-freedom spring-mass systems. The point is that each time the development these models necessitated special analytical methods, special numeric-analytical methods or, at least, the application of the method of finite elements. So, earlier, the computational schemes were different in each of the cases.

The principal difficulties, which arise in process of investigation of the mechanical systems with lumped and distributed parameters, in particular, in the process of consideration of a system of rigid bodies connected to beams by elastic joints, are bound up mainly with the diversity of variants of mounting absolutely rigid bodies on flexible beams (rods). In order to avoid these difficulties, the authors of papers ^{[2,3,4,5,6,7,8,9,10,11]} have proposed to decompose of the beams (rods) into parts, and, next, to sew the solutions together at the points of attachment of elastically mounted masses. Unfortunately, this approach implies a very large volume of computations in the process of finding the analytical solution. Furthermore, the process of numerical solving of the problem necessitates a substantial volume of preliminary work. A different approach, which the author considers as more productive, presumes investigation of the generalized models described by HSDEs with the use of a relatively simple and sufficiently transparent mathematical apparatus of generalized functions. A similar apparatus is widely applied in mathematical physics, quantum mechanics, and in other disciplines for the purpose of describing point masses and charges, point sources of heat, concentrated forces, and moments.

Noteworthy, during the recent years, the Chair of Applied Mathematics, East Siberian State University of Technology and Management, which was headed by the author, conducted the research work oriented to development of theoretical foundations for investigations of linear HSDEs with the coefficients depending on the Dirac delta-functions and on its derivatives.

The class of linear HSDEs implied represents a new (and, so, poorly known) class of differential equations. In the capacity of applications of our research results we have, in particular, considered mechanical systems representing various classes of systems of interconnected rigid bodies and beams described by HSDEs. Furthermore, in the process of constructing the computational schemes for various mechanical systems (a rigid body attached to a beam; a cascade system of rigid bodies attached to a beam; a system of rigid bodies horizontally attached to a beam; several rigid bodies interconnected and attached to a beam), a universal approach to computations has been developed and realized by the author. It is based on application of the mathematical apparatus of generalized functions. Note, there are two papers ^[12,13], which can be found in the literature, in which the mathematical apparatus of generalized functions has been applied in the investigations of free vibrations of the Euler-Bernoulli beam with n parallel mounted masses, but unfortunately, without any strong mathematical grounding. Some results obtained by the Chair and bound up with the problem discussed in the present paper can be found in ^[14]. These results are characterized by a strong mathematical grounding.

The experience of investigations bound up with definite computational schemes of mechanical systems, and the analysis of their equations of motion have allowed us to propose a generalized mathematical model, which is considered in the present paper. In this case, a generalized mathematical model for a system of rigid bodies mounted on the Euler-Bernoulli beam with the aid of springs is understood as a HSDE of some given structure. On the basis of a unified approach, for the case of generalized mathematical model, the theoretical foundations good for investigations of free vibrations for a class mechanical systems have been proposed. The scrutinized mechanical systems represent diverse systems of interconnected rigid bodies mounted on a Euler-Bernoulli beam with the aid of elastic joints.

2.   The principal theoretical assumptions

The generalized mathematical model for a system of interconnected rigid bodies elastically mounted on a Euler-Bernoulli beam, i.e. the HSDE, has the form

where x is a variable describing the coordinate axis, which coincides with the beam at rest; q(t) is an n-dimensional vector function, which describes the transition a system of rigid bodies; u(x, t) is a scalar function, which describes the transversal transitions of points of the beam; u(t) is an m-dimensional vector function with the components u(a₁t), u(a₂, t), …, u(a_m, t); A, C are the given constant n×n -matrices; C is a given constant n×m -matrix; D is a given constant m×n -matrix; dⁱ is an n-dimensional vector composed of the rows of matrix D; a, c, a_i, k_i, (i = $\overline{1, m}$) are given constants, furthermore, 0≤a_i≤l; (∙)^T is (from now on) the operation of transposition.

Function u(x, t) describes transversal transitions of the beam's points. In this connection, there are some boundary conditions imposed on function u(x, t) and corresponding to the techniques of attachment of the beam's ends:

where $l$ is the beam's length.

In particular, in the case of stiff attachment of the beam's end, we have

in the case, when there is a hinge-based joint of the beam's end, we have

in the case of free beam's end, we have

Let us introduce the concept of generalized solution of the boundary-value problem (1)–(2). To this end let us consider the following set of vector functions:

where $D = \left\{ {(x, t) \in {R^2}:\, \, \, 0 \leqslant x \leqslant l, \, \, \, \, 0 \leqslant t \leqslant T} \right\}$ is a rectangle. Let us call the vector functions of set (6) the main vector functions.

Definition 1. Let us call the vector function $q(\cdot) \in C_{2, \left[{o, \, T} \right]}^n$ and the scalar function $u(\cdot, \cdot) \in C_{4, \, 2, \, D}^{}$ the generalized solution of HSDE (1) satisfying the boundary conditions (2) if for any main vector function $\left({\eta (\cdot), \, v(\cdot, \cdot)} \right) \in K$ the following identity holds

Having substituted $q(t) = Z\sin \omega \, t$ and $u(x, t) = V(x)\sin \omega \, t$ into (1), we obtain the following system of algebraic-differential equations

where $\bar V\;$ is an m-dimensional vector with the components $V({a_1}), \cdots, V({a_m})$.

Due to the boundary conditions (2) imposed on function $u(x, t)$, function $V(x)$ shall satisfy some definite boundary conditions

As far as the functions, which define the boundary conditions (8) are concerned, let us suppose that the following property is valid:

where ${\alpha _i}$ are constants, ${\nu _i}(x)$ are functions. Note, satisfaction of (8) is quite obvious in the case of boundary conditions, which correspond to the conditions of attachment of the beam's ends (3)–(5).

Consider the auxiliary boundary-value problem represented by the following differential equation with boundary conditions (8) for some values of $\omega$ and $Z$

Definition 2. The scalar function $V(\cdot) \in {C_{4, \, \left[{0, \, T} \right]}}$ satisfying the boundary conditions (8) is called the generalized solution of the auxiliary boundary-value problem if for any component $v(\cdot, \cdot)$ of the main vector function $\left({\eta (\cdot), \, v(\cdot, \cdot)} \right) \in K$ the following identity holds for any $t \in \left[{0, \, T} \right]$

Theorem 1. The generalized solution of the auxiliary boundary-value problem $V(x)$ has the following representation for any values of $\omega$ and $Z$

where functions ${G_i}(x), \, \, (i = 1, ..., m)$ are generalized solution of equation

which satisfies the boundary conditions

Proof: The plausibility of satisfaction of the boundary conditions (8) for the function $V(x)\,$, which satisfies representation (12), follows immediately from the boundary conditions (14) for the functions ${G_i}(x), \, \, (i = 1, ..., m)$ due to property (9).

Note, it follows from (11) that if function $V(x)$ represents a generalized solution of the differential equation of system (10), then for any component $v(\cdot, \cdot)$ of the main vector function the following identity holds:

Let us rewrite (12) in the following form:

Now let us put (16) into the left-hand side of relation (15). Next, by changing the order of integration and taking account of (13), we obtain:

The latter coincides with the right-hand side of (11).

Therefore, the representation (12) is valid for the generalized solution $V(x)\,$ of the differential equation of system (10). Q.E.D.

In order to find $Z$ and $V(x)$, having initially substituted the values $x = {a_i}, \quad i = 1, 2, ..., m$, sequentially into relation (12), we obtain the following system of linear algebraic equations with respect to $V({a_1}), V({a_2}), V({a_m})$

Having used matrix denotations, we rewrite system (17) in the following form:

where $M\;$ is an $m \times m$-matrix:

$N\;$ is an $m \times n$ -matrix:

Having joined the first equation of system (7) with system (18), we obtain a homogeneous system of linear algebraic equations with respect to $Z, \, \, \, \bar V$.

System (19) has nonzero solutions, when its determinant is zero. By equating the determinant of system (18) to zero we obtain the equation for finding the eigen-frequencies

In order to use the frequency equation (20) for finding the eigen-frequencies, let us find ${G_1}(x), {G_2}(x), ..., {G_m}(x)$ as generalized solutions of the following equation

with the corresponding boundary conditions (14)

The general solution $G(x, {c_1}, {c_2}, {c_3}, {c_4})$ of equation (21) can be found in the form of a sum of the general generalized solution ${G_0}(x, {c_1}, {c_2}, {c_3}, {c_4})$ of the homogeneous equation

and some generalized solution $\tilde G(x)$ of the non-homogeneous equation (21), i.e.

The general solution ${G_0}(x, {c_1}, {c_2}, {c_3}, {c_4})$ of the homogeneous equation (22) may be written in the form

where ${c_1}$, ${c_2}$, ${c_3}$, ${c_4}$ are constants of integration, $\beta = \frac{{\sqrt \omega \, \sqrt[4]{a}}}{{\sqrt[4]{c}}}$,

${S_1}\left({\beta x} \right), {S_2}\left({\beta x} \right), {S_3}\left({\beta x} \right), {S_4}\left({\beta x} \right)$ are the Krylov functions:

In the capacity of the partial generalized solution $\tilde G(x)$ of equation (21), in accordance with ^[1], let us consider

where $g(x)$ is the solution of the homogeneous equation, which satisfies the initial conditions

$\theta (x)$ is a classical Heaviside's function.

The solution of a homogeneous equation, which satisfies the initial conditions (26), can be found in the form

Therefore, in accordance with (23)–(25), the general generalized solution $G(x, {c_1}, {c_2}, {c_3}, {c_4})$ of equation (21) may be represented as follows

Having determined arbitrary constants ${c_1}, {c_2}, {c_3}, {c_4}$, which enter in the general solution (27), proceeding from the conditions of satisfaction of the corresponding ${G_i}(x)$ boundary conditions (14), we can find the generalized solutions ${G_1}(x), {G_2}(x), ..., {G_m}(x)$.

3.   The algorithmic apparatus for investigations of eigen-vibrations

In order to find eigen-frequencies of a mechanical system, which is described by a generalized mathematical model (1), it is necessary to conduct the following undertakings.

1. Development of a procedure for computing the determinant for the matrix of the system of algebraic equations (19)

The functions obtained ${G_1}(x), {G_2}(x), ..., {G_m}(x)$ allow one to construct the matrix of the system of algebraic equations (19) and organize the computation of its determinant (28) for some fixed value of $\varpi$.

2. Elaboration of the procedure of finding the frequencies $\varpi$, for which determinant (28) turns zero with a given accuracy.

To the end of finding the eigen-frequencies $\varpi$, computation of the determinant (28) at the points was conducted, while beginning from the value of $\varpi$ equal to zero, with some step depending on the accuracy, and until defining the first 5 to 7 intervals of changing the sign of the frequency function $\Delta (\varpi)$. For each particular interval, the process of finding the roots of the frequency equation (20) was conducted with the aid one of methods good for finding the roots of the monotonous function on the segment.

The eigen-forms of the beam's vibrations $V(x)$, corresponding to eigen-frequency $\varpi$ can be found by formula (12). For this purpose, it is necessary to obtain nontrivial solutions $Z$ and $\bar V$ of the linear homogeneous algebraic equation (19), which correspond to iegen-ferquency $\varpi$.

The method, which realizes the described approach to the investigation of eigen-frequencies, has been implemented in the form of a software complex written in Fortran. Testing of the software complex has been conducted on the basis of numerical computations for definite computatonal schemes and their comparison with available computations, which can be found in the literature, in particular, in ^[2].

4.   Examples of practical computations

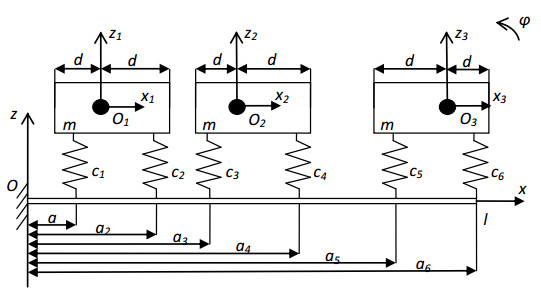
1. Papers ^[2,3,4,5] describe investigations of mechanical systems, whose computational scheme is shown in Figure 1.

In the case of ^[2], the computations were conducted for the following three techniques of attaching the beam's ends: (ⅰ) fixed joint (i.e. stiff attachment of the beam's end), (ⅱ) hinge-based joint (attachment) of the beam's end, (ⅲ) free beam's end. Note, in Fig. 1 one can see the case, when the left end is stiffly fixed, while the right end is free (so, there is a combination of "the fixed end – the free end"). The comparative analysis of the results obtained in our investigations to the results given in ^[2] can be found in Table 1. Here FEM means "the method of finite elements"; NAM – "the method of numerical assembly".

Proceeding from the comparative analysis given in Table 1, it is possible to note that there is a good coincidence of the results obtained in our computations with those given in ^[2].

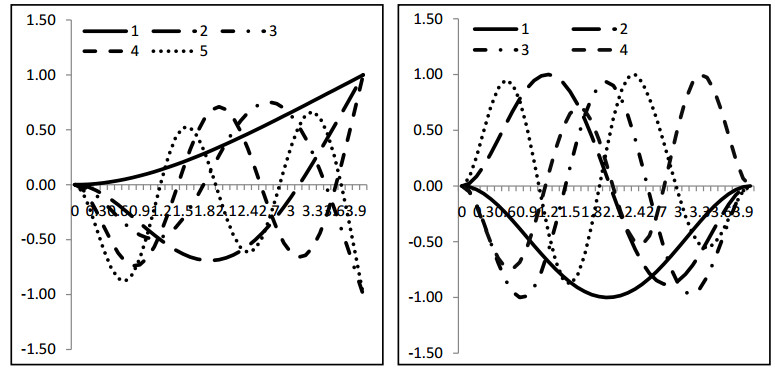
The results (obtained with the use of formula (12)) for the graphs of vibration forms for the beam with a rigid body, which is mounted with the aid of two springs, are given in Figure 2.

In the left-hand side of Fig. 2, one can find the forms of vibrations with the frequencies corresponding to the rows of Table 1, for the case, when one end of the beam is stiffly fixed, and the other one is free. The right-hand side of Fig. 2 relates to the forms of vibrations with the frequencies corresponding to the rows of Table 1, for the case, when both ends of the beam are stiffly fixed.

On the whole, the constructed forms of the beam's vibrations for the first five eigen-frequencies correlate with the computations given in paper ^[2]

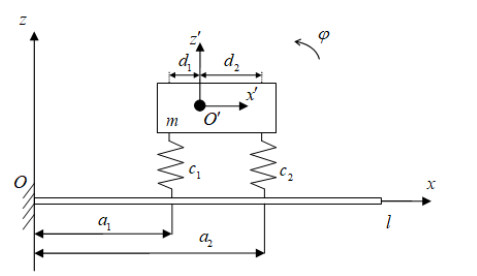
2. The papers ^[2,3] also presented investigations of the mechanical system, whose computational scheme is given below in Figure 3. In this case, each rigid body is attached to an elastic beam with the use of two springs characterized by definite rigidity. One end of the beam is fixed, and the other end is free.

The final results of comparison of the computations for the first five eigen-frequencies of the beam with three elastically mounted rigid bodies to the results given in ^[2] have been summarized in Table 2.

5.   Conclusion

The generalized mathematical model in the form of HSDE (1) proposed in the present paper describes a wide class of mechanical systems, which includes various arbitrary systems of rigid bodies mounted on the Euler-Bernoulli beam with the aid of springs. The process of inference of the dynamic equations for such systems on the basis of the Hamiltonian variation principle leads to the HSDE, which represents a particular case of HSDE (1). The theoretical foundations needed for the study of free vibrations of a given class of mechanical systems in the form of a generalized mathematical model have been proposed.

On the basis of our results we have developed a software complex for analysis of free vibrations of mechanical systems, which represent various systems of interconnected rigid bodies mounted on an Euler-Bernoulli beam with the aid of elastic joints. The software complex elaborated is a universal instrument for the study of free vibrations of mechanical systems, whose mathematical models can be described by HSDEs of form (1). Noteworthy, when the Hamiltonian variation principle is used, the computational schemes of mechanical systems considered in papers ^{[2,3,4,5,6,7,8,9,10,11,12,13]} all lead to HSDEs, whose structures coincides with (1). Presently, the software complex is complemented with the software aids, which ensure the automation of the process of constructing mathematical models in the form of HSDE (1) according to the computational scheme. On the whole, the software complex, which is elaborated on the principles described in the present paper, allows one to investigate any systems discussed in papers ^{[2,3,4,5,6,7,8,9,10,11,12,13]}. Furthermore, now there is no need to conduct investigations bound up with elaboration and application of special (each time new) numerical-analytical methods oriented to definite computational schemes ^{[2,3,4,5,6,7,8,9,10,11]}.

The comparison of the results of computations obtained with the aid of our software complex to the computational results obtained for the similar objects and available from the literature has shown the advantages of the new approach, which is universal and is simpler. The comparison has also proved the plausibility and universality of the computations guaranteed by the software complex elaborated by our team.

Acknowledgments

The work has been financially supported by the Russian Foundation for Basic Research, grant 18-41-030004 and state assignment of the Ministry of Education and Science of the Russian Federation No. 1.5671.2017 / 8.9.

Conflict of interest

The author declares no conflict of interests.