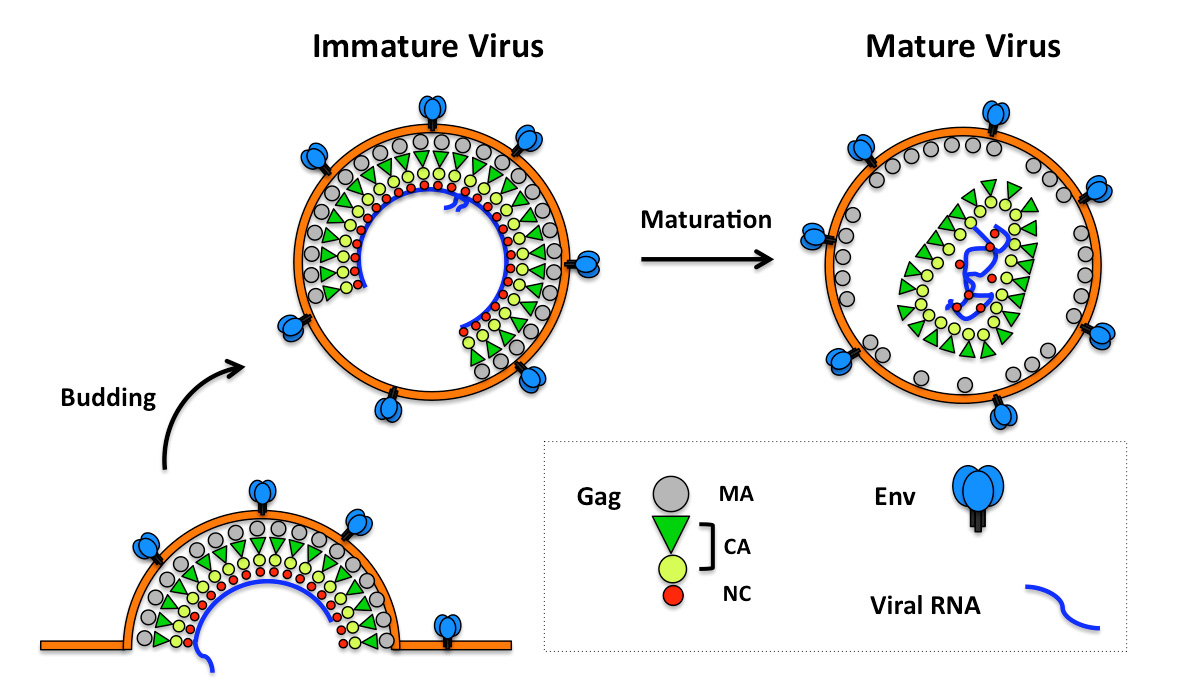
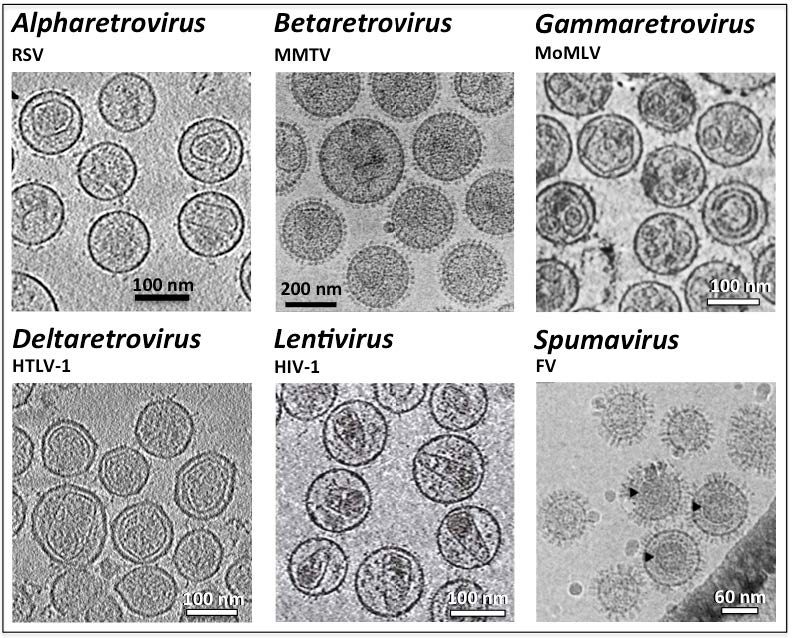
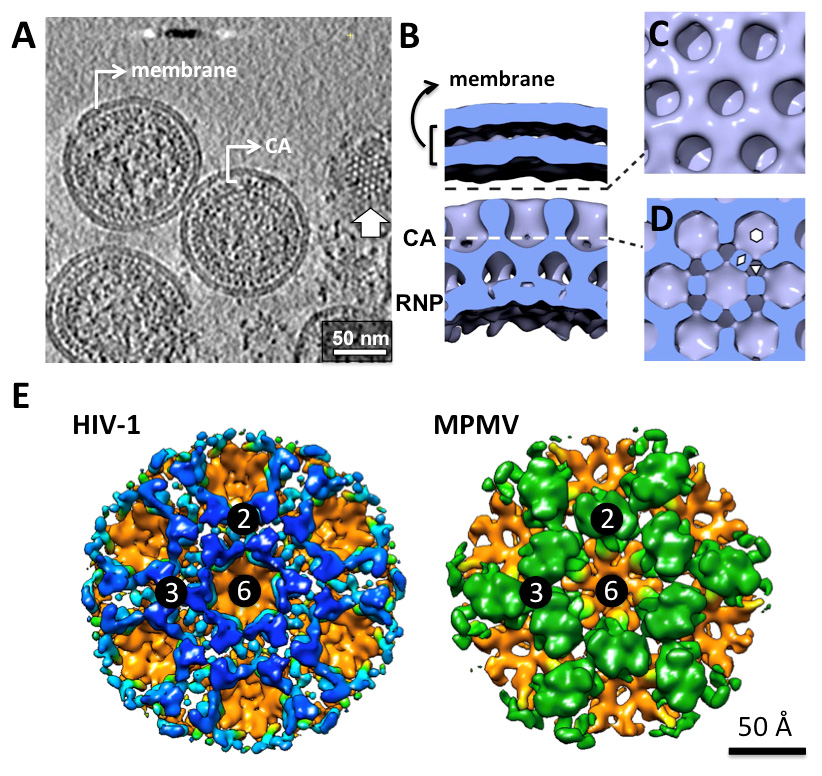
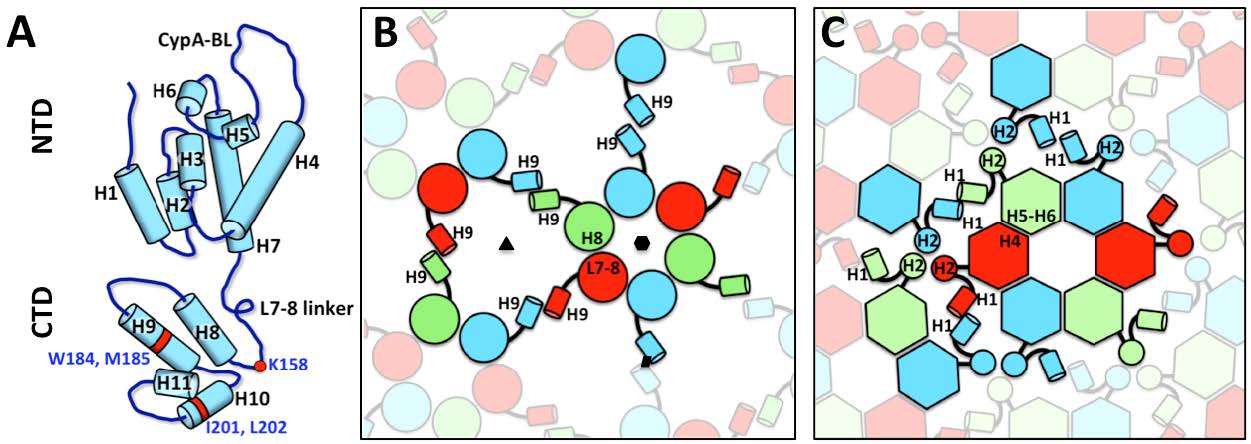
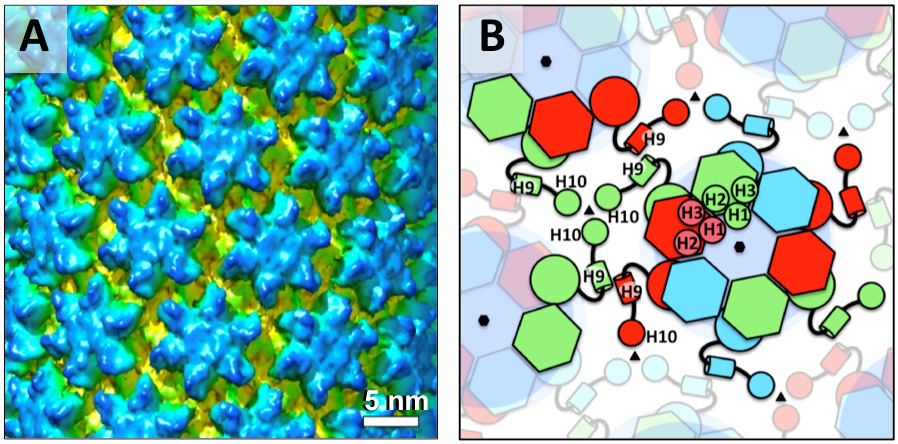
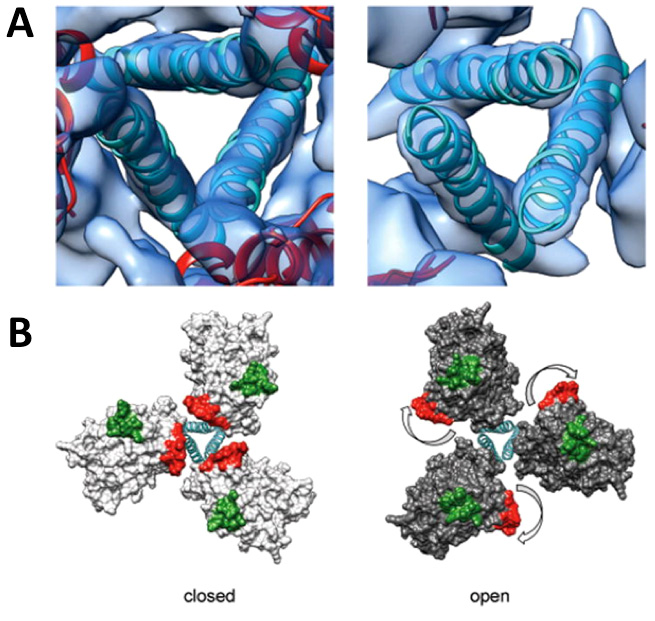
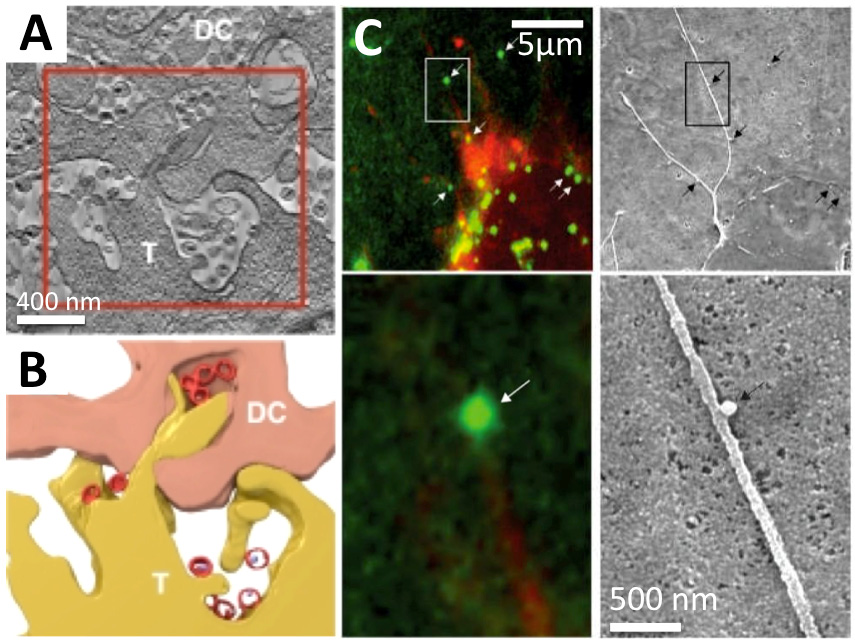
Retrovirus morphogenesis entails assembly of Gag proteins and the viral genome on the host plasma membrane, acquisition of the viral membrane and envelope proteins through budding, and formation of the core through the maturation process. Although in both immature and mature retroviruses, Gag and capsid proteins are organized as paracrystalline structures, the curvatures of these protein arrays are evidently not uniform within one or among all virus particles. The heterogeneity of retroviruses poses significant challenges to studying the protein contacts within the Gag and capsid lattices. This review focuses on current understanding of the molecular organization of retroviruses derived from the sub-nanometer structures of immature virus particles, helical capsid protein assemblies and soluble envelope protein complexes. These studies provide insight into the molecular elements that maintain the stability, flexibility and infectivity of virus particles. Also reviewed are morphological studies of retrovirus budding, maturation, infection and cell-cell transmission, which inform the structural transformation of the viruses and the cells during infection and viral transmission, and lead to better understanding of the interplay between the functioning viral proteins and the host cell.
1.
Introduction
The spread of infectious diseases threatens people's health and social stability. To control the spread of the epidemic, governments usually take some measures, such as developing vaccines and isolating patients carrying the virus. Before the successful promotion of the vaccine, the government's non-pharmaceutical control measures, which reduce people's contact rate through lockdown and isolation, play a leading role in controlling the epidemic. However, it cannot relieve people's fear of the virus and may deteriorate the national or regional economy [1,2].
Mathematical models are useful tools to analyze the formation of social and economic phenomena under various backgrounds. In recent years, the Boltzmann-type equation, which uses the collision theory to study the statistical distribution of rarefied gas molecules [3], is adopted to investigate the socio-economic phenomena of multi-agent systems, such as opinion formation and wealth distribution (see [4,5,6,7,8]). To discover the socio-economic impact of epidemics, researchers extend the classical Susceptible-Infectious-Recovered (SIR) epidemic model [9,10,11,12], in which agents are separated into three categories: susceptible (S), infected (I) and recovered (R), and integrate the SIR model with the socio-economic phenomena of multi-agent systems, such as people's social contact and wealth exchange behavior [13,14].
The description of socio-economic features involves knowledge of mathematics, sociology, economics, psychology and other fields [15,16,17,18]. In the physical-economic dynamic models, the wealth distribution is determined by the continuous trading features of a large number of agents according to a wealth exchange mechanism, which is characterized by the saving (exchange) propensity of agents and uncertain elements. The uncertainty includes market risks and speculative risks [5]. Saving means that agents are risk-conscious and only use part of their wealth for trading. The saving (exchange) propensity reflects agents' trading decision-making. Decision-making problems are common in life, such as commodity selection, product evaluation, company management, etc. (see [19,20,21]). Persons' decision-making behaviors are affected by psychological preferences, health status, wealth and other factors (see [5,13,22,23,24,25,26]).
Dimarco et al. [13] introduce a kinetic system consisting of three Boltzmann-type equations to describe how a wealth distribution might evolve under the course of an epidemic. In the kinetic system, the transport parts reflect the movement of individuals in different infection statuses and the Boltzmann collision operators depict the change in wealth distributions caused by the wealth exchange behaviors. The wealth exchange mechanism is depicted by the Cordier-Pareschi-Toscani (CPT) model
In (1.1), the pre-trade wealth $ (w, w_{*}) $ of two agents with infection status $ L, J\in\{S, I, R\} $ becomes $ (w^{'}, w_{*}^{'}) $ after the transaction, and the constant $ P_{J}\in[0, 1] $ is exchange propensity for the class of agents with the infectious state $ J $. The random variables $ \eta_{LJ} $ and $ \tilde{\eta}_{LJ} $ stand for the uncertain impact of market risks. Dimarco et al. [13] find that epidemics affect wealth distribution.
In [13], agents in the same infection state have the same exchange propensity (see (1.1)) without considering the psychological differences of people when trading. In addition, the impact of government policies and measures on wealth distribution is not considered. Based on the work in [13], the motivation in our work includes two points. Firstly, we explore wealth distribution when the agent's trading decision is influenced by psychology. Secondly, we discuss the impact of contact control measures and vaccination on wealth distribution.
In a speculative market with one stock and two populations of chartists and fundamentalists, Maldarella and Pareschi [27] consider the influence of agents' behavioral and psychological factors on their investment. The psychological impact is represented by an appropriate value function corresponding to the prospect theory in Kahneman and Tversky [28]. The prospect theory is applied to dynamic models of social and biological phenomena, such as social contacts, alcohol consumption, the age of first marriage, the size of cities, tumor growth, etc. (see [14,29,30,31]). In these studies, the micro modification of the social trait $ x $ is expressed as a single interaction model
where $ x_{*} $ denotes the value of the trait after the interaction, and $ \eta $ is a random variable with mean zero and bounded variance. For the variable $ s = x/\bar{x} $, the general function $ \Phi_{\delta}^{\epsilon}(s) $ is given by
The constant parameters $ \bar{x} $, $ \mu\in(0, 1) $, $ \delta\in[-1, 1] $ and $ \epsilon > 0 $ are related to the phenomenon in society.
The parameter $ \delta $ plays a key role in determining the properties of the value function (1.3) and the trait's macroscopic features under the updating rule (1.2). Provided that $ \delta\mapsto 0 $, the value function (1.3) is concave, and the stationary solution of the Boltzmann-type kinetic model is a lognormal density describing situations of call center service time and human behaviors (see [30,32,33]). When $ \delta\neq 0 $, (1.3) possesses properties of the prospect theory in [28,34]. For example, the value function (1.3) is concave above $ \bar{x} $ and convex below it. In the case of $ \delta > 0 $, the stationary distribution of the trait $ x $ is a generalized gamma distribution depicting the alcohol consumption in [29]. $ \delta < 0 $ leads to an Amoroso-type distribution, which depicts the formation of social elites caused by social climbing activities [35].
In this paper, to study the influence of epidemics and the psychology of agents on wealth distribution, we will generalize the CPT model (1.1) in [13]. Assuming that agents' trading behavior is affected by their characteristics (such as health state and wealth level) and the prevalence of infectious diseases, we extend the constant exchange propensity of (1.1) as a function of the infected fraction and wealth. Firstly, as a response to the severity of the epidemic, we multiply the constant exchange propensity $ P_{J} $ by a function of the infected fraction at time $ t $ to describe a possible way for agents to reduce the exchange propensity $ P_{J} $. Secondly, considering that the rich have better anti-risk abilities than the poor, unlike the assumption that agents in the same infection state have the same trading propensity in [13], in this paper, we assume that the rich tend to use more wealth for trading to obtain better life enjoyment or investment return, while the poor tend to save wealth to ensure future life needs. We adopt a function $ \Phi(\cdot) $ (see (2.4)), which is a generalized form of (1.3) with $ \delta = 1 $, as a component of the exchange propensity to represent the disturbance of these psychological factors when making trading decisions. We introduce an additional parameter on the denominator of (1.3) to avoid the extreme situation that the increased investment proportion is too large (small) when the wealth level is high (low).
The stationary solution of the conservative socio-economic dynamic model, whose form is determined by the micro-interaction rules, plays a significant role in describing the large-time behavior of the trait under investigation. In this work, we utilize the Boltzmann system [13] to describe the evolutions of wealth distributions, and generalize the constant contact rate in [13] to a time-dependent function. Under the modified binary wealth exchange mechanism proposed in this paper, the Boltzmann system is transformed into the Fokker-Planck equations with quadratic drift and diffusion coefficients by using the quasi-invariant asymptotic limit method [7]. Specifically, the stationary wealth distribution of susceptible (recovered) agents $ f_{L}^{\infty}(w) $, $ L\in \{S, R\} $ in this work satisfies an ordinary differential equation in the form
where the non-negative coefficients $ \sigma $, $ \tilde{a}_{L} $, $ b $, and $ c > 0 $ rely on the parameters involved in the exchange rule and the epidemic environment. The solution of (1.4) is in the form of the product of an inverse gamma function and an exponential function. Since the microscopic interaction of the trait (alcohol consumption) in [29] is not a binary interaction, the stationary distribution in [29] satisfies Eq (1.4) with $ b\neq0 $ and $ c = 0 $. The stationary distribution in [13] satisfies Eq (1.4) with $ b = 0 $ and $ c\neq0 $. Compared with the work in [13], in our work, the new quadratic term $ b w^{2} $ in the drift coefficient of (1.4) is due to the nonlinear value function $ \Phi(\cdot) $ adopted in the exchange propensity.
The contributions of this paper are summarized as follows. 1) We supplement the exchange propensity form in the wealth distribution literature. Compared with the constant exchange propensity (see [6,13,22,36,37]), the varying exchange propensity in our model reflects people's psychological features. Compared with the exchange propensity in [5], which is a monotone function of wealth, we take into account the asymmetry of the agent's trading psychology at different wealth levels. 2) We supplement the description of the steady-state wealth distribution function in the literature. Polk and Boghosian [38] point out that the expression form of the wealth distribution's tail is not universal. Based on the classical wealth exchange CPT model, if the dynamic model is involved in the feedback control, taxation and redistribution implemented by the government, or the heterogeneity of agents, the steady-state wealth distributions are inverse gamma function (see [5,6,13,22,39,40]). Compared with the inverse gamma wealth distribution obtained in [13], the presence of the exponential function part in the solution of (1.4) makes the wealth distribution curve decay faster as $ w\mapsto\infty $, namely, the slimmer of the tail. This phenomenon corresponds to the decline in the number of super-rich. 3) We verify that the epidemic affects wealth distribution, contact control measures can curb the epidemic and aggravate wealth inequality. Ashraf [41] finds that the increase of COVID-19 confirmed cases has a negative impact on the stock market. Ashraf [2] discovers that social distancing measures are bad for the economy. Dosi et al. [42] point out that COVID-19 and contact controls may aggravate wealth inequality. 4) We illustrate that vaccination can curb the spread of epidemics and help to improve the economy. Hansen and Mano [43] find that vaccination can increase the mobility of the workplace, help to improve the economy and reduce inequality.
The rest of the paper is constructed as follows. In Section 2, we set up the Boltzmann-type system describing the evolution of wealth distribution involving an epidemic environment, and introduce a wealth exchange mechanism containing the environment and agents' psychology. The macroscopic properties of the wealth exchange model, such as the proportion of each group population and their mean wealth, are discussed in Section 3. We obtain a Fokker-Planck system to describe the evolution of wealth distributions in Section 4, and acquire the steady-state wealth distribution under the background of the SIR model. In Section 5, we introduce the government's contact control measures and vaccination into the Boltzmann-type system of wealth distributions and discuss their impact on epidemics and wealth distributions. In addition, we numerically analyze the effect of agents' trading psychology on wealth distribution and verify the existence of bimodal stationary wealth distribution. Conclusions are given in Section 6.
2.
Wealth exchange in a SIR epidemic model
In this paper, under the framework of the SIR epidemic model [10,11], we investigate how wealth distribution might evolve under the course of an epidemic. In the SIR model [11], agents are separated into the susceptible (S), infected (I), and recovered (R) categories. The susceptible group refers to individuals who have no immunity and may be infected by the disease, the infected group includes those who are infectious, and the recovered group includes those who are cured or permanently immunized.
2.1. The Boltzmann system of wealth distribution
As assumed in the wealth exchange dynamics in [5], we regard that agents are indistinguishable. In addition to the difference of infection status, each agent's state at any time $ t $ is characterized by wealth $ w\geq 0 $. We denote $ \Omega = \{S, I, R\} $. Let $ f_{L}(w, t) $ with $ L\in \Omega $ represent the wealth distribution of agents in group $ L $ at time $ t $. In the SIR epidemic model, the birth and mortality factors are not considered, which is a simplification of the actual epidemic dynamics. Then, the whole agent system's wealth distribution is $ f(w, t) = \sum\limits_{L\in \Omega}f_{L}(w, t) $, and satisfies the normalization condition $ \int_{\mathbb{R}_{+}} f(w, t)dw = 1 $.
Following the idea of wealth exchange dynamics in [13], the wealth distribution $ f_{L}(w, t) $, $ L\in \Omega $ satisfies an integro-differential system of three Boltzmann-type equations
where
is a combination of collision operators, and represents the interaction between heterogeneous agents [22,44]. The collision term $ Q(f_{L}, f_{J}) $ describes the changes in wealth distribution resulting from the microscopic interactions between individuals from groups $ L $ and $ J $. The relaxation parameters $ \tau_{LJ} $ ($ L, J\in\Omega $) before the collision operators depend on the behavior patterns of agents and the share of transactions [45], reflecting the impact of the infectious disease on the frequency of wealth exchange.
In (2.1), the time evolution of $ f_{L}(w, t) $ ($ L\in \Omega $) is expressed as the additive coupling of collision process and transport terms. The transport terms $ \Pi(w, t)f_{S}(w, t) $ and $ r f_{I}(w, t) $ consider the shift of agents from one category to another, while the change in health status is due to contact with infected persons or medical treatment. In (2.1b) and (2.1c), constant $ r > 0 $ is the recovery rate and $ 1/r $ represents the average infection period [11]. The spread of the epidemic is governed by the local incidence growth rate
where $ \rho(w, v, t) $ is the contact rate of two agents possessing wealth $ w $ and $ v $ at time $ t $.
Let $ L(t) = \int_{\mathbb{R}_{+}}f_{L}(w, t)dw $, $ L\in \Omega $ represents the proportion of agents in group $ L $. In this work, we take $ \rho(w, v, t) = \rho(t) > \rho_{0} > 0 $, where the constant $ \rho_{0} $ is a lower bound of $ \rho(t) $, then $ \Pi(w, t) = \rho(t)I(t) $.
2.2. Binary wealth exchange model
In the background of an epidemic, we consider the binary wealth exchange model
In the wealth exchange rule (2.2), an agent with infection status $ L\in \Omega $ and wealth $ w $ interacts with another agent with infection status $ J\in \Omega $ and wealth $ v $, and their post-trade wealth is $ w^{*} $ and $ v^{*} $, respectively.
According to (2.2), the change of each agent's wealth in a single interaction comes from two mechanisms, the deterministic exchange part and the random fluctuation caused by market risks. The certain exchange part of each agent's wealth depends on the effect of infectious diseases and the impact of the individual's psychology on the transaction. In terms of a mathematical expression, the exchange propensity of the agent with wealth $ w $ and infection state $ L $ is represented by $ P_{L}\cdot H(I(t))+\Phi(\frac{w}{\overline{W}}) $. Specifically, $ P_{L} $ is the exchange propensity of agents with infection state $ L $ under normal circumstances, which is the same as that in the CPT model (1.1). $ H(I(t))\leq 1 $ is a non-increasing function of the infected fraction $ I(t) $ and is used to measure the impact of the epidemic on people's participation in economic activities. We take $ H(I(t)) = \frac{1}{1+I(t)} $. The value function $ \Phi(\frac{w}{\overline{W}}) $, which measures the psychological impact of an agent's wealth level on his trading decision, is an application of the prospect theory [28]. The constant $ \overline{W} $ represents a reference wealth level, such as average wealth. The uncertainty is represented by the random variable $ \eta $ with mean zero and variance $ \sigma $. To ensure that the post-trade wealth is nonnegative, we suppose that $ \eta\geq P_{L}\cdot H(I(t))+\Phi(\frac{w}{\overline{W}})-1 $. In addition, to guarantee that the kinetic equations (2.1) is well posed [13], we assume that
For the variable $ s\geq 0 $, we consider the value function
where the constant $ \mu\in [0, 1) $ measures the influence of individual psychology on trading decision-making, and the constant $ 0 < \epsilon < 1 $ denotes the intensity of the frequency of wealth interaction. For fixed $ \mu $, $ \epsilon $ and $ s $, function $ |\Phi(s)| $ decreases with respect to parameter $ \nu $. (2.4) is a generalization of the value function $ \Phi_{1}^{\epsilon}(s) $ in [29],
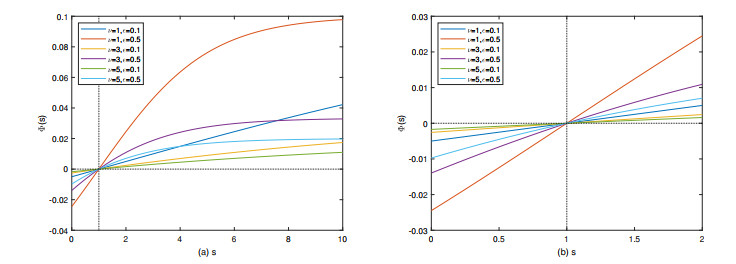
Compared with $ \Phi_{1}^{\epsilon}(s) $, parameter $ \nu > 1 $ in (2.4) prevents the possibility that when the wealth is large, the proportion of increased investment is too high, and when the wealth is small, the conservative psychology leads to little investment. The images of function $ \Phi(s) $ with $ \mu = 0.1 $ and different values of parameters $ \nu $ and $ \epsilon $ are presented in Figure 1.
The Eq (2.4) satisfies the properties of the value function in [28], which are described as follows:
1) $ \Phi(s) $ monotonically increases with $ s $ and has finite upper and lower bounds
2) $ s = 1 $ is the reference point, i.e., $ \Phi(s = 1) = 0 $.
3) In the case of $ \epsilon < \log \nu $, we have $ [\Phi(s)]^{''} < 0 $ for every $ s\geq 0 $. Namely, $ \Phi(s) $ is a concave function on $ \mathbb{R}_{+} $. In the case of $ \log \nu < \epsilon < 1 $, $ s = 1-\frac{1}{\epsilon}\log \nu\in(0, 1) $ is the inflection point, and
4) Since $ \nu\geq1 $, we get
Property 4) states that the value function (2.4) is asymmetric to the point $ s = 1 $, which can also be observed in Figure 1(b). It corresponds to a phenomenon that the decision-making behavior of agents possessing wealth higher than the reference level $ \overline{W} $ is more robust, namely, the fluctuation of decision-making affected by psychology is more gentle. Moreover, this property also indicates that agents with wealth under the reference level $ \overline{W} $ tend to save more wealth.
According to the boundedness (2.5), the parameters in the binary exchange rule (2.2) satisfy $ P_{L}+\mu/\nu < 1 $, $ \eta\geq P_{L}+\mu/\nu -1 $ and $ P_{L}+\frac{\mu}{\nu}(1-\frac{1+\nu}{\nu e^{-\epsilon}+1}) > 0 $ for every $ \epsilon\in(0, 1) $, $ L\in\Omega $. Since $ \frac{\mu}{\nu}(\frac{1+\nu}{\nu e^{-\epsilon}+1}-1) $ increases with $ \epsilon $, we have $ P_{L}\geq \mu\frac{e-1}{\nu+e} $, $ L\in\Omega $.
3.
Macro properties of kinetic model
In (2.1), the Boltzmann-type collision operator $ Q(f_{L}, f_{L}) $ ($ L\in \Omega $) denotes the binary interaction of agents with the same infection state $ L $, and $ Q(f_{L}, f_{J}) $ with $ L\neq J $ ($ L, J\in \Omega $) represents the binary interaction of agents with different infection states $ L $ and $ J $. For any test function $ \psi(w)\in C_{0}^{\infty}(\mathbb{R}_{+}) $, we have [13]
where $ \langle\cdot\rangle $ is the expectation operator with respect to the random variable $ \eta $.
We take the relaxation time $ \tau_{LJ} = 1 $ ($ L, J\in\Omega $) in (2.1). Then, the weak form of the system (2.1) is
where
Substituting $ \psi(w) = 1 $ into (3.2), we obtain that the fractions of the three agent groups satisfy
and $ S(t)+I(t)+R(t)\equiv 1 $, which is due to the normalization condition of $ f(w, t) $. If $ \rho(t) = \rho $ is a constant, (3.3) is the classical SIR model, which is mathematically and epidemiologically well-posed [11]. In the SIR model, the contact number $ \gamma $, which refers to the average number of contacts of an infected person during the period of infection, is equal to the ratio of contact rate $ \rho(t) $ to recovery rate $ r $ (i.e. $ \gamma = \rho(t)/r $) [11]. Let $ \gamma_{0} = \rho/r $. For the classical SIR model (3.3), Hethcote [10] gives the properties of its solution, which is repeated as the following Theorem. Denote $ L^{\infty} = \lim\limits_{t\mapsto +\infty}L(t) $, $ f_{L}^{\infty}(w) = \lim\limits_{t\mapsto +\infty}f_{L}(w, t) $ with $ L\in \Omega. $
Theorem 3.1. ([10]) Let $ (S(t), I(t)) $ be a solution of the classical SIR model in
If $ \gamma_{0}S_{0}\leq 1 $, then $ I(t) $ decreases to zero as $ t\mapsto \infty $. If $ \gamma_{0}S_{0} > 1 $, then $ I(t) $ increases to a maximum $ I_{max} = I_{0}+S_{0}-1/\gamma_{0}-[ln(\gamma_{0}S_{0})]/\gamma_{0} $ and then decreases to 0 as $ t\mapsto\infty $. The susceptible proportion $ S(t) $ is a decreasing function and $ S^{\infty}\in (0, 1/\gamma_{0}) $ is the unique root of the equation
Theorem 3.1 implies that the infected fraction $ I(t) $ tends to zero in the steady-state (i.e., $ I^{\infty} = 0 $). Combined with the non-negativity of the distribution function, the wealth distribution of the infected population in the steady-state is zero, i.e., $ f_{I}^{\infty}(w) = 0 $. Then, in the steady-state, the order moments of wealth distribution of the infected population are zero. When $ I^{\infty} = 0 $, we have $ \lim\limits_{t\mapsto+\infty}\Pi(w, t) = 0 $.
Let $ m_{L}(t) = \int_{\mathbb{R}_{+}}wf_{L}(w, t)dw $ ($ L\in \Omega $) represent the mean wealth of group $ L $. According to (2.2), the whole agent system's wealth is conserved in the mean, i.e., $ \langle w^{*}+ v^{*}\rangle = w+ v $, then $ \sum\limits_{L\in\Omega} m_{L}(t): = m $, $ t\geq 0 $.
Let $ E_{L}(t) = \int_{\mathbb{R}_{+}} w^{2} f_{L}(w, t) dw $ ($ L\in\Omega $) represent the second moment of $ f_{L}(w, t) $. Denote $ m_{L}^{\infty} = \lim\limits_{t\mapsto +\infty}m_{L}(t) $ and $ E_{L}^{\infty} = \lim\limits_{t\mapsto +\infty}E_{L}(t) $.
Taking $ \psi(w) = w $ and substituting (2.2) into (3.1) arise
Denote
We get
where
If $ I^{\infty} = 0 $, we have $ m_{I}^{\infty} = 0 $. Denote $ F_{J}^{\infty} = \lim\limits_{t\mapsto +\infty}F_{J}(t) $. From (3.5a) and (3.5c), the mean wealth $ m_{S}^{\infty} $ and $ m_{R}^{\infty} $ satisfy
where $ R^{\infty} = 1-S^{\infty} $ and $ m_{S}^{\infty}+m_{R}^{\infty} = m $. Since $ \Phi(\frac{v}{\overline{W}}) $ is a nonlinear function of variable $ v $, the mean wealth $ m_{S}^{\infty} $ and $ m_{R}^{\infty} $ cannot be solved explicitly from (3.6), but their upper and lower bounds can be obtained. The value function (2.4) has an upper and lower bound (2.5), so we have $ F_{S}^{\infty} \in\big[\mu \frac{e^{-\epsilon}-1}{\nu e^{-\epsilon}+1} m_{S}^{\infty}, \frac{\mu}{\nu}m_{S}^{\infty} \big] $ and $ F_{R}^{\infty} \in\big[\mu \frac{e^{-\epsilon}-1}{\nu e^{-\epsilon}+1} m_{R}^{\infty}, \frac{\mu}{\nu}m_{R}^{\infty} \big] $. Then we obtain
where $ D_{SR} = S^{\infty} (P_{R}+\frac{\mu}{\nu}) +R^{\infty} (P_{S}+\mu \frac{e^{-\epsilon}-1}{\nu e^{-\epsilon}+1}) $ and $ D_{RS} = S^{\infty} (P_{R}++\mu \frac{e^{-\epsilon}-1}{\nu e^{-\epsilon}+1}) + R^{\infty} (P_{S}+\frac{\mu}{\nu}) $.
4.
Fokker-Planck asymptotic analysis
The Boltzmann-like system (2.1) describes how wealth distribution evolves under the course of an epidemic, but its explicit solutions are difficult to obtain. Utilizing the quasi-invariant limit method [40], the Boltzmann-type equations are turned into the Fokker-Planck equations. We can use the stationary solution of the Fokker-Planck system to depict the large-time behavior of wealth distribution.
Letting $ 0 < \epsilon\ll 1 $ and employing the scaled quantities
The binary wealth exchange model (2.2) becomes
where $ L, J\in\Omega $.
The scaled micro wealth exchange model (4.2) indicates that a single interaction arises only small changes in wealth. To preserve the effects of all parameters in the exchange rule (2.2) when taking the limit $ \epsilon\mapsto 0 $, the agents need to do much more interactions within a time period, that is, to increase the interaction frequency. Therefore, we take $ \tau_{LJ}\to\epsilon\tau_{LJ} $, which also makes the evolution of the distributions independent of the scaling parameter $ \epsilon $. Then, the weak form of the scaled system (2.1) reads
where
Taking a Taylor expansion of $ \psi(w^{*}) $ around $ w $, and substituting the expansion into the collision terms on the right of (4.3), we obtain
The residual $ R_{LJ}(\epsilon) $ describes the higher-order terms of $ \epsilon $. In fact, for any test function $ \psi(w) $ belonging to the second-order $ H\ddot{o}lder $ space $ \mathcal{C}_{0}^{2+\alpha}(R_{+}) $ with $ \alpha\in(0, 1) $, we have
where $ \tilde{w} = \theta w^{*} + (1-\theta)w $ for some $ \theta \in (0, 1) $.
Using
the limit of (4.4) is expressed as
where
Substituting (4.4) into (4.3), setting $ \tau_{LJ} = 1 $ ($ L, J\in\Omega $), taking $ \epsilon\mapsto 0 $ and combining with (4.6), we obtain
where
The boundary conditions are
The system (4.7) maintains the memory of the micro-dynamic (2.2) through relevant parameters $ \mu $, $ \nu $, $ \overline{W} $, $ \sigma $ and $ P_{J} $ ($ J\in\Omega $).
As a special case of explicitly finding the steady-state solution of (4.7), we suppose that the contact rate $ \rho(t) = \rho > 0 $ is a constant. From Theorem 3.1, there are $ I^{\infty} = 0 $, $ f_{I}^{\infty}(w) = 0 $ and $ S^{\infty} $ is the unique solution of (3.4). The mean wealth $ m_{S}^{\infty} $ and $ m_{R}^{\infty} $ are bounded and belong to $ [0, m] $.
Proposition 4.1. When the steady-state infected fraction $ I^{\infty} = 0 $, the moments of the stationary solutions of the Boltzmann-like system (4.3) satisfy the recursive relationship
where
denotes the $ n $-order moment of the stationary wealth distribution of agents with infection state $ L $.
Proof. When $ I^{\infty} = 0 $, we have $ f_{I}^{\infty}(w) = 0 $ and $ M_{I}^{n, \infty} = 0 $.
For the case of $ n = 1 $. Substituting $ \psi(w) = w $ into (4.3), and using the scaled exchange rule (4.2), then the steady-state mean wealth $ m_{L}^{\infty} $ and energy $ E_{L}^{\infty} $ satisfy
which is consistent with (4.8) when $ n = 1 $.
When $ n\geq 2 $, substituting $ \psi(w) = w^{n} $ into (4.3) and (4.4), letting $ \epsilon\mapsto 0 $ and using (4.5), we have
Then the recursive relation (4.8) is deduced through a simple calculation of (4.10).
In the scaling (4.1), condition (2.3) for $ \epsilon\mapsto 0 $ becomes
Using the inequality in (4.5), a sufficient condition for (4.11) is $ P_{L}-\frac{\mu}{\nu+1}-\frac{\sigma}{2} > 0 $ with $ L\in \{S, I, R\} $. Employing the H$ \ddot{o} $lder's inequality, we have
Let $ n = 2 $ in (4.8). Using (4.9) and (4.12), $ E_{L}^{\infty} $ has an upper bound
In the case of $ \mu\neq 0 $, according to the recursive formula (4.8) and the boundedness of the first two moments of wealth distributions (see (4.12) and (4.13)), we can obtain the boundedness of higher-order moments of wealth distributions in the stationary situation.
From (4.7), the stationary distribution $ f_{L}^{\infty}(w) $ ($ L\in \{S, R\} $) satisfies the ordinary differential equation
where
From (4.9), we have
which is independent of the subscript $ L $. Then the stationary wealth distribution of the susceptible (recovered) group is expressed as
where $ C_{L} $ is a regularization parameter such that $ \int_{\mathbb{R}_{+}}f_{L}^{\infty}(w)dw = L^{\infty} $. Note that
Then, $ f_{L}^{\infty}(w) $ is a concave function in $ (0, +\infty) $ and reaches the maximum value at $ \tilde{w}_{L} = c/(\sigma-a_{L}) $ in the case of $ \mu = 0 $. When $ \mu\neq0 $, $ f_{L}^{\infty}(w) $ gets the maximum value at $ \tilde{w}_{L} = \big[(a_{L}-\sigma)+\sqrt{(a_{L}-\sigma)^{2}+4bc}\big]/(2b) $.
The whole stationary wealth distribution is given by
Proposition 4.2. The combination (4.15) of two unimodal distributions (4.14) is a unimodal or bimodal distribution.
Proof. Let
Then
Using $ \lim\limits_{w\mapsto 0^{+}}\Upsilon(w) < 0 $ and $ \lim\limits_{w\mapsto +\infty}\Upsilon(w) > 0 $, thus the function $ \Upsilon(w) $ has at least one positive root, which corresponds to the maximum point of $ f^{\infty}(w) $. Taking the derivative of $ \Upsilon(w) $ with respect to $ w $, we get
where
Since $ f_{S}^{\infty}(w)\geq 0 $, $ f_{R}^{\infty}(w)\geq 0 $ and the number of variations in the sign of the polynomial $ \phi_{L}(w) $ is 2. Using the Descartes' rule of sign, the number of positive roots of $ d \Upsilon(w)/d w $ is 0 or 2. When $ d \Upsilon(w)/d w $ has no positive root, the function $ \Upsilon(w) $ has only on positive root. When $ d \Upsilon(w)/d w $ has two positive roots, the function $ \Upsilon(w) $ has three positive roots, corresponding to two maximum points and one minimum point of $ f^{\infty}(w) $, respectively.
The distribution (4.14) is the product of an inverse-gamma function and an exponential function, which is equivalent to
where
and $ \Gamma(\cdot) $ is the Gamma function. Note that $ g_{L}(w; a_{L}, c, \sigma) $ is the density of the inverse-gamma distribution $ IG_{L}(1-\frac{2a_{L}}{\sigma}, \frac{2c}{\sigma}) $, and $ h(w; b, \sigma) $ is the density of the exponential distribution $ E(\frac{2b}{\sigma}) $.
It is fascinating to note that the appearance of the exponential function part (i.e., $ h(w; b, \sigma) $) is mainly due to the function $ \Phi(\cdot) $ in (2.2). When the psychological factors are not considered in the wealth exchange (i.e., $ \mu = 0 $), (4.14) becomes an inverse-gamma function, which is the same as the stationary wealth distribution in [13], showing polynomial decay when $ w\mapsto\infty $. The decomposition form (4.17) suggests that, due to the exponential function $ h(w; b, \sigma) $, the tail of the wealth distribution (4.15) is slimmer than that of the inverse gamma distribution curve under appropriate parameters, and corresponds to a society with fewer super-rich people.
5.
Numerical analysis
Under the framework of the SIR epidemic dynamic, by coupling the binary wealth exchange rule (2.2) with the Boltzmann-type dynamic system (2.1), we obtain the stationary wealth distribution (4.15), which is impacted by the epidemic-related parameters and the value function (2.4). In this part, we introduce the government contact control measures and vaccination into the kinetic system, and analyze the impact of different measures on epidemic dynamics and wealth distribution. Finally, in a fixed epidemic background, we explore the influence of the value function (2.4) on the stationary wealth distribution, and verify the possible situation that the whole stationary wealth distribution exists double peaks.
The Gini coefficient takes value in $ [0, 1] $ and measures wealth inequality. A larger Gini coefficient indicates a more unequal wealth distribution. The Gini coefficient is equal to the ratio of the area between the equality line and the Lorentz curve to the area below the equality line. Define the Lorenz curve as [40]
then the Gini coefficient is
In the following simulations, if there is no special declaration, we always take $ \rho = 0.3 $, $ I_{0} = 0.01 $, $ S_{0} = 0.99 $, $ P_{S} = 0.075 $, $ P_{R} = 0.15 $, $ m = 1 $, $ \sigma = 0.1 $, $ \overline{W} = 1 $ and $ \nu = 3 $.
5.1. Epidemic dynamics and its impact on the steady-stade wealth distribution
5.1.1. The influence of contact control on the wealth distribution
Considering that the government takes non-drug containment measures to control the spread of infectious diseases. We take $ \rho(t) = \rho-\kappa I(t) > 0 $, where the constant $ \kappa \in [0, \min\{\rho/I(t)\}) $ measures the strength of contact control. Then, (3.3) is rewritten as
System (5.1) is an example of the implicit behavioral SIR model [46], and the contact rate $ \rho(t) $ decreases with the infected fraction $ I(t) $. When $ \kappa = 0 $, (5.1) becomes the classical SIR model in [10]. When $ \kappa\neq0 $, compared with the classical SIR model, a nonlinear term $ \kappa S(t)I^{2}(t) $ appears in (5.1). The contact number $ \gamma_{1} = [\rho-\kappa I(t)]/r\leq \rho/r $ varies with the infected fraction $ I(t) $. Because of $ 0 < \rho-\kappa I(t)\leq \rho $, $ S(t)\geq 0 $ is monotonically decreasing. Similar to Theorem 3.1, the infected fraction in the steady-state is zero, i.e., $ I^{\infty} = 0 $, as verified in Figure 2(a). Then, the wealth distribution of the infected group is zero in the steady-state, and the whole wealth distribution is still in the form of (4.15), in which $ S^{\infty} $ and $ R^{\infty} $ are the stationary solutions of (5.1).
Figure 2 depicts the epidemic dynamics and the wealth distribution with different values of parameters $ \kappa $ and $ r $. We take $ \mu = 0 $. The parameter value $ \rho = 0.3 $ and $ r = 0.04 $ are close to the epidemiological parameters estimated in [14], which are fitted from the COVID-19 data before the lockdown in three European countries (France, Italy and Spain). Figure 2(a) shows that with the increase of the recover rate $ r $ or the contact control strength $ \kappa $, the peak value of the infected fraction becomes smaller, and more agents keep the uninfected state. In particular, when $ r = 0.25 $, more than half of the susceptible people have the opportunity to remain uninfected during the epidemic.
The Gini coefficients of the wealth distributions in Figure 2(b) are $ Gini(r = 0.04, \kappa = 0) = 0.3127 $, $ Gini(r = 0.15, \kappa = 0) = 0.3739 $, $ Gini(r = 0.25, \kappa = 0) = 0.4257 $, $ Gini(r = 0.15, \kappa = 0.5) = 0.3901 $ and $ Gini(r = 0.15, \kappa = 1) = 0.3989 $. In the epidemic backgrounds in Figure 2(a), the wealth distribution curves and Lorentz curves in Figure 2(b) and their corresponding Gini coefficients show that the increase in $ r $ or $ \kappa $ leads the wealth distribution curve shifts to the left, and aggravates the wealth inequality. Combined with Figure 2(a), a reasonable explanation for this phenomenon is that when the contact number $ \gamma_{1} $ is small, the susceptible agents in the steady-state take a large proportion. Affected by the conservative exchange psychology of susceptible agents, that is, the exchange tendency of susceptible individuals is less than the tendency of recovered agents, the inequality of wealth distribution becomes worse.
5.1.2. The influence of vaccination on the wealth distribution
One possible way to deal with the negative effect in Section 5.1.1 is vaccination. Through vaccination, the susceptible agent transforms directly into the recovered person. Compared with (2.1), we introduce a term $ \Xi(w, t)f_{S}(w, t) $ to represent the transfer of agents from the susceptible group to the recovered group due to vaccination. The Boltzmann-type system (2.1) is rewritten as
in which we take the transfer rate $ \Xi(w, t) = \int_{\mathbb{R}_{+}}\theta(t)f_{I}(v, t)dv $. To explore the effect of vaccination on the wealth distribution, we take the contact rate $ \rho(t) = \rho $ as a constant and $ \theta(t) = \beta \cdot \Psi_{\{t\geq T_{0}\}} $. The constant $ \beta > 0 $ represents the vaccination rate, $ T_{0} $ is the time of starting vaccination and $ \Psi_{\{t\geq T_{0}\}} $ denotes the indicator function on $ \{t|t\geq T_{0}\} $. Integrating the Eqs (5.2) over $ \mathbb{R}_{+} $ yields
Since $ \theta(t)\geq 0 $, the consideration of vaccination does not affect the steady-state infected fraction $ I^{\infty} = 0 $, which is verified in Figure 3(a). Therefore, the stationary solution obtained from (5.2) has the same form as (4.15), while the susceptible and recovered fractions $ S^{\infty} $ and $ R^{\infty} $ are calculated from (5.3).
The impact of vaccination on epidemic and wealth distribution is shown in Figure 3, in which we take $ T_{0} = 30 $, $ r = 0.15 $ and $ \mu = 0 $. Figure 3 indicates that as the vaccination rate $ \beta $ increases, more agents become recovered. The total number of infected patients declines, and the distribution of wealth shifts to the right, reflecting an improvement in wealth inequality. The Gini coefficients of the wealth distributions in Figure 3(b) are $ Gini(\beta = 0) = 0.3739 $, $ Gini(\beta = 0.3) = 0.3551 $ and $ Gini(\beta = 0.7) = 0.3395 $. Therefore, according to the simulations in Figure 3, we infer that vaccination plays a role in preventing and controlling the epidemic and improving the economy. This change can not only effectively control the spread of the epidemic and reduce the infected fraction, but also have a positive impact on reducing wealth inequality.
5.2. The influence of value function $ \Phi $ on the wealth distribution
In the exchange mechanism (2.2), the exchange propensity of agents is affected by their psychology, which is measured by the value function (2.4). The stationary wealth distribution of susceptible (infected) populations is obtained in the form of (4.14), which is the product of an inverse-gamma function and an exponential function (see (4.17)). It is different from the inverse-gamma steady-state distribution obtained from the usual socio-economic dynamic models [6,13].
In Figure 4, we compare the wealth distribution $ f^{\infty}(w) $ with different $ \mu $. Moreover, to verify the existence of bimodal distribution, we simulate the distribution $ f^{\infty}(w) $ with different values of the risk parameter $ \sigma $. We take $ P_{R} = 0.2 $ and choose the epidemic background corresponding to a recovery rate $ r = 0.25 $. The Gini coefficients of the wealth distributions in Figure 4(a) are $ Gini(\mu = 0) = 0.4476 $, $ Gini(\mu = 0.001) = 0.4444 $, $ Gini(\mu = 0.01) = 0.4258 $, $ Gini(\mu = 0.05) = 0.3856 $ and $ Gini(\mu = 0.08) = 0.3654 $. The Gini coefficients of the wealth distributions in Figure 4(b) are $ Gini(\mu = 0) = 0.2989 $, $ Gini(\mu = 0.001) = 0.2982 $, $ Gini(\mu = 0.01) = 0.2923 $, $ Gini(\mu = 0.05) = 0.2712 $ and $ Gini(\mu = 0.08) = 0.2591 $.
Figure 4 indicates that with the increase of psychological influence (i.e., the increase of $ \mu $), more agents are at the middle wealth level, the number of agents of both low and high wealth levels has declined. The Gini coefficient of different risk parameter values decreases with the increase of parameter $ \mu $. It also verifies the improvement of wealth inequality. Additionally, Figure 4(b) illustrates that the wealth distribution's tail becomes slimmer with the increase of $ \mu $, which corresponds to a society with fewer super-rich people. From the perspective of mathematical analysis, the larger the value of $ \mu $, the smaller the shape parameter $ 1-2a_{L}/\sigma $ of the inverse-gamma function $ g_{L}(w; a_{L}, c, \sigma) $. This corresponds to a fatter tail. Therefore, the existence of exponential function $ h(w; b, \sigma) $ plays a key role in thinning the tail.
6.
Conclusions
Real economic behavior is complex and is affected by various factors, such as the market environment and the psychology of traders. Under the background of an epidemic, we utilizes the method of mixed rarefied gas dynamics to investigate the distribution of wealth. In the wealth exchange mechanism, the impact of agents' psychology on trading decisions is expressed by a value function, which satisfies the properties of the prospect theory [28]. Under the SIR epidemic, we obtain that the steady-state wealth distribution of the susceptible (recovered) group is the product of an inverse-gamma function and an exponential function, showing a single peak. The emergence of the exponential function part is caused by the nonlinear utility function (2.4). We prove and numerically verify that the wealth distribution of the whole agent system presents a bimodal distribution with appropriate parameters.
An increase in the recovery rate or the strength of contact control helps to curb the epidemic, keeping more people uninfected and reducing the peak value of the infected fraction. However, these measures are imperfect and may lead to economic recession, because the conservative trading psychology of susceptible agents caused by the fear of the virus is not changed. Vaccination, which transfers the susceptible person directly into a recovered individual, is numerically verified to have a positive impact on curbing epidemics and reducing wealth inequality. In addition, numerical simulations state that, with the increase of the psychological effect of agents, the population in the middle wealth level is increased, the Gini coefficient is decreased, and the tail of the multi-agent system's wealth distribution becomes thinner. These results indicate a reduction in the super-rich and wealth inequality.
Acknowledgments
This research is supported by the National Natural Science Foundation of China (No. 11471263). The authors are very grateful to the reviewers for their valuable and meaningful comments of the paper.
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: