Search Advanced

AIMS Environmental Science

2019, Volume 6, Issue 3: 186-221. doi: 10.3934/environsci.2019.3.186
Previous Article Next Article
Review

Implications of climate change on nutrient pollution: a look into the nitrogen and phosphorus loadings in the Great Miami and Little Miami watersheds in Ohio

  • Agricultural Research Development Program (ARDP), Central State University, Wilberforce, OH 45384, USA
  • The Great Miami (GM) and Little Miami (LM) watersheds in Ohio are included in the 51 major river systems in the United States for long-term assessment of conditions of water quality under the USGS National Water-Quality Assessment (NAWQA) Program. Nitrogen (N) and phosphorus (P) loadings have decreased over the years in the GM and LM basins, however, they still remain among the highest concentrations detected in the nation. The latest nutrient loading analysis from Ohio Environmental Protection Agency (OEPA) showed slightly above period of record averages for N and P. Significant amounts of mobilized agricultural N and P from fertilizers in watersheds are transported to the Ohio River and other coastal marine systems such as the Gulf of Mexico, leading to increased growth of harmful algal blooms. In the GM and LM watersheds, changes in flood frequency and intensity are projected to occur in the future as heavy precipitation events are likely to increase as a result of climate change. As climate plays a role for nutrient transformation and transport, studies have shown that N and P inputs to surface waters from agriculture and other sources are projected to continue to increase over the next several decades. This paper reviewed the means of how the GM and LM watersheds are ecologically affected by the N and P nutrient pollution and how climate change impacts the quantity of N and P loadings that go into the river systems. Without better understanding of the nutrient loading processes and their association with various agricultural practices and interactions with climate, there could be additional threats to water quality in both the GM and LM watersheds in decades to come. This literature review has made references to many pertinent new publications that have become available in recent years, as well as to the classic literature.

    Citation: Eric Ariel L. Salas, Sakthi Kumaran Subburayalu. Implications of climate change on nutrient pollution: a look into the nitrogen and phosphorus loadings in the Great Miami and Little Miami watersheds in Ohio[J]. AIMS Environmental Science, 2019, 6(3): 186-221. doi: 10.3934/environsci.2019.3.186

    Related Papers:

    [1] Nathaly A. Díaz Molina, José A. Sosa Olivier, José R. Laines Canepa, Rudy Solis Silvan, Donato A. Figueiras Jaramillo . Evaluation of the bioenergy potential of agricultural and agroindustrial waste generated in southeastern Mexico. AIMS Energy, 2024, 12(5): 984-1009. doi: 10.3934/energy.2024046
    [2] Constantinos S. Psomopoulos . Residue Derived Fuels as an Alternative Fuel for the Hellenic Power Generation Sector and their Potential for Emissions ReductionConstantinos S. Psomopoulos. AIMS Energy, 2014, 2(3): 321-341. doi: 10.3934/energy.2014.3.321
    [3] Gustavo Aguilar, Pranjali D. Muley, Charles Henkel, Dorin Boldor . Effects of biomass particle size on yield and composition of pyrolysis bio-oil derived from Chinese tallow tree (Triadica Sebifera L.) and energy cane (Saccharum complex) in an inductively heated reactor. AIMS Energy, 2015, 3(4): 838-850. doi: 10.3934/energy.2015.4.838
    [4] Ee Sann Tan, Kumaran Palanisamy, Teuku Meurah Indra Mahlia, Kunio Yoshikawa . Performance and emission study on waste cooking oil biodiesel and distillate blends for microturbine application. AIMS Energy, 2015, 3(4): 798-809. doi: 10.3934/energy.2015.4.798
    [5] Rumana Islam, Charushi Panditharatne, John Schellenberg, Richard Sparling, Nazim Cicek, David B. Levin . Potential of thin stillage as a low-cost nutrient source for direct cellulose fermentation by Clostridium thermocellum. AIMS Energy, 2015, 3(4): 711-727. doi: 10.3934/energy.2015.4.711
    [6] Lihao Chen, Hu Wu, Kunio Yoshikawa . Research on upgrading of pyrolysis oil from Japanese cedar by blending with biodiesel. AIMS Energy, 2015, 3(4): 869-883. doi: 10.3934/energy.2015.4.869
    [7] Robinson J. Tanyi, Muyiwa S Adaramola . Bioenergy potential of agricultural crop residues and municipal solid waste in Cameroon. AIMS Energy, 2023, 11(1): 31-46. doi: 10.3934/energy.2023002
    [8] Honnurvali Mohamed Shaik, Adnan Kabbani, Abdul Manan Sheikh, Keng Goh, Naren Gupta, Tariq Umar . Measurement and validation of polysilicon photovoltaic module degradation rates over five years of field exposure in Oman. AIMS Energy, 2021, 9(6): 1192-1212. doi: 10.3934/energy.2021055
    [9] Patrick Moriarty, Damon Honnery . Review: Assessing the climate mitigation potential of biomass. AIMS Energy, 2017, 5(1): 20-38. doi: 10.3934/energy.2017.1.20
    [10] Tuan Le-Anh . Energy benchmark and energy saving potential in the pulp and paper industry. AIMS Energy, 2023, 11(6): 1306-1327. doi: 10.3934/energy.2023059
  • The Great Miami (GM) and Little Miami (LM) watersheds in Ohio are included in the 51 major river systems in the United States for long-term assessment of conditions of water quality under the USGS National Water-Quality Assessment (NAWQA) Program. Nitrogen (N) and phosphorus (P) loadings have decreased over the years in the GM and LM basins, however, they still remain among the highest concentrations detected in the nation. The latest nutrient loading analysis from Ohio Environmental Protection Agency (OEPA) showed slightly above period of record averages for N and P. Significant amounts of mobilized agricultural N and P from fertilizers in watersheds are transported to the Ohio River and other coastal marine systems such as the Gulf of Mexico, leading to increased growth of harmful algal blooms. In the GM and LM watersheds, changes in flood frequency and intensity are projected to occur in the future as heavy precipitation events are likely to increase as a result of climate change. As climate plays a role for nutrient transformation and transport, studies have shown that N and P inputs to surface waters from agriculture and other sources are projected to continue to increase over the next several decades. This paper reviewed the means of how the GM and LM watersheds are ecologically affected by the N and P nutrient pollution and how climate change impacts the quantity of N and P loadings that go into the river systems. Without better understanding of the nutrient loading processes and their association with various agricultural practices and interactions with climate, there could be additional threats to water quality in both the GM and LM watersheds in decades to come. This literature review has made references to many pertinent new publications that have become available in recent years, as well as to the classic literature.


    Abbreviations: % mol: percent mol; ℃: degrees Celsius; ®: trademark; ~: approximate symbol; ≤: equal or minor; ø: diameter; C/N: carbon-nitrogen relation; C/P: carbon-phosphorus relation; cm-1: Wavenumber; g: gram; GWh: Gigawatt hora; h: hours; HHV: Higher Heating Value; J/g: Joule per gram; kg: kilogram; km: kilometer; L: liter; m3: cubic meter; mg/g: milligram per gram; mg/kg: milligram per kilogram; mg: milligram; MJ/kg: Mega Joule per kilogram; mm: millimeter; MPa: Megapascal; mS/cm: milli siemens per centimeter; MXN＄: Mexican peso; t: tons; TWh: Terawatt hora; US＄: American dollar

    1.   Introduction

    During 2019 worldwide, primary energy consumption had an annual growth rate of 1.30%. As a consequence, the carbon emission from energy use increased 0.50% (almost 50% less than in 2018), the main sources of electricity generation were coal (36.38%), natural gas (23.32%), and renewable energies (10.39%), the latter is the source of energy generation with the highest growth (41%), the geothermal and biomass group, represent 6% of renewable energy sources [1]. In Mexico, the electricity demand grew at an average annual rate of 2.50%, with a generation of 329.71 TWh [2]. Nevertheless, 78.90% of the energy in the country is produced through conventional technologies, and the remaining 29.50% comes from clean technologies, including biomass that represents only 0.92%. The use of biomass is divided between cane bagasse (0.75%) and biogas (0.17%), with a growth of 28.60% and 24.20%, respectively, in addition to the existence of 79 plants that use biomass [3]. Biomass is considered a source of clean and renewable energy due to the ability to absorb CO2 from the atmosphere, which helps reduce the greenhouse effect [4], and due to its abundance, large distribution and carbon neutrality are considered a potential substitute for fossil fuels [5]. In Mexico, there are small advances in the use of biomass as a source of clean energy, perhaps the best example is the cane bagasse in the sugar mills. The Santa Rosalia sugar mill (Tabasco, México) generates 100% of the electrical energy from the bagasse generated as a byproduct in sugar production, avoiding the use of fuel oil or any other fossil fuel. Surplus electricity is sold to the Federal Electricity Commission, which is responsible for producing, distributing, and billing electricity in Mexico and industrial customers [6]. The calorific value of cane bagasse varies from 7.53–17.58 MJ/kg, hence using other biomass with similar potentials could be a fuel alternative in combined cycle plants or other combustion power generation systems [7,8,9].

    Aquatic biomass is one of the most abundant renewable energy sources and will be an essential component of a more sustainable energy system [9]. Nevertheless, in recent years an atypical phenomenon has been unleashed, such as the arrival of large volumes of seaweed, on some shores of the Atlantic Ocean. In 2011, the massive influx of brown seaweed occurred, denominated "Sargassum" in the eastern Caribbean, from Trinidad and Tobago to the Dominican Republic, and on the west coast of Africa, from Sierra Leone to Ghana [8]. In 2012, the massive arrival of Sargassum on the coast of Cuba [10], in 2014, many other islands and countries of the Caribbean were affected, including the Mexican Caribbean. These travel routes were verified by Franks et al. [11] when conducting experiments using drift buoys with satellite location, with a 60% similarity. In Mexico, the excessive arrival of the Sargassum has impacted nearly 1,000 km of the Mexican Caribbean coast [12], reaching volumes of up to 2 m3 per linear meter of the beach [13]. During the periods 2017 [13], 2018 [14,15], and 2019 [16], the government of Mexico invested 22.30 million dollars in the collection and management of around 701.67 thousand tons of Sargassum collected off the coast of Quintana Roo. According to DrecKmann & Sentíes [17], the arrival of this biomass in the state of Quintana Roo mainly affects Cancun and Puerto Morelos. It is presumed that this phenomenon originates from the natural detachment of aggregations of free-living species such as Sargassum fluitans Børgesen and Sargassum natans Gaillon, endemic to the Sargasso Sea in the Atlantic Ocean [18]. Subsequently, the hypothesis that originated in northeastern Brazil emerged [19]. It is important to mention that one of the hypotheses of greater debate is the interference of high nutrient loads [20], due to the mouth of the Mississippi rivers (west of the Gulf of Mexico) and the Amazon (southern Ecuador). In the case of the Amazon River, the concentration of inorganic nitrogen is reduced below the detection limit about 200 km from the mouth [21,22], but a higher growth rate has been observed in these neritic zones than in the center of the Sargasso Sea [23]. These nutrients have altered aquatic resources and various economic activities such as tourism, fishing, and shipping, of the coastal areas. Hernández-Zanuy [24] points out that the large accumulation of this material and its natural decomposition causes an increase in the chemical and biochemical oxygen demand, anoxia alters the quality of the sand, affects coastal ecosystems, and generates greenhouse gases (GHG). Lapointe et al. [23] indicate that a low C/N and C/P ratio is attributable to the rapid growth of the Sargassum. The use of macroalgae biomass for direct combustion has been studied by various researchers [25,26,27,28]. Sudhakar and Premalatha [29] indicate that the calorific value of macroalgae biomass is in the range of 4.35–20.10 MJ/kg, relatively lower than the biomass values of terrestrial crops with ranges of 14–20 MJ/kg. The chemical composition of marine biomass (Table 1) is very different from terrestrial biomass due to lower carbon (C) values, hydrogen (H), and oxygen (O), concerning higher values of nitrogen (N) and sulfur (S) [30].

    Table 1.  Characteristics comparison between Sargassum fluitans and others sargassum species.
    Characteristics Units Sargassum tenerrimum Sargassum sp. Sargassum sp. Sargassum horneri Sargassum fluitans
    Dirty Wash
    Moisture % 5.70 6.70 9.80 10.46 5.08 ± 0.31 6.34 ± 0.37
    Ash 26.50 6.60 21.20 29.29 40.52 ± 1.24 16.67 ± 1.17
    Volatile Matter 61.50 54.70 43.90 48.85 52.18 ± 0.79 76.81 ± 1.31
    Fixed Carbon 6.30 32.00 25.10 11.60 7.31 ± 1.90 6.52 ± 0.14
    Carbon 32.10 40.30 25.50 48.93 27.01 ± 1.14 39.05 ± 0.18
    Hydrogen 4.70 5.40 3.81 6.22 3.70 ± 0.08 5.00 ± 0.11
    Oxygen 60.72 51.80 - 42.16 26.07 ± 0.76 36.72 ± 0.86
    Nitrogen 0.93 2.50 1.37 0.92 1.45 ± 0.26 1.65 ± 0.19
    Sulphur 1.55 - - 1.77 1.04 ± 0.19 0.79 ± 0.04
    Chlorine - - - - 0.20 ± 0.00 0.12 ± 0.00
    Calorific values MJ/kg - - 14.70 15.44 9.82 ± 0.52* 13.85 ± 0.19*
    13.87 ± 3.22** 15.27 ± 0.18**
    9.24 ± 0.28*** 12.71 ± 0.07***
    Author [5] [31] [32] [33] This Work
    *Note: * Dulong method; ** Chaniwala method; ***Calorimetric pump method.
     | Show Table
    DownLoad: CSV

    The complexity causes inconsistencies in the stoichiometric calculations of the calorific value of the Sargassum [32]. Although the combustion of macroalgae is economically viable, the technical dimension remains debatable due to the high content of ash and moisture, which reduces its energy efficiency. Sudhakar et al. [34] pointed out that some technical problems are the handling of ash and the presence of alkali metals such as sodium (Na), potassium (K), and halogens, which cause problems of corrosion and saturation of conductive lines. Algae naturally, including Sargassum sp. they can absorb metal ions, such as lead (Pb II), copper (Cu II), and nickel (Ni II), its average removal capacity is 113.50 mg/g, with a range of 10.60 to 357 mg/g [35]. The European Environmental Agency [36] reported that the anthropogenic emission of toxic metals such as arsenic (As), Cadmium (Cd), chrome (Cr), copper (Cu), lead (Pb), nickel (Ni), and zinc (Zn), it is due to the thermal conversion of fuels, for the generation of energy and heat. For this reason, determining the presence or absence of compounds that may pose a risk of pollution to the atmosphere in materials that can be used as fuels must be necessary. Jagustyn et al. [37] mentioned the level limited based on ISO 17225-1, the limits of metals in solid biofuels, particularly for non-woody biomass, both in pellets and briquettes. Some authors highlight the valorization of Sargassum in multiple sectors such as pharmaceuticals, cosmetic, food, and biorefineries, due to the high content of carbohydrates in the form of sulfated alginates and polysaccharides, the presence of metals and high amounts of ash reduce its use in the food or fertilizer sector and biofuel production, respectively [38]. Other authors highlight its use in the biosorption and bioaccumulation of pollutants [39]. Thompson et al. [40] mention that the use of Sargassum in digestion systems, like monodigestion, is not very efficient, but the use of cosubstrates improves the high C/N ratios, but the lack of energy policies, financial and financing in the Caribbean area, this strategy is hindered. Thus, the objective of this work is to determine the calorific value of Sargassum sp. off the coast of the Mexican Caribbean. Three methods are evaluated, two calculable stoichiometric, and a direct method with a calorimeter pump, considering the washing of the Sargassum, as a factor of influence. Moreover, this research aims to outline the presence and concentration of the main toxic metals in the seaweed.

    2.   Materials and methods

    2.1.   Obtaining and characterizing Sargassum sp.

    The material was naturally dehydrated, out of the water, and exposed to the sun, subsequently transferred to pilot plant 3 of Air and Solid Waste Treatment of the Academic Division of Biological Sciences (DACBiol) of the Juarez Autonomous University of Tabasco (UJAT) in México. A sample of Sargassum sp. was hydrated for 24 h with distilled water to be observed under the microscope and to determine the morphological characteristics of the species. It 1.10 kg of Sargassum fluitans was manually sieved on a # 10 sieve (2 mm ø). The biomass was placed in a 19 L container and filled with 12 L of drinking water to reduce the sand and salts content. It was mixed manually for 5 min to wash the material, and the process was repeated up to 10 times. In each wash cycle, 250 mL of drinking water (start) and wash water (end) were sampled. Thus, the electrical conductivity was measured in mS/cm with the help of measuring equipment. Finally, the material was left to dry in an oven at 105 ℃ for 10 h.

    2.2.   Proximal and ultimate characterization

    Samples were taken to perform the proximal analysis determining the gravimetric content (mass loss) by the action of temperature and time, according to the American Society of Testing Methods (ASTM). The humidity was determined at 105 ℃ for 24 h, volatile matter at 550 ℃ for 2 h, and ashes at 800 ℃ for 1 h, based on ASTM D-2974 [41]. Further, the ultimate analysis was carried out, determining the content of C, H, N, and S (elemental composition). Each determination was performed in quadruplicate, using a Perkin Elmer PE2400 CHNS/O Elemental Analyzer (PerkinElmer, Waltham, MA, USA). The presence of O is achieved by the arithmetic difference of the sum of the elements and ash at 100%.

    2.3.   Content of toxic metals

    The presence of toxic metals such as As, Cd, Cr, Pb, Ni, and Zn was determined according to the United States Environmental Protection Agency. Samples were ground and pretreated, based on the ASTM 5468-02 [42] and analyzed US EPA 6010-B [43] method, using a Plasma Atomic Emission Spectrometer Perkin Elmer® Optima 5300 (PerkinElmer, Waltham, MA, USA) for metal arrest heavy and a Leco® AC-500 kit for PC analysis. These analyses were carried out in the coprocessing laboratory at the Macuspana plant of the Geocycle® Company.

    2.4.   Characterization of functional groups by FT-IR

    Fourier Transform Infrared (FT-IR) spectrophotometer was used to identify the functional groups present in each sample. Specimens of both types were first mixed with KBr at an approximate ratio of 1/100 (sample/KBr) and then ground in an agate mortar. The resulting mixture was pressed at 10 tons for 5 min to form the pellet, which was characterized using an FT-IR spectrometer Shimadzu IRAffinity-1 (Shimadzu Scientific Instruments, Columbia, MD, USA). Eighty scans and 2 cm-1 resolutions were applied in the range of 4500–500 cm-1 for recording the spectra. The background obtained from a scan of pure KBr was automatically subtracted from the sample spectra.

    2.5.   Determination of the calorific value using the calorimetric pump method

    The calorific value was determined on a semi-automatic oxygen bomb calorimeter A4000 from Heedding. The calibration of the oxygen bomb is made with standard benzoic acid (calorific value 26433 J/g). For the Sargassum samples, weighed a mass close to 1 g in an analytical balance VE-204 from VELAB (precision 0.1 mg); in the bottom of the reaction vessel, was added 10 ml of deionized water and fill the vessel with reactive degree oxygen (purity greater than 99.50% mol) up to a pressure of 3 MPa, to achieve an oxygen-excess atmosphere. All the measurements are carried out in triplicate.

    2.6.   Higher heating value (HHV)

    The calorific value of a material such as biomass is equal to the sum of the calorific value of the simple elements that form it, multiplied by the mass quantity of the elements present. The calorific value can also be determined by calculating the HHV, which is an important characteristic of fuels, and this can be calculated from their elemental composition (C, H, N, O, and S) [44] and their respective combustion products [45]. Two equations with multiple citations were used to determine HHV, employing the stoichiometric composition of Sargassum.

    2.7.   HHV by Dulong method

    The equation proposed by Dulong [44] expresses the HHV (MJ/kg) of dry fuel solid or liquid, containing C, H, and S in its composition.

    HHVDulong(MJkg)=[(0.3383∗C)+[1.443∗(H−O8)]+(0.0942∗S)] (1)

    2.8.   HHV by Channiwala method

    The equation reported by Channiwala et al. [44] determines the HHV (MJ/kg) considering a higher number of components such as O, N, and ash.

    HHV Channiwala(MJkg)=(0.3491∗C)−(1.1783∗H)+(0.1005∗S)−(0.1034∗O)−(0.0151∗N)−(0.0211∗Ash) (2)

    2.9.   Ash-free calorific value (AFCV)

    An adjustment was made to analyze the effect of washing on removing impurities such as ash. The ash-free calorific value (AFCV) was calculated by applying the following equation reported by Wang et al. [45] for each calorific value method.

    AFCV=100∗calorifc value100−Ash (3)

    2.10.   Analysis of results

    Analysis of variances was performed to determine the statistical similarity between the calorific value determination methods in response to the washing factor. This factor was also analyzed using linear regressions. The analyses were carried out using the statistical package Statgraphics® Centurion XVIII.

    To have knowledge for the precision of the methods used, a relative error analysis was carried out using the calorific values calculated, thereby determining the mean percentage error (MPE) and the mean absolute percentage error (MAPE), using Eqs 4 and 5, reported by Huang and Lo [46].

    MPE=1n∑ni=1HHVc−HHVDHHVD∗100% (4)
    MAPE=1n∑ni=1|HHVc−HHVDHHVD|∗100% (5)

    Where HHVC is the calorific value calculated (Dulong and Channiwala), and HHVD is the calorific value determined (calorimetric pump). A positive MPE value indicates overestimation, and a negative value suggests underestimation in the method used. For its part, the MAPE helps us to know the proximity of the calculated value of the determined one. The lower the MAPE, the greater the precision.

    2.11.   Unit Cost

    The unit cost per ton of pretreated biomass and the cost of calorific value per ton were estimated. Therefore, the costs of the inputs required in three stages of pretreatment, collection, washing, and crushing of Sargassum Fluitans were estimated. The costs were obtained by calculating the consumption of inputs on a small scale in the laboratory and scaled to one metric ton. Investment and equipment acquisition costs were not considered.

    3.   Results and discussion

    Figures 1 A) and B) show the most characteristic difference between the species Sargassum fluitans and Sargassum natans, which is the upper spine of the air bladder. In Figure 1C, it can be seen that the gas bladders of Sargassum sp. analyzed under the microscope lack the upper column in the air bladder, which indicates that it is Sargassum fluitans as reported by Oyesiku & Egunyomi [47].

    Figure 1.  Characteristics of Sargassum sp. A) Sargassum fluitans; B) Sargassum natans (Own image, based on Oyesiku and Egunyomi [47]); C) Sargassum fluitans observed under a microscope.
    DownLoad: Full-Size Img PowerPoint

    3.1.   Washing

    In Figure 2, see the decreasing electric conductivity (EC) for the wash water, regarding drinking water, during the Sargassum wash.

    Figure 2.  Decreased EC due to washing effect.
    DownLoad: Full-Size Img PowerPoint

    The EC measure of the water of the first washing of the material reached 8.02 mS/cm, concerning 0.34 mS/cm, that had drinking water before its use. After each washing session, it was possible to notice a reduction until reaching an average value of 0.38 mS/cm after 10 wash times. In the first two wash times, the reduction was 88%. Finally, the washing ratio was 0.25 L to 10 g of Sargassum to achieve similar EC values. This process differs from reported by Milledge [48], those who have washed the material for 30 seconds in running water.

    3.2.   Elementary characterization, metal content, and washing effect

    The results of the proximal and ultimate characterizations and calorific values for the three theoretical methods are shown in Table 1.

    The results of the proximal analysis ranged according to the reported by Li et al. [31], Ali & Bahadar [32], Biswas et al. [5] and Li et al. [33]. Nevertheless, the effect of washing is noticeable since the ash content was reduced and it was increased volatile matter significantly; this is attributed to reducing the content of sand and salts and the manual removal of shells from mollusk and waste plastic.

    The elemental analysis results also showed an improvement in the effect of washing. The element values ​​of C, H, and N of dirty Sargassum fluitans are similar to those reported by Ali & Bahadar [32]. No higher proportions were observed in N and S, concerning the content of C, H, and O, as indicated by Ghadiryanfar et al. [30]. In washed Sargassum, the results of C, H, O, and N are very similar to those reported by Wei et al. [31], with the use of Sargassum sp. Significant differences were found in the elemental results reported by Biswas et al. [5]; this could be because of the use of Sargassum tenerrimum or that they did not report a previous separation of the sands as in this work, they only mention washing with water. The notable increase in the elemental proportions is due to the elimination of sand, waste, and impurities in the screening and washing steps, which is related to the reduction of ashes mentioned above.

    The determined content of the metals is observed in Table 2.

    Table 2.  Reported values of heavy metals content and regulatory limit (mg/kg).
    Toxic metals ISO 17225:2014 Microalgae
    Nanno chloropsis gaditana    		 Sea balls Dirty Wash
    Ar ≤1 < 1 > 10 < 0.1 < 0.1
    Cd ≤0.5 < 0.5 < 0.5 < 0.1 < 0.1
    Cr ≤50 < 10 20 < 0.1 < 0.1
    Cu ≤20 10 < 10 -* -*
    Pb ≤10 < 10 < 20 < 0.1 < 0.1
    Ni ≤10 < 5 < 10 < 0.1 < 0.1
    Zn ≤100 < 100 < 50 < 0.1 < 0.1
    Ba - - - 10.2 5.67
    Mn - - - 14.2 < 0.1
    [49] [37] This work
    *Note: * Not determinated.
     | Show Table
    DownLoad: CSV

    The low presence of toxic metals is evident regarding the limits of the ISO 17225-1 [49]. Nevertheless, a difference in barium (Ba) and manganese (Mn) values could be observed since Mn is not soluble in water, unlike Ba, the effect is attributed to the cleaning of the material, both sand removal, and the washing. In general terms, the concentration of toxic metals in biomass is below the limits reported by Jagustyn et al. [37].

    3.3.   The Fourier Transform Infrared Spectroscopy (FT-IR)

    The spectra in Figure 3 show typical absorption bands of Sargassum fluitans.

    Figure 3.  Functional groups detected by FT-IR.
    DownLoad: Full-Size Img PowerPoint

    The strong absorption bands around 3200–3600 cm-1 may be attributed to the stretching vibrations of hydroxyl groups (-OH) in the hydrogen bond of the molecules [50], which can also be attributed to the overlapping of -OH and -NH stretching bands [49,50]. Weak bands around 2900 cm−1 are due to C-H stretching vibrations [48,51]; the bands at ~2923 and ~2853 cm-1 are due to the stretching vibration of -CH3 and -CH2- groups, respectively. The absorption peak of weak bands around 2300 cm-1 may correspond to the C-O stretching band [54]. In both spectrums, the absorbance at wavenumber around 1640 and 1420 cm-1 correspond to stretching vibrations of carbonyl double bond (ʋC = O) and carbon-oxygen single bond (ʋC-O), respectively [51]. However, in the spectrum of the dirty sample, more intense signals were observed at ~1630 cm−1 corresponded to carboxylate O-C-O asymmetric, stretching vibration and to C = O asymmetric stretching vibrations of uronic acids and band at ~1430 cm−1 can be attributed to C-OH deformation vibration [48,51,53]. In this regard, it is important to mention that it is possible to identify carboxylate bands (COO-) in natural Sargassum sp., related to carboxylic acid groups bound to metal ions (nickel and copper) in the 1635 and 1427 cm-1 regions [56]. In the spectrum of the washed samples, weak bands around 1541 cm-1 represent C = C stretch vibration indicative of the lignin were observed [54]. The absorption band at ~1246 cm-1 and ~1270 cm-1 are due to S = O (sulfate esters) [52,53]. These wide bands around 1200 cm-1 were observed with greater intensity in the spectrum of the dirty sample. They were attributed to sulfonate salts resulting from the formation of salts of the sulfonic acid of polysaccharides [56]. The absorption bands at ~1100–1030 cm-1 in the fingerprint region indicate several modes such as C-H deformation or C-O or C-C stretching, pertaining to carbohydrates and polysaccharides [48,52]. In the dirty sample, strong absorption bands were observed at approximately 1400 and 874 cm-1, the calcium carbonate (CaCO3) shows strong bands in these regions. The sharp band at ~874 cm-1 corresponded to the symmetric deformation of the CO3 group. The wideband centered at ~1400 cm-1 corresponded to an asymmetric stretch of the CO3 group. The peak at ~713 cm-1 was due to bending vibration [55,56]. In this regard, the presence of crystals biominerals that have been reported in algal samples was quantified based on the specific λmax referred from the existing literature for calcite, 706–716 cm-1, 869–877 cm-1, 1414–1439 cm-1, and 2920–2952 cm-1 [57].

    3.4.   Directly and theoretical calorific value

    The calculated and measured calorific value results are shown in Table 1. The calorific values are slightly similar to those reported by Li et al. [33]. The increase in the values is noted due to the effect of the Sargassum fluitans washing, increasing to 41.04%, 10.09%, and 36.80% in the Dulong, Channiwala, and Calorimetry pump methods, respectively. This increase is attributed to the decrease in the content of sand and salts, which do not add calorific value to the biomass.

    The results of the AFCV applying equation 3 on the calorific values of dirty Sargassum fluitans showed an increase of these, being slightly higher than the calorific values of washed Sargassum fluitans, 16.58 MJ/kg and 17.36 MJ/kg, in the Dulong methods. and Channiwala, respectively. This contributes to the hypothesis that the content of impurities removed in the washing process has a positive impact on increasing the calorific values of the biomass. However, in the calorific values of the direct method (calorimetric bomb), the AFCV obtained was significantly higher, reaching 22.81 MJ/kg. The great difference with the values of the direct method responds to the overestimation of the values of the stoichiometric methods, as shown in Figure 5.

    3.5.   Statistical analysis

    Figure 4 A) and B) show the ANOVA tests for each type of Sargassum fluitans (dirty and washed) and compare the three calorific value methods. The lowercase letters at the top indicate differences or similarities, depending on their repetition.

    Figure 4.  ANOVA graphics of calorific values, A) Dirty Sargassum fluitans, B) Wash Sargassum fluitans. Linear regression graphics, by the interaction between methods, C) Dirty Sargassum fluitans, D) Wash Sargassum fluitans, E) ANOVA graphic by groups.
    DownLoad: Full-Size Img PowerPoint

    The results indicate that there are statistically significant differences in both materials. Applying a Tukey test (Figure 4A), a dirty Sargassum p-value = 0.0028 was obtained. Using a Kruskal-Wallis test (Figure 4B) in the washed Sargassum values, a p-value = 0.0047 was obtained. It is noteworthy the similarity in the stoichiometric methods' calorific variables and the differences with the direct method. It is possible to miss the mistake of inferring that the Channiwala method offers us a better result. These inequalities refer to overestimations in the calculations, which are best described in the relative and absolute error analysis.

    The linear regression analyses performed, shown in Figure 4 C) and D), indicate the trends of the models used. The R2 values of the adjusted model explain 59.53% (Figure 4C) and 97.78% (Figure 4D) of the variability of each factor. The washing effect promotes a better adjustment of the calorific values of Sargassum fluitans, demonstrating the importance and possible need to implement this pretreatment.

    In Figure 4 E), the ANOVA graphic performed at calorific values by combining groups is shown, all dirty and all wash. The results indicate statistically significant differences; the p-value = 0.00001 was obtained by applying a Bonferroni test. A statistically significant effect on the two conditions of use of Sargassum can be demonstrated in the methods to determine the calorific values. These results would be similar to those reported by Choi et al. [59], who used different proportions and washing times with Saccharina Japan.

    3.6.   Relative and absolute error analysis

    Figure 5 shows the results of the analysis of percentage error (MPE) and absolute percentage error (MAPE).

    Figure 5.  Relative error graphic by each method.
    DownLoad: Full-Size Img PowerPoint

    Both methods present a slight overestimation (MPE), being the Dulong equation the one with the lowest MPE. However, the MAPE values indicate an important difference between the calculated and determined values, of 9.90% for the Channiwala method and 4.44% for Dulong. This indicates that the Dulong method would be most similar to the values determined with the bomb calorimetric method. The MAPE obtained from both methods is different from those reported by Huang and Lo [46], who reported 6.73% in Dulong and 2.49% in Channiwala; however, the authors use these methods in lignocellulosic biomass. Although authors such as Channiwala and Parikh [44] also reported 6.94% for the Dulong method, authors such as Vardon et al. [9] used this method to determining HHV of three species of marine algae. It would be important to obtain a greater number of results (n > 100), as mentioned by Huang and Lo [46], to analyze the overestimation of calorific values more effectively. Although there are differences in each method (Dulong and Channiwala), both equations at a practical or pilot level are useful, specifically in determining the value of the gross calorific value, based on the elemental composition of the biomass, like the Sargassum fluitans.

    3.7.   Unit cost

    The cost of collecting Sargassum fluitans was estimated by relating the annual expenditure reported by the Mexican government with the amounts collected per year (2017–2019). The cost of washing was determined based on the water consumed in the process. The cost per grinding was determined by the time of electrical consumption by using an electrical mill at a certain amount of dough. Finally, the quantities were extrapolated to a base quantity of one ton, and the costs were integrated (Table 3).

    Table 3.  Unit cost analysis integration.
    Activity (inputs) Unit Quantity per t Price (＄) Cost (＄)
    Dirty Wash
    Recollection t - 31.75 31.75 31.75
    Water (washing) m3 96* 0.74 - 71.04
    Electricity (grinding) kW 32.40** 1.09 35.21 35.21
    Cost per ton 66.96 138.00
    Cost per calorific value
    Dirty (9,242 MJ/t)
    Wash (12,705 MJ/t)
    		0.007***
    -    		 -
    0.011***
    *Note : * Costs of the industrial tariff in water consumption (10 m3) of the Potable Water and Sewerage Commission of Quintana Roo; ** Average costs of medium voltage electricity tariff (25 kW) from Mexico's Federal Electricity Commission (CFE); *** The quotient obtained between the calorific value and the price per ton.
     | Show Table
    DownLoad: CSV

    The cost of US＄ 0.007 per MJ of dirty Sargassum fluitans is similar to the US＄ 0.006 per MJ reported by Tauro et al. [60] with the use of sawdust pellets. The cost of US＄ 0.011 per MJ of washed Sargassum fluitans is similar to the US＄ 0.013 per MJ reported by Tauro et al. [60] in cane bagasse pellets. Park et al. [61] report a price of US＄ 0.010 per MJ of LPG, which is very similar to the price per MJ of the washed Sargassum fluitans used in this research. BP [1] reports a price of US＄ 57.16 per t of coal in North America, with dirty Sargassum being the closest to this price. The cost of Sargassum fluitans with only two wash times (Figure 2) could be reduced to US＄ 84.80 per t. Costs in dollars were calculated at an exchange rate of MXN＄ 20.00 per USD.

    4.   Conclusions

    The washing mechanism had favorable effects on the bioenergetic characteristics of Sargassum fluitans.

    ● Removing sand, salts, and residues reduce the ash content by 58%. Volatile matter increased by 47%. There was an increase in the percentage content of C, H, O, and N and a reduction in the content of S and Cl. A decrease in the concentration of heavy metals was observed at levels below international standards. In addition, the decrease in the concentration of Ba and Mn.

    ● The reduction of the impurity content allowed the calorific values to increase by 36.80% in the direct measurement by the calorimetric pump. The MPE and MAPE analysis in the indirect methods indicate a slight overestimation and lower proximity in washed Sargassum. Dulong's method showed the least overestimation and the greatest proximity. It is very important to standardize the washing process. Improving the screening process with the use of mechanized equipment could substantially improve the elemental and calorific value characteristics and reduce wash times.

    ● The calorific value of Sargassum fluitans that reaches the shores of the Mexican Caribbean could be compared to other types of biomass used as fuels. It could be used as an input in combustion processes, being a potentially economical option in already proven systems such as sugar mills or cement kilns with co-processing of solid waste, especially given the emerging need to remove it from the coast and while developing methods and technologies of better application, efficiency, and profitability.

    Authors' contributions

    José Aurelio Sosa (ORCID: https://orcid.org/0000-0001-6786-0521): Ph.D. student, performed the calculations of calorific values and statistical analysis. aurelio.sosa@ujat.mx; ing-jaso@hotmail.es.

    José Ramón Laines (ORCID: https://orcid.org/0000-0002-6770-5596): Research Professor, performed the proximal analysis. josra_2001@yahoo.com.mx.

    Donato Antonio Figueiras: Laboratorian, performed the heavy metal content analysis. donato.figueiras@geocycle.com.

    Anabel González (ORCID: https://orcid.org/0000-0002-6855-788X): Laboratorian, performed the FTIR analysis and elementary mapping. anaiq86@hotmail.com.

    David Guerrero (ORCID: https://orcid.org/0000-0002-7762-0246): Research Professor, performed the calorimetry tests. iqguerrero@gmail.com.

    Heidi Kimberly Osorio García and Berenice Evia López: Environmental engineering students carried out the washing material tests and the ultimate analysis. kim159h@gmail.com (Osorio), bereniceevialopez@gmail.com (Evia).

    Acknowledgments

    We are grateful for the collaboration of the co-processing laboratory of the company Geocycle® S.A de CV.

    We acknowledge and appreciate the support received by Dr. Alejandro Padilla (University of Calgary, Canada).

    Conflicts of interest

    The authors have no conflicts of interest to declare relevant to this article content.



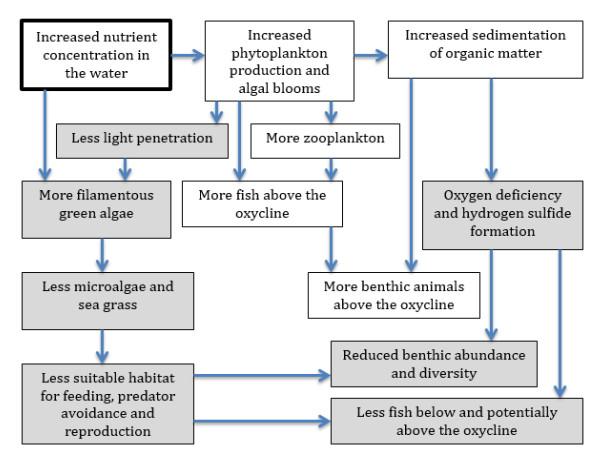
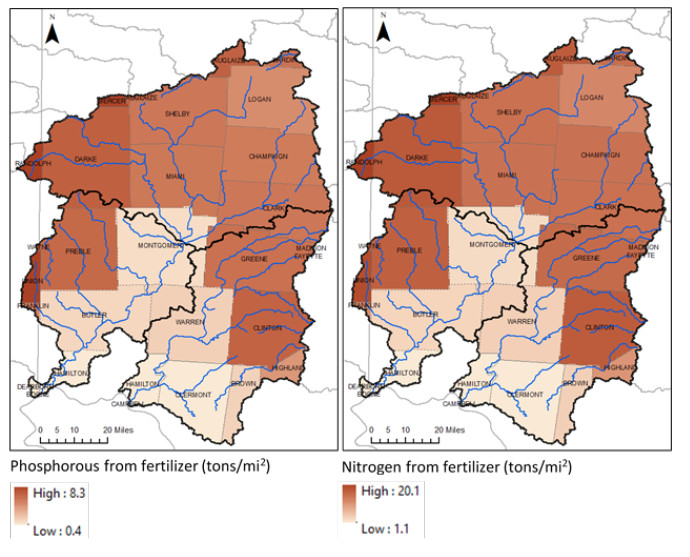
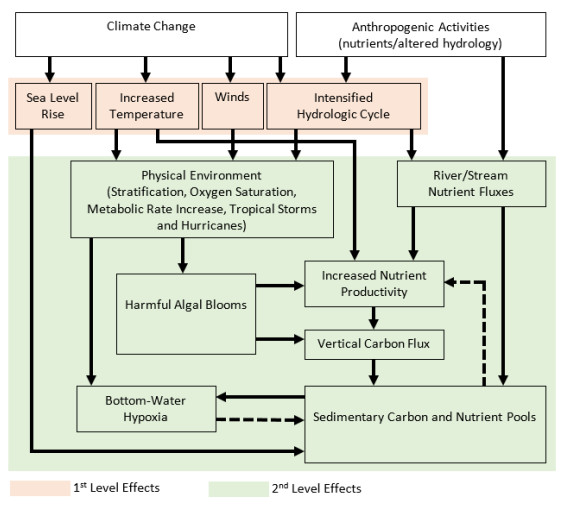
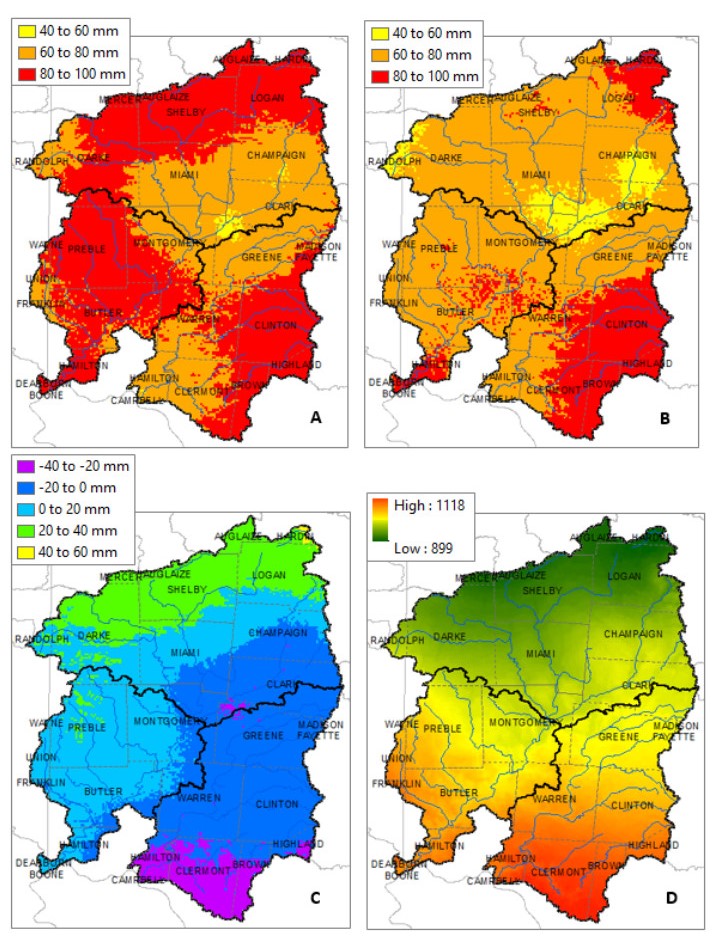
    [1] Ohio Department of Development (ODD) Population and Housing: Ohio's population; Ohio Development Services Agency, 2010. Available from: https://development.ohio.gov/reports/reports_pop_proj_map.htm.
    [2] Tong STY, Sun Y, Ranatunga T, et al. (2012) Predicting plausible impacts of sets of climate and land use change scenarios on water resources. Appl Geogr 32: 477–489. doi: 10.1016/j.apgeog.2011.06.014
    [3] Debrewer LM, Rowe GL, Reutter DC, et al. Environmental setting and effects on water quality in the Great and Little Miami River basins, Ohio and Indiana: Water-Resources Investigations Report, 2000. Available from: https://pubs.usgs.gov/wri/1999/4201/report.pdf.
    [4] OEPA biological and water quality study of the Upper Little Miami River. Clark, Clinton, Greene, Madison, Montgomery, and Warren Counties, Ohio. OHIO EPA Technical Report: Division of Surface Water, 2011. Available from: https://epa.ohio.gov/Portals/35/documents/LMR_Upper_Basin_2011_TSD.pdf.
    [5] Pitt R, Bozeman M. Water quality and biological effects of urban runoff in Coyote Creek, U.S. Ohio Environmental Protection Agency, 1980. Available from: https://nepis.epa.gov/Exe/ZyPURL.cgi?Dockey=30000C3M.TXT.
    [6] Tong STY (1990) The hydrologic effects of urban land use: A case study of the little Miami River Basin. Landsc and Urban Plan 19: 99–105. doi: 10.1016/0169-2046(90)90037-3
    [7] Turner RE, Rabalais NN (2004) Suspended sediment, C, N, P, and Si yields from the Mississippi River Basin. Hydrobiologia 511: 79–89. doi: 10.1023/B:HYDR.0000014031.12067.1a
    [8] Rowe GL, Reutter DC, Runkle DL, et al. Water quality in the Great and Little Miami River Basins, Ohio and Indiana, 1999–2001, USGS, 2004. Available from: https://pubs.er.usgs.gov/publication/cir1229.
    [9] Kaushal SS, Groffman PM, Band LE, et al. (2008) Interaction between urbanization and climate variability amplifies watershed nitrate export in Maryland. Environ Sci Technol 42: 5872–5878. doi: 10.1021/es800264f
    [10] OEPA Nutrient Mass Balance Study for Ohio's Major Rivers, Ohio Environmental Protection Agency, Division of Surface Water Modeling, Assessment and TMDL Section, 2016. Available from: https://epa.ohio.gov/Portals/35/documents/Nutrient%20Mass%20Balance%20Study%202018_F inal.pdf.
    [11] Yu S, Yu GB, Liu Y, et al. (2012) Urbanization impairs surface water quality: Eutrophication and metal stress in the Grand Canal of China. River Res Appl 28: 1135–1148. doi: 10.1002/rra.1501
    [12] EPA National Nonpoint Source Program-a catalyst for water quality improvements, 2017. Available from: https://www.epa.gov/sites/production/files/2016-10/documents/nps_program_highlights_report-508.pdf.
    [13] MCD Lower Great Miami River Nutrient Management Project, 2017. Available from: https://www.mcdwater.org/wp-content/uploads/2017/06/2017-LGMR_Report-FINAL_02-28-17_Compressed_Graphics.pdf.
    [14] Naramngam S, Tong STY (2013) Environmental and economic implications of various conservative agricultural practices in the Upper Little Miami River basin. Agric Water Manag 119: 65–79. doi: 10.1016/j.agwat.2012.12.008
    [15] Paul MJ, Meyer JL (2001) Streams in the urban landscape. Annu Rev Ecol Syst 32: 333–365. doi: 10.1146/annurev.ecolsys.32.081501.114040
    [16] Center for Watershed Protection, Impacts of impervious cover on aquatic ecosystems, Watershed Protection Research Monograph No. 1. Center for Watershed Protection, 2003. Available from: https://clear.uconn.edu/projects/TMDL/library/papers/Schueler_2003.pdf.
    [17] OEPA Ohio Nutrient Reduction Strategy, Ohio Environmental Protection Agency, 2013. Available from: https://epa.ohio.gov/Portals/35/wqs/ONRS_final_jun13.pdf.
    [18] Townsend AR, Howarth RW, Bazzaz FA, et al. (2003) Human health effects of a changing global nitrogen cycle. Front Ecol Environ 1: 240–246. doi: 10.1890/1540-9295(2003)001[0240:HHEOAC]2.0.CO;2
    [19] Newcomber G, House J, Ho L, et al. Management strategies for cyanobacteria (blue-green algae) and their toxins: A guide for water utilities. Water Quality Research Australia Limited, 2009. Available from: https://www.researchgate.net/profile/Lionel_Ho/publication/242740698_Management_Strategie s_for_Cyanobacteria_Blue-Green_Algae_A_Guide_for_Water_Utilities/links/02e7e52d62273e8f70000000/Management-Strategies-for-Cyanobacteria-Blue-Green-Algae-A-Guide-for-Water-Utilities.pdf.
    [20] Graham J, Loftin K, Meyer M, et al. (2010) Cyanotoxin mixtures and taste-and-odor compounds in cyanobacterial blooms from the Midwestern United States. Environ Sc. Technol 44: 7361–7368. doi: 10.1021/es1008938
    [21] MCD nitrogen and phosphorus concentrations and loads in the Great Miami River Watershed, Ohio 2005 – 2011, 2012. Available from: https://www.mcdwater.org/wp-content/uploads/PDFs/2012NutrientMonitoringReport_Final.pdf.
    [22] OEPA biological and water quality study of the Middle and Lower Great Miami River and selected tributaries, 1995-Volume I, Ohio Environmental Protection Agency, 1997. Available from: https://epa.ohio.gov/portals/35/documents/lmgmr95.pdf.
    [23] Smith JH. Miami River algae draws local attention, 2011. Available from: https://www.daytondailynews.com/news/local/miami-river-algae-draws-local- attention/Rh715SpRPOMoJsF6qMyghK.
    [24] NPS Nonpoint Source Management Plan Update, Ohio Environmental Protection Agency, 2018. Available from: https://www.epa.ohio.gov/portals/35/nps/nps_mgmt_plan.pdf.
    [25] OEPA Integrated Water Quality Monitoring and Assessment Report, Ohio Environmental Protection Agency, 2018. Available from: https://www.epa.ohio.gov/Portals/35/tmdl/2018intreport/2018IR_Final.pdf.
    [26] Takle ES, Xia M, Guan F, et al. (2006) Upper Mississippi River basin modeling system part 4: climate change impacts on flow and water quality, In: Coastal Hydrology and Processes, Water Resources Publications, 135–142.
    [27] Luo Y, Ficklin DL, Liu X, et al. (2013) Assessment of climate change impacts on hydrology and water quality with a watershed modeling approach. Sci Total Environ 450–451: 72–82.
    [28] Ekness P, Randhir TO (2015) Effect of climate and land cover changes on watershed runoff: A multivariate assessment for storm water management. J Geophys Res-Geosciences 120: 1785–1796. doi: 10.1002/2015JG002981
    [29] Rahman K, da Silva AG, Tejeda EM (2015) An independent and combined effect analysis of land use and climate change in the upper Rhone River watershed, Switzerland. Appl Geogr 63: 264–272. doi: 10.1016/j.apgeog.2015.06.021
    [30] Li Z, Fang H (2017) Modeling the impact of climate change on watershed discharge and sediment yield in the black soil region, northeastern China. Geomorphology 293: 255–271. doi: 10.1016/j.geomorph.2017.06.005
    [31] Barnett TP, Adam JC, Lettenmaier DP (2005) Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 438: 303–309. doi: 10.1038/nature04141
    [32] Wang GQ, Zhang JY, Xuan YQ (2013) Simulating the Impact of Climate Change on Runoff in a Typical River Catchment of the Loess Plateau, China. J Hydrometeor 14: 1553–1561. doi: 10.1175/JHM-D-12-081.1
    [33] Barranco LM, Álvarez-Rodríguez J, Olivera F (2014) Assessment of the expected runoff change in Spain using climate simulations. J Hydrol Eng 19: 1481–1490. doi: 10.1061/(ASCE)HE.1943-5584.0000920
    [34] Demaria EMC, Roundy JK, Wi S (2016) The effects of climate change on seasonal snowpack and the hydrology of the Northeastern and Upper Midwest United States. J Climate 29: 6527–6541. doi: 10.1175/JCLI-D-15-0632.1
    [35] Wagena MB, Collick AS, Ross AC (2018) Impact of climate change and climate anomalies on hydrologic and biogeochemical processes in an agricultural catchment of the Chesapeake Bay watershed, USA. Sci Total Environ 637–638: 1443–1454.
    [36] Gleick PH (1989) Climate change, hydrology, and water resources. Rev Geophys 27: 329–344. doi: 10.1029/RG027i003p00329
    [37] Dyer F, ElSawah S, Croke B, et al. (2014) The effects of climate change on ecologically-relevant flow regime and water quality attributes. Stoch Environ Res Risk Assess 28: 67–82. doi: 10.1007/s00477-013-0744-8
    [38] Ferrer J, Pérez-Martín MA, Jiménez S, et al. (2012) GIS-based models for water quantity and quality assessment in the Júcar River Basin, Spain, including climate change effects. Sci Total Environ 440: 42–59. doi: 10.1016/j.scitotenv.2012.08.032
    [39] Van Liew M, Feng S, Pathak T (2013) Assessing climate change impacts on water balance, runoff, and water quality at the field scale for four locations in the heartland. Transactions of the ASABE 56: 833–900.
    [40] Butterbach-Bahl K, Dannenmann M (2011) Denitrification and associated soil N2O emissions due to agricultural activities in a changing climate. Curr Opin Env Sust 3: 389–395. doi: 10.1016/j.cosust.2011.08.004
    [41] OEPA Ohio Nutrient Reduction Strategy, Ohio Environmental Protection Agency, 2016. Available from: https://epa.ohio.gov/Portals/35/wqs/ONRS_addendum.pdf.
    [42] OEPA Ohio water resource inventory, executive summary: Summary, conclusions, and recommendations Division of Surface Water and Monitoring Assessment Section, Ohio Environmental Protection Agency, 1996. Available from: https://www.epa.ohio.gov/portals/35/documents/exsumm96.pdf.
    [43] Tong STY, Liu AJ, Goodrich JA (2007) Climate change impacts on nutrient and sediment loads in a Midwestern agricultural watershed. J Environ Inform 9: 18–28. doi: 10.3808/jei.200700084
    [44] Rowe GL, Baker NT. National Water-Quality Assessment Program, Great and Little Miami River Basins, 1997. Available from: https://pubs.water.usgs.gov/circ1229.
    [45] Cross WP, Drainage areas of Ohio streams, supplement to Gazetteer of Ohio streams; Ohio Water Plan Inventory Report: Ohio Department of Natural Resources, 1967, 61.
    [46] OEPA East Fork Little Miami River comprehensive water quality report, Little Miami River Basin, Clinton, Highland, Brown, and Clermont Counties: Ohio Environmental Protection Agency, 1985. Available from: http://msdgc.org/downloads/initiatives/water_quality/2012_lmr_biological_water_quality_study. pdf.
    [47] Rankin ET, Yoder CO, Mishne D. Ohio water resources inventory executive summary-Summary, conclusions and recommendation: Ohio Environmental Protection Agency, 1996, 75 p. Available from: https://www.epa.ohio.gov/portals/35/documents/exsumm96.pdf.
    [48] Miami Conservancy District Flood protection dams: Miami Conservancy District, 2018. Available from: http://www.conservancy.com/dams.asp#dams.
    [49] National Research Council Alternative agriculture, National Academy Press, 1989. Available from: https://www.nap.edu/catalog/1208/alternative-agriculture.
    [50] Dickey E, Shelton DP, Jasa P, et al. (1985) Soil erosion from tillage systems used in soybean and corn residues. T ASAE 28: 1124–1130. doi: 10.13031/2013.32399
    [51] Walters D, Jasa P. Conservation tillage in the United States: An overview, 2018. Available from: http://agecon.okstate.edu/isct/labranza/walters/conservation.doc.
    [52] Tebrügge F, Düring R-A (1999) Reducing tillage intensity - a review of results from a long-term study in Germany. Soil Tillage Res 53: 15–28. doi: 10.1016/S0167-1987(99)00073-2
    [53] Armand R, Bockstaller C, Auzet A-V, et al. (2009) Runoff generation related to intra-field soil surface characteristics variability: Application to conservation tillage context. Soil Tillage Res 102: 27–37. doi: 10.1016/j.still.2008.07.009
    [54] Borie F, Rubio R, Ruanet JL, et al. (2006) Effects of tillage systems on soil characteristics, glomalin and mycorrhizal propagules in a Chilean Ultisol. Soil Tillage Res 88: 253–261. doi: 10.1016/j.still.2005.06.004
    [55] Rocha EO, Calijuri ML, Santiago AF, et al. (2012) The contribution of conservation practices in reducing runoff, soil loss, and transport of nutrients at the watershed level. Water Resour Manage 26: 3831–3852. doi: 10.1007/s11269-012-0106-1
    [56] Jarecki MK, Lal R (2003) Crop management for soil carbon sequestration. Crit Rev Plant Sci 22: 471–502. doi: 10.1080/713608318
    [57] Mangalassery S, Sjögersten S, Sparkes DL, et al. (2014) To what extent can zero tillage lead to a reduction in greenhouse gas emissions from temperate soils? Sci Rep 4: 4586.
    [58] Baker NT. Tillage practices in the conterminous United States, 1989–2004-Datasets aggregated by watershed, USGS, 2011, 22 p. Available from: https://pubs.usgs.gov/ds/ds573/pdf/dataseries573final.pdf.
    [59] Cox WJ, Zobel RW, van Es HM, et al. (1990) Growth development and yield of maize under three tillage systems in the northeastern U.S.A. Soil Tillage Res 18: 295–310. doi: 10.1016/0167-1987(90)90067-N
    [60] Ruffo ML, Bollero GA (2003) Modeling rye and hairy vetch residue decomposition as a function of degree-days and decomposition-days. Agron J 95: 900–907. doi: 10.2134/agronj2003.9000
    [61] Findlater PA, Carter DJ (1990) A model to predict the effects of prostrate ground cover on wind erosion. Aust J Soil Res 28: 609–622. doi: 10.1071/SR9900609
    [62] Staver KW, Brinsfield RB (1998) Using cereal grain winter cover crops to reduce groundwater nitrate contamination in the mid-Atlantic coastal plain. J Soil Water Conserv 53: 230–240.
    [63] Whish JPM, Price L, Castor PA (2009) Do spring cover crops rob water and so reduce wheat yields in the northern grain zone of eastern Australia? Crop Pasture Sci 60: 517–525. doi: 10.1071/CP08397
    [64] Fageria NK, Baligar VC, Bailey BA (2018) Role of cover crops in improving soil and row crop productivity. Commun Soil Sci Plant Anal 36: 19–20.
    [65] Hoorman JJ. Using cover crops to convert to no-till, 2018. Available from: https://ohioline.osu.edu/factsheet/SAG-11.
    [66] Dabney SM, Delgado JA, Reeves DW (2001) Using winter cover crops to improve soil and water quality. Commun Soil Sci Plant Anal 32: 1221–1250. doi: 10.1081/CSS-100104110
    [67] SARE- CTIC Report of the 2013–2014 Cover Crop Survey. Joint publication of the Conservation Technology Information Center and the North Central Region Sustainable Agriculture Research and Education Program.; Conservation Technology Information Center: West Lafayette, Indiana, 2014. Available from: https://www.sare.org/Learning-Center/From-the-Field/North-Central-SARE-From-the-Field/2013-14-Cover-Crops-Survey-Analysis.
    [68] Creamer NG, Baldwin KR (2000) An evaluation of summer cover crops for use in vegetable production systems in North Carolina. HortScience 35: 600–603. doi: 10.21273/HORTSCI.35.4.600
    [69] SARE- CTIC Cover Crop survey report. Conservation Technology Information Center. 2014. Report of the 2013-14 Cover Crop Survey. Joint publication of the Conservation Technology Information Center and the North Central Region Sustainable Agriculture Research and Education Program; Conservation Technology Information Center: West Lafayette, Indiana, 2015. Available from: https://www.sare.org/Learning-Center/From-the-Field/North-Central-SARE-From-the-Field/2016-Cover-Crop-Survey-Analysis.
    [70] Nokes S, Ward A. Surface water quality best management practices summary guide: Columbus, The Ohio State University Extension Factsheet, 1997. Available from: http://epa.ohio.gov/dsw/storm/technical_guidance.
    [71] Gorham T, Jia Y, Shum CK, et al. (2017) Ten-year survey of cyanobacterial blooms in Ohio's waterbodies using satellite remote sensing. Harmful Algae 66: 13–19. doi: 10.1016/j.hal.2017.04.013
    [72] Goolsby DA, Battaglin WA, Lawrence GB, et al. Flux and sources of nutrients in the Mississippi-Atchafalaya River Basin: Topic 3 Report for the Integrated Assessment on Hypoxia in the Gulf of Mexico, 1999. Available from: http://www.cop.noaa.gov/pubs/das/das17.pdf.
    [73] Baker DB, Richards RP, Kramer JW. Point source-nonpoint source trading: applicability to stream TMDLs in Ohio. In Proceedings of the Proceedings – Innovations in Reducing Nonpoint Source Pollution, 2006, 328–337.
    [74] Scavia D, Justic D, Bierman VJ (2004) Reducing hypoxia in the Gulf of Mexico: Advice from three models. Estuaries 27: 419–425. doi: 10.1007/BF02803534
    [75] Smith RA, Schwarz GE, Alexander RB (1997) Regional interpretation of water-quality monitoring data. Water Resour Res 33: 2781–2798. doi: 10.1029/97WR02171
    [76] Battaglin WA, Goolsby DA. Spatial data in geographic information system format on agricultural chemical use, land use, and cropping practices in the United States, 1995. Available from: https://pubs.usgs.gov/wri/1994/4176/report.pdf.
    [77] Rabalais NN, Turner RE, Díaz RJ, et al. (2009) Global change and eutrophication of coastal waters. ICES J Mar Sci 66: 1528–1537. doi: 10.1093/icesjms/fsp047
    [78] Midwest Biodiversity Institute Biological and water quality assessment of the Great Miami River and tributaries 2013 Hamilton County, Ohio, 2014, 121. Available from: https://midwestbiodiversityinst.org/reports/biological-and-water-quality-study-of-the-little-miami-river-and-tributaries-2012-hamilton-county-ohio/LMR%202012%20MSDGC%20FINAL%20REPORT%2020130930.pdf.
    [79] OEPA Integrated Water Quality Monitoring and Assessment Report: Ohio Environmental Protection Agency, 2002. Available from: https://www.epa.ohio.gov/portals/35/tmdl/2002IntReport/Ohio2002IntegratedReport_100102.pdf.
    [80] MCD Water Data Report, Great Miami River Watershed, Ohio, 2015. Available from: https://www.mcdwater.org/wp-content/uploads/PDFs/2015-Water-Data-Report-FINAL-reduced.pdf.
    [81] Hayhoe K, Edmonds J, Kopp RE, et al. (2017) Climate models, scenarios, and projections: Climate Science Special Report: Fourth National Climate Assessment; U.S. Global Change Research Program, 133–160.
    [82] IPCC Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change: Geneva, Switzerland,. Available from: https://www.ipcc.ch/report/ar5/syr.
    [83] IPCC Contribution of Working Groups I, II and III to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change Core Writing Team; Geneva, Switzerland, 2007. Available from: https://www.ipcc.ch/report/ar4/syr.
    [84] Meehl GA, Tebaldi C (2004) More intense, more frequent, and longer lasting heat waves in the 21st century. Science 305: 994–997. doi: 10.1126/science.1098704
    [85] Rosenzweig C, Major DC, Demong K, et al. (2007) Managing climate change risks in New York City's water system: assessment and adaptation planning. Mitig Adapt Strat Glob Change 12: 1391–1409. doi: 10.1007/s11027-006-9070-5
    [86] Karl TR, Melillo JM, Peterson TC. Global climate change impacts in the United States, Cambridge University Press: UK, 2009. Available from: http://www.nrc.gov/docs/ML1006/ML100601201.pdf.
    [87] Lawrimore JH, Menne MJ, Gleason BE, et al. (2011) An overview of the Global Historical Climatology Network monthly mean temperature data set, version 3. JGR Atmospheres 2011, 116.
    [88] Vörösmarty CJ, McIntyre PB, Gessner MO, et al. (2010) Global threats to human water security and river biodiversity. Nature 467: 555–561. doi: 10.1038/nature09440
    [89] Lettenmaier DP, Milly PCD (2009) Land waters and sea level. Nature Geoscience 2009, 2, 3.
    [90] Hatfield JL, Prueger JH (2004) Impacts of changing precipitation patterns on water quality. J Soil Water Conserv 59: 51–58.
    [91] Prowse TD, Beltaos S, Gardner JT, et al. (2006) Climate change, flow regulation and land-use effects on the hydrology of the Peace-Athabasca-Slave System; Findings from the Northern Rivers Ecosystem Initiative. Environ Monit Assess 113: 167–197. doi: 10.1007/s10661-005-9080-x
    [92] Zhang A, Zhang C, Fu G, et al. (2012) Assessments of impacts of climate change and human activities on runoff with SWAT for the Huifa River Basin, Northeast China. Water Resour Manage 26: 2199–2217. doi: 10.1007/s11269-012-0010-8
    [93] Ye L, Grimm NB (2013) Modelling potential impacts of climate change on water and nitrate export from a mid-sized, semiarid watershed in the US Southwest. Climatic Change 120: 419–431. doi: 10.1007/s10584-013-0827-z
    [94] Zahabiyoun B, Goodarzi MR, Bavani ARM, et al. (2013) Assessment of climate change impact on the Gharesou River Basin using SWAT hydrological model. CLEAN – Soil, Air, Water 41: 601–609. doi: 10.1002/clen.201100652
    [95] Backlund,P, Janetos A Schimel D. The effects of climate change on agriculture, land resources, water resources, and biodiversity in the United States. Synthesis and Assessment Product 4.3. Washington, DC: U.S. Environmental Protection Agency, Climate Change Science Program, 2008, 240.
    [96] Peterson TC, Heim RR, Hirsch R, et al. (2013) Monitoring and understanding changes in heat waves, cold waves, floods, and droughts in the United States: State of knowledge. Bull Amer Meteor Soc 94: 821–834. doi: 10.1175/BAMS-D-12-00066.1
    [97] Dudula J, Randhir TO (2016) Modeling the influence of climate change on watershed systems: Adaptation through targeted practices. J Hydrol 541: 703–713. doi: 10.1016/j.jhydrol.2016.07.020
    [98] Davis MB, Shaw RG (2001) Range shifts and adaptive responses to quaternary climate change. Science 292: 673–679. doi: 10.1126/science.292.5517.673
    [99] Feeley KJ, Silman MR (2010) Land-use and climate change effects on population size and extinction risk of Andean plants. Glob Chang Biol 16: 3215–3222. doi: 10.1111/j.1365-2486.2010.02197.x
    [100] Parmesan C (2006) Ecological and evolutionary responses to recent climate change. Annu Rev Ecol Evol Syst 37: 637–669. doi: 10.1146/annurev.ecolsys.37.091305.110100
    [101] Poloczanska ES, Brown CJ, Sydeman WJ, et al. (2013) Global imprint of climate change on marine life. Nature Clim Chang 3: 919–925. doi: 10.1038/nclimate1958
    [102] Runion GB (2003) Climate change and plant pathosystems: Future disease prevention starts here. New Phytol 159: 531–533. doi: 10.1046/j.1469-8137.2003.00868.x
    [103] Smith DL, Almaraz JJ (2004) Climate change and crop production: contributions, impacts, and adaptations. Can J Plant Pathol 26: 253–266. doi: 10.1080/07060660409507142
    [104] Ashmore M, Toet S, Emberson L (2006) Ozone – a significant threat to future world food production? New Phytol 170: 201–204. doi: 10.1111/j.1469-8137.2006.01709.x
    [105] Alexander JM, Diez JM, Levine JM (2015) Novel competitors shape species' responses to climate change. Nature 525: 515–518. doi: 10.1038/nature14952
    [106] Duku C, Zwart SJ, Hein L (2018) Impacts of climate change on cropping patterns in a tropical, sub-humid watershed. PLOS ONE 13, e0192642.
    [107] Aguilera R, Marcé R, Sabater S (2015) Detection and attribution of global change effects on river nutrient dynamics in a large Mediterranean basin. Biogeosciences 12: 4085–4098. doi: 10.5194/bg-12-4085-2015
    [108] Cousino LK, Becker RH, Zmijewski KA (2015) Modeling the effects of climate change on water, sediment, and nutrient yields from the Maumee River watershed. J Hydrol Reg Stud 4: 762–775. doi: 10.1016/j.ejrh.2015.06.017
    [109] Cordovil C, Cruz S, Brito A, et al. (2018) A simplified nitrogen assessment in Tagus River Basin: A management focused review. Water 10, 406.
    [110] Easterling DR (2002) Recent changes in frost days and the frost-free season in the united states. Bull Amer Meteor Soc 83: 1327–1332. doi: 10.1175/1520-0477-83.9.1327
    [111] Easterling DR, Evans JL, Groisman PY, et al. (2000) Observed variability and trends in extreme climate events: A brief review. Bull Amer Meteor Soc 81: 417–426. doi: 10.1175/1520-0477(2000)081<0417:OVATIE>2.3.CO;2
    [112] Williamson S, Lakhey S, Karetnikov D, et al. Economic impacts of climate change on Ohio; Center for Integrative Environmental Research, University of Maryland: College Park, Maryland, USA, 2008, 20.
    [113] Kundzewicz ZW, Mata LJ, Arnell NW, et al. (2008) The implications of projected climate change for freshwater resources and their management. Hydrolog Sci J 53: 3–10. doi: 10.1623/hysj.53.1.3
    [114] Milly PCD, Dunne KA, Vecchia AV (2005) Global pattern of trends in streamflow and water availability in a changing climate. Nature 438: 347–350. doi: 10.1038/nature04312
    [115] Wu S-Y (2010) Potential impact of climate change on flooding in the Upper Great Miami River Watershed, Ohio, USA: a simulation-based approach. Hydrolog Sci J 55: 1251–1263. doi: 10.1080/02626667.2010.529814
    [116] Jha M, Pan Z, Takle ES, et al. (2004) Impacts of climate change on streamflow in the Upper Mississippi River Basin: A regional climate model perspective. JGR Atmospheres 2004, 109.
    [117] Pathak P, Kalra A, Ahmad S (2017) Temperature and precipitation changes in the Midwestern United States: implications for water management. Int J Water Resour Dev 33: 1003–1019. doi: 10.1080/07900627.2016.1238343
    [118] Milly PCD, Dunne KA (2001) Trends in evaporation and surface cooling in the Mississippi River Basin. Geophys Res Lett 28: 1219–1222. doi: 10.1029/2000GL012321
    [119] WorldClim - Global Climate Data, Free climate data for ecological modeling and GIS. Available from: http://www.worldclim.org.
    [120] Gent PR, Danabasoglu G, Donner LJ, et al. (2011) The Community Climate System Model Version 4. J Climate 24: 4973–4991. doi: 10.1175/2011JCLI4083.1
    [121] Watanabe M, Suzuki T, O'ishi R, et al. (2010) Improved climate simulation by MIROC5: Mean States, Variability, and Climate Sensitivity. J Climate 23: 6312–6335. doi: 10.1175/2010JCLI3679.1
    [122] Collins WJ, Bellouin N, Doutriaux-Boucher M, et al. (2011) Development and evaluation of an Earth-System model – HadGEM2. Geosci Model Dev 4: 1051–1075. doi: 10.5194/gmd-4-1051-2011
    [123] Taylor KE, Stouffer RJ, Meehl GA (2011) An overview of CMIP5 and the experiment design. Bull Amer Meteor Soc 93: 485–498.
    [124] Sheffield J, Barrett AP, Colle B, et al. (2013) North American climate in CMIP5 experiments. Part I: Evaluation of historical simulations of continental and regional climatology. J Climate 26: 9209–9245.
    [125] van Vuuren DP, Edmonds J, Kainuma M, et al. (2011) The representative concentration pathways: an overview. Climatic Change 109: 5. doi: 10.1007/s10584-011-0148-z
    [126] Knutti R, Sedláček J (2013) Robustness and uncertainties in the new CMIP5 climate model projections. Nat Clim Chang 3: 369–373. doi: 10.1038/nclimate1716
    [127] Zwiers FW, Kharin VV (1998) Changes in the extremes of the climate simulated by CCC GCM2 under CO2 doubling. J Climate 11: 2200–2222. doi: 10.1175/1520-0442(1998)011<2200:CITEOT>2.0.CO;2
    [128] Kharin VV, Zwiers FW (2000). Changes in the extremes in an ensemble of transient climate simulations with a coupled atmosphere–ocean GCM. J Climate 13: 3760–3788. doi: 10.1175/1520-0442(2000)013<3760:CITEIA>2.0.CO;2
    [129] Cubash U, Meehl GA. Projections of future climate change. In Climate Change 2001: The Scientific Basis.; Contribution of Working Group 1 to the Third IPCC Scientific Assessment; Cambridge University Press: UK, 2001: 524–582.
    [130] Semenov V, Bengtsson L (2002) Secular trends in daily precipitation characteristics: greenhouse gas simulation with a coupled AOGCM. Clim Dyn 19: 123–140. doi: 10.1007/s00382-001-0218-4
    [131] Murdoch PS, Baron JS, Miller TL (2000) Potential effects of climate change on surface water quality in North America 1. JAWRA 36: 347–366.
    [132] Srinivasan R, Arnold JG, Jones CA (1998) Hydrologic modelling of the United States with the Soil and Water Assessment Tool. Int J Water Resour Dev 14: 315–325. doi: 10.1080/07900629849231
    [133] Arnold JG, Williams JR, Srinivasan R, et al. SWAT-Soil and Water Assessment Tool User Manual, 2018. Available from: https://swat.tamu.edu/media/69296/swat-io-documentation-2012.pdf.
    [134] Pease LM, Oduor P, Padmanabhan G (2010) Estimating sediment, nitrogen, and phosphorous loads from the Pipestem Creek watershed, North Dakota, using AnnAGNPS. Comput Geosci 36: 282–291. doi: 10.1016/j.cageo.2009.07.004
    [135] Borah DK, Xia R, Bera M. DWSM−A dynamic watershed simulation model for studying agricultural nonpoint−source pollution. Paper number 012028, ASAE Annual Meeting St. Joseph, Michigan, 2001.
    [136] Bicknell BR, Imhoff JC, Kittle JL, et al. Hydrological Simulation Program--Fortran, User's manual for version 11: U.S. Environmental Protection Agency; U.S. Environmental Protection Agency: National Exposure Research Laboratory, 1997, 755.
    [137] Singh VP, Frevert DK (2002) Mathematical models of large watershed hydrology. J Hydrol Eng 7: 270–292. doi: 10.1061/(ASCE)1084-0699(2002)7:4(270)
    [138] Shen Z, Liao Q, Hong Q, Gong Y (2012) An overview of research on agricultural non-point source pollution modelling in China. Sep Pur Technol 84: 104–111. doi: 10.1016/j.seppur.2011.01.018
    [139] Weller DE, Baker ME (2014) Cropland riparian buffers throughout Chesapeake Bay Watershed: Spatial patterns and effects on nitrate loads delivered to streams. JAWRA 50: 696–712.
    [140] Sharifi A, Lang MW, McCarty GW, et al. (2016) Improving model prediction reliability through enhanced representation of wetland soil processes and constrained model auto calibration – A paired watershed study. J Hydrol 541: 1088–1103. doi: 10.1016/j.jhydrol.2016.08.022
    [141] Borah DK, Bera M (2003) Watershed-scale hydrologic and nonpoint-source pollution models: Review of mathematical bases. T ASAE 46: 1553–1566. doi: 10.13031/2013.15644
    [142] Robson BJ (2014) State of the art in modelling of phosphorus in aquatic systems: Review, criticisms and commentary. Environ Modell Softw 61: 339–359. doi: 10.1016/j.envsoft.2014.01.012
    [143] Rinke A, Dethloff K, Cassano JJ, et al. (2006) Evaluation of an ensemble of Arctic regional climate models: spatiotemporal fields during the SHEBA year. Clim Dyn 26: 459–472. doi: 10.1007/s00382-005-0095-3
    [144] Mohammed IN, Bomblies A, Wemple BC (2015) The use of CMIP5 data to simulate climate change impacts on flow regime within the Lake Champlain Basin. J Hydrol Reg Stud 3: 160–186. doi: 10.1016/j.ejrh.2015.01.002
    [145] Nour MH, Smith DW, El-Din MG, et al. (2008) Effect of watershed subdivision on water-phase phosphorus modelling: An artificial neural network modelling application. J Environ Eng Sci 7: 95–108. doi: 10.1139/S08-043
    [146] Kim RJ, Loucks DP, Stedinger JR (2012) Artificial neural network models of watershed nutrient loading. Water Resour Manage 26: 2781–2797. doi: 10.1007/s11269-012-0045-x
    [147] Tang X, Xia M, Guan F, et al. (2016) Spatial distribution of soil nitrogen, phosphorus and potassium stocks in Moso bamboo forests in subtropical China. Forests 7, 267.
    [148] Mohanty S, Jha MK, Kumar A, et al. (2010) Artificial neural network modeling for groundwater level forecasting in a river island of eastern India. Water Resour Manage 24: 1845–1865. doi: 10.1007/s11269-009-9527-x
    [149] Kalin L, Isik S, Schoonover JE, et al. (2010) Predicting water quality in unmonitored watersheds using artificial neural networks. J Environ Qual 39: 1429–1440. doi: 10.2134/jeq2009.0441
    [150] Fogelman S, Blumenstein M, Zhao H (2006) Estimation of chemical oxygen demand by ultraviolet spectroscopic profiling and artificial neural networks. Neural Comput Applic 15: 197–203. doi: 10.1007/s00521-005-0015-9
    [151] Dogan E, Sengorur B, Koklu R (2009) Modeling biological oxygen demand of the Melen River in Turkey using an artificial neural network technique. J Environ Manag 90: 1229–1235. doi: 10.1016/j.jenvman.2008.06.004
    [152] Iliadis LS, Maris F (2007) An artificial neural network model for mountainous water-resources management: The case of Cyprus mountainous watersheds. Environ Modell Softw 22: 1066–1072. doi: 10.1016/j.envsoft.2006.05.026
    [153] Noori N, Kalin L (2016) Coupling SWAT and ANN models for enhanced daily streamflow prediction. J Hydrol 533: 141–151. doi: 10.1016/j.jhydrol.2015.11.050
    [154] Okkan U, Serbes ZA (2012) Rainfall–runoff modeling using least squares support vector machines. Environmetrics 23: 549–564. doi: 10.1002/env.2154
    [155] Huang S, Chang J, Huang Q, Chen Y (2014) Monthly streamflow prediction using modified EMD-based support vector machine. J Hydrol 511: 764–775. doi: 10.1016/j.jhydrol.2014.01.062
    [156] Jajarmizadeh M, Harun S, Salarpour M. An assessment of a proposed hybrid neural network for daily flow prediction in arid climate, 2014. Available from: https://www.hindawi.com/journals/mse/2014/635018.
    [157] Gassman P, Reyes M, Green C, Arnold J (2007) The Soil and Water Assessment Tool: Historical development, applications, and future research directions. T ASABE 7: 1211–1250.
    [158] Niraula R, Kalin L, Wang R, et al. (2012) Determining nutrient and sediment critical source areas with SWAT model: effect of lumped calibration. T ASABE 55: 137–147.
    [159] White M, Gambone M, Yen H, et al. (2015) Regional blue and green water balances and use by selected crops in the U.S. JAWRA 51: 1626–1642.
    [160] Wang R, Bowling LC, Cherkauer KA (2016) Estimation of the effects of climate variability on crop yield in the Midwest USA. Agric For Meteorol 216: 141–156. doi: 10.1016/j.agrformet.2015.10.001
    [161] Yen H, White MJ, Arnold JG, et al. (2016) Western Lake Erie Basin: Soft-data-constrained, NHDPlus resolution watershed modeling and exploration of applicable conservation scenarios. Sci Total Environ 569–570: 1265–1281.
    [162] Arnold JG, Fohner N (2005) Current capabilities and research opportunities in applied watershed modeling. Hydrol Process 19: 563–572. doi: 10.1002/hyp.5611
    [163] Santhi C, Arnold JG, Williams JR, et al. (2001) Validation of the Swat Model on a Large Rwer Basin with Point and Nonpoint Sources. JAWRA 37: 1169–1188.
    [164] Bosch DD, Sheridan JM, Batten HL, et al. (2004) Evaluation of the SWAT model on a coastal plain agricultural watershed. T ASAE 47: 1493–1506. doi: 10.13031/2013.17629
    [165] Saleh A, Du B (2004) Evaluation of SWAT and HSPF within BASINS program for the Upper North Bosque River watershed in central Texas. T ASAE 47: 1039–1049. doi: 10.13031/2013.16577
    [166] Tripathi MP, Panda RK, Raghuwanshi NS (2005) Development of effective management plan for critical subwatersheds using SWAT model. Hydrol Process 19: 809–826. doi: 10.1002/hyp.5618
    [167] Grunwald S, Qi C (2006) Gis-Based Water Quality Modeling in the Sandusky Watershed, Ohio, USA. JAWRA 42: 957–973.
    [168] Setegn SG, Srinivasan R, Dargahi B (2008) Hydrological Modelling in the Lake Tana Basin, Ethiopia Using SWAT Model. TOHJ, 2: 49–62.
    [169] SWAT Literature Database SWAT Literature Database for Peer-Reviewed Journal Articles Available from: https://www.card.iastate.edu/swat_articles.
    [170] Tuo Y, Chiogna G, Disse M, et al. (2015) A multi-criteria model selection protocol for practical applications to nutrient transport at the catchment scale. Water 7: 2851–2880. doi: 10.3390/w7062851
    [171] Krysanova V, Hattermann F, Huang S, et al. (2015) Modelling climate and land-use change impacts with SWIM: lessons learnt from multiple applications. Hydrol Sci J 60: 606–635. doi: 10.1080/02626667.2014.925560
    [172] Čerkasova N, Umgiesser G, Ertürk A (2018) Development of a hydrology and water quality model for a large transboundary river watershed to investigate the impacts of climate change – A SWAT application. Ecol Eng 124: 99–115. doi: 10.1016/j.ecoleng.2018.09.025
    [173] Cho J, Oh C, Choi J, et al. (2018) Climate change impacts on agricultural non-point source pollution with consideration of uncertainty in CMIP5. Irrig Drain 65: 209–220.
    [174] Yang X, Warren R, He Y, et al. (2018) Impacts of climate change on TN load and its control in a River Basin with complex pollution sources. Sci Total Environ 615: 1155–1163. doi: 10.1016/j.scitotenv.2017.09.288
    [175] Lee S, Yeo I-Y, Sadeghi AM, et al. (2018) Comparative analyses of hydrological responses of two adjacent watersheds to climate variability and change using the SWAT model. Hydrol Earth Syst Sci 22: 689–708. doi: 10.5194/hess-22-689-2018
    [176] Jha MK, Gassman PW, Panagopoulos Y (2015) Regional changes in nitrate loadings in the Upper Mississippi River Basin under predicted mid-century climate. Reg Environ Change 15: 449–460. doi: 10.1007/s10113-013-0539-y
    [177] Chiew FHS, McMahon TA (1993) Detection of trend or change in annual flow of Australian rivers. Int J Clim 13: 643–653. doi: 10.1002/joc.3370130605
    [178] Gellens D, Roulin E (1998) Streamflow response of Belgian catchments to IPCC climate change scenarios. J Hydrol 210: 242–258. doi: 10.1016/S0022-1694(98)00192-9
    [179] Jha M, Gassman PW, Secchi S, et al. (2004) Effect of watershed subdivision on Swat flow, sediment, and nutrient predictions. JAWRA 40: 811–825.
    [180] Glavan M, Ceglar A, Pintar M (2015) Assessing the impacts of climate change on water quantity and quality modelling in small Slovenian Mediterranean catchment – lesson for policy and decision makers. Hydrol Process 29: 3124–3144. doi: 10.1002/hyp.10429
    [181] Kroeze C, Seitzinger SP (1998) Nitrogen inputs to rivers, estuaries and continental shelves and related nitrous oxide emissions in 1990 and 2050: a global model. Nutr Cycl Agroecosys 52: 195–212. doi: 10.1023/A:1009780608708
    [182] Seitzinger SP, Kroeze C, Bouwman AF, et al. (2002) Global patterns of dissolved inorganic and particulate nitrogen inputs to coastal systems: Recent conditions and future projections. Estuaries 25: 640–655. doi: 10.1007/BF02804897
    [183] Galloway JN, Dentener FJ, Capone DG, et al. (2004) Nitrogen cycles: Past, present, and future. Biogeochemistry 70: 153–226. doi: 10.1007/s10533-004-0370-0
    [184] Bouwman AF, Drecht GV, Knoop JM, et al. (2005) Exploring changes in river nitrogen export to the world's oceans. Global Biogeochem Cy 19: GB1002.
    [185] Tilman D, Fargione J, Wolff B, et al. (2001) Forecasting agriculturally driven global environmental change. Science 292: 281–284. doi: 10.1126/science.1057544
    [186] Fisher R (2013) Cost estimates of phosphorus removal at wastewater treatment plants.; Ohio Environmental Protection Agency, p. 50.
    [187] Kronvang B, Bechmann M, Pedersen ML, et al. (2003) Phosphorus dynamics and export in streams draining micro-catchments: Development of empirical models. J Plant Nutr Soil Sci 166: 469–474. doi: 10.1002/jpln.200321164
    [188] Osmond D, Meals D, Hoag D, et al. (2012). Improving conservation practices programming to protect water quality in agricultural watersheds: Lessons learned from the National Institute of Food and Agriculture–Conservation Effects Assessment Project. J Soil Water Conserv 67: 122–127. doi: 10.2489/jswc.67.2.122
    [189] Gburek WJ, Drungil CC, Srinivasan MS, et al. (2002) Variable-source-area controls on phosphorus transport: Bridging the gap between research and design. J Soil Water Conserv 57: 534–543.
    [190] Gitau MW, Veith TL, Gburek WJ (2004) Farm-level optimization of BMP placement for cost-effective pollution reduction. T ASAE 47: 1923–1931. doi: 10.13031/2013.17805
    [191] Arabi M, Govindaraju RS, Hantush MM (2006) Cost‐effective allocation of watershed management practices using a genetic algorithm - Arabi. Water Resouce Res 42: W10429.
    [192] Caswell M, Fuglie K, Ingram C, et al. Adoption of agricultural production practices. Economic Research Service, Agricultural Economic Report No. 792, USDA, 2001.
    [193] Gabriel M, Knightes C, Cooter E, et al. (2018) Modeling the combined effects of changing land cover, climate, and atmospheric deposition on nitrogen transport in the Neuse River Basin. J Hydrol Reg Stud 18: 68–79. doi: 10.1016/j.ejrh.2018.05.004
    [194] Holman IP, Rounsevell MDA, Shackley S, et al. (2005) A regional, multi-sectoral and integrated assessment of the impacts of climate and socio-economic change in the UK. Climatic Change 71: 9–41. doi: 10.1007/s10584-005-5927-y
    [195] Dowd BM, Press D, Huertos ML (2008) Agricultural nonpoint source water pollution policy: The case of California's Central Coast. Agr Ecosyst Environ 128: 151–161. doi: 10.1016/j.agee.2008.05.014

  • This article has been cited by:

    1. Judith Rosellón-Druker, Edith Calixto-Pérez, Elva Escobar-Briones, Jaime González-Cano, Luis Masiá-Nebot, Fernando Córdova-Tapia, A Review of a Decade of Local Projects, Studies and Initiatives of Atypical Influxes of Pelagic Sargassum on Mexican Caribbean Coasts, 2022, 2, 2673-9410, 254, 10.3390/phycology2030014
    2. Nour Sh. El-Gendy, Mohamed Hosny, Abdallah R. Ismail, Ahmed A. Radwan, Basma A. Ali, Hager R. Ali, Radwa A. El-Salamony, Khaled M. Abdelsalam, Manal Mubarak, Kaliannan Durairaj, A Study on the Potential of Valorizing Sargassum latifolium into Biofuels and Sustainable Value‐Added Products, 2024, 2024, 1687-8787, 10.1155/2024/5184399
    3. Judith Rosellón-Druker, Laura McAdam-Otto, Justin J. Suca, Rachel Seary, Adriana Gaytán-Caballero, Elva Escobar-Briones, Elliott L. Hazen, Frank Muller-Karger, Local ecological knowledge and perception of the causes, impacts and effects of Sargassum massive influxes: a binational approach , 2023, 19, 2639-5908, 10.1080/26395916.2023.2253317
    4. Nathaly A. Díaz Molina, José A. Sosa Olivier, José R. Laines Canepa, Rudy Solis Silvan, Donato A. Figueiras Jaramillo, Evaluation of the bioenergy potential of agricultural and agroindustrial waste generated in southeastern Mexico, 2024, 12, 2333-8334, 984, 10.3934/energy.2024046
    5. Kalyan Annamalai, Breathing Planet Earth: Analysis of Keeling’s Data on CO2 and O2 with Respiratory Quotient (RQ), Part I: Global Respiratory Quotient (RQGlob) of Earth, 2024, 17, 1996-1073, 299, 10.3390/en17020299
    6. Amalinalli Velázquez-Hernández, Javier E. Aguillón-Martínez, Aspen plus simulation of sargassum for quality synthesis gas, 2023, 9, 24058440, e17731, 10.1016/j.heliyon.2023.e17731
    7. María I. López-Torres, José A. Sosa-Olivier, José R. Laines-Canepa, Alejandro Padilla-Rivera, Irma Santiago-Cortez, Fabiola J. Jiménez-Hernández, Aerobic biotransformation of Sargassum fluitans in combination with sheep manure: optimization of control variables , 2023, 39, 0275-7540, 823, 10.1080/02757540.2023.2263427
    8. Norma P. Muñoz Sevilla, Samuel Pérez Rodríguez, Enrique Morales Acuña, Diana Cecilia Escobedo-Urias, 2025, 9780443292408, 223, 10.1016/B978-0-443-29240-8.00017-1
  • Reader Comments
  • © 2019 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)
通讯作者: 陈斌, bchen63@163.com
  • 1. 

    沈阳化工大学材料科学与工程学院 沈阳 110142

  1. 本站搜索
  2. 百度学术搜索
  3. 万方数据库搜索
  4. CNKI搜索
AIMS Environmental Science
1.6 2.9

Metrics

Article views(9695) PDF downloads(2034) Cited by(5)

Preview PDF
Download XML
Export Citation
Article outline
Abstract
   Introduction
   Materials and methods
   Results and discussion
   Conclusions
Authors' contributions
Acknowledgments
Conflicts of interest
References

Figures and Tables

Figures(10)  /  Tables(7)

Other Articles By Authors

Related pages

Tools

Copyright © AIMS Press

/

DownLoad:  Full-Size Img  PowerPoint
Return
Return

Catalog