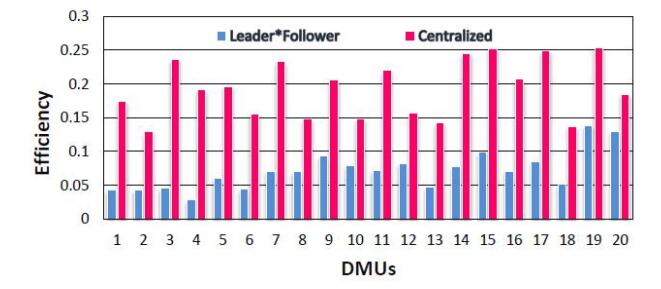
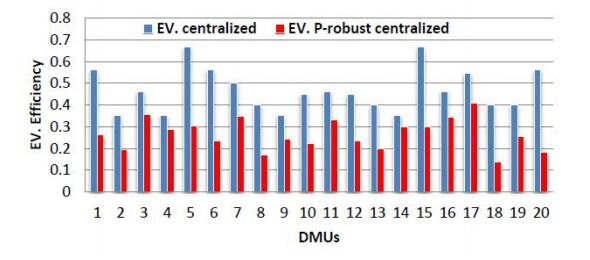
Data Envelopment Analysis (DEA) is a method for evaluating the performance of a set of homogeneous Decision Making Units (DMUs). When there are uncertainties in problem data, original DEA models might lead to incorrect results. In this study, we present two stochastic p-robust two-stage Network Data Envelopment Analysis (NDEA) models for DMUs efficiency estimation under uncertainty based on Stackelberg (leader-follower) and centralized game theory models. This allows a deleterious effect to the objective function to better hedge against the uncertain cases those are commonly ignored in classical NDEA models. In the sequel, we obtained an ideal robustness level and the maximum possible overall efficiency score of each DMU over all permissible uncertainties, and also the minimal amount of uncertainty level for each DMU under proposed models. The applicability of the proposed models is shown in the context of the analysis of bank branches performance.
1.
Introduction
As far as the built environment is concerned, improving performance implies reasoning on multiple levels and taking action on a variety of elements in a building or a building unit. The expression building performance is a broad concept with no univocal definition in the literature, possibly because constructions are durable goods and complex systems. Forasmuch as building performance is difficult to define, it is also hard to evaluate. Early examples of building performance evaluation were developed in the US between the late sixties and the mid-seventies, leading authors to use the expression post-occupancy evaluation for the methodologies meant to evaluate building performance after their construction and occupation. More recently, the academic and professional debate has further evolved, expanding the research interest in performance evaluation to the whole building life-cycle [1,2].
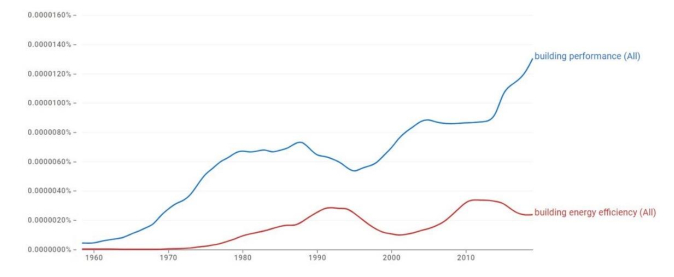
A broad research strand has long since focused on building performance from the perspective of energy saving and efficiency [3,4,5], especially concerning energy consumption from non-renewable sources, not least because of the implications in the matter of greenhouse gas emissions [6,7,8,9]. Over time, the research strand mentioned above branched out into several specific fields of study, some of which—among the primary ones—can be identified as follows: 1) building system optimization as well as integration of innovative technologies into the building and use of advanced and highly performing building materials [10,11]; 2) integration of passive systems and architectural design optimization concerning the characteristics that influence the most energy consumption, such as orientation and shape [12,13]. Nonetheless, the topic of building performance improvement is much broader, encompassing issues such as the home and workplace healthiness and safety [14,15,16], the comfort perceived by the users [17,18], and other aspects [19]. Actually, the attention paid by authors in the literature to the overall building performance increased earlier and faster than the focus on building energy efficiency, and is still growing stronger (Figure 1).
In this position paper, we argue that two somewhat niche topics—whether the focus is on energy efficiency or other aspects shaping the notion of building performance—are deeply intertwined with the issue of improving that performance, and thus, they deserve greater attention. The first topic—discussed below in Section 2—is hinged upon the notion of budget constraint, which plays a crucial role in the decision-making processes on the construction of new buildings or the renovation of existing ones, as it significantly affects the planning and execution stages, as well as the outcomes. The second topic discussed later in Section 3 is related to operating in critical scenarios, meaning dealing with building performance improvement while facing problematic situations, such as rapidly developing demographic phenomena and other anthropological changes, for instance, overcrowding due to fast population growth and recurrent natural disasters such like sea level rise and flash flooding due to climate change.
2.
Budget constraints
Economic issues are known to be tied to achievable levels of building performance [20]. The role played by economic parameters in shaping the viability of adopting efficiency measures is a case in point [21,22,23]. An additional case in point is represented by the examination of the financial incentives to push the adoption of efficiency measures, in addition to the rise and growth of innovative business models [24,25] to exploit those incentives in the building industry [26,27,28]. Another pertinent example is given in the studies dealing with the appraisal of the cost premium [29,30] and the price premium [31,32] of highly efficient buildings compared to conventional ones [33,34,35]. Nonetheless, the comparative analysis of the profitability of investing in high-performance constructions—whether performed through well-known cost-benefit or life-cycle cost models [36,37,38], or even novel economic and multi-criteria models [39,40]—often misses considering a second feasibility dimension, namely, the ability to meet a given budget constraint.
The early literature on the topic explored a variety of market failures and barriers—such as imperfect and asymmetric information, bounded rationality, split incentives, transaction costs, and more [41,42,43]—that hinder the adoption of state-of-the-art and high-performance solutions in buildings. While the actual occurrence of all these barriers is disputed [44,45,46], consumers' and firms' spending ability is recognized as a barrier itself [47,48]. There is an inherent conflict - apparent and yet still partly neglected - between the substantial costs required to get high-performance buildings and the limited ability to incur capital expenditures by property owners and other investors (Figure 2). A budget constraint is seldom included in the evaluation of performance optimization measures to be adopted in new [49,50] and existing buildings [51]. Its consideration is largely connected with the use of analytical models derived from the life-cycle costing approach and the cost-optimal methodology [52,53]. It is additionally linked to the planning of maintenance and renovation actions of building elements according to their deterioration function in a couple of research papers [54,55], as well as used among the inputs in investment decision optimization tools concerning retrofit measures in multiple buildings in another couple of studies [56,57,58].
3.
Critical scenarios
There is a case for arguing that the research on the investments meant to improve building energy efficiency—and building performance, more broadly—has been focused primarily in Western economies and developed countries [59]. Thus, it has predominantly advanced in the EU and US contexts [60] with a few other additional areas, following the adoption and implementation of targeted policies, codes, and regulations in those countries, as also shown by the International Energy Agency in its 2018 report (Figure 3). Only recently, the literature reported studies of efficiency and performance in the least-developed countries. Such studies are still limited to a small number [61,62].
One of the issues with that lies in the lack of representativeness [63]. Western economies and developed countries hardly provide a comprehensive representation of the various situations the majority of the world's population faces, both in terms of rapidly evolving demographic phenomena— or other anthropological changes—and recurring natural disasters. We refer to them as critical scenarios. On the demographic and anthropological side, they include exponential population growth, fast rural-to-urban migration resulting in intensive land-use changes, overcrowding of urban areas, and other migratory movements with related shifts in needs and wants, tastes, and preferences [64,65,66]. On the environmental side, they also include sea level rise, flash flooding, drought, overheating, and desertification due to ongoing climate change, which represents a source of substantial risk for urban areas [67,68,69,70].
4.
Conclusions and further developments
Since many of the above-mentioned disruptive phenomena are bound to occur in developing and underdeveloped countries [71,72,73], the dynamic interplay between budget constraints and critical scenarios looks like an interesting field of study. From a normative analysis perspective, what strategies and tactics should be adopted to cope with limitations on spending power while simultaneously dealing with challenging situations? Also, from a positive analysis perspective, what actual actions do the affected people, households, and firms put into play? How much do critical scenarios worsen the burden of budget constraints, especially in large urban areas and in developing countries? Thus, how much does exposure to critical scenarios exacerbate budget constraints? How do budget constraints in critical scenarios interact with medium-to long-run policy goals as far as building performance is concerned? These are just a few instances of the research questions populating this field of inquiry.
In the near future, we expect more and more studies to address the above research issues and, perhaps, other related research topics so as to start shedding light on this under-explored topic.
Acknowledgments
This paper is meant as the opening of the special issue "Budget constraints in critical scenarios: challenges to improving building performance" in the journal AIMS Energy. Please see: https://www.aimspress.com/aimse/article/6744/special-articles.
Conflict of interest
The authors declare no conflicts of interest.









 DownLoad:
DownLoad: