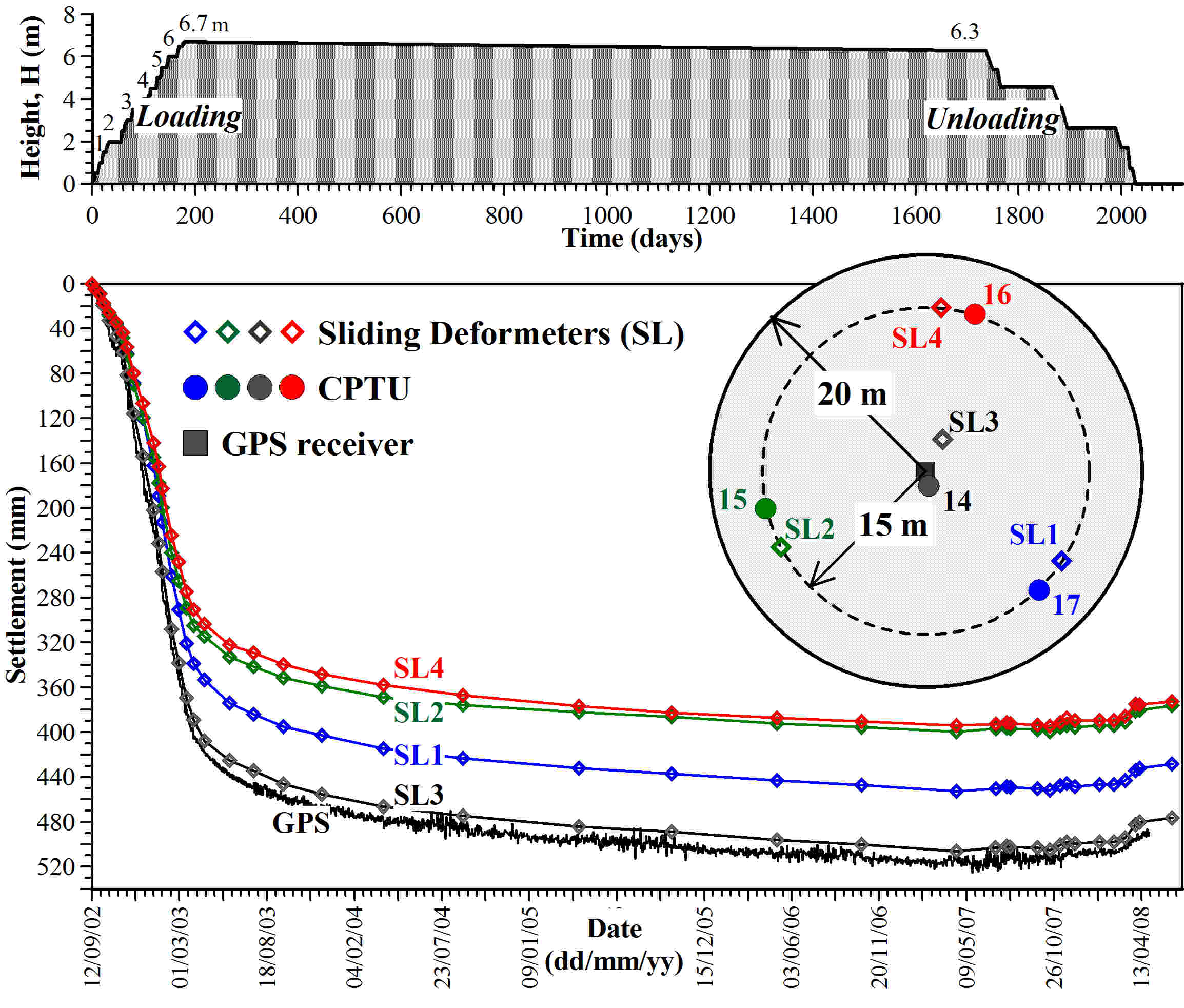
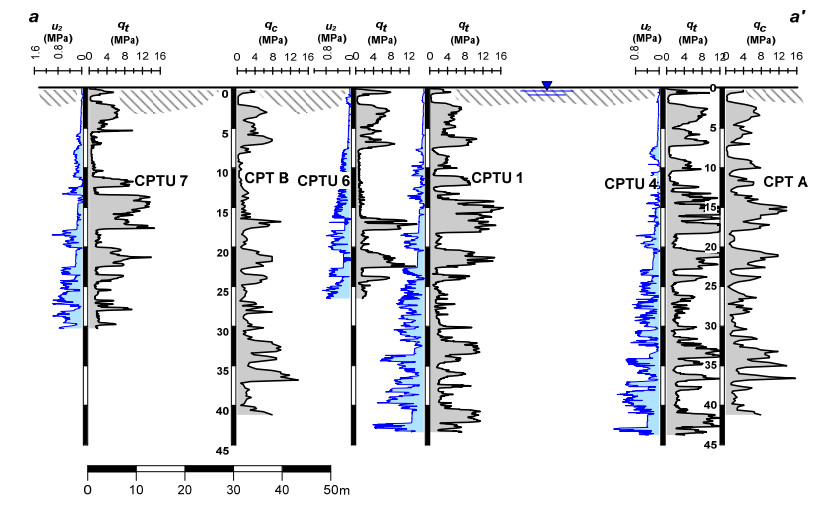
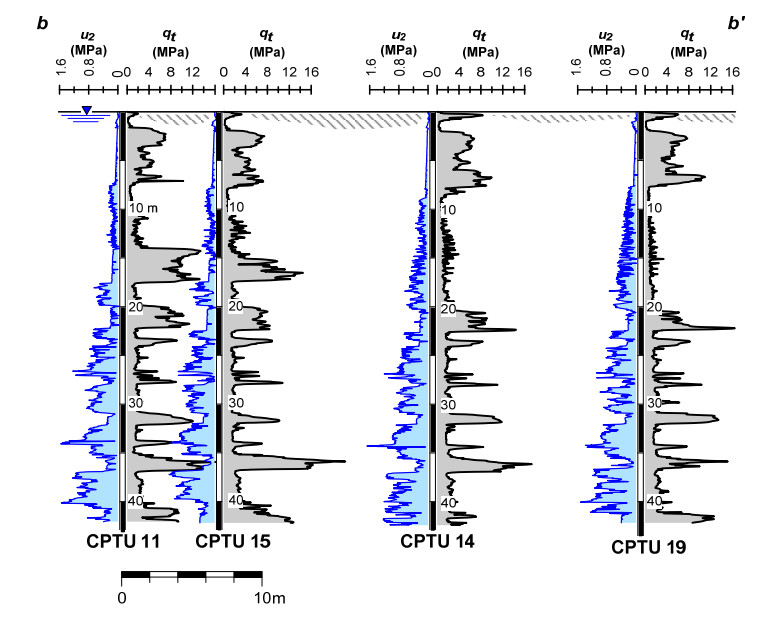
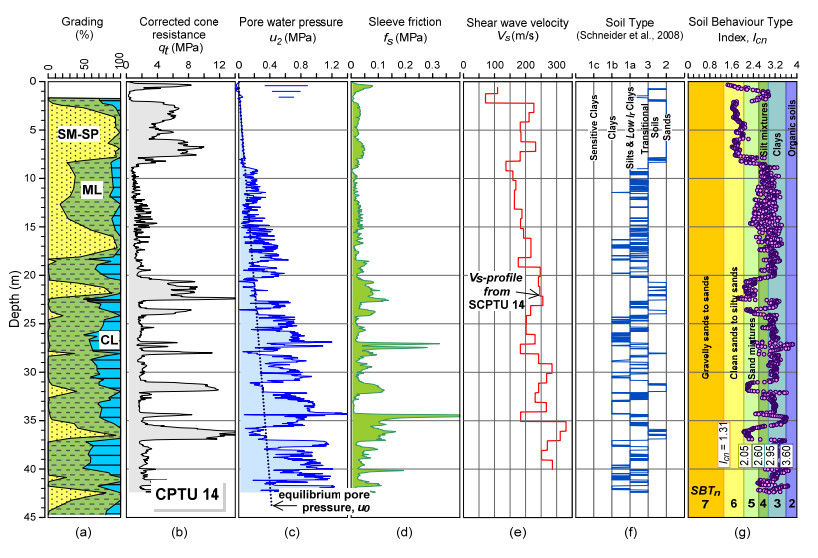
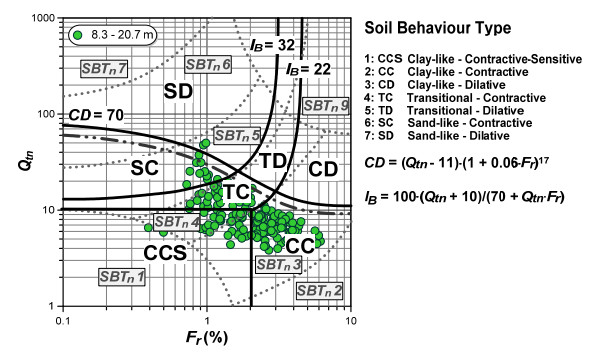
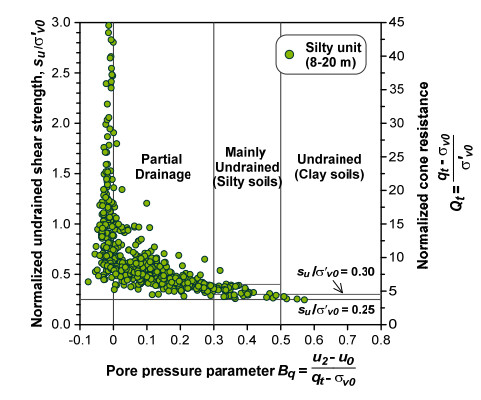
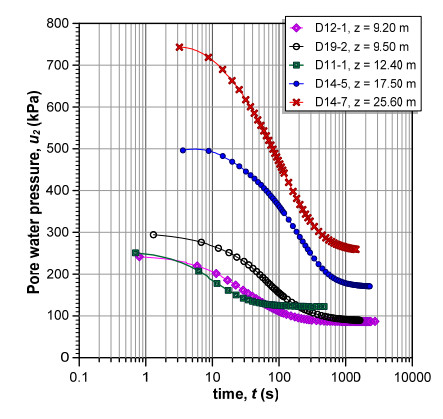
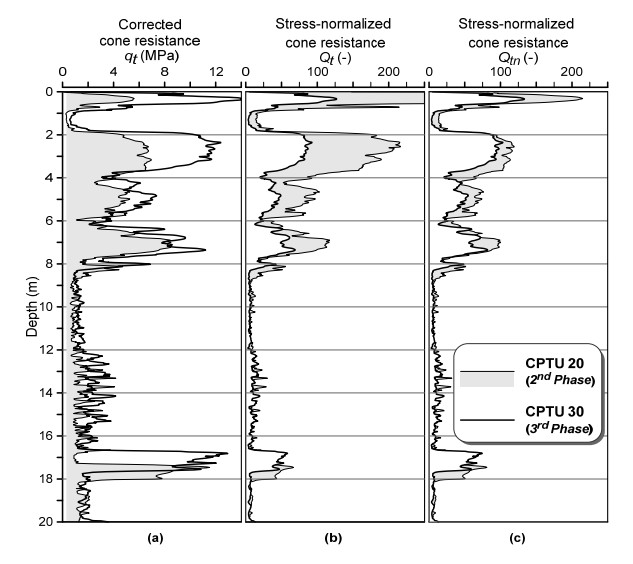
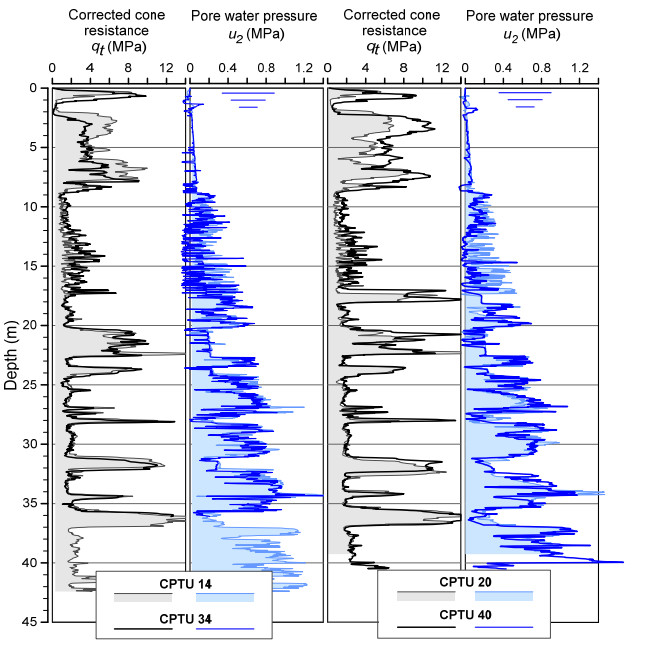
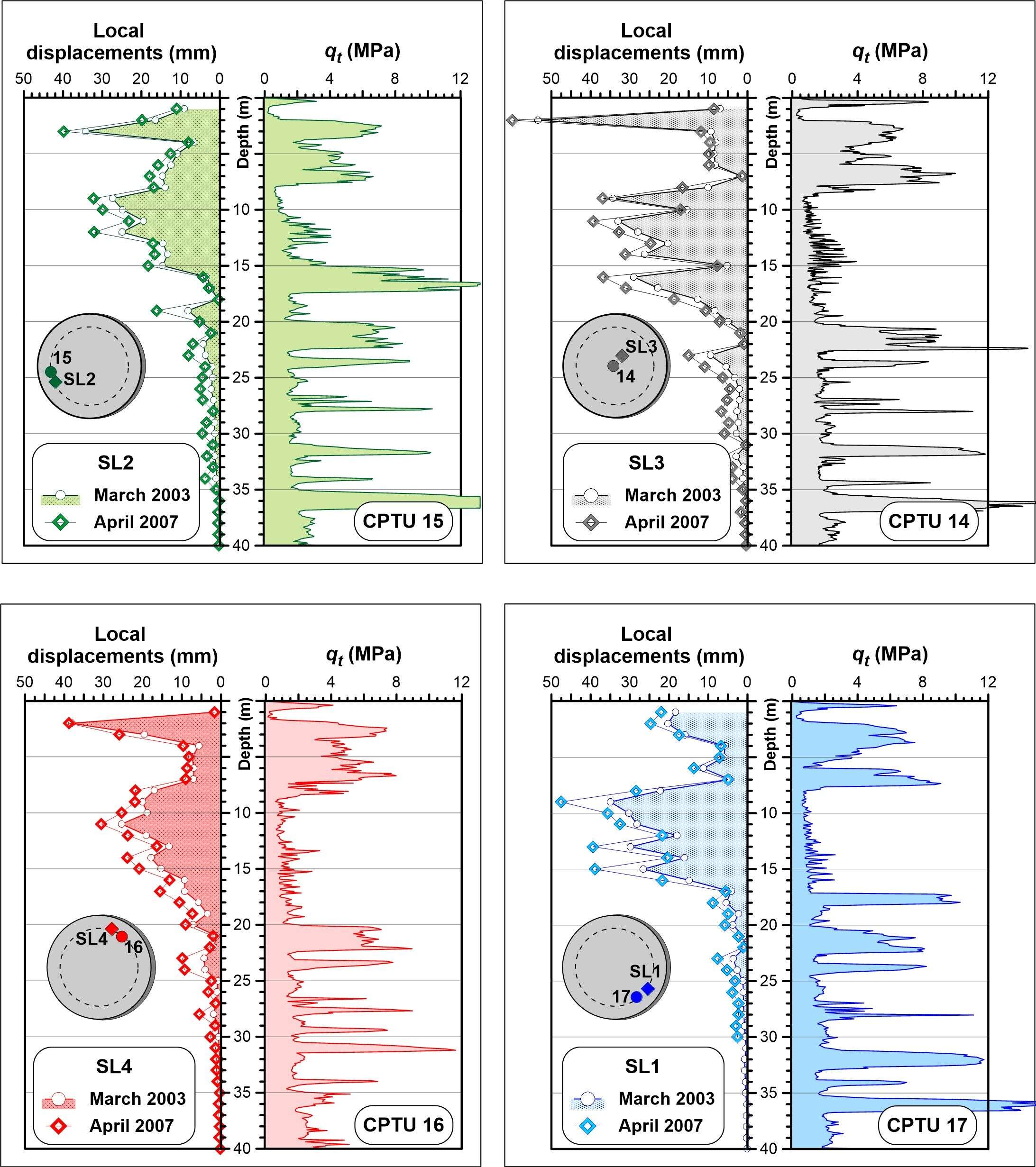
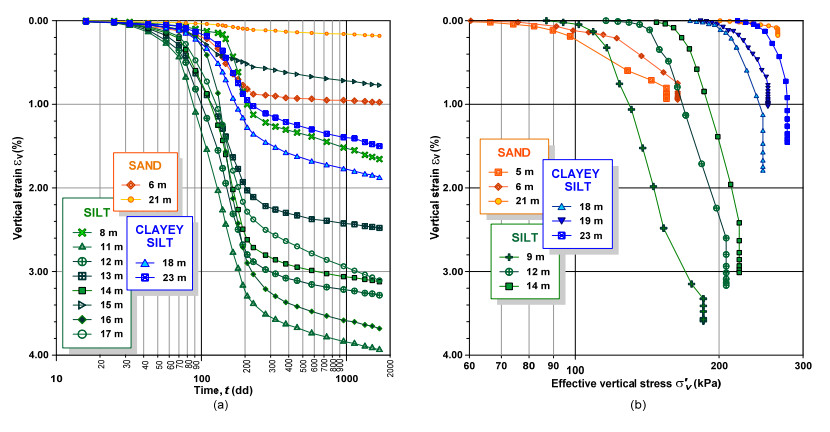
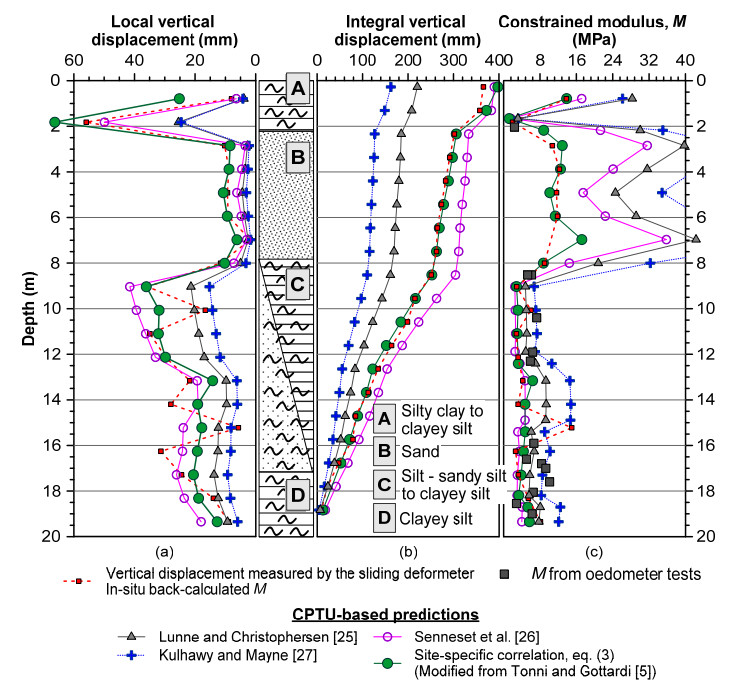
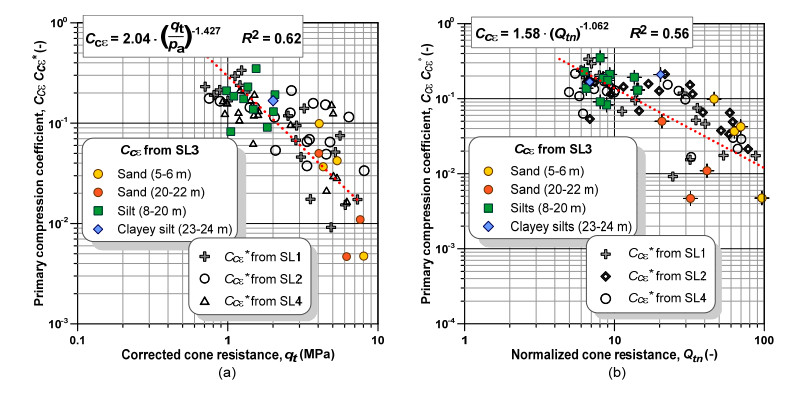
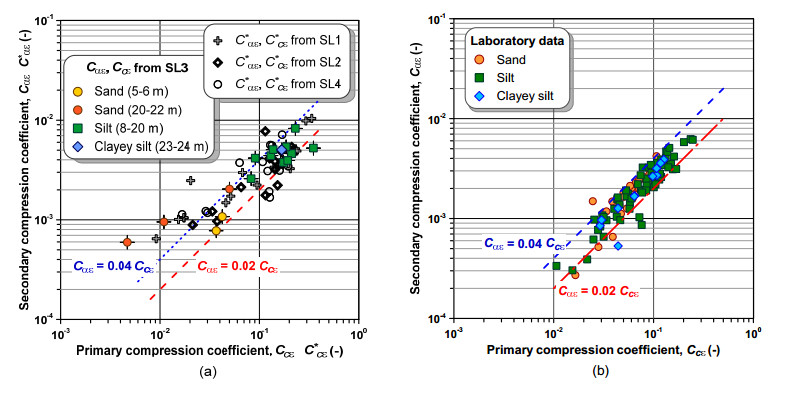
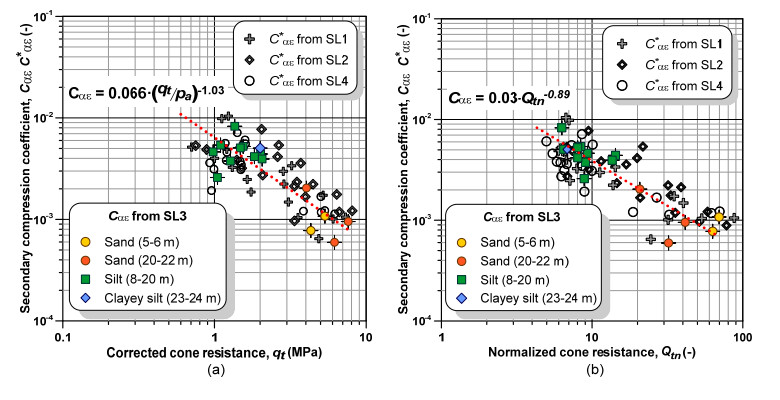
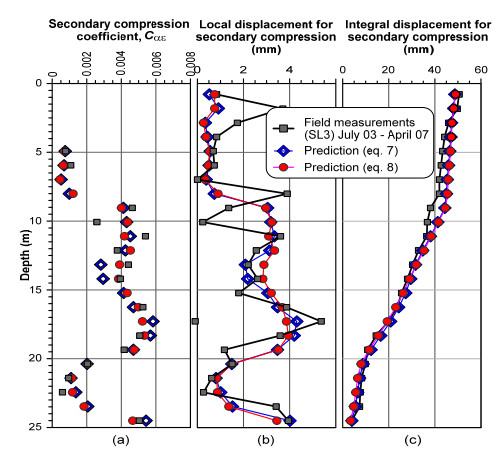
This paper explores the capability of cone penetration testing as an effective tool to estimate the compressibility characteristics of silts, silt mixtures and sand mixtures. The study uses part of the large amount of piezocone (CPTU) data and subsoil deformation measurements assembled over approximately 6 years at the Treporti Test Site (Venice, Italy), within an extensive research project aimed at thoroughly analyzing the stress-strain-time response of the complex assortment of sandy and silty sediments forming the Venetian lagoon subsoil. The combined analysis of piezocone data and subsoil deformations measured beneath a full-scale test embankment primarily showed that the existing interpretation approaches developed for 'standard' sands or clays - and thus based on the idealized assumption of fully drained or fully undrained testing conditions - generally result in invalid estimates of soil compressibility parameters. Therefore, site-specific correlations have been developed in order to correctly predict the compressibility of Venetian sediments, both primary and secondary, and consequently obtain the best fit of the measured settlements. By taking this very well documented case study as a base, the proposed paper aims at discussing some key issues on the use of piezocone tests for the geotechnical characterization of silts and other sedimentary soils with very scattered grain size distributions, thus falling in the so-called intermediate permeability range. The idea is basically to provide a critical appraisal of the CPTU-based approaches currently available for the mechanical characterization of natural soils, and explore potential advances in the interpretation methods, which might take account of possible partial drainage phenomena around the advancing cone during the test.
1.
Introduction
The Fibonacci sequence is defined Fn=Fn−1+Fn−2 for n⩾2 with the initial conditions F0=0,F1=1. The Fibonacci sequence and the golden ratio are used in many fields such as cryptology, coding theory and quantum physics in [1,2,3,4,5,6,7,8,9,10,11]. Horadam defined the Gaussian Fibonacci numbers in [12,13] and gave some general identities about the Gaussian Fibonacci numbers. Jordan generalized the Gaussian Fibonacci numbers with a similar definition in [14]. The Gaussian Fibonacci sequence is defined as GFn=GFn−1+GFn−2 with n>1 where GF0=i,GF1=1 in [14]. It can also be easily seen Fn that GFn=Fn+iFn−1 where Fn is the nth Fibonacci number.
Asci and Gurel generalized these studies and defined the k-order Gaussian Fibonacci numbers in [15] by the following recurrence relation
with boundary conditions for 1−k⩽n⩽0,
It can also be seen that GF(k)n=F(k)n+iF(k)n−1 where F(k)n is the nth k-order Fibonacci number.
In [16], Asci and Aydinyuz defined the k-order Gaussian Fibonacci polynomials and gave some important results. The k-order Gaussian Fibonacci polynomials {GFn(k)}∞n=0 are
for n>0 and k⩾2 with the initial conditions for 1−k⩽n⩽0,
It can be seen that
where F(k)n(x) is the nth k-order Fibonacci polynomial.
In order to ensure information security in terms of data transfer over communication channels, a lot of work has been done on this subject and continues to be done. Therefore, coding/decoding algorithms play an important role to ensure information security. Especially, Fibonacci coding theory is one of the most preferred in this field. We can see examples of these in many studies. For example, in [17], Stakhov gave a new approach to a coding theory using the generalization of the Cassini formula for Fibonacci p-numbers and Qp− matrices in 2006. In 2009, Basu and Prasad in [18] presented the generalized relations among the code elements for the Fibonacci coding theory. Also, Basu and Das introduced a new coding theory for Tribonacci matrices in [19] and in 2014 they defined the coding theory for Fibonacci n-step numbers by generalizing the coding theory for Tribonacci numbers in [20]. Esmaeili in [21] also described a Fibonacci polynomial-based coding method with error detection and correction.
In this paper, we remember the coding theory for k-order Gaussian Fibonacci polynomials given in [16] by taking x=1 for k-order Gaussian Fibonacci numbers. We describe the coding theory for the k-order Gaussian Fibonacci numbers. We give illustrative examples. The interesting relation between the elements of the code-message matrix is analyzed and derived. The most important of this paper is that we deal with error detection and error correction methods and examples of error probability is given.
2.
k-Order Gaussian Fibonacci coding theory
When we take x=1 in the coding theory defined in [16], we obtain the k-order Gaussian Fibonacci coding method. First, we define the Qk, Rk and En(k) matrices, which plays an important role in this coding theory. Qk, Rk and En(k) are defined the k×k matrices as the following:
and
where GF(k)n is the nth k-order Gaussian Fibonacci number.
Theorem 2.1. For n⩾1, we get in [15] as follow:
Corollary 2.1. For k=2, we get
where GFn is the nth usual Gaussian Fibonacci number in [15].
Corollary 2.2. For k=3, we get
where GTn is the nth Gaussian Tribonacci number in [23].
2.1. Applications of k-order Gaussian Fibonacci numbers to coding theory
In this section, we redefine k-order Gaussian Fibonacci coding theory using k-order Gaussian Fibonacci numbers and Qk, Rk and En(k) play very important role in the construction of k-order Gaussian Fibonacci coding theory.
We now obtain the matrix En(k) using Qk, Rk matrices for the k=2,k=3 values and examine the inverse.
• For k=2, introducing the square matrix Q2 of order 2 as:
and the square matrix R2 of order 2 as:
for n=1, we can use (2.1)
such that
The inverse of E(2)1 is as:
such that
Also, by (2.1) for n=2, we can get E(2)2 as follows:
such that
The inverse of E(2)2 is as:
such that
Theorem 2.1.1. E(2)n=[GF(2)n+1GF(2)nGF(2)nGF(2)n−1] where E(2)1=[1+i11i].
Theorem 2.1.2. (E(2)n)−1=1detE(2)n[GF(2)n−1−GF(2)n−GF(2)nGF(2)n+1]
• For k=3, introducing the square matrix Q3 of order 3 as:
and the square matrix R3 of order 3 as:
for n=1, we can use (2.1)
such that
The inverse of E(3)1 is as:
such that
Also, by (2.1) for n=2, we can get E(3)2 as follows:
such that
The inverse of E(3)2 is as:
Theorem 2.1.3. E(3)n=[GF(3)n+2GF(3)n+1GF(3)nGF(3)n+1GF(3)nGF(3)n−1GF(3)nGF(3)n−1GF(3)n−2] where E(3)1=[2+i1+i11+i1010i].
Theorem 2.1.4.
For arbitrary k-positive integers, the square matrix E(k)n of order k and inverses can be found similarly.
2.2. k-order Gaussian Fibonacci coding/decoding method
In this section, we describe a new k-order Gaussian Fibonacci coding theory. We put our message in a matrix of M and let us represent the initial message in the form of the square matrix M of order k. We take the k-order Gaussian Fibonacci matrix E(k)n as a coding matrix and its inverse matrix (E(k)n)−1 as a decoding matrix for an arbitrary positive integer k. The transformation M×E(k)n=C is called k-order Gaussian Fibonacci coding and we name the transformation C×(E(k)n)−1=M as k-order Gaussian Fibonacci decoding. We define C as a code matrix.
2.3. Illustrative examples of k-order Gaussian Fibonacci coding/decoding method
The given example is solved using the alphabet table below.
Using the arbitrary value of s⩾0, we write the following alphabet according to mod30. We can extend the characters in the table according to our wishes. We begin the “s†for the first character in Table 1.
Example 2.3.1. Let us consider the message matrix for the following message text:
• Step 1: Let’s create the message matrix using the message text:
• Step 2: Let’s write the message matrix M according to the alphabet table for the arbitrary value “s†we choose. For s = 2 ;
• Step 3: For k = 2 , n = 2 , we use (2.1);
• Step 4: The code message is:
• Step 5: The decode message is:
Example 2.3.2. Let us consider the message matrix for the following message text:
• Step 1: Let’s create the message matrix using the message text:
• Step 2: Let’s write the message matrix M according to the alphabet table for the arbitrary value “s†we choose. For s = 5 :
• Step 3: For k = 3 , n = 6 , we use (2.1):
• Step 4: The code message is:
• Step 5: The decode message is:
3.
Connections between the code matrix elements
In this section, we consider the k-order Gaussian Fibonacci coding/decoding method for k = 2 . We have an interesting relation among the elements of a code matrix C that has a crucial role in the error-correction process, outlined as follows:
and
For the case for an even integer n = 2m , we obtain the following equation
since the \det \left({{Q_2}} \right) = 1 and \det \left({{R_2}} \right) = 2 - i .
It follows from (3.5) that the elements of the matrix M can be obtained according to the following formulas:
Since the s \geqslant 0 , the elements of the matrix M are
Because of the condition (3.10) we can write the equalities (3.6)–(3.9) as:
From the Eqs (3.11) and (3.12), we can get
or
Similarly, from (3.13) and (3.14), we can obtain:
or
Since two consecutive Gaussian Fibonacci numbers approach the golden ratio, we also obtain the following equations in (3.16) and (3.18) that connect the elements of the code matrix in (3.1):
where \tau = \frac{{1 + \sqrt 5 }}{2} is the “golden ratioâ€.
Similarly, for an odd integer n = 2m + 1 , we can write the same approximate equalities (3.19) and (3.20) that connect the elements {c_1}, {c_2}, {c_3} and {c_4} of the code matrix in (3.1).
Thus, we have generated some important identities that connect the elements of the code matrix in (3.1) for the case k = 2 .
If we consider the coding/decoding method for k = 3 , we can obtain interesting identities as in k = 2 . Since two consecutive Gaussian Tribonacci numbers approach \Phi where \Phi = 1.8393. However, for general case of k we can find mathematical identities that connect the code matrix elements similar to the (3.19) and (3.20).
Example 3.1. Suppose k = 2 . Thus, we have \tau = \frac{{1 + \sqrt 5 }}{2} \cong 1.618 . Assume that the following message-matrix is to be transmitted in (2.2):
For s = 2 , we can get
• If n = 2 then
In this case, we have the following numbers rounded off to their first five digits:
• For n = 5 , we have
In this case
• For n = 10 , we have
In this case
• For n = 15 , we have
In this case
These show that for n = 15 the relation (3.19) and (3.20) holds very well.
Therefore, we select the value of n large enough, as seen in Examples 2.3.1 we get a good approximation of \tau . If we apply similar operation in Example 2.3.2, when n is chosen large enough we get a good approximation of \Phi where \Phi = 1.8393 and \Phi is the ratio between two Gaussian Tribonacci numbers.
4.
Error detection and correction
The k-order Gaussian Fibonacci coding/decoding method considered above provides an interesting possibility to detect and correct “errors†in code message C . Error detection and correction for k = 2 depends on the states of the determinant of the matrix C and the connections with the code matrix elements at (3.19) and (3.20). These mathematical relations given by (3.19), (3.20) and the determinant of the code matrix C play a role in checking relations of the k-order Gaussian Fibonacci coding/decoding method. The error-correction algorithm for Fibonacci coding has been explained in [10] and [13]. This defined algorithm is valid and applicable to the k-order Gaussian Fibonacci numbers we have given in this study.
First, let’s calculate the determinant of our message matrix M and send it to the communication channel right after the code matrix elements. Here, the determinant of M will be the control element for the C code matrix received from the communication channel. After taking the determinant of the code matrix C and its control element M , we can calculate the determinant of the code matrix C and compare the determinant of M with the determinant of C with respect to the control relation. If the operations we have done after this check are exactly appropriate, we can conclude that the elements of the code matrix C are transmitted on the communication channel without errors. If the opposite happens, we can say that there are errors in the elements of the code matrix C or the determinant of the control element M .
Suppose the elements of the C code matrix errors. This matrix can have a one-fold error, double-fold error or {k^2} - fold error. To explain how to correct these errors, we consider the 2 \times 2 type matrix obtained for k = 2 . These cases are considered.
Our first hypothesis is that we have the case of a “single†error in the code matrix C received from the communication channel. It is clearly seen that there are four types of single-fold errors in the C code matrix:
where x, y, z, t are possible “destroyed†elements.
Since it is C = M \times E_n^{(2)} , if we take the determinant of both sides, we get the following equations:
or equivalently
The formulas (4.6)–(4.9) give four possible states of a “single errorâ€. However, we need to choose the correct case from among x, y, z, t integer solutions. We have to choice such solutions, which satisfies to the additional “checking relations†(3.19) and (3.20). If calculations by formulas (4.6)–(4.9) do not give an integer result, we can conclude that our “single error†hypothesis is incorrect or that the determinant of control element M is “errorâ€. In the second case, we can use approximate Eqs (3.19) and (3.20) to check the correctness of the C code matrix.
Similarly, we can easily check “double errors†of the C code matrix. Suppose that the code matrix C has elements x and y error as shown below:
Then,
However, according to the (3.19) there is the following relation between x and y
Again, only integer solutions are acceptable. If no integer solution is obtained, then two-fold errors have not occurred.
Hence, we can show that with this type of approach, there is the possibility to correct all possible triple-fold errors in the C code matrix.
Therefore, our method of error correction depends on the verification of different hypotheses regarding errors in the code matrix using the determinant of the control relationship C matrix, (3.19) and (3.20), and the elements of the code matrix as integers. If all our solutions do not reach integer solutions, it means that the determinant of the control item M is wrong or there is a four-fold error in the C code matrix, and we should reject it. The code matrix C is defective and not correctable.
As a result, there are 15 error conditions in the C code matrix. According to the method given in [17], it means that the correctable probability of the method is equal since 14 cases between them can be corrected and
If we generalize this equation as in [20], since only {k^2} - fold errors cannot be corrected with this method, the error correction capacity of the method is
where k is the order of the message-matrix. So far sufficiently large values of k , the probability of decoding error is almost zero.
Consequently, for a sufficiently large value of k , in the case of n = k , the correct ability of this method is
Therefore, for large value of k , the correct possibility of the method is
5.
Conclusions
In this paper, we obtained the coding theory for k-order Gaussian Fibonacci polynomials given in [16] by taking x = 1 for k-order Gaussian Fibonacci numbers and gave illustrative examples. This coding method differs from classical algebraic coding methods in this respect. We can show this difference with the following features:
1) Since the n, k and s \geqslant 0 values are arbitrarily chosen in the k-order Gaussian Fibonacci coding theory, it is difficult to estimate the information transmission between the two channels by a third channel, which increases the reliability of the information transmission. In addition, this method depends on matrix multiplication and can be performed quickly and easily by today’s computers.
2) With k-order Gaussian Fibonacci coding theory, we can encrypt and send messages of the desired length by enlarging the k value sufficiently.
3) The main practical feature of this method is that matrix elements are error detection and correction objects.
4) The Gaussian Fibonacci coding method, which is the simplest coding method obtained for the k = 2 value, has been redefined by handling the 2 \times 2 type matrices with “single-fold, double-fold and triple-fold errorsâ€.
5) In the simplest case, for k = 2 , the correct capability of the method is essentially equal to 93.33%, exceeding all well-known correction codes.
6) This error correction method given for k = 2 is generalized and the correct ability of the errors of this method increases as k increases, and the correct ability approaches 100% for a sufficiently large value of k .
7) This article is just a brief outline of a new coding theory based on the k-order Gaussian Fibonacci matrices of the articles in [17,18,20,21] and [22].
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: