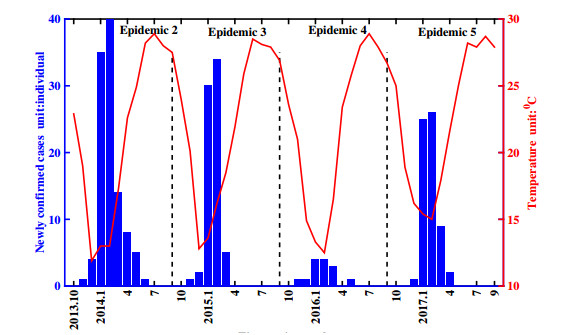
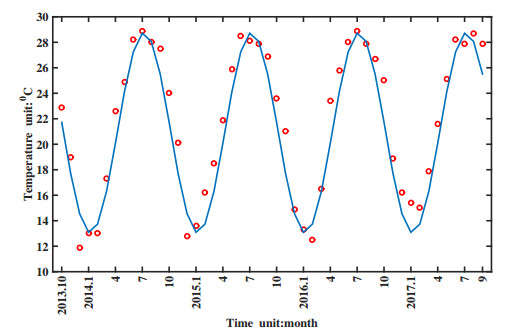
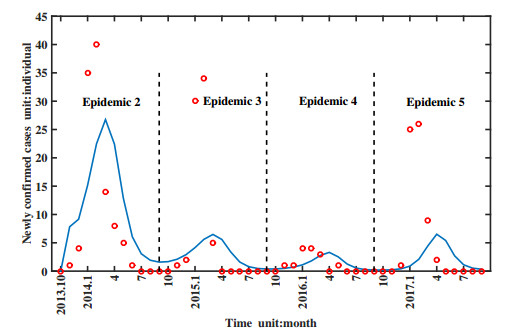
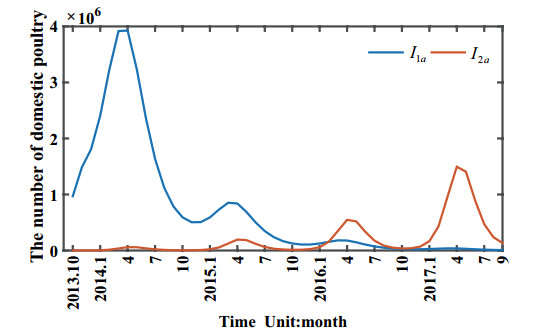
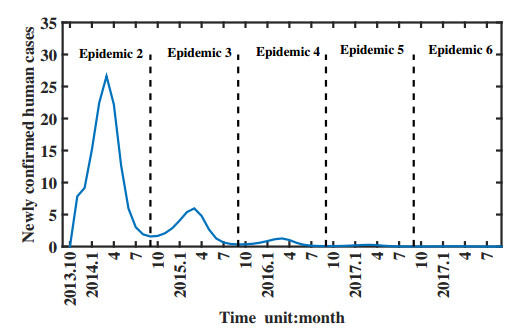
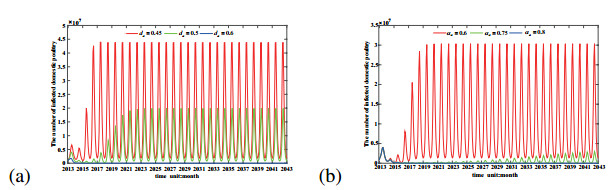
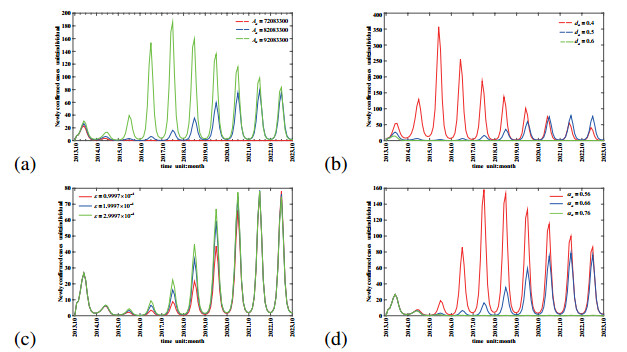
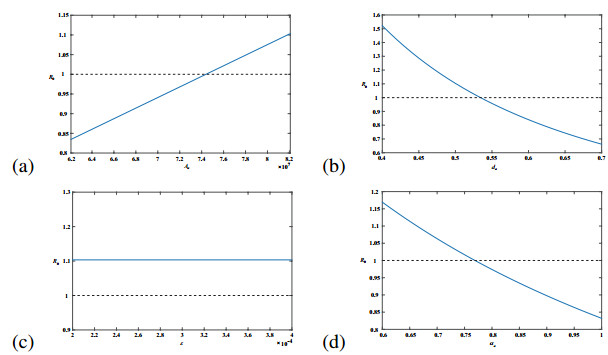
In 2017, the low pathogenic avian influenza H7N9 virus in China had mutated into high pathogenicity to domestic poultry, and led to a large number of poultry death and human cases. To evaluate the effect of virus mutation on the transmission of avian influenza H7N9 virus, this paper takes Guangdong province for the research area, takes domestic poultry, virus in the domestic poultry survival environment and human beings for the research objects, and establishes a non-autonomous dynamical model. By fitting model with the newly confirmed human cases in Guangdong province, the model we established is confirmed and applied to explain the dynamics of historical human cases. By carrying on parameter estimation, it is deduced that at least 5279376 human beings in Guangdong province had been infected with avian influenza H7N9 virus from March 2013 to September 2017, but most of them were not confirmed, since they had no obvious symptoms or had been cured as common influenza. And comparing with the low pathogenic avian influenza H7N9 virus (H7N9 LPAIV), the transmission rate of the highly pathogenic avian influenza H7N9 virus (H7N9 HPAIV) to human is almost unchanged, but to domestic poultry is about 3.87 times higher. Also, we calculate the basic reproduction number R0 = 1.3042, which indicates that the virus will persist in Guangdong province with time. Besides, we also perform some sensitivity analysis of the newly confirmed human cases and R0 in terms of model parameters and conclude that reducing the birth population of domestic poultry, speeding up the circulation of domestic poultry in the market and raising the rate of disease-related death of domestic poultry are benefit to control the transmission of the avian influenza H7N9 virus.
1.
Introduction
In biological systems, the continuous predator-prey model has been successfully investigated and many interesting results have been obtained (cf. [1,2,3,4,5,6,7,8,9] and the references therein). Moreover, based on the continuous predator-prey model, many human factors, such as time delay [10,11,12], impulsive effect [13,14,15,16,17,18,19,20], Markov Switching [21], are considered. The existing researches mainly focus on stability, periodic solution, persistence, extinction and boundedness [22,23,24,25,26,27,28].
In 2011, the authors [28] considered the system incorporating a modified version of Leslie-Gower functional response as well as that of the Holling-type Ⅲ:
With the diffusion of the species being also taken into account, the authors [28] studied a reaction-diffusion predator-prey model, and gave the stability of this model.
In model (1) x represents a prey population, y represents a predator with population, a1 and a2 represent the growth rate of prey x and predator y respectively, constant b represents the strength of competition among individuals of prey x, c1 measures the maximum value of the per capita reduction rate of prey x due to predator y, k1 and k2 represent the extent to which environment provides protection to x and to y respectively, c2 admits a same meaning as c1. All the constants a1,a2,b,c1,c2,k1,k2 are positive parameters.
However, provided with experimental and numerical researches, it has been obtained that bifurcation is a widespread phenomenon in biological systems, from simple enzyme reactions to complex ecosystems. In general, the bifurcation may put a population at a risk of extinction and thus hinder reproduction, so the bifurcation has always been regarded as a unfavorable phenomenon in biology [29]. This bifurcation phenomenon has attracted the attention of many mathematicians, so the research on bifurcation problem is more and more abundant [30,31,32,33,34,35,36,37,38,39,40].
Although the continuous predator-prey model has been successfully applied in many ways, its disadvantages are also obvious. It requires that the species studied should have continuous and overlapping generations. In fact, we have noticed that many species do not have these characteristics, such as salmon, which have an annual spawning season and are born at the same time each year. For the population with non-overlapping generation characteristics, the discrete time model is more practical than the continuous model [38], and discrete models can generate richer and more complex dynamic properties than continuous time models [39]. In addition, since many continuous models cannot be solved by symbolic calculation, people usually use difference equations for approximation and then use numerical methods to solve the continuous model.
In view of the above discussion, the study of discrete system is paid more and more attention by mathematicians. Many latest research works have focused on flip bifurcation for different models, such as, discrete predator-prey model [41,42]; discrete reduced Lorenz system [43]; coupled thermoacoustic systems [44]; mathematical cardiac system [45]; chemostat model [46], etc.
For the above reasons, we will study from different perspectives in this paper, focusing on the discrete scheme of Eq (1).
In order to get a discrete form of Eq (1), we first let
and rewrite u,v,τ as x,y,t, then (1) changes into:
where β1=b2c1a1,h1=b2k1a21,α=a2c1,β2=c2bc1a2,h2=bk2a1.
Next, we use Euler approximation method, i.e., let
where △t denotes a time step, xn,yn and xn+1,yn+1 represent consecutive points. Provided with Euler approximation method with the time step △t=1, (2) changes into a two-dimensional discrete dynamical system:
For the sake of analysis, we rewrite (3) in the following map form:
In this paper, we will consider the effect of the coefficients of map (4) on the dynamic behavior of the map (4). Our goal is to show how a flipped bifurcation of map (4) can appear under some certain conditions.
The remainder of the present paper is organized as follows. In section 2, we discuss the fixed points of map (4) including existence and stability. In section 3, we investigate the flip bifurcation at equilibria E2 and E∗. It has been proved that map (4) can undergo the flip bifurcation provided with that some values of parameters be given certain. In section 4, we give an example to support the theoretical results of the present paper. As the conclusion, we make a brief discussion in section 5.
2.
Existence and stability of fixed points
Obviously, E1(1,0) and E2(0,h2β2) are fixed points of map (4). Given the biological significance of the system, we focus on the existence of an interior fixed point E∗(x∗,y∗), where x∗>0,y∗>0 and satisfy
i.e., x∗ is the positive root of the following cubic equation:
Based on the relationship between the roots and the coefficients of Eq (5), we have
Lemma 2.1 Assume that β1h22−β22h1<0, then Eq (5) has least one positive root, and in particular
(ⅰ) a unique positive root, if β1≥β22;
(ⅱ) three positive roots, if β1<β22.
The proof of Lemma 2.1 is easy, and so it is omitted.
In order to study the stability of equilibria, we first give the Jacobian matrix J(E) of map (4) at any a fixed point E(x,y), which can be written as
For equilibria E1, we have
The eigenvalues of J(E1) are λ1=0,λ2=1+α with λ2>1 due to the constant α>0, so E1(1,0) is a saddle.
For equilibria E2, note that
then the eigenvalues of J(E2) are λ1=2−β1h22β22h1,λ2=1−α, and so we get
Lemma 2.2 The fixed point E2(0,h2β2) is
(ⅰ) a sink if 1<β1h22β22h1<3 and 0<α<2;
(ⅱ) a source if β1h22β22h1<1 or β1h22β22h1>3 and α>2;
(ⅲ) a a saddle if 1<β1h22β22h1<3 and α>2, or, β1h22β22h1<1 or β1h22β22h1>3 and 0<α<2;
(ⅳ) non-hyperbolic if β1h22β22h1=1 or β1h22β22h1=3 or α=2.
3.
Flip bifurcation
In this section, we will use the relevant results of literature [38,39,40] to study the flip bifurcation at equilibria E2 and E∗.
3.1. Flip bifurcation at equilibria E2
Based on (ⅲ) in Lemma 2.2, it is known that if α=2, the eigenvalues of J(E2) are: λ1=2−β1h22β22h1,λ2=−1. Define
We conclude that a flip bifurcation at E2(0,h2β2) of map (4) can appear if the parameters vary in a small neighborhood of the set Fl.
To study the flip bifurcation, we take constant α as the bifurcation parameter, and transform E2(0,h2β2) into the origin. Let e=2−β1h22β22h1,α1=α−2, and
then map (4) can be turned into
Let
then by the following invertible transformation:
map (6) turns into
where
Provided with the center manifold theorem (Theorem 7 in [40]), it can be obtained that there will exist a center manifold Wc(0,0) for map (7), and the center manifold Wc(0,0) can be approximated as:
As the center manifold satisfies:
it can be obtained by comparing the coefficients of the above equality that a=0,b=0,c=0, so the center manifold of map (7) at E2(0,h2β2) is s=0. Then map (7) restricted to the center manifold turns into
Obviously,
so
Therefore, Theorem 4.3 in [38] guarantees that map (3) undergoes a flip bifurcation at E2(0,h2β2).
3.2. Flip bifurcation at equilibria E∗
Note that
then the characteristic equation of Jacobian matrix J(E∗) of map (3) at E∗(x∗,y∗) is:
where
Firstly, we discuss the stability of the fixed point E∗(x∗,y∗). The stability results can be described as the the following Lemma, which can be easily proved by the relations between roots and coefficients of the characteristic Eq (8), so the proof has been omitted.
Lemma 3.1 The fixed point E∗(x∗,y∗) is
(ⅰ) a sink if one of the following conditions holds.
(ⅰ.1) 0<α0+η<1, and α0−1α0+η<α<2(1+α0)1+α0+η;
(ⅰ.2) −1<α0+η<0, and α<min{α0−1α0+η,2(1+α0)1+α0+η};
(ⅰ.3) α0+η<−1, and α0−1α0+η>α>2(1+α0)1+α0+η;
(ⅱ) a source if one of the following conditions holds.
(ⅱ.1) 0<α0+η<1, and α<min{α0−1α0+η,2(1+α0)1+α0+η};
(ⅱ.2) −1<α0+η<0, and α0−1α0+η<α<2(1+α0)1+α0+η;
(ⅱ.3) α0+η<−1, and α>max{α0−1α0+η,2(1+α0)1+α0+η};
(ⅲ) a saddle if one of the following conditions holds.
(ⅲ.1) −1<α0+η<1, and α>2(1+α0)1+α0+η;
(ⅲ.2) α0+η<−1, and α<2(1+α0)1+α0+η;
(ⅳ) non-hyperbolic if one of the following conditions holds.
(ⅳ.1) α0+η=1;
(ⅳ.2) α0+η≠−1; and α=2(1+α0)1+α0+η;
(ⅳ.3) α0+η≠0,α=α0−1α0+η and (1+α0−α)2<4((1−α)α0−ηα).
Then based on (ⅳ.2) of Lemma 3.1 and α≠1+α0,3+α0, we get that one of the eigenvalues at E∗(x∗,y∗) is −1 and the other satisfies |λ|≠1. For α,β1,β2,h1,h2>0, let us define a set:
We assert that a flip bifurcation at E∗(x∗,y∗) of map (3) can appear if the parameters vary in a small neighborhood of the set Fl.
To discuss flip bifurcation at E∗(x∗,y∗) of map (3), we choose constant α as the bifurcation parameter and adopt the central manifold and bifurcation theory [38,39,40].
Let parameters (α1,β1,β2,h1,h2)∈Fl, and consider map (3) with (α1,β1,β2,h1,h2), then map (3) can be described as
Obviously, map (9) has only a unique positive fixed point E∗(x∗,y∗), and the eigenvalues are λ1=−1,λ2=2+α0−α, where |λ2|≠1.
Note that (α1,β1,β2,h1,h2)∈Fl, then α1=2(1+α0)1+α0+η. Let |α∗| small enough, and consider the following perturbation of map (9) described by
with α∗ be a perturbation parameter.
To transform E∗(x∗,y∗) into the origin, we let u=x−x∗,v=y−y∗, then map (10) changes into
where
a1=2−2x∗−β1(y∗)2f(0)−β1x∗(y∗)2f′(0); a2=−2β1x∗y∗f(0);
a3=−1−β1(y∗)2f′(0)−12β1x∗(y∗)2f″(0); a4=−2β1y∗f(0)−2β1x∗y∗f′(0);
a5=−β1x∗f(0); a6=−12β1(y∗)2f″(0)−16β1x∗(y∗)2f‴(0);
a7=−β1x∗y∗f″(0)−2β1y∗f′(0); a8=−β1f(0)−β1x∗f′(0),a9=0;
f(0)=1(x∗)2+h1,f′(0)=−2x∗[(x∗)2+h1]2,f″(0)=6(x∗)2−2h1[(x∗)2+h1]3,f‴(0)=24x∗(h1−(x∗)2)[(x∗)2+h1]4.
b1=α1β2(y∗)2(x∗+h2)2; b2=1+α1−α1β2y∗x∗+h2; b3=−α1β2(y∗)2(x∗+h2)3; b4=2α1β2y∗(x∗+h2)2;
b5=−α1β2x∗+h2; c1=β2(y∗)2(x∗+h2)2; c2=1−β2y∗x∗+h2; c3=−β2(y∗)2(x∗+h2)3;
c4=2β2y∗(x∗+h2)2; c5=−β2x∗+h2; b6=α1β2(y∗)2(x∗+h2)4; b7=−2α1β2y∗(x∗+h2)3;
Now let's construct an matrix
It's obvious that the matrix T2 is invertible due to λ2≠−1, and then we use the following invertible translation
map (11) can be described by
where
with
u=a2(s+w),v=(λ2−a1)w−(a1+1)s;
u2=(a2(s+w))2;
uv=(a2(s+w))((λ2−a1)w−(a1+1)s);
v2=((λ2−a1)w−(a1+1)s)2;
u3=(a2(s+w))3;
u2v=(a2(s+w))2((λ2−a1)w−(a1+1)s);
uv2=(a2(s+w))((λ2−a1)w−(a1+1)s)2;
v3=((λ2−a1)w−(a1+1)s)3.
In the following, we will study the center manifold of map (12) at fixed point (0, 0) in a small neighborhood of α∗=0. The well-known center manifold theorem guarantee that a center manifold Wc(0,0) can exist, and it can be approximated as follows
which satisfies
By comparing the coefficients of the above equation, we have
So, restricted to the center manifold Wc(0,0), map (12) turns into
where
e1=A1a22−A2a2(a1+1)+A3(a1+1)2;
e2=−A8a2+A9(a1+1);
e3=2A1d2a22+A2a2d2(λ2−2a1−1)−2A3d2(λ2−a1)(a1+1)−A8a2d1
−A9(λ2−a1)d1−A10a22+A11a2(a1+1)−A12(a1+1)2;
e4=−A8a2d2−A9(λ2−a1)d2;
e5=2A1a22d1+A2a2d1(λ2−2a1−1)−2A3d1(λ2−a1)(a1+1)+A4a32
−A5a22(a1+1)+A6a2(a1+1)2−A7(a1+1)3;
with
A1=(λ2−a1)a3−a2b3a2(λ2+1);A2=(λ2−a1)a4−a2b4a2(λ2+1);A3=(λ2−a1)a5−a2b5a2(λ2+1);A4=(λ2−a1)a6−a2b6a2(λ2+1);
A5=(λ2−a1)a7−a2b7a2(λ2+1);A6=(λ2−1)a8−a2b8a2(λ2+1);A7=(λ2−a1)a9−a2b9a2(λ2+1);A8=a2c1a2(λ2+1);
A9=a2c2a2(λ2+1);A10=a2c3a2(λ2+1);A11=a2c4a2(λ2+1);A12=a2c5a2(λ2+1).
To study the flip bifurcation of map (13), we define the following two discriminatory quantities
and
which can be showed in [38]. Then provided with Theorem 3.1 in [38], the following result can be given as
Theorem 3.1. Assume that μ1 and μ2 are not zero, then a flip bifurcation can occur at E∗(x∗,y∗) of map (3) if the parameter α∗ varies in a small neighborhood of origin. And that when μ2>0(<0), the period-2 orbit bifurcated from E∗(x∗,y∗) of map (3) is stable (unstable).
4.
Example
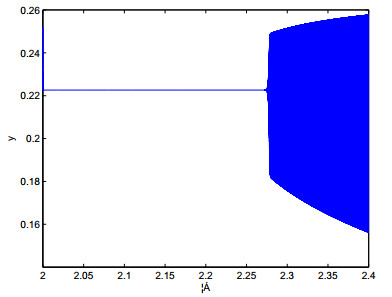
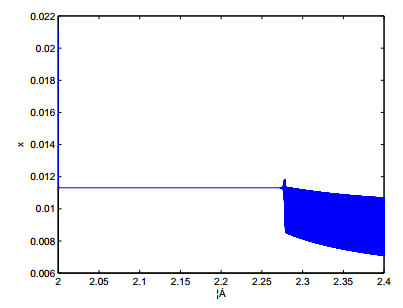
As application, we now give an example to support the theoretical results of this paper by using MATLAB. Let β1=1,β2=0.5,h1=0.05,h2=0.1, then we get from (5) that map (3) has only one positive point E∗(0.0113,0.2226). And we further have μ1=e2=0.1134≠0,μ2=e5+e21=−4.4869≠0, which implies that all conditions of Theorem 3.1 hold, a flip bifurcation comes from E∗ at the bifurcation parameter α=2.2238, so the flip bifurcation is supercritical, i.e., the period-2 orbit is unstable.
According to Figures 1 and 2, the positive point E∗(0.0113,0.2226) is stable for 2≤α≤2.4 and loses its stability at the bifurcation parameter value α=2.2238. Which implies that map (3) has complex dynamical properties.
5.
Conclusions
In this paper, a predator-prey model with modified Leslie-Gower and Holling-type Ⅲ schemes is considered from another aspect. The complex behavior of the corresponding discrete time dynamic system is investigated. we have obtained that the fixed point E1 of map (4) is a saddle, and the fixed points E2 and E∗ of map (4) can undergo flip bifurcation. Moreover, Theorem 3.1 tell us that the period-2 orbit bifurcated from E∗(x∗,y∗) of map (3) is stable under some sufficient conditions, which means that the predator and prey can coexist on the stable period-2 orbit. So, compared with previous studies [28] on the continuous predator-prey model, our discrete model shows more irregular and complex dynamic characteristics. The present research can be regarded as the continuation and development of the former studies in [28].
Acknowledgments
This work is supported by the National Natural Science Foundation of China (60672085), Natural Foundation of Shandong Province (ZR2016EEB07) and the Reform of Undergraduate Education in Shandong Province Research Projects (2015M139).
The authors would like to thank the referee for his/her valuable suggestions and comments which led to improvement of the manuscript.
Conflict of interest
The authors declare that they have no competing interests.
YYL carried out the proofs of main results in the manuscript. FXZ and XLZ participated in the design of the study and drafted the manuscripts. All the authors read and approved the final manuscripts.









 DownLoad:
DownLoad: