The survival analysis of a stochastic Lotka-Volterra competition model with a coexistence equilibrium

In Memory of Geoffrey J. Butler and Herbert I. Freedman

1.   Introduction

The classical two-species Lotka-Volterra competition model takes the form

where all parameters are positive with clear biological meanings in literature. It has been one of the most popular models in ecology and its dynamic behaviors have been fully studied as summarized in ^[1]. In fact, only when $\frac{b_{12}}{b_{2}} < \frac{a_{1}}{a_{2}} < \frac{b_{1}}{b_{21}}$ or $\frac{b_{1}}{b_{21}} < \frac{a_{1}}{a_{2}} < \frac{b_{12}}{b_{2}}$, the unique positive equilibrium $(X^{\ast}, Y^{\ast})$ exists.

In reality, population dynamics are inevitably affected by environmental noises. Different kinds of random perturbations have been considered in literature, such as ^{[2,3,4,5,6,7,8,9,10,11]} and references therein. Persistence and extinction of a competitive system with linear random perturbations have been studied in ^[4,9].

In particular, a Lotka-Volterra competition system with nonlinear random perturbations

was studied in ^[8], where $B_{i}(t)\ (i = 1, 2, 3)$ are three independent Brownian motions. The authors constructed two threshold values $\lambda_{i}\ (i = 1, 2)$ that only depend on the coefficients of (1.2) by using the invariant probability densities of diffusions on the axes, and obtained that the signs of $\lambda_{i}\ (i = 1, 2)$ determine if the two species could coexist or one species excludes the other, and additionally estimated the Lyapunov exponents.

In ^[12], a stochastic competition model with time-dependent delays

was considered, where the random perturbations were related to the coexistence equilibrium state $(X^{\ast}, Y^{\ast})$ of the corresponding deterministic system. Here the intrinsic rates $r_{i}\ (i = 1, 2)$ are subject to the environmental noises, and clearly $(X^{\ast}, Y^{\ast})$ is also the equilibrium of the above stochastic system. The sufficient conditions of the asymptotic stability of its positive equilibrium were obtained by using the method of Lyapunov function.

In ^[13], we studied the following stochastic system

which was obtained by perturbing $b_{12}$ and $b_{21}$ in (1.1), and investigated the asymptotic stability of its positive equilibrium by constructing an appropriate Lyapunov function. However, due to the limitation of methods, the case of competitive exclusion had not been considered in ^[13], and we will investigate this case completely in this paper.

In fact, the two-species Lotka-Volterra competition model (1.1) can be simplified as

where $r$ is the ratio of the intrinsic rates of the two species, and $k_{1}, k_{2}$ represent the abilities of their competition between each other. Clearly, only when $k_{1}, k_{2} < 1$ or $k_{1}, k_{2} > 1$, the positive equilibrium exists, and the corresponding results are showed as follows:

(ⅰ) if $k_{1}, k_{2} < 1$, all positive solutions $\big(X(t), Y(t)\big)$ to (1.4) converge to the unique positive equilibrium $(X^{\ast}, Y^{\ast}) = \left(\frac{1-k_{1}}{1-k_{1}k_{2}}, \frac{1-k_{2}}{1-k_{1}k_{2}}\right)$;

(ⅱ) if $k_{1}, k_{2} > 1$, there is an unstable manifold (called the separatrix) splitting the interior of the positive quadrant $\mathbb{R}_{+}^{2, o}$ into two regions. Solutions above the separatrix converge to $(0, 1)$, while solutions below the separatrix converge to $(1, 0)$.

In this paper, for simplicity we assume $r = 1$ and consider the following stochastic system

where $(X^{\ast}, Y^{\ast}) = \left(\frac{1-k_{1}}{1-k_{1}k_{2}}, \frac{1-k_{2}}{1-k_{1}k_{2}}\right)$ is the coexistence (or positive) equilibrium of the corresponding deterministic system (1.4), and the inter-specific competition rates $k_{1}, k_{2}$ are subject to white noises. In reality, the stochasticity in inter-specific competition is more important than that in intra-specific competition. In fact, system (1.5) is a special case of system (1.3).

In this paper, we consider a Lotka-Volterra competition model with special stochastic terms related to its positive equilibrium, which implies that system (1.5) makes sense only for $k_{1}, k_{2} < 1$ or $k_{1}, k_{2} > 1$. Above all, $(X^{\ast}, Y^{\ast})$ is also the unique positive equilibrium of the stochastic differential equation (1.5), which is the main difference between our model and other stochastic models. Thus it is significant to investigate whether and how the existence of such environmental noises regulates the dynamic behaviors of the deterministic system.

We first pose an assumption $(H_{0})$ about the restriction on $\sigma_{i}\ (i = 1, 2)$, which guarantees that all solutions to system (1.5) remain positive and non-explosive in any finite time. Subsequently, we use the main ideas in ^[8] to consider the equations on the two axes and calculate two critical values $\lambda_{1}$ and $\lambda_{2}$ via these coefficients of (1.5) under another assumption $(H_{1})$. We obtain that if they are both positive, the two species coexist, and moreover all solutions converge to the coexistence equilibrium $(X^{\ast}, Y^{\ast})$, and while they are both negative, the two species go extinct with positive probabilities and these two probability values add up to one. Moreover, if $Y(t)\ $ (or $X(t)$) converges to zero, its Lyapunov exponent is exactly $\lambda_{1}\ $(or $\lambda_{2}$), that is also the rate at which the corresponding species goes extinct.

Following the same logic in ^[8], we obtain quite different results due to the special stochastic terms, that is, $(X^{\ast}, Y^{\ast})$ is also the positive equilibrium of the stochastic system (1.5). In this paper, we just consider the stochastic system under the two cases of the corresponding deterministic system in which $(X^{\ast}, Y^{\ast})$ is globally asymptotically stable or the bistability occurs. Here the intensity of noises $\sigma_{i}\ (i = 1, 2)$ cannot be too strong (the assumption $(H_{0})$ is a restriction), otherwise the solutions to system (1.5) make no biological sense. Moreover, assumption $(H_{1})$ guarantees the existence of $\lambda_{i}\ (i = 1, 2)$, which have precise expressions. Different from that in ^[8], $\lambda_{1}\lambda_{2} < 0$ should not happen according to many numerical trials, and we find that the dynamic behaviors of the deterministic system will not be destroyed if the random perturbations are relatively small, which will be discussed in the final part.

The rest of the paper is organized as follows. Some preliminaries and the main ideas are presented in Section 2, and the main results in this paper are listed in Sections 3. In Sections 4 and 5, the cases of coexistence and competitive exclusion are considered, respectively. Finally in Section 6, some discussions about this model and some numerical examples are provided to illustrate our mathematical results.

2.   Preliminaries

Let $\left(\Omega, \mathcal{F}, \{\mathcal{F}_{t}\}_{t\geq 0}, \mathbb{P} \right)$ be a complete filtered probability space with the filtration $\{\mathcal{F}_{t}\}_{t\geq 0}$ satisfying the usual condition, i.e. it is increasing and right continuous while $\mathcal{F}_{0}$ contains all $\mathbb{P}$-null sets. Throughout this paper, we denote $\mathbb{R}_{+}^{2, o} = \left\{(x, y):x > 0, \ y > 0\right\}$ and let $Z_{z}(t) = \big(X_{z}(t), Y_{z}(t)\big)$ be the solution to system (1.5) with initial value $z = (x, y)$.

First of all, we pose an assumption under which all solutions to system (1.5) are reasonable in biological sense, the similar proof can be found in ^[13] and we omit it here.

Lemma 2.1. Under the assumption $(H_{0}):\sigma_{1} < \sqrt{2}, \ \sigma_{2} < \sqrt{2}$, there is a unique global positive solution $\big(X(t), Y(t)\big)^{T}$ to system (1.5) on $\mathbb{R}_{+}^{2, o}$ for any given initial value $\big(X_{0}, Y_{0}\big)\in \mathbb{R}_{+}^{2, o}$ a.s..

Therefore the rest of this paper is carried out under this assumption and below we provide some important properties of the solutions to system (1.5). In fact, they are based on the results in Lemma 2.1 and the detailed proofs are similar to that in ^[2].

Corollary 2.2. For any $\varepsilon > 0, \ H > 1, \ T > 0$, there is an $\overline{H} = \overline{H}(\varepsilon, H, T) > 1$ such that

and

Now we consider the equations on the boundary. On the $x$-axis,

Let $\xi_{t} = \ln \varphi(t)$, where $\xi_{t}$ is a function of $t$, then

According to the method in ^[7], if $\sigma_{1} < \frac{\sqrt{2}}{Y^{\ast}}$, the diffusion (2.1) has a unique invariant probability measure $\pi_{1}^{\ast}$ in $(0, \infty)$ with density

where $c_{1}^{\ast}$ is the normalizing constant and

According to the Ergodic Theorem in ^[14,15], for any measurable function $g(\cdot):\mathbb{R}_{+}\rightarrow \mathbb{R}$ satisfying that $\int_{0}^{\infty}{\left|g(\phi)\right| f_{1}^{\ast}(\phi) d\phi} < \infty$, we have

where $\varphi_{x}(t)$ is the solution to (2.1) starting at $x$. In particular, for any $p \in (-\infty, 3)$,

In fact, $Q_{1}$ and $Q_{2}$ can be calculated directly by the expression of $c_{1}^{\ast}$, that is,

Analogously, $Q_{2} = 1-\frac{1}{2}\sigma_{1}^{2}(Y^{\ast})^{2}$. Define

Similarly, the diffusion equation on the $y$-axis is

which has a unique invariant probability measure $\pi_{2}^{\ast}$ in $(0, \infty)$ if $\sigma_{2} < \frac{\sqrt{2}}{X^{\ast}}$. Likewise, define

Below we explain the definitions of $\lambda_{i}\ (i = 1, 2)$ and how to use them. To investigate whether $Y_{z}(t)$ converges to zero or not, we consider the Lyapunov exponent of $Y_{z}(t)$ when $Y_{z}(t)$ is small for a sufficiently long time. Therefore, we consider the following equation

which is derived from Itô's formula. Moreover, it can be rewritten as

When $T$ is sufficiently large, on the right side of (2.6), the first term tends to zero, and the third term is also very small according to the strong law of large numbers for martingales. Intuitively, if $Y_{z}(t)$ is small in $[0, T]$, then $X_{z}(t)$ is close to $\varphi_{x}(t)$. By the ergodicity, $\frac{\ln Y_{z}(T)}{T}$ is close to $\lambda_{1}$.

In order to study the relationship between the two values $\lambda_{i}\ (i = 1, 2)$ and the survival situation of the two species, the assumption

should be satisfied, because it guarantees the existence of $\lambda_{1}$ and $\lambda_{2}$. Moreover, the following assumption

is essential in the latter sections.

3.   Main results

Recall that $(X^{\ast}, Y^{\ast}) = \left(\frac{1-k_{1}}{1-k_{1}k_{2}}, \frac{1-k_{2}}{1-k_{1}k_{2}}\right)$, then $X^{\ast}, Y^{\ast} < 1$ whether $k_{1}, k_{2} < 1$ or $k_{1}, k_{2} > 1$. Obviously, assumption $(H_{1})$ implies assumption $(H_{0})$, which implies that $\lambda_{i}\ (i = 1, 2)$ can exist with assumption $(H_{0})$. Interestingly, we find that assumption $(H_{1})$ also implies assumption $(H_{2})$, but there is no relationship between assumptions $(H_{0})$ and $(H_{2})$.

From now on, we always assume that assumptions $(H_{0})$ and $(H_{2})$ are satisfied. In addition, we use the definitions of stochastic coexistence and competitive exclusion in ^[8] as follows.

Definition 3.1 The populations of two species modeled by (1.5) are said to stochastically coexist if for any $\varepsilon > 0$, there is an $M = M(\varepsilon) > 1$ such that

The competitive exclusion is said to take place almost surely if

Below we present our main results of the coexistence and the competitive exclusion of the two species in system (1.5), the detailed proofs are provided in the next two sections, respectively.

Theorem 3.2. Under assumptions $(H_{0})$ and $(H_{2})$, if $\lambda_{1} > 0$ and $\lambda_{2} > 0$, then the two species coexist. Moreover, all solutions converge to the positive equilibrium $(X^{\ast}, Y^{\ast})$.

Theorem 3.3. Under assumptions $(H_{0})$ and $(H_{2})$, if $\lambda_{1} < 0$ and $\lambda_{2} < 0$, then $X(t)$ or $Y(t)$ goes extinct. For any $z\in \mathbb{R}_{+}^{2, o}$, we have

where $p_{z} > 0, \ q_{z} > 0$ and $p_{z}+q_{z} = 1$. Moreover, if $Y_{z}(t)$ converges to zero, then the distribution of $X_{z}(t)$ converges weakly to $\pi_{1}^{\ast}$, and the other case is analogous.

Remark 3.4 We remark that since $\lambda_{1}$ and $\lambda_{2}$ can be rewritten as

then when $\sigma_{i}\ (i = 1, 2)$ are relatively small, $k_{1}, k_{2} < 1$ leads to $\lambda_{1}, \lambda_{2} > 0$, while $k_{1}, k_{2} > 1$ leads to $\lambda_{1}, \lambda_{2} < 0$. Therefore, relatively small random perturbations will not destroy the dynamic behaviors of the deterministic system.

4.   Stochastic coexistence

In this section, we consider the stochastic coexistence of system (1.5) and prove Theorem 3.2. Define the stopping time

Lemma 4.1. For any $T > 1, \ \varepsilon > 0, \ \sigma > 0$, there is a $\delta = \delta(T, \varepsilon, \sigma) > 0$ such that

Proof. By the exponential martingale inequality, we have $\mathbb{P}(\Omega_{1}^{z})\geq 1-\varepsilon$, where

In view of (2.5), for any $\omega \in \Omega_{1}^{z}$ we have

By choosing $\delta = \sigma \varepsilon e^{-T}$, moreover if $y < \delta$, then $Y_{z}(t) < \sigma$ for any $t < T$ and any $\omega\in \Omega_{1}^{z}$.

Lemma 4.2. For any $H > 1, \ T > 1, \ \varepsilon > 0, \ \nu > 0$, there is a $\sigma > 0$ such that for all $z\in [H^{-1}, H]\times(0, \sigma]$,

Proof. According to Corollary 2.2, there is an $\overline{H} = \overline{H}(H, T, \varepsilon)$ sufficiently large such that

It follows from Itô's formula that

which leads to

Together with the elementary inequality $\left(\sum\limits_{i = 1}^{n} a_{i}\right)^{2}\leq 2^{n}\sum\limits_{i = 1}^{n} a_{i}^{2}$, we have

where $\xi_{z}: = \tau_{z}^{\sigma}\wedge \inf \left\{u: \big(\varphi_{x}(u)\big) \vee \big(X_{z}(u)\big) \geq \overline{H} \right\}$.

For any $t\in [0, T]$, it can be estimated that

where (4.2) and (4.3) follow from Martingale inequality. By Hölder's inequality,

Applying (4.2), (4.3), (4.4) and (4.5) to (4.1), we obtain that

for some $\overline{m} = \overline{m}(\overline{H}, T) > 0$. Then it follows from Gronwall's inequality that

Hence

for sufficiently small $\sigma$. Equivalently,

In fact,

Applying (4.7) to (4.6), we have

which yields the desired result.

Lemma 4.3. For any $H > 1, \ T > 0, \ \varepsilon > 0$, there is an $\widehat{M} = \widehat{M}(\varepsilon, H, T) > 0$ such that

Proof. Since

together with Corollary 2.2, for $\overline{H} = \overline{H}(\varepsilon, H, T) > 1$, we have

Then

By choosing $\widehat{M} > \sigma_{2}\big(\overline{H}+X^{\ast}\big)$, we have

Thus the above result is proved.

Proposition 4.4. Assume that $\lambda_{1} > 0$, then for any $\varepsilon > 0, \ H > 1$, there are $T = T(\varepsilon, H) > 0$ and $\delta_{0} = \delta_{0}(\varepsilon, H) > 0$ satisfying that for any $z\in [H^{-1}, H]\times (0, \delta_{0}]$, $\mathbb{P}(\widehat{\Omega}^{z}) > 1-4\varepsilon$, where

Proof. By the definition of $\lambda_{1}$, for sufficiently small $\nu$,

Let $\widehat{M}$ be in Lemma 4.3 and by the ergodicity of $\varphi_{x}(t)$ [see (2.2)], there is a $T = T(\varepsilon, H) > \frac{25\widehat{M}^{2}}{\varepsilon^{2}\lambda_{1}^{2}}$ such that

In fact, $\varphi_{x}(t) < \varphi_{H}(t)$ a.s. for all $x\in (H^{-1}, H)$. Otherwise there is a $t_{0}\in (0, +\infty)$ such that $\varphi_{x}(t_{0}) = \varphi_{H}(t_{0})$ because of the continuity of $\varphi(t)$, which contradicts the uniqueness of solutions. Hence, according to assumption $(H_{2})$, we have $\mathbb{P}(\Omega_{2}^{z})\geq 1-\varepsilon$, where

By Lemma 4.2, there is a $\sigma = \sigma(\varepsilon, H) > 0$ such that $\sigma < \frac{\lambda_{1}}{5}$ and $\mathbb{P}(\Omega_{3}^{z})\geq 1-\varepsilon$, where

According to Lemma 4.1, for definite $\sigma$, there is a $\delta_{0} = \delta_{0}(\varepsilon, H) > 0$ satisfying that for all $z\in [H^{-1}, H]\times(0, \delta_{0}]$, $\mathbb{P}(\Omega_{4}^{z})\geq 1-\varepsilon$, where $\Omega_{4}^{z} = \big\{ \tau_{z}^{\sigma}\geq T \big\}$. Since $T > \frac{25\widehat{M}^{2}}{\varepsilon^{2}\lambda_{1}^{2}}$, it follows from Lemma 4.3 that $\mathbb{P}(\Omega_{5}^{z})\geq 1-\varepsilon$, where

Hence, for any $z\in [H^{-1}, H]\times(0, \delta_{0}], \ \omega\in \widehat{\Omega}^{z} = \cap_{i = 2}^{5}\Omega_{i}^{z}$, we obtain

The proof is completed by noting that $\mathbb{P}(\widehat{\Omega}^{z}) = \mathbb{P}(\cap_{i = 2}^{5} \Omega_{i}^{z}) > 1-4\varepsilon$.

Proposition 4.5. Suppose that $\lambda_{1} > 0$, then for any $\rho > 0$, there is a $T = T(\rho) > 0$ and a $\delta_{2} = \delta_{2}(\rho) > 0$ such that

The above result indicates that if $\lambda_{1} > 0$, then $Y(t)$ will not go extinct in finite time. The similar proof can be found in ^[8], thus we omit the details here.

Proof of Theorem 3.2. Similar to that in ^[8], for any $\varepsilon > 0$ and $z\in \mathbb{R}_{+}^{2, o}$, there is a $T = T(\varepsilon) > 0$ and a sufficiently large $M$, such that

Then

which implies the existence of an invariant probability measure $\mu_{\ast}$ and indicates that the two species coexist. Moreover, $(X^{\ast}, Y^{\ast})$ is also the unique positive equilibrium of the stochastic system (1.5), it has invariant Dirac measure, thus $\mu_{\ast} = \delta_{(X^{\ast}, Y^{\ast})}$, which implies that all solutions converge to $(X^{\ast}, Y^{\ast})$ and remain unchanged afterwards.

5.   Competitive exclusion

In this section, we consider the competitive exclusion of system (1.5). If one species goes extinct, we estimate the corresponding Lyapunov exponent of the population, and analyze the behaviors of the other one. For example, if $Y_{z}(t)$ converges to zero, we can obtain the difference between $X_{z}(t)$ and $\varphi_{x}(t)$ by estimating $\big|\ln \varphi_{x}(t)-\ln X_{z}(t)\big|$ for $t\geq 0$.

Lemma 5.1. For any $H > 1, \ T > 1, \ \varepsilon > 0, \ \gamma > 0$, there is a $\tilde{\sigma} > 0$ such that for any $z\in [H^{-1}, H]\times (0, \tilde{\sigma}]$,

Proof. In view of Corollary 2.2, there is an $\overline{H} = \overline{H}(\varepsilon, H, T) > 1$ sufficiently large such that for any $z\in [H^{-1}, H]\times[0, H]$,

It follows from $\overline{H}^{-1}\leq \varphi_{x}(t), \ X_{z}(t)\leq \overline{H}$ that

Thus the desired result is obtained from Lemma 4.2.

Proposition 5.2. Assume that $\lambda_{1} < 0$. For any $H > 1, \ \varepsilon > 0, \ \gamma > 0$, and $\lambda\in (0, -\lambda_{1})$, there is a $\tilde{\delta} > 0$ such that for any $z\in [H^{-1}, H]\times[0, \tilde{\delta}]$,

Proof. From the definition of $\lambda_{1}$, we have

For any $\lambda\in (0, -\lambda_{1})$, let $d = \frac{-\lambda_{1}-\lambda}{4}$, then by the continuity of integration there are $\eta_{1}, \eta_{2}, \eta_{3} \in (0, 1)$ sufficiently small such that

By the ergodicity in (2.2), there is a $T_{1} = T_{1}(\varepsilon, H)$ such that with a probability greater than $1-\varepsilon$ we have

The uniqueness of solutions implies that for any $x\in [H^{-1}, H]$, $\varphi_{H^{-1}}(s)\leq \varphi_{x}(s)\leq \varphi_{H}(s)$ a.s. $s\geq 0$. According to assumption $(H_{2})$, with a probability greater than $1-\varepsilon$, we have that $\varphi_{x}(t)$ also satisfies (5.1) and (5.2). Then for any $t \geq T_{1}$, $\mathbb{P}(\Omega_{6}^{z})\geq 1-\varepsilon$, where

In fact, $x\geq (\phi-\eta_{1})\mathbf{1}_{\{\eta_{1}\leq \phi \leq \eta_{2}^{-1}\}}$ if $|\ln \phi-\ln x|\leq \eta_{1}\eta_{2}$. Define the stopping time

Consequently, for any $\omega \in \Omega_{6}^{z}\cap \{\vartheta_{z}\geq T_{1}\}$ and $t\in [T_{1}, \vartheta_{z}]$, we have

Recall that

It follows from exponential martingale inequality that

which implies that $\mathbb{P}(\Omega_{7}^{z})\geq 1- \varepsilon$, where

From (5.3) and (5.4), for any $\omega\in \Omega_{6}^{z}\cap \Omega_{7}^{z}\cap \{\vartheta_{z}\geq T_{1}\}$, we have

In particular, if $y\leq 1$, putting $\tilde{m}_{1} = \exp(\frac{1}{\eta_{3}}\ln \frac{1}{\varepsilon}) = \frac{\exp \left(\eta_{3}^{-1}\right)}{\varepsilon}$, then

Next we estimate $\big|\ln \varphi_{x}(t)-\ln X_{z}(t)\big|$ for a larger time interval. It follows from Itô's formula that

where

and

which implies that

Set $U = \big|\ln \phi-\ln x\big|^{2}$, then (5.7) becomes

Let $V = \sqrt{U}$, it follows from Itô's formula that

In fact, $V = |\ln \phi-\ln x|$, thus

By exponential martingale inequality, $\mathbb{P}(\Omega_{8}^{z})\geq 1-\varepsilon$, where

Thus for any $\omega \in \Omega_{8}^{z}$, we have

where $\tilde{m}_{2} = \sigma_{1}^{2}\left(\frac{3}{2}+\frac{1}{\gamma_{0}}\ln \frac{1}{\varepsilon}\right)$.

By assumption $(H_{2})$, there is a $T_{2} = T_{2}(\varepsilon, H)\geq T_{1}$ sufficiently large such that

and a $\tilde{\sigma} = \tilde{\sigma}(\varepsilon, H) < 1$ sufficiently small such that

In view of Lemma 4.1 and Lemma 5.1, there is a $\tilde{\delta} = \tilde{\delta}(\varepsilon, H)$ so small that

and

Set $\tilde{\Omega}^{z} = \cap_{i = 6}^{9}\Omega_{i}^{z}$, then $\mathbb{P}(\tilde{\Omega}^{z})\geq 1-4\varepsilon$. For any $\omega\in \tilde{\Omega}^{z}, \ t\geq T_{2}$, by using (5.6), (5.9) and (5.10) we obtain

Therefore, together with (5.8), we have

As a result, in $\tilde{\Omega}^{z}$, $t\wedge \zeta_{z} < \vartheta_{z}$ for any $t\geq T_{2}$, which implies that $\tilde{\Omega}^{z}\subset \{\zeta_{z}\leq \vartheta_{z}\}$. Notice that $\zeta_{z} = \vartheta_{z}\wedge \tau_{z}^{\tilde{\sigma}}$, then $\tilde{\Omega}^{z}\subset \{\tau_{z}^{\tilde{\sigma}}\leq \vartheta_{z}\}$. For any $z\in [H^{-1}, H]\times(0, \tilde{\delta}]$ and $\omega\in \tilde{\Omega}^{z}$, it follows from (5.5) and (5.11) that

which means that $t\wedge \tau_{z}^{\tilde{\sigma}} < \tau_{z}^{\tilde{\sigma}}$ for any $t\geq T_{2}$, $z\in [H^{-1}, H]\times(0, \tilde{\delta}]$ and $\omega\in \tilde{\Omega}^{z}$. In other word, $\tau_{z}^{\tilde{\sigma}} = \vartheta_{z} = \infty$.

Hence, for any $z\in [H^{-1}, H]\times(0, \tilde{\delta}]$,

which completes the proof.

Proposition 5.3. Assume that $\lambda_{1} < 0$. For any $H > 1, \ \varepsilon > 0$, there is a $\overline{\delta} > 0$ such that for any $z\in [H^{-1}, H]\times(0, \overline{\delta}]$,

Proof. For any $\epsilon > 0$, let $\overline{\eta}_{1}, \overline{\eta}_{2}\in (0, 1)$ be sufficiently small such that

According to Proposition 5.2, there is a $\overline{\delta} > 0$ such that for any $z\in [H^{-1}, H]\times(0, \overline{\delta}]$, $\mathbb{P}(\overline{\Omega}_{1}^{z})\geq 1-\varepsilon$, where

Similar to (5.3), for $\omega \in \overline{\Omega}_{1}^{z}$, we have

On the other hand, it follows from Itô's formula that

and

By the ergodicity of $\varphi_{x}(t)$ and the strong law of large numbers for martingales, we have

which implies that

Notice that for any $\omega \in \overline{\Omega}_{1}^{z}$, $\big|\ln \varphi_{x}(t)-\ln X_{z}(t)\big|\leq \overline{\eta}_{1}\overline{\eta}_{2}$, then $\ln X_{z}(t)\geq \ln \varphi_{x}(t)-\overline{\eta}_{1}\overline{\eta}_{2}$. Therefore

Moreover, $Y_{z}(t)$ converges to zero in $\overline{\Omega}_{1}^{z}$, then

Together with (5.12), for $\omega \in \overline{\Omega}_{1}^{z}$, we have

Recall that

which implies that

Let $t\to \infty$, then it follows from (2.3) and (5.13) that

Hence

Proof of Theorem 3.3. Similar to that in ^[8], if $\lambda_{1} < 0, \ \lambda_{2} < 0$, then for any $\varepsilon > 0$ and $z\in \mathbb{R}_{+}^{2, o}$ we obtain

Since $\varepsilon$ is taken arbitrarily, and according to Proposition 5.2, we claim $p_{z}+q_{z} = 1$, where

If for some $z\in \mathbb{R}_{+}^{2, o}$, $Y_{z}(t)$ converges to zero, by Propositions 5.2 and 5.3, we obtain that $\big|X_{z}(t)-\varphi_{x}(t)\big|$ is sufficiently small and the distribution of $X_{z}(t)$ converges weakly to $\pi_{1}^{\ast}$. More details can be found in ^[8], thus we omit here.

6.   Discussion

In this paper, we consider a stochastic Lotka-Volterra competition model (1.5) and analyze the cases of coexistence and competitive exclusion, respectively. Firstly, the model makes sense under the assumption that the positive equilibrium $(X^{\ast}, Y^{\ast})$ of the corresponding deterministic system exists, and it is obtained by perturbing inter-specific competition rates $b_{12}, b_{21}$, therefore this model is reasonable mathematically. Secondly, $(X^{\ast}, Y^{\ast})$ is also the coexistence equilibrium of the stochastic system (1.5), which implies that there is an invariant Dirac measure, and which is the biggest difference between our model and other stochastic competitive models. Therefore, the survival analysis for model (1.5) is significative.

Recall that only if $k_{1}, k_{2} < 1$ or $k_{1}, k_{2} > 1$, the unique positive (coexistence) equilibrium $(X^{\ast}, Y^{\ast})$ of system (1.4) exists, which guarantees the rationality of the stochastic system (1.5). Therefore, we consider system (1.5) in the above two cases.

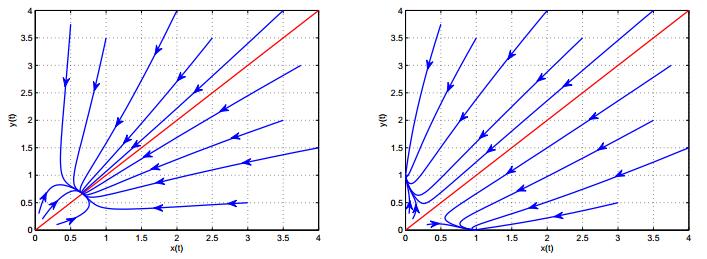
Firstly, we provide an example to demonstrate the mathematical results of the deterministic system (1.4) by choosing many different initial values.

Example 1. Consider the deterministic system (1.4) with $r = 1$ and parameters $k_{1} = k_{2} = 0.5$ and $k_{1} = k_{2} = 2$, respectively. Many solutions are obtained by choosing different initial points from either side of the diagonal line. Moreover, the same set of initial points are used in both cases, which is more convenient for comparison. In the former case, $(X^{\ast}, Y^{\ast}) = (\frac{2}{3}, \frac{2}{3})$, and it can be seen from the left panel of Figure 1 that all solutions converge to $(X^{\ast}, Y^{\ast})$. In the latter case, $(X^{\ast}, Y^{\ast}) = (\frac{1}{3}, \frac{1}{3})$, and solutions with different initial values converge to $(1, 0)$ or $(0, 1)$, which can be seen clearly from the right panel of Figure 1.

In this paper, we construct two values $\lambda_{1}, \lambda_{2}$ that can be directly calculated via those coefficients of system (1.5), and obtain that if they are both positive, all solutions to system (1.5) converge to the unique positive (coexistence) equilibrium $(X^{\ast}, Y^{\ast})$, and if they are both negative, $X(t)$ or $Y(t)$ goes extinct. Below we present two examples to illustrate the main mathematical results in this paper by choosing appropriate parameters, and obtain corresponding figures according to the method in ^[16]. In addition, we just consider the two cases $k_{1}, k_{2} < 1$ and $k_{1}, k_{2} > 1$, and choose some relatively small values for $\sigma_{1}, \sigma_{2}$ such that assumptions $(H_{0})$ and $(H_{2})$ both hold.

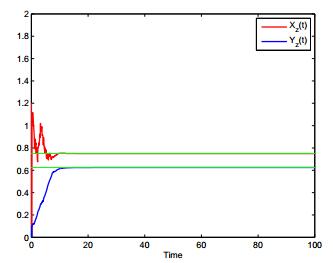
Example 2. Consider system (1.5) with parameters $k_{1} = 0.4, \ k_{2} = 0.5$, then $k_{1}, k_{2} < 1$ and $(X^{\ast}, Y^{\ast}) = (0.75, 0.625)$. Let $\sigma_{1} = \sigma_{2} = 0.5$, it can be easily verified that assumptions $(H_{0})$ and $(H_{2})$ both hold. Moreover, by direct calculation, $\lambda_{1} = 0.51 > 0, \ \lambda_{2} = 0.61 > 0$. According to Theorem 3.2, the two species coexist, moreover the solution converges to $(X^{\ast}, Y^{\ast})$ and keeps on it afterwards, which can be seen clearly from Figure 2.

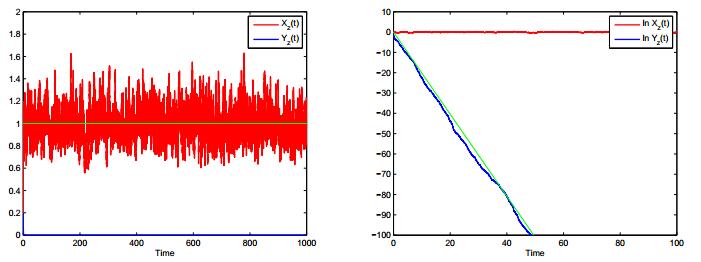
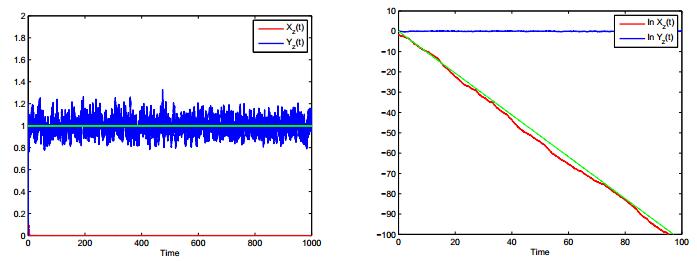
Example 3. Consider system (1.5) with parameters $k_{1} = 2, \ k_{2} = 3$, then $k_{1}, k_{2} > 1$ and $(X^{\ast}, Y^{\ast}) = (0.2, 0.4)$. Let $\sigma_{1} = \sigma_{2} = 0.5$, clearly assumptions $(H_{0})$ and $(H_{2})$ are both satisfied, and $\lambda_{1} = -2.02 < 0, \ \lambda_{2} = -1.03 < 0$. By Theorem 3.3, $X(t)$ or $Y(t)$ goes extinct, and below two trials with initial values $z_{1} = (1.2, 0.2)$ and $z_{2} = (0.2, 1.2)$ are provided, respectively. Here the two initial values are chosen symmetrically, which makes it easier to be compared. See Figure 3 and Figure 4.

From Figure 3 we can see that $Y_{z_{1}}(t)$ converges to zero and $\lim\limits_{t\to \infty}\frac{\ln Y_{z_{1}}(t)}{t} = \lambda_{1}$, and $X_{z_{1}}(t)$ keeps floating up and down around one. Similarly, Figure 4 shows that $X_{z_{2}}(t)$ converges to zero and $\lim\limits_{t\to \infty}\frac{\ln X_{z_{2}}(t)}{t} = \lambda_{2}$, and $Y_{z_{2}}(t)$ keeps floating up and down around one.

After many trials, we find that if $\sigma_{i}\ (i = 1, 2)$ satisfy assumptions $(H_{0})$ and $(H_{2})$, $k_{1}, k_{2} < 1$ will lead to $\lambda_{1}, \lambda_{2} > 0$, while $k_{1}, k_{2} > 1$ leads to $\lambda_{1}, \lambda_{2} < 0$. In other words, in either case, we cannot find appropriate $\sigma_{1}, \sigma_{2}$ satisfying these two assumptions such that $\lambda_{1}\lambda_{2} < 0$.

According to the results in ^[13], if the noise intensities $\sigma_{1}, \sigma_{2}$ satisfy assumption $(H_{0})$ and

then the positive (coexistence) equilibrium $(X^{\ast}, Y^{\ast})$ of the stochastic system (1.5) is globally asymptotically stable. In this paper, similar results are obtained if $\lambda_{1}, \lambda_{2} > 0$. The two kinds of conditions must have some connections although there is no obvious relationship between their expressions.

Especially, if $\sigma_{1} = \sigma_{2} = 0$, system (1.5) actually becomes the deterministic system (1.4), and $\lambda_{1}^{0} = 1-k_{2}, \ \lambda_{2}^{0} = 1-k_{1}$. As claimed before, if $k_{1}, k_{2} < 1$, then $\lambda_{1}^{0}, \lambda_{2}^{0} > 0$, and the positive (coexistence) equilibrium $(X^{\ast}, Y^{\ast})$ is globally asymptotically stable; if $k_{1}, k_{2} > 1$, then $\lambda_{1}^{0}, \lambda_{2}^{0} < 0$, and the case of bistability occurs. It implies that our mathematical results for the stochastic system (1.5) can go back to that of the corresponding deterministic system.

According to the above statements, we obtain that if the random perturbations are relatively weak, the dynamic behaviors of the stochastic system (1.5) are similar to those of the corresponding deterministic system (1.4). However, the conjecture that there is no appropriate $\sigma_{1}, \sigma_{2}$ satisfying assumptions $(H_{0})$ and $(H_{2})$ such that $\lambda_{1}\lambda_{2} < 0$ has not been rigorously proved mathematically, and that will be our future work.

Acknowledgments

This work was partially supported by an NSFC (11571041) and partially supported by an NSERC grant (RGPIN-2015-04581).

Conflict of interest

The authors declare that they have no competing interests.