Abbreviations: IDP: Intrinsically disordered protein; IDR: Intrinsically disordered region; YPRA: Yeast proteinase A; TFE: 2,2,2-trifluoroethanol; CD: Circular dichroism; SDSL: Site-directed spin labeling; CW-EPR: Continuous wave electron paramagnetic resonance; IAP: 3-(2-Iodoacetamido)-PROXYL; MTSL: (1-oxyl-2,2,5,5-tetramethyl-Δ3-pyrroline-3-methyl) methanethiosulfonate; MSL: 4-maleimido-TEMPO; DTT: Dithiothreitol
1. Introduction
Proteins or protein regions of 50 or more residues, which do not have stable secondary or tertiary structure under physiological conditions, are characterized as intrinsically disordered proteins (IDPs) or intrinsically disordered regions (IDRs) [1,2,3,4,5,6,7]. Although the structure-function paradigm suggests that 3D structure is necessary for function, the discovered importance of intrinsic disorder within proteins or protein regions of higher eukaryotic systems shows how function could arise from various unstructured states [3,4,8,9]. IDPs have important roles in cellular signal transduction, translation, and transcription, influencing the study of disordered proteins, focusing on both the functions provided by IDPs, and the conformational changes associated with target binding [4,7,10].
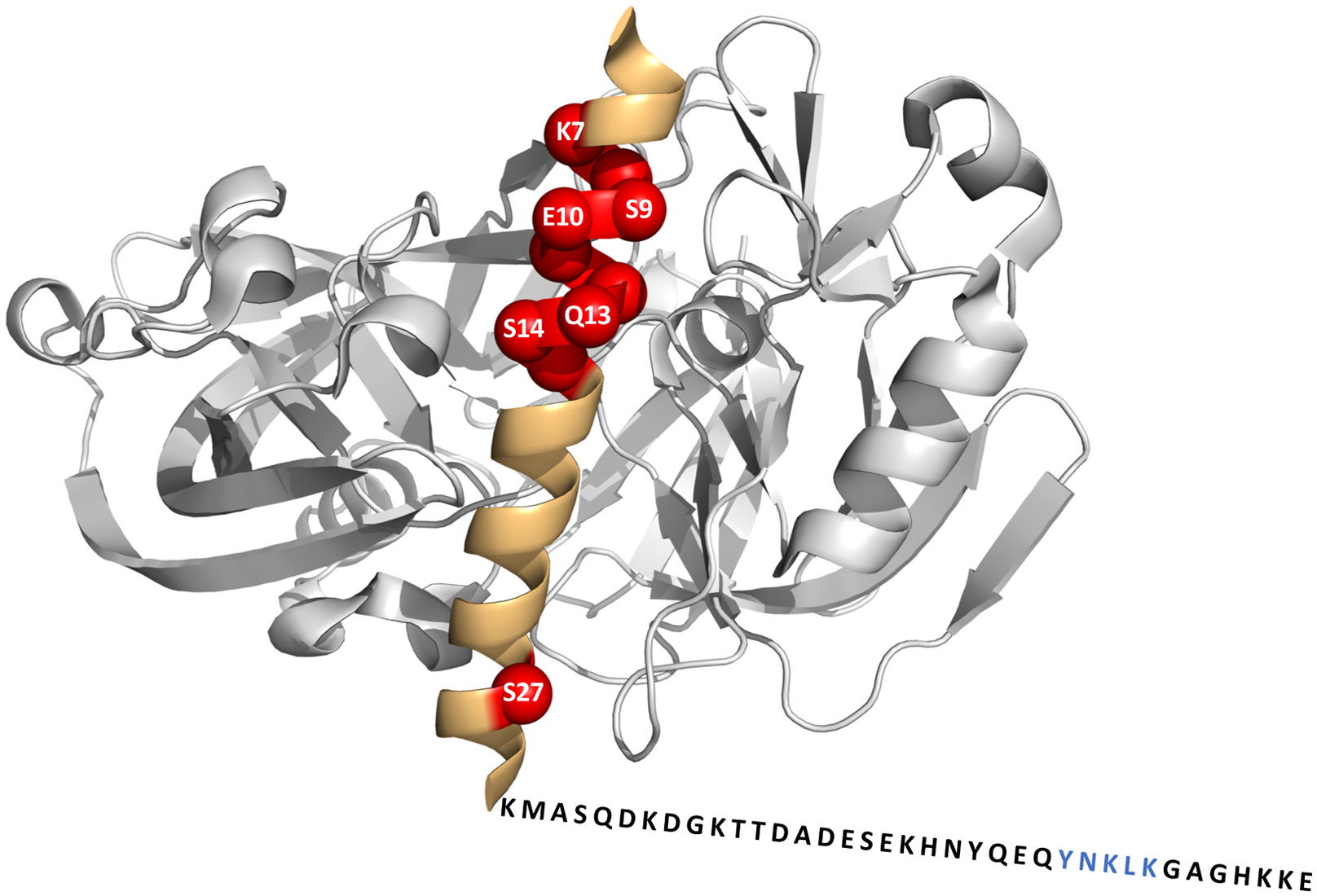
IA3, an IDP found in Sacchoromyeces cerevisiae, is composed of 68 amino acid residues and acts as an inhibitor of yeast proteinase A (YPRA). Previous studies have shown IA3 to adopt an α-helical conformation when bound in the active site of YPRA and when exposed to the secondary structure stabilizer 2,2,2-trifluoroethanol (TFE). These observed helical tendencies of IA3 differ between the N-terminal residues (2-34) and C-terminal residues (35-68) [11,12,13,14,15]. X-ray crystallographic models of IA3 bound to YPRA indicate α-helical structure in the N-terminal region (residues 2-34). In contrast, the C-terminal region (residues 35-68) has unresolved electron density, suggesting disorder (Figure 1) [11]. Biophysical methods of circular dichroism (CD) spectroscopy, 2D H1 N15 nuclear magnetic resonance spectroscopy, molecular dynamics simulations, laser temperature-jump fluorescence spectroscopy, fluorescence resonance energy transfer spectroscopy, and site directed spin labeling (SDSL), provide data supporting a two-state transition for IA3, where the C-terminus undergoes a helical transition but is less pronounced than the N-terminus [13,14,15,16,17,18].
SDSL, in combination with continuous wave electron paramagnetic resonance (CW-EPR) spectroscopy is a biophysical tool for probing structure, dynamics, and conformational changes in macromolecules [19,20,21,22,23]. For proteins, typically a CW-EPR active chemical group, such as a nitroxide spin label, is incorporated at desired locations by chemical modification of a substituted cysteine. The introduction of an active chemical group provides a reactive side group for covalent bond spin labeling. Recent progress in spin labeling methodology has also demonstrated the ability to incorporate non-natural amino acids for subsequent chemical modification, as well as novel schemes for specifically labeling tyrosine residues; a potentially very useful strategy for spin labeling IDPs [24,25,26,27].
The resultant CW-EPR spectral line shape reflects motional averaging of the nitroxide spin label [20,21,28]. Typically, the effects are described by three main types of motion, occurring in the 0.1-50 ns time scale [29,30]. The corresponding correlation times are referred to as the following: τR, the overall tumbling of the protein, τI, the movement of the spin label about the bonds connecting it to the protein, and τB, the motion of the spin labeled protein backbone. SDSL CW-EPR has been applied to study structure-to-unstructured transitions in proteins as well as to IDP systems [5,17,22,31,32]. For structured proteins ≥ 15 kDa, line shape parameters such as the second moment and scaled mobility readily reveal conformational changes without the need to increase solution viscosity [29,33]. Ordered to disordered transitions in structured proteins are readily characterized by these “traditional” line shape parameter analyses [34,35]. However, in IDPs, the degree of disorder and the dynamics of the system often times results in “isotropic-like” spectra that fall into the fast motional averaging limit. In these cases, for relatively fast motional averaging, the ratio of the intensities of the low field (h(+1)) and central field (h(0)) transitions provide an alternative line shape analysis parameter, h(1)/h(0), that is useful to describe conformational changes [5,17,22,36].
Here, extending upon previous work, we performed a spin-labeled cysteine scanning profile of the N- and C-termini of IA3, where a series of fifteen singly spin-labeled IA3 constructs consisting of ten and five cysteine substitutions in the N- and C-terminus were generated, respectively (Figure 1) [17]. A comparison is provided between the termini on a site by site basis revealing variations in the degree of transition of the two termini, and sensitivity of the helical content of the N-terminus to the spin-labeled cysteine substitution and select amino acid substitutions. As these results show, the degree of site-specific helical propensity of the N-terminus is modulated by the introduction of a chemically modified cysteine residue. By further probing site V8 of IA3, the specific effects on secondary structure due to site-specific amino acid substitution and spin labeling are analyzed. The size of an introduced residue or chemical modification has marked effects on the helical propensity within the N-terminal region of IA3, whether found on the buried (concave) or solvent exposed (convex) side of the helix when bound to YPRA. By comparing SDSL and CD results, we are able to determine sites within IA3 that can tolerate spin-label incorporation and retain WT helical tendencies; thus, we label those our “wild-type mimics”.
2. Materials and methods
2.1. Materials
BL21(DE3) pLysS cells were purchased from Invitrogen (Carlsbad, CA). E. coli codon-optimized DNA for the IA3 gene from S. cerevisiae, and DNA primers used for site-directed mutagenesis were purchased from DNA2.0 (Newark, CA). DNA taq polymerase and Dpn1 were purchased from New England Biolabs (Ipswich, MA). A 5-mL chelating column was purchased from GE Healthcare (Wauwatosa, WI). A HiPrep 26/10 desalting column was purchased from Amersham (Pittsburgh, PA). The 16.5% Tris-Tricene gels were purchased from Bio-Rad (Hercules, CA). 3-(2-Iodoacetamido)-PROXYL (IAP), (1-oxyl-2,2,5,5-tetramethyl-Δ3-pyrroline-3-methyl) methanethiosulfonate (MTSL), and 3-maleimido-TEMPO (MSL) spin label was purchased from Sigma Aldrich (St. Louis, MO). The 0.60 i.d. × 0.84 o.d. capillary tubes were purchased from Fiber Optic Center (New Bradford, MA). Unless otherwise stated, all other reagents and products were purchased from Fisher Scientific (Pittsburgh, PA) and used as received.
2.2. Protein expression and purification of IA3 wild type and mutants
The optimized IA3 gene was cloned into the pET-22b+ vector containing a C-terminal 6× His-tag, adding the sequence LEHHHHHH to the C-terminus as described previously [17]. Site directed mutagenesis via polymerase chain reaction was used to introduce non-native cysteines by designing mutagenic primers. The substituted sequence in each resultant plasmid was confirmed via Sanger DNA sequencing. WT and cysteine substituted constructs were purified as described previously [17]. Following affinity chromatography, residual nickel from the column was removed by addition of EDTA to a concentration of 100 mM and cysteine reduction was ensured by addition of dithiothreitol (DTT) to a concentration of 0.1 mM. Protein purity was assessed using a 16.5% tris-tricene SDS-PAGE gel.
2.3. Spin labeling of IA3 mutants
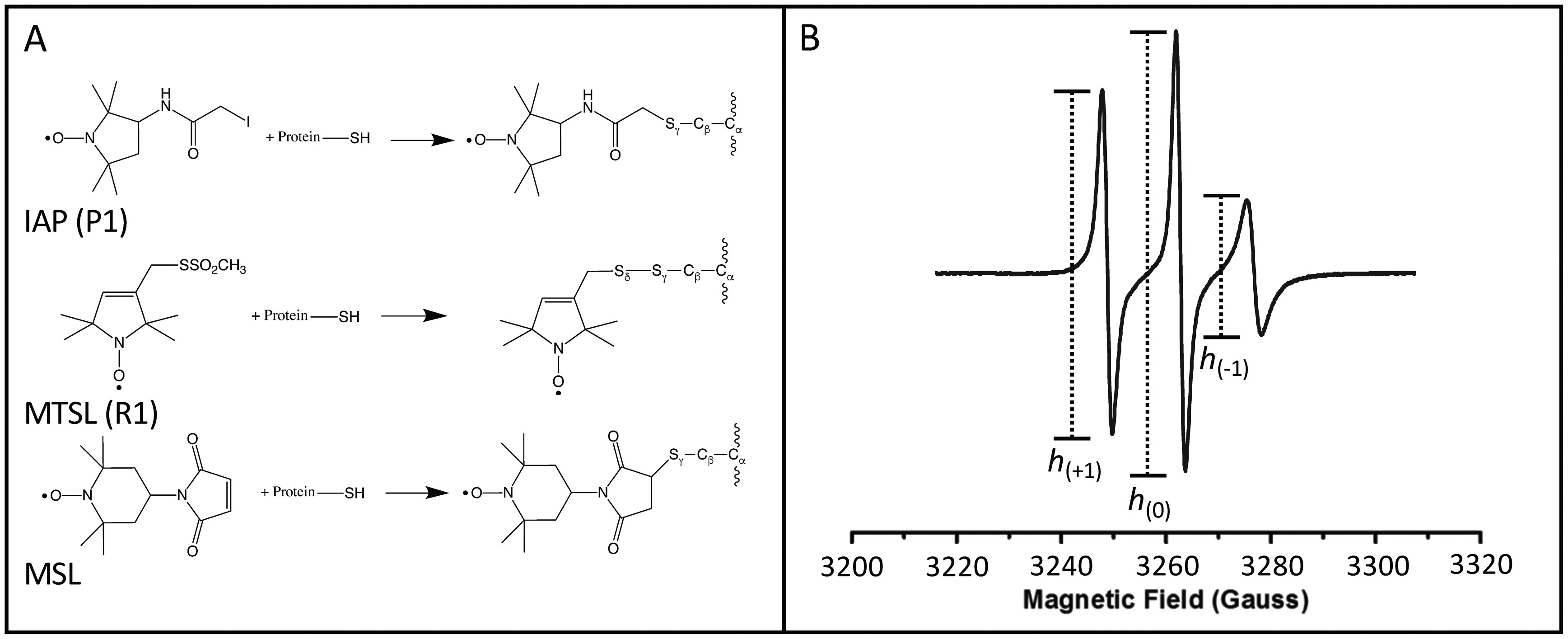
WT and cysteine substituted proteins were buffer exchanged into 50 mM sodium phosphate, 300 mM sodium chloride, pH 7.4 using a desalting column. This step also removed residual nickel, EDTA, and DTT that were added as described above. After desalting, IAP, MTSL, or MSL nitroxide spin label, dissolved in ethanol, was added in excess (5-10× molar ratio) and allowed to react with cysteine substituted constructs for 10-12 h at room temperature, in the dark. Spin labeling schemes are represented in Figure 2A. Excess spin label was removed by repeating the desalting buffer exchange process as described above.
2.4. Sample preparation for CW-EPR experiments
For each spin labeled construct, nine separate samples were prepared with increasing 5% (v/v) increments of 2,2,2-trifluoroethanol (TFE) that spanned 0-40%. Each individual sample was prepared at a final volume of 500 µL: 300 µL of 50 mM sodium phosphate, 300 mM sodium chloride, pH 7.4 buffer, (200−x) µL of TFE, where x ranged from 0-200 µL, and x µL of appropriately prepared solution of 5× stock buffer diluted with water to keep all samples at equal ionic strength and pH. These larger 500 µL sample volumes were prepared to help mitigate pipetting errors of small volumes. Samples of ∼10 µL were drawn into 0.60 i.d. × 0.84 o.d. capillary tubes, which were then flame sealed on both ends ensuring minimal to no TFE evaporation.
2.5. Sample preparation for CD experiments
For each spin labeled construct, samples were prepared with varying percentages of increasing TFE concentrations. For IAP labeled cysteine scanning and the V8C construct with varying spin label attachments, three samples were prepared with increasing 15% (v/v) increments of TFE from 0-30%. For amino acid scanning at the 8th position of the IA3 sequence and cysteine or alanine substitution at the 11th position, six or nine samples were prepared with increasing 7% (v/v) increments of TFE from 0-35% or increasing 5% (v/v) increments of TFE from 0-40%, respectively. Samples were prepared with 80-120 μL of protein sample in 50 mM sodium phosphate, 300 mM sodium chloride, pH 7.4 to reach a final concentration of 10 μM protein in 1000 μL. The final volume was adjusted using 10 mM sodium phosphate, pH 7.0 buffer or TFE to reach appropriate % (v/v) TFE. For the V8C un-labeled construct, 0.1 mM DTT was present to prevent disulfide bonding of free cysteine residues.
2.6. CW X-band EPR data collection and analysis
Either a Bruker ER200 spectrometer with an ER023 M signal channel, an ER032 M field control unit or a Bruker E500 with a loop gap resonator (Medical Advances, Milwaukee, WI) was used to collect CW X-band EPR spectra. For all experiments the temperature was kept at a constant 27 ± 0.2 °C using a nitrogen gas passed through a copper coil submersed into a water bath, while monitored with a temperature probe and thermometer from OMEGA Engineering Inc (Norwalk, CT). All spectra are reported as an average of four scans, collected as 100 G sweep width, 0.6 modulation amplitude, 70 ms conversion time, 100 kHz modulation amplitude, and 2 mW incident microwave power. Spectra were normalized using labVIEW software allowing for baseline correction and double integral area normalization. A representative nitroxide EPR spectrum with the typical three-line transition pattern is shown and labeled in Figure 2B. Spectral line shapes were analyzed by calculating the ratio of the intensities of the low field and center field transitions, h(+1)/h(0) as a function of TFE percentage. Although the low field and center field transitions individually are not as sensitive to motion as the high field transition (h(−1)), this ratio has been previously shown to change considerably as the unstructured-to-structured transition occurs and is not sensitive to errors in baseline correction or double integration [17,36]. We have used this analysis previously to monitor the unstructured to helical transition in IA3 by % TFE. Plots of h(+1)/h(0) values versus the % TFE are sigmoidal in shape and are well fit by a two-state Boltzmann transition, given by Eq 1.
| y=(A1−A2)1+e(x−x0)/dx+A2 |
(1) |
A1 is the initial value of the curve, A2 is the final value of the curve and x0 is the midpoint of the curve—which corresponds well to the midpoint of folding transitions observed by CD and NMR [14]. Data were fit using Origin 8.5 software.
2.7. CD data collection and analysis
CD measurements were collected using an AVIV model 202 CD spectrometer set at 27 °C. To collect the spectra, 400 μL of each sample were loaded into a 1mm path length quartz cuvette, cleaned between runs with nanopure H2O and ethanol. Typically, four scans of each buffer blank and sample were collected between wavelengths of 200-250 nm with 1 nm increments and a four second averaging time. Each set of CD scans for each construct was averaged, and the averaged buffer baseline was subtracted from each individual construct averaged scan. Units were converted to Δε (molar circular dichroism, M−1 cm−1) from the instruments output unit of Θ (ellipticity, mdeg) using Eq 2.
| Δε (M−1cm−1)=Θ (mdeg)xCxL100xM |
(2) |
Θ is the output ellipticity value from the CD measurement, C is the concentration of sample in g/L, L is the path length in cm, and M is the average molecular weight in g/mol.
3. Results and discussion
3.1. SDSL CW-EPR spectroscopy reveals sites where spin-label incorporation alters helicity
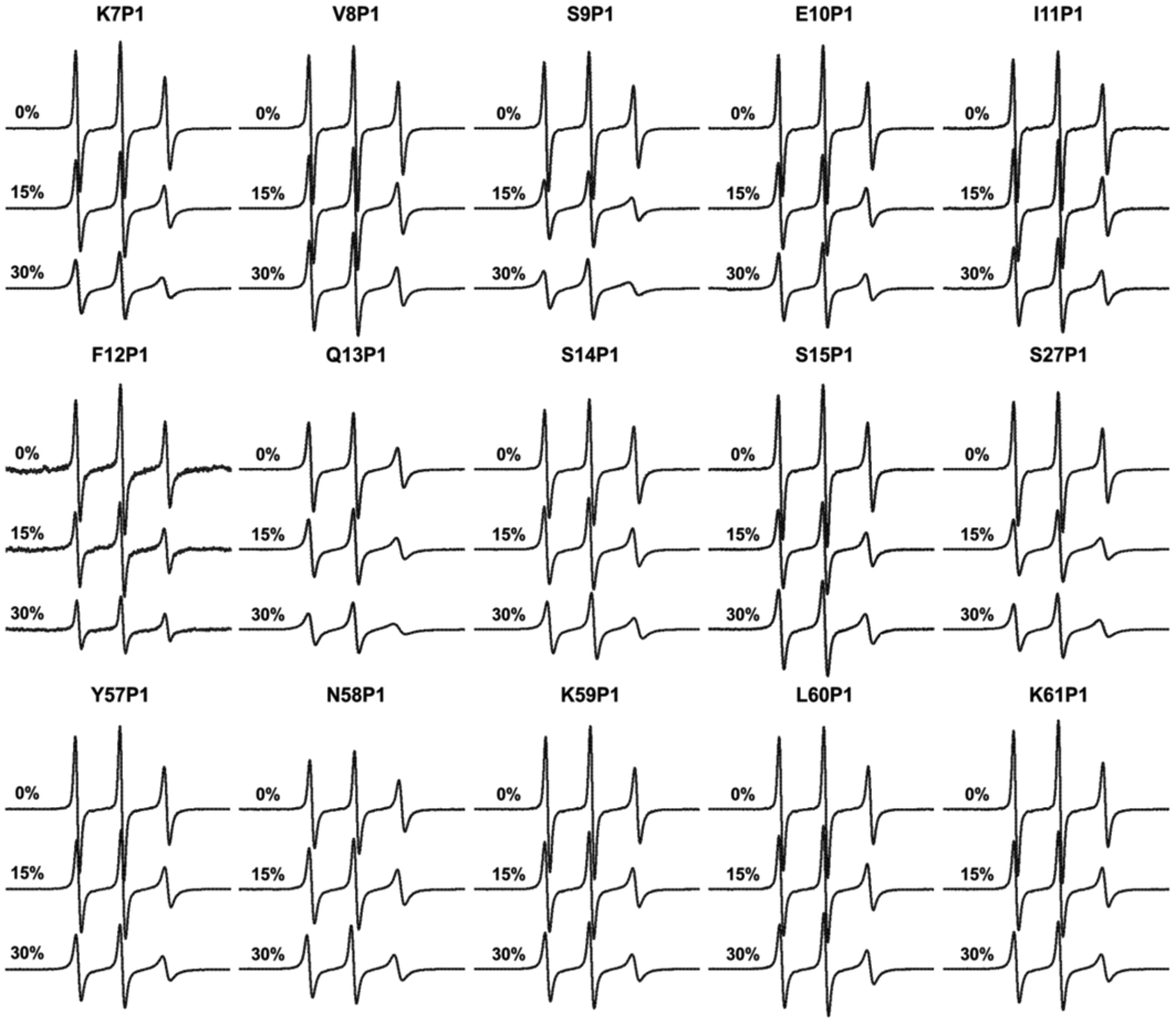
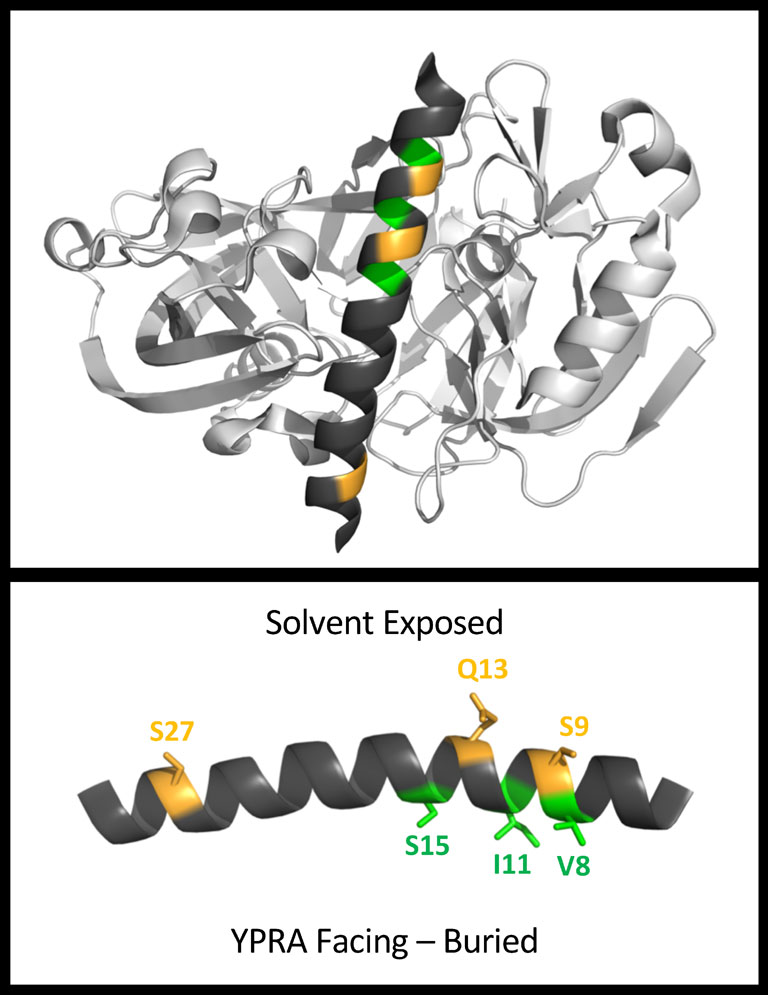
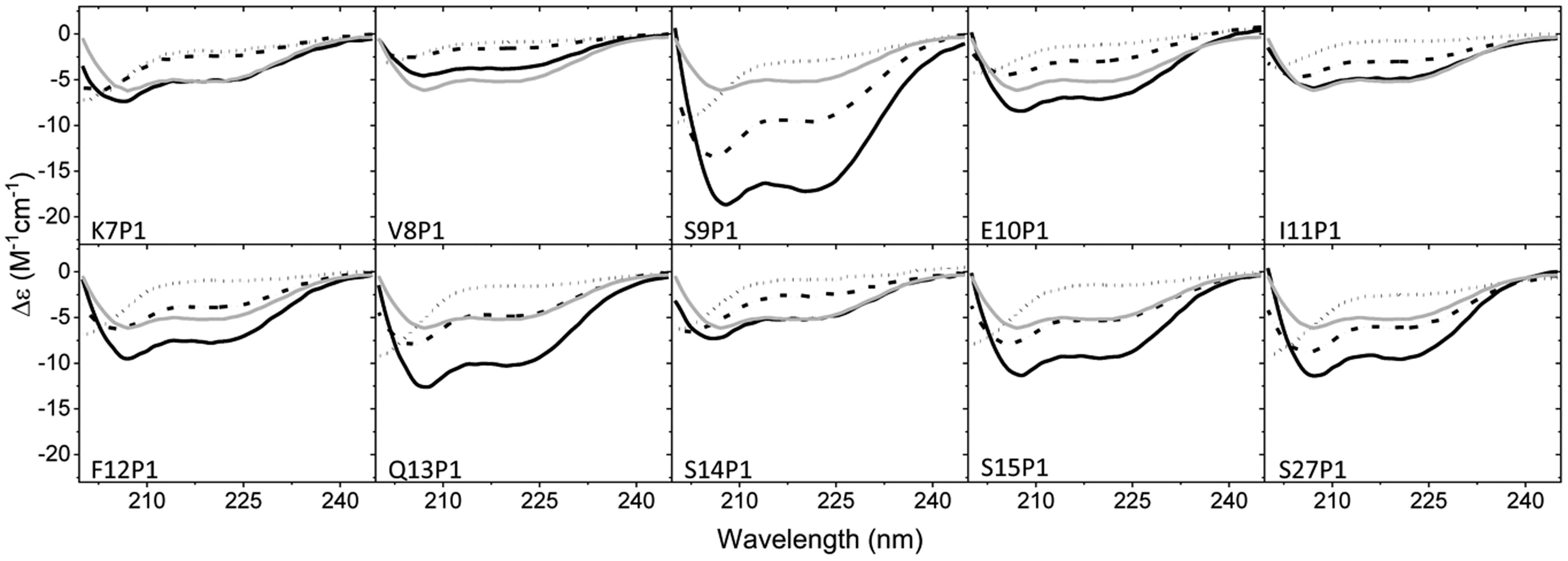
It is well known that the labeling of a naturally occurring or substituted cysteine may impact the native function of a protein. To understand if spin-label and cysteine substitution within IA3 impacted folding or folding propensity, cysteine scanning was performed across the N- and C-termini of IA3. Sites K7, V8, S9, E10, I11, F12, Q13, S14, S15, and S27 were chosen within the N-terminus and span two helical turns containing both solvent exposed and buried residues in the α-helix when bound to YPRA. Sites Y57, N58, K59, L60, and K61, were selected in the C-terminus (Figure 1).
CW X-band EPR spectra were collected for the fifteen IAP spin labeled-IA3 variants (referred to within as P1-IA3) as a function of TFE concentration that ranged from 0-40% (v/v) TFE. Figure 3 shows representative CW-EPR spectra for 0%, 15%, and 30% (v/v) TFE for each P1-IA3 variant. Spectra are plotted with normalized double integral area to allow for easy visualization of changes in mobility. As mobility (defined as both the rate of motion and order of motion) decreases, the line shape broadens. As a result, when plotted with normalized area, the intensity appears to be less. A decrease in mobility upon increasing TFE percentage is observed for nearly all sites and indicates a conformational change upon increasing TFE concentration (earlier work has ruled out the impact of increased solution viscosity) [17]. Inspection of the line shapes shows that the change in mobility differs among these 15 P1-IA3 variants, indicating that some spin-labeled cysteine substitutions affect the conformation of each state, altering the TFE-induced helical propensity of IA3.
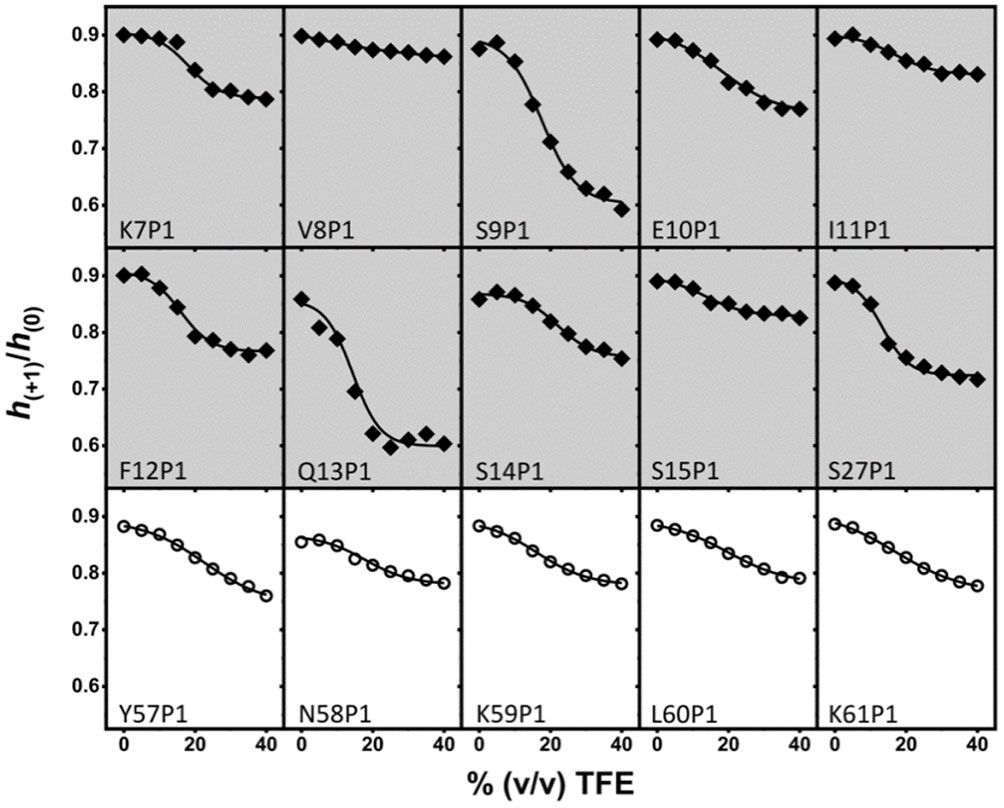
A more quantitative way to analyze the TFE-induced conformational changes for each variant is to plot h(+1)/h(0) values as a function of TFE % (Figure 4). For isotropic motion, the h(+1)/h(0) value is expected to be 1. As the mobility decreases as the protein becomes helical, lower values of h(+1)/h(0) are expected. In the unfolded state (absence of TFE), all P1-IA3 variants have similar CW-EPR spectra indicative of similar high nitroxide mobility (indicated by values of h(+1)/h(0) ∼ 0.9). As a function of TFE concentration, the shape of each h(+1)/h(0) plot can be well fit by Eq 1, indicative of a two-state transition.
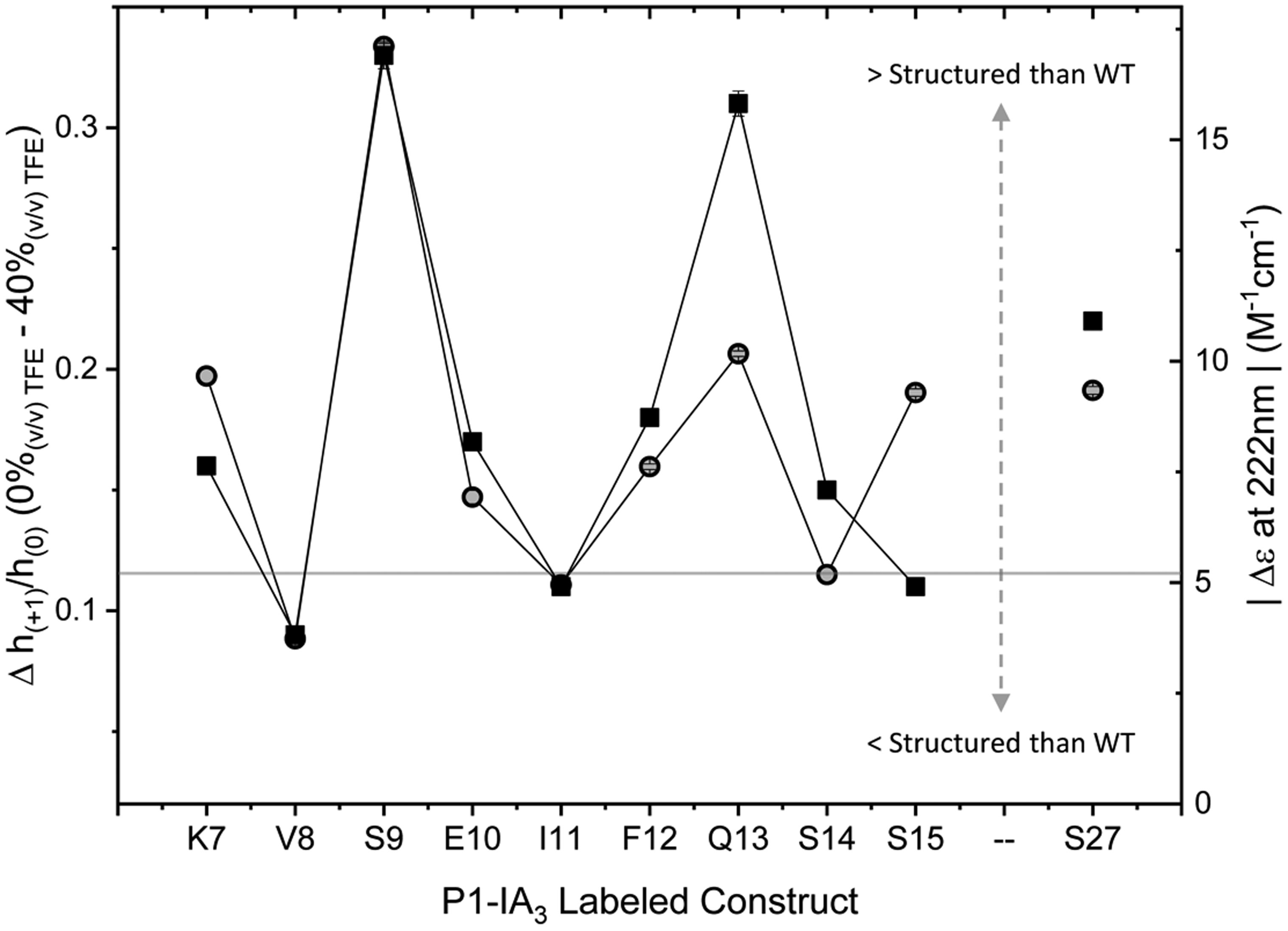
Several conclusions can be drawn from the data in Figure 4. Firstly, the sigmoidal behavior of the h(+1)/h(0) parameter for N-terminal P1-IA3 variants (gray shade, solid diamonds) varies both in sharpness and extent of transition, which is defined by the limiting h(+1)/h(0) value. In contrast C-terminal P1-IA3 variants (no shade, open circles) exhibit similar behavior, both in the sharpness and extent of transition. Secondly, there are site specific variations in the behavior of the h(+1)/h(0) parameter in the N-terminus that follow a helical trend that maps to the surface of IA3 in the YRPA bound site. Specifically, sites V8P1, I11P1, and S15P1 which are located on the concave buried face of the peptide when bound to YPRA, have small changes (<0.05 over the 0-40% (v/v) TFE range) in their h(+1)/h(0) values. In contrast, sites S9P1, Q13P1 and S27P1, which reside on the convex solvent exposed face when bound to YPRA, pose large changes in their h(+1)/h(0) values (>0.3 over the 0-40% TFE range). Figure 5 shows the location of these residues in the IA3: YPRA complex crystal structure. These results indicate a sensitivity of the N-terminal helicity to amino acid substitution.
To further explore these observations, CD spectroscopy was performed on each of the N-terminal P1-IA3 variants with 0%, 15%, and 30% (v/v) TFE. Data are shown in Figure 6, which also overlays results from WT IA3 (gray solid line) in 30% (v/v) TFE for comparison. For wild type IA3, CD data reveal a predominantly random coil conformation for 0% (v/v) TFE, whereas with 30% (v/v) TFE the spectra reflect a mostly helical conformation with features at 208 nm and 222 nm indicative of helix formation [37,38]. For all N-terminal P1-IA3 variants, CD data confirm that in the absence of TFE, all constructs adopt a random coil conformation and that the addition of TFE induces a helical conformation. As was observed with the CW-EPR data, the degree of the helical transition, as reflected in the values of Δε222nm in CD spectra, varies when compared to WT for the P1 variants. It can be seen that I11P1 and S14P1 possess CD spectra that very closely match that of WT (i.e., represent SL wild-type mimics). V8P1 is found to be less helical than WT, whereas all other variants have greater helicity than WT. To directly compare the SDSL CW-EPR characterized unstructured-to-structured transition within the N-terminus to the degree of α-helicity from CD spectroscopy, we plotted the values of Δh(+1)/h(0), or degree of transition (h(+1)/h(0) (40% (v/v) TFE) − h(+1)/h(0) (0% (v/v) TFE)) against the Δε222nm (30% (v/v) TFE) (Eq 2) values from CD spectra for each P1-IA3 variant (Figure 7). The Δε222nm value for WT IA3 is displayed in Figure 7 as a gray line to represent how the helical conformation of each variant compares to WT behavior. As can be seen, there is remarkable agreement in overall trend between these two parameters, confirming that the helical propensity of the N-terminal region in IA3 is particularly sensitive to amino acid substitution/spin-labeling. It is striking that CW-EPR line shape analysis readily reflects this sensitivity to amino acid substitution/modification and in most cases the incorporation of the spin-label is found to enhance the helicity of IA3.
3.2. Helical propensity at site V8 in IA3 is modulated by amino acid substitution and size
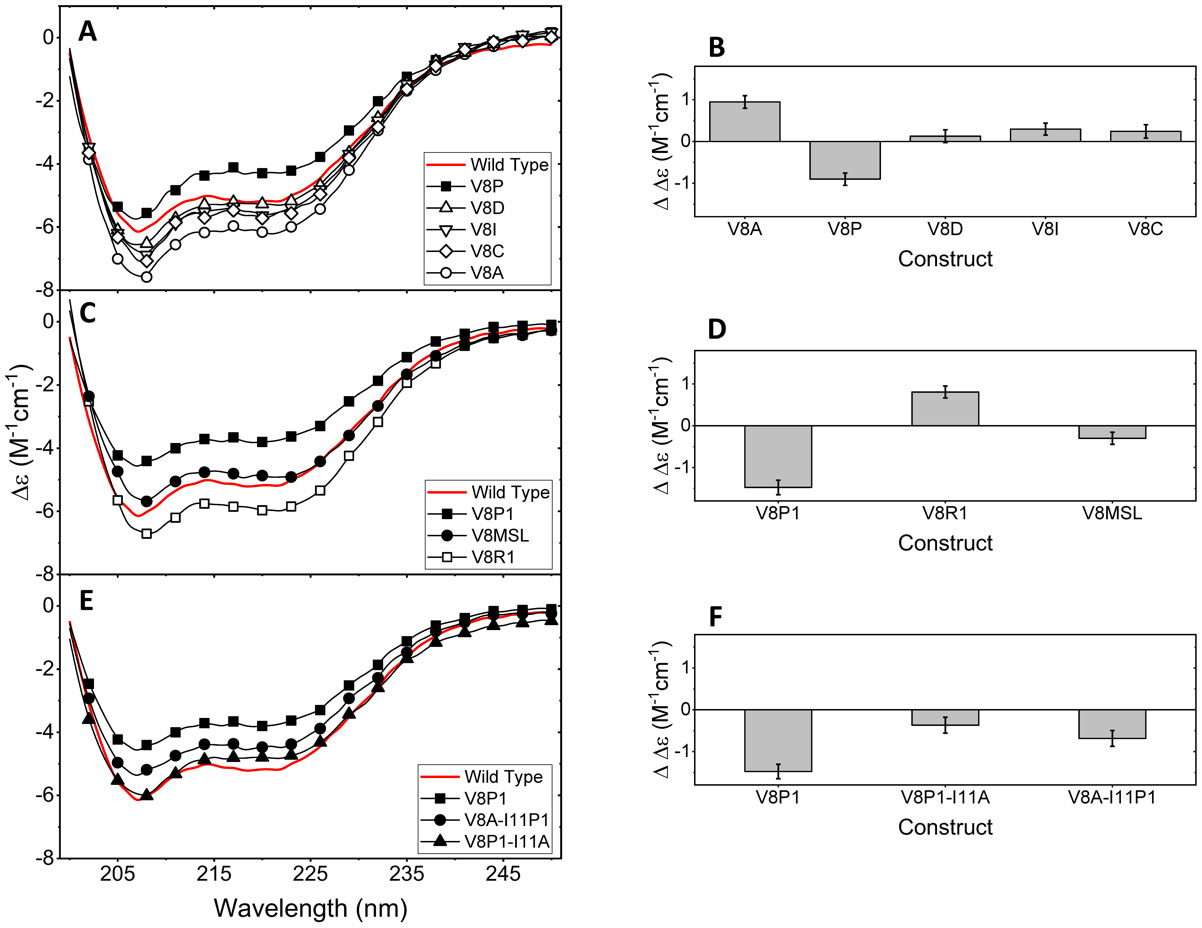
Because the P1 substitution at site V8 revealed less helical character than WT, we proceeded to generate a series of substitutions at this site to probe how amino acid size and type impacted helical propensity. The following constructs were chosen: V8A and V8I (smaller and larger than V; respectively), V8P (typical helical disrupter), V8D (charged), and V8C (our cysteine mutation without spin-label). CD spectroscopy was performed on each of the V8 variants with 0-40% or 0-35% (v/v) TFE (Figures S1 and S2, respectively). CD spectra of each construct in 30% (v/v) TFE are given in Figure 8A. It is found that TFE does induce a helical transition in each of these constructs. We assessed the impact of each substitution on helical content by calculating the difference in Δε222nm of the variant to WT. Figure 8B plots values of Δ(Δε222nm), showing that, as expected, the proline substitution at site 8 is less helical than WT. Also as expected, the alanine substitution induces the greatest increase in helical content, whereas other substitutions resulted in near WT behavior.
3.3. Choice of spin-label at site V8C alters helical behavior of IA3
The result that V8C contained WT helicity was surprising, which prompted us to examine if and how spin-label structure influenced helicity when incorporated at this site. CD spectroscopy was performed on the V8C spin-labeled variants from 0-40% or 0-30% (v/v) TFE (Figures S1 and S3, respectively). Interestingly, we found that the P1 substitution disrupted helicity compared to WT, MSL-CYS behaved like WT, and R1 substitution slightly increased helical content (Figure 8C, D). Perhaps the structure of the P1 label, which contains a pseudo-peptide bond interferes with TFE induced folding. MSL is a bulkier label than P1, and R1 is oftentimes considered a compact label because of potential sulfur interactions with the protein backbone [39].
Nevertheless, results appear to indicate a dependency of structural bulkiness for disruption or enhancement of helical propensity. Indeed, the structure of IA3 bound to YPRA shows a slight concave bend on the buried interface, making substitution to larger residues disrupt helical behavior and conversely, a smaller residue would enhance helicity. To test this idea, we made two additional constructs, V8P1-I11A and V8A-I11P1, which would place the smaller alanine residue next to the P1 spin-label. CD spectroscopy was performed on each additional construct from 0-40% or 0-35% (v/v) TFE (Figures S1 and S2, respectively). V8P1-I11A shows nearly WT helical behavior and although V8A-I11P1 is less helical than WT, it is more helical than V8P1 (Figure 8E, F).
4. Conclusions
It was determined through SDSL CW-EPR that the extent of helical order within the N-terminal region of IA3 is easily perturbed by amino acid substitution and IAP labeling. The C-terminal region did not have similar susceptibility, where changes in labeled amino acid substitution did not reveal drastic changes in the unstructured-to-structured transition, and as we showed previously, retained WT behavior [17]. CD results confirmed that the helical order within the N-terminus varied due to the location of the altered residue in relation to the buried or solvent-exposed, or the concave or convex face of the protein, respectively. The concave face of IA3, is negatively affected by cysteine mutation and labeling, whereas the convex surface increases in helical order. It is proposed that the change in helical propensity on either side of the protein is due to spatial availability when incorporating a cysteine residue and nitroxide probe. Residue V8, located on the concave side of the N-terminal region showed the greatest negative perturbation due to cysteine substitution, and spin labeling. Mutations to the V8 residue, including substitutions in residue, charge, and size did not drastically affect the helical propensity, but rather the addition of the IAP nitroxide probe had the greatest effect on helical formation.
These experiments demonstrate the care that must be taken when spin-labeling IDPs. Proper checks-and-balances are needed to ensure that a labeled site retains WT helical propensity (in addition to any other functional assays). Overall, the results identify key sites for spin-label incorporation that mimic WT helical tendencies that can be used in future studies of IA3 conformational sampling studies.
Acknowledgements
This work was supported by NSF MCB 1329467 & MCB 1715384 and NIH 1S10-RR031603-01 to GEF. The authors would like to thank Stephen J. Hagen and Robert McKenna for access to the Aviv CD spectrometer, and Christian Altenbach for Labview software to analyze the EPR data.
Conflict of interest
All authors declare no conflict of interest in this paper.









 DownLoad:
DownLoad: