| 1.
|
Xia Wang, Yuming Chen, Shengqiang Liu,
Global dynamics of a vector-borne disease model with infection ages and general incidence rates,
2018,
37,
0101-8205,
4055,
10.1007/s40314-017-0560-8
|
|
| 2.
|
Cruz Vargas-De-León,
Global stability properties of age-dependent epidemic models with varying rates of recurrence,
2016,
39,
01704214,
2057,
10.1002/mma.3621
|
|
| 3.
|
Edwin Setiawan Nugraha, Janson Naiborhu, Nuning Nuraini,
2017,
1825,
0094-243X,
020015,
10.1063/1.4978984
|
|
| 4.
|
Gang Huang, Chenguang Nie, Yueping Dong,
Global stability for an SEI model of infectious diseases with immigration and age structure in susceptibility,
2019,
12,
1793-5245,
1950042,
10.1142/S1793524519500426
|
|
| 5.
|
Xia Wang, Ying Zhang, Xinyu Song,
An age-structured epidemic model with waning immunity and general nonlinear incidence rate,
2018,
11,
1793-5245,
1850069,
10.1142/S1793524518500699
|
|
| 6.
|
Rui Xu, Zhili Wang, Fengqin Zhang,
Global stability and Hopf bifurcations of an SEIR epidemiological model with logistic growth and time delay,
2015,
269,
00963003,
332,
10.1016/j.amc.2015.07.084
|
|
| 7.
|
Danga Duplex Elvis Houpa, Tagne Eric Miamdjo, Tchaptchie Yannick Kouakep,
A General Model for Hepatitis B Disease with Age-Dependent Susceptibility and Transmission Probabilities,
2014,
05,
2152-7385,
707,
10.4236/am.2014.54068
|
|
| 8.
|
Lili Liu, Xianning Liu,
Mathematical Analysis for an Age-Structured Heroin Epidemic Model,
2019,
164,
0167-8019,
193,
10.1007/s10440-018-00234-0
|
|
| 9.
|
Carles Barril, Andrei Korobeinikov,
2014,
Chapter 18,
978-3-319-08137-3,
99,
10.1007/978-3-319-08138-0_18
|
|
| 10.
|
Jinliang Wang, Ran Zhang, Toshikazu Kuniya,
Global dynamics for a class of age-infection HIV models with nonlinear infection rate,
2015,
432,
0022247X,
289,
10.1016/j.jmaa.2015.06.040
|
|
| 11.
|
Suxia Zhang, Hongbin Guo,
Global analysis of age-structured multi-stage epidemic models for infectious diseases,
2018,
337,
00963003,
214,
10.1016/j.amc.2018.05.020
|
|
| 12.
|
Kosaku Kitagawa, Toshikazu Kuniya, Shinji Nakaoka, Yusuke Asai, Koichi Watashi, Shingo Iwami,
Mathematical Analysis of a Transformed ODE from a PDE Multiscale Model of Hepatitis C Virus Infection,
2019,
81,
0092-8240,
1427,
10.1007/s11538-018-00564-y
|
|
| 13.
|
Chuncheng Wang, Dejun Fan, Ling Xia, Xiaoyu Yi,
Global stability for a multi-group SVIR model with age of vaccination,
2018,
11,
1793-5245,
1850068,
10.1142/S1793524518500687
|
|
| 14.
|
Toshikazu Kuniya, Jinliang Wang, Hisashi Inaba,
A multi-group SIR epidemic model with age structure,
2016,
21,
1531-3492,
3515,
10.3934/dcdsb.2016109
|
|
| 15.
|
Xia Wang, Yijun Lou, Xinyu Song,
Age-Structured Within-Host HIV Dynamics with Multiple Target Cells,
2017,
138,
00222526,
43,
10.1111/sapm.12135
|
|
| 16.
|
Jinliang Wang, Min Guo, Shengqiang Liu,
SVIR epidemic model with age structure in susceptibility, vaccination effects and relapse,
2017,
82,
0272-4960,
945,
10.1093/imamat/hxx020
|
|
| 17.
|
Cruz Vargas-De-León, Lourdes Esteva, Andrei Korobeinikov,
Age-dependency in host-vector models: The global analysis,
2014,
243,
00963003,
969,
10.1016/j.amc.2014.06.042
|
|
| 18.
|
Xia Wang, Yuming Chen, Xinyu Song,
Global dynamics of a cholera model with age structures and multiple transmission modes,
2019,
12,
1793-5245,
1950051,
10.1142/S1793524519500517
|
|
| 19.
|
Leonid Shaikhet, Andrei Korobeinikov,
Stability of a stochastic model for HIV-1 dynamics within a host,
2016,
95,
0003-6811,
1228,
10.1080/00036811.2015.1058363
|
|
| 20.
|
Xia Wang, Yuming Chen, Shengqiang Liu,
Dynamics of an age‐structured host‐vector model for malaria transmission,
2018,
41,
0170-4214,
1966,
10.1002/mma.4723
|
|
| 21.
|
Raúl Peralta, Cruz Vargas-De-León, Pedro Miramontes,
Global Stability Results in a SVIR Epidemic Model with Immunity Loss Rate Depending on the Vaccine-Age,
2015,
2015,
1085-3375,
1,
10.1155/2015/341854
|
|
| 22.
|
Shengfu Wang, Lin-Fei Nie,
Global Dynamics for a Vector-Borne Disease Model with Class-Age-Dependent Vaccination, Latency and General Incidence Rate,
2020,
19,
1575-5460,
10.1007/s12346-020-00407-z
|
|
| 23.
|
Jinliang Wang, Xianning Liu, Toshikazu Kuniya, Jingmei Pang,
Global stability for multi-group SIR and SEIR epidemic models with age-dependent susceptibility,
2017,
22,
1553-524X,
2795,
10.3934/dcdsb.2017151
|
|
| 24.
|
Toshikazu Kuniya,
Existence of a nontrivial periodic solution in an age-structured SIR epidemic model with time periodic coefficients,
2014,
27,
08939659,
15,
10.1016/j.aml.2013.08.008
|
|
| 25.
|
Toshikazu Kuniya,
Global Behavior of a Multi-Group SIR Epidemic Model with Age Structure and an Application to the Chlamydia Epidemic in Japan,
2019,
79,
0036-1399,
321,
10.1137/18M1205947
|
|
| 26.
|
Hisashi Inaba,
2017,
Chapter 6,
978-981-10-0187-1,
287,
10.1007/978-981-10-0188-8_6
|
|
| 27.
|
Toshikazu Kuniya,
Hopf bifurcation in an age-structured SIR epidemic model,
2019,
92,
08939659,
22,
10.1016/j.aml.2018.12.010
|
|
| 28.
|
Xia Wang, Yuming Chen, Maia Martcheva, Libin Rong,
Asymptotic analysis of a vector-borne disease model with the age of infection,
2020,
14,
1751-3758,
332,
10.1080/17513758.2020.1745912
|
|
| 29.
|
Faïçal Ndaïrou, Delfim F. M. Torres,
Mathematical Analysis of a Fractional COVID-19 Model Applied to Wuhan, Spain and Portugal,
2021,
10,
2075-1680,
135,
10.3390/axioms10030135
|
|
| 30.
|
Suxia Zhang, Yanna Liu, Hui Cao,
Bifurcation analysis of an age‐structured epidemic model with two staged‐progressions,
2021,
44,
0170-4214,
11482,
10.1002/mma.7508
|
|
| 31.
|
Manoj Kumar, Syed Abbas,
Age-Structured SIR Model for the Spread of Infectious Diseases Through Indirect Contacts,
2022,
19,
1660-5446,
10.1007/s00009-021-01925-z
|
|
| 32.
|
Jiaji Pan, Zhongxiang Chen, Yixuan He, Tongliang Liu, Xi Cheng, Jun Xiao, Hao Feng,
Why Controlling the Asymptomatic Infection Is Important: A Modelling Study with Stability and Sensitivity Analysis,
2022,
6,
2504-3110,
197,
10.3390/fractalfract6040197
|
|
| 33.
|
Ruyan Su, Wensheng Yang,
Global stability of a diffusive HCV infections epidemic model with nonlinear incidence,
2022,
68,
1598-5865,
2685,
10.1007/s12190-021-01637-3
|
|
| 34.
|
Xin Jiang,
Global Dynamics for an Age-Structured Cholera Infection Model with General Infection Rates,
2021,
9,
2227-7390,
2993,
10.3390/math9232993
|
|
| 35.
|
Chunrong Xue, Xin Ning,
Study on the Global Stability for a Generalized SEIR Epidemic Model,
2022,
2022,
1687-5273,
1,
10.1155/2022/8215214
|
|
| 36.
|
Xiaogang Liu, Yuming Chen, Xiaomin Li, Jianquan Li,
Global stability of latency-age/stage-structured epidemic models with differential infectivity,
2023,
86,
0303-6812,
10.1007/s00285-023-01918-4
|
|
| 37.
|
Yi Chen, Lianwen Wang, Jinhui Zhang,
Global asymptotic stability of an age-structured tuberculosis model: An analytical method to determine kernel coefficients in Lyapunov functional,
2024,
181,
09600779,
114649,
10.1016/j.chaos.2024.114649
|
|
| 38.
|
Abderrazak NABTi,
Dynamical analysis of an age-structured SEIR model with relapse,
2024,
75,
0044-2275,
10.1007/s00033-024-02227-6
|
|
| 39.
|
Qian Jiang, Zhijun Liu, Lianwen Wang,
Global threshold dynamics of an HIV/AIDS model with multi-class-age structure,
2024,
0,
1531-3492,
0,
10.3934/dcdsb.2024068
|
|
| 40.
|
Kailong Zhao, Zhijun Liu, Caihong Guo, Huili Xiang, Lili Liu, Lianwen Wang,
Modeling and analysis of transmission dynamics of tuberculosis with preventive treatment and vaccination strategies in China,
2025,
138,
0307904X,
115779,
10.1016/j.apm.2024.115779
|
|
| 41.
|
Abderrazak Nabti, Salih Djilali, Malek Belghit,
Dynamics of a Double Age-Structured SEIRI Epidemic Model,
2025,
196,
0167-8019,
10.1007/s10440-025-00723-z
|
|










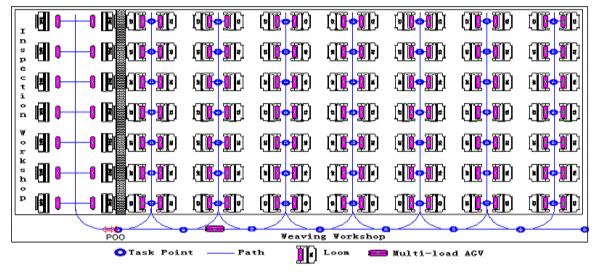
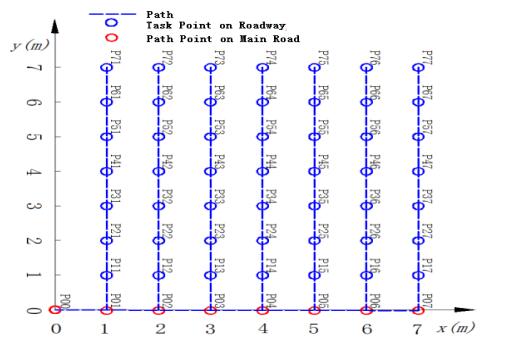
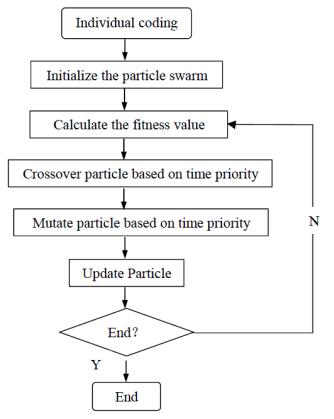
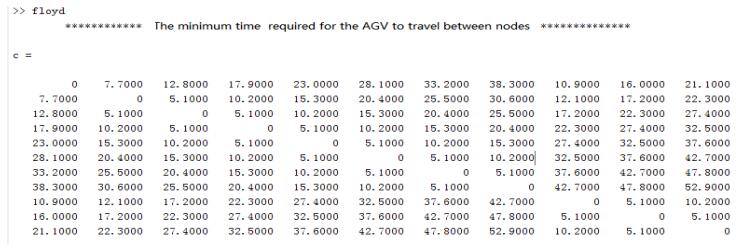

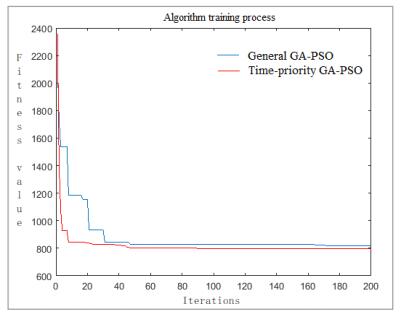
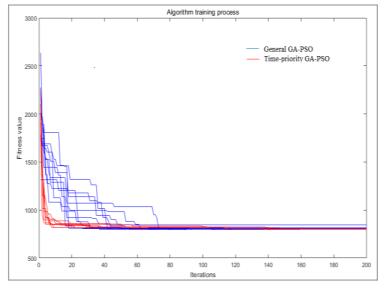
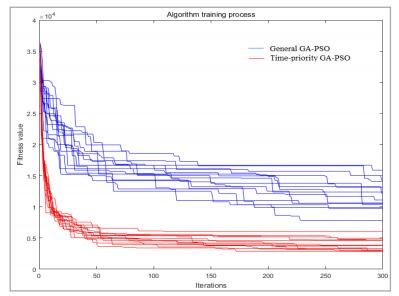
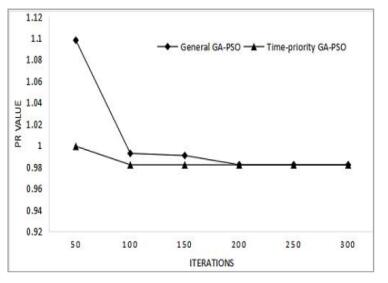


 DownLoad:
DownLoad: