1. Introduction
MicroRNAs (miRNAs) are distinctive regulatory member of the small RNAs that regulate gene silencing at post-transcriptional level. Gene silencing by miRNAs is an important, advance and exciting area of present regulatory RNA research. They are endogenous, non-coding in nature and about 18 to 26 nucleotides (nt) in size. They are the negative regulator at post-transcriptional stage of gene regulation [1]. Initially, a self-folded stable hair-pin/stem-loop secondary structure termed as precursor-miRNAs (pre-miRNAs) is generate from long single strand RNA known as primary miRNA (pri-miRNA). Later the pre-miRNAs give rise a small sized (18–26nt) functional RNA known as mature miRNA. This mature miRNA is integrate into argonaute protein and advanced into the RNA induced silencing complex (RISC) [2,3]. The RISC complex having mature miRNA triggers post-transcriptional gene suppression of the messenger RNA (mRNA) either by inhibiting protein encoding or by activating mRNA degradation. This inhibition and degradation capability of the miRNA depends on the scale of complementarity between miRNA and its targeted mRNA [4]. In case of partial pairing between miRNAs and its mRNA target causes its inhibition. While, the complete pairing of miRNAs with it mRNA target causes the mRNAs degradation [1,5]. They participate as gene regulator in almost each and every life activity, such as growth and development, foreign genes suppression, signal transduction, environmental stresses and as a defense against the attacking microbes in various living organisms [1,6,7,8,9]. Majority of the miRNAs show conserved behavior among various plant species. Many researchers, based on this conserved nature, have identified a huge number of miRNAs using comparative genomic approaches in a wide range of plant species, including cowpea [10], Brassicanapus
[11], Glycinemax [12], cotton species [13,14], Zeamays [15], tobacco [16], switch grass [17], Phaseolus [18], tomato [19], eggplant [20] and chilli [21]. These reports strongly suggest that comparative genomic strategies are valid, highly efficient, convenient, and economical-friendly methods to identify new miRNAs.
Cowpea (Vigna unguiculata L.) is an important leguminous crop of Asia, Africa, Southern Europe and USA [22]. It is a good food due to the presence of carbohydrate and high protein contents. This makes it not only essential diet to the human, but also serve as fodder to livestock. Cowpea is also significant to grow under low soil fertility, heat and drought. It is a key constituent of low-input farming systems for farmers. Cowpea also play vital role in the nitrogen fixation which is necessary for the enhancement of soil productiveness [22,23]. Very little reports and data are available about the miRNAs in this important plant. According to the latest version of miRNA registry database (Version Rfam 21.0, released June, 2014) [24], only few miRNAs are available for cowpea. This situation demands to focus and profile new miRNAs and their targets in cowpea that will act as preliminary data to manage and understand the cowpea at molecular level.
Consequently, a total of 46 new miRNAs belonging to 45 families in cowpea were identified. In this study, one miRNA gene was also found as pre-miRNA cluster (vun-mir4414). Furthermore, these newly identified miRNAs were also validated for their protein targets.
2. Materials and methods
2.1. Identification of raw sequences
A similar methodology [15] with a little modification as described by Barozai MYK, et al. [13] was applied to profile the potential miRNAs from cowpea expressed sequence tags (ESTs). As reference miRNAs, a total of 4739 known plant miRNA sequences, both precursors and matures, were downloaded from the microRNA registry database (Version Rfam 21.0 released June, 2014) [24], and subjected to basic local alignment search tool (BLAST) for alignment against publicly available 187487 ESTs of cowpea from the dbEST (database of EST), release 130101 at http://blast.ncbi.nlm.nih.gov/Blast.cgi, using BLASTn program [25].
2.2. Creation of single tone EST
The repeated ESTs from the same gene were eliminated and a single tone EST per miRNA was produced by using BLASTn program against the cowpea EST database with default parameters [25].
2.3. Elimination of coding sequences
The initial potential miRNA sequences of cowpea, predicted by the mature source miRNAs, were checked for protein coding. The FASTA format of initial potential sequences were subjected against protein database at NCBI using BLASTX with default parameter [26] and the protein coding sequences were removed.
2.4. Creation of hair-pen structures
The initial potential candidate cowpea miRNA sequences, confirming as non-protein coding nature, having 0–4 mismatches with the reference miRNAs and representing single tone gene were subjected to generate hair-pen or secondary structures. Publicly available Zuker folding algorithm http://www.bioinfo.rpi.edu/applications/mfold/rna/form1.cgi, known as MFOLD (version 3.6) [27] was used to predict the secondary structures. The MFOLD parameters were adjusted same as published by various researchers for the identification of miRNAs in various plant and animal species [7,8,28]. For physical scrutinizing, the hair-pen structures either showing the lowest free energy ≤−18 kcal mol−1 or less than or equal to the lowest free energy of the reference miRNAs were preferred. The Ambros et al. [29] threshold values were applied as reference to finalize the potential miRNAs in cowpea. The stem regions of the stem-loop structures were checked and confirmed for the mature sequences with either at least 16 or equal to the reference miRNAs base pairing involved in Watson-Crick or G/U base pairing between the mature miRNA and the opposite strand (miRNA*).
2.5. Convergence and phylogenetic analysis
The convergence and phylogenetic analysis was carried out for the one of conserved cowpea miRNA (vun-mir398). Simply, the vun-mir398, for its conserved behavior in different plant species was checked for convergence and phylogenetic investigation. The vun-mir398 alignment was created with Glycine max (gma), Nicotiana tabacum (nta) and Cucumis melo (cme) by the publicly accessible web logo: a sequence logo generator and ClustalW to produce cladogram tree using neighbor joining clustering method respectively. The results were saved.
2.6. Prediction of miRNAs targets
Dual schemes were used to predict the potential targets for cowpea miRNAs. In the first scheme, the newly identified cowpea miRNAs were subjected to psRNATarget (http://bioinfo3.noble.org/psRNATarget), with default parameters [30]. The cowpea miRNAs that not produced potential targets through psRNATarget, were subjected to the second scheme as described by Barozai [31]. Briefly, the cowpea mature miRNA sequences were subjected as queries through BLASTn program. The parameters were adjusted as, database: reference mRNA sequences (refseq_rnat); organism: Vigna unguiculata (taxid:4072) and Program Selection: highly similar sequences (megablast). The mRNA sequences showing ≥75% query coverage were selected and further subjected to RNA hybrid—a miRNA target prediction tool [32]. Only targets, confirming stringent seed site located at either positions 2–7 and/or 8–13 from the 5′ end of the miRNAs along with the supplementary site and having minimum free energy (MFE) ≤−20 kcal mol−1 were selected. For more stringency, these targets were subjected to the NTNU microRNA target prediction tool available at http://tare.medisin.ntnu.no/mirna_target/search#results, to confirm the RNA hybrid results. These predicted targets were further analyzed through Gene Ontology (GO) on AmiGO website.
3. Results and discussion
3.1. The new cowpea miRNAs
In order to identify and characterize the potential miRNAs in cowpea, a comparative genomic approach was applied using bioinformatics tools. This is in agreement with the previous reports [8,28,31] that the homology based search by applying comparative genomics is a valid and logical approach to find interesting findings in plants at genomic level. The current study resulted a total of 46 new conserved miRNAs from the analyses of 187487 cowpea ESTs using bioinformatics tools (Table 1). The 46 potential cowpea miRNAs belong to 45 families (vun-miR: 398,413,435,834,1512,1514,1525,1848,2095,2606,2609,2622,2630,2636,2657,2678,2950,3434,4351,4392,4408,4414 (cluster), 4992,4996,5012,5043,5215,5216,5219,5227,5241,5246,5255,5261,5280,5290,5298,5376,5561,5758,5770,6252,7696,8182,9748). The vun-miR4414 family is observed as cluster pre-miRNA. Available miRNAs literature revealed that all these 46 miRNAs are profiled for the first time in cowpea. In the light of the empirical formula for biogenesis and expression of the miRNAs suggested by Ambros et al. [29], these miRNAs are considered as a valid candidate after justifying the criteria B, C and D. According to Ambros et al. [29] only the criterion D is enough for homologous sequences to validate as potential miRNAs in other species. The present study is in agreement with the other research groups [21,33,34,35,36] where similarity based search by applying comparative genomics has produced novel and interesting findings in plants genomics.
Table 1. The newly identified conserved cowpea miRNAs characterization. Cowpea miRNAs were characterized in terms of precursor miRNA length (PL), minimum free energy (MFE), mature sequence (MS), number of mismatches (NM) (represented in bold red and enlarged font size), mature sequence length (ML), source EST (SE), mature sequence arm (MSA), GC content percentage (GC%), SL = Strand Location and organ of expression (OE).
| vun miRNAs |
Ref. miRNAs |
PL |
MFE |
MS |
NM |
ML |
SE # |
MSA |
GC% |
SL |
OE |
| vun-mir398 |
mtr-mir398a |
131 |
−32.24 |
TGTGTTCTCAGGTCGCCCCTG |
2 |
21 |
FF542932 |
5' |
61.90 |
+ |
leaves |
| vun-mir413 |
ath-mir413 |
353 |
−88.55 |
TTAGTTTCTCTTGTTCTGCTT |
2 |
21 |
FG940215 |
5' |
33.33 |
+ |
mixed |
| vun-mir435 |
osa-mir435 |
347 |
−124.38 |
TTATGAGGCTTTGGAGTTGA |
4 |
20 |
FG811172 |
3' |
40.00 |
+ |
mixed |
| vun-mir834 |
ath-mir834 |
135 |
−52.95 |
TGGTAGCAGTGGCGGTGGTGG |
3 |
21 |
FG822669 |
3' |
66.66 |
− |
mixed |
| vun-mir1512 |
gma-mir1512a |
46 |
−10.60 |
CCTTTAAGAATTTCA-TTA-- |
4 |
18 |
FG880488 |
3' |
22.22 |
− |
mixed |
| vun-mir1514 |
gma-mir1514 |
127 |
−31.70 |
TTCATTTCTAAAATAGGCATC |
2 |
21 |
FF388166 |
5' |
28.57 |
− |
root |
| vun-mir1525 |
gma-mir1525 |
78 |
−14.10 |
GGGGTTAAATATGTTTTTAGT |
3 |
21 |
FG845219 |
5' |
28.57 |
+ |
mixed |
| vun-mir1848 |
osa-mir1848 |
77 |
−32.20 |
CGCTCGCCGGCGCGCGCGTCCA |
2 |
22 |
FG920123 |
3' |
86.36 |
+ |
mixed |
| vun-mir2095 |
osa-mir2095 |
57 |
−17.20 |
CTTCCATTTATGACATGTTT |
3 |
20 |
FG838629 |
5' |
30.00 |
− |
mixed |
| vun-mir2606 |
mtr-mir2606a |
69 |
−13.00 |
TTGAAGTGCTTGGTTCTCACT |
4 |
21 |
FG931806 |
5' |
42.85 |
+ |
mixed |
| vun-mir2609 |
mtr-mir2609a |
70 |
−13.00 |
TTGAAGTGCTTGGTTCTCACT |
4 |
21 |
FG931806 |
5' |
42.85 |
+ |
mixed |
| vun-mir2622 |
mtr-mir2622 |
210 |
−36.85 |
CTTGTGTGCCATTGTGAGCTTA |
3 |
22 |
FG900047 |
3' |
42.85 |
− |
mixed |
| vun-mir2630 |
mtr-mir2630a |
114 |
−24.70 |
TGGTTTTGGTCTTTGGTTTTA |
3 |
21 |
FF391380 |
5' |
33.33 |
+ |
root |
| vun-mir2636 |
mtr-mit2636 |
191 |
−29.40 |
GGATGTTAGTGTGCTGAATAT |
4 |
21 |
FG814033 |
5' |
38.09 |
− |
mixed |
| vun-mir2657 |
mtr-mir2657 |
156 |
−35.38 |
TTTTATTGTATTGATTTTGTTG |
4 |
22 |
FG926034 |
5' |
18.18 |
− |
mixed |
| vun-mir2678 |
mtr-mir2678 |
136 |
−39.32 |
TAAAGTTGTTGCGCGTGTC |
3 |
19 |
FF389500 |
3' |
47.36 |
− |
root |
| vun-mir2950 |
mes-mir2950 |
347 |
−83.20 |
TTCCATCTCTTGCAGACTGAA |
2 |
21 |
FG872933 |
5' |
42.85 |
− |
mixed |
| vun-mir3434 |
ath-mir3434 |
78 |
−17.40 |
TGAGAGTATCAGCCATGAGA |
2 |
20 |
FF392538 |
3' |
45.00 |
− |
root |
| vun-mir4351 |
gma-mir4351 |
148 |
−63.30 |
GTTAGGGTTCAGTTGGAGTTGG |
3 |
22 |
FG936300 |
3' |
50.00 |
− |
mixed |
| vun-mir4392 |
gma-mir4392 |
306 |
−80.53 |
TCTGTGAGAACGTGATTTCGGA |
3 |
22 |
FG857306 |
5' |
45.45 |
+ |
mixed |
| vun-mir4408 |
gma-mir4408 |
66 |
−20.70 |
CAACAACATTGGATGAGTATAGGA |
4 |
24 |
FG894682 |
3' |
37.5 |
+ |
mixed |
| vun-mir4414a vun-mir4414b |
mtr-mir4414a |
120 |
−42.20 |
AGCTGCTGACTCGTTGGTTCAATTCAACGATGCGGGAGCTGC |
0 1 |
21 21 |
FF537171 |
5' 3' |
52.38 57.14 |
+ + |
leaves |
| vun-mir4992 |
gma-mir4992 |
63 |
−21.20 |
CATCTAAGATGGTTTTTTTCAG |
4 |
22 |
FG926352 |
3' |
31.81 |
− |
mixed |
| vun-mir4996 |
gma-mir4996 |
163 |
−49.83 |
TAGAAGTTACCCATGTTCTC |
2 |
20 |
FF388735 |
3' |
40.00 |
− |
root |
| vun-mir5012 |
ath-mir5012 |
172 |
−43.44 |
TTTTGCTGCTCCGTGTGTTCC |
3 |
21 |
FG809429 |
3' |
52.38 |
+ |
mixed |
| vun-mir5043 |
gma-mir5043 |
125 |
−48.20 |
CTTCTCCTTCTCTGCACCACC |
3 |
21 |
FG810406 |
5' |
57.14 |
+ |
mixed |
| vun-mir5215 |
mtr-mir5215 |
181 |
−49.63 |
AGGAGGATGAGCTAGTTGATT |
3 |
21 |
FG939979 |
5' |
42.85 |
+ |
mixed |
| vun-mir5216 |
mtr-mir5216a |
124 |
−27.58 |
TTGGGAGTGAAAAACAGTGGAA |
2 |
22 |
FF399948 |
5' |
40.90 |
+ |
root |
| vun-mir5219 |
mtr-mir5219 |
107 |
−25.23 |
TCATGGAATCTCAGCTGCAGCAG |
1 |
23 |
FG850600 |
3' |
52.17 |
− |
mixed |
| vun-mir5227 |
mtr-mir5227 |
140 |
−18.04 |
AGAACAGAAGAAGATTGAAGAA |
3 |
22 |
FG915684 |
5' |
31.81 |
− |
mixed |
| vun-mir5241 |
mtr-mir5241a |
381 |
W#8722;119.80 |
TGGGTGAATGGAAGAGTGAAT |
3 |
21 |
FG904590 |
3' |
42.85 |
+ |
mixed |
| vun-mir5246 |
mtr-mir5246 |
68 |
−18.70 |
CACCAGAGAGCTTTGAAGGTT |
4 |
21 |
FG856911 |
3' |
47.61 |
+ |
mixed |
| vun-mir5255 |
mtr-mir5255 |
54 |
−10.40 |
TGACAGGATAGAGGACATGAC |
4 |
21 |
FG910302 |
5' |
47.61 |
− |
mixed |
| vun-mir5261 |
mtr-mir5261 |
311 |
−71.81 |
CGATTGTAGATGGCTTTGGCT |
3 |
21 |
FG838847 |
5' |
47.61 |
− |
mixed |
| vun-mir5280 |
mtr-mir5280 |
90 |
−20.22 |
TAAGTAGAAACGGGCCGAGATCGGGG |
4 |
26 |
FG915361 |
5' |
57.69 |
− |
mixed |
| vun-mir5290 |
mtr-mir5290 |
217 |
−30.24 |
AAAGTAGAGAGAGAAAGACACATA |
4 |
24 |
FG852502 |
5' |
33.33 |
+ |
mixed |
| vun-mir5298 |
mtr-mir5298a |
192 |
−36.58 |
TGGATTTCAAGATGAAGATGAAGAA |
4 |
25 |
FF402284 |
3' |
32.00 |
− |
root |
| vun-mir5376 |
gma-mir5376 |
341 |
−132.02 |
TGGAGATTGTGAAGAATTTGAGA |
3 |
23 |
FG872123 |
3' |
34.78 |
+ |
mixed |
| vun-mir5561 |
mtr-mir5561 |
346 |
−69.34 |
ATCTCTCTCTCTCTAAATGTA |
3 |
21 |
FF390124 |
5' |
33.33 |
− |
root |
| vun-mir5758 |
mtr-mir5758 |
91 |
−22.60 |
TAAGTTGGATCTATGTATTTG |
3 |
21 |
FG893334 |
3' |
28.57 |
+ |
mixed |
| vun-mir5770 |
gma-mir5770a |
98 |
−30.40 |
TTAGGACTATGGTTTGGATGA |
1 |
21 |
FG937135 |
3' |
38.09 |
− |
mixed |
| vun-mir6252 |
osa-mir6252 |
90 |
−20.90 |
ATGAGTTGTGTTGAGAGAGGGTT |
4 |
23 |
FG841373 |
3' |
43.47 |
− |
mixed |
| vun-mir7696 |
mtr-mir7696a |
173 |
−33.67 |
ACAAGTACTTA-AATTCAAAA |
4 |
20 |
FG864277 |
3' |
20.00 |
− |
mixed |
| vun-mir8182 |
ath-mir8182 |
170 |
−31.80 |
TTGTGTTGCGTTTGTGATGACT |
3 |
22 |
FG942892 |
5' |
40.90 |
− |
mixed |
| vun-mir9748 |
gma-mir9748 |
98 |
−32.45 |
GAAGGAAGTGTTGAGGGAGGAG |
3 |
22 |
FG921211 |
5' |
54.54 |
+ |
mixed |
3.2. Characterization of cowpea miRNAs
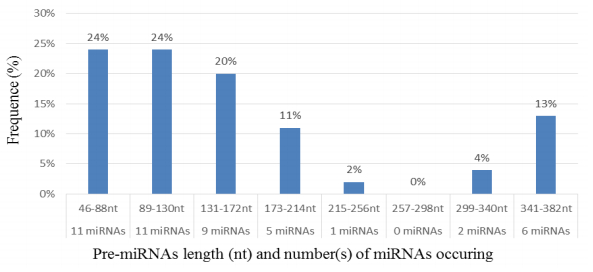
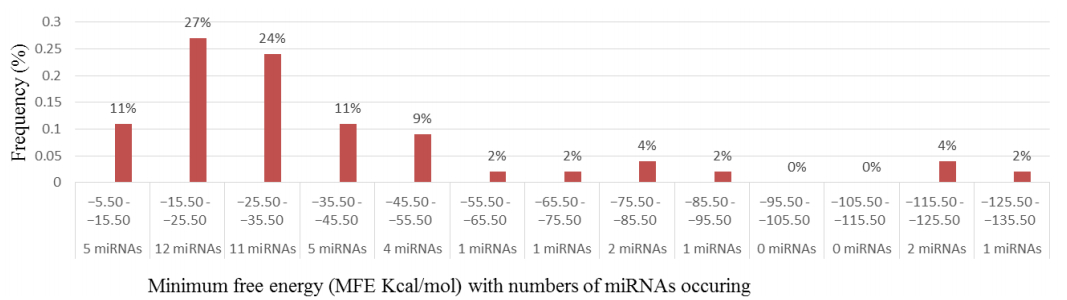
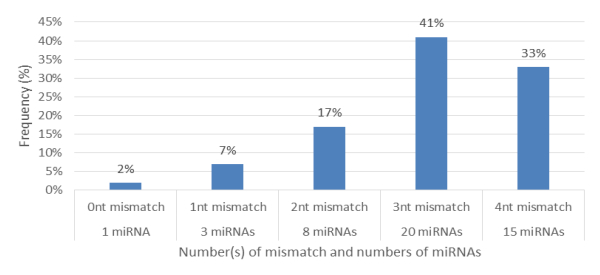
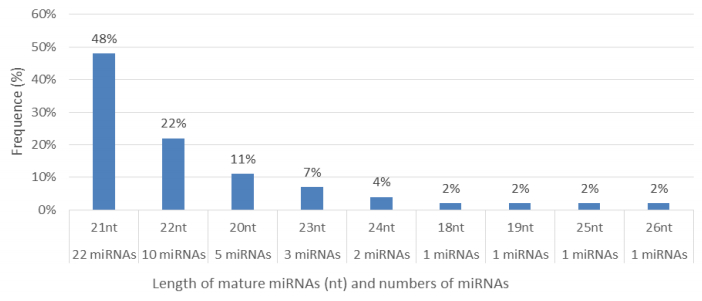
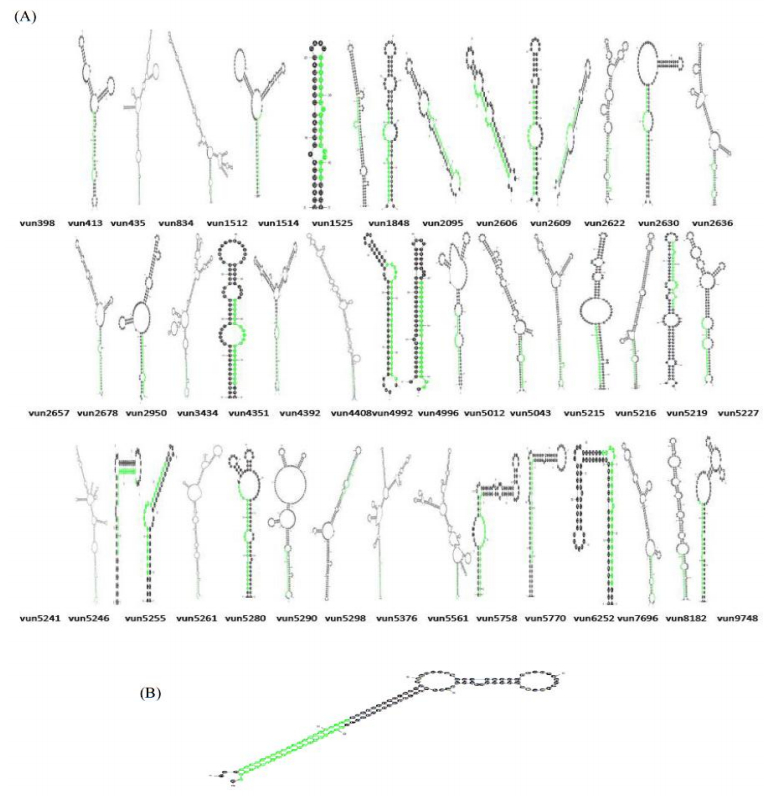
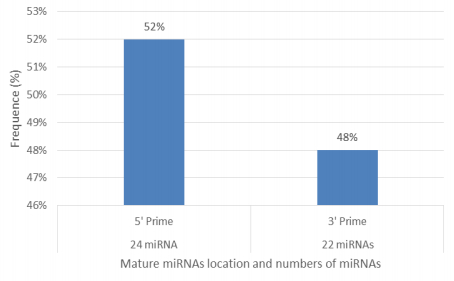
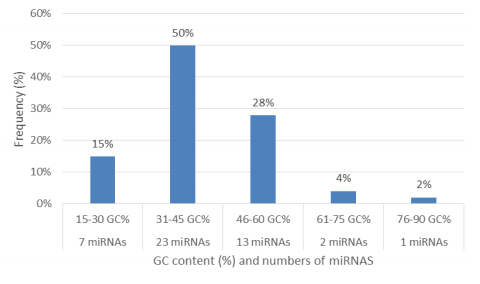
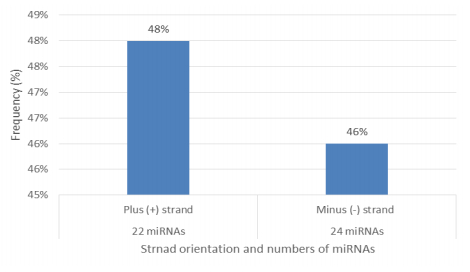
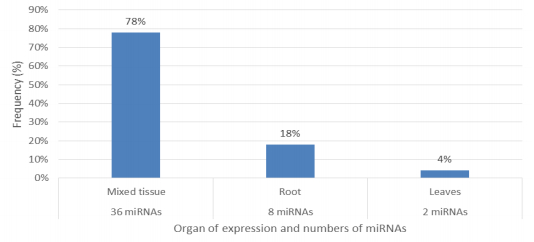
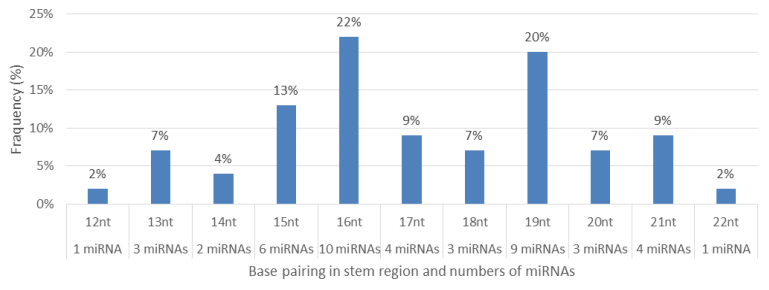
Characterization of newly identified candidate miRNAs is a set crucial step for their validation, as reported earlier [16,17,37]. The pre-miRNA length of the profiled cowpea miRNAs ranges from 46 to 381 nt with an average of 159 nt. The pre-miRNAs were further illustrated on the basis of their length (Figure 1). The minimum folding free energy (MFE) of pre-miRNA is a vital and valid term of characterization. The newly identified potential cowpea pre-miRNAs have shown MFEs in range from −10 to −132 kcal mol−1 with an average of −40 kcal mol−1 as shown in Figure 2. The numbers of mismatches of mature sequences with their reference sequences were observed in a range of 0–4 with an average of three mismatches as categorized in Figure 3. These values are matched with the previously reported values in different plants [21,37,38,39]. Mature miRNA sequences lengths were observed from 18 to 26 nt with an average of 21 nt as explained in Figure 4. These findings of mature sequences length are in agreement to prior published data in other plant species [16,17,18,36]. The 52% cowpea miRNAs sequences were found at 5′ arm, while 48% were at 3′ arm (Figure 5(A), 6). The GC content was found from 18 to 86% with an average of 42% as shown in Figure 7. Strand orientation is another important character for the generation of mature miRNAs transcripts. In this study, 24 mature miRNAs were found on minus strand while 22 were observed on plus strand of the transcripts (Figure 8). The same results for plus and minus strand orientation of mature miRNAs are in agreement with the earlier research work [40]. The identified conserved cowpea miRNAs were also characterized on the basis of their organ of expression as presented in Figure 9. These findings are similar with the earlier reports [37] and suggesting organ dependent expression pattern of miRNAs in cowpea. The miRNA organ specific expression would be utilized to manage the organogenesis in cowpea. The secondary self-folded stem-loop structures of the cowpea pre-miRNAs are observed with at least 17 nucleotides engaged in Watson-Crick or G/U base pairing between the mature miRNA and the opposite arms (miRNAs*) in the stem region (Figure 10). Except few where the reference miRNAs have also less base pairing and these precursors do not contain large internal loops or bulges. The mature miRNA sequences are observed in the double stranded stem region of the pre-miRNA secondary structures, as shown in Figure 5(A). Almost similar findings for various plant and animal species were reported by many researchers [16,17,20,37,41,42]. Furthermore, the newly identified cowpea miRNAs were also confirmed as non-protein coding nature by showing no significant similarity with known proteins. This validation strengthens the expressed nature for computationally identified miRNAs as non-coding RNAs. Similar results were observed in various research papers by many groups [16,43,44].
3.3. Cluster pre-miRNA gene in cowpea
In animals, a large number of miRNAs have been found in clusters and have been predicted to have similar expression profiles and functions [45]. The miRNA clusters have rarely been detected in plants. They were first reported by Jones-Rhoades and Bartel [46]. In this study, we also identified one pre-miRNA (mir4414) as cluster in cowpea having two mature miRNAs within Figure 5(B). On the basis of current available literature, this miRNA family (miR4414) was found for the first time in cowpea as a cluster.
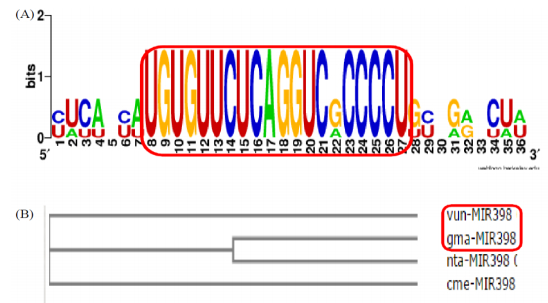
3.4. Convergence and phylogenetic studies
The newly characterized cowpea miRNA vun-mir398, due to its conserved nature, was investigated for convergence and phylogeny. Simply, the cowpea miRNA vun-mir398 alignment and cladogram tree, using neighbour joining clustering method, were created with Glycine max (gma), Nicotiana tabacum (nta) and Cucumis melo (cme) by the publicly available Web-Logo, a sequence logo generator [47] and ClustalW, a multiple sequence alignment tool [48]. The cowpea miRNA vun-mir398 is observed in convergence with Glycine max (gma), Nicotiana tabacum (nta) and Cucumis melo (cme) as shown in Figure 11(A). The Phylogenetic cladogram tree, as illustrated in Figure 11(B), clearly showed that on the basis of sharing a more recent common ancestor the cowpea miRNA is more closely related to Glycine max (gma) than Nicotiana tabacum (nta) and Cucumis melo (cme). Zeng et al. [49] have also reported conserved nature in Euphorbiaceous plants.
3.5. The potential cowpea miRNAs targeted genes
Profiling the potential cowpea miRNAs targeted genes is a vital step for validation of the computationally identified miRNAs. A total of 138 targeted genes were predicted for the 46 potential cowpea miRNAs. The detail description is mentioned in Table 2. Different cowpea miRNAs targeting same proteins and vice versa were predicted here. This showed that one miRNA target more than one mRNAs and a single mRNA targets by many miRNAs [50]. The profiled targeted genes are categories as, 27% (37 of 138) are engaged in metabolism, 26% (36 of 138) are playing role as transcription factors, 11% (15 of 138) are involved in transport activities, 11% (15 of 138) are shown with stress related, and the rest are engaged in hypothetical protein, signal transduction, growth and development, structural proteins and diseases related. Almost all of these targets were already reported as miRNA targets in other plants [7,16,17].
Table 2. Targets of cowpea miRNAs: As predicted by psRNAtarget and RNA hybrid in terms of miRNA family number, target acc., target description and function.
| miRNA |
Target Acc. |
Target Description |
Function |
Alignment |
| vun-mir398 |
TC8412 |
Predicted protein |
Hypothetical protein |
miRNA 21 GUCCCCGCUGGACUCUUGUGU 1
::::::::.:::: ::::::
Target 24 CAGGGACGAUCUGAUAACACA 44 |
| vun-mir413 |
TC18010 |
H/ACA ribonucleoprotein complex |
Transcription factor |
miRNA 21 UUCGUCUUGUUCUCUUUGAUU 1
:::::::::::::::::::::
Target 432 AAGCAGAACAAGAGAAACUAA 452 |
| vun-mir413 |
FF538223 |
Tropinone reductase |
Metabolism |
miRNA 21 UUCGUCUUGUUCUCUUUGAUU 1
.:::::::.::.:.::::::
Target 321 GAGCAGAAUAAUGGGAACUAA 341 |
| vun-mir413 |
TC16544 |
Valyl-tRNA synthetase |
Metabolism |
miRNA 21 UUCGUCUUGUUCUCUUUGAUU 1
:.::::::::::.:::. :::
Target 1013 AGGCAGAACAAGGGAAGAUAA 1033 |
| vun-mir413 |
TC9044 |
Uroporphyrinogen decarboxylase |
Metabolism |
miRNA 21 UUCGUCUUGUUCUCUUUGAUU 1
.:: :::: :::::::.::.:
Target 59 GAGAAGAAGAAGAGAAGCUGA 79 |
| vun-mir435 |
TC9534 |
Chromosome chr12 scaffold_238, |
Hypothetical protein |
miRNA 20 AGUUGAGGUUUCGGAGUAUU 1
:::::::::: :..::::.:
Target 242 UCAACUCCAAUGUUUCAUGA 261 |
| vun-mir435 |
FF387447 |
Chromosome chr9 scaffold_7, |
Hypothetical protein |
miRNA 20 AGUUGAGGUUUCGGAGUAUU 1
::::.:.:::.::::: :::
Target 386 UCAAUUUCAAGGCCUCCUAA 405 |
| vun-mir435 |
TC16349 |
Ripening related protein |
Growth and development |
miRNA 20 AGUUGAGGUUUCGGAGUAUU 1
:.::::::::: :.:.::.:
Target 523 UUAACUCCAAAACUUUAUGA 542 |
| vun-mir435 |
FG810938 |
Protein kinase |
Signal transduction |
miRNA 20 AGUUGAGGUUUCGGAGUAUU 1
::: :::::: :::::.::.
Target 474 UCACCUCCAAUGCCUCGUAG 493 |
| vun-mir834 |
TC4272 |
SCOF-1 |
Transcription factor |
miRNA 21 GGUGGUGGCGGUGACGAUGGU 1
:::::.::::::: :.:::::
Target 281 CCACCGCCGCCACCGUUACCA 301 |
| vun-mir834 |
TC8566 |
Cytochrome P450 monooxygenase CYP83E9 |
Metabolism |
miRNA 20 GUGGUGGCGGUGACGAUGGU 1
::::: : ::::::::::::
Target 465 CACCAACACCACUGCUACCA 484 |
| vun-mir834 |
TC7191 |
DnaJ-like protein |
Stress related |
miRNA 21 GGUGGUGGCGGUGACGAUGGU 1
::.::::::::::::: :::.
Target 173 CCGCCACCGCCACUGCAACCG 193 |
| vun-mir834 |
FG876294 |
Zinc finger-like protein |
Transcription factor |
miRNA 21 GGUGGUGGCGGUGACGAUGGU 1
::::::::::::: :: ::::
Target 138 CCACCACCGCCACCGCCACCA 158 |
| vun-mir834 |
TC4023 |
GroEL-like chaperone, ATPase |
Stress related |
miRNA 21 GGUGGUGGCGGUGACGAUGGU 1
:: ::.:::::.:::::.:::
Target 78 CCUCCGCCGCCGCUGCUGCCA 98 |
| vun-mir834 |
TC7031 |
Oxophytodienoate reductase |
Metabolism |
miRNA 21 GGUGGUGGCGGUGACGAUGGU 1
.::.::.:::::::::: :::
Target 19 UCAUCAUCGCCACUGCUUCCA 39 |
| vun-mir834 |
TC15421 |
MYB |
Transcription factor |
miRNA 20 GUGGUGGCGGUGACGAUGGU 1
..:.::.::.::::::::::
Target 955 UGCUACUGCUACUGCUACCA 974 |
| vun-mir834 |
GH622195 |
Ribosomal protein |
Structural protein |
miRNA 21 GGUGGUGGCGGUGACGAUGGU 1
:::::.:::::::: :::::
Target 110 CCACCGCCGCCACUUCUACCU 130 |
| vun-mir834 |
TC7768 |
Calcium-binding EF-hand) |
Transcription factor |
miRNA 21 GGUGGUGGCGGUGACGAUGGU 1
..::.::.:..::::.:::::
Target 470 UUACUACUGUUACUGUUACCA 490 |
| vun-mir1512 |
XM_013230906 |
Biomphalaria glabrata dual oxidase |
Metabolism |
target 5' C U 3'
AAUGAAAUUCUUAAAGG
UUACUUUAAGAAUUUCC
miRNA 3' A 5' |
| vun-mir1512 |
XM_006957329 |
Nucleoside triphosphate hydrolase protein |
Transcription factor |
target 5' U A 3'
UAAUGAAAUUCUUAAAG
AUUACUUUAAGAAUUUC
miRNA 3' C 5' |
| vun-mir1512 |
KC463855 |
NB-LRR receptor (RSG3-301) |
Transcription factor |
target 5' C CCC GG U 3'
AAUGA AA CUUGAAGG
UUACU UU GAAUUUCC
miRNA 3' A AA 5' |
| vun-mir1512 |
EF076031 |
Phosphatidic acid phosphatase alpha (PAPa) |
Metabolism |
target 5' A AAGGGG G A 3'
UGGUGAAA UC UAAAGG
AUUACUUU AG AUUUCC
miRNA 3' A A 5' |
| vun-mir1512 |
AF413209 |
Dolichos biflorus chloroplast ribulose-1, 5-bisphosphate carboxylase |
Metabolism |
target 5' C G 3'
UGGUGAAAU UAAAGG
AUUACUUUA AUUUCC
miRNA 3' AGA 5' |
| vun-mir1514 |
FF388166 |
NAC domain-containing protein 78 |
Transcription factor |
miRNA 21 CUACGGAUAAAAUCUUUACUU 1
:::::::::::::::::::::
Target 687 GAUGCCUAUUUUAGAAAUGAA 707 |
| vun-mir1514 |
FF540114 |
Phosphate transporter family protein |
transporter |
miRNA 20 UACGGAUAAAAUCUUUACUU 1
::::::.::::.::::::::
Target 461 AUGCCUGUUUUGGAAAUGAA 480 |
| vun-mir1514 |
TC15423 |
NAM-like protein |
Transcription factor |
miRNA 20 UACGGAUAAAAUCUUUACUU 1
::::::.::::.::::::::
Target 589 AUGCCUGUUUUGGAAAUGAA 608 |
| vun-mir1514 |
TC869 |
ATP-binding cassette sub-family f member 2 |
Transporter |
miRNA 21 CUACGGAUAAAAUCUUUACUU 1
:: ::.:::: ::::::::::
Target 733 GAGGCUUAUUCUAGAAAUGAA 753 |
| vun-mir1514 |
FG830151 |
Starch branching enzyme |
Metabolism |
miRNA 20 UACGGAUAAAAUCUUUACUU 1
::::: ::::::::.::::
Target 314 AUGCCAAUUUUAGAGAUGAU 333 |
| vun-mir1514 |
TC5197 |
Cytochrome c biogenesis protein-like |
Transporter |
miRNA 20 UACGGAUAAAAUCUUUACUU 1
::.::::::::::.::::
Target 749 AUAUCUAUUUUAGAGAUGAU 768 |
| vun-mir1525 |
TC17248 |
Salt-tolerance protein |
Stress related |
miRNA 21 UGAUUUUUGUAUAAAUUGGGG 1
::::::::::::::::::.:.
Target 306 ACUAAAAACAUAUUUAACUCU 326 |
| vun-mir1525 |
FG915097 |
UDP-N-acetylmuramoylalanine-D-glutamate ligase |
Transcription factor |
miRNA 21 UGAUUUUUGUAUAAAUUGGGG 1
::::::::.::::::.::::
Target 468 ACUAAAAAUAUAUUUGACCCA 488 |
| vun-mir1525 |
TC14268 |
Non-specific lipid-transfer protein |
transporter |
miRNA 20 GAUUUUUGUAUAAAUUGGGG 1
::.:::...:::::::::.:
Target 505 CUGAAAGUGUAUUUAACCUC 524 |
| vun-mir1525 |
TC18336 |
Heat shock protein |
Stress related |
miRNA 20 GAUUUUUGUAUAAAUUGGGG 1
.:.:..:.::::::.:::::
Target 166 UUGAGGAUAUAUUUGACCCC 185 |
| vun-mir1848 |
EG424245 |
Radical SAM domain protein |
Metabolism |
miRNA 20 CUGCGCGCGCGGCCGCUCGC 1
:: ::: :::: ::::::::
Target 110 GAAGCGAGCGCAGGCGAGCG 129 |
| vun-mir2095 |
FF402667 |
Resistance protein MG55 |
Stress related |
miRNA 20 UUUGUACAGUAUUUACCUUC 1
.: :.::::::::::::::
Target 592 GAUCGUGUCAUAAAUGGAAU 611 |
| vun-mir2095 |
TC2784 |
Vacuolar protein sorting-associated protein 26-like protein |
transporter |
miRNA 20 UUUGUACAGUAUUUACCUUC 1
:::::::::::.: :::::
Target 824 AAACAUGUCAUCGAAGGAAG 843 |
| vun-mir2606 |
TC406838 |
SNF1 related protein kinase |
Signal transduction |
miRNA 20 CACUCUUGGUUCGUGAAGUU 1
: :::::. :::::::::::
Target 1051 GAGAGAAUAAAGCACUUCAA 1070 |
| vun-mir2606 |
TC401737 |
ATP binding protein |
Transcription factor |
miRNA 20 CACUCUUGGUUCGUGAAGUU 1
:::::::.::::.:::::
Target 242 UCGAGAACCGAGCAUUUCAA 261 |
| vun-mir2606 |
NP305366 |
Hypothetical protein |
Hypothetical protein |
miRNA 21 UCACUCUUGGUUCGUGAAGUU 1
: ::::::.:.::.::::::.
Target 420 ACUGAGAAUCGAGUACUUCAG 440 |
| vun-mir2609 |
NP038997 |
Jasmonate induced protein |
Stress related |
miRNA 21 UCACUCUUGGUUCGUGAAGUU 1
: ::.:: :::::::::::::
Target 220 ACUGGGAUCCAAGCACUUCAA 240 |
| vun-mir2609 |
NP568563 |
SEC14-like protein |
Transcription factor |
miRNA 21 UCACUCUUGGUUCGUGAAGUU 1
:: :::::::::: ::::.::
Target 417 AGCGAGAACCAAGGACUUUAA 437 |
| vun-mir2609 |
TC406838 |
SNF1 related protein kinase-like protein |
Signal transduction |
miRNA 20 CACUCUUGGUUCGUGAAGUU 1
: :::::. :::::::::::
Target 1051 GAGAGAAUAAAGCACUUCAA 1070 |
| vun-mir2609 |
TC401737 |
ATP binding protein |
Signal transduction |
miRNA 20 CACUCUUGGUUCGUGAAGUU 1
:::::::.::::.:::::
Target 242 UCGAGAACCGAGCAUUUCAA 261 |
| vun-mir2622 |
TC9003 |
Alpha-expansin 2 |
Metabolism |
miRNA 22 AUUCGAGUGUUACCGUGUGUUC 1
::::::::::::::::::::::
Target 64 UAAGCUCACAAUGGCACACAAG 85 |
| vun-mir2630 |
TC15462 |
Auxin influx transport protein |
Transporter |
miRNA 20 UUUUGGUUUCUGGUUUUGGU 1
::::::::: :::::::::
Target 293 AAAACCAAAAACCAAAACCU 312 |
| vun-mir2630 |
FF390661 |
Serine/arginine repetitive matrix 1 |
Transcription factor |
miRNA 20 UUUUGGUUUCUGGUUUUGGU 1
::::: ::: ::::::::::
Target 349 AAAACAAAAAACCAAAACCA 368 |
| vun-mir2630 |
FG865319 |
Monosaccharid transport protein |
Transporter |
miRNA 20 UUUUGGUUUCUGGUUUUGGU 1
:::.:::::::.::.::::
Target 109 UAAAUCAAAGACUAAGACCA 128 |
| vun-mir2630 |
TC4441 |
Ras-related protein RAB8-1 |
Transcription factor |
miRNA 20 UUUUGGUUUCUGGUUUUGGU 1
::::.:::: ::::::::::
Target 75 AAAAUCAAA-ACCAAAACCA 93 |
| vun-mir2630 |
TC1550 |
Homeodomain leucine zipper protein HDZ3 |
Transcription factor |
miRNA 21 AUUUUGGUUUCUGGUUUUGGU 1
:.::::..:. ::::::::::
Target 1253 UGAAACUGAGAACCAAAACCA 1273 |
| vun-mir2630 |
FC457466 |
Pseudouridylate synthase |
Metabolism |
miRNA 21 AUUUUGGUUUCUGGUUUUGGU 1
:::::. :..:::.:::::::
Target 504 UAAAAUGAGGGACUAAAACCA 524 |
| vun-mir2630 |
TC6720 |
Ubiquitin carrier protein |
Transporter |
miRNA 20 UUUUGGUUUCUGGUUUUGGU 1
:::::::::: :::::.::
Target 685 AAAACCAAAGCCCAAAUUCA 704 |
| vun-mir2636 |
TC7750 |
NADH-ubiquinone oxidoreductase chain 2 |
Metabolism |
miRNA 21 UAUAAGUCGUGUGAUUGUAGG 1
:::::.::::::::::.:.:
Target 225 AUAUUUAGCACACUAAUAAUC 245 |
| vun-mir2636 |
FF537611 |
Na+/H+ antiporter |
Metabolism |
miRNA 20 AUAAGUCGUGUGAUUGUAGG 1
: :::::::::::..:::..
Target 25 UCUUCAGCACACUGGCAUUU 44 |
| vun-mir2636 |
TC1711 |
Beta-1, 3-glucanase-like protein |
Metabolism |
miRNA 19 UAAGUCGU-GUGAUUGUAGG 1
: :::::: :::::::::::
Target 1279 AAUCAGCAACACUAACAUCC 1298 |
| vun-mir2657 |
TC7897 |
Proteinase inhibitor 20 |
Metabolism |
miRNA 20 UGUUUUAGUUAUGUUAUUUU 1
:.::::: ::::.:::::::
Target 934 AUAAAAUAAAUAUAAUAAAA 953 |
| vun-mir2657 |
FG852576 |
Heat shock protein 70 cognate |
Stress related |
miRNA 22 GUUGUUUUAGUUAUGUUAUUUU 1
:::.:.:::::::. :::.:::
Target 77 CAAUAGAAUCAAUGAAAUGAAA 98 |
| vun-mir2657 |
TC5942 |
2, 4-D inducible glutathione S-transferase |
Metabolism |
miRNA 21 UUGUUUUAGUUAUGUUAUUUU 1
::.:::::. ::..:::::::
Target 745 AAUAAAAUUUAUGUAAUAAAA 765 |
| vun-mir2678 |
EF472252 |
Bound starch synthase |
Metabolism |
target 5' U UG UG A 3'
GGC G GCA GAC
CUG C CGU UUG
miRNA 3' UG G UG AAAU 5' |
| vun-mir2678 |
D88122 |
CPRD46 protein |
Stress related |
target 5' U C G 3'
GCGCGUA CAACUU
UGCGCGU GUUGAA
miRNA 3' CUG U AU 5' |
| vun-mir2678 |
AY466858 |
Peroxisomal ascorbate peroxidase |
Metabolism |
target 5' U A C A 3'
GGCACG UG CGGC ACUU
CUGUGC GC GUUG UGAA
miRNA 3' U AU 5' |
| vun-mir2678 |
AB028025 |
YLD mRNA for regulatory protein |
Metabolism |
target 5' A CCA C G 3'
GCGC GCG CGGCGAC
UGUG CGC GUUGUUG
miRNA 3' C AAAU 5' |
| vun-mir2950 |
TC11773 |
F-box/Kelch-repeat protein |
Transcription factor |
miRNA 21 AAGUCAGACGUUCUCUACCUU 1
:::::::::::::::::::::
Target 614 UUCAGUCUGCAAGAGAUGGAA 634 |
| vun-mir2950 |
TC2831 |
Ethylene responsive protein |
Stress related |
miRNA 20 AGUCAGACGUUCUCUACCUU 1
:..:: ::.::::::::::.
Target 1700 UUGGUAUGUAAGAGAUGGAG 1719 |
| vun-mir3434 |
TC7167 |
Protein transport protein Sec24-like At3g07100 |
Transporter |
miRNA 20 AGAGUACCGACUAUGAGAGU 1
:::.::::.:::: ::.:::
Target 662 UCUUAUGGUUGAUUCUUUCA 681 |
| vun-mir4351 |
TC5899 |
Expressed protein |
Hypothetical protein |
miRNA 22 GGUUGAGGUUGACUUGGGAUUG 1
::::::::::::::::::::::
Target 27 CCAACUCCAACUGAACCCUAAC 48 |
| vun-mir4351 |
FF391835 |
NADH-ubiquinone oxidoreductase chain 2 |
Metabolism |
miRNA 20 UUGAGGUUGACUUGGGAUUG 1
::: ::::.: ::::::::.
Target 22 AACCCCAAUUAAACCCUAAU 41 |
| vun-mir4392 |
TC14606 |
AKIN beta1 |
Signal transduction |
miRNA 22 AGGCUUUAGUGCAAGAGUGUCU 1
: : :::::::::.:::.:::
Target 791 UGCUAAAUCACGUCUUCAUAGA 812 |
| vun-mir4392 |
TC9038 |
SNF1-related protein kinase regulatory beta subunit 1 |
Signal transduction |
miRNA 22 AGGCUUUAGUGCAAGAGUGUCU 1
: : :::::::::.:::.:::
Target 979 UGCUAAAUCACGUCUUCAUAGA 1000 |
| vun-mir4408 |
TC2049 |
Monooxygenase |
Metabolism |
miRNA 24 AGGAUAUGAGUAGGUUACAACAAC 1
:: :::.::::: :: :::::::
Target 369 UCAGAUAUUCAUCAAAAGUUGUUG 392 |
| vun-mir4992 |
FG809835 |
TfIIE |
Transcription factor |
miRNA 22 GACUUUUUUUGGUAGAAUCUAC 1
::::::::::::::::::::::
Target 247 CUGAAAAAAACCAUCUUAGAUG 268 |
| vun-mir4992 |
TC11468 |
Uncharacterized protein At2g03890.2 |
Hypothetical protein |
miRNA 22 GACUUUUUUUGGUAGAAUCUAC 1
:::::::: :::::.:::::::
Target 836 CUGAAAAAUACCAUUUUAGAUG 857 |
| vun-mir4992 |
TC414 |
Zinc finger protein 7 |
Transcription factor |
miRNA 22 GACUUUUUUUGGUAGAAUCUAC 1
.:::.:.:::::::.::.:::
Target 739 UUGAGAGAAACCAUUUUGGAUC 760 |
| vun-mir4992 |
TC2268 |
Zinc finger protein 4 |
Transcription factor |
miRNA 22 GACUUUUUUUGGUAGAAUCUAC 1
.:::.:.:::::::.::.:::
Target 857 UUGAGAGAAACCAUUUUGGAUC 878 |
| vun-mir5012 |
TC1335 |
Ribosomal protein L30 |
Structural protein |
miRNA 21 CCUUGUGUGCCUCGUCGUUUU 1
::::.::. ::::::::::::
Target 209 GGAAUACGAGGAGCAGCAAAA 229 |
| vun-mir5012 |
TC59 |
Acireductone dioxygenase |
Metabolism |
miRNA 21 CCUUGUGUGCC-UCGUCGUUUU 1
::::::::: : ::::::::::
Target 19 GGAACACACUGUAGCAGCAAAA 40 |
| vun-mir5012 |
TC12731 |
Mn-specific cation diffusion facilitator transporter |
Transporter |
miRNA 20 CUUGUGUGCCUCGUCGUUUU 1
::.::::::::: :::::.
Target 186 GAGCACACGGAGAAGCAAGU 205 |
| vun-mir5043 |
FF401363 |
Ran-specific GTPase-activating protein |
Transcription factor |
miRNA 21 CCACCACGUC-UCUUCCUCUUC 1
: :::::::: :::.:::::::
Target 444 GAUGGUGCAGGAGAGGGAGAAG 465 |
| vun-mir5215 |
FG909052 |
Ferredoxin Ⅰ precursor |
Metabolism |
miRNA 21 UUAGUUGAUCGAGUAGGAGGA 1
:::::::::::::::::::::
Target 179 AAUCAACUAGCUCAUCCUCCU 199 |
| vun-mir5215 |
GH620837 |
L-lactate dehydrogenase |
Metabolism |
miRNA 20 UAGUUGAUCGAGUAGGAGGA 1
:::.:: :::::.:::::::
Target 491 AUCGACGAGCUCGUCCUCCU 510 |
| vun-mir5215 |
TC8326 |
50S ribosomal protein L21 |
Structural protein |
miRNA 21 UUAGUUGAUCGAGUAGGAGGA 1
:::.::.:.:::.::::::.:
Target 943 AAUUAAUUGGCUUAUCCUCUU 963 |
| vun-mir5215 |
FG849457 |
Vancomycin resistance protein |
Stress related |
miRNA 20 UAGUUGAUCGAGUAGGAGGA 1
::::::.:::::::::.:
Target 340 AUCAACAGGCUCAUCCUUCG 359 |
| vun-mir5215 |
TC6816 |
General substrate transporter |
Transporter |
miRNA 21 UUAGUUGAUCGAGUAGGAGGA 1
::::::::.:::: :.:::::
Target 1035 AAUCAACUGGCUC-UUCUCCU 1054 |
| vun-mir5216 |
FG851044 |
Metal ion binding |
Transcription factor |
miRNA 22 AAGGUGACAAAAAGUGAGGGUU 1
:.:::: :::::.:::.::::
Target 227 UAUCACUUUUUUUUACUUCCAA 248 |
| vun-mir5216 |
FG841236 |
T5I8.13 |
Transcription factor |
miRNA 22 AAGGUGACAAAAAGUGAGGGUU 1
:::::.: :: ::::.::::::
Target 132 UUCCAUUCUUCUUCAUUCCCAA 153 |
| vun-mir5216 |
FG931306 |
Predicted protein |
Hypothetical protein |
miRNA 21 AGGUGACAAAAAGUGAGGGUU 1
:.:::::::: ::..:.::::
Target 2 UUCACUGUUUCUCGUUUCCAA 22 |
| vun-mir5219 |
TC16320 |
Tumor-related protein |
Growth and development |
miRNA 20 GACGUCGACUCUAAGGUACU 1
::::: :::::.:: :::::
Target 141 CUGCACCUGAGGUUACAUGA 160 |
| vun-mir5227 |
TC9947 |
TINY-like protein |
Transcription factor |
miRNA 22 AAGAAGUUAGAAGAAGACAAGA 1
::.::::: ::::::.::::::
Target 1075 UUUUUCAA-CUUCUUUUGUUCU 1095 |
| vun-mir5227 |
FG842691 |
HMG1/2-like protein |
Transcription factor |
miRNA 20 GAAGUUAGAAGAAGACAAGA 1
:::::::.::.:::: ::.:
Target 27 CUUCAAUUUUUUUCUAUUUU 46 |
| vun-mir5227 |
FG886406 |
Probable intracellular septation protein |
Growth & development |
miRNA 22 AAGAAGUUAGAAGAAGACAAGA 1
:.::::: :::.::.::::.:
Target 48 UGUUUCAACCUUUUUUUGUUUU 69 |
| vun-mir5227 |
TC17852 |
Glutathione S-transferase PM24 |
Metabolism |
miRNA 20 GAAGUUAGAAGAAGACAAGA 1
:::::::.:::: ::::::
Target 1044 CUUCAAUUUUCUCGUGUUCU 1063 |
| vun-mir5227 |
TC10272 |
DNA-directed RNA polymerase subunit |
Transcription factor |
miRNA 20 GAAGUUAGAAGAAGACAAGA 1
:::::: ::.::.::::::
Target 288 CUUCAAGAUUUUUUUGUUCU 307 |
| vun-mir5241 |
TC10790 |
VDAC-like porin |
Transporter |
miRNA 20 AAGUGAGAAGGUAAGUGGGU 1
::::::::::::::::..::
Target 201 UUCACUCUUCCAUUCAUUCA 220 |
| vun-mir5241 |
TC18525 |
Peptidyl-prolyl cis-trans isomerase |
Metabolism |
miRNA 20 AAGUGAGAAGGUAAGUGGGU 1
:::..::::::.::::::.:
Target 58 UUCGUUCUUCCGUUCACCUA 77 |
| vun-mir5241 |
FG863193 |
Probable plastid-lipid-associated protein 13 |
Stress related |
miRNA 20 AAGUGAGAAGGUAAGUGGGU 1
::::.:: :.:::::::.::
Target 158 UUCAUUCAUUCAUUCACUCA 177 |
| vun-mir5241 |
TC7362 |
Serine/threonine protein kinase |
Signal transduction |
miRNA 20 AAGUGAGAAGGUAAGUGGGU 1
::..::.:::.:::::..::
Target 934 UUUGCUUUUCUAUUCAUUCA 953 |
| vun-mir5241 |
TC16629 |
Multidrug resistance protein |
Disease related |
miRNA 20 AAGUGAGAAGGUAAGUGGGU 1
:::::::::::: :: :.::
Target 915 UUCACUCUUCCAGUCUCUCA 934 |
| vun-mir5241 |
TC2781 |
Non-specific lipid-transfer protein |
Transporter |
miRNA 20 AAGUGAGAAGGUAAGUGGGU 1
::::::::::: ::: :.::
Target 20 UUCACUCUUCCUUUCUCUCA 39 |
| vun-mir5241 |
TC212 |
Chaperone GrpE type 2 |
Stress related |
miRNA 20 AAGUGAGAAGGUAAGUGGGU 1
::::.:::.: ::::::::
Target 207 UUCAUUCUCUCCUUCACCCA 226 |
| vun-mir5255 |
TC8912 |
Pyruvate kinase |
Signal transduction |
miRNA 20 AGUACAGGAGAUAGGACAGU 1
:.:::::.:::.::.:::.:
Target 71 UUAUGUCUUCUGUCUUGUUA 90 |
| vun-mir5255 |
TC18327 |
Cysteine protease |
Metabolism |
miRNA 20 AGUACAGGAGAUAGGACAGU 1
::: :::::. ::.::::::
Target 605 UCAAGUCCUUGAUUCUGUCA 624 |
| vun-mir5261 |
FG838847 |
Chromosome undetermined scaffold_221 |
Hypothetical protein |
miRNA 21 UCGGUUUCGGUAGAUGUUAGC 1
:::::::::::::::::::::
Target 540 AGCCAAAGCCAUCUACAAUCG 560 |
| vun-mir5261 |
FF398912 |
TIR |
Stress related |
miRNA 21 UCGGUUUCGGUAGAUGUUAGC 1
::::::::.::::::::::::
Target 413 AGCCAAAGUCAUCUACAAUCG 433 |
| vun-mir5290 |
TC3168 |
Hydroxyproline-rich glycoprotein |
Disease related |
miRNA 24 AUACACAGAAAGAGAGAGAUGAAA 1
: : : :::::::::.::::.:::
Target 82 UCUCUUUCUUUCUCUUUCUAUUUU 105 |
| vun-mir5290 |
FG844083 |
PAS sensor protein |
Signal transduction |
miRNA 24 AUACACAGAAAGAGAGAGAUGAAA 1
: : : :::::::.:::.::.:::
Target 99 UUUCUCUCUUUCUUUCUUUAUUUU 122 |
| vun-mir5290 |
FG871448 |
Eco57I restriction endonuclease |
Metabolism |
miRNA 20 ACAGAAAGAGAGAGAUGAAA 1
: ::::::::::::: ::::
Target 42 UCUCUUUCUCUCUCUCCUUU 61 |
| vun-mir5290 |
TC11392 |
Ribonuclease Ⅲ |
Transcription factor |
miRNA 24 AUACACAGAAAGAGAGAGAUGAAA 1
::: :: ::: ::::.:.::::::
Target 841 UAUAUGACUUCCUCUUUUUACUUU 864 |
| vun-mir5290 |
TC12655 |
Calcium dependent protein kinase |
Signal transduction |
miRNA 20 ACAGAAAGAGAGAGAUGAAA 1
::::::.:.:::.:.::::
Target 1254 GGUCUUUUUUUCUUUGCUUU 1273 |
| vun-mir5290 |
TC4908 |
ACC oxidase |
Growth & development |
miRNA 22 ACACAGAAAGAGAGAGAUGAAA 1
: : ::::::::::::::. ::
Target 1376 UCUCUCUUUCUCUCUCUAUCUU 1397 |
| vun-mir5290 |
FG874464 |
RNA-binding protein |
Transcription factor |
miRNA 20 ACAGAAAGAGAGAGAUGAAA 1
: :::::::::::::.:::
Target 14 UCUCUUUCUCUCUCUCUUUU 33 |
| vun-mir5298 |
TC16082 |
Translation initiation factor IF |
Transcription factor |
miRNA 25 AAGAAGUAGAAG-UAGAACUUUAGGU 1
:.::::::::: : :::::::::::
Target 34 UCUUUCAUCUUCGAACUUGAAAUCCA 59 |
| vun-mir5298 |
TC11481 |
Non-specific lipid-transfer protein |
Transporter |
miRNA 24 AGAAGUAGAAGUAGAACUUUAGGU 1
:.: ::: ::.:::::::.::..:
Target 614 UUUACAUGUUUAUCUUGAGAUUUA 637 |
| vun-mir5298 |
TC16211 |
(Iso) Flavonoid glycosyltransferase |
Metabolism |
miRNA 25 AAGAAGUAGAAGUAGAACUUUAGGU 1
: ::.. :::: ::::::::::::
Target 233 UCCUCUGCCUUCUUCUUGAAAUCCA 257 |
| vun-mir5376 |
TC18575 |
Zgc:158399 protein |
Hypothetical protein |
miRNA 23 AGAGUUUAAGAAGUGUUAGAGGU 1
:::::::::::::::::::::::
Target 517 UCUCAAAUUCUUCACAAUCUCCA 539 |
| vun-mir5376 |
TC16446 |
Predicted protein |
Hypothetical protein |
miRNA 23 AGAGUUUAAGAAGUGUUAGAGGU 1
:::::::::::::: :::.: ::
Target 687 UCUCAAAUUCUUCAGAAUUUACA 709 |
| vun-mir5376 |
FC457472 |
Chromosome chr1 scaffold_135 |
Hypothetical protein |
miRNA 20 GUUUAAGAAGUGUUAGAGGU 1
.: ::::::::::::::.:
Target 141 AGAUUUCUUCACAAUCUCUA 160 |
| vun-mir5561 |
TC1062 |
H+/Ca2+ exchanger 2 |
Transporter |
miRNA 20 UGUAAAUCUCUCUCUCUCUA 1
: :::::::::::::::::
Target 8 AGAUUUAGAGAGAGAGAGAG 27 |
| vun-mir5561 |
TC8162 |
GTPase |
Metabolism |
miRNA 20 UGUAAAUCUCUCUCUCUCUA 1
:..: ::::::::::::::
Target 102 AUGUAUAGAGAGAGAGAGAG 121 |
| vun-mir5561 |
TC11798 |
Cold shock domain |
Stress related |
miRNA 20 UGUAAAUCUCUCUCUCUCUA 1
::: : : ::::::::::::
Target 2 ACAGUGACAGAGAGAGAGAU 21 |
| vun-mir5758 |
TC975 |
Chromosome chr11 scaffold_13 |
Hypothetical protein |
miRNA 21 GUUUAUGUAUCUAGGUUGAAU 1
:::::::::::::::::::::
Target 213 CAAAUACAUAGAUCCAACUUA 233 |
| vun-mir5758 |
TC5742 |
Pyrophosphate-dependent phosphofructo-1-kinase |
Signal transduction |
miRNA 21 GUUUAUGUAUCUAGGUUGAAU 1
.:::::.::::::::::: ::
Target 306 UAAAUAUAUAGAUCCAACCUA 326 |
| vun-mir5758 |
TC16939 |
Chromosome undetermined scaffold_310 |
Hypothetical protein |
miRNA 20 UUUAUGUAUCUAGGUUGAAU 1
:::::::: :::::::: ::
Target 509 AAAUACAUUGAUCCAACGUA 528 |
| vun-mir5770 |
TC1925 |
Amine oxidase |
Metabolism |
miRNA 21 AGUAGGUUUGGUAUCAGGAUU 1
:::::::::::::::::::::
Target 165 UCAUCCAAACCAUAGUCCUAA 185 |
| vun-mir5770 |
TC5168 |
Copper amine oxidase |
Metabolism |
miRNA 21 AGUAGGUUUGGUAUCAGGAUU 1
:..::::::::::::::: ::
Target 148 UUGUCCAAACCAUAGUCCAAA 168 |
| vun-mir5770 |
TC18480 |
Ribonuclease H |
Transcription factor |
miRNA 20 GUAGGUUUGGUAUCAGGAUU 1
:::.:::.:.:::::..:::
Target 613 CAUUCAAGCUAUAGUUUUAA 632 |
| vun-mir5770 |
TC1738 |
Allyl alcohol dehydrogenase |
Metabolism |
miRNA 20 GUAGGUUUGGUAUCAGGAUU 1
::::.::::. ::::.::.:
Target 766 CAUCUAAACUUUAGUUCUGA 785 |
| vun-mir6252 |
FG841373 |
Nucleoporin-like protein |
Transcription factor |
miRNA 23 UUGGGAGAGAGUUGUGUUGAGUA 1
:::::::::::::::::::::::
Target 24 AACCCUCUCUCAACACAACUCAU 46 |
| vun-mir6252 |
FG857360 |
Membrane protein |
Transporters |
miRNA 21 GGGAGAGAGUUGUGUUGAGUA 1
.::::::::::::: :::::
Target 247 UCCUCUCUCAACACUCCUCAU 267 |
| vun-mir6252 |
TC15301 |
Homeobox domain, ZF-HD class |
Transcription factor |
miRNA 23 UUGGGAGAGAGUUGUGUUGAGUA 1
: : :::::::::: :::::::
Target 9 AUCACUCUCUCAACUCAACUCAA 31 |
| vun-mir7696 |
FG864277 |
BZIP transcription |
Transcription factor |
miRNA 20 AAAACUUAAAUUCAUGAACA 1
::::::::::::::::::::
Target 17 UUUUGAAUUUAAGUACUUGU 36 |
| vun-mir7696 |
FF383199 |
Olfactory receptor |
Signal transduction |
miRNA 20 AAAACUUAAAUUCAUGAACA 1
:::: : ::::::::::::
Target 141 UUUUUAUUUUAAGUACUUGG 160 |
| vun-mir8182 |
TC3507 |
Pectin methylesterase |
Metabolism |
miRNA 21 CAGUAGUGUUUGCGUUGUGUU 1
::::::::::..:::::: :.
Target 654 GUCAUCACAAGUGCAACAGAG 674 |
| vun-mir9748 |
TC16306 |
Lectin-like protein kinase |
Signal transduction |
miRNA 22 GAGGAGGGAGUUGUGAAGGAAG 1
:.:::..:::::::::::::.
Target 17 CGUCUCUUUCAACACUUCCUUU 38 |
| vun-mir9748 |
TC1064 |
Zinc finger, RING-type: Thioredoxin-related |
Transcription factor |
miRNA 22 GAGGAGGGAGUUGUGAAGGAAG 1
.:::::.::::::.::.::::
Target 16 UUCCUCUCUCAACUUUUUCUUC 37 |
| vun-mir9748 |
TC9843 |
Beta-xylosidase/alpha-L-arabinosidase |
Metabolism |
miRNA 20 GGAGGGAGUUGUGAAGGAAG 1
:.::..:::::::::::::
Target 478 CUUCUUUCAACACUUCCUUG 497 |
| vun-mir9748 |
TC15743 |
Heat shock protein |
Stress related |
miRNA 22 GAGGAGGGAGUUGUGAAGGAAG 1
:::.:::::::::.::.::::
Target 244 CUCUUCCCUCAACGCUCUCUUC 265 |
| vun-mir9748 |
TC15591 |
Transcription factor AHAP2 |
Transcription factor |
miRNA 22 GAGGAGGGAGUUGUGAAGGAAG 1
.::.:::::::: :::::: ::
Target 64 UUCUUCCCUCAAGACUUCCAUC 85 |
| vun-mir9748 |
TC298 |
Glutathione reductase |
Metabolism |
miRNA 20 GGAGGGAGUUGUGAAGGAAG 1
.:::.:::::::::.::::
Target 95 UCUCUCUCAACACUCUCUUC 114 |
| vun-mir9748 |
TC1040 |
Glycine-rich protein 2b |
Transcription factor |
miRNA 20 GGAGGGAGUUGUGAAGGAAG 1
::.::::.::::::::::
Target 567 ACUUCCUCUGCACUUCCUUC 586 |
Majority (27%) of the newly characterized cowpea miRNAs are observed to regulate the metabolic proteins. Such findings regarding metabolism related genes targeted by miRNAs are similar with the prior publications in plants and animals [28,43,44]. Pectin methylesterase (PME) is an important enzyme that acts on pectin, a major component of plant cell wall. PME catalyzes reactions according to the double-displacement mechanism [51]. In this study, the PME is predicted as a putative target for vun-miR1882. Thus the vun-miR1882 is a valuable resource to regulate cell wall. Another important enzyme ribulose-1, 5-bisphosphate carboxylase (Rubisco) is a key enzyme in photosynthesis and photorespiration, where it catalyzes the fixation of CO2 and O2, respectively. Due to its rate-limiting property in photosynthesis, it is the prime focus of improving the plant productivity [52]. The cowpea miRNA (vun-miR2657) is predicted to target this important enzyme which is the potential resource to modify Rubisco expression and ultimately plant productivity.
The transcription factor myeloblastosis (MYB) is an important regulator of many developmental and physiological processes in plants. Ballester et al. [53], suggested that the MYB also plays a significant role in regulating the flavonoid pathway in plants. The newly identified cowpea miRNA family vun-834 is found to target the MYB transcription factors. Thus this miRNA is an important resource to fine tune the MYB regulation for the desirable traits in cowpea fruit. The transcription factor, zinc finger is believed to be involved in many biotic and abiotic stresses as responding gene to manage the plant under these stresses [54]. The same family of transcription factor is also reported to play a crucial role in plant development [55]. The newly identified cowpea miRNA families vun-miR834 and 4992 are found to target this zinc finger transcription factor family. These miRNAs are important resources to regulate the zinc finger family proteins for the betterment of cowpea under various biotic and abiotic stresses and fruit development.
Similarly 12% targeted genes by cowpea miRNAs are engaged in transport activities. ATP-binding cassette transporters comprise a highly conserved family of ATP-binding proteins that are involved in transporting of various molecules across plasma membrane. Here vun-miR1514 is identified to target ATP-binding cassette transporters. Such findings are in agreement with the other workers in the miRNA field [37,43].
Biotic and abiotic stresses like salinity, drought, temperature extremities, heavy metals, pathogen attacks, and pollution cause huge yield reductions in plants [56]. Naturally plants have various systems to protect themselves from these stresses that occur at various levels, i.e., at whole plant, tissue, cellular, sub-cellular, genetic and molecular levels [56,57,58,59,60]. Many studies suggest that plant miRNAs are involved in these stresses [9,17,61]. In this study identified miRNAs such as vun-miR1525,2657 and 9748 also targeted heat shock proteins that expressed in response of heat stress. This suggests the role of these miRNAs during the heat stressed condition of plants. Similar findings were reported in switch grass [17].
Some miRNAs of cowpea were observed to target the protein functioning in the process of cell signal transduction. Almost similar findings were observed by many researchers in various organisms [42,43]. Protein kinases are key regulators of cell function and play crucial role in protein phosphorylation and dephosphorylation that are major signaling pathways induced by osmotic stress in higher plants. Similarly, SNF1 (sucrose non-fermenting-1) is an osmotic-stress-activated protein kinase in Arabidopsis thaliana that can significantly impact drought tolerance of Arabidopsis thaliana plants [62]. These two important proteins were targeted by cowpea miRNAs families, like vun-miR435,2606,2609 and 4392 respectively. Serine/threonine protein kinase (STPKs) is another protein kinase that is targeted by miRNA family (miR5241), act as sensors of environmental signals and regulate different developmental changes and also host pathogen interactions [63].
In this study, newly profiled cowpea miRNAs were also observed to target hypothetical proteins, growth and development, structural proteins and disease related proteins. Such findings were also published earlier [19,21,37].
4. Conclusion
The current study is resulted 46 new miRNAs and their 138 targeted genes in an important commercial plant cowpea. All these miRNAs are profiled for the first time in cowpea. These findings will serve as resources to fine tune cowpea plant at micro-molecular level. This will help us to enhance the production ability of cowpea against biotic and abiotic stress tolerance. Furthermore these miRNAs and their targets are also powerful functional genomic resources in the Kingdom plantae.
Conflict of Interest
The authors declare that there is no conflict of interest regarding the publication of this article.









 DownLoad:
DownLoad: