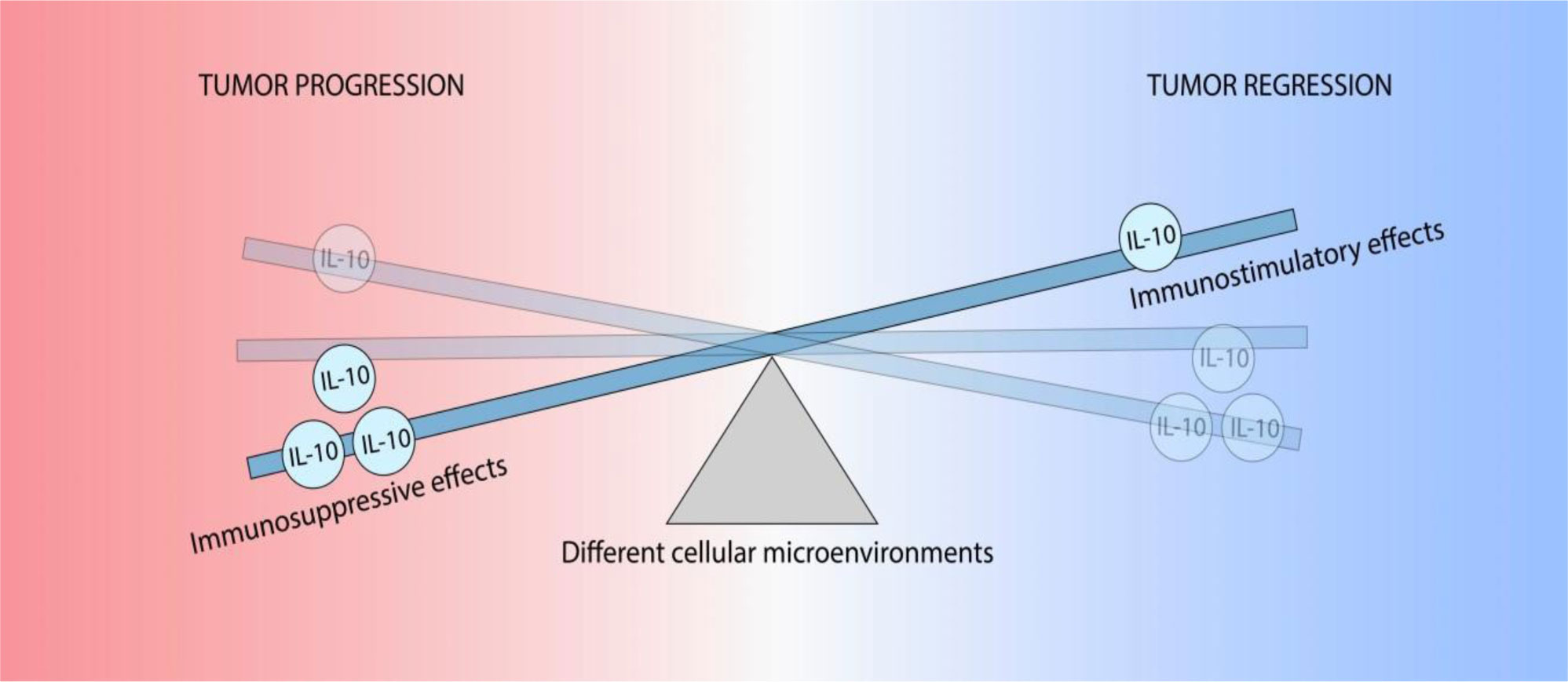
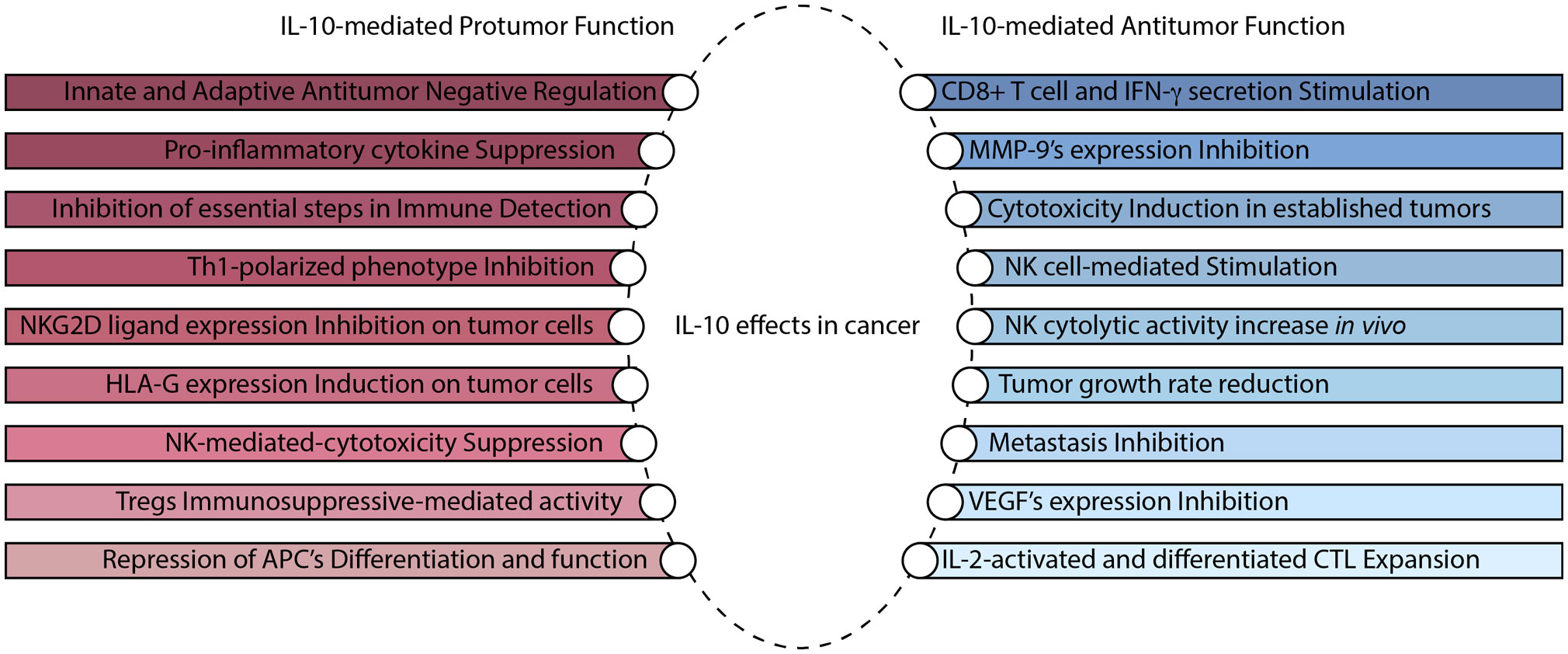
It is generally well-accepted and established the IL-10-mediated protumor function in cancer, based on its immunosuppressive properties. However, new evidences from in vitro and in vivo murine models have emerged showing a potential immunostimulating activity of this cytokine, which may sustain IL-10-mediated antitumor function in cancer, hence favoring tumor regression. Here, we attempt to clarify IL-10’s role in cancer, by conducting a literature review of previously published studies, presenting information about IL-10 immunosuppressive and/or immunostimulating properties. Different and contradictory IL-10 effects leading to tumor growth (e.g., suppression of pro-inflammatory cytokines or inhibition of immune response recognition steps) or tumor regression (e.g., stimulation of cytotoxic and cytolytic activities of immune cells or inhibition of angiogenic factors) were found in distinct scenarios, hindering the establishment of a general role for IL-10 in cancer. Such definition is still a challenge, maybe due to a lack of sufficient information to support it, or perhaps based on the fact that IL-10 role in distinct cancer contexts may vary, switching from a classical immunosuppressive factor to an immunostimulating one.
1.
Introduction
IBD, which includes Crohn's disease (CD) and ulcerative colitis (UC), characterized by chronic inflammation of the gastrointestinal tract and is on the rise worldwide [1]. Symptoms of CD include abdominal pain, diarrhea, etc. [2], while those of UC include hemorrhagic diarrhea, faecal incontinence, and abdominal discomfort [3]. Many studies noted that IBD is not only an immune-mediated disease, but also a psychiatric disorder, where mood disorders, depression, and anxiety are more common in patients with IBD compared to the general population [4,5,6,7,8,9]. It has been reported that 16 to 30% of patients with IBD suffer from depression in remission, and 34 to 60% of patients had active depression [10,11]. The above mentioned physical and psychological symptoms seriously affect the daily life and social communication of each patient, decreasing the quality of life and resulting in huge medical costs.
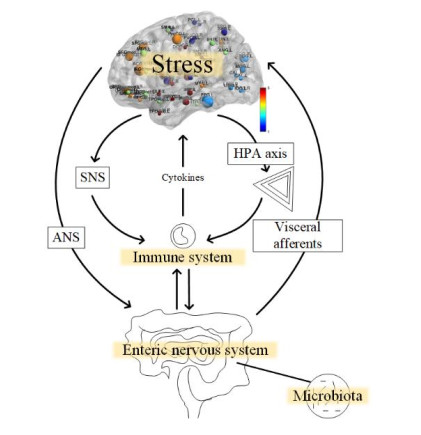
Bidirectional interactions between the gut and the nervous system include the central nervous system (CNS; brain, and spinal cord), the autonomic nervous system (ANS), the enteric nervous system (ENS), and the hypothalamic-pituitary-adrenal (HPA) pathway [12], which comprise the brain-gut axis. Environmental stress activates the hypothalamic corticotropin-releasing factor (CRF), which stimulates pituitary adrenocorticotropin (ACTH) secretion. This, in turn, leads to the release of the major stress hormone, cortisol, which affects many human organs, including the brain [13]. It is particularly important to note that the connection between the human gastrointestinal tract and the CNS is not only physiological, but also active through endocrine, humoral, metabolic, and immune communication pathways [14] (see Figure 1 below). The role of the brain-gut axis in IBD has received increasing attention, as it allows for a further interpretation of brain structure and function in IBD [15]. Recent studies have found more pronounced differences between IBD and healthy control (HC), with variations in gray matter volume in the middle frontal and temporal regions, and variations in the function of the supra-frontal, middle frontal, infra-frontal, inferotemporal, rectus and inferior frontal gyrus regions [16].
As the role of the brain-gut axis in IBD has been increasingly emphasized [17,18], it has become more important to study the functional changes in the brains of patients with IBD. The differences between IBD and HC brain function are centered on the middle frontal and temporal regions, as well as the left superior frontal gyrus. In addition, patients who suffer from major depressive disorder (MDD) have abnormal function in the frontal cortex (PFC), anterior cingulate cortex (ACC), and limbic system (amygdala) [19]. Many researchers worldwide have focused their attention on the two belligerent subtypes of IBD. On the one hand, they studied the functional differences between the brains of individuals with CD and HC [20,21,22,23,24,25,26,27,28,29], where the brain function of the paracentral lobule, the cingulate gyrus, and the medial frontal gyrus were partially altered in patients with CD as compared to those with HC [30]. On the other hand, they focused on the study of UC [31,32,33,34], but there was little consensus on the conclusions [35]. It is essential to investigate changes in the brain function of patients with IBD.
Electroencephalography (EEG) recordings are capable of assessing brain activity during various experiments with a millisecond precision and high temporal resolution. Functional magnetic resonance imaging (fMRI) typically images the brain using blood-oxygen level-dependent (BOLD) contrast and has an excellent spatial resolution (millimeters). These are two of the most popular, non-invasive brain imaging techniques in cognitive neuroscience. Therefore, an orderly fusion of the two becomes an even better neurobiological technique, and it becomes especially important to find a suitable and accurate fusion method. Several EEG-fMRI fusion multimodal data methods exist, including those based on independent component analysis (ICA), CCA and a parallel factor analysis (PARAFAC) [36]. There are three mainstream simultaneous EEG-fMRI fusion methods, namely, symmetric fusion of two modalities of EEG and fMRI data [37], source localization fusion using fMRI data as a constraint on the traceability of the EEG data [38,39], and predictive fusion using EEG data as a constraint on the traceability of the fMRI data [40]. This paper adopts symmetric fusion of multimodal data, which has been used in a wide range of areas, including the coupling and decoupling mechanisms between EEG and fMRI [41,42], prediction of epileptic disease lesions [43], brain activity during mood swings in individuals with depression [44], and changes in the brain regions involved in emotional processing [45,46,47].
The symmetric fusion method has achieved remarkable success in different areas. The technical core of symmetric fusion is mainly the use of joint decomposition methods to separate the sources of EEG and fMRI data. Among them, the brightest method belongs to the typical tool for unlocking complex relationships between multiple variables, and can be used to identify links between sets of variables from different modalities. The main mechanism of action is to identify linear associations between two random variables in order to maximize the correlation between the variables [48], which is particularly suitable for obtaining activation maps at various locations in the brain. CCA was first applied in the field of neuroimaging data to filter spatial signals [49,50,51,52]; later on, it was used to classify data [53]. Recently, researchers have attempted to use CCA to combine imaging data from different modalities for computation [54]. The data from different modalities include but are not limited to, fMRI, EEG, and gray and white matter [55].
Moreover, CCA has some limitations. Generally, CCA is only applicable when two different sets of modal data are treated as linear. However, in practical applications, most of the relationships between multiple random variables are nonlinear. Therefore, KCCA has been developed to map the low-dimensional data to a high-dimensional kernel function space (feature space), and to perform a correlation analysis in the feature space through the kernel function. As the research progressed, it was found that a part of high-dimensional datasets had much larger dimensions than the sample size, and the use of classical CCA to process the data would crash the system [56,57,58]. Therefore, attempts were made to introduce a sparse retention term on the basis of the original CCA, which is called SPCCA [59]. First the sparse reconstruction coefficients among samples in each feature set are learned by sparse representation, and the sparse reconstruction weight matrix is constructed. Then, it is necessary for the two groups of features extracted by the algorithm to not only meet the requirement of maximum correlation but to also ensure that the sparse reconstruction relationship in each feature set can be maintained as a kind of structural information, so as to improve the stability and robustness of the algorithm in complex environments. In SPCCA, in addition to the correlation between two modal datasets from the same sample, cross-correlations between two datasets from different in-class samples are also utilized, which are automatically determined by performing sparse representations for good performance [60]. Rosa et al. [61] adopted CCA, KCCA, and other algorithms to verify the utility of multivariate linear relationships among high-dimensional, intra-modal, neuroimage datasets obtained by the same group of subjects to find meaningful multivariable image-to-image correspondence in the intra-modal study. Yang et al. [62] compared whether CCA and KCCA algorithms could provide useful technical means for fusing brain region localization, ERP induction time determination, and brain imaging feature extraction in the field of brain-human interfaces in an neural activity analysis under cognitive reassessment. However, the existing literature has not applied SPCCA algorithm to EEG-fMRI fusion research.
In this paper, CCA, KCCA, and SPCCA were used in the fusion step to combine different modal data, and to explore the functional brain changes in IBD disease, which is the first instance this has been performed. Differences in activation intensity between IBD and HC were compared and further interpreted and analyzed. This method allows us to discover structural changes that occur in different brain regions of individuals with IBD, which have been neglected in medical research. Meanwhile, the application of the SPCCA algorithm can also promote the sustainable development of CCA series algorithms.
2.
Materials and methods
Simultaneous EEG-fMRI data from IBD patients and healthy individuals were collected for analysis. After preprocessing and feature extraction, the extracted features were fused using the CCA, KCCA, and SPCCA methods, and the differential activation intensities were calculated for 90 brain regions divided by anatomical automatic labeling (AAL). The mean difference in activation intensity between patients with IBD and healthy individuals was calculated separately, and the differences between patients with IBD and healthy individuals were summarized by analyzing relevant medical conclusions. Figure 2 depicts the complete process, from data preprocessing to results.
2.1. Participants
The following exclusion criteria were applied: (1) use of corticosteroids and psychotropic medications within the past 30 days; (2) current or previous history of neurologic, medical, or psychiatric disorders; (3) current or previous history of neurosurgery, head injury, cerebral vascular injury, or traumatic brain injury involving loss of consciousness; (4) presence of a learning disability; (5) presence of claustrophobia; (6) refusal to give informed consent; (7) the presence of magnetic implants in the body; and (8) a under 18 years or over 70 years.
This study involved a total of 40 participants with a mean age of 36 years (age range 19–63 years; SD ± 14.01). The Ethics Committee (Changzhou University, Changzhou, China) approved the experiment, and all participants signed an informed consent form before the experiment. The study was conducted in accordance with the Declaration of Helsinki. They received comprehensive instructions related to the experimental process, and each subject was given a one-on-one introduction and explanation to avoid unnecessary errors during the experiment.
2.2. Data acquisition
The simultaneous EEG-fMRI experiment was performed in the imaging department of Changzhou Hospital. The experiment was a resting-state experiment with an eye-closing task and 240 time-points of fMRI scanning. The EEG equipment was a 64-lead nuclear magnetic resonance (NMR) EEG acquisition system from EGI, and the electrode positions followed the international 10–10 electrode system spatial distribution, in which the midline central (Cz) electrode was utilized as the experiment reference electrode. The EEG acquisition software was adopted from EGI, which could display the acquired EEG signals in real time; therefore, the quality of the acquired EEG signals could be observed in real time. Among them, the sampling frequency was set to 1000 Hz.
The MRI equipment was a 3.0T superconducting functional magnetic resonance imaging system from Philips. The fMRI scanning parameters were ae follows: repetition time (TR) 2000 ms, echo time (TE) 35 ms, field angle (FOV) 230 mm, turning angle (FA) 90°, matrix size 128 × 128, layer thickness of 4mm, and consecutive scanning of 24 layers. The experiment was performed using the scanning method of sequential scanning without an interval. A clock synchronization box was used in the fusion experiment to synchronize the time of the EEG and FMRI data acquisitions.
2.3. Data preprocessing
All experiments were performed in an magnetic resonance (MR) environment, which is very noisy, thus resulting in a high likelihood that the quality of the EEG data would be impaired [63]. Therefore, the quality of data preprocessing must be very high. In this paper, EEGLAB [64,65], the Functional MRI Center for the Brain (FMRIB) [66], and customized codes were used for processing. First, gradient field denoising with impulse artifact removal was performed using a plug-in for EEGLAB, which was freely available from the FMRIB at the University of Oxford [67,68]. Then, a bandpass filter with cutoff frequencies of 0.01 and 40 Hz was applied for denoising to remove DC drift and high-frequency artifacts unrelated to neuronal oscillations. At the same time, a 50 Hz bandpass filter was used to remove noise from the device wires. Next, the EEG data was segmented using the laboratory's immediate "TREV" scan markers as a reference, and the baseline was corrected so that the number of EEG segments was equal to the fMRI volume. Then the EEG data was averaged for reference. Finally, an independent component analysis (ICA) was selected to remove components related to blinks and movements and components not related to neural data [69].
In this paper, the DPABI toolbox [70] in MATLAB was used for fMRI data processing. First, the fMRI data was converted from the Digital Imaging and Communications in Medicine (DICOM) format to the Neuroimaging Information Technology Initiative (NIfTI) format. Then, the fMRI images were slice-time corrected, motion corrected, normalized to the Montreal Neurological Institute (MNI) space, and resampled to a voxel size of 3 × 3 × 3 mm3. Next, smoothing was performed using an 8 mm half-peak full width (FWHM) Gaussian kernel. Additionally, bandpass filters with cutoff frequencies of 0.01 and 0.08 Hz were applied for filtering. In particular, it should be noted that, fMRI data with a head motion amplitude of more than 2 mm of horizontal motion or 2 degrees of rotation angle were regarded as poor-quality data and were discarded.
2.4. EEG feature extraction
Feature extraction was performed on the pre-processed and normalized EEG signals. First, the resting-state wave amplitude at 40 TR times was extracted as the EEG features for the subsequent fusion analysis. Next, the E9 electrode was selected as the baseline EEG signal. However, after extracting the wave amplitude for 40 TR times, the current EEG data lost synchronization with the fMRI data. Therefore, in order to be consistent with the time course of the fMRI data, the 40 trails of EEG data were subjected to the zero-completion operation, which turned one trail of the EEG data into 5 trails, and the number of trails was 40 × 5. Finally, the resting state information and the hemodynamic response function (HRF) function of each TR time were convolved to obtain the final required EEG characteristics, which were recorded as $ {Y_{\_EEG}} $.
2.5. fMRI feature extraction
Preprocessed fMRI data are usually delayed by 4–8 s due to the blood-oxygen-level-dependent (BOLD) signal; therefore, in this paper, the fMRI data of five time-points (10 s) after each trail corresponding to the EEG signal were selected as the data involved in the calculation. Meanwhile, in order to extract more accurate regions of interest, k-means clustering was performed on all voxel time series, and a mask was created. Next, the data was simplified and streamlined according to the created mask. Finally, using the SPM8 software [71], the mean of 90 regions of interest in the whole brain was calculated for each time-point according to the AAL90 template to represent each region of interest, denoted as $ {Y_{\_fMRI}} $. Figure 3 shows the schematic diagram of the fMRI feature extraction process.
2.6. Introduction to the CCA algorithm
The theory of the CCA algorithm [49,50,51,52] is briefly described below.
The two sample sets $ X $ and $ Y $ obtained in the same experiment both contain $ N $ samples. Assume that the dimension of the $ X $ sample set is $ p $ and the $ Y $ sample set is $ q $, as shown in Eq (1).
On the other hand, the purpose of CCA is to find some linear combination of $ X $ and $ Y $ that can maximize the degree of correlation, which can be translated into calculating the maximum value of the correlation function of Eq (2):
where $ {w_x} $ and $ {w_y} $ denote the linear combination coefficients of $ X $ and $ Y $, respectively, and $ {S_{XX}} $, $ {S_{XY}} $ and $ {S_{YY}} $ denote the variance and covariance matrices of $ X $ and $ Y $, respectively.
2.7. Introduction to the KCCA algorithm
Since CCA cannot handle nonlinear data, kernel canonical correlation algorithms can solve this problem by mapping data to high-dimensional feature spaces [72,73], a kernel $ \kappa $ for all $ X, Y \in R $ is defined as Eq (3):
where $ \varphi $ is a mapping from the original data space $ R $ to a new feature space $ F $.Based on kernel, the directions $ {\alpha _{Xk}} $ and $ {\alpha _{Yk}} $ can be represented as Eq (4):
where $ {K_X} $ and $ {K_Y} $ represent the RBF kernel matrices.
2.8. Introduction to the SPCCA algorithm
SPCCA utilizes the method of solving the sparse weight matrix in the Sparsity preserving projections (SPP) algorithm to obtain the global sparse reconstruction weights between samples [59] and uses an optimization strategy to introduce the theory of CCA as a kind of discriminatory information of the data.
Foe the two sample sets, $ X = \left[ {{x_1}, {x_2}, \cdots , {x_N}} \right] \in {R^{p \times N}} $ and $ Y = \left[ {{y_1}, {y_2}, \cdots , {y_N}} \right] \in {R^{q \times N}} $, in the same model, $ N $ denotes the number of samples, $ p $ denotes the feature dimension of the $ X $ sample set, $ q $ denotes the feature dimension of the $ Y $ sample set, and each column of $ X $ and $ Y $ denotes a sample. Construct the sparse reconstruction weight matrices $ R = \left[ {{r_1}, {r_2}, \cdots , {r_N}} \right] \in {R^{N \times N}} $, and $ S = \left[ {{s_1}, {s_2}, \cdots , {s_N}} \right] \in {R^{N \times N}} $ for the two sets of sample sets $ X $ and $ Y $. The objective functions of Eqs (5) and (6) are defined to seek the projections $ {w_x} $ and $ {w_y} $ that are able to maintain the optimal sparse weight vectors $ {r_i} $ and $ {s_i} $, namely.
where $ {\tilde r_i} $ and $ {\tilde s_i} $ denote the optimal solution for the solution of the $ {L_1} $ minimization problem on $ X $ and $ Y $, respectively.
Combined with the core thrust of the CCA–maximization of mutual covariance, the objective function can be obtained as shown in Eq (7):
where $ {\tilde S_{xx}} = X(I - R){(I - R)^T}{X^T} $ and $ {\tilde S_{yy}} = Y(I - S){(I - S)^T}{Y^T} $ denote the sparse holding scatter matrices of $ X $ and $ Y $, respectively, and both of them satisfy the positive definiteness of the matrix. If a singularity occurs, a small perturbation is added to the matrix to eliminate the singularity.
2.9. Data fusion and reconfiguration
The features of the EEG and fMRI data after feature extraction were performed as superposition averaging, after which they were used as input signals for fusion of the data in two modalities. The typical variable matrix $ M $ was calculated by CCA, KCCA, and SPCCA. Finally, the data was reconstructed according to Eq (8), and the correlation components $ C $ in the time and spatial domains were obtained from the typical variable matrix $ M $.
Then, the IBD and HC data were analyzed separately to obtain the activation intensity required for the final study of this paper. Figure 4 shows the flow of data fusion and reconstruction.
2.10. Activation intensity difference calculation method
The fMRI-related components obtained after remodeling were written as $ {C^{'}} $. The activation intensity difference were written as $ J $. Then, the average fMRI-related components after analysis in the IBD patient group were recorded as $ C_{IBD}^{'} $, and the average fMRI-related components after analysis in the healthy participant group were recorded as $ C_{HC}^{'} $. The difference in activation intensity was calculated as shown in Eq (9):
3.
Results
3.1. CCA processing results
The group analysis of IBD and HC data was performed. CCA fusion was used to obtain different activation intensity differences in 90 brain regions. As shown in Table 1, the top 10 brain regions with large activation intensity differences and the six brain regions known to have large activation intensity differences are listed with ROIs, ROIs numbers, automated anatomical labelling (AAL) and their specific activation intensity differences.
As can be seen from the table, those that meet expectations were as follows: the Temporal pole: superior temporal gyrus, temporal pole: middle temporal gyrus, and Middle frontal gyrus, orbital part. Changes in the activation intensity of these brain regions have been previously mentioned in the literature. In contrast, the Posterior cingulate gyrus, Amygdala, Thalamus, Cuneus, Precuneus, and Caudate nucleus were not mentioned as being involved in IBD disorders. Additionally, in this paper, the brain regions mentioned in the medical literature have been divided according to AAL90. Six brain regions with known large activation differences were randomly selected for analysis and are presented in the bottom half of the table. According to the analysis of CCA calculations, the activation differences in the Superior frontal gyrus, medial, Middle frontal gyrus, Superior temporal gyrus, and Middle temporal gyrus were very small, which is inconsistent with the known conclusions. This shows that CCA does not process simultaneous EEG-fMRI data well.
3.2. KCCA processing results
Similarly, IBD and HC data were analysed separately by using KCCA fusion. Differences in activation intensity were obtained for 90 brain regions. As shown in Table 2, the top 10 brain regions with large activation intensity differences and the six brain regions with known large activation intensity differences are listed with ROIs, ROIs numbers, AAL labels, and their specific activation intensity differences.
As can be seen in the table, the Heschl gyrus, Middle frontal gyrus, and Superior frontal gyrus, medial orbital regions all met previous expectations. Structural changes in the Superior parietal gyrus, Gyrus rectus, Parahippocampal gyrus, and Posterior cingulate gyrus have not been previously mentioned in the literature. However, the activation difference between the Middle temporal gyrus and Superior temporal gyrus was partially improved compared with the CCA calculations. Moreover, the Middle frontal gyrus and Heschl gyrus were among the top 10 brain regions with large activation intensities. It can be seen that KCCA performs better than CCA in the fusion of multimodal nonlinear data.
3.3. SPCCA processing results
Similarly, a group analysis of IBD and HC data, alongside data fusion using the SPCCA method, also obtained the difference in activation intensity of 90 brain regions. As shown in Table 3, the top 10 brain regions with large activation intensity differences and the six brain regions with known large activation intensity differences are listed with ROIs, ROIs numbers, AAL labels, and their specific activation intensity differences. The details of the difference in activation intensity across the 90 brain regions are shown in Figure 5 and 6.
As can be seen from the table, those that met expectations were the Middle frontal gyrus, Superior frontal gyrus, medial orbital, and Inferior frontal gyrus. Structural changes in the Middle frontal gyrus, Gyrus rectus, and Amygdala have not been previously reported. In addition, the Superior frontal gyrus, medial orbital had the highest activation intensity difference of 75; the Gyrus rectus had the lowest activation intensity difference of 46. The SPCCA showed a mean difference in activation intensity of 60.1 among the six brain regions known to have significant activation differences. However, the mean difference in activation intensity between the six brain regions obtained by CCA was 36.9, and the mean difference in activation intensity between the six brain regions obtained by KCCA was 49.8. Meanwhile, although the Inferior temporal gyrus and Heschl gyrus were not among the top 10 brain regions with large activation intensity differences, their activation strengths were also considerable. The results calculated by SPCCA in the six brain regions with known large activation differences were generally much higher than those calculated by CCA and KCCA. It can be seen that SPCCA not only has the highest activation intensity difference compared with CCA and KCCA, but also has the highest average difference value of the six known brain regions, which is more in line with the facts. It is concluded that SPCCA is the most suitable algorithm among the above three methods.
3.4. Connection matrix results discussion
By extracting the data for different voxels throughout time, a time series for different voxels can be obtained. This time series represents the change in blood oxygen levels of that voxel over time, which reflects the performance of the function. Based on the correlation between the time series, a functional correlation can be obtained. By calculating the average time series for each brain region and the pairwise correlation coefficient, the correlation matrix for the whole brain during this period can be obtained, that is, the functional connection matrix.
Using the average time series of fMRI data from 25 IBD patients and 15 healthy people, the connection matrix of IBD patients to healthy subjects was plotted, as shown in Figure 7. According to the figure, the differences between the two aforementioned connection matrices can be clearly seen, and the brain regions with the most obvious changes are indicated by the red boxes.
Activation differences were analyzed and calculated for 90 brain regions. The most basic connection matrix method was used to analyze the parts of the brain regions with large activation differences between IBD patients and healthy individuals, namely the Superior occipital gyrus, Middle occipital gyrus, Inferior occipital gyrus, and Caudate nucleus. However, these regions do not contain relevant brain regions known in the medical literature. Therefore, it can be judged that the results obtained when using a single data analysis are not satisfactory. In this paper, the simultaneous EEG-fMRI fusion method was used to calculate the brain regions associated with IBD more correctly and excellently.
3.5. Two-sample t-test
A two-sample t-test (also known as an independent-sample t-test) is a statistical method used to test the degree of difference between two groups; the smaller the p-value, the greater the difference [72]. The calculation results are shown in Table 4.
According to the results described in the table, it can be seen that not only the activation intensity of the two brain regions, namely the frontal and temporal regions, differ considerably, and were mentioned in relevant literature. In addition, the Posterior cingulate gyrus, Gyrus rectus, and Amygdala proposed in the results of this paper are also statistically significantly different. The above results demonstrate the validity of the computational methods used in this paper, as well as the large degree of activation differences in Posterior cingulate gyrus, Gyrus rectus, and Amygdala regions, that is, there were significant differences between IBD and HC in the Posterior cingulate gyrus, Gyrus rectus, and Amygdala regions. Due to the large number of brain regions, a single brain region was selected for the t-test, and this test is generally applicable to the examination of the results of each fusion.
3.6. Use relational degrees for comparison
The CCA family of algorithms searches a pair of linear transformations of a set of variables in a one-to-one manner. Given two dataests and $ X\left( {{Y_{\_EEG}}} \right) $, their generative models are given by Eq (10):
where $ {A_X} $ and $ {A_Y} $ are canonical variate matrices and $ {C_X} $ and $ {C_Y} $ are associated EEG and fMRI components. $ {a_{Xk}} $ and $ {a_{Yk}} $ represent the $ {k^{th}} $ column of $ {A_X} $ and $ {A_Y} $, respectively. The relational degree is defined in the following equation:
where $ {{\rm{ \mathsf{ ρ}}} _k} $ indicates the relational degree of the $ {k^{th}} $ pair of associated components.
The activation differences of 90 brain regions were reconstructed using the CCA, KCCA, and SPCCA algorithms fused with simultaneous EEG and fMRI data, through the judgement of the algorithms based on the differences was one-sided. Therefore, the correlation degree of different components of HC and IBD data under the three algorithms was compared: the greater the degree of correlation, the higher the degree of matching, which can prove the excellence of the algorithm. The correlation components with a correlation degree greater than 0.55 are shown in Table 5. In order to facilitate the comparison of data differences, the data with the highest correlation degree obtained from the HC and IBD data of the three algorithms are bolded within the table.
As shown in the table, there are four pairs of correlated components when using CCA for fusion. When KCCA was used for fusion, there were five pairs of correlations. When fused using SPCCA, there were six pairs of correlations. It is clear that the correlations obtained with SPCCA are greater than those obtained with KCCA and even greater than those obtained with CCA.
4.
Discussion
The functional changes of 90 brain regions of IBD and HC individuals were studied by applying the CCA, KCCA, and SPCCA algorithms for capturing higher-order structures and the complementarity of multimodal data. The fusion of CCA and KCCA is widely used in simultaneous EEG-fMRI fusion analyses [60,61,62]. However, the noise contained in simultaneous EEG-fMRI fusion data is huge, and the nonlinearity of the data may lead to the decrease of fusion accuracy. Therefore, this paper introduces the SPCCA algorithm to improve the robustness of the algorithm in a complex environment. As shown in Table 4, the t-test method [74,75,76] was used to verify the excellence of SPCCA calculation results. The smaller the p-value, the greater the difference between different brain regions of IBD and HC, which indicates that the SPCCA calculation results were correct. As shown in Table 5, the correlation degree derived [77,78,79] from SPCCA fusion is generally greater than that derived from the fusion of CCA and KCCA. At the same time, the greater the degree of correlation, the stronger the relationship between the two components. Therefore, the results in the table can show that SPCCA fusion is superior to traditional CCA fusion.
The results can be analyzed from three perspectives. On the one hand, the KCCA algorithm, which is upgraded from CCA and designed for nonlinear multimodal data, and the SPCCA algorithm, which is more accurate for feature recognition, were used to process the same batch of data. Judging by the difference in activation intensity of different brain regions and the correlation of the data, SPCCA performs well. The algorithm is more suitable for processing synchronous EEG-fMRI data, and the data presentation is more accurate and complete. On the other hand, SPCCA proceeds to analyze the structural status of the brain in IBD patients. According to the treatment results corresponding to the brain region, the Frontal lobe and Temporal lobe regions mentioned in the literature were found in the results. The attention to the brain-gut axis around the world has brought new opportunities for the treatment of IBD. The human gastrointestinal tract and central nervous system are connected by the brain-gut axis, and the discomfort caused by the gastrointestinal tract is easily imaged by the brain-gut axis. The analysis of simultaneous EEG-fMRI fusion concluded that images of the brain regions of IBD patients are highly likely to be present not only in the Frontal and Temporal regions, but also in the Posterior cingulate gyrus, Gyrus rectus, and Amygdala. This means that the Posterior cingulate gyrus, Gyrus rectus, and Amygdala communicate with the gastrointestinal tract in the brain-gut axis. This discovery will definitely open up a new situation for IBD-related medical research. More importantly, the high activation intensity in the Amygdala region indicates that most of the patients with IBD also suffer from major depressive disorder (MDD), and healthcare professionals should pay more attention to the psychological status of patients with IBD.
Based on a series of analyses presented here, simultaneous EEG-fMRI fusion analysis appears to be a potential approach to study functional and structural changes in IBD brain regions. This complex technique is very practical and provides a new perspective for IBD research. At the same time, the SPCCA algorithm can still maintain a certain stability and robustness in complex environments; therefore, it is also suitable for the study of other diseases or task state data. For example, the EEGs of epilepsy patients show characteristics of a strong sudden onset, rapid amplitude change, and a large range of change [80,81,82]. A more stable algorithm for analysis may obtain better results.
5.
Conclusions
In this paper, CCA, KCCA, and SPCCA methods were used to study the differences in brain function between IBD and HC patients. This series of methods uses the complementarity of multimodal data and the interdependence of different dimensions to identify the association between two modal datasets and maximize the correlation between variables to obtain the activation intensity of each region in the brain. SPCCA performs well in synchronous EEG-fMRI data processing, and its calculated correlation components are highly correlated. At the same time, the calculated average activation intensity difference is 60.1, which is 36.9 and 49.8 when compared with the average activation intensity difference calculated by CCA and KCCA, respectively; this also implies a higher robustness of the SPCCA distinguishing features. This paper identifies significant differences in the functioning of IBD and HC brain regions proposed in other literature, as well as significant changes in the Posterior cingulate gyrus, Gyrus rectus, and Amygdala, which have been overlooked in previous research works.
Among them, the presence of the Amygdala means that MDD follows IBD patients closely, and healthcare professionals should pay more attention to the mental health status of IBD patients and provide them with additional support. The results of this study help to further expand the research methods of brain function and contribute to the study of the SPCCA algorithm and brain function changes in IBD diseases. Meanwhile, it also brings new perspectives to the medical research of the brain axis.
The fusion method proposed in this paper has some limitations. (1) Prior knowledge is a necessary condition for the KCCA fusion method. It is important to select appropriate parameters to obtain satisfactory fusion results, though there is no standard to determine the threshold of correlation degree. (2) In the face of a large number of nonlinear problems, the focus of future research will be how to use relevant techniques of sparse representation to study and develop a nonlinear and sparse CCA. (3) Due to the difficulty of simultaneous EEG-fMRI fusion experiments and the extensive personnel involved, the sample size obtained in this paper was relatively small, and the evaluation may not be convincing. In future work, more simultaneous EEG-fMRI fusion data from additional IBD and HC patients will be collected to further validate the results. In addition, a new computational model will be built to analyze the brain differences between IBD and HC, and different subtypes of IBD will be analyzed and discussed.
Acknowledgments
This work was supported by the project of Jiangsu Key Research and Development Plan (BE2021012-2 and BE2021012-5), Changzhou Science and Technology Bureau Plan (CE20225034), Key Laboratory of Brain Machine Collaborative Intelligence Foundation of Zhejiang Province (2020E10010-04), Human-Machine Intelligence, Interaction International Joint Laboratory Project and Interaction International Joint Laboratory Project and Postgraduate Research & Practice Innovation Program of Jiangsu Province (KYCX23_3170).
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: