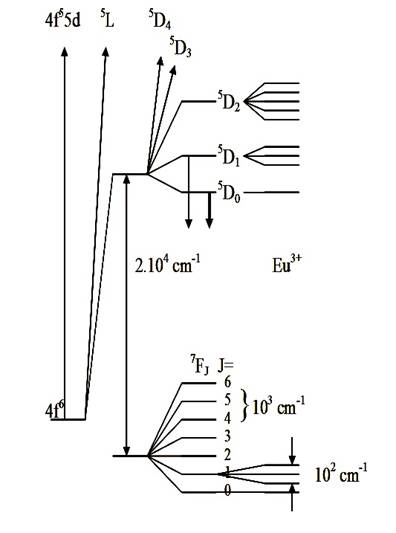
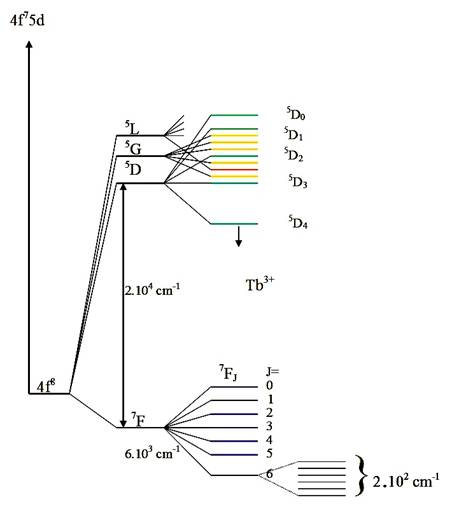
The basic theories of electronic levels and transition probabilities of lanthanides are summarized. Their interpretation allows practical preparation of new materials having application in lighting, solar energy utilization, optoelectronics, biological sensors, active waveguides and highly sensitive bioassays for in vitro detection in medical applications. The ways by which the weak fluorescence arising from electronic transition within the four f-configurations can be intensified will be discussed. This includes the intermixing of the four f-states with ligands of the host matrix, excitation to higher d-electronic states. Additional intensification of luminescence by plasmonic interaction with gold, silver and copper nanoparticles will be discussed. A short history of the time development of the research and the names of the scientists who made the major contribution of our understanding of lanthanides spectroscopy are presented.
1.
Introduction
The arm is an important part of the human body, and human participation in various social activities is inseparable from the arm. However, war, disease and accidents have caused many people to lose a hand or an entire arm, causing a variety of inconveniences in their lives. As a result, the number of amputees fitted with prosthetic hands or arms has increased over the past years. Therefore, the design and manufacture of a humanoid arm with various functions of human arm and the realization of accurate and stable control of humanoid arm have become the hot spot of rehabilitation medical treatment [1,2].
During the contraction of skeletal muscle, a series of biochemical changes take place inside the muscle fibers, and at the same time, action potentials are generated. All the action potentials generated by muscle fibers are superimposed on the electrodes attached to the skin, which is the surface electromyography (sEMG) signal. Thus, the sEMG signal can be used as a control signal for the humanoid arm. Compared with Electroencephalogram (EEG) signal and invasive sEMG signal, sEMG signal is the best control signal for artificial arm, because it is easy, cheap and harmless to control prosthetic hand [3,4,5,6,7]. Although surface sEMG signal acquisition has non-invasive advantages, it will be interfered by skin impedance, electromagnetic interference, surrounding environment and many other factors due to the direct use of electrodes to collect signals at the corresponding muscle positions. In addition, surface sEMG signal itself is weak, with low signal-to-noise ratio (SNR) and poor stability. Under ideal experimental conditions, most of the noise can be eliminated. However, human movement is carried out in various unpredictable environments, so the sEMG signals will be mixed with various inevitable noises and artifacts, which will make the control effect of the prosthesis not meet the expectation. Therefore, it is necessary to use an effective algorithm to de-noising the sEMG signals [8,9].
Wavelet transform has become a common method for nonstationary signal processing [10] and exerts a significant effect. The most common denoising method is wavelet threshold method, including hard and soft thresholds [11]. After processing the wavelet coefficients through the hard threshold method, the wavelet coefficients become discontinuous. Therefore, the original signal may oscillate when it is reconstructed using the processed coefficients. The wavelet coefficients after soft threshold processing are however continuous, and hence the deviation between the processed wavelet coefficients and the original ones will affect the similarity between the reconstructed signal and the original one. In the literature [12,13], an improved wavelet threshold function is presented. When two parameters of the threshold function are adjusted, the processed threshold can be adjusted continuously between soft and hard thresholds. Thus, the performance is altered. Srivastava et al. [14] proposed a new wavelet denoising method for selecting the decomposition levels and noise thresholds. Their threshold function is different from the traditional denoising method. The useful signal can also be easily extracted from the signal with a high magnitude of noise. It has been successful for the sEMG signal denoising method based on wavelet on pre-processing stage of movement recognition of the upper and lower limbs [14,15,16]. Raurale et al. [17] proposed a wrist motion recognition system for embedded platforms to control prostheses and gesture devices. Their research promotes real-time control on embedded devices, but the quality of the signal is not considered in the experiment. Mastinu et al. [18] have come up with a way to control a prosthetic hand, but they can only control the movement of the hand, not the entire arm, which is limited
The empirical mode decomposition (EMD) method, which has numerous advantages for nonstationary signal analysis [19,20,21], was first introduced by Huang et al. [22], and the EMD method can be used for sEMG noise reduction. However, the EMD method has a disadvantage, that is, the so-called mode mixing effect. Wu and Huang proposed an ensemble empirical mode decomposition (EEMD) algorithm to overcome mode mixing [23,24]. Torres et al. [24] proposed the complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) algorithm to improve EEMD. CEEMDAN obtains IMF modes by calculating the unique residue after adding adaptive white Gaussian noise in every stage of EMD. The CEEMDAN algorithm can effectively overcome the mode-mixing problem and reduce the reconstruction error, which has been studied extensively from various fields [25,26,27]. EMD based method may be used alone for sEMG signal denoising [28,29], e.g., EEMD or CEEMDAN decomposition are applied and then certain part of the IMF with high noise is discarded. In such a process some useful signal components may be lost, especially when the signal contains more sharp components like sEMG signal.
In this study, a novel sEMG signal denoising algorithm is proposed based on the EEMD, an improved wavelet threshold, and the extracted IMF1, which combine the advantages of wavelet and EMD. The methodology is validated through experiments on different sEMG signals, and results show that the random noise in the sEMG signal can be effectively denoised, so as to make prosthetic limb control more accurate, fast and robust.
The remainder of this paper is organized as follows. In section 2, we present the proposed new method in detail. In section 3, we discuss the experimental results. In section 4, we draw the conclusion.
2.
Denoising algorithm for sEMG
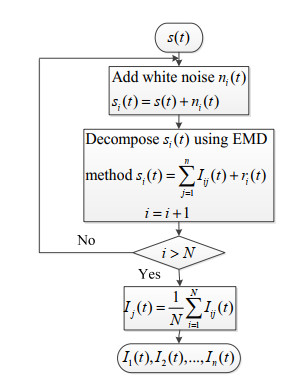
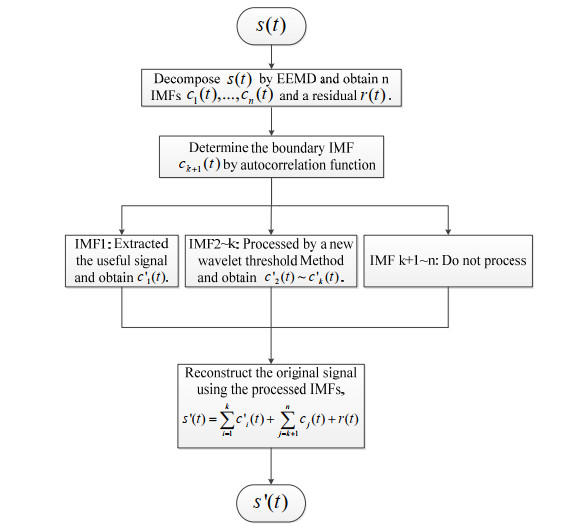
The current de-noising algorithm may not completely de-noising or remove some useful signals, which makes it difficult for the control of the prosthesis to meet people's expectations. We propose a new sEMG denoising method based on EEMD and wavelet transform, whose flow diagram is shown in Figure 1. Using the method the noised sEMG signal is first decomposed into several intrinsic mode functions (IMFs), and each IMF is analyzed by the autocorrelation method to determine the high-frequency IMFs containing random noise [30]. Second, the useful signal from IMF1 is extracted by a new processing method based on wavelet transform [13], and the remainder of the IMFs containing random noise is processed using an improved wavelet threshold denoising method [12]. Finally, the processed high-frequency IMFs and low-frequency IMFs are used to reconstruct the denoised sEMG signals.
The steps of the denoising algorithm are as follows:
(1) Decompose the noised sEMG signal using the EEMD method and obtain n IMFs.
(2) Calculate the autocorrelation function of each IMF and their normalization results.
(3) Calculate the variance of each normalized autocorrelation function to measure the noise component of each IMF.
(4) Find the boundary IMF $ {c}_{k+1}\left(t\right) $ through the variance. If the variance is less than a certain threshold, the corresponding IMF is considered to be a high-frequency IMF with a high noise component, whereas other IMFs are considered to be low-frequency IMFs with a low noise component.
(5) Process $ {c}_{1}\left(t\right) $ alone using wavelet extraction to obtain $ c{\mathrm{\text{'}}}_{1}\left(t\right) $. Process the remaining high-frequency IMFs using an improved wavelet threshold denoising method to obtain $ c{\mathrm{\text{'}}}_{2}\left(t\right) \sim c{\mathrm{\text{'}}}_{k}\left(t\right) $.
(6) Reconstruct the original signal, $ s\mathrm{\text{'}}\left(t\right) = c{\mathrm{\text{'}}}_{1}\left(t\right)+{\sum }_{i = 2}^{k}c{\mathrm{\text{'}}}_{i}\left(t\right)+{\sum }_{j = k+1}^{n}{c}_{j}\left(t\right)+r\left(t\right) $, where $ s\mathrm{\text{'}}\left(t\right) $ is the denoised signal.
2.1. Decompose the signal using EEMD and determine the boundary of IMF
EMD divides signals into several IMFs and a residual [22], as follows:
The EEMD method is proposed based on EMD and white noise to solve the modal mixing problem of the EMD. The details are shown in Figure 2, where N is the time to add the noise.
The autocorrelation function is used to measure the similarity between signals $ x\left(t\right) $ and $ x(t+\tau ) $. The normalized autocorrelation function is defined as follows:
where $ {R}_{x}\left(\tau \right) $ represents the normalized autocorrelation function and $ E(\cdot ) $ denotes the mean value.
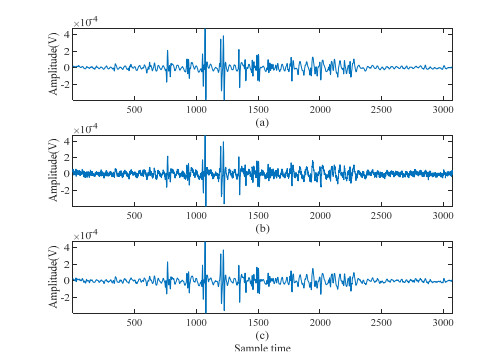
The autocorrelation function diagram of random noise is a sharp pulse. However, the diagram of a noised EMG signal has a certain width. The sEMG signal is decomposed into several IMFs by the EEMD. If the IMF contains more random noise, then the middle part of the autocorrelation function diagram narrows. Therefore, in this study, we determine the noise component of each IMF by the autocorrelation function. Then, we obtain the boundary IMF, which determines the IMFs that should be processed. Finally, we conduct further denoising of the IMF with high noise component.
2.2. Extract the useful component from the first IMF and Remove the noise
In traditional signal denoising using the EEMD method, the first IMF is considered the noise. However, it is realized that the first IMF contains certain amount of useful signal [31]. In particular, some peak positions of the signal often have a small component in the first IMF. The sEMG signals often have some abrupt peaks. Therefore, the extraction of useful signals from IMF1 can reduce signal distortion. In this study, a processing method [13] based on wavelet transform is used to extract the useful signal from IMF1. The details are as follows:
(1) Take the $ {k}^{th} $ level discrete wavelet transform (DWT) of the IMF1, and define the “peak-to-sum ratio” of the detail coefficients, as follows:
where $ {w}_{j} $ is the wavelet coefficient of the level j. If $ {S}_{j}\le 0.2<{S}_{j+1} $, then j is selected as the decomposition level for the wavelet transform of IMF1. For the parameter settings in this subsection please refer to Ref. [13].
(2) Select two thresholds $ {\lambda }_{L} $ and $ {\lambda }_{H} $ to deal with the wavelet coefficients of each level, as follows:
where $ {\lambda }_{j, L} $ and $ {\lambda }_{j, H} $ are the upper and lower thresholds of the decomposition level j, respectively, $ {\mu }_{j} $ and $ {\sigma }_{j} $ are the mean and standard deviation of the wavelet coefficients at decomposition level j, respectively, and $ {\kappa }_{j, L} $, $ {\kappa }_{j, H} $ are the adjustable parameters for each threshold calculated as follows:
① If $ {S}_{j}\le 0.01 $,
② If $ 0.01<{S}_{j}\le 0.2 $, we use the peak positive and negative coefficient values in the following manner:
where $ {S}_{r, L} $ and $ {S}_{r, H} $ are defined as $ {S}_{r, L}\equiv \frac{{S}_{k, L}+{S}_{k+1, L}}{2} $ and $ {S}_{r, H}\equiv \frac{{S}_{k, H}+{S}_{k+1, H}}{2} $, respectively, which mean the reference peak-to-sum coefficient values. $ {S}_{j, L} $ and $ {S}_{j, H} $ are the peak-to-sum ratios of the positive and negative coefficient values, respectively.
(3) After determining the threshold of each layer, hard thresholding is processed in the following manner:
(4) Reconstruct the wavelet coefficients after hard thresholding to obtain the new IMF1, which is the useful signal component extracted from IMF1.
An improved wavelet threshold denoising method is used to remove the noise from high-frequency IMFs.
2.2.1. Selection of the wavelet basis function
When analyzing the original signal using wavelet transform, selecting the appropriate wavelet function is vital. The maximum entropy method is commonly used. First, the signal is decomposed by wavelet transform. Then, the entropy of the wavelet coefficients is calculated. Finally, the wavelet function which obtain the maximum entropy is selected as the optimal wavelet function. The entropy is calculated in the following manner: First, the wavelet coefficient $ \left\{\left.{w}_{j}\right\}\right.(j = \mathrm{1, 2}, \cdots , N) $ is normalized, as follows:
Then, the entropy of the wavelet coefficient is calculated as follows:
For the EMG signal, through numerous experiments, the use of the sym8 wavelet can often derive the maximum entropy and the best denoising effect. Therefore, we will use the sym8 wavelet as the denoising wavelet basis function in subsequent experiments.
2.2.2. Selection of decomposition level
A decomposition level that results in the best denoising effect exists. By testing the white noise characteristics of the obtained wavelet coefficients sequence, we can determine the decomposition level adaptively [32]. The specific process is as follows:
(1) Take one level wavelet transform for the pending signal.
(2) Test the white noise characteristics of the high frequency wavelet coefficients obtained by step (1). If the coefficients belong to white noise, then we continue decompose to obtain the second-level high frequency wavelet coefficients and the white noise characteristics is tested. This process is repeated until the wavelet coefficients of one level do not belong to white noise.
(3) According to Step (2), if Step (2) decomposes n times, then the selected decomposition level is n − 1.
2.2.3. Improved threshold function
A novel improved two-parameter threshold function [12] is used in this study to overcome the disadvantages of the soft and hard threshold functions. By adjusting two parameters of the threshold function, we can change the denoising performance by adjusting the threshold value through different parameters in different circumstances.
The improved threshold function is defined as follows:
where $ \alpha $ and $ \beta $ are variable parameters and $ \beta $ is an integer [12],
3.
Experimental results and discussions
In this experiment, the original sEMG signal was obtained from the standard database, BioPatRec open source platform [33]. The sampling frequency is 2000 Hz, bandwidth at 20–400Hz. The sampling duration is 3–4 s. Part of the signal generated by one motion was selected, and white noise was added to obtain the noised sEMG signal. The experiment was recorded from four bipolar electrodes, distributed on average about a third of the way up the forearm, at a sampling frequency of 2 KHZ and a resolution of 14 bits. The average age of the subjects was 33.9 ± 13 years, and 60% of them were male. Six motion categories (hand opening/closing, wrist flexion and extension, forearm inward and outward rotation) were investigated using four disposable pairs of electrodes, using the same method as offline evaluation. Subjects were visually guided through the biomedical recording user interface. Each movement was repeated three times for three seconds, with the same length of rest between each contraction. The intensity of muscle contraction is required to be around 70–80% of the maximum voluntary contraction, which can be visually verified by the total sEMG strength during muscle contraction.
In this section, first, the sEMG signal produced by the flexor carpi radialis when bending the elbow is selected as the research object. Then, 10 dB Gaussian white noise was added to the sEMG signal to obtain a noised sEMG signal.
3.1. Experiment procedure
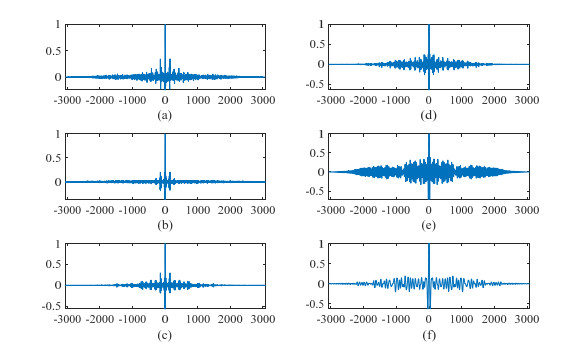
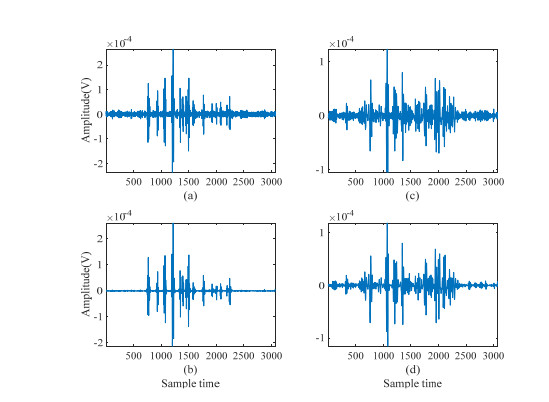
The noised sEMG signal is decomposed into several IMFs and one residue by the EEMD method to reduce the noise. Figure 3 shows the noised sEMG signal and the first five IMFs.
The normalized autocorrelation function of each IMF and their variance are calculated. Figure 4 shows the normalized autocorrelation function of the first five IMFs. Table 1 shows the variance of each normalized autocorrelation function. According to a large number of experimental results, the threshold of the variance is set to 0.005. The variance of the first three IMFs’ normalized autocorrelation function are less than 0.005, whereas that of the others are greater than 0.005. From the properties of the autocorrelation function and the variance threshold method, we need a de-noising algorithm to make the original signal undergo EEMD decomposition, so that the variance of the first three IMF components is also less than 0.05. Because of the high noise component of the high frequency IMF will cause a large deviation in the control of the prosthesis.
During signal denoising by the traditional EMD or EEMD method, the first IMF is usually regarded as noise and discarded. Indeed, the noise will be eliminated. However, in this manner, the useful signal component in IMF1 is also discarded. After reconstructing the signal, many parts are distorted. If some useful components are treated as noise removal, the details of some people's movements may not be collected, which is one of the reasons why the current de-noising algorithm is not effective in practical application.
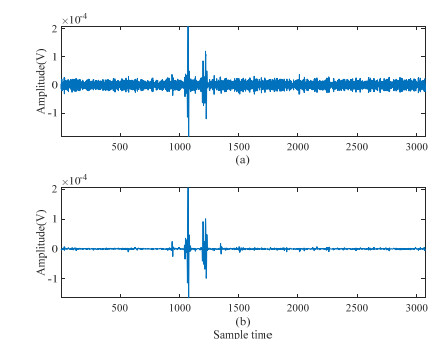
The first IMF is shown in Figure 3(b). Clearly, most of IMF1 are random noise, but some are still useful signals. Given that the sEMG signals often have some peaks, some useful components from the mutated peaks exist in IMF1.
A wavelet extraction is used to improve the denoising effect of the sEMG signal, and the useful signal component extracted from IMF1 is shown in Figure 5.
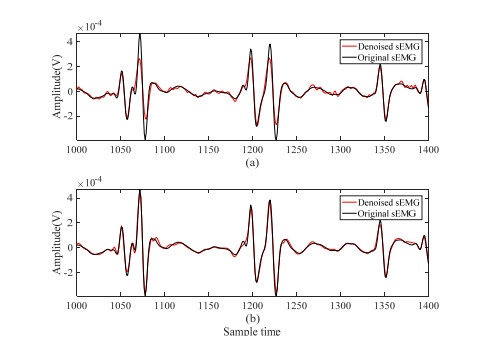
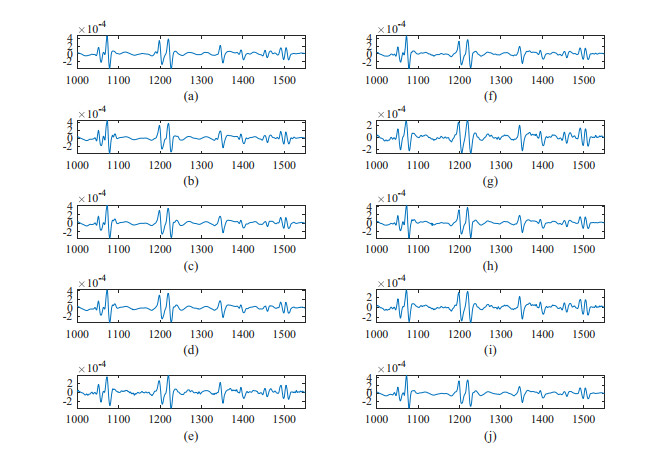
Figure 6 shows the denoising effect with IMF1 discarded and IMF1 processed. The denoised sEMG signal and original sEMG signal are part of the complete signal from sampling points 1,000 to 1,400. As shown in Figure 6(a), the denoised sEMG signal obtained using the traditional EEMD method is compared with the original sEMG signal, and some peak parts of the sEMG signal are lost.
On the contrary, Figure 6(b) illustrates that the peak parts of the sEMG signal are not lost when the useful signal component extracted from the IMF1 is added before reconstructing the signal. This allows us to eliminate unwanted noise while preserving the useful details of human motion signals, thus greatly improving the accuracy and robustness of prosthetic control.
The remainder of the high-frequency IMF, IMF2, and IMF3 are processed by the improved wavelet threshold denoising method. Figure 7 shows the original IMF2 and IMF3 and the processed IMF2 and IMF3.
We reconstruct the original signal. Figure 8 shows the original sEMG signal, noised sEMG signal, and denoised sEMG signal.
3.2. Experimental results
Figures 9(a) to 9(h) show the denoising results of the noised sEMG signal using different denoising methods. EEMDWT means the proposed new method based on EEMD and wavelet transform. EMDWT means the method based on EMD and wavelet transform. CEEMDAN & WT means the method based on CEEMDAN and wavelet transform.
First, 5, 10, 15, and 20 dB Gaussian white noise were added to the noise-free sEMG signal to illustrate the advantages of the proposed algorithm quantitatively. Then, the traditional method and the proposed improved method are used to denoise the signal. Signal-to-noise ratio (SNR), Peak Signal-to-Noise Ratio (PSNR) and root mean square (RMSE) will be used as the indices of the denoising effect. SNR defines the signal energy with respect to the energy of the error. PSNR is an engineering term for the ratio between the maximum possible power of a signal and the power of corrupting noise that affects the fidelity of its representation. RMSE defines the energy of the error signal during denoising. SNR, PSNR and RMSE are defined as follows:
where $ {x}_{i} $ is the original sEMG signal, $ {\widehat{x}}_{i} $ is the denoised sEMG signal, N is the signal length, $ MSE = RMS{E}^{2} $ and $ MA{X}_{{x}_{i}} $ is the maximum of $ {x}_{i} $.
Table 2 presents the performance indices computed under different noise intensities by various denoising methods. The SNR, PSNR and RMSE values are the average value of ten experiments.
Table 2 indicates that the improved threshold methods had higher SNR, PSNR and lower RMSE than the traditional threshold methods. In all methods, the proposed new method EEMDWT had the highest SNR, PSNR and lowest RMSE, which illustrates the superiority of the proposed new method over the other methods to denoise the sEMG signal.
In the experiment, we also selected the sEMG signal produced by the flexor carpi radialis when bending the wrist to verify the superiority of the proposed new method for the sEMG signal produced by different motions. The selected sEMG signal was processed. Table 3 shows the performance indices computed under different noise intensities by various denoising methods.
As shown in Table 3, the proposed new method has the highest SNR, PSNR and lowest RMSE. The denoising effect of the traditional hard and soft wavelet threshold methods is poor. Tables 2 and 3 show the denoising effect of the sEMG signal produced by two motions on the same muscle. We observe that the denoising effect of traditional EMD, EEMD and CEEMDAN are unstable for different sEMG signals. As for CEEMDAN & WT, the performance may sometimes be superb and sometimes poor, leading to a lower average value than EEMDWT. This instability of CEEMDAN & WT makes us choose EEMD in the proposed method.
In the experiment, the sEMG signals produced by the soleus when rotating and lifting the foot were selected to verify the superiority of the proposed new method for sEMG signals produced by different muscles. Tables 4 and 5 show the results. The proposed new method always had a significant denoising effect compared with the other methods.
In summary, this study aimed to analyze the method of denoising the sEMG signal and propose a new effective method to improve the robustness and accuracy of prosthetic control. As shown in Tables 2 to 5, the improved threshold method always has a better effect than the traditional hard and soft threshold denoising methods. Therefore, in the proposed new method, the improved threshold method is used to remove the noise in the high-frequency IMFs. In the traditional EMD based methods, the denoising effect is unstable. The effect may sometimes be good, but it may sometimes be bad, which depends on the sEMG signal. In three combination methods, EMDWT, EEMDWT and CEEMDAN & WT, the IMFs are processed in the same manner, but the decomposition method is different. The combined method EMDWT based on EMD has a good denoising effect. However, the denoising effect is not good enough because of the drawback of mode mixing. The combined method CEEMDAN & WT based on CEEMDAN also has a good denoising effect. However, the denoising effect is not good enough because of its instability. Therefore, the proposed method selects the EEMD method as the decomposition method, which can overcome mode mixing and have a stable denoising effect. As shown in each table, the proposed methods all have the best denoising effect. The results illustrate that the proposed algorithm can improve the robustness of emg to changing noises. In addition, in the case of low or no noise, there is no defect of information loss, which plays a significant role in promoting the field of prosthetic limb control and medical rehabilitation.
4.
Discussions and conclusions
Prosthetic limb control is currently the focus of rehabilitation in the field of medical rehabilitation and the signal to control the prosthesis must be of high quality. Therefore, how to obtain pure EMG signals is an important issue. Since its birth, EMD has been widely used in various fields of signal processing and analysis. However, the modal decomposition method has some shortcomings in practical applications, such as modal aliasing, which greatly hinders its further application in practice. There are two reasons for modal aliasing: on the one hand, it is related to the EMD algorithm itself; on the other hand, the frequency characteristics of the original signal will also affect the decomposition result, and even produce modal aliasing. For example, white noise residuals and false modes after EEMD decomposition, and as the EEMD method becomes more and more widely used, the defects of the EEMD method gradually become prominent. However, EEMD cannot effectively solve the modal aliasing phenomenon, and effective IMF requires manual screening. Other scholars have proposed improved EEMD methods based on the EEMD method, such as SVM-based EEMD improvement methods, complementary generalized empirical mode decomposition (CEEMD) and other auxiliary methods in noise, and complementary set overall empirical mode decomposition (CEEMD) The generalized empirical mode decomposition (ceemdan) of the complete auxiliary noise set restores the integrity of the emd decomposition, but these methods require many iterations, long calculation time, and low decomposition efficiency. In addition to EEMD, wavelet transform plays an important role in non-stationary signal processing. The most commonly used denoising method is wavelet threshold method, including hard threshold method and soft threshold method. The wavelet coefficients become discontinuous after hard thresholding. Therefore, when reconstructing the original signal with the processed wavelet coefficients, oscillations may occur in some places. Although the wavelet coefficients obtained after soft threshold processing are continuous, the deviation between the processed wavelet coefficients and the original coefficients will affect the degree of approximation between the reconstructed signal and the original signal.
In order to solve the problems of existing denoising algorithms, this paper proposes a new sEMG signal denoising algorithm based on EEMD. This algorithm is an improved wavelet threshold algorithm and extracts useful signal components from IMF1. The noisy surface EMG signal is decomposed into a series of internal mode functions. Through autocorrelation analysis, the high frequency internal mode function containing random noise is determined. A new method is used to process the first IMF with the most random noise to extract useful signal components. For other internal model functions containing random noise, an improved wavelet threshold is used to denoise. Finally, reconstruct the remaining internal mode functions to obtain clean surface EMG signals. The surface EMG signals generated by the flexor carpi radialis and soleus muscles during elbow flexion, wrist rotation, and foot lift were verified experimentally. As mentioned earlier, we use SNR, PSNR and RMSE as quality estimators for denoising. The results show that the method has high signal-to-noise ratio, peak signal-to-noise ratio and the lowest root mean square error, and can stably remove random noise in surface EMG signals, and the effect is significant. This work lays the foundation for the subsequent study of EMG signal feature extraction and action recognition, and ensures its usability in prosthetic control.
In this study, we found that CEEMDAN & WT can sometimes achieve good results, but its performance lacks stability. Making this method feasible will be one of our future research directions. If this method can achieve a stable denoising effect, it will greatly promote the process of prosthesis control and medical rehabilitation. At present, the algorithm has a good denoising effect under the interference of white noise, but no experiments have been carried out on motion artifact noise and electromagnetic interference noise. In future work, we will try to extract these noise signals and further verify the effect of our algorithm.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Nos. 61971169, and 60903084), and Jinhua Science and Technology Bureau (Nos. 2019–3–020 and 2020–3–036).
Conflict of interest
No potential conflict of interest was reported by the authors.









 DownLoad:
DownLoad: