1. Introduction
It is widely recognized that adenosine triphosphate (ATP) acts as an extracellular messenger by activating purinergic receptors via autocrine and paracrine signaling [1]. In addition to its physiological role, an increase in extracellular ATP concentrations has been implicated as a “danger signal” or “danger-associate molecular pattern (DAMP)” in the pathophysiology of pulmonary diseases such as cystic fibrosis, asthma, chronic obstructive pulmonary disease (COPD) and pulmonary fibrosis [2,3,4,5,6]. Therefore, the concentration of extracellular ATP in vivo is strictly controlled at a baseline steady state by balancing the amounts of ATP release and hydrolysis of ATP by ecto-ATPases [7,8]. In the respiratory system, ATP is released from various kinds of cells including neurons, immune cells, cancer cells, airway epithelial cells, alveolar epithelial cells, airway smooth muscle (ASM) cells, lung fibroblasts and pulmonary artery endothelial cells in response to chemical and mechanical stimuli [9,10,11,12,13,14,15]. In this review, we focus on cellular ATP release, specifically methods for visualization and mechanisms, in the lung and airway resident cells.
2. Roles of Extracellular ATP in Normal Respiratory Physiology and Pathogenesis of Respiratory Diseases
ATP plays a pivotal role in homeostasis of the airway by regulating epithelial mucociliary clearance and host defenses against bacterial infection [1]. The effects of extracellular purine nucleotides are mediated by their specific P2 receptors, subclassified as P2X and P2Y receptors [1]. P2X receptors are members of Ca2+-permeable ion channels, while P2Y receptors are coupled to G proteins [16]. Extracellular ATP causes anion secretion from airway epithelial cells [17,18] and stimulates surfactant secretion from type II alveolar epithelial cells [19]. ATP and its metabolite adenosine are important luminal autocrine and paracrine signals that regulate the hydration of airway epithelial cells [20,21]. In the lung, ATP released from alveolar epithelial cells stimulates endothelial nitric oxide (NO) production by pulmonary microvascular endothelial cells [22], indicating that ATP is involved in regulation of mechanisms of gas exchange by affecting microvascular circulation.
Cystic fibrosis lung disease, an extremely rare disease in Japanese, is a hereditary disease caused by a mutation in the cystic fibrosis transmembrane regulator (CFTR) gene [23]. Because CFTR is essential for maintaining water balance via the transport of Cl- ions across cell membranes of airway epithelial cells, its dysfunction results in the production of thick mucus and airway dehydration in patients with cystic fibrosis [1,23]. The levels of lipoxin A4, which is synthesized from arachidonic acid by the action of 5-lipoxygenase, have been reported to be decreased in cystic fibrosis [24]. Application of lipoxin A4 to airway epithelial cell lines derived from cystic fibrosis induces ATP release and subsequent activation of P2Y11 receptor, which leads to an increase in height of airway surface liquid layer [25]. Therefore, lipoxin A4 and ATP/purinergic signaling is expected as potentially a novel therapy for patients with cystic fibrosis lung disease [1].
In addition to its physiological roles, extracellular ATP is recognized as one of the DAMPs, which contribute to apoptosis and inflammation in the lung and airway [26]. Therefore, extracellular ATP and purinergic signaling are considered to be involved in various respiratory diseases including asthma, COPD, pulmonary fibrosis, lung injury and lung cancer [1,3,4,9,15,27,28]. Lung hypoxia causes ATP release, which leads to proliferation of adventitial fibroblasts of the pulmonary artery and induces transformation to myofibroblasts via autocrine/paracrine mechanisms [29], indicating the role of ATP in vascular remodeling inpulmonary arterial hypertension. A blockade of purine receptors may represent a potential therapy for abnormal inflammatory responses to extracellular ATP [30]. Here, we briefly summarize examples of the roles of extracellular ATP in the pathogenesis of asthma, COPD, pulmonary fibrosis and lung injury.
2.1. Asthma and COPD
An association between ATP and the pathogenesis of asthma and COPD has been proposed [1,2,4,9,31,32]. Contraction of ASM, which is regulated by intracellular Ca2+ concentrations ([Ca2+]i) and sensitivity to intracellular Ca2+, plays a central role in the airway narrowing of asthma and is partially involved in the pathophysiology of COPD [33]. Activation of P2X and P2Y receptors by ATP causes contraction of ASM tissues [34,35]. Extracellular ATP directly mobilizes [Ca2+]i in ASM cells [34,36,37]. In tracheal smooth muscle tissues isolated from guinea pigs, ATP enhances methacholine-induced contraction [38]. This agonist-synergism of purinergic and muscarinic receptors mediated by the Ca2+ sensitivity of contractile proteins [38] may lead to airway hyperresponsiveness in patients with asthma. The binding of extracellular ATP to P2X and P2Y receptors induces the recruitment and activation of inflammatory cells such as neutrophils, macrophages and dendritic cells [39]. Mortaz et al. demonstrated that exposure to cigarette smoke leads to the release of ATP into the airways, which may induce release of IL-8 and elastase by neutrophils [28], both of which are directly related to development of pulmonary emphysema and inflammatory response in the pathophysiology of COPD. There is evidence that ATP accumulates in the airways of patients with asthma and COPD [3,28]. Thus, it is suggested that ATP contributes to contraction of ASM and inflammation in the pathophysiology of asthma and COPD.
2.2. Pulmonary fibrosis and lung injury
A major cause of progressive pulmonary fibrosis is dysregulated wound healing after lung inflammation or damage in patients with idiopathic pulmonary fibrosis (IPF) or severe lung injury such as acute respiratory distress syndrome (ARDS). ATP concentrations in bronchoalveolar lavage fluid are increased in patients with IPF and murine models of experimental lung fibrosis [5]. Extracellular ATP and purinergic signaling plays an important role in the pathogenesis of pulmonary fibrosis [40]. Previous studies have shown that ATP regulates cellular properties and differentiation of lung fibroblasts, a key player in lung fibrosis. ATP elevates [Ca2+]i and induces expression of P2Y6 and P2Y11 receptor genes in human lung fibroblasts [41].
Mechanical cues including shear stress, matrix stiffness and stretching are involved in the mechanisms underlying the pathogenesis of pulmonary fibrosis and lung injury [42,43,44,45]. These mechanical stimuli regulate cellular properties such as proliferation, differentiation, migration, cytokine production and ion channel gating via activating mechanotransduction in the lung and airway resident cells [46,47,48,49,50,51,52]. In mechanically ventilated patients with respiratory failure due to acute lung injury, ARDS and acute exacerbation of IPF, the lung is exposed to excessive stretch, which often causes further damage and fibrosis, called ventilator-induced lung injury (VILI) [53,54,55]. In rat models of VILI, ATP levels of bronchoalveolar lavage fluid were significantly increased by high pressure mechanical ventilation [56]. Intratracheal ATP administration also directly increased pulmonary edema [56]. These findings further suggest that ATP acts as an inflammatory mediator and regulates permeability of pulmonary microvasculature in pathophysiology of VILI.
3. Cellular ATP Releasefrom Lung and Airway Cells
ATP is released from cells upon cellular injury as a “find-me signal” as well as from pathogens in diseased conditions [57]. Moreover, ATP is released from normal cells as a physiological phenomenon [8,58,59]. For example, ATP released from vascular endothelial cells in response to shear stress by fluid flow tightly regulates pulmonary circulation [60]. Endothelial cells of mice lacking P2X4 channels fail to induce [Ca2+]i elevation and NO production in response to blood flow, which results in impaired flow-dependent control of vascular tone and remodeling [14,15,61]. In addition to physiological phenomena, cellular ATP release is enhanced by stress conditions such as inflammatory processes, hypoxia and mechanical stresses without cell damage. Mechanical stresses such as stretch and hypotonic cell swelling induce ATP release from the cells including A549 lung adenocarcinoma cell lines, Calu-3 cells, airway epithelial cells, ASM cells and lung fibroblasts [12,13,40,62,63,64,65]. In several kinds of cell types, mechanically-induced ATP regulates Ca2+ signaling, a universal second messenger for most important cellular functions, via an autocrine/paracrine mechanism. Shear stress evokes ATP release, which induces subsequent intracellular Ca2+ waves in pulmonary artery endothelial cells [14]. In HaCaT keratinocytes, ATP released in response to mechanical stretch leads to a subsequent [Ca2+]i elevation by activating P2Y receptors [49]. Inconsistent with these findings, the [Ca2+]i elevation caused by mechanical stretch was not inhibited by ATP diphosphohydrolase apyrase or the purinergic receptor antagonist suramin in primary human lung fibroblasts [12]. Thus, the contribution of autocrine/paracrine mechanisms by released ATP on regulation of [Ca2+]i differs among cell types.
3.1. Measurements of extracellular ATP concentrations
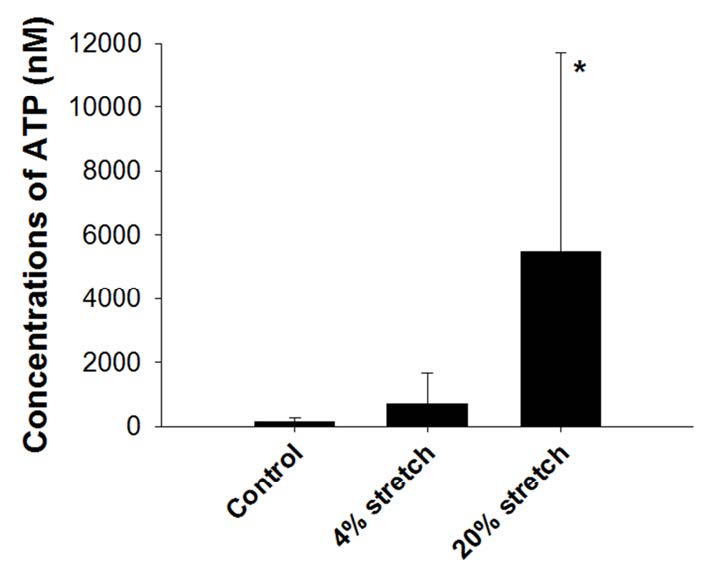
The standard technique to assess extracellular ATP in bulk solutions is observing the bioluminescence of the ATP-dependent luciferase-mediated oxidation of luciferin. This luciferin-luciferase (L-L) biuoluminescence assay is a useful tool to quantify ATP concentrations in bulk media both in vitro and in vivo. An example for measurements of ATP released from human pulmonary microvascular endothelial cells is shown in Figure 1. Using a cell stretch apparatus, uniaxial cyclic stretch (30 cycle/min for 15 min) was applied to the silicone chamber on which the cells were grown. The bulk concentrations of ATP in the cell culture supernatant were significantly elevated by 20% strain but not by 4% strain (Figure 1).
3.2. Visualization of released ATP
Several laboratories have attempted to visualize the ATP release from individual cells in real time using biosensor techniques [14,58,66,67,68,69]. As for fluorescent methods, Corriden et al. utilized a tandem-enzyme system that generates fluorescent NADPH when ATP is present and visualizes released ATP from individual Jurkat T cells and human neutrophils [70]. Recently, using novel small molecular fluorescent ATP probes 1-2Zn (II) (water soluble) and 2-2Zn (II) (membrane bounded), developed by Ojida et al. [71,72], Ledderose et al. demonstrated that immune stimulation of neutrophils and T cells caused an instantaneous ATP release, followed by a second phase of ATP release that was localized to the immune synapse of T cells or the leading edge of polarized neutrophils [73]. Combining these ATP imaging with mitochondrial probes provided evidence for a close spatial relationship between mitochondrial activation and localized ATP release in these immune cells [73].
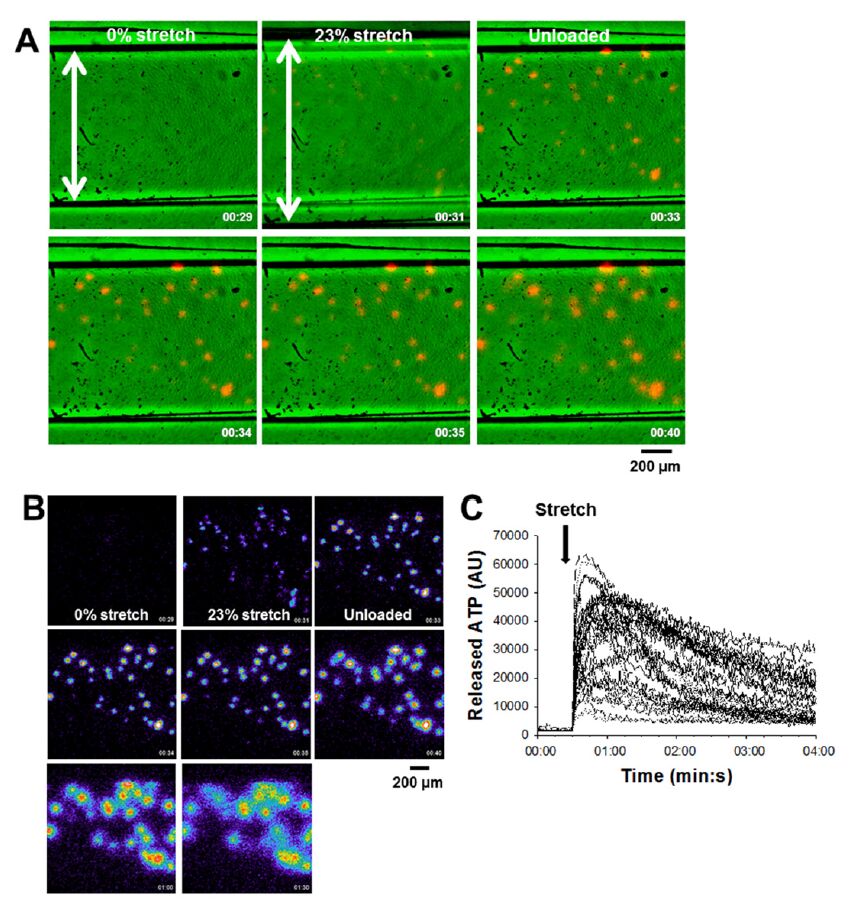
As for bioluminescent methods using L-L, Nakamura et al. developed a novel chemiluminescence imaging method by utilizing a biotin-luciferase chimera protein that can be stably immobilized on a biotinylated cell surface with streptavidin [67]. Using this probe and high-sensitive EM-CCD camera, Yamamoto et al. demonstrated that the localized ATP release in response to fluid shear stress occurred at caveolae in pulmonary artery endothelial cells [14]. Furuya et al. improved the luminescence imaging using an image intensifier with EM-CCD camera under a upright microscope and enabled simultaneous observation of bioluminescence of ATP and differential interference contrast (DIC) images of the cells and tissues using infrared (IR) optics [13,49,65,69]. Using this imaging system coupled with a cell-stretching apparatus, we visualized the extracellular ATP released from human ASM cells [13] and pulmonary microvascular endothelial cells in response to a single mechanical stretch in real time. Figure 2A shows representative luminescent images of released ATP (red) and IR-DIC images for pulmonary microvascular endothelial cells (green) during stretching (23% strain, 1 s) (see also Supplemental movie E1). Although ATP responses to stretch were increase in number of the responded cells with stretching strength, the spatial distribution of releasing cells were restricted and heterogeneous even in cultured homogeneous cells, consistent with findings in mammary epithelial cells, ASM cells and A549 cells [13,65,69]. Figure 2B and 2C show the pseudo color images of the luminescence and the time course of the luminescence changes in 30 responded cells, respectively. The intensity and duration of ATP release from individual cells were rather variable. The duration of ATP release was in the range from about 10 to 80 s and seemed to be separated into two groups, fast and slow. Taken together, the real-time ATP imaging has an advantage in assessing cell populations with heterogeneous responsibility as well as in analyzing kinetic aspects of released ATP at the single cell and tissue levels [13,69].
Recently, Furuya et al. have successfully visualized inflation induced ATP release in the rat lung tissue ex vivo [74]. With L-L solution introduced into airspaces brief inflation of the lung (1 s, ~20 cm H2O) induced transient ATP release in a limited number of air-inflated alveolar sacs. Released ATP remained spatially restricted to single alveolar sacs or their clusters. With L-L introduced into blood vessels, inflation induced transient ATP release, which occurred in small patch-like areas, the size of alveolar sacs and spread to surrounding capillaries. Findings suggest that physiological and pathophysiological inflation of the lung induces ATP release in both alveoli sacs and the surrounding blood capillary network and the functional units of ATP release presumably consist of alveolar sacs or their clusters [74]. These imaging approaches will enable future investigations of ATP release in tissues, organs and in vivo, giving new insights into the working mechanisms and complexity of the purinergic signaling in the respiratory system.
4. Mechanisms of ATP Release
Multiple mechanisms and pathways by which cells release ATP during mechanical deformation and chemical stimulation have been proposed [59,75]. It has been suggested that various kinds of membrane channels such as connexin and pannexin hemichannels, maxi-anion channels, volume-regulated anion channels, CFTR and P2X7 receptor mediate ATP release [8,49,58,76,77]. In addition to a conductive pathway via channels, exocytosis of ATP-enriched vesicles is involved in the mechanisms of ATP release [8,78]. Here, we summarize the role of vesicular exocytosis in ATP release.
4.1. Vesicular exocytosis in the mechanism of stretch-induced ATP release
Staining of cellular ATP stores with quinacrine or the fluorescent ATP analogue reveals a distribution of fluorescence consistent with ATP-enriched vesicles [68,78,79]. Thus, an active transport system for ATP uptake into vesicles is present. Sawada et al. identified SLC17A9 protein as the vesicular nucleotide transporter (VNUT) that plays a central role in the mechanisms of ATP uptake into intracellular vesicles [80]. There is strong evidence that the vesicular exocytosis is the major pathway for cellular ATP release in the lung and airway cells [13,64,65]. Exocytosis of vesicles is regulated by intracellular free Ca2+ [81,82]. Okada et al. found that inhibitors of Ca2+-regulated vesicular exocytosis such as 1, 2-bis(o-aminophenoxy)ethane-N, N, N’, N’-tetraacetic acid tetraacetoxymethyl ester (BAPTA-AM), an intracellular Ca2+ chelator, N-ethylmaleimide (NEM), an inhibitor of the fusion of vesicles to the plasma membrane and bafilomycin A1, which depletes ATP within vesicular pools by inhibiting vesicular H+-ATPase, significantly inhibited the ATP release induced by hypotonic stress in human bronchial epithelial cells [64]. Similar results were observed in primary human ASM cells. BAPTA-AM, NEM, bafilomycin A1 and monensin, an inhibitor of vesicular transport, significantly inhibited the increase of ATP concentrations in the cell supernatant induced by cyclic stretch in human ASM cells [13]. The results in the previous studies further suggest that transport of ATP into vesicular pools plays a role in the ATP release from human ASM cells, A549 adenocarcinoma cell lines and normal airway epithelial cells [13,64]. Sesma et al. found that VNUT regulates the ATP concentration in mucin granules as well as the amount of released ATP in human airway epithelial Calu-3 cells [83]. Expression of VNUT mRNA and ATP release was enhanced by inflammation in primary human bronchial epithelial cells obtained from patients with cystic fibrosis and normal subjects [64]. Therefore, VNUT plays a key role in ATP uptake and subsequent ATP release via vesicular exocytosis in the lung and airway cells.
It is likely that the relative contribution of vesicular exocytosis and conductive pathways to the amount of ATP released depends on cell type. The stretch-induced ATP release from human ASM cells was not significantly affected by carbenoxolone, an inhibitor of pannexins and connexins [13]. Similar findings were observed in A549 cells [65]. In contrast, pannexin 1 contributes to ATP release onto the apical airway surface from normal human bronchial epithelial cells [62]. However, the mechanisms of cellular ATP release have not been fully elucidated.
4.2. Extracellular vesicles and exosomes
Extracellular vesicles, exosomes and membrane-derived microvesicles, are released from the cell. Because extracellular vesicles contain cytoplasmic proteins, cytokines, mRNA and microRNA, they act as important mediators of cell-to-cell communication and the intercellular microenvironment [84]. Moreover, extracellular vesicles are considered to play a role in maintenance of normal lung physiology as well as pathogenesis of respiratory diseases such as COPD and lung cancer[85]. Unlike cytoplasmic vesicles, it is not known whether the released extracellular vesicles contain ATP as a tool for cell-to-cell communication. In macrophages, monocytes, dendritic cells and microglial cells, which express P2X7 receptors, extracellular ATP induces maturation and subsequent release of IL-1β via activating P2X7 receptors [86]. Interestingly, exosome and membrane-derived microvesicles, which contain IL-1β, have been proposed as one of pathways for the ATP-induced IL-1β release [86]. Because an increase in [Ca2+]i has been proposed as a mechanism of formation of membrane-derived microvesicles [87], extracellular ATP or released ATP may regulate the formation of microvesicles via purinergic receptors in the lung and airway cells. Future studies are required to elucidate this possibility.
5. Conclusions
In this review, we focused on the pathophysiology and possible mechanisms of ATP release from the airway and lung cells. However, the precise mechanisms of ATP release from the cell have not been fully elucidated. For example, we know little about how ATP release is related to the dynamics of mitochondria in which ATP is synthetized.Understanding the mechanisms of ATP dynamics will bring important insights into the pathophysiology of respiratory diseases and normal respiratory physiology.
Acknowledgements
This work was supported by JSPS KAKENHI Grant Numbers 25461188 and 16K09578 to S.I. and 24590274 and 15K09174 to K.F. The authors thank Ms. Katherine Ono for providing language help. We thank Dr. Norihiro Takahara for his experimental work.
Conflict of Interest
The authors declare that there is no conflict of interests.









 DownLoad:
DownLoad: