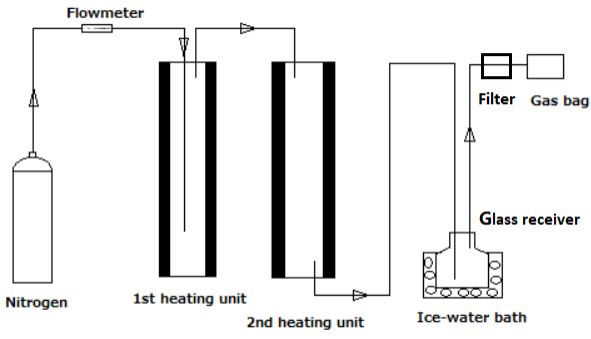
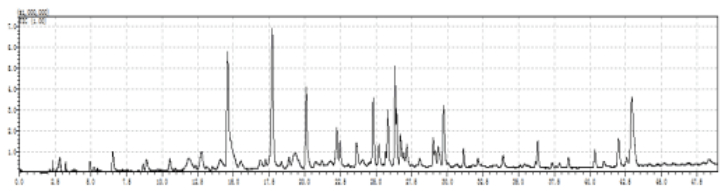
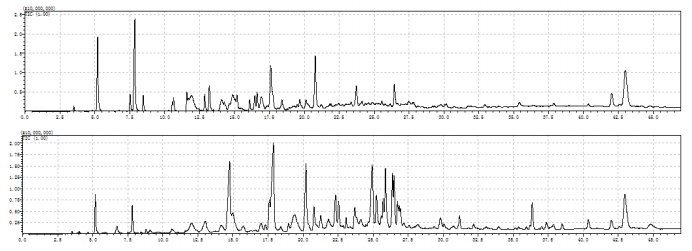
The objective of this research is to explore the possibility to upgrade gasified bio-oil in bench-scale fixed bed reactors with two heating units using the cracking method. The bio-oil is derived from Japanese cedars which are widely distributed in Japan. The catalyst is HZSM-5 zeolite, which is commonly used in bio-oil upgrading. The result showed that by using two heating units, even without catalyst, the upgrading was achieved as well. The catalytic cracking promoted the deoxygenation rate and further improved the quality of the upgraded oil compared with the non-catalytic cracking case. By separating two heating units with different operating condition, the catalytic effect and the deactivation of the catalyst was clarified. The raw bio-oil and the upgraded oil were characterized by measuring their element content, water content and the chemical composition of its organic fraction.
1.
Introduction
Consider a symplectic manifold (M,ω), a coisotropic submanifold N⊆M, and a Hamiltonian diffeomorphism ψ:M→M. The isotropic (or characteristic) distribution TNω on N gives rise to the isotropic foliation on N. A leafwise fixed point for ψ is a point x∈N for which ψ(x) lies in the leaf through x of this foliation. We denote by Fix(ψ,N) the set of such points. A fundamental problem in symplectic geometry is the following:
Problem. Find conditions under which Fix(ψ,N) is non-empty and find lower bounds on its cardinality.
This generalizes the problems of showing that a given Hamiltonian diffeomorphism has a fixed point and that a given Lagrangian submanifold intersects its image under a Hamiltonian diffeomorphism. References for solutions to the general problem are provided in [20,22].
Example(translated points). As explained in [19,p. 97], translated points of the time-1-map of a contact isotopy starting at the identity are leafwise fixed points of the Hamiltonian lift of this map to the symplectization.
We denote
We call N regular (or "fibering") iff there exists a smooth manifold structure on Nω, such that the canonical projection from N to Nω is a smooth submersion.1 Let X be a manifold and h∈C([0,1]×X,M). We call h a semistrong (N,ω)-homotopy iff for every t∈[0,1] there is a leaf F of N that contains the image of {t}×∂X under h.
1Such a structure is unique if it exists. In this case the symplectic quotient of N is well-defined.
We denote by D the closed unit disk in R2. We call (N,ω) (or simply N) adiscal iff every map u∈C(D,M) that sends ∂D=S1 to a leaf of N, is semistrongly (N,ω)-homotopic to a constant map.
The main result of [20] (Theorem 1.1) implies the following. We denote by bi(N) the i-th Z2-Betti-number of N.
Theorem 1.1 (leafwise fixed points for adiscal coisotropic). Assume that (M,ω) is geometrically bounded, N is closed2, regular, and adiscal, and that (N,ψ) is nondegenerate in the sense of [20,p. 105]. Then the following estimate holds:
2This means compact and without boundary.
This bound is sharp if there exists a Z2-perfect Morse function on N, see [20,Theorem 1.2]. The idea of the proof of Theorem 1.1 given in [20], is to find a suitable Lagrangian embedding ιN of N into a geometrically bounded symplectic manifold, see (5) below. We then apply Y. Chekanov's Main Theorem in [3], which implies the result in the Lagrangian case.3 The Lagrangian intersection points of the image of ιN correspond to leafwise fixed points of ψ.
3[20,Theorem 1.1] is formulated in a more general setting than Theorem 1.1. Chekanov's result is needed to deal with that setting, whereas in the setting of Theorem 1.1 Floer's original article [5] suffices.
Similarly to Theorem 1.1, in [21] for a regular N, we defined monotonicity and the minimal Maslov number m(N), and we proved the following result ([21,Theorem 3]):
Theorem 1.2 (leafwise fixed points for monotone coisotropic). Assume that (M,ω) is geometrically bounded or convex at infinity4, N⊆M is closed, monotone, and regular, and (N,ψ) is non-degenerate. Then the following estimate holds:
4[20,Theorem 1.1] is stated for the geometrically bounded case, but the proof goes through in the convex at infinity case.
The idea of the proof of this theorem given in [21], is to use the same Lagrangian embedding as in the proof of Theorem 1.1. We then apply P. Albers' Main Theorem in [2], which states Theorem 1.2 in the Lagrangian case.
Finally, the main result of [22] (Theorem 1) implies that leafwise fixed points exist for an arbitrary closed coisotropic submanifold if the Hamiltonian flow is suitably C0-small. More precisely, it implies the following:
Theorem 1.3 (leafwise fixed points for C0-close coisotropic). Let (M,ω) be a symplectic manifold and N⊆M be a closed coisotropic submanifold. Then there exists a C0-neighbourhood U⊆C(N,M) of the inclusion N→M with the following property. Let (φt)t∈[0,1] be a Hamiltonian flow on M satisfying φt|N∈U, for every t∈[0,1]. If (N,φ1) is nondegenerate then the following estimate holds:
This result is optimal in the sense that the C0-condition cannot be replaced by Hofer smallness of φ1. The idea of the proof of Theorem 1.3 given in [22], is to find a suitable embedding of N as a Lagrangian submanifold ˜N of some symplectic manifold ˜M that is a Weinstein neighbourhood of ˜N, see (7) below. We then use Weinstein's neighbourhood theorem and the existence of Lagrangian intersection points for the zero-section in the cotangent bundle. These points correspond to leafwise fixed points for φ1. Since N is not assumed to be regular in Theorem 1.3, in contrast with Theorems 1.1 and 1.2, we can construct ˜M only locally around ˜N.
The point of this note is to reinterpret the proofs of Theorems 1.1 and 1.2 in terms of a version of Floer homology for an adiscal or monotone regular coisotropic submanifold. I also outline a definition of a local version of Floer homology for an arbitrary closed coisotropic submanifold and use it to reinterpret the proof of Theorem 1.3. Details of the construction of this homology will be carried out elsewhere. For the extreme cases N=M and N Lagrangian, local versions of Floer homology were developed in [7,15,16,4,18,9]; see also the book [17,Section 17.2].
5
5In [1] a Lagrangian Floer homology was constructed that is "local" in a different sense.
Potentially a (more) global version of coisotropic Floer homology may be defined under a suitable condition on N that is weaker than regularity, so that the C0-condition on (φt) in Theorem 1.3 can be relaxed.
6 This may also yield a lower bound on |Fix(ψ,N)| that is higher then the sum of the Betti numbers of N, for a suitably generic pair (ψ,N).
6This can only work under suitable conditions on N. The reason is that by [10,Theorem 1.1], there exists a closed hypersurface N in R2n and a Hamiltonian diffeomorphism on R2n that is arbitrarily Hofer-close to id and has no leafwise fixed points w.r.t. N.
Based on the ideas outlined below, one can define a Floer homology for certain regular contact manifolds and use it to show that a given time-1-map of a contact isotopy has translated points. Namely, consider a closed manifold N and a contact form α on N. Assume that α is regular, i.e., that its symplectic quotient is well-defined. Then N is naturally a smooth principal S1-bundle, which is called a Boothby-Wang fibration. The associated real two-dimensional vector bundle E is equipped with a natural symplectic form, see e.g. [8,proof of Lemma 3,p. 200]. The idea is now to define the Floer homology of (N,α) to be the Floer homology of the circle bundle in E of some radius r. If the symplectic quotient of N is monotone then for a suitable choice of r this circle bundle is a monotone coisotropic submanifold with minimal Maslov number at least 2. Hence its Floer homology is well-defined. Since part of the symplectization of (N,α) symplectically embeds into E, it follows that translated points exist under suitable hypotheses.
Various versions of coisotropic Floer homology may play a role in mirror symmetry, as physicists have realized that the Fukaya category should be enlarged by coisotropic submanifolds, in order to make homological mirror symmetry work, see e.g. [11].
2.
Floer homology for an adiscal or monotone regular coisotropic submanifold
To explain the coisotropic Floer homology in the regular case, consider a geometrically bounded symplectic manifold (M,ω), and a closed, regular coisotropic submanifold N⊆M.
Suppose first also that N is adiscal. We define the Floer homology of N as follows. Let φ=(φt)t∈[0,1] be a Hamiltonian isotopy starting at id, such that (N,φ1) is nondegenerate. We call a point x0∈M a (N,φ)-contractible leafwise fixed point iff the path x:[0,1]→M, x(t):=φt(x0), is semistrongly (N,ω)-homotopic to a constant path.7 We define
7 By definition, for every such point x0, the point x(1)=φ1(x0) lies in the isotropic leaf of x0. Hence x0 is a leafwise fixed point of φ1.
Remark. By definition this direct sum contains one copy of Z2 for each point in Fixc(N,φ).
We now define a collection of boundary operators on CF(N,φ), one for each (N,φ1)-regular time-dependent almost complex structure. To explain this, observe that, since N is regular, Nω carries canonical smooth and symplectic structures AN,ω and ωN. We define
The map ιN is a ˆω-Lagrangian embedding of N into ˆM, see [20,Lemma 3.2]. It follows from [21,Proposition 61,p. 43] that the restriction of the map ιN, given by
is well-defined and injective. A straightforward argument shows that it is surjective.
Let p∈(2,∞) and ψ be a Hamiltonian diffeomorphism on M. We call a t-dependent ˆω-compatible smooth almost complex structure ˆJ on ˆM (N,ψ)-regular, iff the vertical differential of its Cauchy-Riemann operator is surjective for all finite-energy ˆJ-holomorphic strips with compact image and boundary on ˆN and ˆψ(ˆN). (For definitions see [5,Proposition 2.1].8) We define Jreg(N,ψ):=Jreg(M,ω,N,ψ,p) to be the set of all (N,ψ)-regular ˆJ.9 For every ˆJ∈Jreg(N,φ1) we define the Floer boundary operator
8 The exponent p enters the Banach bundle setup of that proposition.
9 It follows from the proof of [5,Proposition 2.1] that this set is dense in the set of all t-dependent ˆω-compatible almost complex structures, and therefore nonempty. See [6,Theorem 5].
to be the (Lagrangian) Floer boundary operator of (ˆM,ˆω,ˆN,ˆφ,ˆJ), where CF(N,φ) is as in (4). (See [5,Definition 3.1].)
To see that this operator is well-defined, recall that it is defined on the direct sum of Z2's indexed by the set occurring on the right hand side of (6).10 Using the bijection (6), we identify this direct sum with CF(N,φ). Hence ∂N,φ,ˆJ is defined between the right spaces.
10 Sometimes this is called the "Z2-vector space spanned by this index set". Here we identify the intersection ˆN∩(ˆφ1)−1(ˆN) with ˆφ1(ˆN)∩ˆN via the map ˆφ1.
We check the conditions of [5,Definition 3.1]. Since N is closed, the same holds for Nω. Since (M,ω) is geometrically bounded, it follows that (ˆM,ˆω) is geometrically bounded. The Lagrangian ˆN is diffeomorphic to N via ιN, and therefore also closed. Since N is adiscal, it follows from [21,Proposition 61,p. 43] that the same holds for ˆN. Since (N,φ1) is nondegenerate, by [20,Lemma 3.2(c)] the intersection of ˆN and ˆφ−1(ˆN) is transverse. Hence the conditions of [5,Definition 3.1] are satisfied, and therefore the boundary operator ∂N,φ,ˆJ is well-defined.11 By [5,Lemma 3.2] it squares to 0. Hence we may define the Floer homology of (N,φ,ˆJ) to be the homology
11In [5] Floer assumes that the symplectic manifold is closed. However, the same construction of Floer homology works for geometrically bounded symplectic manifolds. Here we use that we only consider Floer strips with compact image.
Let G be a Z-grading of the Z2-vector space CF(N,φ), which via the identification (6) is compatible with the Viterbo-Maslov index for strips satisfying Lagrangian boundary conditions.12 Such a G induces a grading on HF(N,φ,ˆJ). For every pair ^J0,^J1∈Jreg(N,φ1) we denote by
12By [5,Proposition 2.4] such a grading exists and each two gradings differ by an additive constant.
the canonical isomorphism provided by the proof of [5,Proposition 3.1,p. 522]. This isomorphism respects the grading G. It does not depend on the choice of G.
Definition 2.1 (Floer homology for adiscal coisotropic). We define the Floer homology of (N,φ) to be
Remarks. ● This is a collection of graded Z2-vector spaces together with grading-preserving isomorphisms.
● Philosophically, the Floer homology of (N,φ) is defined to be HF(N,φ,ˆJ), for some choice of ˆJ. The collection of isomorphisms (Φ^J0,^J1) encodes the sense in which this does "not depend" on this choice.
By the proof of [5,Theorem 1] HF(N,φ) is isomorphic to the singular homology of ˆN (hence of N) with Z2-coefficients. Since HF(N,φ) is generated by the (N,φ)-contractible leafwise fixed points of φ1, this reproves Theorem 1.1.
Suppose now that N is monotone in the sense of [21] and of minimal Maslov number m(N)≥2. 13
13We continue to assume that (M,ω) is geometrically bounded, N is closed and regular, and that (N,φ1) is nondegenerate.
Definition 2.2 (Floer homology for monotone coisotropic). We define the Floer homology of (N,φ) to be the Floer homology of (ˆN,ˆφ), as defined in [13,14].
Since N is monotone, the same holds for ˆN. The minimal Maslov numbers of N and ˆN agree, see the proof of [21,Theorem 3,p. 17]. It follows that the Floer homology of (N,φ) is well-defined. By [2,Corollary 2.1] it is isomorphic to singular homology in degrees i=dimN−m(N)+2,…,m(N)−2. It follows that (2) holds. This reproves Theorem 1.2.
3.
Local Floer homology for an arbitrary coisotropic submanifold
Consider now the situation in which (M,ω) is any symplectic manifold, N an arbitrary closed coisotropic submanifold of M, and φ=(φt) a Hamiltonian flow on M whose restriction to N stays "C0-close" to the inclusion N→M, such that (N,φ1) is nondegenerate. We also fix an ω-compatible almost complex structure J on M. Heuristically, we define the local Floer homology HF(N,φ,J) as follows. Its chain complex is generated by the points x∈Fix(N,φ1), for which there is a "short" path from x to φ1(x) within the isotropic leaf through x.
To explain the boundary operator ∂=∂N,φ,J, we denote by iN:N→M the inclusion map. We equip the product M×N with the presymplectic form ω⊕(−i∗Nω). By [22,Lemma 4] there exists a symplectic submanifold ˜M of M×N that contains the diagonal
as a Lagrangian submanifold. We shrink ˜M, so that it is a Weinstein neighbourhood of ˜N. The flow φ induces a Hamiltonian flow ˜φ that is defined on an open neighbourhood ˜N of ˜M. The structure J induces an almost complex structure ˜J on ˜M that is ˜ω-compatible.
The boundary operator ∂ is now defined to be the boundary operator of the "local Lagrangian Floer homology" of (˜M,˜ω,˜N,˜φ,˜J). This map counts finite energy ˜J-holomorphic strips in ˜M that stay "close" to ˜N, have Viterbo-Maslov index 1, map the lower and upper boundaries of the strip to ˜N and (˜φ1)−1(˜N), and connect two intersection points of ˜N and (˜φ1)−1(˜N). Such points correspond to points x∈Fix(N,φ1), for which there exists a short path from x to φ1(x) within a leaf. (See [22,Lemma 6].)
To understand why heuristically, the boundary operator ∂ is well-defined and squares to zero, observe that ˜N intersects (˜φ1)−1(˜N) transversely, since (N,φ1) is nondegenerate. (See [22,Lemma 7].) Therefore, for generic ˜J
14, the moduli space of ˜J-strips is a 0-dimensional manifold in a natural sense. (Here we divided by the translation action.) It is compact for the following reasons:
14Here one needs to work with a family of almost complex structures depending on the time t.
● Holomorphic strips with boundary on ˜N and (˜φ1)−1(˜N) stay inside some fixed compact neighbourhood of ˜N, provided that ˜φ1 is close enough to the identity. This follows from the fact that there is a neighbourhood ˜U of ˜N and an exhausting ˜J-plurisubharmonic function on ˜U.
● Disks or spheres cannot bubble off. This follows from our assumption that ˜M is a Weinstein neighbourhood of ˜N, which implies that ˜N is an exact Lagrangian in ˜M.
● Index-1-strips generically do not break.
It follows that heuristically, ∂ is well-defined. For similar reasons we have ∂2=0.
Given two choices of symplectic submanifolds ˜M,˜M′⊆M×N containing ˜N, one obtains a symplectomorphism between open neighbourhoods of ˜N in ˜M and ˜M′, by sliding ˜M to ˜M′ along the isotropic leaves of N. This symplectomorphism intertwines the corresponding ˜φ's and ˜J's. It follows that the boundary operator does not depend on the choice of ˜M, and therefore, heuristically, is well-defined.
To make the outlined Floer homology rigorous, the words "close" and "short" used above, need to be made precise. To obtain an object that does not depend on the choice of "closeness", the local Floer homology of (N,J) should really be defined to be the germ of the map
around id:M→M.
By showing that HF(N,φ,J) is isomorphic to the singular homology of ˜N, it should be possible to reproduce the lower bound (1) of Theorem 1.3.
Remark(local presymplectic Floer homology). A presymplectic form on a manifold is a closed two-form with constant rank. By [12,Proposition 3.2] every presymplectic manifold can be coisotropically embedded into some symplectic manifold. By [12,4.5. Théorème on p. 79] each two coisotropic embeddings are equivalent. Hence heuristically, we may define the local Floer homology of a presymplectic manifold to be the local Floer homology of any of its coisotropic embeddings.
Remark (relation between the constructions). Assume that N is regular. Then the constructions of its "global" and local Floer homologies are related as follows. Namely, the symplectic submanifold ˜M⊆M×N can be viewed as a local version of ˆM. More precisely, shrinking ˜M if necessary (so that it still contains ˜N), the manifold ˜M symplectically embeds into ˆM via the map
Acknowledgments
I would like to thank Will Merry for an interesting discussion and the anonymous referees for valuable suggestions.













 DownLoad:
DownLoad: