Hydrodynamic limit for a Fokker-Planck equation with coefficients in Sobolev spaces

1.   Introduction

Fractional partial differential equations (FPDEs) have attracted considerable attention in various fields. Though research shows that many phenomena can be described by FPDEs such as physics ^[1], engineering ^[2], and other sciences ^[3,4]. However, finding the exact solutions of FPDEs by using current analytical methods such as Laplace transform, Green's function, and Fourier-Laplace transform (see ^[5,6] for examples) are often difficult to achieve^[7]. Thus, proposing numerical methods to find approximate solutions of these equations has practical importance. Due to this fact, in recent years a large number of numerical methods have been proposed for solving FPDEs, for instances see ^{[8,9,10,11,12]} and the references therein.

The time fractional diffusion-wave equation is obtained from the classical diffusion-wave equation by replacing the second order time derivative term with a fractional derivative of order $\alpha$, $1 < \alpha < 2$, and it can describe the intermediate process between parabolic diffusion equations and hyperbolic wave equations. Many of the universal mechanical, acoustic and electromagnetic responses can be accurately described by the time fractional diffusion-wave equation, see ^[13,14] for examples. The fourth order space derivative arises in the wave propagation in beams and modeling formation of grooves on a flat surface, thus considerable attention has been devoted to fourth order fractional diffusion-wave equation and its applications, see ^[15]. In this paper, the following nonlinear time fractional diffusion-wave equation with fourth order derivative in space and homogeneous initial boundary conditions will be considered

where $1 < \alpha < 2$, $f(x, t)$ is a known function, $g(u)$ is a nonlinear function of $u$ with $g(0) = 0$ and satisfies the Lipschitz condition, and ${}^{C}_{0}D_{t}^{\alpha}u(x, t)$ denotes the temporal Caputo derivative with order $\alpha$ defined as

Recently, there exist many works on numerical methods for time fractional diffusion-wave equations (TFDWEs), see ^{[16,17,18,19,20,21,22]} and the references therein. Chen et al. ^[17] proposed the method of separation of variables with constructing the implicit difference scheme for fractional diffusion-wave equation with damping. Heydari et al. ^[19] have proposed Legendre wavelets (LWs) for solving TFDWEs where fractional operational matrix of integration for LWs was derived. Bhrawy et al. ^[16] have proposed Jacobi tau spectral procedure combined with the Jacobi operational matrix for solving TFDWEs. Ebadian et al. ^[18] have proposed triangular function (TFs) methods for solving a class of nonlinear TFDWEs where fractional operational matrix of integration for the TFs was derived. Mohammed et al. ^[21] have proposed shifted Legengre collocation scheme and sinc function for solving TFDWEs with variable coefficients. Zhou et al. ^[22] have applied Chebyshev wavelets collocation for solving a class of TFDWEs where fractional integral formula of a single Chebyshev wavelets in the Riemann-Liouville sense was derived. Khalid et al. ^[20] have proposed the third degree modified extended B-spline functions for solving TFDWEs with reaction and damping terms. Some other numerical methods were presented for solving time fractional diffusion equations, one can see ^{[23,24,25,26]} and the references therein.

To the best of our knowledge, there is no existing numerical method which can be used to solve Eq (1.1) neither directly nor by transferring Eq (1.1) into an equivalent integro-differential equation. Thus, the aim of this study is devoted to constructing the high order numerical schemes to solve Eq (1.1), and carrying out the corresponding numerical analysis for the proposed schemes. Herein, we firstly transform Eq (1.1) into the equivalent partial integro-differential equations by using the integral operator. Secondly, the Crank-Nicolson technique is applied to deal with the temporal direction. Then, we use the midpoint formula to discretize the first order derivative, use the weighted and shifted Gr$\ddot{\text{u}}$nwald difference formula to discretize the Caputo derivative, and apply the second order convolution quadrature formula to approximate the first order integral. The classical central difference formula, the fourth order Stephenson scheme, and the fourth order compact difference formula are applied for spatial approximations.

The rest of this paper is organized as follows. In Section 2, some preparations and useful lemmas are provided and discussed. In Section 3, the finite difference scheme is constructed and analyzed. In Section 4, the compact finite difference scheme is deduced, and the convergence and the unconditional stability are strictly proved. Numerical experiments are provided to support the theoretical results in Section 5. Finally, some concluding remarks are given.

2.   Preliminaries

Lemma 2.1. (see Lemma 6.2 in ^[27]) Eq (1.1) is equivalent to the following partial integro-differential equation,

where $F(x, t) = {}_{0}J_{t}f(x, t)$ and ${}_{0}J_{t}$ is first order integral operator, i.e., ${}_{0}J_{t}u(\cdot, t) = \int_{0}^{t}u(\cdot, s)ds$.

To discretize Eq (2.1), we introduce the temporal step size $\tau = T/N$ with a positive integer $N$, $t_n = n\tau$, and $t_{n+1/2} = (n + 1/2)\tau$. Similarly, define the spatial step size $h = L/M$ with a positive integer $M$, and denote $x_i = ih$. Then, define a grid function space $\Theta_h = \{v_i^n|\text{ }0 \leq n \leq N, 0 \leq i \leq M, v^n_0 = v^n_M = 0\}$, and introduce the following notations, inner product, and norm, i.e., for $u^n, v^n \in \Theta_h$, we define

Lemma 2.2. (see Lemmas 2.2 and 2.3 in ^[28]) If $u(\cdot, t) \in C^2([0, T])$ and $0 < \gamma < 1$, then it holds

Furthermore, if $u(\cdot, t)\in C^3([0, T])$, then we have

and

Lemma 2.3. (see Theorem 4.1 in ^[29]) Let $\{\omega_{k}\}$ be the weights from generating function $\left(3/2 - 2z + z^2/2\right)^{-1}$, i.e., $\omega_k = 1-3^{-(k+1)}$. If $u(\cdot, t) \in C^2\left([0, T]\right)$ and $u(\cdot, 0) = u_t(\cdot, 0) = 0$, then we have

Lemma 2.4. (see Theorem 2.4 in ^[30]) For $u(\cdot, t) \in L^1(\mathbb{R})$, ${}_{-\infty}^{RL}D_{t}^{\gamma +2}u(\cdot, t)$ and its Fourier transform belong to $L^1(\mathbb{R})$, if we use the weighted and shifted Gr$\ddot{\mathit{\text{u}}}$nwald difference operator to approximate the Riemann-Liouville derivative, then it holds

where

and $c_j^{(\gamma)} = (-1)^j\left(\begin{array}{c} \gamma \\ j \end{array}\right)$ for $j\geq 0$.

Lemma 2.5. (see Lemma 1.2 in ^[31]) Suppose $u(x, \cdot)\in C^4([x_{i-1}, x_{i+1}])$, let $\zeta(s) = u^{(4)}(x_i+sh, \cdot) + u^{(4)}(x_i-sh, \cdot)$, then

Lemma 2.6. (see Page 6 of ^[32]) Assume that $u(x, \cdot)\in C^8\left([0, L]\right)$ with $u(0, \cdot) = u(L, \cdot) = u_x(0, \cdot) = u_x(L, \cdot) = 0$, and define the operator $\delta_x^4$ by

where $v_i^n$ is a compact approximation of $u_x(x_i, t_n)$, i.e.,

Then, we have the following approximation

Furthermore, let $u^n = \left(u_1^n, u_2^n, \cdots, u_{M-1}^n\right)^T$, then the matrix representation of the operator $\delta_x^4$ is

where

and $\mathbf{D} = 6\mathbf{I} - \mathbf{P}$ with the identity matrix $\mathbf{I}$.

Lemma 2.7. (see Lemma 3.3 in ^[32]) The matrix $\mathbf{S}$ defined in Lemma 2.6 is symmetric positive definite.

It follows from Lemma 2.7, there is an invertible matrix $\mathbf{B}$ such that, $\mathbf{S} = \mathbf{B}^T\mathbf{B}$. Then for $w^n, v^n \in \Theta_h$, we have

The following lemma is required when we use compact operator $\mathcal{H}$ to increase the spatial accuracy.

Lemma 2.8. (see Lemma 1.2 in ^[31]) Suppose $u(x, \cdot) \in C^6\left([x_{i-1}, x_{i+1}]\right)$, $1 \leq i\leq M-1$, and $\zeta(s) = 5\left(1-s\right)^3 - 3\left(1-s\right)^5$. Then it holds that

In order to linearize the nonlinear function $g(u)$, we can easily get the following lemma by Taylor expansions.

Lemma 2.9. Assume that $u(\cdot, t)\in C^1([0, T]) \cap C^2((0, T])$, then the following approximation holds

3.   Derivation and analysis of the finite difference scheme

3.1.   The derivation of the finite difference scheme

In this subsection, a finite difference scheme with the accuracy $O(\tau^2 + h^2)$ for nonlinear Problem (2.1) is constructed.

Assume that $u(x, t) \in C_{x, t}^{8, 3}([0, L]\times[0, T])$, and $u(\cdot, 0) = u_t(\cdot, 0) = 0$. Consider Eq (2.1) at the point $u(x_i, t_{n+1/2})$, we have

The Crank-Nicolson technique and Lemma 2.2 for the above equation yield

Let $u(x_i, t_n) = u_i^n$. Since the initial values are $0$, thus the Riemann$-$liouville derivative is equivalent to Caputo derivative. We apply Lemmas 2.3 and 2.4 to discretize the first order integral operator and Caputo derivative in Eq (3.1) respectively, apply Lemma 2.6 to discretize $\frac{\partial^4u(x_i, t)}{\partial x^4}$, and Lemma 2.5 to discretize $\frac{\partial^2u(x_i, t)}{\partial x^2}$, then we get

where $(R_1)_i^{n+1} = O(\tau^2 + h^2 + h^4) = O(\tau^2 + h^2).$

It is clear that Eq (3.2) is a nonlinear system with respect to the unknown $u_i^{n+1}$. To linearly solve Eq (3.2), we use $u_i^1 = u_i^0 + \tau(u_t)_i^0 +O(\tau^2)$ and Lemma 2.9 to linearize Eq (3.2) for $n = 0$ and $1\leq n \leq N-1$, respectively, and then multiply Eq (3.2) by $\tau$, i.e.,

and

Noting $(u_t)_i^0 = 0$, neglecting the truncation error term $O(\tau^{3} + \tau h^2)$ in both above equations, and replacing the $u_i^n$ with its numerical solution $U_i^n$, we deduce the following finite difference scheme for Problem (2.1)

and

Remark 3.1. In case of $g(u) = f(x, t) = 0$, the only solution of the finite difference Scheme (3.5) and (3.6) is zero solution.

3.2.   Analysis of the finite difference Scheme (3.5) and (3.6)

In this subsection, the convergence and stability of the finite difference Scheme (3.5) and (3.6) will be discussed. For convenience, let $C$ be a generic constant, whose value is independent of discretization parameters and may be different from one line to another. To begin, we provide two lemmas that will be used in our convergence and stability analysis.

Lemma 3.2. (see Proposition 5.2 in ^[33] and Lemma 3.2 in ^[34]) Let $\{\omega_k\}$ and $\{\sigma_k^{(\alpha-1)}\}$ be the weights defined in Lemmas 2.3 and 2.4, respectively. Then for any positive integer $K$ and real vector $\left(V_1, V_2, \cdots, V_K\right)^{T}$, the inequalities

and

hold.

Lemma 3.3. (see Lemma 4.2.2 in ^[35]) For any grid function $w^n, v^n \in \Theta_h$, it holds

Theorem 3.4. Assume $u(x, t)\in C_{x, t}^{8, 3}\left([0, L] \times[0, T]\right)$ and $u(\cdot, 0) = u_t(\cdot, 0) = 0$, and let $u(x, t)$ be the exact solution of Eq (2.1) and $\{U_i^n|\mathit{\text{}}0\leq i \leq M, 1 \leq n \leq N\}$ be the numerical solution for Scheme (3.7) and (3.8). Then, for $1 \leq n \leq N$, it holds that

Proof. Let us start by analyzing the error of (3.6). Subtracting Eq (3.6) from Eq (3.4), we have

where $e_i^n = u_i^n - U_i^n$. Since $e_i^0 = 0$, the above equation becomes

Multiplying the both sides of the above equation by $h(e_i^{n+1} + e_i^{n})$ and summing over $1\leq i \leq M-1$. Then using Lemmas 3.3, 2.6, and Eq (2.2), we have

Summing the above equation over $n$ from $1$ to $J-1$ leads to

Now, we turn to analyze $\|e^1\|$. Subtracting Eq (3.5) from Eq (3.3), and by the similar deductions as above, we can derive that

Sum up Eq (3.7) and Eq (3.8), and apply Lemma 3.2, it deduces that

Using the Lipschitz condition of $g$ and exchanging the order of two summations in the above inequality, we have

Assuming ${\|e^P\| = \max\limits_{0 \leq p \leq N} \|e^p\|}$. Since ${\tau \sum\limits_{n = k}^{N}\left(\omega_{n+1-k} + \omega_{n-k}\right)}$ is bounded (see ^[29]), then the above inequality yields

Once the discrete Gronwall inequality has been applied to Inequality (3.11), we arrive at the estimate

thus the proof is completed.

Theorem 3.5. Let $\{U_i^n|\mathit{\text{}}0\leq i \leq M, 0\leq n \leq N\}$ be the numerical solution of Scheme (3.5) and (3.6) for Problem (2.1). Then for $1 \leq K \leq N$, it holds

Proof. Multiplying (3.6) by $h(U_i^{n+1}+U_i^n)$ and summing up for $i$ from $1$ to $M - 1$, we have

Note that Eq (1.1) is equipped with the homogeneous initial conditions, thus it deduces

Applying the similar deductions to get Eq (3.9), it achieves that

One can estimate $\| g(2U^n -U^{n-1}) \|$ as the following

Substituting Eq (3.14) into Eq (3.13) and using Young's inequality, then we have

By applying the Gronwall inequality to (3.15), it becomes

and this completes the proof.

4.   Derivation and analysis of the compact finite difference scheme

4.1.   The derivation of the compact finite difference scheme

In this subsection, a compact finite difference scheme with accuracy $O(\tau^2 + h^4)$ for nonlinear Problem (2.1) is presented.

Now let us act on both sides of Eq (3.1) with the compact operator $\mathcal{H}$. Then, by using Lemma 2.8, we obtain

Apply the similar deductions to get Eqs (3.3) and (3.4), it achieves

and

Neglecting the truncation error term $O(\tau^{3} + \tau h^4)$ in both above equations, and replacing the $u_i^n$ with its numerical solution $U_i^n$, we deduce the following compact finite difference scheme for Problem (2.1)

and

Remark 4.1. In case of $g(u) = f(x, t) = 0$, the only solution of the compact finite difference Scheme (4.4) and (4.5) is zero solution.

4.2.   Analysis of the compact finite difference Scheme (4.4) and (4.5)

In this subsection, we turn to analyze the convergence and stability of the compact finite difference Scheme (4.4) and (4.5). Firstly, we provide the following lemmas, which will be used in our convergence and stability analysis.

Lemma 4.2. (see Lemma 5 in ^[36]) Let $\{\sigma_k^{(\alpha-1)}\}$ be the weighted coefficients defined in Lemma 2.4, then for any positive integer $n$ and $w^n \in \Theta_h$, it holds that

Lemma 4.3. (see Lemma 4.2 in ^[37]) For any grid function $w^n \in \Theta_h$, we have

Theorem 4.4. Assume $u(x, t)\in C_{x, t}^{8, 3}\left([0, L] \times[0, T]\right)$ and $u(\cdot, 0) = u_t(\cdot, 0) = 0$, and let $u(x, t)$ be the exact solution of Eq (2.1) and $\{U_i^n|\mathit{\text{}}0\leq i \leq M, 1 \leq n \leq N\}$ be the numerical solution for Scheme (4.4) and (4.5). Then, for $1 \leq n \leq N$, it holds that

Proof. Let us start by analyzing the error of (4.5). Subtracting Eq (3.5) from Eq (4.3), we have

where $e_i^n = u_i^n - U_i^n$. Since $e_i^0 = 0$, the above equation becomes

Multiplying the both sides of the above equation by $h(e_i^{n+1} + e_i^{n})$ and summing over $1\leq i \leq M-1$. Then using Lemmas 2.6, 3.2, 4.2, and Eq (2.2), we have

Summing the above inequality over $n$ from $1$ to $J-1$ leads to

Now, we turn to analyze $\|e^1\|$. From Eqs (4.4), (4.2), and by the similar deductions as above, we can derive that

Sum up Eqs (4.6) and (4.7), and apply Lemmas 3.2 and 4.2, it deduces that

According to the same technique as for dealing with (3.9), we can achieve

thus completes the proof.

Theorem 4.5. Let $\{U_i^n|\mathit{\text{}}0\leq i \leq M, 0\leq n \leq N\}$ be the numerical solution of Scheme (4.4) and (4.5) for Problem (2.1). Then for $1 \leq K \leq N$, it holds

5.   Numerical experiments

In this section, we carry out numerical experiments to verify the theoretical results and demonstrate the performance of our new schemes. All of the computations are performed by using a MATLAB on a computer with Intel(R) Core(TM) i5-8265U CPU 1.60GHz 1.80GHz and 8G RAM.

Example 5.1. Consider the following problem with exact solution $u(x, t) = t^{2+\alpha} \sin^2(\pi x)$

where $T = 1$, $0 < x < 1$, $0 < t \leq T$, and $1 < \alpha < 2$. The nonlinear function $g(u) = u^2$ and $f(x, t)$ is

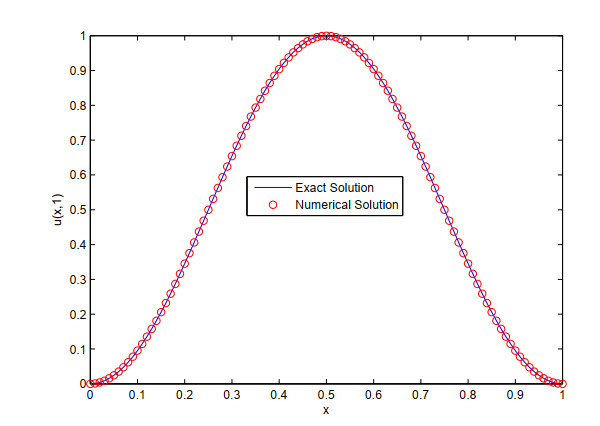
It is clear that $u(x, t)$ satisfies all smoothness conditions required by Theorems 3.4 and 4.4, so that both of our schemes can be applied in this example. In Figures 1 and 2, we compare the exact solution with the numerical solution of finite difference Scheme (3.5) and (3.6) and compact finite difference Scheme (4.4) and (4.5). We easily see that the exact solution can be well approximated by the numerical solutions of our schemes.

First, we in Tables 1, 2 and 3 show that the errors, time and space convergence order $\thickapprox 2$ and CPU times (second) of the finite difference Scheme (3.5) and (3.6) for $\alpha = 1.25, 1.5, 1.75$. The average CPU time, expressed as the mean time (mean) for $\alpha = 1.25, 1.5, 1.75$. Specifically, Table 1 tests the case that when $\tau = h$. In Table 2, we set $h = 0.001$, a value small enough such that the spatial discretization errors are negligible as compared with the temporal errors, and choose different time step size. In Table 3, we set $\tau = 0.001$, a value small enough such that the temporal discretization errors are negligible as compared with the spatial errors, and choose different space step size. From all scenarios above, we conclude that the temporal and spatial convergence order is 2. It verifies Theorem 3.4.

On the other hand, we check the numerical convergence orders and CPU times (second) in time and space of the compact finite difference Scheme (4.4) and (4.5) for $\alpha = 1.25, 1.5, 1.75$ in Tables 4 and 5, respectively. The average CPU time, expressed as the mean time (mean) for $\alpha = 1.25, 1.5, 1.75$. As expected, the numerical results reflect that the compact finite difference has a convergence order of $2$ and $4$ in time and space, respectively, which verifies our Theorem 4.4.

6.   Conclusions

We in this paper constructed two linearized finite difference schemes for time fractional nonlinear diffusion-wave equations with the space fourth-order derivative. The equations were transformed into equivalent partial integro-differential equations. Then, the Crank-Nicolson technique, the midpoint formula, the weighted and shifted Gr$\ddot{\text{u}}$nwald difference formula, the second order convolution formula, the classical central difference formula, the fourth-order approximation and the compact difference technique were applied to construct the two proposed schemes. The finite difference Scheme (3.5) and (3.6) has the accuracy $O(\tau^2 + h^2)$. The compact finite difference Scheme (4.4) and (4.5) has the accuracy $O(\tau^2 + h^4)$. It should be mentioned that our schemes require the exact solution $u(\cdot, t) \in C^3([0, T])$, while it requires $u(\cdot, t)\in C^4([0, T])$ if one discretizes Eq (1.1) directly to get the second order accuracy in time. Theoretically, the convergence and the unconditional stability of the two proposed schemes are proved and discussed. All of the numerical experiments can support our theoretical results.

Acknowledgments

This research is supported by Natural Science Foundation of Jiangsu Province of China (Grant No. BK20201427), and by National Natural Science Foundation of China (Grant Nos. 11701502 and 11871065).

Conflict of interest

The authors declare that they have no competing interests.