Failure of quasi-brittle materials such as concrete needs a proper description of strain softening due to progressive micro-cracking and the introduction of an internal length in the constitutive model in order to achieve non zero energy dissipation. This paper reviews the main results obtained with the non local damage model, which has been among the precursors of such models. In most cases up to now, the internal length has been considered as a constant. There is today a consensus that it should not be the case as models possess severe shortcomings such as incorrect averaging near the boundaries of the solid considered and non local transmission across non convex boundaries. An interaction-based model in which the weight function is constructed from the analysis of interaction has been proposed. It avoids empirical descriptions of the evolution of the internal length. This model is also recalled and further documented. Additional results dealing with spalling failure are discussed. Finally, it is pointed out that this model provides an asymptotic description of complete failure, which is consistent with fracture mechanics.
1.
Introduction
Population growth and changing lifestyle with industrialization and urbanization are the added sinks for soaring energy demand. Present energy security is predominantly drifting around the fossil resources and alternative fuels are being searched [1]. However, the faster depletion of fossil resources and accelerated accumulation of greenhouse gases (GHGs) in the environment that already has exceeded the "dangerously high" threshold of 450 ppm CO2, stressing the fossil fuel to be an unsustainable source of energy. The conventional fossil-based fuels contributed major share in the global primary energy consumption [2]. Global dependence on fossil fuels has led to the release of over 1,100 GtCO2 into the atmosphere since the mid-nineteenth century. Currently, energy related GHG emissions, mainly from fossil fuel combustion for heat supply, electricity generation and transport, account for around 70% of total emissions including carbon dioxide, methane and some traces of nitrous oxide [3].
The concerns related to energy security, environmental safety and sustainability have encouraged researchers towards alternative, renewable, sustainable, efficient and cost effective energy sources with lesser emissions [4]. Renewable energy can play a decisive role at global and national levels in dealing with the concerns related to energy security, climate change, eco-friendliness and sustainability [5,6,7,8,9]. With the situation of increasing energy demand, its prices and implementation of policies for global warming reduction, the sources of renewable energy have popularized [10,11]. Renewable energy is not only providing the sustainable energy, but also considered as a tool to solve several other problems associated with the fossil energy, viz., improving the energy security, resolving the health and environmental anxiety, decreasing greenhouse gas emissions and reducing poverty by increasing employment [2].
The increasing demand for biofuels has encouraged researchers and policy makers to find sustainable biofuel production systems in accordance with regional conditions and needs. The sustainability of a biofuel production system must include energy and greenhouse gas (GHG) saving along with environmental and social acceptability [12].
The studies reviewed in various publications are mainly focused on very specific aspects of bio-hydrogen production such as reactor design, molecular tools, production pathway, etc., however, this article exclusively reviews the biological production of hydrogen and its sustainability as an economical clean fuel in present scenario and also discusses its future perspective.
2.
Classification of biofuel
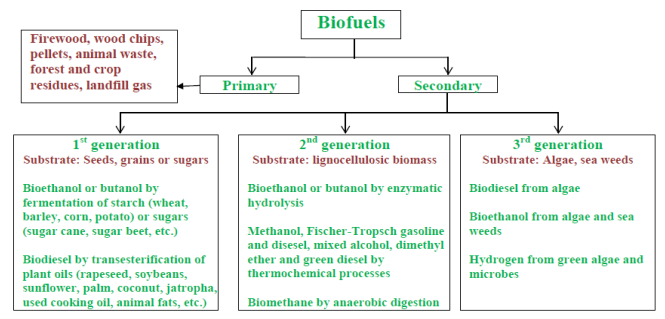
There are some recent publications on types of biofuels and their production from different substrates [13] and waste bioresources [10,14]. Biofuels can broadly be categorised into two groups:
Primary biofuel: In this category, all those biomass materials can be included which were traditionally used i.e. firewood, wood chips, pellets, animal waste, forest, crop residue, landfill gas etc.
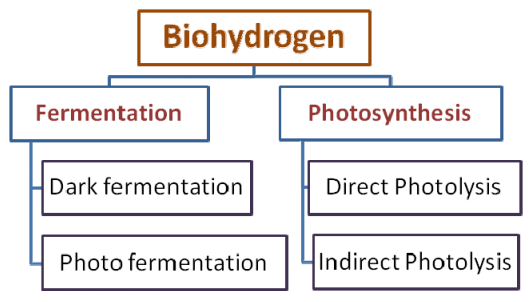
Secondary biofuel: In this category, all other products and processes, which use biomass and provide fuel in the form of liquid, solid or gas. On the basis of substrate utilization, this group can further be divided into three categories viz. 1st, 2nd and 3rd generation biofuel (Figure 1).
3.
Biohydrogen production
3.1. Scientometric analysis
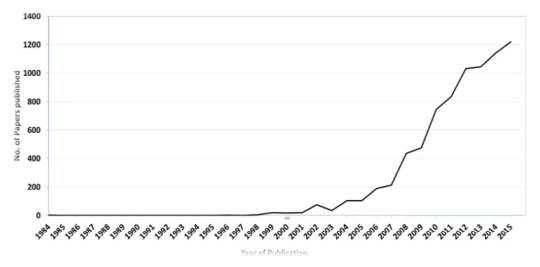
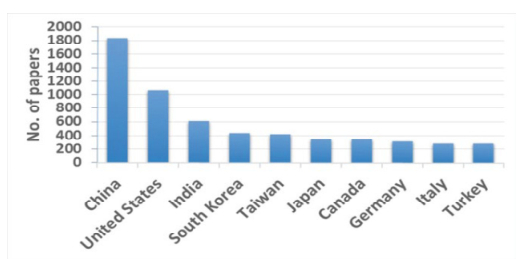
Though, research on the biohydrogen production is not new and basic photolytic hydrogen production during photosynthesis was explained long back, currently a possibility for industrial production of hydrogen from biological sources provides a boost in the field. After the possibility of hydrogen usage as transportation fuel, the research in this field has fuelled up and a tremendous improvement is seen since 2003. Published databases showed as much as 146 journals are publishing research results on biohydrogen. Among them, some are completely devoted towards the bioenergy i.e. International Journal of Hydrogen, Energy, Renewable and Sustainable Energy Reviews. Biohydrogen research are being conducted by more than 100 nations and around 7834 papers have been published since 1984 (Figure 2). Major contribution on this research have come from China followed by USA. India hold third position on this research (Figure 3) [2]. Most of the publications on biohydrogen are research articles (73%) followed by conference papers (11%) and Review articles (10%) (SCOPUS, 2016).
3.2. Production processes
Present hydrogen production system (Figure 4) is mainly based on electrolysis of water, and thermocatalytic reformation of hydrogen rich compounds, but these processes are energy intensive. Biological hydrogen production can solve this problem by utilizing biomass and microorganisms. Biohydrogen can be produced in two broad ways: By photosynthesis using microalgae, and by fermentation [15,16,17,18,19]. The organism involved and maximum H2 yield in different process are summarized in Table 1, and the pros and cons of different process are summarized in Table 2.
3.2.1. Photosynthetic biohydrogen production
Photosynthetic biohydrogen is either direct photolysis of water or indirect photolysis using sunlight. Unfortunately, H2 released by microorganisms during the photosynthetic process are in low yields. The increased order-of-magnitude of its volumetric productivity will be required before becoming reasonable for industrial-scale production. Further, the oxygen sensitivity of hydrogenase restricts the process in natural conditions. The Present photosynthetic biohydrogen production research is directed towards the enhancement of hydrogenase activity by identifying new organisms or using engineered organisms. Since the Rhodospirillum rubrum was found to produce H2 photosynthetically using organic acids as a carbon source and amino acid as a nitrogen source [22], many photosynthetic bacteria have been reported with hydrogen production efficiency under appropriate conditions [23,24,25,26]. Hwang et al. [27] reported enzymatic hydrogen production of Chlorella vulgaris YSL01 and YSL16 using CO2 as a carbon source under atmospheric conditions. Cyanothece sp. strain ATCC 51142 is capable of performing simultaneous oxygenic photosynthesis and H2 production by dinitrogenase NifHDK, an enzyme complex [28]. Bayro-Kaiser, V. and Nelson [29] randomly mutagenized the green microalgae Chlamydomonas reinhardtii to generate mutants that exhibited temperature-sensitive photoautotrophic growth. Eilenberg et al. [30] engineered the HydA enzyme and reported that the in vivo photosynthetic activity of the Fd-HydA enzyme surpasses that of the native HydA and shows higher oxygen tolerance. Recently, Batyrova and Hallenbeck reported another genetically modified Chlamydomonas reinhardtii strain cy6Nac2.49, which activates photosynthesis in a cyclical manner, so that photosynthesis will not be active in the presence of oxygen, but only in response to a metabolic trigger i.e. anaerobiosis [31]. Krassen et al. showed the stepwise assembly of a hybrid complex consisting of photosystem I and [NiFe] hydrogenase on a solid gold surface which can give rise to light-induced H2 evolution which converted solar energy to hydrogen energy [32].
3.2.2. Fermentative biohydrogen production
Present fermentative biohydrogen production research are concentrating on feedstock selection and process optimization. Azman et al. [33] used de-oiled rice bran, obtained after the extraction of oil content of rice bran, for dark fermentative biohydrogen production. Oil-extracted rice bran was hydrolyzed by dilute H2SO4 (1%, v/v) to obtain de-oiled rice bran hydrolyzate as a substrate for hydrogen generation. A recent comprehensive literature survey, on efficient biohydrogen generation and long-term operation in microbial fuel cell (MFC), concluded that to obtain high process efficiencies, cell design ought to be of primary concern [34]. Stanislaus et al. [35] used Ipomoea aquatica as a substrate with digested sludge as inoculum for biohydrogen production. Process optimization in this experiment through response surface methodology indicated 90 ℃ temperature for 60 min as the optimum pre-treatment condition of inoculum. Also, frozen dry I. aquatic demonstrated the highest hydrogen yield among all the other substrate pre-treatment conditions along with positive energy production. Kirili and Kapdan [36] applied a novel technique for biohydrogen production process enhancement, by adding microbial support particles namely; plastic scouring sponge pad, plastic nylon sponge, black porous sponge, plastic scouring sponge pad with metal mesh, and plastic nylon sponge with metal mesh, using waste wheat as feedstock. The experiment resulted into increased yield with decreasing retention time from 5 days to 1 day for all particles and achieved maximum yield with metal mesh covered plastic scouring sponge pad at 1 day retention time in repeated batch operation. Sarkar and Venkata Mohan [37] also concluded that application of pre-treated inoculum as biocatalyst and high substrate concentration resulted in substantial enhancement of both hydrogen and volatile fatty acid production. Radha and Murugesan [38] suggested that pre-treatment of marine microalgae is effective in removing phenolic content and enhancing biohydrogen production.
Bharathiraja et al. [39] reviewed the variable feedstock resources and process enhancement criterion for dark fermentative biohydrogen production. Sivagurunatahn and Lin [40] conducted a process optimization experiment using beverage wastewater as a feedstock with enriched mixed microflora dominated by Clostridium sp. in a continuously-stirred tank reactor (CSTR) under mesophilic conditions. The results revealed that a peak hydrogen production rate was observed at HRT 1.5 h while, maximum hydrogen yield was achieved at HRT 6 h. Another experiment with psychrophilic G088 strain (EU636029), closely related to Polaromonas rhizosphaerae (EF127651) was evaluated for its hydrogen production efficiency using different carbon sources, such as xylose, glucose, fructose, galactose, lactose or sucrose [41]. Experiment results showed glucose as the substrate with the highest consumption rate, accompanied by the maximum values of biohydrogen production rate and yield. Wen et al. [42] achieved stable and efficient photo-fermentative hydrogen production by forming biofilm on the surface of carrier in the biofilm reactor.
Dark fermentation process is considered to be promising and favourable over the photo fermentation process. Although, selection of one process over the other depends on several factors, such as availability of feedstock, selection of process organism, process condition for consortium, compatibility of feedstock with applied microorganism etc. Some workers also used the hybrid reactor to combine photo and dark fermentation processes. A combined process showed a positive result and an increase in total hydrogen yield. Several other researchers with variable feedstock and optimised process conditions also reported potential of industrial hydrogen production [43,44,45,46,47,48,49]. However, most of these results are limited to laboratory scales, none of them reached to the industrial production and failed to contribute in the hydrogen economy.
3.3. Benefits of biohydrogen
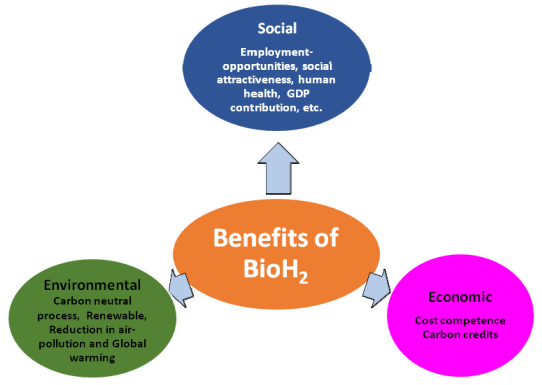
Among the four strategically important alternative fuel sources viz. biofuels, hydrogen (H2), natural gas and syngas (synthesis gas), hydrogen emerges as superior, since it is renewable, does not emit the greenhouse gases, liberates large amount of energy per unit weight in combustion and can be easily converted into electricity by fuel cell. Biological H2 production delivers clean H2 in a sustainable manner with simple technology and more attractive potential than the current chemical production of H2. Biohydrogen holds the potential for a substantial contribution to the future renewable energy demands. Biohydrogen production delivers clean H2 in a sustainable manner using simple technology and has more attractive potential than the current chemical production of H2, since it is suited for the conversion of a wide spectrum of substrate utilization such as organic wastes, industrial manufacturing process by-products and biomass as feedstock, mostly available free or at a low cost [50]. The sustainability of all products depends mainly on its impact on society, economy and environment. Figure 5 summarizes the social, economic and environmental benefits of biohydrogen.
3.4. Limitations
The main limitation of biological hydrogen production is lower rate and yields as compared to the other hydrogen production methods. Therefore, there is a necessity to develop strategies to increase the yield and production rate of biohydrogen. The main obstacles to achieve high rates and yields include, partial pressure of hydrogen gas in the produced gas mixture, competing reactions, bioprocess technology, insufficient active hydrogenase enzyme, and efficient hydrogen-producing cultures [51,52]. Hallenbeck [51] suggested that partial pressure of hydrogen can be reduced by sparging inert gas to derive electrons form NADH, while there is a need to develop a cost-effective and technologically sound method for the same [52].
The metabolic shift from acetic acid generation to solvent or hydrogen-consuming organic acid generation, and consumption of hydrogen by uptake of hydrogenase and homoacetogens, reduces biohydrogen production [51,53]. The metabolic shift can be controlled by using a bioreactor, which has been reviewed in detail by Argun et al. [52]. The purity of hydrogen in gas phase is also a challenge, as it varies from 30–60%. The separation of hydrogen by using selective membranes in the production process could help in reducing hydrogen partial pressure and increasing purity of hydrogen [52,54].
4.
Sustainability assessment of biohydrogen
The sustainability of biohydrogen production is driven by production rate and its purity, to get biohydrogen at an affordable cost. Physicochemical methods are highly efficient in both productivity and purity of hydrogen but they are not cost-effective due to high energy demands during the production. However, the use of biological methods for hydrogen production have acquired significant attention in the last decades as they operate in mild conditions and have lower energy demands, which make the process cost-effective. There are some other factors seeking the attentions of researchers and industrialists for biohydrogen production, such as utilization of organic residues; but it involved high technologies to operate safely and to convert it into biohydrogen in an environmentally-acceptable form [52].
The criteria for sustainability assessment concerns three aspects, including economics, environmental performance and social issues. Sustainability usually refers to simultaneously achieving economic prosperity, environmental cleanness and social parity [55]. Several investigations have been conducted to improve the biological hydrogen production and develop a biohydrogen economy. However, development of biofuel industries is recognized as a complex system and besides experimental studies, social, economical and environmental aspects of biofuel system in a country or region should be considered. Aspects are estimated by feasibility assessments, evaluation of biofuels sustainability, and life-cycle and techno-economic analysis [56]. The energy ratio and GHG emissions of biohydrogen compared favourably with diesel and other H2 production pathways. The energy ratio (may be called as Net Energy Ratio or Energy Balance) of biohydrogen production pathways must be positive for sustainable replacement of fossil sources. Consequently, biohydrogen is worthy of consideration in the planning and development of a H2 economy, both from an energy and from an environmental perspective [57].
4.1. Economic feasibility of biohydrogen
A detailed financial feasibility analysis by Lee [58], indicated that an attractive investment proposal or business plan, is critical in attracting investment for long-term biohydrogen production on a small or commercial scale. His results explained that the levelized cost of energy (LCOE) of biohydrogen will be approximately USD 2 to 3 kg. All financial indices revealed that biohydrogen is economically feasible of investment and will be commercialized successfully before the timelines in many official reports. Results revealed decision-making criteria should include the economic incentives. LCOE of biohydrogen is less sensitive to the cost of biomass feedstock, which is more sensitive to the capital cost, operating and maintenance cost. Another study by Lee [59] reported that the biohydrogen and biobutanol can replace fossil fuels with high economic feasibility. Biohydrogen has the most flexibility under variation in the production cost of biomass feedstock. Algae biodiesel is less financially competitive than biohydrogen and biobutanol.
Three sources of bioenergy are cost-competitive with fossil fuels under ideal conditions. Lee and Chiu [60] investigated the development of the biohydrogen sector in four countries, US, Japan, China and India. His study stated China as the largest biohydrogen market with the highest total output multiplier by 2050, followed by the US, Japan and India (in that order). High investment will encourage the rapid development of the biohydrogen industry in all four countries. Therefore, investing US$1 in the biohydrogen industry will generate a total output of US$3.22, 3.50, 3.09 and 3.00 in the four economies, respectively, in 2011–2050. Study also revealed that investing in the development of biohydrogen technology will provide more benefits than investing in hydrogen infrastructure. Han et al. [61] conducted a techno-economic analysis for fermentative hydrogen production from food waste. Study exhibited 26.75% return on investment (ROI) and 24.07% internal rate of return (IRR) within 5 years of payback period (PBP).
4.2. Societal parity of biohydrogen
However, societal impact of biohydrogen production and its use were less quantified due to complexity in societal structure, a few reports suggested an edge of biohydrogen on other fuels. Ren et al. [55] described ten societal criteria to assess the societal aspect in a sustainability study. The criterion were: Inherent safety index, occupational index, social attractiveness, human health and safety of employees, per capita GDP contribution, taxes contribution, cultural influence, political acceptability, security of primary supply and contribution for energy sufficiency. Sun et al. [62] quantified potential societal benefits of hydrogen fuel cell vehicles (FCVs) using the societal lifetime cost (SLC). The study included the vehicle retail cost (a function of vehicle performance), the cost of energy use (a function of vehicle fuel economy), operating and maintenance costs, externality costs of oil-use, damage costs of noise and emissions from air pollutants and GHGs, and other factors. Results of the study showed the cost difference between FCVs and gasoline vehicles is initially very large. FCVs eventually become lifetime cost competitive with gasoline vehicles, as their production volume increases, even without accounting for externalities. High valuation of externalities and high oil price could reduce the buy-down cost (the cumulative investment needed to bring hydrogen FCVs to lifetime cost parity with gasoline vehicles by $10 billion relative to the reference case. According to Ogden et al. [63] "the hydrogen fuel cell car stands out as having the lowest externality costs of any option, and when mass produced with high valuations of externalities, the least projected lifecycle cost". These costs are estimated over the full fuel-cycle from "well-to-wheels" and the entire vehicle lifetime and include adjustments for non-cost social transfers, such as taxes and fees, and producer overhead costs associated with fuel and vehicles [62].
In a study Stanislaus et al. [35] has studied the production of biohydrogen from Ipomoea aquatica using digested sludge as inoculum and reported that the energy consumed in the fermentation process was lesser than energy produced in the process, which shows a positive energy balance or NER. The biohydrogen system succeeds in obtaining a negative global warming impact with a low cumulative non-renewable energy demand. This indicates that biohydrogen can be produced with positive NER, which could be a sustainable approach. Sekoai and Daramola [64] and Singh et al. [65] reviewed the published reports and concluded hydrogen as the safest fuel due to its non-toxicity, dispersive in nature, and with the least dangers in terms of a fire hazard. Although, it can cause fire but the clear flame cannot perch skin at a distance because of the little thermal radiation emitted by the flame due its lack of soot content.
4.3. Environmental safety through biohydrogen
Romangnoli et al. [66] conducted an LCA study of biohydrogen by photosynthesis and the results of the analysis, showed that using biohydrogen to produce electricity offers more environmental benefits than using a fossil fuel based source. Wulf and Kaltschmitt [67] estimated that total 29.9 Mio t CO2-eq could be reduced by using compact class hydrogen fuel cell vehicle over compact class gasoline vehicle over the 15 years life time. The life cycle study of Djomo and Blumberga [57] compared the energetic and environmental performances of hydrogen from wheat straw (WS-H2), sweet sorghum stalk (SSS-H2) and steam potato peels (SPP-H2), and found comparable energy ratios (ER) among the three raw materials used i.e. 1.08 for WS-H2, 1.14 for SSS-H2 and 1.17 for SPP-H2; and a GHG savings by 52–56% compared to diesel and by 54–57% compared to steam methane reforming production of H2.
Dadak et al. [68] carried out an exergy analysis and concluded that the eco-exergy concept could provide unique insights beyond those of conventional exergy analysis, which thereby provides a useful design tool for photobiological hydrogen production. The researchers further added that the sodium acetate concentration of 1 g L−1 and light intensity of 1000 lux were found to be the most suitable conditions for biohydrogen production, according to the normalized exergy destruction obtained using both concepts. In another exergy analysis, no noticeable changes were observed in the conventional exergetic and eco-exergetic performance parameters of the bioreactor over 540 h of continuous operation. Nevertheless, eco-exergetic analysis owing to the inclusion of the work of information embedded in the genomes of living organisms is still recommended for improving the design features of photobioreactors for hydrogen production [68]. In a study with Rhodopseudomonas palustris PT, Hosseini et al. [69] provided a comprehensive insight into the exergetic parameters of a bioreactor for hydrogen production using a locally isolated light-dependent photosynthetic bacterium to select the best carbon source dosage for efficient and eco-friendly biohydrogen production. According to the experiment normalized exergy destruction and sustainability index, 1.5 g/L sodium acetate dosage was found to be an optimal carbon source for the industrial applications phase.
Wulf et al. [70] has performed a life cycle assessment of different biohydrogen production processes to examine environmental impact, such as anthropogenic climate change, acidification, eutrophication and human toxicity. They considered biohydrogen production from biomass sources derived from forestry and short rotation coppice (SRC), herbaceous biomass, energy crops and biowaste in Germany. They reported that biomass source has significant influence on the environmental impact of biohydrogen production pathways, and concluded that the gasification and the reforming of biomass have the potential to be climate friendly. They also reported that steam methane reforming (SMR) technology is the most promising technology regarding the environmental impact [70].
4.4. Challenges in development of sustainable biohydrogen
Though the biohydrogen production and its utilization seems to be an environmentally safe and feasible alternative for fossil based fuel however, shifting from present fuel economy to biohydrogen economy is still in its infancy stage. Despite being several research groups working on it, its industrial production, storage and transportation have not yet reached on a satisfactory level. The major constraints in biological hydrogen production processes are raw material cost, low hydrogen evolution rate and yield at large scale [71].
Dadak et al. [68] suggested eco-exergy concept as an effective tool to assess the sustainability and productivity of biohydrogen production from a thermodynamic point of view. Bretner et al.
[72] and Miandad et al. [20] summarised the technological challenges for sustainable use of biohydrogen fuel. Briefly these challenges are:
1. Low Photochemical efficiency.
2. Efficiency of employed bacterial strain.
3. Instability of hydrogenase over-expression.
4. Sensitivity of hydrogenase to oxygen and feedback inhibition.
5. Competition for reductant from ferredoxin between hydrogenases and other cellular functions.
6. Suitability of low cost substrates.
7. Industrially feasible production process and yield. Substrate use competence of used strain.
8. Kinetics suitable design of reactors.
9. Thermodynamic barrier.
10. Low cost material for hydrogen storage for economic feasibility.
5.
Future perspective
Biohydrogen production provides clean H2 with the help of simple technology and a more attractive potential than the current chemical production of H2, makes it sustainable. Although, present hydrogen production industries are based on chemical processing units, but the research trend on biohydrogen production promises a booming potential of industrial biohydrogen production in the near future. Global utilization of confined and trader hydrogen is projected to increase more than 300 billion cubic through 2018 with an annual growth rate of 3.5%. Recent global research trends showed that the world's largest hydrogen consumption will continue with US having the maximum share of growth, although in 2018 it is likely to occur in China.
Biohydrogen production from the Asian countries is mainly focusing on dark fermentation while the European countries are focusing on dark and photo fermentation. So far, the current biohydrogen production system is appropriate for decentralized small scale systems, integrated with waste from agriculture and industries or from waste processing facilities, using reactors operating with mixed microflora (aerobic, anaerobic, thermophillic, photo non-sulphur producing bacteria) or pure cultures enriched from natural sources. Seed inocula for biohydrogen production have been obtained from heat sludge, compost, waste water, and food waste etc.
Production of hydrogen using biological tool is the predominant challenge for biotechnology, concerning present and future environmental problems. Future of biological hydrogen production is not only determined by research advances, including genetic engineering of microorganisms for efficiency improvement and designing complications of bioreactor, but also by fuel economics (cost of fuel), societal adaptation and the development of systems for hydrogen energy [73]. Current strategies geared towards improving biohydrogen production include microbial culture immobilisation, bioreactor modifications, the optimisation of process conditions (temperature, pH, OLR and HRT), culture selection and enrichments, substrate choice and the metabolic engineering of biohydrogen specialists [74,75,76,77].
Cost factor is an important aspect for sustainability of fuel. Metabolic and genetic engineering can play a vital role in bringing down the production cost and increasing the H2 yield. By an estimate 80 kg of hydrogen per acre per day could be produced by diverting the entire photosynthetic efficiency of the algae toward hydrogen production. In a realistic efficiency of 50%, hydrogen production cost comes close to a $2.80 a kilogram [78]. However, in the current scenario below, 10% of the algae's photosynthetic capacity was utilized for biohydrogen production [79,80]. Research on biotechnological approach to improve algal photosynthetic biohydrogen production are underway and demonstrating a promising result [81]. There are two major factors that would have an important impact on the cost of biohydrogen production for commercial use: The cost of the photo-bioreactor and storage system has to be brought down, which will depend on appropriate and less expensive materials to be used in the fabrication of the photo-bioreactors.
The reports published by several researchers have clearly indicated that the cost-effective production of biohydrogen with a positive energy balance is the key feature to get sustainable biohydrogen production, as summarised in Table 3.
After reviewing all information this can be emphasized that the sustainable biohydrogen production can be generated in the future by exploration of the following technologies:
a. Utilization of molecular tools for identification of robust hydrogen producing micro-organisms.
b. Advancement in the bioreactor development.
c. Fine tuning of pre-treatment techniques.
d. Integration of other energy generation systems such as biogas, bioethanol, etc.
6.
Conclusion
The studies reviewed in various publications are mainly focused on very specific aspects of bio-hydrogen production, such as biomass gasification [82], reactor design [83], molecular tools [84], and production pathway [85], etc. However, this article has exclusively reviewed the biological production of hydrogen and its sustainability as an economical clean fuel currently and has also discussed its future perspective.
This review with the following points concludes that biohydrogen is a renewable and sustainable source of energy and a clean economical fuel in comparison to other biofuels [86] for the near future:
● Various types of biomass can be used for sustainable biohydrogen production.
● The selection of pre-treatment technology for biohydrogen production process depends on substrate composition.
● The simultaneous use of more than one pre-treatment technology can lead to improvements in substrate-biodegradability along with increase in hydrogen production.
● Development of biohydrogen economy is a feasible alternative for sustainable fuel as it provides energy security, societal parity and environmental safety.
● Hybrid or biorefinery concept can lead to commercialization of biohydrogen production.
● Metabolic and genetic engineering can play a vital role in bringing down the production cost and increasing the yield of biohydrogen.
Conflict of interest
The authors declare there are no conflicts of interest in this paper.









 DownLoad:
DownLoad: