Groundwater flow in a fissurised porous stratum

1.   Introduction

Rice is the staple food for most Asian people. Due to the conversion of lowland to infrastructure and plantation development, the best paddy fields tend to decrease ^[1]. Increased production will depend on the greater use of suboptimal land areas ^[2]. Among the potential lands in this category are coastal regions. As the largest archipelago country, Indonesia has extensive coastal areas ^[3]. However, these areas have some constraints for rice cultivation, including a high level of salinity ^[1].

In general, rice is one of the most sensitive plants to salinity stress and has a narrow tolerance variability ^[4,5]. The rice productivity in the coastal regions is relatively low compared to the optimal land areas ^[1,6]. According to Rad et al. ^[7] salinity at 6 dS m^-1 can reduce rice productivity by 50-100%. Therefore, increasing rice productivity in saline areas is very important for maintaining the sustainability of food production in Indonesia and elsewhere. Among the solutions for this critical issue is the use of rice varieties tolerant to salinity stress.

Development of varieties can be done through doubled-haploid technology by anther culture ^[8,9]. The approach is efficient in producing homozygous lines in a shorter period compared to the conventional breeding process ^[10]. However, the response of doubled-haploid rice lines is still influenced by their interactions with the environment ^[11], so effective selection of salinity tolerance is crucial. Reproductive screening is considered the most crucial because, at this stage, plants are unable to escape from the salinity stress ^[12]. In addition, salinity toxicity is cumulative as the longer the plant is exposed to salinity the greater the accumulation of Na⁺ in tissues ^[13]. High accumulation of Na⁺ can negatively impact the development of rice reproductive traits which are economically valuable ^[12]. Therefore, the selection of tolerant rice lines under salinity stress in the reproductive phase is essential.

The salinity screening performed in the greenhouse until the reproductive phase can be conducted in pots as an artificial screening method. It is preferred as compared to the actual selection in the field ^[14,15,16]. The salinity treatment can be controlled under a greenhouse condition according to the desired stress level, whereas in the field it is difficult to control because each field has specific spatial and temporal characteristics of salinity stress ^[6,17] as well as other stresses. Therefore, the artificial screening method as a selection approach is a good alternative for screening genotypes for salinity tolerance. However, the combination of main and secondary characters through a selection index model under the greenhouse environment is rarely performed. According to Mansuri et al. ^[18], selection based on stable secondary characters related to yield can increase yield stability under different environments. In the selection index model, character weighting is an important step in determining priorities in selection ^[19,20,21]. One of the methods for determining character weighting is factor analysis. Factor analysis is a multivariate analysis approach used to identify the internal covariate among variables in one dimension ^[22,23,24]. It is useful in random data analysis ^[25]. Godshalk and Timothy ^[26] and Rocha et al. ^[27] have reported the use of factor analysis in selection index development as an alternative to the Smith-Hazel index. Thus, the factor analysis in selection index development can also be applied to the selection of doubled-haploid rice lines under salinity stress. The objective of this study was to develop a selection index model based on factor analysis and select doubled-haploid rice lines tolerant to high salinity stress using an artificial screening in the greenhouse.

2.   Materials and methods

2.1.   Plant materials and experimental design

The salinity screening was conducted in a pot under a greenhouse condition at the Indonesian Center for Agricultural Biotechnology and Genetic Resources Research and Development (ICABIOGRAD): Bogor from March to July 2018. The minimum and maximum temperature and humidity in the greenhouse during the screening experiments were 21.6–37.5 ℃ and 38.9–87.4%, respectively. The photoperiod is normal in the tropical area as 12 h per day. The experimental design used was split plot in a randomized complete block design with the main plot being salinity stress treatments (normal (0 mM NaCl) and saline (25 mM NaCl)) and the subplot was the genotypes. Forty-two rice genotypes were used, consisting of 36 doubled-haploid lines from 4 crosses (F1–F11 = Inpara 5/IR77674, F12–F52 = IR77674/Inpari 29, F53 = IR78788/Inpari 29, and F54–F56 = Dendang/Inpari 30) ^[28], four cultivated varieties (Ciherang, Inpara 5, Inpari 29, Inpari 34 Salin Agritan): Pokkali (salinity tolerant check variety) and IR29 (salinity sensitive check variety). The concentration of NaCl used was 0 (electrical conductivity (EC) = 0.46 dS m⁻¹) and 25 mM NaCl or 17.55 in 4 L water and 8 kg soil (EC = 5.6–5.8 dS m⁻¹). The NaCl concentration was adjusted with the critical EC as reported by Anshori et al. ^[29]. The experiment was replicated three times so that there were 252 experimental units, each consisting of one plant in one pot. The soil description used before the NaCl application is as follows: soil type: Latosol, cation exchange capacity (CEC) = 16.43 cmol (+) kg⁻¹, Ca = 5.62 cmol (+) kg⁻¹, Mg = 1.11cmol (+) kg⁻¹, K = 0.6 cmol (+) kg⁻¹, Na = 0.24 cmol (+) kg⁻¹, N total (Kjeldahl) = 0.09%, C-organic (Walkley and Black) = 2.31%, exchangable Al = 0.06 cmol (+) kg⁻¹, pH (H₂O) = 5.95, P Bray I = 2.74 ppm.

2.2.   Experimental procedures

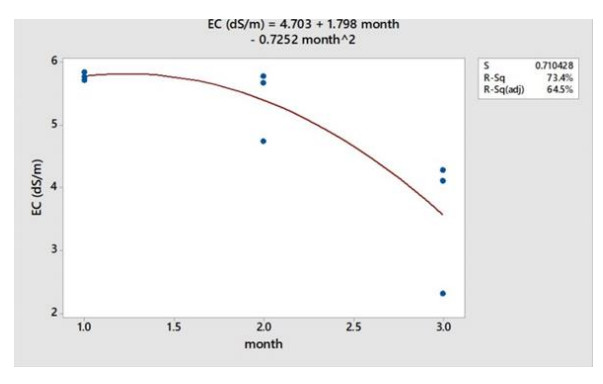
The experimental procedure was conducted according to Anshori et al. ^[29]. The salinity stress (NaCl) treatment was applied at the early vegetative stage or 22 days after germination (DAG) and it was employed until the end of the reproductive stage or 2 weeks (101 DAG) before harvest time. The NaCl solution was added to the media according to the treatment and stirred slowly until the soil became muddy. The preparation of saline media had been completed 3 days before transplanting. Before transplanting, i.e., at 20 DAG, all seedlings were treated with 3 dS m⁻¹ or 1.755 g/L salinity stress solution to prevent osmotic stress in the chamber for two days. Electrical conductivity (EC) was measured in standing water to verify the level of salinity stress. The maintenance of the plants included watering, fertilizing, and weeding. Watering was carried out at least once a day to keep the water condition relatively the same every day. NPK 15:15:15 fertilizer (6 g per pot) was applied one week after planting (WAP) and urea fertilizer (1.5 g per-pot) was applied at 3 and 7 WAP. Plants were harvested when 80% of the panicles had turned yellow. The observations were conducted on the following traits: vegetative and reproductive plant height, number of total tillers, number of productive tillers, days to flowering, flag leaf length, panicle length, number of grains (filled, unfilled, and total) per panicle, 100-grain weight, percentage of filled grains, and yield (g per-plant). The level of EC was monitored during experiment at 1, 2 and 3 months after planting (Figure 1).

Figure 1.  The EC level during the experiment.

DownLoad: Full-Size Img PowerPoint

2.3.   Data analyis

Data were analyzed with the analysis of variance (ANOVA). Relative performance decrease between normal and saline conditions was calculated. The mean squares from the ANOVA were the basis for calculating repeatability ^[24]. Phenotypic and genetic correlations in each environment were calculated for selecting secondary characters ^[30,31]. Trait average in each treatment was used to calculate the stress tolerance index (STI) as described by Fernandez ^[32]. The use of STI is intended to increase and stabilize the genotype variance in the saline environment. The STI results were correlated and analyzed further using stepwise multiple regression ^[33] and path analysis ^[34]. Determination of the weight of the selection index was based on factor analysis ^[25]. The weight of a secondary character in the selection index model was corrected with its repeatability and its direct effect on the yield. The statistical software used in this analysis were META R ^[35], STAR 2.0.1, R with Agricolae package ^[36], and Minitab 17.

2.3.1.   Relative decrease

The relative decrease in each character was estimated by the following formula ^[21]:

where: X₀ = genotype value under normal condition; X_s = genotype value under saline condition.

2.3.2.   Standardization of stress tolerance index ^[20]:

where: z_n = Standardized of STI variable; x_i = STI value of genotypes; µ₀ = STI average of population; ${\sigma }^{2}$ = STI variance of population.

3.   Result and discussion

3.1.   Analysis of variance and relative decrease

The analysis of variance (ANOVA) and relative decrease (from normal to saline conditions) for all characters are shown in Table 1. The genotype and salinity treatment (G x E) interaction effect was significant on the number of filled grains, number of unfilled grains, 100-grains weight, percentage of filled grains, and yield. The relative decreases of the number of total tillers, number of productive tillers, number of filled grains, and yield were greater than 50%. Based on the ANOVA and relative decrease, the number of filled grains and the yield were identified as the traits least impacted by saline conditions.

Table 1.  Analysis of variance of morphological and physiological characters towards a number of synthetic rice genotypes in varied environments.

Character	MS of stress (E)	MS of Genotype (G)	MS G*E	CV	Average		RD (%)
					Normal	Saline
VH (cm)	43279.61ns	272.41**	109.55ns	10.22	117.89 ±12	89.85 ± 16.85	23.78
GH (cm)	5900.88ns	203.75**	85.71ns	9.25	93.85 ± 7.58	82.52 ±14.11	12.08
TT	1707.76*	8.51**	3.96ns	24.50	9.4 ± 2.2	3.8 ± 1.9	59.45
PT	1630.18*	10.54**	4.46ns	27.12	9.6 ± 2.4	4.1 ± 2.3	57.45
DF	656.30ns	26.69**	13.37ns	4.15	89.3 ±11.7	92.0 ± 11.3	−3.04
FLL (cm)	9462.65*	161.90**	48.37ns	14.53	48.99 ± 8.37	36.30 ± 6.82	25.91
PL (cm)	1254.97*	38.39**	13.95ns	14.97	29.36 ± 4.47	24.96 ± 3.92	14.98
NFG	340249.31*	1087.72**	903.71**	25.19	120.4 ± 26.9	44.3 ± 27.3	63.17
NUG	3277.55ns	410.57**	249.71**	38.97	24.5 ± 10.4	30.7 ± 18.3	−25.42
NTG	276737.81*	2351.67**	708.74ns	20.02	144.9 ± 30.4	75.1 ±31.7	48.18
100w (g)	27.50*	0.26**	0.17*	14.88	2.52 ± 0.16	1.78 ± 0.64	29.52
PFG (%)	46091.85ns	218.50ns	300.38*	20.36	83.15 ± 6.57	53.61 ± 25.7	35.52
Yield (g)	29676.44*	43.72ns	52.38*	36.66	26.58 ± 8.32	3.98 ±3.89	85.01
Note: * significantly influential at 5% level, ** significantly influential at 1%, ns not significant; C = characters, CV = coefficient of variation, MS = means square, RD = relative decrease; 100W: 100-grain weight, DF = days to flowering, FLL = flag leaf length, GH = generative plant height, NFT = number of filled grains, NTG = number of total grains, NUG = number of unfilled grains, PFG = percentage of filled grains, PL = panicle length, PT = number of productive tillers, TT = number of total tillers, VH = vegetative plant height.

---

 | Show Table

DownLoad: CSV

The amount of interaction variance and the relative decrease could be indicators for the complexity of the trait and stress degree of the environment on rice growth characters ^{[15,21,37,38,39]}. Based on this study, the salinity treatment has a large effect on the genotype yield as the main character (Table 1). The high influence of the environment on the yield indicated that the selection of genotypes should be analyzed in-depth by including genetic variance in each analysis ^[40]. Krishnamurthy et al. ^[41] also reported that environmental influences have a large impact on the yield, so selecting the characters with considerably large genetic variance would be useful. If such characters were correlated with yield decrease, then they might imply tolerance. The consideration of genetic variance in salinity selection has been reported by Mohammadi et al. ^[42] in the selection of salinity tolerant rice and by Yadav et al. ^[43] in determining the important characters under salinity stress.

The high environment effect and G x E reduce genetic variance, especially for polygenic characters such as the yield ^[30]. The low genetic variance of yield indicates that the selection index required additional secondary characters which are stable (i.e., less affected by environment) and have a strong correlation with yield. Such secondary characters may be used to predict the yield of genotypes in other environments ^[18]. To determine the stable secondary characters under high environment effect, the analysis should be performed independently between normal and stress conditions. This approach has been used by Garg et al. ^[44] to determine the important characters involved in drought stress based on the high heritability in both stress and normal environments. Therefore, the independent analysis between normal and saline conditions could be the basis for identifying the secondary characters.

3.2.   Determination of selection character in the pot salinity screening

The determination of selection characters in this research was analyzed through two approaches. The first approach was an analysis of phenotypic and genetic correlations towards normal and saline conditions independently. Based on phenotypic and genetic correlations shown in Table 2, the normal condition has a more stable correlation than the saline condition. It was shown on the low difference between phenotypic (P) and genetic (G) correlations in normal conditions rather than saline conditions, especially on characters with significant phenotypic correlation to the yield. Based on the correlation stability with regard to the yield under normal and saline conditions, the productive tiller trait was stable under both normal (rP/rG = 0.63/0.60) and saline conditions (rP/rG = 0.79/0.62).

Table 2.  Phenotypic and genotypic correlation between yield and agronomic traits in normal and saline conditions.

C	VH	TT	DF	GH	PT	FLL	PL	NFG	NUG	NTG	100W	PFG
Normal
Yld-P	0.22	$\underline{0.65^{**}}$	0.01	0.09	$\underline{0.63^{**}}$	0.01	0.17	0.40*	0.09	0.36	0.02	0.13
Yld-G	0.23	$\underline{0.76^{**}}$	0.16	−0.16	$\underline{0.60^{**}}$	−0.24	$\underline{0.44^{**}}$	0.2	0.26	0.23	−0.26	−0.14
Saline
Yld-P	$\underline{0.64^{**}}$	$\underline{0.65^{**}}$	−0.07	$\underline{0.62^{**}}$	$\underline{0.74^{**}}$	0.39	0.27	$\underline{0.84^{**}}$	−0.04	$\underline{0.56^{*}}$	$\underline{0.53^{*}}$	$\underline{0.62^{**}}$
Yld-G	$\underline{1.00^{**}}$	0.23	NA	$\underline{1.00^{**}}$	$\underline{0.62^{**}}$	0.17	$\underline{−0.62^{**}}$	$\underline{0.93^{**}}$	0.09	$\underline{0.56^{*}}$	$\underline{0.87^{**}}$	$\underline{0.72^{**}}$
Notes: * significant correlation at α = 5%, ** significant correlation at α = 1%, 100W: 100-grain weight, C = characters, DF = days to flowering, FLL = flag leaf length, GH = generative plant height, NFT = number of filled grains, NTG = number of total grains, NUG = number of unfilled grains, PFG = percentage of filled grains, PL = panicle length, PT = number of productive tillers, TT = number of total tillers, VH = vegetative plant height. Yld-P: phenotypic correlation with yield, Yld-G: genotypic correlation with yield.

---

 | Show Table

DownLoad: CSV

Phenotypic and genetic correlation analyses and the employment of a tolerance index are useful for identification of secondary traits. The use of phenotypic and genetic correlation in the normal and saline environment was reported by Krishnamurthy et al. ^[41] for determining the selection character supporting rice yield. The phenotypic and genetic correlation could identify the effect of the environment on the correlation variance. The greater the difference between the two correlations, the greater the role of the environment in influencing the phenotype correlation among these characters ^[45,46,47]. The difference can be an indicator to identify the stable secondary characters to the yield.

The second approach for determining selection characters involved the use of stress tolerance index (STI) as the basis for stepwise multiple regression analysis and path analysis. Before these analyses, the STI was subjected to correlation analysis to the yield. This analysis showed that all characters were highly significantly correlated with yield except for days to flowering and panicle length (Figure 2). Number of total tillers (r = 0.65), number of productive tillers (r = 0.73), number of filled grains (r = 0.72) and percentage of filled grains (r = 0.61) were the better characters as having correlation coefficient of more than 0.6. These characters could be the basis for secondary characters in stepwise multiple regression and path analysis.

Figure 2.  Pearson correlation among the STI of the characters (white background of cell indicates non-significance at α = 5%, 100W: 100-grain weight, DF = days to flowering, FLL = flag leaf length, GH = generative plant height, NFT = number of filled grains, NTG = number of total grains, NUG = number of unfilled grains, PFG = percentage of filled grains, PL = panicle length, PT = number of productive tillers, TT = number of total tillers, VH = vegetative plant height).

DownLoad: Full-Size Img PowerPoint

The use of tolerance index was a good approach to apply in determining the genotype adaptability under stress ^[48], especially on the low yield genetic variance level. The index assessed the yield stability by considering the response in normal and stress conditions ^[32] so that the selection was more representative compared to direct selection in a saline environment. According to Anshori et al. ^[29], there were three tolerance indices which were well used in the pot salinity screening, namely stress tolerance index (STI), geometric mean productivity (GMP), and yield stability index (YSI). The STI tolerance index was selected as the tolerance index in this experiment. The STI index is considered the average response of all genotypes under normal conditions so that the selection is more dynamic than GMP and YSI indices which focus on individual genotypes. The use of STI was also reported by Krishnamurthy et al. ^[41] in rice and Singh et al. ^[49] in wheat to evaluate salinity tolerance in a genotype.

Determination of characters for in-depth analysis based on high STI correlation became necessary for determining the secondary characters. It was also consistent with assumptions in path analysis, such as independent and dependent variables should have a linear and strong relationship with each other ^[50]. The high STI correlation has a strong relationship with the yield tolerance response under salinity stress. Therefore, these characters were expected to provide better information regarding the specific relationships to the yield.

The results of stepwise multiple regression analysis showed that the number of productive tillers and the number of filled grains were the best secondary characters in predicting the yield STI (Table 3). This was also supported by the path analysis which showed that the number of productive tillers (direct effect = 0.67) and the number of filled grains (direct effect = 0.55) had a significant direct effect on the yield STI (Table 4). Based on these two approaches, the number of productive tillers was determined to be the most appropriate character associated with yield in the development of the selection index model.

Table 3.  Stepwise multiple linear regression to the stress tolerance index (STI) of yield.

Variabel	Estimate	Std. Error	t value	Pr(>|t|)
(Intercept)	−0.082	0.013	−6.159	0.000**
Productive tiller	0.269	0.025	10.635	0.000**
Number of filled grains	0.291	0.028	10.435	0.000**
Notes = ** significant at 1%, Multiple R-squared: 0.7519 dan Adjusted R-squared: 0.748.

---

 | Show Table

DownLoad: CSV

Table 4.  Path analysis results based on selected highly correlated characters to the stress tolerance index (STI) of yield. (R² path analysis: 0.512; bold numbers indicated the direct effect).

Characters	Total tillers	Number of Productive tillers	Number of filled grains	Percentage of filled grains	Corelation total
Number of total tillers	−0.13	0.61	0.20	−0.04	0.65
Number of productive tillers	−0.12	0.67	0.22	−0.04	0.73
Number of filled grains	−0.05	0.26	0.55	−0.05	0.72
Percentage of filled grain	−0.07	0.38	0.36	−0.07	0.61

---

 | Show Table

DownLoad: CSV

Stepwise multiple regression analysis can determine the independent characters in predicting the main character ^[51]. Whereas path analysis can determine the direct and indirect effects of independent variables on the main character ^{[21,25,41,52,53]}. Thus, stepwise multiple regression analysis and path analysis are good combinations to determine the specific supporting characters of the main variable ^[21,25,29]. Based on all analyses, the number of productive tillers is the best stable secondary character which could be used as selection character under salinity screening in the pot. This character had been reported by Anshori et al. ^[20], Anshori et al. ^[21], and Mohammadi et al. ^[42]. On other hand, the other study of Anshori et al. ^[29] showed different from the result, where the total tiller trait was the best selection character for pot screening under salinity stress. However, their study only used two genotypes, Pokkali (tolerant check) and IR 29 (sensitive check): while we used 42 genotypes in this study. Therefore, the productive tiller is suitable for supporting the yield in line selection under salinity stress.

3.3.   Development of selection index and selection of double-haploid rice lines under salinity stress

The results of factor analysis showed that there were four representative factors with an eigenvalue above 1 (Table 5). Based on factor analysis, the days to flowering, the 100-grain weight, and the percentage of filled grains were strongly influenced the selected doubled-haploid populations. Meanwhile, the yield as the main character had the greatest variance in factor 2 (0.3). While the value did not reach the standard of 0.32, the yield score was still good considering the large environmental variance. The yield in factor 2 was grouped with the number of total tillers and the number of productive tillers. This was a strong indication that the number of productive tillers is a stable selection character for yield under salinity stress under greenhouse condition. Based on factor 2, the selection index was formulated as 0.3 (productivity) + 0.416 (productive tillers). However, the index needs to be corrected considering that the number of productive tillers had a direct effect of 0.67 on the yield with a total general variance of the path analysis of 0.512 (Table 4) and a combination (normal and saline conditions) repeatability of 0.58 (Supplement 1). Based on the results of direct effect and repeatability, the final selection index formed as follows:

Table 5.  Result of factor analysis based on principal component analysis of stress tolerance index (STI).

Characters	Factor 1	Factor 2	Factor 3	Factor 4	Communality
Vegetative plant height	0.259	−0.100	0.056	−0.173	0.632
Number of total tillers	−0.143	0.412	0.009	0.118	0.883
Days to flowering	0.394	−0.168	0.091	0.256	0.647
Generative plant height	0.182	−0.014	−0.113	0.161	0.658
Number of productive tillers	−0.168	0.416	−0.003	0.005	0.919
Flag leaves length	−0.059	−0.029	0.052	−0.731	0.871
Panicle length	−0.053	−0.064	−0.248	−0.25	0.659
Number of filled grains	0.079	0.097	−0.169	0.083	0.830
Number of unfilled grains	−0.153	−0.006	−0.402	0.078	0.828
Number of total grains	−0.054	0.071	−0.362	0.126	0.940
Weight of 100-grains	0.310	−0.143	0.099	−0.223	0.731
Percentage of filled grains	0.304	−0.006	0.170	−0.022	0.845
Yield	−0.09	0.300	−0.078	−0.066	0.825
Eigenvalue	5.427	2.531	1.246	1.066	10.269
Variance	0.417	0.195	0.096	0.082	0.790

---

 | Show Table

DownLoad: CSV

The results indicated that based on index selection values there were 19 genotypes (15 doubled-haploid (DH) lines) tolerant to salinity through the saline soil screening in pots under a greenhouse condition (Table 6).

Table 6.  The results of the doubled-haploid rice lines screening under greenhouse condition based on the selection index.

R	Genotype	PT (0)	Yld (0) (g)	PT (1)	Yld (1) (g)	STI PT	STI Yld	zSTI PT	zSTI Yld	Index
1	F11	10.3	23.32	7.0	10.19	0.79	0.34	1.84	2.30	0.84
2	F42	11.0	32.19	5.7	7.20	0.68	0.33	1.27	2.20	0.77
3	F10	8.7	22.77	7.7	9.67	0.72	0.31	1.50	2.00	0.72
4	F41	11.0	29.06	5.7	6.70	0.68	0.28	1.27	1.56	0.57
5	F22	12.7	34.95	4.3	5.64	0.60	0.28	0.84	1.60	0.55
6	F26	11.7	29.96	5.3	6.35	0.68	0.27	1.26	1.48	0.55
7	Inpari 34 Salin Agritan	12.7	25.51	7.3	6.10	1.01	0.22	3.02	0.88	0.51
8	F2	10.7	27.49	5.0	5.39	0.58	0.21	0.75	0.75	0.29
9	F49	11.3	37.17	4.3	3.97	0.53	0.21	0.51	0.74	0.26
10	F44	10.0	24.79	4.3	6.11	0.47	0.22	0.18	0.81	0.26
11	F37	9.0	21.24	4.7	6.90	0.46	0.21	0.10	0.72	0.23
12	F20	9.0	34.79	3.0	4.38	0.29	0.22	−0.76	0.83	0.19
13	F45	11.0	32.74	4.3	3.54	0.52	0.17	0.43	0.19	0.09
14	F28	8.7	20.89	4.7	5.83	0.44	0.17	0.01	0.30	0.09
15	F8	7.5	22.25	5.0	5.56	0.41	0.18	−0.16	0.33	0.09
16	Pokkali	9.0	21.00	3.3	5.94	0.33	0.18	−0.59	0.35	0.06
17	Inpara 5	11.3	27.93	5.0	3.54	0.62	0.14	0.94	−0.10	0.05
18	Inpari 29	6.0	19.25	4.5	6.35	0.29	0.17	−0.76	0.30	0.03
19	F14	6.3	27.39	2.7	4.62	0.18	0.18	−1.34	0.38	0.00
20	F56	14.0	35.47	5.3	1.93	0.81	0.10	1.98	−0.62	−0.02
41	IR29	8.7	25.58	2.3	1.34	0.22	0.05	−1.15	−1.22	−0.46
42	Ciherang	9.0	22.19	2.3	0.60	0.23	0.02	−1.11	−1.58	−0.57
Notes: PT = productive tiller, STI = stress tolerance index, Yld =Yield, zSTI= STI standardized.

---

 | Show Table

DownLoad: CSV

The determination of the main character in the factor analysis was based on a factor loading score above 0.32, which is the standard for factor analysis based on PCA variance ^[54]. In this study, factor analysis had sufficient power to detect good secondary characters from random data or data with a high environment effect ^[27]. Therefore, factor loading could be employed as the basis for weighting of character priority in the selection index.

The yield was the main character, so that its weight should be greater than the number of productive tillers character in the selection index. The direct effect value and heritability may be employed to correct the secondary character weighting. The use of path analysis as the weighting basis for the selection index in rice has also been reported by Sabouri et al. ^[55]. Meanwhile, the use of repeatability or heritability is also used in the formation of the Smith-Hazel selection index combined with economic correlations and weightings on selection character ^[56]. Based on these, the combination of direct effect from path analysis and repeatability could be an alternative for determining the index weight of the supporting character, especially in the low-yield genetic variance. Therefore, the productive tiller character must be corrected by direct effect and repeatability to increase its effectiveness and genetic stability in predicting the yield.

The determination of selected genotypes was based on the positive standardization value concept from the selection index. This concept has been reported by Tobi et al. ^[40] on Moroccan sugar beet. The high index value of a genotype indicates the genotype has the same variance direction with a high value of the yield and the number of productive tillers. Meanwhile, the positive index values were around 0, indicating that there was the larger positive value of a character toward other characters with negative values directions. Another assumption was that both characters have the same positive direction of variance, but both have a low value.

Based on the results of index selection, the index was considered better to use than only used the yield on pot artificial screening. It was proven by P values of regression of index that was significant (0.027), whereas the pot yield has no significant regression (0.056). Besides, the index could group Pokkali and Inpari 34 Salin Agritan as the tolerant varieties while Ciherang and IR 29 as sensitive varieties. The classification of Pokkali as tolerant and IR 29 as sensitive control varieties was consistent with the findings of Safitri et al. ^[15] who also conducted salinity screening in pots under a greenhouse condition. Besides, based on the regression analysis to Sukra yield by Anshori et al. ^[21] (Figure 3), this index has p-value of 0.027 or less than alpha of 0.05 and there was no outlier in prediction interval regression. This regression analysis is a good validation concept and has been reported by Fadhli et al. ^[52], Farid et al. ^[53], and Anshori et al. ^[21]. This result indicates that the use of the selection index model in this screening was more beneficial in selecting the salinity tolerant rice line than solely using the yield character on pot artificial screening. Therefore, the selected 15 DH lines that are classified as salinity tolerant based on the model could be subjected to further evaluations.

Figure 3.  Validation of index (A) and pot yield (B) toward Sukra field.

DownLoad: Full-Size Img PowerPoint

4.   Conclusions

Number of productive tillers is the best yield-supporting character in the salinity screening under greenhouse condition. Stress tolerance index (STI), path analysis, stepwise regression analysis and factor analysis could be used in the development of a salinity selection index model. The selection index model for salinity screening is 0.3 (yield) + 0.083 (productive tillers). The index can distinguish tolerant and non-tolerant varieties and 15 doubled haploid rice lines are identified as tolerant lines under salinity stress in soil artificial screening. These lines are recommended for further evaluation in developing the rice variety adapted to salinity stress.

Acknowledgements

We acknowledge the Ministry of Research, Technology, and Higher Education of the Republic of Indonesia for providing financial support to this research through the PMDSU Scholarship and Research Scheme with contract number 136/SP2H/LT/DRPM/IV/2017. The authors wish to express their gratitude toward the Indonesian Center for Agricultural Biotechnology and Genetic Resources Research and Development for providing the facilities for this study.