1. Introduction
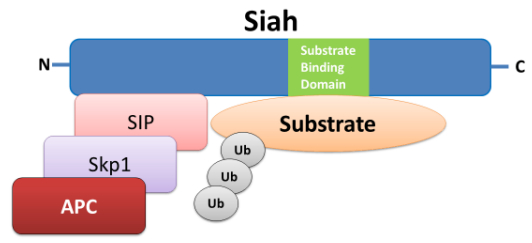
The seven in absentia (Sina) gene was initially identified to be critical for photoreceptor cell development in Drosophila [1]. As its mammalian orthologs, murine and human homologs of the Sina gene have also been identified. In Xenopus and mice, Sina homologs (Siahs) were isolated as three Siah proteins, Siah1a, Siah1b, and Siah2, which are encoded by different genes [2]. In contrast, the human Siah proteins consist of two homologs, Siah1 and Siah2, which are encoded by the SIAH1 and SIAH2 genes, respectively [3]. Siah1 and Siah2 have the high sequence similarity of their N-terminal RING finger domain, central cysteine-rich domain, and C-terminal substrate binding domain (SBD); however, Siah1 and Siah2 apparently have distinct but overlapping functions as proteins of a tumor suppressor gene and a proto-oncogene, respectively (Figure 1) [4]. Siah forms homodimers and heterodimers, which directly binds to their substrates or acts as the subunit of an E3 multi-protein complex through their anchoring proteins. A peptide motif RPVAxVxPxxR or AxVxP, which mediates an interaction of SBD with the substrates of Siah, was identified [5]. The various substrates and upstream regulatory molecules of Siah proteins have recently been identified and reviewed. Siah2 is phosphorylated by p38 mitogen-activated protein kinase (MAPK) to increase its ubiquitin activity [6]. In contrast, ubiquitin-specific protease 13 (USP13) is a deubiquitinase that forms a complex with Siah proteins and attenuates the E3 ligase activity [7]. In cancer cell lines, several functions of Siah in cancer progression regulated by Ras, p53, and hypoxia inducible factor (HIF), have been identified [8,9,10].
In this review, we discuss the critical functions of Siah proteins in variety of conditions, including cancer progression and ischemia reperfusion, and also discuss the evidence for oncogenic and tumor-suppressive functions of Siah to provide the clues for understanding the potential clinical applications by targeting Siah.
2. The critical functions of Sina and Siah proteins
The Sina protein is required for specification of R7 photoreceptor cell fate during Drosophila eye development. Sina down-regulates the expression of proteins that inhibit the differentiation of R7 photoreceptor cell [11]. The loss of Sina protein results in a deficiency of R7 precursor. Sina binds to Phyllopod (PHYL) and a transcriptional repressor, Tramtrack (TTK88), for ubiquitin-dependent proteolysis, proceeding R7 cell fate specification in the development of Drosophila eye [12].
Later, vertebrate homologs of Drosophila Sina are characterized, and termed as seven in absentia homolog (Siah). In Xenopus, Siah2, a protein with 67% identity to Drosophila Sina, was isolated. Siah2 expression is restricted to the brain, spinal cord and the developing and mature eyes. In Siah2 overexpressed Xenopus, the formation of a small eye phonotype is observed. The small eyes are characterized by a reduced size of the lens, the retina and the pigmented epithelium [13]. In contrast, in Siah1a overexpressed Xenopus, severe suppression of embryo cleavage is observed, while Siah1b overexpression does not influence during the development.
On the other hand, in mammals, similar ubiquitin ligase complex such as Skp, Cullin, F-box containing complex (SCF complex) or anaphase-promoting complex (APC complex) is formed and functions in ubiquitin-dependent proteolysis. Siah proteins with a catalytic RING domain on their N-terminus, followed by two zinc fingers and C-terminal SBDs are potent RING finger type E3 ubiquitin ligases that catalyze the ubiquitination of specific proteins, bind to E2 enzymes, and target their substrates for ubiquitin degradation [4]. Siah contains functional binding sites that recognize a peptide motif RPVAxVxPxxR or AxVxP within many substrates [5], and interact with a number of cellular proteins such as the oncogenic protein, β-catenin [8]; a nuclear receptor co-repressor, N-CoR [14]; a motor protein Kid [12]; the tumor suppressor homeodomain-interacting protein kinase 2 (HIPK2) and the tumor suppressor TGF-β inducible early gene 1 (TIEG-1) [15,16]. The interaction of Siah1 or Siah2 with APC/Axin complex is required for the degradation of β-catenin in mammalian cells [8]. Siah2 is also known as a regulator of hypoxia-activated signaling pathways and limits its own availability through self-ubiquitination under normoxia [17].
3. Upstream or downstream signaling pathways of Siah proteins
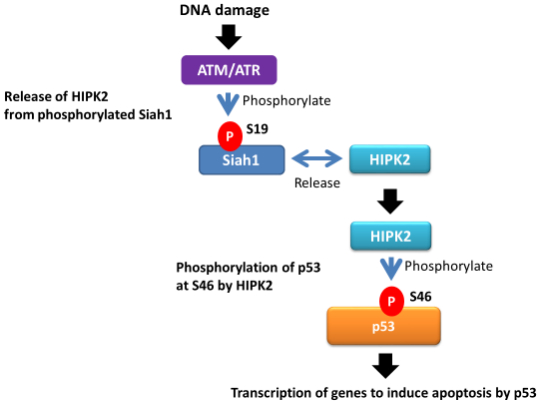
After DNA damage, activated p53 induces the expression of Siah1, but not Siah2. Siah1 is phosphorylated by check point kinases, Ataxia Telangiectasia Mutated (ATM) /Ataxia Telangiectasia and Rad3 related protein (ATR) in response to DNA damage [9]. The phosphorylation of Siah1 by ATM/ATR disrupts the interaction of HIPK2 and Siah1, thereby stabilizing HIPK2, resulting in the phosphorylation of p53 at Ser 46 and subsequent p53-mediated apoptosis induction (Figure 2) [15].
In estrogen receptor (ER)-positive breast cancer cells, ER up-regulates the expression of Siah2 at a transcriptional level, inducing the degradation of proteins such as the repressor of ER signaling, N-CoR, and activated Cdc42-associated kinase 1 (ACK1) and strengthening the subsequent resistance to apoptosis induction and affecting mitochondrial function [14].
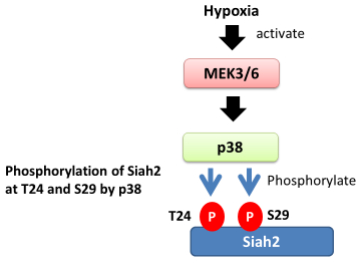
Recently, the up-regulatory mechanisms of Siah2 expression in response to oxygen concentration have been reviewed and discussed elsewhere. Under hypoxic condition, treatment with a chemical inhibitor against phosphoinositide 3-kinase (PI3K) decreases Akt activity and the expression levels of hypoxia-induced Siah2 mRNA, while expression of an active form of Akt by the cDNA transfection into cells induces the expression of Siah2 [10]. Therefore, the PI3K/Akt axis dependent pathway may be one of the critical signaling pathways to induce Siah2, although the transcription factor that induces Siah2 mRNA remains unknown. In addition, under hypoxia, Siah2 is subjected to phosphorylation, which increases its activity. This phosphorylation of Siah2 is inhibited when cells are exposed to a chemical inhibitor against p38 MAPK. Siah2 contains the conserved SQ/TQ amino acid sequence motif for the phosphorylation by p38 MAPK [6]. Amino acid residues, serine S29 and threonine T24 are major phosphorylation sites of Siah2. The phosphorylation of Siah2 by p38 MAPK results in stabilization and subsequent activation of the Siah2 protein in the cytoplasm (Figure 3). Furthermore, the deubiquitinating enzyme USP13 decreases Siah2 activity, resulting in the reduction of substrate degradation of Siah2 protein under normoxia [7]. In melanoma cells, USP13 expression is downregulated under hypoxia, hereby increasing Siah2 activity.
4. Function of Siah in response to hypoxia and ROS
Under normal conditions, the expression of HIF-1a, which is a master transcriptional factor to protect cells against hypoxic stress, is regulated by the hydroxylation of its two proline residues [18]. The stability of HIF-1a is regulated by prolyl hydroxylases (PHD) 1 and 3-mediated hydroxylation. Siah2 protein targets PHD 1 and 3, concomitantly facilitating HIF-1a stabilization under an oxygen concentration of 2−5% [19]. The deficiency of Siah2 induces the reduction of HIF-1a protein expression levels, leading to decreased proliferation, and increased apoptosis induction in cancer cells. In Siah2 knockout mice, an abrogated response to hypoxic conditions was exhibited, and tumor onset was delayed. At cellular and tissue levels, the expression of Siah2 mutants under hypoxic conditions led to significantly lower protein levels of HIF-1α, resulting in reduced hypoxia-induced proteins-mediated angiogenesis [20].
Recent studies have also suggested that Siah2 is involved in reactive oxygen species (ROS) metabolism. NF-E2-related factor (Nrf2), which is a transcriptional master regulator to protect cells against ROS, is negatively regulated by Siah2 under stressful conditions [21,22]. Under basal conditions, Nrf2 is known to be a substrate and negatively regulated by Kelch-like ECH-associated protein 1 (Keap1) [23]; however, Siah2, but not Keap1, is involved in the degradation of Nrf2 under particular conditions as follows. Under hypoxia, Nrf2 is phosphorylated by protein kinase C (PKC), which triggers the release of Nrf2 from Keap1. The knockdown of Siah2, but not Keap1, was shown to rescue hypoxia-induced reduction of Nrf2 irrespective of its phosphorylation status [21]. In addition, the knockdown of Siah2, but not Keap1, significantly attenuates the hypoglycemia-mediated reduction of Nrf2 expression [22]. These works have suggested that inhibition of the expression and function of Siah might be an attractive approach to regulate ROS metabolism. Interfering with Nrf2 down-regulation through the inhibition of expression or function of Siah is effective to induce the expression of cytoprotective genes, as it may have an impact on the cellular adaptive responses to oxidative stress more broadly than the inhibition of Keap1 function alone.
Ischemia reperfusion generates ROS and leads to cellular damage and oxidative stress in hypoxia and subsequent reoxygenation. In ischemia-induced cell death in cardiomyocytes, Siah2 regulates the availability of the mitochondrial scaffolding protein, A-kinase anchoring protein AKAP121, and subsequent mitochondrial dynamics [24]. Mitochondria are well known to be critical for cell survival, and their morphology is associated with susceptibility to cell death signals. Reduced availability of AKAP121 due to Siah2 relieves the inhibition of dynamin-related protein 1 (DRP1) by PKA and increases its interaction with mitochondrial fisson1 (FIS1), resulting in enhanced mitochondrial fission. In cells lacking Siah2, the level of this fission is decreased and ischemia-induced apoptosis of cardiomyocytes is reduced. Inhibition of both Siah1 and Siah2 expression by RNAi reduces infarct size and improves cardiac function after ischemia-reperfusion injury of hearts. Moreover, in vivo RNAi-induced inhibition of both Siah1 and Siah2 expression was found to augment the cardioprotective function of netrin-1 [25].
5. Function of Siah proteins as proto-oncogene products and tumor suppressor proteins
Due to increasing evidences, our understanding of the critical role of Siah proteins in tumor development and progression has vastly developed by verifying cell-based findings in animal models. The function of Siah in tumor progression was first investigated in pancreatic cancer [26]. In human pancreatic cancer cells, overexpression of a dominant-negative, RING-mutated Siah1 and Siah2, was found to cause tumor growth arrest. This study was the first to show that targeting Siah proteins induces the inhibition of tumor growth, and was also validated in a subsequent study in other types of cancers, suggesting a similar tumor-promoting role for both Siah1 and Siah2 proteins. In other cancers, such as liver and gastric cancers, low levels of Siah1 expression inhibited apoptosis and promoted cancer progression [27]. A dominant negative Siah protein was found to inhibit ERK signaling and cell proliferation, to induce apoptosis, and to reduce tumorigenesis of A549 human lung cancer cells, when injected into nude mice, and to reduce tumor growth by affecting Sprouty2 in the Ras signaling pathway in solid tumors [28]. Blocking of the expression of Siah had an anti-tumorigenic effect in mouse melanoma cell, SW1, and breast cancer cell, MCF7 [29]. Inhibition of the binding of Siah with the substrates through PHYL due to high homology sequence in the SBD also reduced tumor growth, angiogenesis, and metastatic spread by the inactivated hypoxic response pathway [20].
Furthermore, in vivo, a chemical inhibitor of Siah2, menadione, abolished the growth of xenograft tumors in nude mice [30]. The genetic knockout of SIAH in mice is valuable in establishing the significance of biochemical and cell biological studies. Finally, in both Siah1a and Siah2 null mice, tumor progression to an advanced stage was inhibited and metastasis was reduced [31]. These findings suggest that the inhibition of Siah expression is effective in attenuating tumor growth.
Previous several studies suggested the tumor suppressive role of Siah proteins, as shown that overexpression of Siah1 arrested the growth of hepatoma cells [32]. The expression of Siah1 transfected into U937 lymphoma cell suppressed the tumorigenesis of these cells when injected into mice [33]. In addition, in situ hybridization on cancer tissue microarrays revealed that expression of both SIAH1 and SIAH2 genes were down-regulated in tumor tissues. Expression of Siah1 is also decreased in human breast cancer tissue compared with normal tissue. These evidences strongly suggest that Siah1 functions as a tumor suppressor.
As described above, Siah1 seems to act as a tumor suppressor and Siah2 as an oncogene product. A correct difference between the oncogenic and tumor-suppressive roles of Siah in tumor progression remains unknown. One study has reported that nuclear accumulation of Siah1 and Siah2 proteins in patients with hepatocellular carcinoma (HCC) were inversely correlated, and that Siah2 accumulation was correlated with hepatocarcinogenesis and tumor dedifferentiation, suggesting potentially exclusive expression patterns and highlighting an association between Siah2 levels and cancer progression [34]. Evidence from the clinical studies describes distinct roles for Siah1 and Siah2. The different roles are due to the ubiquitination of substrate proteins by the distinct complex formation. The molecular basis of substrate specificity with Siah leads to the identification of potential inhibitors against Siah proteins for therapeutic responses of the cancer patients [35].
Recent studies have revealed that cancer development is associated with the loss of circadian homeostasis. RevErbα, the nuclear hormone receptor, is known to be a key constituent of the circadian clock. Siah2 is found to be involved in the regulation of the dynamic rhythmicity of RevErbα stability and circadian clock function [36].
SIAH1 gene is located on chromosome 16q12.1, which is found to be deleted in a variety of other cancers. In contrast, SIAH2 gene is located on chromosome 3q25.1, genomic copy number of which is gained in basal-like breast cancer. Indeed, it is reported that copy number of gain of the SIAH2 gene was more frequently detected in these tumors than luminal tumors and that basal-like tumors copy number gain was related to high expression of Siah2 protein [37]. Therefore, depending on the cancer types, and stage of metastasis, Siah1 and/or Siah2 may have opposing roles on the tumor progression.
6. Conclusion
Siah2 protein is a regulator of several pathways mediated by signaling molecules such as Ras, p53, ER, and HIF [9,14,20,38]. Recent work has described contradictory roles for Siah1 and Siah2 in cancer progression, metastasis, and therapeutic responses. Evidence suggests that Siah2 acts in an oncogenic manner, and is also a promising therapeutic target in pathological conditions accompanied by a low level of Nrf2 expression [21,22]. The inhibition of Siah2 expression reduces tumorigenesis and/or metastasis, and restores the decreased expression of Nrf2-inducible genes and subsequently improves symptoms, while, Siah1 often functions as a tumor suppressor. Past data focuses on the inhibition of Siah2 expression, consequently, vitamin K3 (menadione) was identified as an inhibitor of Siah2 ubiquitin ligase activity and inhibited both Ras and the hypoxic response pathways [30]. In fact, mice treated with menadione had reduced tumor growth rates, showing the significance of the screening and functional validation of Siah inhibitors to prevent cancer progression. Identification of the inhibitors against either or both Siah1 and Siah2 proteins will be necessary to fine-tune this therapeutic approach for the effective treatment. Therefore, more precise investigations are needed for a novel understanding of the molecular mechanism underlying the relationship between Siah proteins and their substrates, and the modulation of the activity or expression level of Siah proteins, in vivo, since Siah proteins play central roles in key signaling pathways during the course of tumor progression.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: