1.
Introduction
In 1964, Hopf first proposed Hopf algebra in order to study the properties of algebraic topology and algebraic groups [1]. In 1965, Milnor and Moore introduced the basic definitions and properties of Hopf algebras [2], then Chase and Sweedler did some relevant works and introduced common notations [3,4]. After that, Hopf algebra has been used to study a lot of objects, such as posets [5], symmetric functions [6,7], quantum groups [8], and Clifford algebras [9].
In 1979, Joni and Rota first studied Hopf algebras on combinatorial objects, such as polynomials and puzzles [10]. In 1994 and 1995, Schmitt studied incidence Hopf algebras and a Hopf algebra on graphs with an addition invariant and introduced a variety of examples of incidence Hopf algebras arising from families of graphs, matroids, and distributive lattices, many of which generalize well-known Hopf algebras [11,12].
In 1997 and 1999, Connes and Kreimer studied Hopf algebra structures on rooted trees and rooted forests and their applications in renormalization in quantum field theories [13,14]. This promotes the study of Hopf algebras on graphs. In 2020, Aval et al. mentioned a Hopf algebra on labeled graphs arising from the unshuffle coproduct [15]. For more Hopf algebras on graphs, please refer to [16,17,18,19,20].
Permutations are related to graphs closely. In 1995, Malvenuto and Reutenauer studied a Hopf algebra on permutations, where the product is the classic shuffle Ⅲ [21]. In 2014, Vargas defined a commutative but non-cocommutative Hopf algebra on permutations by the super-shuffle product Ⅲ and the cut-box coproduct Δ⋄ without a proof [22], which was done by Liu and Li in 2021 [23]. In 2020, Zhao and Li defined another commutative Hopf algebra structure on permutations and its duality and figured out closed-formulas of the antipodes [24]. It is well-known that permutations are elements of symmetric groups, which are widely used in various fields, such as the algebraic number theory [25].
A labeled simple graph is a simple graph with vertices labeled by distinct positive integers. In this paper, we generalize the super-shuffle product and the cut-box coproduct on permutations to labeled simple graphs. We prove that the vector space spanned by labeled simple graphs with these two operations is a Hopf algebra.
This paper is organized as follows. In Section 2, we review some basic concepts of Hopf algebra, give the definition of labeled simple graphs, and define the super-shuffle product and the cut-box coproduct on labeled simple graphs. In Section 3, we prove that the vector space spanned by labeled simple graphs is a graded algebra with the super-shuffle product and a graded coalgebra with the cut-box coproduct. Furthermore, we prove the compatibility of these operations, then the vector space is a Hopf algebra. Finally, we summarize our main conclusions in Section 4.
2.
Basic definitions
2.1. Preliminaries
Here, we recall some basic definitions related to Hopf algebra and see [4] for more details. Let C be a K-module over commutative ring K.
Define K-bilinear mappings m from C⊗C to C and μ from K to C, such that the diagrams in Figure 1 are commutative, then (C,m,μ) is a K-algebra. Here, m and μ are called a product and a unit, respectively.
Define K-linear mappings Δ from C to C⊗C and ν from C to K, such that the diagrams in Figure 2 are commutative, then (C,Δ,ν) is a K-coalgebra. Here, Δ and ν are called a coproduct and a co-unit, respectively.
We say (C,m,μ,Δ,ν) is a bialgebra if (C,m,μ) is an algebra, (C,Δ,ν) is a coalgebra, and one of the following compatibility conditions holds:
(ⅰ) Δ and co-unit ν are algebra homomorphisms;
(ⅱ) m and unit μ are coalgebra homomorphisms.
In fact, (ⅰ) and (ⅱ) are equivalent; see [26] for details.
A vector space C is graded if
and we call it connected when C0≅K [26]. The algebra (C,m,μ) is graded if the product m satisfies
and
Similarly, the coalgebra (C,Δ,ν) is graded if the coproduct Δ satisfies
and
when n⩾1. A bialgebra is graded when its algebra and coalgebra structures are both graded.
For bialgebra (C,m,μ,Δ,ν), we call S: C→C an antipode if it satisfies
i.e., the diagram in Figure 3 is commutative. A bialgebra is a Hopf algebra when it has an antipode.
Actually, a graded connected bialgebra must be a Hopf algebra [26].
2.2. Main concepts
In this subsection, we recall some basic concepts of graph theory, which can be found in [27].
A labeled simple graph Γ=(V,E) is a finite graph with no cycles and no multiple edges whose vertices are distinct positive integers, where V is the set of all vertices of Γ, also denoted by V(Γ), and E is the set of all edges of Γ, also denoted by E(Γ). Obviously, E⊆V×V. If (i1,i2)∈E, then i1≠i2 and (i2,i1)∉E, since the graph Γ has no cycles and no multiple edges. In particular, Γ is the empty graph when V=∅, denoted by ϵ.
Let Γ=(V,E) and I⊆V. Define the restriction of Γ on I by ΓI=(I,EI), where
and we call ΓI a subgraph of Γ. If I is a nontrivial subset of V, we call ΓI a true subgraph of Γ. If the vertex sets of two subgraphs of Γ are disjoint, then we say that the subgraphs are disjoint subgraphs. If
and
then denote
Obviously, there are no edges between V1 and V2.
We introduce the following notations for convenience:
and
Example 1. The labeled simple graph
can be represented as the graph
then
Let
and Hn be the vector space spanned by Hn over field K, for a nonnegative integer n. In particular, H0={ϵ} and H0=KH0. Denote
Let Γ=(V,E) be a nonempty labeled simple graph, where
Define the restructure of Γ=(V,E) by ˆV to be ˆΓ=(ˆV,ˆE), where
is a set of distinct positve integers satisfying
and ˆE satisfies
for any 1⩽i,j⩽n.
Example 2. For
the restructure of Γ by [5] is 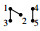 and the restructure of Γ by {1,3,5,7,9} is
and the restructure of Γ by {1,3,5,7,9} is 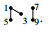
Let I be the set {i1,i2,⋯,in} of distinct positive intergers with i1<i2<⋯<in. We define a mapping stI from I to [|I|] to be the standardization of I satisfying stI(ia)=a for 1⩽a⩽n. For x,y∈I, we have stI(x)<stI(y) if, and only if, x<y. For a subset S of I, denote
In general, the standardizations of a number in different sets are different. For example, let I1={6,7,9} and I2={1,3,7,9,11}, then stI1(7)=2 and stI2(7)=3. For convenience, we omit the subscript of the set.
Define the standard form of Γ=(V,E) by st(Γ)=(st(V),st(E)), where st(V)=[|V|] and st(E) satisfies
Obviously, the above standardizations are of the vertex set V, so we omit the subscript. In particular, we have st(ϵ)=ϵ. Thus, st(⋅) is a mapping from the set of all labeled simple graphs to H. In fact, the standard form of Γ=(V,E) is the restructure of Γ by [|V|].
In addition, for a positive integer n, let Γ↑n be the restructure of Γ by the set
Similarly, let Γ↓n be the restructure of Γ by the set
provided n is less than the minimum of V.
Example 3. For labeled simple graphs
their standard forms are
and
For nonempty Γ in H, the standard form of any restructure of Γ must be Γ, i.e.,
where the ˆΓ is a restructure of Γ. Conversely, if the standard form of a labeled simple graph is Γ, then it must be a restructure of Γ.
Example 4. For
the restructure of Γ by [4,8] is 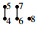 and the restructure of Γ by {1,3,5,7,9} is
and the restructure of Γ by {1,3,5,7,9} is 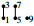 . We have
. We have
For Γ=([n],E) in Hn, we call i a split of Γ if
where 0⩽i⩽n. Obviously, i is a split of Γ if, and only if, there are no edges between [i] and [i+1,n] in Γ. By the definition, 0 and n, called trivial splits, are always splits of labeled simple graphs in Hn when n⩾1. We call Γ indecomposible if it is nonempty and only has trivial splits.
For Γ=([n],E) in Hn, n⩾1, assume that {i0,i1,⋯,is} is the set of all splits of Γ, where
then we call Γ[ik−1+1,ik] an atom of Γ, 1⩽k⩽s. Obviously, the standard form of an atom is indecomposible since there is no split of Γ in [ik−1+1,ik] for 1⩽k⩽s. Let
for 1⩽k⩽s. We define the decomposition of Γ by
Actually, if jk: =ik−ik−1, then Γk∈Hjk for 1⩽k⩽s, and
In particular, when Γ=ϵ, its decomposition is itself.
Example 5. (1) The set of splits of 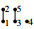 is {0,2,5} and its decomposition is
is {0,2,5} and its decomposition is
The atoms of 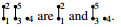
(2) The set of splits of 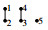 is {0,2,4,5}, so its decomposition is
is {0,2,4,5}, so its decomposition is
The atoms of 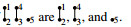
(3) The set of splits of 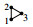 is {0,3}, so it is indecomposible. Its decomposition is itself, and so is its atom.
is {0,3}, so it is indecomposible. Its decomposition is itself, and so is its atom.
Define the cut-box coproduct Δ on H by
for nonempty
in Hn with splits
Define the co-unit ν from H to K by
for Γ in H.
Example 6.
Theorem 2.1. (H,Δ,ν) is a graded coalgebra.
Proof. It is easy to verify that ν is a co-unit. Obviously,
Suppose Γ=([n],E) with n⩾1, and its decomposition is
then,
where
for 0⩽k⩽s. So, Δ satisfies the coassociative law. Hence, (H,Δ,ν) is a coalgebra.
By the definition of the coproduct Δ, we have
and
when n⩾1. So, (H,Δ,ν) is a graded coalgebra. □
Define the super-shuffle product ∗ on H by
for Γ1 in Hm and Γ2 in Hn. Sometimes, we denote it by ∗(Γ1,Γ2). Obviously, the product ∗ is commutative on H. Define the unit μ from K to H by μ(1)=ϵ.
Actually, ΓI is the restructure of Γ1 by I, and ΓJ is the restructure of Γ2 by J in (2.1). Given I and J satisfying |I|=m, |J|=n, and I∪J=[m+n], Γ traverses all graphs in Hm+n, which is a union of the restructure of Γ1=(V1,E1) by I, the restructure of Γ2=(V2,E2) by J, and some edges between ˆV1 and ˆV2. That is, Γ traverses the set
So, we rewrite (1) as
That is, each term Γ in Γ1∗Γ2 is a graph by adding some edges between ˆV1 and ˆV2 to ˆΓ1∪ˆΓ2, where
i.e.,
where C is a set of edges between ˆV1 and ˆV2. Conversely, (ˆV1,ˆV2,C) can uniquely determine a term in Γ1∗Γ2, where
and C is a set of edges between ˆV1 and ˆV2. We consider two terms in Γ1∗Γ2 the same if, and only if, their corresponding ˆV1, ˆV2 and C are the same. Thus, each term in Γ1∗Γ2 is unique.
Example 7.
Here, we color the vertices of the term Γ in Γ1∗Γ2 restricted to Γ1 red and to Γ2 blue, respectively. In this example, although 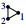 and
and 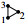 are the same as graphs, we consider that they are different in Γ1∗Γ2 because their ˆV1 and ˆV2 are not the same. So, each term in Γ1∗Γ2 is unique.
are the same as graphs, we consider that they are different in Γ1∗Γ2 because their ˆV1 and ˆV2 are not the same. So, each term in Γ1∗Γ2 is unique.
In order to represent vertices in each term of Γ1∗Γ2 before restructure, we name the vertices in Γ1 and Γ2, respectively, as
and
where v11<v12<⋯<v1m and v21<v22<⋯<v2n. Although v11 and v21 are both equal to 1, we consider that they are different because they belong to different graphs, then the vertex set of a term in Γ1∗Γ2 is
Theorem 2.2. (H,∗,μ) is a graded algebra.
Proof. It is easy to verify that μ is a unit. Suppose
and
in H. For any term Γ in (Γ1∗Γ2)∗Γ3, it corresponds to two disjoint subsets J and K of [n1+n2+n3] with |J|=n1+n2 and |K|=n3, such that st(ΓJ) is a term in Γ1∗Γ2 and st(ΓK)=Γ3. It means
For a fixed J in (4), st(ΓJ) corresponds to two disjoint subsets P and Q of [n1+n2] with |P|=n1 and |Q|=n2, such that
and
Therefore, there is a subset M of J with |M|=n1 corresponding to P, i.e., stJ(M)=P, such that
Similarly, there is a subset N of J with |N|=n2 corresponding to Q, i.e., stJ(N)=Q, such that
That means (4) can be rewritten as
For a fixed subset J in [n1+n2+n3] with cardinality n1+n2, P traverses all subsets with cardinality n1 in [n1+n2] since st(ΓJ) traverses all terms in Γ1∗Γ2. Meanwhile, M traverses all subsets with cardinality n1 in J. Therefore, M traverses all subsets with cardinality n1 in [n1+n2+n3] since J traverses all subsets with cardinality n1+n2 in [n1+n2+n3]. At the same time, N traverses all subsets with cardinality n2 in [n1+n2+n3] from J=M∪N. Thus, (5) can be rewritten as
Similarly, Γ1∗(Γ2∗Γ3) is equal to (6). Hence, ∗ satisfies the associative law and (H,∗,μ) is an algebra.
By the definition of the product ∗, we have
and
So, (H,∗,μ) is a graded algebra. □
3.
Main theorems
In this section, we will prove that (H,∗,μ,Δ,ν) is a Hopf algebra. Now, we give two lemmas.
Let Γ1=(V1,E1) in Hm and Γ2=(V2,E2) in Hn be nonempty graphs and Γ be a term in Γ1∗Γ2. Thus, Γ can be represented by (ˆV1∪ˆV2,ˆE1∪ˆE2∪C) from (3), where
is the restructure of Γ1 by ˆV1 and
is the restructure of Γ2 by ˆV2. Obviously,
Lemma 3.1. Each atom of Γ in Γ1∗Γ2 can only contain subgraphs of ˆΓ1 or ˆΓ2 corresponding to some complete atoms in Γ1 or Γ2.
Proof. Let
and
be nonempty in H, where v11<⋯<v1m and v21<⋯<v2n. Consider a term Γ in Γ1∗Γ2. Suppose Γ[i,j] is an atom of Γ containing a nonempty subgraph of ˆΓ1{ˆv1k}qk=p, where ˆΓ1{ˆv1k}qk=p corresponds to the atom Γ1{v1k}qk=p of Γ1.
When p=q, there is only one element in {ˆv1k}qk=p, then Γ[i,j] contains the complete atom ˆΓ1{ˆv1k}qk=p. Hence, the conclusion holds.
When 1⩽p<q⩽m, {v1k}qk=p contains at least two vertices. Suppose that Γ[i,j] contains a true subgraph of ˆΓ1{ˆv1k}qk=p. In fact, since {ˆv1k}qk=p maintains the order relationship in {v1k}qk=p, the vertices of this true subgraph correspond to a true subinterval in {v1k}qk=p. Let
and
We have i⩽ˆv1ω⩽ˆv1Ω⩽j, then
and ω≠p or Ω≠q because Γ[i,j] contains a true subgraph of ˆΓ1{v1k}qk=p.
If ω≠p, then ω>p. From
and
From Γ[i,j] is an atom of Γ and i−1 is a split of Γ, there are no edges between [i−1] and [i,m+n] in Γ. Therefore,
By the definition of ∗, we have
and
Hence,
where p−1<ω−1<q, i.e., ω−1 is a split of Γ1. However, there is no split of Γ1 between p−1 and q, since Γ1{v1k}qk=p is an atom of Γ1, which is a contradiction. Similarly, when Ω≠q, we have p−1<Ω<q and Ω is a split of Γ1, a contradiction.
Thus, if an atom of Γ contains a true subgraph in ˆΓ1, then this subgraph must correspond to some complete atoms of Γ1. Similarly, we can prove the conclusion holds for atoms in Γ2. □
For simplicity, we restate Lemma 3.1 as: for any term Γ in Γ1∗Γ2, any atom of Γ can only contain some complete original atoms of Γ1 or Γ2.
Remark 3.1. For Γ in Hn, suppose its decomposition is
with splits
then
If Θ1⊗Θ2 is the term in Δ(Γ), then Θ1 is a standard form of the first k atoms of Γ for some 0⩽k⩽s. Let Γ be a term in Γ1∗Γ2 and Θ1⊗Θ2 be a term in Δ(Γ). From Lemma 3.1, Θ1 only contains the standard forms of some complete original atoms of Γ1 or Γ2. If the first few atoms of a labeled simple graph contain l vertices, then these vertices must be [l]. So, if Θ1 contains i original atoms of Γ1, then they must be the first i atoms of Γ1. Similarly, if Θ1 contains j original atoms of Γ2, then they must be the first j atoms of Γ2.
Let Γ1 and Γ2 be nonempty in H. Suppose their decompositions are
and
Define Δij(Γ1∗Γ2) to be the sum of all terms Θ1⊗Θ2 in Δ(Γ1∗Γ2), where Θ1 contains the first i complete original atoms in Γ1 and the first j complete original atoms in Γ2, 0⩽i⩽s, and 0⩽j⩽t.
Lemma 3.2. Let Γ1 and Γ2 be nonempty in H. Assume their decompositions are
then,
for 0⩽i⩽s and 0⩽j⩽t.
Proof. Denote
and
Similarly,
and
Obviously,
and
Next, we denote ˆV11 as the subset corresponding to V11 in ˆV1 and (ˆV11,ˆE11) as the restructure (V11,E11) by ˆV11. Similarly, we have ˆV12, ˆE12, ˆV21, ˆE21, ˆV22, and ˆE22.
By (3), each term Γ in Γ1∗Γ2,
where C is a set of edges between ˆV1 and ˆV2. Let Θ1⊗Θ2 be a term in Δ(Γ) and in Δij(Γ1∗Γ2). By the definition of Δij, h1+h2 is a split of Γ,
and
Since h1+h2 is a split of Γ, there are no edges between [h1+h2] and [h1+h2+1,m+n] in Γ. Thus, there are no edges between ˆV11 and ˆV22 and no edges between ˆV12 and ˆV21. Therefore, C is C1∪C2, where
and
Hence,
Therefore,
and
then Θ1 is a term in
for
and
Similarly, Θ2 is a term in
For given Θ1 in Γ11⋄⋯⋄Γ1i∗Γ21⋄⋯⋄Γ2j, let
For each Γ in S,
by (7), where ˆV11,ˆV21, and C1 are fixed, since Θ1 is fixed.
By (3), when Γ traverses all terms in Γ1∗Γ2, its ˆV1 and ˆV2 traverse all disjoint subsets of [m+n] with cardinalities m and n, respectively, and C traverses all subsets in ˆV1׈V2 for fixed ˆV1 and ˆV2. Thus, ˆV12 and ˆV22 of Γ in S traverse all disjoint subsets of [h1+h2+1,m+n] with cardinalities m−h1 and n−h2, respectively. Also, C2 of Γ in S traverses all subsets of ˆV12׈V22 for fixed ˆV12 and ˆV22. Correspondingly, for ˆV12 and ˆV22 of Γ in S, stˆV12∪ˆV22(ˆV12) and stˆV12∪ˆV21(ˆV22) traverse all disjoint subsets of [m+n−h1−h2] with cardinalities m−h1 and n−h2, respectively. Also, stˆV12∪ˆV22(C2) traverses all subsets in
for fixed ˆV12 and ˆV22. From the arguments above and (2), for fixed Θ1 in Γ11⋄⋯⋄Γ1i∗Γ21⋄⋯⋄Γ2j, Θ2 traverses all terms in Γ1,i+1⋄⋯⋄Γ1s∗Γ2,j+1⋄⋯⋄Γ2t. Similarly, for fixed Θ2 in Γ1,i+1⋄⋯⋄Γ1s∗Γ2,j+1⋄⋯⋄Γ2t, Θ1 traverses all terms in Γ11⋄⋯⋄Γ1i∗Γ21⋄⋯⋄Γ2j. Therefore,
□
Next, we show that (H,∗,μ,Δ,ν) is a Hopf algebra.
Theorem 3.1. (H,∗,μ,Δ,ν) is a bialgebra.
Proof. It is easy to verify ν is an algebra homomorphism. We only need to prove Δ is an algebra homomorphism, i.e.,
for Γ1 and Γ2 in H.
If Γ1 or Γ2 is an empty graph, then (8) holds. Suppose
in Hm and
in Hn are nonempty graphs. Let
By Lemma 3.2, we have
Furthermore,
Hence, (H,∗,μ,Δ,ν) is a bialgebra. □
Example 8.
Corollary 3.1. (H,∗,μ,Δ,ν) is a Hopf algebra.
Proof. Since (H,∗,μ,Δ,ν) is a graded connected bialgebra, it is a Hopf algebra. □
4.
Conclusions
Many combinatorial objects have Hopf algebra structures. The labeled simple graphs are important combinatorial objects. In this paper, we generalize the super-shuffle product and the cut-box coproduct on permutations to labeled simple graphs. We prove that the vector space spanned by labeled simple graphs with the super-shuffle product and the cut-box coproduct is a Hopf algebra. In the future, we will study the duality of the Hopf algebra (H,∗,μ,Δ,ν).
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This work is supported by National Natural Science Foundation of China (Nos. 11701339 and 12071265).
Conflict of interest
The authors declare that there are no conflicts of interest in this paper.










 DownLoad:
DownLoad:





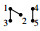 and the restructure of
and the restructure of 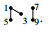





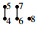 and the restructure of
and the restructure of 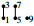 . We have
. We have
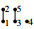 is
is 
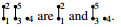
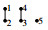 is
is 
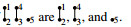
 is
is 

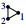 and
and 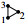 are the same as graphs, we consider that they are different in
are the same as graphs, we consider that they are different in 


