Mixing is the basis of stable and efficient combustion in air-breathing power systems, and it is also an important problem in fluid mechanics, which has been extensively studied from various perspectives. The purpose of this review is to investigate mixing mechanisms based on two commonly-used mixing indicators, namely ci (c refers to concentration, and i is either 1 or 2, indicating first- or second-order statistics), with a focus on passive-scalar (PS) and variable-density (VD) mixing. For PS mixing, the flow is not influenced by the mixing process. By using first-order statistics with concentration as the core, the PS mixing mechanisms on lamella structures can be described as stretching enhancing diffusion and promoting mixing. On the other hand, second-order statistics represented by the scalar dissipation rate can investigate mixing mechanisms on specific type of flow structures described by the invariants of velocity gradient tensors and the rotation of principal strain axis. As such, it has been found that strain-dominated flow structures can promote mixing, while rotation-dominated flow structures hinder it. For VD mixing, it has two distinct characteristics: flow changes due to baroclinic vorticity, and the inherent velocity divergence alters the mixing indicators. Studies using first-order statistics center on the mixing time in different types of VD flows, leading to the discovery of new phenomena. For instance, the second baroclinic vorticity can promote stretching in shock bubble interactions. Studies on second-order statistics for VD mixing have defined several mixing indicators from the component-transport equation, which have been utilized in phenomenological studies on VD mixing. This review aims to provide an overview of mixing phenomena, mixing indicators, and mixing mechanisms, and proposes research directions for understanding the mixing characteristics, flow structures, and their relationship with specific combustion phenomena particularly by second-order statistics.
Citation: Xu Han, Bin Yu, Hong Liu. Mixing mechanisms in the view of mixing indicators: from passive-scalar mixing to variable-density mixing[J]. Metascience in Aerospace, 2024, 1(1): 1-37. doi: 10.3934/mina.2024001
| [1] | Wei Qi . The polycyclic codes over the finite field Fq. AIMS Mathematics, 2024, 9(11): 29707-29717. doi: 10.3934/math.20241439 |
| [2] | Xiying Zheng, Bo Kong, Yao Yu . Quantum codes from σ-dual-containing constacyclic codes over Rl,k. AIMS Mathematics, 2023, 8(10): 24075-24086. doi: 10.3934/math.20231227 |
| [3] | Fatma Zehra Uzekmek, Elif Segah Oztas, Mehmet Ozen . (θi,λ)-constacyclic codes and DNA codes over Z4+uZ4+u2Z4. AIMS Mathematics, 2024, 9(10): 27908-27929. doi: 10.3934/math.20241355 |
| [4] | Hongfeng Wu, Li Zhu . Repeated-root constacyclic codes of length p1pt2ps and their dual codes. AIMS Mathematics, 2023, 8(6): 12793-12818. doi: 10.3934/math.2023644 |
| [5] | Irwansyah, Intan Muchtadi-Alamsyah, Fajar Yuliawan, Muhammad Irfan Hidayat . Generalized Reed-Solomon codes over number fields and exact gradient coding. AIMS Mathematics, 2024, 9(4): 9508-9518. doi: 10.3934/math.2024464 |
| [6] | Yanyan Gao, Yangjiang Wei . Group codes over symmetric groups. AIMS Mathematics, 2023, 8(9): 19842-19856. doi: 10.3934/math.20231011 |
| [7] | Ted Hurley . Ultimate linear block and convolutional codes. AIMS Mathematics, 2025, 10(4): 8398-8421. doi: 10.3934/math.2025387 |
| [8] | Yuezhen Ren, Ruihu Li, Guanmin Guo . New entanglement-assisted quantum codes constructed from Hermitian LCD codes. AIMS Mathematics, 2023, 8(12): 30875-30881. doi: 10.3934/math.20231578 |
| [9] | Chaofeng Guan, Ruihu Li, Hao Song, Liangdong Lu, Husheng Li . Ternary quantum codes constructed from extremal self-dual codes and self-orthogonal codes. AIMS Mathematics, 2022, 7(4): 6516-6534. doi: 10.3934/math.2022363 |
| [10] | Hao Song, Yuezhen Ren, Ruihu Li, Yang Liu . Optimal quaternary Hermitian self-orthogonal [n,5] codes of n≥492. AIMS Mathematics, 2025, 10(4): 9324-9331. doi: 10.3934/math.2025430 |
Mixing is the basis of stable and efficient combustion in air-breathing power systems, and it is also an important problem in fluid mechanics, which has been extensively studied from various perspectives. The purpose of this review is to investigate mixing mechanisms based on two commonly-used mixing indicators, namely ci (c refers to concentration, and i is either 1 or 2, indicating first- or second-order statistics), with a focus on passive-scalar (PS) and variable-density (VD) mixing. For PS mixing, the flow is not influenced by the mixing process. By using first-order statistics with concentration as the core, the PS mixing mechanisms on lamella structures can be described as stretching enhancing diffusion and promoting mixing. On the other hand, second-order statistics represented by the scalar dissipation rate can investigate mixing mechanisms on specific type of flow structures described by the invariants of velocity gradient tensors and the rotation of principal strain axis. As such, it has been found that strain-dominated flow structures can promote mixing, while rotation-dominated flow structures hinder it. For VD mixing, it has two distinct characteristics: flow changes due to baroclinic vorticity, and the inherent velocity divergence alters the mixing indicators. Studies using first-order statistics center on the mixing time in different types of VD flows, leading to the discovery of new phenomena. For instance, the second baroclinic vorticity can promote stretching in shock bubble interactions. Studies on second-order statistics for VD mixing have defined several mixing indicators from the component-transport equation, which have been utilized in phenomenological studies on VD mixing. This review aims to provide an overview of mixing phenomena, mixing indicators, and mixing mechanisms, and proposes research directions for understanding the mixing characteristics, flow structures, and their relationship with specific combustion phenomena particularly by second-order statistics.
Major applications of remote sensing in geoscience are detecting and monitoring geomorphological structures. Generally, the overall aim of most geomorphological studies is assessing terrain features in an area of interest (AOI) with a sufficiently high topographic and objective differentiation [1]. Innovations and technical progresses in the field of remote sensing caused a rapid increase in the number of available sensors and methods of capturing surfaces in 3D. Even though these remote sensing methods allow a reliable surface mapping, investigating the subsurface is almost impossible. This would however be beneficial for investigations in which surface changes might be explainable by subterraneous processes. Hence, it is desirable to combine surface and subsurface data.
Investigations in karstic regions are one example where such combined investigations should be worthwhile, since subterraneous solution and subsidence processes are likely to cause surfaces changes. In this study, a karst depression in south-west Germany was investigated, where surface changes are expected based on human-based long-term observations. Monitoring campaigns with terrestrial laser scanning (TLS) during the last two years, have however not shown discernible movements yet [2]. This detection of temporal changes is not the primary topic of this contribution. Instead, the focus lies on a better understanding of the surface and subsurface structures and their interrelation. Strictly speaking, the results of a comprehensive campaign are presented, where TLS and low-altitude airborne imaging from an unmanned aerial vehicle (UAV) were applied for capturing the surface, and electrical resistivity tomography (ERT) was conducted for imaging subsurface structures. This contribution follows two aims: (Ⅰ) investigating the usability of both remote sensing systems for capturing fine karstic structures and (Ⅱ) establishing a suitable way of combining the surface mapping with the data from the subsurface and examining its benefit. The latter presupposes the visualization of the ERT measurements.
A large number of remote sensing approaches already exist for capturing surfaces in 3D. With regard to the topic of this paper, a short introduction into laserscanning and into low-altitude airborne imaging are in the focus of this paragraph. Measurements based on Light Detection and Ranging (LiDAR) are generally widely applied due to their known accuracy and reliability [3]. LiDAR measurements may be performed as airborne laser scanning (ALS) or terrestrial laser scanning (TLS) depending on factors such as the targeted spatial and temporal resolution, the desired level of detailedness, or the extent and accessibility of the AOI. Examples for both methods can be widely found [4,5,6]. Even though TLS measurements are considerably cheaper and easier to perform than ALS approaches, the effort and expense should still not be underestimated. Beside the costs, major issues are the unsuitability in terrains with difficult access or the time requirement.
An important step in the evolution of remote sensing was the development of UAVs as platform for different remote sensing sensors over the last several years. Further benefited by the rapidly increasing quality of affordable conventional digital cameras, a growing research interest on low-cost UAV-based imaging for scientific studies can be determined [7,8]. Key features of most approaches are to be as flexible and time-and cost-effective as possible. Moreover, areas which are not or less accessible with ground-based sensors can be investigated. The captured images are commonly used to derive 3D information based on the structure from motion (SfM) approach [9,10]. Only little research has however been done so far on the accuracy and reliability of collected data in comparison to traditional remote sensing methods. The integration of UAV-based photogrammetry and TLS for the mapping of open-pit mine areas for example was performed by Tong et al. [11]. Moreover, Smith et al. [12] and Ouédraogo et al. [13] outlined the benefits and challenges of low-altitude airborne imaging for studies in physical geography. Nevertheless, the widespread and further growing number of available systems still requires research focusing on the practical application. Moreover, validation analyses against reliable reference data are required. Comparative studies with trustworthy data and measuring procedures are therefore necessary.
Capturing information about the subsurface is generally more difficult than investigations of the surface since the access is obviously limited. Different approaches of deriving information exist, which can be divided into destructive and non-destructive methods. The latter ones are often based on near-surface geophysical prospection methods, such as ground penetrating radar, seismic surveying, or electrical resistivity tomography (ERT) [14]. A major advantage of these non-destructive measurements is that, information can be gained without disturbing the subsurface. Moreover, with most of the methods quite large areas can be assessed in a short time. In this study, ERT measurements were performed, as they are known for their suitability in karstic regions [15,16,17]. Moreover, ERT was already successfully used in combination with TLS [18,19]. The result of an ERT profile is a visualization of the suspected subsurface, derived from the measured apparent resistivity. This 2D image can indicate the existence of different layers in the subsurface. The resistivity values are plotted as pseudosections, resulting from an inversion model. Thus, these pseudosections can show the variation of the measured resistivity in relation to the position and the effective depth of penetration but cannot show the exact depths of layer borders. Moreover, the material of the subsurface cannot be determined from ERT measurements alone.
In contrast, destructive measurements, such as borehole drillings, can be used for specific statements about the material of the subsurface or the depths of layer borders. Borehole drilling is a commonly used method of investigating the subsurface and also applied in karstic regions [17,20]. A major limitation of borehole drilling is that only data at single locations can be achieved in a time consuming process, which limits the recordable data in a short campaign. Overall, an efficient approach should base on the combination of geophysical prospecting and borehole drilling.
Large parts of the land surface which are today located in the temperate zone of central Europe were situated in the subtropics and below sea level during the Triassic, lasting from ~230 to ~195 million years BP [21]. Calcareous sediments, shells, and other marine features were hence deposited under marine environs and later fossilized. This is also indicated by the name of this lithostratigraphic unit Muschelkalk (shellbearing limestone), which covers the older Buntsandstein (colorful sandstone) and lies below the younger Keuper. Outcrops of Muschelkalk can be found in Middle and South Germany, where weathering of the limestone induces the development of karstic phenomena. Such regions are marked by sinkholes, ponors, or karst depressions [1].
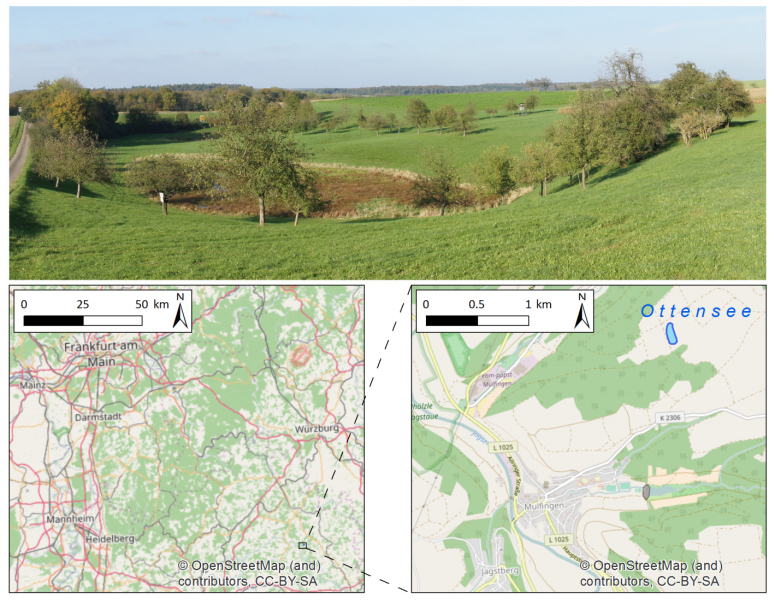
In this study, an episodically water-filled karst depression, named Ottensee, in the region of Hohenlohe in the German federal state Baden-Württemberg was investigated (Figure 1). The area, which is protected as a small nature reserve, is about 100 m by 200 m in size and embedded in a larger and geologically older valley [22]. The area surrounded by the trees (Figure 1 top) can roughly be regarded as AOI. Since only a very small part of the depression is constantly filled with water, the rest of the area is used for pasture farming. However, torrential rain and the consequential subterranean run-off through southern lying higher aquifers cause a flooding of the depression from time to time. This results in a small lake, which lasts for a few hours to weeks, depending on the filling level and the general natural inflow. Then the water drains off through ponors in the northern part of the depression, where the entire terrain is also a bit lower. This episodic flooding is likely to change the surface and to induce dissolution processes in the subsurface.
Figure 1. Karst depression Ottensee in the region of Hohenlohe, Baden-Württemberg. Top: Picture captured from the south side. Area surrounded by the trees can roughly be regarded as AOI. Bottom: Map of the closer region (right) and its location in the South of Germany (left).An extensive field campaign was carried out between the 26th and 29th of May 2016. The surface was almost continuously captured in 3D with terrestrial laser scanning and low-altitude airborne imaging. The pasture in the AOI was previously mown for an easier detection of the bare ground. Several point measurements were carried out with the high-accurate differential global positioning system (DGPS) device Topcon HiPer Pro [23] for acquiring two reference point data sets. A relative accuracy of 1 cm is reached with this device. The subsurface was investigated with geoelectrical measurements. As mentioned above, such ERT profiles can only provide a suspected 2D image of the subsurface derived from the measured apparent resistivity and illustrate the existence of different layers or structures in the subsurface. Hence, borehole drilling was performed to analyze the material of the subsurface and detecting the specific depths of layer borders. These analyses were however neglected in this contribution, due to the focus on imaging methods. The general detection of subsurface structures from the ERT measurements and their interrelation with the surface data were of primary importance.
Laser scanning was performed using the Riegl LMS-Z420i with the digital camera Nikon D200 mounted on top [24]. This time-of-flight scanner applies a near-infrared laser beam with a beam divergence of 0.25 mrad. It can record up to 11,000 points/sec with a field of view up to 80° in the vertical and 360° in the horizontal direction. In this study, a resolution of 0.04° was used. The point clouds gained from the laser scanner can be colorized from the images taken by the camera. Six scan positions were established to attain an almost uniform spatial coverage of the whole AOI (marked in Figure 2). The coordinates of the scan positions and additional reference targets were measured with the DGPS device. These targets are required for the georeferencing and merging of the positions in the post-processing. Highly reflective cylinders arranged on ranging poles act as reference targets. They can be easily detected by the scanner and thus their exact position in relation to the scan position can be measured.
Figure 2. Orthophoto of the Ottensee derived from the UAV-based imaging. Scan positions (SCP) marked in red and electrical resistivity tomography (ERT) profiles marked in blue.In contrast to the expensive TLS system, a low-cost approach was pursued for the low-altitude airborne imaging. The DJI Phantom 3 Professional was therefore used [25]. This UAV is equipped with a camera, which is attached via a gimbal and thus stabilized in the three axes (roll, pitch, and yaw). The camera has a 1/2.3" CMOS sensor with an effective number of pixels of 12.4 M and a 94° field of view. During the campaign, the UAV was remotely piloted with the included controller and the DJI GO app [26], installed on an attached tablet PC. The real-time downlink during the flight allows seeing exactly which area is covered. Moreover, software options enable to define waypoints. During the final image acquisition, the thereby predefined flight paths can be controlled by an autopilot. Hence, a constant height and speed can be ensured. Since the maximal flight time of the Phantom 3 with one battery pack is about 23 minutes, two battery packs were necessary for the entire acquisition process. The final image capturing was carried out in 38 m altitude with a speed of 0.8 m/s and continuous shooting (1 image per 5 sec). About 200 images were taken to cover the AOI. This resulted in an image overlap of > 9 in almost the entire area and a ground resolution of 1.32 cm/pixel. Before the flight, 50 ground control points (GCPs) were distributed in the AOI and their coordinates were measured with the DGPS device. These GCPs can be detected in the images during the post-processing and are used to enhance the georeferencing.
Electrical resistivity tomography (ERT) was carried out with the multi-electrode system GeoTomMK8E1000RES/IP/SP [27]. Four ERT profiles were taken with lengths of 50 m to 100 m and electrode spacings of 0.5 m to 1.0 m (marked in Figure 2). The exact position of each electrode was measured with the DGPS device for a topographic correction of the data in the post-processing. Various measuring methods and arrangements are generally possible, differing in features, such as electrode spacing and design [28,29]. The Wenner array is known of having a high sensitivity to vertical resistivity changes and is well suitable for detecting horizontal structures [30,31]. Thus, it was used in this study. The result of one ERT measurement is a 2D image of the vertical cross section, showing the apparent resistivity. They are referred to as 2D images of apparent resistivity in the following.
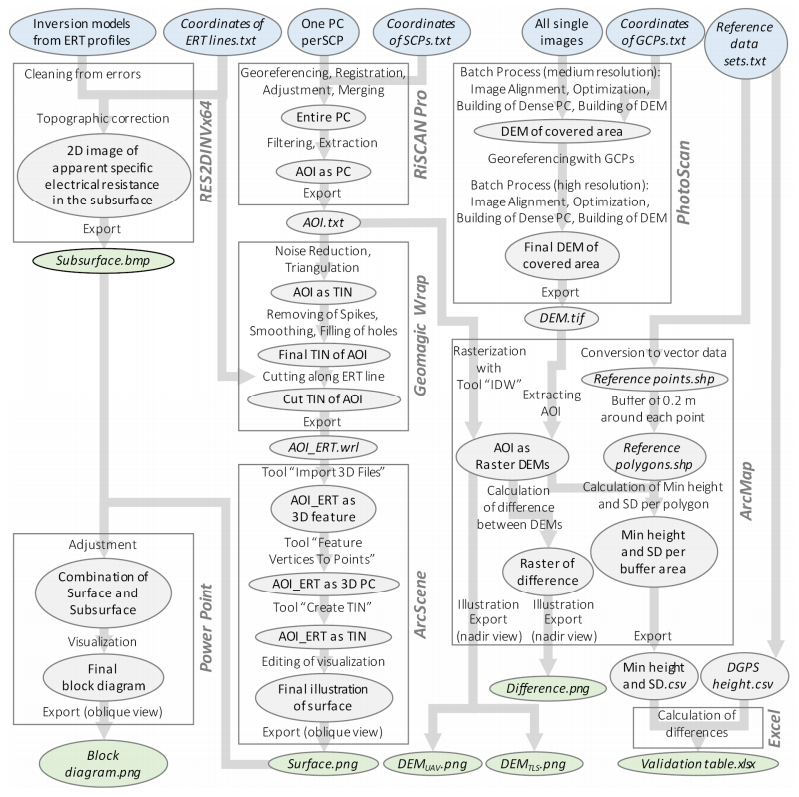
During the field campaign an extensive data set was acquired, including: (Ⅰ) one TLS point cloud per scan position, (Ⅱ) the coordinates of these scan positions, (Ⅲ) all single images from the low-altitude airborne imaging, (Ⅳ) the coordinates of the GCPs, (Ⅴ) two reference point data sets, (Ⅵ) four 2D images of apparent resistivity from the ERT profiles, and (Ⅶ) the coordinates of each electrode. Consequently, the post-processing and analysis process were quite extensive, involving overall eight software programs as shown in the workflow (Figure 3). According to the aims stated at the beginning, this complex scheme could be divided into two main analysis paths, which will be explained in the following. The first aim was mapping the surface from the TLS data and from the UAV-derived images, compare the results, and validate them with the reference data sets. The second aim was combining the surface visualization with the suspected image of the subsurface. Prior to that, visualizing the subsurface was necessary.
Figure 3. Workflow of the the post-processing and analysis process. The following abbreviations are used: Area of interest (AOI); Differential global positioning system (DGPS); Digital elevation model (DEM); Electrical resistivity tomography (ERT); Ground control points (GCPs); Inverse distance weighting (IDW); Minimum (Min); Point cloud (PC); Scan position (SCP); Standard deviation (SD); Terrestrial laser scanning (TLS); Triangulated irregular network (TIN); unmanned aerial vehicle (UAV).The scanner software RiSCAN Pro was applied for the first post-processing steps of the TLS data (Figure 3 center top). A software implemented terrain filter was used to remove most of the vegetation, complemented by a manual editing. Then the AOI was extracted. A common way for analyzing and presenting such data is the visualization as digital elevation models (DEMs). Hence, after importing the point cloud to Esri ArcMap 10.4.1, a raster data set containing the height values was created using the inverse distance weighting (IDW) algorithm. IDW is an exact, deterministic algorithm. The accuracy of measurements with a high density is maintained, since it retains measured values at their discrete sample location [32]. The result of the interpolation is a DEM raster data set.
All single UAV-derived images were merged to an orthophoto and the DEM covering the entire area was generated with the SfM-based software Agisoft PhotoScan 1.2.0 (Figure 3 right top). A coarse georeferencing is already achievable with the GPS information stored for each image. The DGPS-derived coordinates of the GCPs were however used to enhance this georeferencing. The final DEM was exported and then ArcMap was used to extract the AOI in conformity with the DEMTLS.
Due to the different acquisition methods, the resulting point densities and distributions were quite heterogeneous in the AOI. The TLS-and UAV-derived raster data sets were resampled to a common resolution of 0.05 m, which can still be regarded as being a sufficiently high resolution for this study. The difference between these comparable DEMs was calculated with the ArcGIS raster calculator. The result is a raster data set, showing the spatially resolved difference between the DEMTLS and the DEMUAV. This raster data set as well as the DEMTLS and DEMUAV were finally cartographically illustrated and exported.
The DGPS-derived reference data sets were used for validating the DEMs. Two data sets, namely set A and B, were acquired with 20 and 18 points, respectively (Figure 3 very right). It has to be mentioned that set A was already part of the GCPs for the georeferencing of the UAV-derived orthophoto. Hence, this data set is only for the DEMTLS a completely independent reference. Both data sets were converted to vector point data for automatically extracting the height values from the DEMs. The minimum height of the respective DEM was extracted for a created buffer area around each point (radius of 0.20 m). These values were used to prevent overestimations caused by remaining vegetation in the calculated DEMs. In addition, the standard deviation per buffer area was calculated to check whether the extracted heights could be regarded as representative for their particular location. Finally, these DEM heights were validated against the DGPS-derived heights of the reference data sets.
The 2D images of apparent resistivity achieved from the ERT profiles were post-processed with the RES2DINVx64 software [33] (Figure 3 left top). This post-processing included a cleaning of errors (values with a standard deviation > 5 %) and the topographic correction of the surface contour. The latter was based on the DGPS-derived coordinates of each electrode. Such topographic corrections are recommended in the case of considerable altitudinal differences or complex relief structures for a better positioning of the measured values in the subsurface. Moreover, the correct surface contour is necessary for merging the images of the subsurface with the surface data. The measured apparent resistance values were inverted according to the method of Loke & Barker [34] for a rapid least-square model optimized by a quasi-Newton method. An initial model of the subsurface, consisting of the same number of rectangular blocks as measuring points, is optimized in several iterations to minimize the difference between measured and calculated values.
The created raster DEMs are sufficient for exclusively visualizing the surface and a resultant interpretation and validation. They are however less suitable for visualizations with an oblique viewing perspective on the surface, which is necessary for the combination with the 2D images of the subsurface in a block diagram. Triangulated irregular networks (TINs) are recommendable for such pseudo 3D visualizations. For this first approach, the TLS-derived point cloud was used, as it better presents the bare ground of the karst depression since the vegetation was removed. The UAV-derived data set was neglected so far, but in principle, a similar approach can be carried out.
A first attempt was made to create a TINTLS with the software tools in Esri ArcScene 10.4.1. Unfortunately, the result was very edgy with sharp corners and could not be regarded as realistic depiction of the surface. Thus, an additional software, namely Geomagic Wrap 2015.1.3, was applied (Figure 3 center). This software can be used to transform 3D scan data into 3D models with a stronger focus on computer-aided design (CAD) features than in ArcScene. After importing the TLS point cloud, a noise reduction was executed and the resulting point cloud was triangulated to a TINTLS. Software implemented functions were then used for removing spikes, smoothing the surface, and filling holes in the mesh. The coordinates of two ERT profiles were also imported. The final TINTLS was cut along these lines for the later visualization in block diagrams.
From this processing, a realistic depiction of the supposed bare surface could be achieved, but for the final visualization further features were desired, such as a coloring of the TINTLS by height and a vertical exaggeration of the TINTLS. A transfer of the data to ArcScene was necessary, since this was not possible in Geomagic Wrap. As shown in the bottom center of Figure 3, a series of tools from the ArcGIS toolbar was therefore necessary. Finally, the cartographically illustrated TINTLS with a vertical exaggeration of 1.5 was exported as image with an oblique viewing perspective on the surface. Generally, any image processing software can then be used to combine this pseudo 3D visualization and the 2D image of the apparent resistivity in the subsurface. In this study, Microsoft PowerPoint 2016 was used (Figure 3 left bottom). The images of the surface and subsurface were adjusted and finally visualized as block diagram.
Terrestrial laser scanning and low-altitude airborne imaging were performed for capturing the surface of the karst depression Ottensee in a high resolution. Due to the almost simultaneous acquisition, comparing both models is possible and the DGPS-derived reference data sets allowed validating the measured heights. In addition, geoelectrical measurements were performed for investigating the subsurface. Finally, the combined visualization of these data sets aims to increase the understanding of the connection between surface and subsurface structures. According to the workflow, in the following the derived DEMs are presented and discussed first, followed by discussing the images of the subsurface. Finally, the combined visualization as block diagram is assessed.
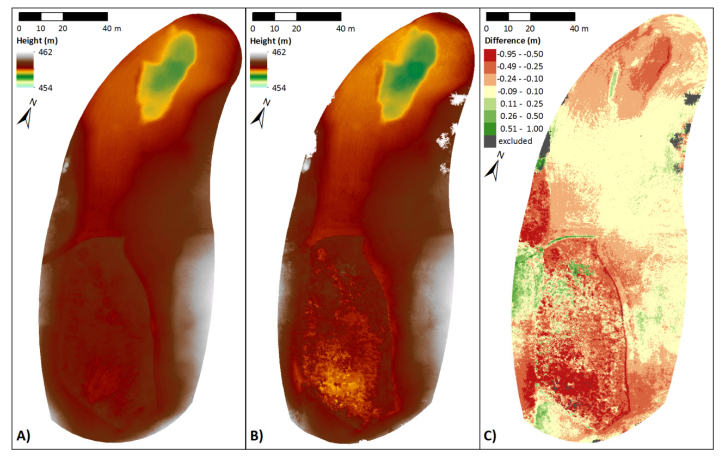
A common way to present the surface of a terrain captured by remote sensing is to visualize the achieved DEM as raster data set colored by height. Such maps were generated for the DEMTLS (Figure 4A) and the DEMUAV (Figure 4B). Figure 4C) shows the spatially calculated difference between the DEMs to compare the results of both sensors. In general, the differences between the DEMs are quite marginal. Since the vegetation was however not removed in the low-altitude airborne imaging approach, the height values are mostly slightly higher than in the TLS-derived model. In particular, the trees at the edges of the AOI cause very high values. Differences between the DEMs larger than 1 m were excluded from the classification since they can be regarded as error due to the vegetation (grey color in Figure 4C). In most parts of the AOI the difference between the DEMs is less than 25 cm (very light red/ green in Figure 4C), or even less than 10 cm (off-white in Figure 4C).
Figure 4. Digital elevation models (DEMs) as raster data sets, derived by A) Terrestrial laser scanning and B) low-altitude airborne imaging. Height values > 462 m were excluded from the color ramp and colored in white as they are caused by trees. C) Spatially calculated difference between both raster data sets, calculated by subtracting the DEMTLS from the DEMUA V.As already mentioned for Figure 1 the AOI can be roughly defined by the trees at the edges of the depression. This area can be described as kidney-shaped valley with a flat hollow in the southern part and a deeper one in the norther part. The southern one is almost constantly filled with water, allowing sedge and reeds to grow there. This vegetation is mainly responsible for the differences between the DEMs. The nadir perspective of the UAV-based camera allows capturing very low points between the vegetation, which cannot be reached from the oblique perspective of the laser scanner. However, since the vegetation was removed from the TLS-derived point cloud the DEMTLS shows a smooth surface in this area. In contrast, the DEMUAV shows a rougher surface with high values due to the remaining vegetation and low values from the ground between it. The northern hollow is generally deeper and only covered by pasture, as the rest of the AOI. Hence, the DEMs are more similar with quite small differences in this part.
The DGPS-derived reference data sets were used for validating the DEMs (Table 1). While both data sets are an independent reference for validating the DEMTLS, set A was already used for the georeferencing of the DEMUAV and had thus an influence on the accuracy of this model already. The minimum height and standard deviation in the circular buffer area around each reference point are given for both DEMs. The standard deviation (SD) is with 0.01 m to 0.04 m per buffer area very low and thus, the stated values can be regarded as representative for the particular location. In addition to the difference between the DEM height and the vertical coordinate of each reference point (Z), the absolute value is given for a more reliable comparability of the discrepancies. The DEMTLS can generally be regarded as being accurate with a mean absolute difference of 0.05 m and 0.03 m and SD values of 0.07 m and 0.03 m for set A and B, respectively. The discrepancies between the DEMUAV and the reference data sets are generally slightly higher with a mean absolute difference of 0.13 m and 0.11 m and SD values of 0.11 m and 0.09 m for set A and B, respectively.
| Reference data sets | DEMTLS | DEMUAV | |||||||
| Name | Z (m) | Height (m) | SD (m) | Diff. (m) | Abs. Diff. (m) | Height (m) | SD (m) | Diff. (m) | Abs. Diff. (m) |
| Set-A_P01 | 459.97 | 459.93 | 0.02 | 0.04 | 0.04 | 459.87 | 0.03 | 0.10 | 0.10 |
| Set-A_P02 | 460.43 | 460.28 | 0.04 | 0.16 | 0.16 | 460.18 | 0.03 | 0.26 | 0.26 |
| Set-A_P03 | 460.89 | 460.88 | 0.02 | 0.01 | 0.01 | 460.94 | 0.02 | -0.05 | 0.05 |
| Set-A_P04 | 458.55 | 458.60 | 0.02 | -0.05 | 0.05 | 458.52 | 0.01 | 0.02 | 0.02 |
| Set-A_P05 | 458.62 | 458.66 | 0.04 | -0.04 | 0.04 | 458.42 | 0.02 | 0.20 | 0.20 |
| Set-A_P06 | 461.19 | 461.23 | 0.02 | -0.04 | 0.04 | 461.17 | 0.02 | 0.03 | 0.03 |
| Set-A_P07 | 459.75 | 459.77 | 0.02 | -0.02 | 0.02 | 459.74 | 0.01 | 0.02 | 0.02 |
| Set-A_P08 | 459.00 | 459.07 | 0.01 | -0.06 | 0.06 | 459.00 | 0.01 | 0.00 | 0.00 |
| Set-A_P09 | 458.45 | 458.48 | 0.01 | -0.03 | 0.03 | 458.33 | 0.02 | 0.12 | 0.12 |
| Set-A_P10 | 458.51 | 458.78 | 0.04 | -0.27 | 0.27 | 458.74 | 0.04 | -0.23 | 0.23 |
| Set-A_P11 | 458.67 | 458.82 | 0.01 | -0.15 | 0.15 | 458.28 | 0.02 | 0.38 | 0.38 |
| Set-A_P12 | 458.52 | 458.52 | 0.01 | -0.01 | 0.01 | 458.46 | 0.01 | 0.06 | 0.06 |
| Set-A_P13 | 458.57 | 458.57 | 0.02 | 0.00 | 0.00 | 458.60 | 0.01 | -0.03 | 0.03 |
| Set-A_P14 | 459.47 | 459.56 | 0.02 | -0.09 | 0.09 | 459.65 | 0.01 | -0.18 | 0.18 |
| Set-A_P15 | 458.62 | 458.66 | 0.02 | -0.04 | 0.04 | 458.58 | 0.02 | 0.04 | 0.04 |
| Set-A_P16 | 457.32 | 457.29 | 0.01 | 0.02 | 0.02 | 457.18 | 0.01 | 0.14 | 0.14 |
| Set-A_P17 | 458.25 | 458.27 | 0.01 | -0.02 | 0.02 | 458.32 | 0.01 | -0.08 | 0.08 |
| Set-A_P18 | 458.01 | 458.03 | 0.01 | -0.01 | 0.01 | 457.81 | 0.01 | 0.21 | 0.21 |
| Set-A_P19 | 457.83 | 457.84 | 0.01 | -0.01 | 0.01 | 457.51 | 0.02 | 0.33 | 0.33 |
| Set-A_P20 | 458.64 | 458.64 | 0.02 | 0.00 | 0.00 | 458.68 | 0.04 | -0.05 | 0.05 |
| Mean | 0.05 | 0.13 | |||||||
| SD | 0.07 | 0.11 | |||||||
| Set-B_P01 | 458.26 | 458.19 | 0.03 | 0.07 | 0.07 | 458.22 | 0.02 | 0.04 | 0.04 |
| Set-B_P02 | 458.12 | 458.13 | 0.01 | -0.01 | 0.01 | 458.13 | 0.02 | -0.01 | 0.01 |
| Set-B_P03 | 456.53 | 456.57 | 0.01 | -0.04 | 0.04 | 456.32 | 0.02 | 0.20 | 0.20 |
| Set-B_P04 | 458.01 | 458.01 | 0.01 | 0.00 | 0.00 | 457.81 | 0.01 | 0.20 | 0.20 |
| Set-B_P05 | 459.93 | 459.95 | 0.02 | -0.03 | 0.03 | 460.06 | 0.02 | -0.14 | 0.14 |
| Set-B_P06 | 459.92 | 459.95 | 0.03 | -0.03 | 0.03 | 459.86 | 0.03 | 0.06 | 0.06 |
| Set-B_P07 | 461.09 | 461.12 | 0.03 | -0.03 | 0.03 | 461.10 | 0.01 | -0.01 | 0.01 |
| Set-B_P08 | 459.13 | 459.12 | 0.02 | 0.00 | 0.00 | 458.81 | 0.02 | 0.32 | 0.32 |
| Set-B_P09 | 458.66 | 458.59 | 0.03 | 0.07 | 0.07 | 458.66 | 0.02 | 0.00 | 0.00 |
| Set-B_P10 | 458.58 | 458.61 | 0.01 | -0.04 | 0.04 | 458.38 | 0.03 | 0.20 | 0.20 |
| Set-B_P11 | 459.27 | 459.28 | 0.02 | -0.01 | 0.01 | 459.30 | 0.02 | -0.03 | 0.03 |
| Set-B_P12 | 458.75 | 458.77 | 0.02 | -0.02 | 0.02 | 458.80 | 0.01 | -0.05 | 0.05 |
| Set-B_P13 | 458.48 | 458.50 | 0.01 | -0.02 | 0.02 | 458.53 | 0.02 | -0.06 | 0.06 |
| Set-B_P14 | 457.23 | 457.24 | 0.01 | -0.02 | 0.02 | 457.07 | 0.01 | 0.16 | 0.16 |
| Set-B_P15 | 458.39 | 458.40 | 0.01 | -0.01 | 0.01 | 458.28 | 0.02 | 0.11 | 0.11 |
| Set-B_P16 | 458.46 | 458.47 | 0.01 | -0.01 | 0.01 | 458.34 | 0.03 | 0.11 | 0.11 |
| Set-B_P17 | 458.61 | 458.71 | 0.02 | -0.10 | 0.10 | 458.81 | 0.03 | -0.21 | 0.21 |
| Set-B_P18 | 459.38 | 459.45 | 0.01 | -0.07 | 0.07 | 459.39 | 0.02 | -0.01 | 0.01 |
| Mean | 0.03 | 0.11 | |||||||
| SD | 0.03 | 0.09 | |||||||
DownLoad: CSVIn summary, it should be recalled that TLS is known as an trustworthy and accurate approach for geomorphological studies [4,5,35]. The here generated DEMTLS proves the suitability for capturing the relief of small-scale karstic forms, such as the investigated karst depression. However, low-altitude airborne imaging is increasingly used for geomorphological studies or more generally in physical geography [10,12,36]. The here followed UAV-based approach aims to be simple to perform as well as cost-and time-efficient. In this sense, the post-processing was reduced to a minimum. Vegetation was not removed prior to the DEM generation for example. Considering this, the results of the low-altitude airborne imaging are also satisfying and confirm the promising potential of low-altitude airborne imaging for geomorphological studies.
One aim of the entire project, which was neglected in this contribution, is the detection of temporal changes in the karst depression Ottensee. Thus, further research is necessary to investigate whether the accuracy and detailedness of the low-altitude airborne imaging approach is sufficient for detecting changes. Obvious benefits of the UAV-based approach are the very fast data acquisition, the easy handling, and the possibility to capture areas which are not or less accessible with the ground-based laser scanner. In contrast, areas where dense vegetation obscures a nadir perspective can hardly be captured and hitherto available systems are prone to poor weather.
A laser scanner is more robust against poor weather but due to the manual transportation and the measuring time, TLS measurements are quite time consuming. The here used Riegl LMS-Z420i is however quite an old system. Several available newer high-end sensors with the focus on longer scanning ranges, higher measuring rates, or a more lightweight buildup would already diminish some difficulties. Examples are the Riegl VZ-2000 [37] or the Leica Scan Station P40 [38]. A contrasting development are upcoming cost-effective systems like the Velodyne HDL-64E LiDAR sensor [39]. Such systems strongly reduce the cost for TLS measurements and thus increase the availability for a broader audience. Moreover, backpack systems like the AKHKA R2 [40] or hand-held mobile laser scanner such as the ZEB1 [41] might be useful alternatives, as they simplify the data acquisition. So far, such systems are only used in pioneering studies on the detection of trees.
For this study, it can be summarized that the high quality of TLS measurements is worthwhile for capturing small-scale topographic features. Thus, such data sets are still required as trustworthy data for comparative studies with low-altitude airborne imaging. Nevertheless, UAV-based approaches offers a promising time-and cost-effective alternative for the rough acquisition of a terrain. Furthermore, it can be assumed that the entire potential of photogrammetric approaches cannot be evaluated yet since the performance capabilities of such systems are still rapidly increasing. Thus, the combination of laser scanning and photogrammetry-based approaches should be a conceivable option [42,43,44].
The 2D image of apparent resistivity was created for each ERT profile. Some limitations of the method have to be reconsidered before the interpretation. First, the resistivity values of the different ERT values cannot be compared, since the measured resistivity strongly depends on the moisture content. This soil moisture, in turn, is quite variable over time and space and since the measurements were carried out across a few days, similar conditions cannot be assumed. Second, the depth axis can only be used as rough orientation since the resistivity values are plotted as pseudosections resulting from the inversion model. These pseudosections show the variation of the measured resistivity in relation to the position and the effective depth of penetration. Hence, the 2D images can be used for detecting subsurface structures and changes of material, such as the depth of the bedrock or the existence of different sediment layers. Destructive in-situ measurements, such as borehole drilling, are necessary for accurate statements.
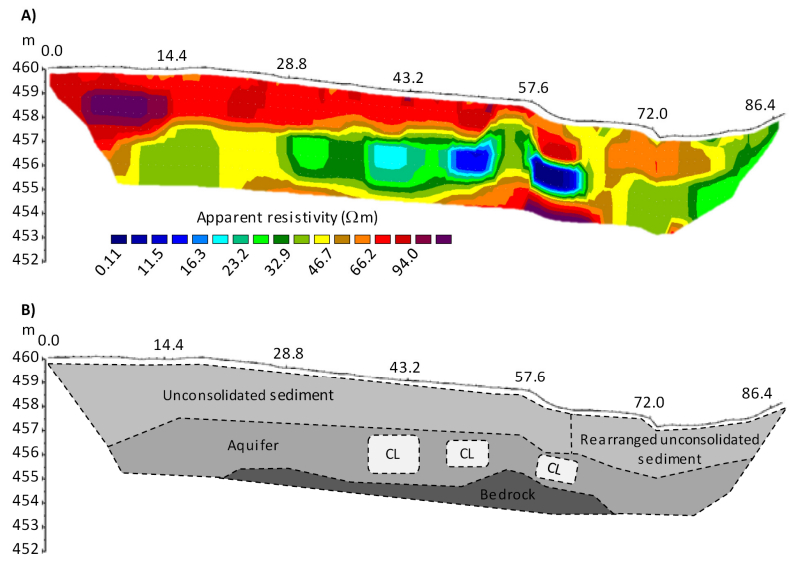
In Figure 5A) the image of apparent resistivity is shown for the 90 m long profile ERT01. Its location is marked in Figure 2. With a thickness of 2 m to 3 m, the reddish superficial layer of the southern part, starting at 0.0 m till ~55.0 m shows the generally highest values of ~60 Ωm to ~100 Ωm. This part of the surface has quite a flat topography, slightly dipping northwards. From the little slope at ~57.6 m northwards the surface is slightly wavy and resistivity variations in the superficial layer between ~30 Ωm to ~60 Ωm can be detected. In this part, the profile crosses the deeper hollow, already stated for the DEMs (Figure 4). Starting again from the southern end of the profile, the yellowish to greenish next layer below the first one, with a thickness of 2 m to 3 m, shows an apparent resistivity of ~20 Ωm to ~50 Ωm. Noteworthy are the three bluish ellipses in the center with lower values of ~0.11 Ωm to ~20 Ωm. Only in the center of the image, another deeper reddish layer with again higher values of ~60 Ωm to ~100 Ωm can be detected.
Figure 5. A) Apparent resistivity in the subsurface along the north-south oriented electrical resistivity tomography profile ERT01, location marked in Figure 2. B) Supposed geological structure (CL: clayish lens).Based on that image the following geological structure can be supposed (Figure 5B): the deepest lying reddish layer in the center is part of the bedrock. The yellowish to greenish layer is an aquifer made of consolidated soil with clayish lenses, visible as bluish ellipses. The latter are marked by a higher water content and thus a lower resistivity. The reddish superficial layer is made of unconsolidated sediment with a low water content, which might have its origin further uphill, in the south-east of the AOI and which was fluvial deposited. However, one has to keep in mind that the range of the resistivity values is quite small. Thus, the classification used in Figure 5A) influences this image interpretation. Further research is necessary to confirm and supplement the here achieved results. As already mentioned, borehole drillings are useful for validating the presumably detected structures. Furthermore, additional ERT profiles can be worthwhile for capturing how these structures change horizontally.
It can be summarized that, images of apparent resistivity derived by geoelectrical measurements are worthwhile for non-destructive investigations of the subsurface and detecting geological structures. The results should be interpreted with care, due to the stated limitations. Further combined analyses with the borehole drillings are planned for the future. The general usability of ERT for detecting karstic structures as shown in other studies [15,16,45] was here confirmed.
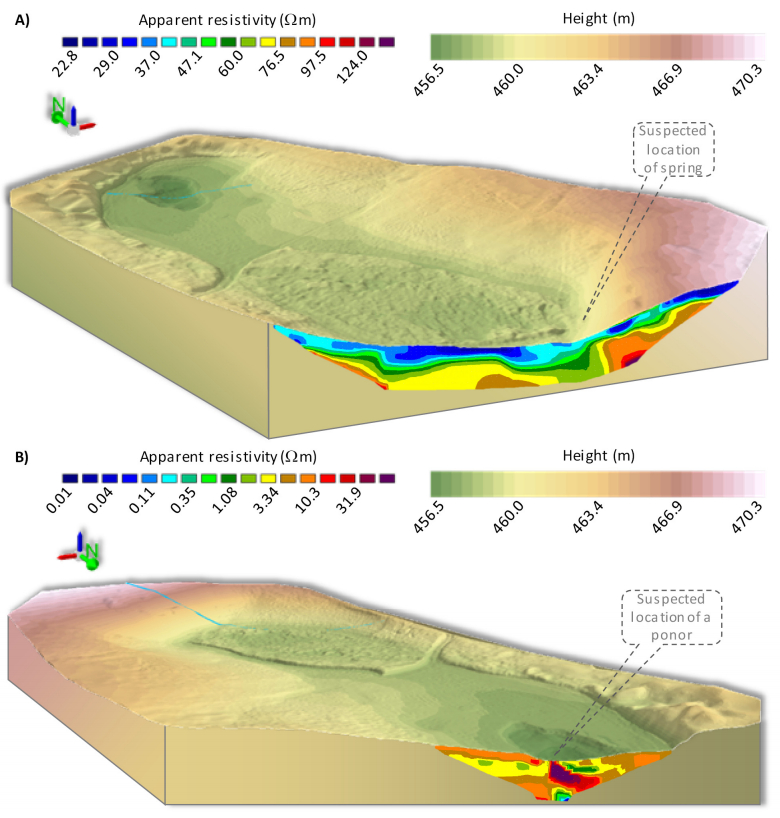
The targeted combination of surface and subsurface data was more time-consuming than expected at the beginning. First attempts with the conventionally used tools in Esri ArcScene 10.4.1 did not yield any satisfactory result. The here proposed method (Figure 3) based on the creation of the TINTLS in the CAD software Geomagic Wrap 2015.1.3 and its visualization in Esri ArcScene 10.4.1 finally yielded good results. An image with oblique perspective to the TINTLS, which almost represents the bare ground of the karst depression, was used for the pseudo 3D visualizations. The TINTLS of the entire AOI was previously cut along the ERT profiles for merging it with the 2D images of the subsurface in block diagrams. This is exemplary shown for the profiles ERT02 and ERT04 in Figure 6. Their locations in the karst depression are shown in Figure 2. In Figure 6 the bluish lines also show the location of the respective other profile for a better orientation. As stated for Figure 5A) the range of the resistivity values is quite small, which biases the classification and thus the interpretation. Further investigations on this issue are planned.
Figure 6. Block diagrams showing the surface captured with terrestrial laser scanning and the apparent resistivity in the subsurface derived by geoelectrical measurements. The surface as triangulated irregular network was cut along two electrical resistivity tomography (ERT) profiles. The bluish lines show the location of the respective other profile. A) View from the south side on the 100 m long ERT02 profile. B) View from the north side on the 50 m long ERT04 profile.The 100 m long ERT02 profile in the southern part of the depression (Figure 6A) crosses the suspected location of the spring, where subterraneous water reaches the surface. An evidence therefore might be found in the geoelectrical measurements. The bluish superficial layer indicates low values of apparent resistivity. In the center, this can be attributed to lake sediments, which are saturated with water since this part of the depression is almost constantly filled with water. Trees are located at both ends of the profile, whose roots can enhance the soil water holding capacity and in turn reduce the apparent resistivity. The yellowish to greenish next layer below has a higher apparent resistivity, possibly due to a water-impermeable layer. This layer is closer to the surface at the suspected location of the spring. The deepest reddish layer, indicating the highest apparent resistivity, might be attributed to the bedrock. This assumption can be confirmed with the TINTLS. Considering that the assumed bedrock is closest to the surface in the eastern part, the TINTLS shows the highest elevation and steepest slope here as well. Around the spring the slope changes and the surface gets quite flat. The exact boundary of the constantly water-filled area can hardly be determined from the TINTLS, since the above mentioned mowing of the pasture was not homogeneously possible. Thus, the surface is quite uneven in this part and the height is influenced by the vegetation.
The 50 m long ERT04 profile in the northern part of the depression (Figure 6B) crosses the location where one ponor is suspected. A remarkable structure in the image of apparent resistivity is the deep reddish to purplish elongated ellipse in the center of the deep layer that reaches the surface in a small part. This high resistivity might be attributed to very porous and thus water-permeable material, creating good conditions for water to drain off. The overall lowest height value of the TINTLS can also be found in this part, which confirms this assumption. The yellowish to greenish colors around the ellipse indicate a lower apparent resistivity, which might be interpreted as water-impermeable layer. The small bluish part at the bottom of the image indicates an even lower apparent resistivity, which might be the edge of another layer or just a measurement error. A reliable statement is not possible as the deeper and the more eastern subsurface is unknown. It is worth striving for further ERT measurements in this part of the depression, since another ponor is supposed to be around the eastern end of this profile.
In summary, combing the surface and subsurface data is worthwhile for a better understanding of how the karst depression Ottensee was formed and how current changes are occurring. So far, only a few studies on such combined approaches exist. However, Siart et al. [18,19] investigated the combined use of TLS and ERT for achieving a comprehensive presentation of karst landforms and achieved good results. In contrast to the capturing of the surfaces, an issue for common ERT profile measurements is the limitation to 2D acquisitions. Thus, an entire link of surface structures to the underlying subsurface is hardly possible and limited to the analysis of several profiles. Only a few approaches for entirely capturing the subsurface exist so far. One of this is the 3D geoelectric tomography approach, presented by Mauriello et al. [46]. It was successfully applied for detecting archaeological structures by Alaia et al. [47]. A first step for the here investigated karst depression could be increasing the number of ERT profiles, which are ideally arranged raster-like.
Two main objectives were investigated in this contribution, based on a comprehensive field campaign carried out in May 2016 in the episodically water-filled karst depression Ottensee. The first was to investigate the usability of terrestrial laser scanning (TLS) and low-altitude airborne imaging from an unmanned aerial vehicle (UAV) for capturing fine karstic structures. The second objective was to establish a suitable way of combining this surface mapping with subsurface data achieved by geophysical prospecting and examine its benefit. The visualization of the apparent resistivity in the subsurface derived by the electrical resistivity tomography (ERT) measurements is a prerequisite for the latter.
The known trustworthiness and accuracy of TLS was confirmed in this study. Validations against high-accurate reference data sets revealed mean absolute differences of 0.03 m to 0.05 m with a standard deviation of 0.03 m to 0.07 m. Since TLS approaches are however quite time–and cost-intensive, a more efficient approach was pursued for the low-altitude airborne imaging. The latter one has several advantages compared to TLS, regarding the data acquisition and post-processing, such as the use of a low-cost system, quite a short acquisition time, or an extensively automatized post-processing. Disadvantages should however be kept in mind, such as the sensitivity to rain and wind or the lower influenceability of the post-processing, due to this automatized processes. Comparing the results, the discrepancies between the UAV-derived values and the reference data sets are slightly higher, having a mean absolute difference of 0.11 m to 0.13 m with a standard deviation of 0.09 m to 0.11 m.
The spatially calculated difference between the digital elevation models (DEMs) leads to the conclusion, that the weaker performance of the DEMUAV is mainly caused by the vegetation, which was not removed prior to this DEM generation. In summary, the low-altitude airborne imaging approach can be regarded as promising alternative to common remote sensing methods like TLS. However, the detection of suspected temporal changes in the karst depression Ottensee was excluded in this contribution. Further field campaigns are necessary to investigate whether the accuracy and detailedness of the low-altitude airborne imaging are sufficient high enough for detecting such changes and whether an accurate merging of the temporal differing data sets is possible.
The visualization of the ERT-derived apparent resistivity as prerequisite for the combined visualization was carried out following conventional methods. Overall, this geophysical prospecting was worthwhile for non-destructively investigate the subsurface and detecting geological structures. However, since only a suspected image of the subsurface can be achieved further research of the subsurface is necessary. The first step will be to analyze the cores taken with borehole drilling in the campaign in May 2016, regarding the material of the subsurface and detecting the specific depths of layer borders. This information might than be used to concretize the ERT-derived results.
The second objective of combining the surface mapping and the suspected image of the subsurface was so far limited to the combination of the latter with the TLS data. Developing the here proposed method was overall more time-consuming than expected at the beginning, but finally satisfying results were achieved. The TLS-derived point cloud was meshed to a triangulated irregular network (TIN) with a computer-aided design (CAD) software and then visualized with a geographic information system (GIS) software. The CAD software was used since implemented functions allowed an appropriate creating and editing of the TINTLS. GIS functionalities were however required for the desired visualization, such as coloring the TINTLS by height and a vertical exaggeration. The final merging of the image with an oblique view on the 3D surface and the 2D image of the apparent resistivity in the subsurface was simple. Establishing a similar approach based on the UAV-derived data is targeted for the future.
The final outlook refers again to one of the main overall aims of this project, namely the detection of suspected temporal changes in the karst depression Ottensee. The day after the campaign in May 2016 was marked by heavy rain in south-west Germany. Consequently, the karst depression was filled with water, which lasted several weeks. According to human-based observations, remarkable surface changes occurred. Thus, in the field campaign, already scheduled for June 2017, a remote sensing based detection of changes might be possible.
The first initiative for this study came from Dr. Reinhard Zeese, who already carried out plenty of geomorphological studies in the region of Hohenlohe. We would like to thank him for this initiative and for the ongoing knowledgeable support. In this context, we acknowledge the permission for the field campaign by the Agency for Nature Conservation and Landscape Management of Baden-Württemberg. Our thanks also go to Daniel Wunderlich. He is responsible for cultivating and protecting the study area and was always very helpful. For the provision of the geoelectric equipment we thank Prof. O. Bubenzer. The data acquisition was carried out as part of a field experience course with students from the Institute of Geography, University of Cologne. Accordingly, we would like to thank the students for their support, namely A. Berghaus, M. Drahs, S. Esser N. Gerdes, M. Holthausen, M. Kanig, S. Keßler, L. Meine, J. Menne. E. Quix, S. Ranke, A. Symanczyk, F. Weber. In particular, Maximilian Kanig is acknowledged for supervising the geophysical prospecting.
All authors declare no conflicts of interest in this paper.
| [1] |
Cetegen BM, Mohamad N (1993) Experiments on liquid mixing and reaction in a vortex. J Fluid Mech 249: 391–414. https://doi.org/10.1017/S0022112093001223 doi: 10.1017/S0022112093001223
|
| [2] |
Verzicco R, Orlandi P (1995) Mixedness in the formation of a vortex ring. Phys Fluids 7: 1513–1515. https://doi.org/10.1063/1.868538 doi: 10.1063/1.868538
|
| [3] |
Urzay J (2018) Supersonic combustion in air-breathing propulsion systems for hypersonic flight. Annu Rev Fluid Mech 50: 593–627. https://doi.org/10.1146/annurev-fluid-122316-045217 doi: 10.1146/annurev-fluid-122316-045217
|
| [4] | Ferri A, Libby PA, Zakkay V (1964) Theoretical and experimental investigation of supersonic combustion, in High Temperatures in Aeronautics, Elsevier, 55–118. https://doi.org/10.1016/B978-0-08-010558-1.50011-6 |
| [5] |
Ferri A (1973) Mixing-controlled supersonic combustion. Annu Rev Fluid Mech 5: 301–338. https://doi.org/10.1146/annurev.fl.05.010173.001505 doi: 10.1146/annurev.fl.05.010173.001505
|
| [6] | Gupta AK, Lilley DG, Syred N (1984) Swirl flows. Tunbridge Wells. |
| [7] |
Candel S, Durox D, Schuller T, et al. (2014) Dynamics of swirling flames. Annu Rev Fluid Mech 46: 147–173. https://doi.org/10.1146/annurev-fluid-010313-141300 doi: 10.1146/annurev-fluid-010313-141300
|
| [8] | Bahr D (1987) Technology for the design of high temperature rise combustors. J Propuls Power 3: 179–186. |
| [9] |
An Q, Steinberg AM (2019) The role of strain rate, local extinction, and hydrodynamic instability on transition between attached and lifted swirl flames. Combusti Flame 199: 267–278. https://doi.org/10.1016/j.combustflame.2018.10.029 doi: 10.1016/j.combustflame.2018.10.029
|
| [10] |
Caulfield C (2021) Layering, instabilities, and mixing in turbulent stratified flows. Annu Rev Fluid Mech 53: 113–145. https://doi.org/10.1146/annurev-fluid-042320-100458 doi: 10.1146/annurev-fluid-042320-100458
|
| [11] |
Crimaldi JP, Zimmer RK (2014) The physics of broadcast spawning in benthic invertebrates. Annu Rev Mar Sci 6: 1. https://doi.org/10.1146/annurev-marine-010213-135119 doi: 10.1146/annurev-marine-010213-135119
|
| [12] |
Mingotti N, Wood R, Noakes C, et al. (2020) The mixing of airborne contaminants by the repeated passage of people along a corridor. J Fluid Mech 903: A52. https://doi.org/10.1017/jfm.2020.671 doi: 10.1017/jfm.2020.671
|
| [13] |
Lohse D, Xia KQ (2010) Small-scale properties of turbulent rayleigh-bénard convection. Annu Rev Fluid Mech 42: 335–364. https://doi.org/10.1146/annurev-fluid-10908.165152 doi: 10.1146/annurev-fluid-10908.165152
|
| [14] |
Kolmogorov AN (1941) The local structure of turbulence in incompressible viscous fluid for very large reynolds numbers. Cr Acad Sci URSS 30: 301–305. https://doi.org/10.1007/978-94-011-3030-1_45 doi: 10.1007/978-94-011-3030-1_45
|
| [15] |
Batchelor GK (1959) Small-scale variation of convected quantities like temperature in turbulent fluid Part 1. general discussion and the case of small conductivity. J Fluid Mech 5: 113–133. https://doi.org/10.1017/S002211205900009X doi: 10.1017/S002211205900009X
|
| [16] |
Warhaft Z (2000) Passive scalars in turbulent flows. Annu Rev Fluid Mech 32: 203–240. https://doi.org/10.1146/annurev.fluid.32.1.203 doi: 10.1146/annurev.fluid.32.1.203
|
| [17] |
Schwertfirm F, Manhart M (2007) Dns of passive scalar transport in turbulent channel flow at high schmidt numbers. Int J Heat Fluid Fl 28: 1204–1214. https://doi.org/10.1016/j.ijheatfluidflow.2007.05.012 doi: 10.1016/j.ijheatfluidflow.2007.05.012
|
| [18] |
Dimotakis PE (2000) The mixing transition in turbulent flows. J Fluid Mech 409: 69–98. https://doi.org/10.1017/S0022112099007946 doi: 10.1017/S0022112099007946
|
| [19] |
Meunier P, Villermaux E (2003) How vortices mix. J Fluid Mech 476: 213–222. https://doi.org/10.1017/S0022112002003166 doi: 10.1017/S0022112002003166
|
| [20] |
Souzy M, Zaier I, Lhuissier H, et al. (2018) Mixing lamellae in a shear flow. J Fluid Mech 838: R3. https://doi.org/10.1017/jfm.2017.916 doi: 10.1017/jfm.2017.916
|
| [21] |
Buaria D, Clay MP, Sreenivasan KR, et al. (2021) Turbulence is an ineffective mixer when schmidt numbers are large. Phys Rev Lett 126: 074501. https://doi.org/10.1103/PhysRevLett.126.074501 doi: 10.1103/PhysRevLett.126.074501
|
| [22] |
Raynal F, Gence JN (1997) Energy saving in chaotic laminar mixing. Int J Heat Mass Trans 40: 3267–3273. https://doi.org/10.1016/S0017-9310(96)00383-3 doi: 10.1016/S0017-9310(96)00383-3
|
| [23] |
Dimotakis PE (2005) Turbulent mixing. Annu Rev Fluid Mech 37: 329–356. https://doi.org/10.1146/annurev.fluid.36.050802.122015 doi: 10.1146/annurev.fluid.36.050802.122015
|
| [24] |
Thiffeault JL (2012) Using multiscale norms to quantify mixing and transport. Nonlinearity 25: R1. https://doi.org/10.1088/0951-7715/25/2/R1 doi: 10.1088/0951-7715/25/2/R1
|
| [25] |
Duplat J, Jouary A, Villermaux E (2010) Entanglement rules for random mixtures. Phys Rev Lett 105: 034504. https://doi.org/10.1103/PhysRevLett.105.034504 doi: 10.1103/PhysRevLett.105.034504
|
| [26] |
Kree M, Duplat J, Villermaux E (2013) The mixing of distant sources. Phys Fluids 25: 091103. https://doi.org/10.1063/1.4820015 doi: 10.1063/1.4820015
|
| [27] |
Villermaux E, Rehab H (2000) Mixing in coaxial jets. J Fluid Mech 425: 161–185. https://doi.org/10.1017/S002211200000210X doi: 10.1017/S002211200000210X
|
| [28] | Vidick B (1989) Critical mixing parameters for good control of cement slurry quality. in SPE Production Operations Symposium. OnePetro. https://doi.org/10.2118/18895-PA |
| [29] |
Poulain S, Villermaux E, Bourouiba L (2018) Ageing and burst of surface bubbles. J Fluid Mech 851: 636–671. https://doi.org/10.1017/jfm.2018.471 doi: 10.1017/jfm.2018.471
|
| [30] | Marble F (1985) Growth of a diffusion flame in the field of a vortex, in Recent advances in the aerospace sciences, Springer, 395–413. https://doi.org/10.1007/978-1-4684-4298-4_19 |
| [31] |
Villermaux E (2019) Mixing versus stirring. Annu Rev Fluid Mech 51: 245–273. https://doi.org/10.1146/annurev-fluid-010518-040306 doi: 10.1146/annurev-fluid-010518-040306
|
| [32] |
Ranz WE (1979) Applications of a stretch model to mixing, diffusion, and reaction in laminar and turbulent flows. AIChE J 25: 41–47. https://doi.org/10.1002/aic.690250105 doi: 10.1002/aic.690250105
|
| [33] | Marble FE, Broadwell JE (1977) The coherent flame model for turbulent chemical reactions. Purdue Univ Lafayette in project squid head quaters. Tech Rep. Available from: https://api.semanticscholar.org/CorpusID:45411925. |
| [34] |
Villermaux E, Duplat J (2003) Mixing is an aggregation process. Comptes Rendus Mécanique 331: 515–523. https://doi.org/10.1016/S1631-0721(03)00110-4 doi: 10.1016/S1631-0721(03)00110-4
|
| [35] |
Duplat J, Villermaux E (2008) Mixing by random stirring in confined mixtures. J Fluid Mech 617: 51–86. https://doi.org/10.1017/S0022112008003789 doi: 10.1017/S0022112008003789
|
| [36] |
Duplat J, Innocenti C, Villermaux E (2010) A nonsequential turbulent mixing process. Phys Fluids 22: 035104. https://doi.org/10.1063/1.3319821 doi: 10.1063/1.3319821
|
| [37] |
Haller G (2015) Lagrangian coherent structures. Annu Rev Fluid Mech 47: 137–162. https://doi.org/10.1146/annurev-fluid-010313-141322 doi: 10.1146/annurev-fluid-010313-141322
|
| [38] |
Hang H, Yu B, Xiang Y, et al. (2020) An objective-adaptive refinement criterion based on modified ridge extraction method for finite-time lyapunov exponent (ftle) calculation. J Visual 23: 81–95. https://doi.org/10.1007/S12650-019-00605-1 doi: 10.1007/S12650-019-00605-1
|
| [39] |
Liang G, Yu B, Zhang B, et al. (2019) Hidden flow structures in compressible mixing layer and a quantitative analysis of entrainment based on lagrangian method. J Hydrodyn 31: 256–265. https://doi.org/10.1017/jfm.2020.295 doi: 10.1017/jfm.2020.295
|
| [40] |
Zheng Z, Fan Z, Wang Z, et al. (2021) Lagrangian visualization of mixing enhancement induced by finite-time stretching in compressible vortex interaction. J Visual 24: 19–28. https://doi.org/10.1007/s12650-020-00698-z doi: 10.1007/s12650-020-00698-z
|
| [41] |
Götzfried P, Emran MS, Villermaux E, et al. (2019) Comparison of lagrangian and eulerian frames of passive scalar turbulent mixing. Phys Rev Fluids 4: 044607. https://doi.org/10.1103/PhysRevFluids.4.044607 doi: 10.1103/PhysRevFluids.4.044607
|
| [42] |
Meunier P, Villermaux E (2022) The diffuselet concept for scalar mixing. J Fluid Mech 951: A33. https://doi.org/10.1017/jfm.2022.771 doi: 10.1017/jfm.2022.771
|
| [43] |
Meunier P, Villermaux E (2010) The diffusive strip method for scalar mixing in two dimensions. J Fluid Mechanics 662: 134–172. https://doi.org/10.1017/S0022112010003162 doi: 10.1017/S0022112010003162
|
| [44] |
Martínez-Ruiz D, Meunier P, Favier B, et al.(2018) The diffusive sheet method for scalar mixing. J Fluid Mech 837: 230–257. https://doi.org/10.1017/S0022112010003162 doi: 10.1017/S0022112010003162
|
| [45] |
Sen S, Singh P, Heyman J, et al. (2020) The impact of stretching-enhanced mixing and coalescence on reactivity in mixing-limited reactive flows. Phys Fluids 32: 106602, 2020. https://doi.org/10.1063/5.0022798 doi: 10.1063/5.0022798
|
| [46] |
Heyman J, Lester DR, Turuban R, et al. (2020) Stretching and folding sustain microscale chemical gradients in porous media. P Natl Acad Sci 117: 13 359–13 365. https://doi.org/10.1073/pnas.2002858117 doi: 10.1073/pnas.2002858117
|
| [47] |
Guilbert E, Almarcha C, Villermaux E (2021) Chemical reaction for mixing studies. Phys Rev Fluids 6: 114501. https://doi.org/10.1103/PhysRevFluids.6.114501 doi: 10.1103/PhysRevFluids.6.114501
|
| [48] |
Guilbert E, Metzger B, Villermaux E (2022) Chemical production on a deforming substrate. J Fluid Mech 934: R1. https://doi.org/10.1017/jfm.2021.1122 doi: 10.1017/jfm.2021.1122
|
| [49] |
Buch KA, Dahm WJ (1996) Experimental study of the fine-scale structure of conserved scalar mixing in turbulent shear flows. part 1. sc [dbl greater-than sign] 1. J Fluid Mech 317: 21–71. https://doi.org/10.1017/s0022112096000651 doi: 10.1017/s0022112096000651
|
| [50] |
Cetegen B, Aguirre J (1990) Analysis of molecular mixing and chemical reaction in a vortex pair. Phys Fluids 2: 2211–2216. https://doi.org/10.1063/1.857807 doi: 10.1063/1.857807
|
| [51] |
Basu S, Barber T, Cetegen B (2007) Computational study of scalar mixing in the field of a gaseous laminar line vortex. Phys Fluids 19: 053601. https://doi.org/10.1063/1.2732454 doi: 10.1063/1.2732454
|
| [52] |
Flohr P, Vassilicos J (1997) Accelerated scalar dissipation in a vortex. J Fluid Mech 348: 295–317. https://doi.org/10.1017/S0022112097006927 doi: 10.1017/S0022112097006927
|
| [53] |
Bilger R (1976) The structure of diffusion flames. Combust Sci Technol 13: 155–170. https://doi.org/10.1080/00102207608946733 doi: 10.1080/00102207608946733
|
| [54] |
Bilger RW (1989) Turbulent diffusion flames. Annu Rev Fluid Mech 21: 101–135. https://doi.org/10.1146/annurev.fl.21.010189.000533 doi: 10.1146/annurev.fl.21.010189.000533
|
| [55] |
Yeung P, Girimaji S, Pope S (1990) Straining and scalar dissipation on material surfaces in turbulence: implications for flamelets. Combust Flame 79: 340–365. https://doi.org/10.1016/0010-2180(90)90145-H doi: 10.1016/0010-2180(90)90145-H
|
| [56] |
Kim SH, Pitsch H (2007) Scalar gradient and small-scale structure in turbulent premixed combustion. Phys Fluids 19: 115104. https://doi.org/10.1063/1.2784943 doi: 10.1063/1.2784943
|
| [57] |
Boratav O, Elghobashi S, Zhong R (1996) On the alignment of the alpha-strain and vorticity in turbulent nonpremixed flames. Phys Fluids 8: 2251–2253. https://doi.org/10.1063/1.869000 doi: 10.1063/1.869000
|
| [58] |
Boratav O, Elghobashi S, Zhong R (1998) On the alignment of strain, vorticity and scalar gradient in turbulent, buoyant, nonpremixed flames. Phys Fluids 10: 2260–2267. https://doi.org/10.1063/1.869747 doi: 10.1063/1.869747
|
| [59] |
Attili A, Bisetti F (2019) Statistics of scalar dissipation and strain/vorticity/scalar gradient alignment in turbulent nonpremixed jet flames. Flow Turbul Combust 103: 625–642. https://doi.org/10.1007/s10494-019-00044-w doi: 10.1007/s10494-019-00044-w
|
| [60] |
McManus TA, Sutton JA (2022) Conditional analysis of temperature and strain rate effects on dissipation structure in turbulent non-premixed jet flames. P Combust Inst. https://doi.org/10.1016/j.proci.2022.07.052 doi: 10.1016/j.proci.2022.07.052
|
| [61] |
Chakraborty N, Swaminathan N (2007) Influence of the damköhler number on turbulence-scalar interaction in premixed flames. i. physical insight. Phys Fluids 19: 045103. https://doi.org/10.1063/1.2714070 doi: 10.1063/1.2714070
|
| [62] |
Zhao S, Er-Raiy A, Bouali Z, et al. (2018) Dynamics and kinematics of the reactive scalar gradient in weakly turbulent premixed flames. Combust Flame 198: 436–454. https://doi.org/10.1016/j.combustflame.2018.10.002 doi: 10.1016/j.combustflame.2018.10.002
|
| [63] |
Batchelor GK (1952) The effect of homogeneous turbulence on material lines and surfaces. Proc Math Phys Sci 213: 349–366. https://doi.org/10.1098/rspa.1952.0130 doi: 10.1098/rspa.1952.0130
|
| [64] |
Girimaji S, Pope S (1990) 'Material-element deformation in isotropic turbulence. J Fluid Mech 220: 427–458. https://doi.org/10.1017/S0022112090003330 doi: 10.1017/S0022112090003330
|
| [65] |
Dresselhaus E, Tabor M (1992) The kinematics of stretching and alignment of material elements in general flow fields. J Fluid Mech 236: 415–444. https://doi.org/10.1017/S0022112092001460 doi: 10.1017/S0022112092001460
|
| [66] |
Lapeyre G, Klein P, Hua B (1999) Does the tracer gradient vector align with the strain eigenvectors in 2d turbulence? Phys Fluids 11: 3729–3737. https://doi.org/10.1063/1.870234 doi: 10.1063/1.870234
|
| [67] |
Klein P, Hua BL, Lapeyre G (2000) Alignment of tracer gradient vectors in 2d turbulence. Physica D 146: 246–260. https://doi.org/10.1016/S0167-2789(00)00119-6 doi: 10.1016/S0167-2789(00)00119-6
|
| [68] |
Swaminathan N, Grout R (2006) Interaction of turbulence and scalar fields in premixed flames. Phys Fluids 18: 045102. https://doi.org/10.1063/1.2186590 doi: 10.1063/1.2186590
|
| [69] |
Minamoto Y, Jigjid K, Igari R, et al. (2022) Effect of flame–flame interaction on scalar pdf in turbulent premixed flames. Combust Flame 239: 111660. https://doi.org/10.1016/j.combustflame.2021.111660 doi: 10.1016/j.combustflame.2021.111660
|
| [70] |
Holzner M, Lüthi B (2011) Laminar superlayer at the turbulence boundary. Phys Rev Lett 106, : 134503. https://doi.org/10.1103/PhysRevLett.106.134503 doi: 10.1103/PhysRevLett.106.134503
|
| [71] |
Townsend AA (1951) The diffusion of heat spots in isotropic turbulence. Proc Math Phys Sci 209: 418–430. https://doi.org/10.1098/rspa.1951.0216 doi: 10.1098/rspa.1951.0216
|
| [72] |
Cocke W (1969) Turbulent hydrodynamic line stretching: consequences of isotropy. Phys Fluids 12: 2488–2492. https://doi.org/10.1063/1.1692385 doi: 10.1063/1.1692385
|
| [73] |
Ashurst WT, Kerstein A, Kerr R, et al. (1987) Alignment of vorticity and scalar gradient with strain rate in simulated navier–stokes turbulence. Phys Fluids 30: 2343–2353. https://doi.org/10.1063/1.866513 doi: 10.1063/1.866513
|
| [74] |
Vincent A, Meneguzzi M (1991) The spatial structure and statistical properties of homogeneous turbulence. J Fluid Mech 225: 1–20. https://doi.org/10.1017/S0022112091001957 doi: 10.1017/S0022112091001957
|
| [75] |
Carter HH, Okubo A (1972) Longitudinal dispersion in non-uniform flow. Water Resour Res 8: 648–660. https://doi.org/10.1029/WR008i003p00648 doi: 10.1029/WR008i003p00648
|
| [76] |
Weiss J (1991) The dynamics of enstrophy transfer in two-dimensional hydrodynamics. Physica D 48: 273–294. https://doi.org/10.1016/0167-2789(91)90088-Q doi: 10.1016/0167-2789(91)90088-Q
|
| [77] | Hunt JC, Wray AA, Moin P (1988) Eddies, streams, and convergence zones in turbulent flows. Studying turbulence using numerical simulation databases, 2. Proceedings of the 1988 summer program. Available from: https://ntrs.nasa.gov/citations/19890015184 |
| [78] |
Basdevant C, Philipovitch T (1994) On the validity of the "weiss criterion" in two-dimensional turbulence. Physica D 73: 17–30. https://doi.org/10.1016/0167-2789(94)90222-4 doi: 10.1016/0167-2789(94)90222-4
|
| [79] |
Hua B, Klein P (1998) An exact criterion for the stirring properties of nearly two-dimensional turbulence. Physica D 113: 98–110. https://doi.org/10.1016/S0167-2789(97)00143-7 doi: 10.1016/S0167-2789(97)00143-7
|
| [80] |
Galanti B, Gibbon J, Heritage M (1997) Vorticity alignment results for the three-dimensional euler and navier-stokes equations. Nonlinearity 10: 1675. https://doi.org/10.1088/0951-7715/10/6/013 doi: 10.1088/0951-7715/10/6/013
|
| [81] |
Ohkitani K, Kishiba S (1995) Nonlocal nature of vortex stretching in an inviscid fluid. Phys Fluids 7: 411–421. https://doi.org/10.1063/1.868638 doi: 10.1063/1.868638
|
| [82] |
Tsinober A, Ortenberg M, Shtilman L (1999) On depression of nonlinearity in turbulence. Phys Fluids 11: 2291–2297. https://doi.org/10.1063/1.870091 doi: 10.1063/1.870091
|
| [83] |
Wacks DH, Chakraborty N, Klein M, et al. (2016) Flow topologies in different regimes of premixed turbulent combustion: A direct numerical simulation analysis. Phys Rev Fluids 1: 083401. https://doi.org/10.1103/PhysRevFluids.1.083401 doi: 10.1103/PhysRevFluids.1.083401
|
| [84] |
Meneveau C (2011) Lagrangian dynamics and models of the velocity gradient tensor in turbulent flows. Annu Rev Fluid Mech 43: 219–245. https://doi.org/10.1146/annurev-fluid-122109-160708 doi: 10.1146/annurev-fluid-122109-160708
|
| [85] |
Jeong J, Hussain F (1995) On the identification of a vortex. J Fluid Mech 285: 69–94. https://doi.org/10.1017/S0022112095000462 doi: 10.1017/S0022112095000462
|
| [86] |
Chong MS, Perry AE, Cantwell BJ (1990) A general classification of three-dimensional flow fields. Phys Fluids A 2: 765–777. https://doi.org/10.1063/1.857730 doi: 10.1063/1.857730
|
| [87] |
Perry AE, Chong MS (1987) A description of eddying motions and flow patterns using critical-point concepts. Annu Rev Fluid Mech 19: 125–155. https://doi.org/10.1146/annurev.fl.19.010187.001013 doi: 10.1146/annurev.fl.19.010187.001013
|
| [88] |
Danish M, Suman S, Girimaji SS (2016) Influence of flow topology and dilatation on scalar mixing in compressible turbulence. J Fluid Mech 793: 633–655. https://doi.org/10.1017/jfm.2016.145 doi: 10.1017/jfm.2016.145
|
| [89] |
Gao X, Bermejo-Moreno I, Larsson J (2020) Parametric numerical study of passive scalar mixing in shock turbulence interaction. J Fluid Mech 895: A21. https://doi.org/10.1017/jfm.2020.292 doi: 10.1017/jfm.2020.292
|
| [90] |
Cifuentes L, Dopazo C, Martin J, et al. (2014) Local flow topologies and scalar structures in a turbulent premixed flame. Phys Fluids 26: 065108. https://doi.org/10.1063/1.4884555 doi: 10.1063/1.4884555
|
| [91] |
Han W, Scholtissek A, Dietzsch F, et al. (2019) Influence of flow topology and scalar structure on flame-tangential diffusion in turbulent non-premixed combustion. Combust Flame 206: 21–36. https://doi.org/10.1016/j.combustflame.2019.04.038 doi: 10.1016/j.combustflame.2019.04.038
|
| [92] |
Heyman J, Lester D, Le Borgne T (2021) Scalar signatures of chaotic mixing in porous media. Phys Rev Lett 126: 034505. https://doi.org/10.1103/PhysRevLett.126.034505 doi: 10.1103/PhysRevLett.126.034505
|
| [93] |
Waitz I, Qiu Y, Manning T, et al. (1997) Enhanced mixing with streamwise vorticity. Prog Aerosp Sci 33: 323–351. https://doi.org/10.1016/S0376-0421(96)00008-5 doi: 10.1016/S0376-0421(96)00008-5
|
| [94] |
Vergine F, Ground C, Maddalena L (2016) Turbulent kinetic energy decay in supersonic streamwise interacting vortices. J Fluid Mech 807: 353–385. https://doi.org/10.1017/jfm.2016.611 doi: 10.1017/jfm.2016.611
|
| [95] |
Wu Z, He M, Yu B, et al. (2022) A circulation prediction model for ramp and vortex generator in supersonic flow: A numerical study. Aerosp Sci Technol 127: 107688. https://doi.org/10.1016/j.ast.2022.107688 doi: 10.1016/j.ast.2022.107688
|
| [96] |
Wang Z, Yu B, Zhang B, et al. (2021) Kinematic and mixing characteristics of vortex interaction induced by a vortex generator model: a numerical study. Appl Math Mech 42: 387–404. https://doi.org/10.1007/s10483-021-2711-5 doi: 10.1007/s10483-021-2711-5
|
| [97] |
Schetz JA, Maddalena L, Burger SK (2010) Molecular weight and shock-wave effects on transverse injection in supersonic flow. J Propuls Power 26: 1102–1113. https://doi.org/10.2514/1.49355 doi: 10.2514/1.49355
|
| [98] |
Tew DE, Hermanson JC, Waitz IA (2004) Impact of compressibility on mixing downstream of lobed mixers. AIAA J 42: 2393–2396. https://doi.org/10.2514/1.11004 doi: 10.2514/1.11004
|
| [99] |
Brouillette M (2002) The richtmyer-meshkov instability. Annu Rev Fluid Mech 34: 445–468. https://doi.org/10.1146/annurev.fluid.34.090101.162238 doi: 10.1146/annurev.fluid.34.090101.162238
|
| [100] |
Zhou Y (2017) Rayleigh–taylor and richtmyer–meshkov instability induced flow, turbulence, and mixing. ii. Phys Rep 723: 1–160. https://doi.org/10.1016/j.physrep.2017.07.008 doi: 10.1016/j.physrep.2017.07.008
|
| [101] |
Zhou Y (2017) Rayleigh–taylor and richtmyer–meshkov instability induced flow, turbulence, and mixing. i. Phys Rep 720-722: 1–136. https://doi.org/10.1016/j.physrep.2017.07.005 doi: 10.1016/j.physrep.2017.07.005
|
| [102] |
Peng G, Zabusky NJ, Zhang S (2003) Vortex-accelerated secondary baroclinic vorticity deposition and late-intermediate time dynamics of a two-dimensional richtmyer–meshkov interface. Phys Fluids 15: 3730–3744. https://doi.org/10.1063/1.1621628 doi: 10.1063/1.1621628
|
| [103] |
Livescu D (2020) Turbulence with large thermal and compositional density variations. Annu Rev Fluid Mech 52: 309-341. https://doi.org/10.1146/annurev-fluid-010719-060114 doi: 10.1146/annurev-fluid-010719-060114
|
| [104] |
Weber C, Haehn N, Oakley J, et al. (2012) Turbulent mixing measurements in the richtmyer-meshkov instability. Phys Fluids 24: 074105. https://doi.org/10.1063/1.4733447 doi: 10.1063/1.4733447
|
| [105] |
Mikaelian KO (1998) Analytic approach to nonlinear rayleigh-taylor and richtmyer-meshkov instabilities. Phys Rev Lett 80: 508–511. https://doi.org/10.1103/PhysRevLett.80.508 doi: 10.1103/PhysRevLett.80.508
|
| [106] |
Zabusky NJ (1999) Vortex paradigm for accelerated inhomogeneous flows: Visiometrics for the rayleigh-taylor and richtmyer-meshkov environments. Annu Rev Fluid Mech 31: 495–536. https://doi.org/10.1146/annurev.fluid.31.1.495 doi: 10.1146/annurev.fluid.31.1.495
|
| [107] |
Kumar S, Orlicz G, Tomkins C, et al. (2005) Stretching of material lines in shock-accelerated gaseous flows. Phys Fluids 17: 082107. https://doi.org/10.1063/1.2031347 doi: 10.1063/1.2031347
|
| [108] |
Zhou Y, Cabot WH, Thornber B (2016) Asymptotic behavior of the mixed mass in rayleigh–taylor and richtmyer–meshkov instability induced flows. Phys Plasmas 23: 052712. https://doi.org/10.1063/1.4951018 doi: 10.1063/1.4951018
|
| [109] |
Richtmyer RD (1960) Taylor instability in shock acceleration of compressible fluids. Commun Pure Appl Math 13: 297–319. https://doi.org/10.1002/cpa.3160130207 doi: 10.1002/cpa.3160130207
|
| [110] |
Meshkov E (1969) Instability of the interface of two gases accelerated by a shock wave. Fluid Dyn 4: 101–104. https://doi.org/10.1007/BF01015969 doi: 10.1007/BF01015969
|
| [111] |
Klein RI, McKee CF, Colella P (1994) On the hydrodynamic interaction of shock waves with interstellar clouds. 1: Nonradiative shocks in small clouds. Astrophys J 420: 213–236. https://doi.org/10.1086/173554 doi: 10.1086/173554
|
| [112] |
Cabot WH, Cook AW (2006) Reynolds number effects on rayleigh–taylor instability with possible implications for type ia supernovae. Nat Phys 2: 562–568. https://doi.org/10.1038/nphys361 doi: 10.1038/nphys361
|
| [113] |
Lindl JD, McCrory RL, Campbell EM (1992) Progress toward ignition and burn propagation in inertial confinement fusion. Phys Today 45: 32–40. https://doi.org/10.1063/1.881318 doi: 10.1063/1.881318
|
| [114] |
EOran ES, Gamezo VN (2007) Origins of the deflagration-to-detonation transition in gas-phase combustion. Combust Flame 148: 4–47. https://doi.org/10.1016/j.combustflame.2006.07.010 doi: 10.1016/j.combustflame.2006.07.010
|
| [115] |
Yang J, Kubota T, Zukoski EE (1994) A model for characterization of a vortex pair formed by shock passage over a light-gas inhomogeneity. J Fluid Mech 258: 217–244. https://doi.org/10.1017/S0022112094003307 doi: 10.1017/S0022112094003307
|
| [116] |
Yu B, He M, Zhang B, et al. (2020) Two-stage growth mode for lift-off mechanism in oblique shock-wave/jet interaction. Phys Fluids 32: 116105. https://doi.org/10.1063/5.0022449 doi: 10.1063/5.0022449
|
| [117] |
Zhang B, Liu H, Yu B, et al. (2022) Numerical investigation on combustion-enhancement strategy in shock–fuel jet interaction. AIAA J 60: 393–410. https://doi.org/10.2514/1.J060168 doi: 10.2514/1.J060168
|
| [118] |
Zhang B, Chen H, Yu B, et al. (2019) Molecular simulation on viscous effects for microscale combustion in reactive shock-bubble interaction. Combust Flame 208: 351–363. https://doi.org/10.1016/j.combustflame.2019.07.001 doi: 10.1016/j.combustflame.2019.07.001
|
| [119] |
Liu H, Yu B, Chen H, et al. (2020) Contribution of viscosity to the circulation deposition in the richtmyer–meshkov instability. J Fluid Mech 895: A10. https://doi.org/10.1017/jfm.2020.295 doi: 10.1017/jfm.2020.295
|
| [120] |
Wang Z, Yu B, Chen H, et al. (2018) Scaling vortex breakdown mechanism based on viscous effect in shock cylindrical bubble interaction. Phys Fluids 30: 126103. https://doi.org/10.1063/1.5051463 doi: 10.1063/1.5051463
|
| [121] |
Ding J, Si T, Yang J, et al. (2017) Measurement of a richtmyer-meshkov instability at an air-sf 6 interface in a semiannular shock tube. Phys Rev Lett 119: 014501. https://doi.org/10.1103/PhysRevLett.119.014501 doi: 10.1103/PhysRevLett.119.014501
|
| [122] |
Cook AW, Dimotakis PE (2001) Transition stages of rayleigh–taylor instability between miscible fluids. J Fluid Mech 443: 69–99. https://doi.org/10.1017/S0022112002007802 doi: 10.1017/S0022112002007802
|
| [123] |
Cook AW, Cabot W, Miller PL (2004) The mixing transition in rayleigh–taylor instability. J Fluid Mech 511: 333–362. https://doi.org/10.1017/S0022112004009681 doi: 10.1017/S0022112004009681
|
| [124] |
Ristorcelli J, Clark T (2004) Rayleigh–taylor turbulence: self-similar analysis and direct numerical simulations. J Fluid Mech 507: 213–253. https://doi.org/10.1017/S0022112004008286 doi: 10.1017/S0022112004008286
|
| [125] |
Samtaney R, Zabusky NJ (1993) On shock polar analysis and analytical expressions for vorticity deposition in shock-accelerated density-stratified interfaces. Phys Fluids A: Fluid Dyn 5: 1285–1287. https://doi.org/10.1063/1.858618 doi: 10.1063/1.858618
|
| [126] |
Marugan-Cruz C, Rodriguez-Rodriguez J, Martinez-Bazan C (2013) Formation regimes of vortex rings in negatively buoyant starting jets. J Fluid Mech 716: 470–486. https://doi.org/10.1017/jfm.2012.554 doi: 10.1017/jfm.2012.554
|
| [127] |
Soteriou MC, Ghoniem AF (1995) Effects of the free stream density ratio on free and forced spatially developing shear layers. Phys Fluids 7: 2036–2051. https://doi.org/10.1063/1.868451 doi: 10.1063/1.868451
|
| [128] |
Livescu D, Ristorcelli J, Petersen M, et al. (2010) New phenomena in variable-density rayleigh–taylor turbulence. Phys Scripta 2010: 014015. https://doi.org/10.1088/0031-8949/2010/T142/014015 doi: 10.1088/0031-8949/2010/T142/014015
|
| [129] |
Zhai Z, Si T, Luo X, et al. (2011) On the evolution of spherical gas interfaces accelerated by a planar shock wave. Phys Fluids 23: 084104. https://doi.org/10.1063/1.3623272 doi: 10.1063/1.3623272
|
| [130] |
Si T, Long T, Zhai Z, et al. (2015) Experimental investigation of cylindrical converging shock waves interacting with a polygonal heavy gas cylinder. J Fluid Mech 784: 225–251. https://doi.org/10.1017/jfm.2015.581 doi: 10.1017/jfm.2015.581
|
| [131] |
Luo X, Wang M, Si T, et al. (2015) On the interaction of a planar shock with an polygon. J Fluid Mech 773: 366–394. https://doi.org/10.1017/jfm.2015.257 doi: 10.1017/jfm.2015.257
|
| [132] |
Ding J, Si T, Chen M, et al. (2017) On the interaction of a planar shock with a three-dimensional light gas cylinder. J Fluid Mech 828: 289–317. https://doi.org/10.1017/jfm.2017.528 doi: 10.1017/jfm.2017.528
|
| [133] |
Li D, Guan B, Wang G (2022) Effects of interface diffusion and shock strength on shock-accelerated sf6 cylinder. Phys Fluids 34: 076109. https://doi.org/10.1063/5.0099353 doi: 10.1063/5.0099353
|
| [134] |
Vorobieff P, Rightley PM, Benjamin RF (1998) Power-law spectra of incipient gas-curtain turbulence. Phys Rev Lett 81: 2240. https://doi.org/10.1103/PhysRevLett.81.2240 doi: 10.1103/PhysRevLett.81.2240
|
| [135] |
Niederhaus JH, Greenough J, Oakley J, et al. (2008) A computational parameter study for the three-dimensional shock–bubble interaction. J Fluid Mech 594: 85–124. https://doi.org/10.1017/S0022112007008749 doi: 10.1017/S0022112007008749
|
| [136] |
Lombardini M, Pullin D, Meiron D (2012) Transition to turbulence in shock-driven mixing: a mach number study. J Fluid Mech 690: 203–226. https://doi.org/10.1017/jfm.2011.425 doi: 10.1017/jfm.2011.425
|
| [137] |
Oggian T, Drikakis D, Youngs D, et al. (2015) Computing multi-mode shock-induced compressible turbulent mixing at late times. J Fluid Mech 779: 411–431. https://doi.org/10.1017/jfm.2015.392 doi: 10.1017/jfm.2015.392
|
| [138] |
Liu H, Yu B, Zhang B, et al. (2020) On mixing enhancement by secondary baroclinic vorticity in shock bubble interaction. J Fluid Mech 931: A17. https://doi.org/10.1017/jfm.2021.923 doi: 10.1017/jfm.2021.923
|
| [139] |
Li Y, Wang Z, Yu B, et al. (2019) Gaussian models for late-time evolution of two-dimensional shock–light cylindrical bubble interaction. Shock Waves 1–16. https://doi.org/10.1007/s00193-019-00928-w doi: 10.1007/s00193-019-00928-w
|
| [140] |
Thornber B, Griffond J, Poujade O, et al. (2017) Late-time growth rate, mixing, and anisotropy in the multimode narrowband richtmyer–meshkov instability: The θ-group collaboration. Phys Fluids 29: 105107. https://doi.org/10.1063/1.4993464 doi: 10.1063/1.4993464
|
| [141] |
Li H, He Z, Zhang Y, et al. (2019) On the role of rarefaction/compression waves in richtmyer-meshkov instability with reshock. Phys Fluids 31: 054102. https://doi.org/10.1063/1.5083796 doi: 10.1063/1.5083796
|
| [142] |
Bin Y, Xiao M, Shi Y, et al. (2021) A new idea to predict reshocked richtmyer–meshkov mixing: constrained large-eddy simulation. J Fluid Mech 918: R1. https://doi.org/10.1017/jfm.2021.332 doi: 10.1017/jfm.2021.332
|
| [143] |
Ruan YC, Zhang YS, Tian BL, et al. (2020) Density-ratio-invariant mean-species profile of classical rayleigh-taylor mixing. Phys Rev Fluids 5: 054501. https://doi.org/10.1103/PhysRevFluids.5.054501 doi: 10.1103/PhysRevFluids.5.054501
|
| [144] |
Yu B, Liu H, Liu H (2021) Scaling behavior of density gradient accelerated mixing rate in shock bubble interaction. Phys Rev Fluids 6: 064502. https://doi.org/10.1103/PhysRevFluids.6.064502 doi: 10.1103/PhysRevFluids.6.064502
|
| [145] |
Yu B, Li L, Xu H, et al. (2022) Effects of reynolds number and schmidt number on variable density mixing in shock bubble interaction. Acta Mech Sinica 38: 121256. https://doi.org/10.1007/s10409-022-09011-9 doi: 10.1007/s10409-022-09011-9
|
| [146] |
Tian Y, Jaberi FA, Li Z, et al. (2017) Numerical study of variable density turbulence interaction with a normal shock wave. J Fluid Mech 829: 551–588. https://doi.org/10.1017/jfm.2017.542 doi: 10.1017/jfm.2017.542
|
| [147] |
Wong ML, Livescu D, Lele SK (2019) High-resolution navier-stokes simulations of richtmyer-meshkov instability with reshock. Phys Rev Fluids 4: 104609. https://doi.org/10.1103/PhysRevFluids.4.104609 doi: 10.1103/PhysRevFluids.4.104609
|
| [148] |
Livescu D, Ryu J (2016) Vorticity dynamics after the shock–turbulence interaction. Shock Waves 26: 241–251. https://doi.org/10.1007/s00193-015-0580-5 doi: 10.1007/s00193-015-0580-5
|
| [149] |
Aslangil D, Livescu D, Banerjee A (2020) Variable-density buoyancy-driven turbulence with asymmetric initial density distribution. Physica D 406: 132444. https://doi.org/10.1016/j.physd.2020.132444 doi: 10.1016/j.physd.2020.132444
|
| [150] |
Tian Y, Jaberi FA, Livescu D (2019) Density effects on post-shock turbulence structure and dynamics. J Fluid Mech 880: 935–968. https://doi.org/10.1017/jfm.2019.707 doi: 10.1017/jfm.2019.707
|
| [151] |
Orlicz G, Balasubramanian S, Prestridge K (2013)Incident shock mach number effects on richtmyer-meshkov mixing in a heavy gas layer. Phys Fluids 25: 114101. https://doi.org/10.1063/1.4827435 doi: 10.1063/1.4827435
|
| [152] |
Tomkins C, Kumar S, Orlicz G, et al. (2008) An experimental investigation of mixing mechanisms in shock-accelerated flow. J Fluid Mech 611: 131–150. https://doi.org/10.1017/S0022112008002723 doi: 10.1017/S0022112008002723
|
| [153] |
Marble FE, Zukoski EE, Jacobs JW, et al. (1990) Shock enhancement and control of hypersonic mixing and combustion. AIAA Pap 1981: 1990. https://doi.org/10.2514/6.1990-1981 doi: 10.2514/6.1990-1981
|
| [154] |
Ottino JM (1990) Mixing, chaotic advection, and turbulence. Annu Rev Fluid Mech 22: 207–254. https://doi.org/10.1146/annurev.fl.22.010190.001231 doi: 10.1146/annurev.fl.22.010190.001231
|
| [155] |
Sreenivasan KR (2019) Turbulent mixing: A perspective. P Natl Acad Sci 116: 18 175–18 183. https://doi.org/10.1073/pnas.1800463115 doi: 10.1073/pnas.1800463115
|
| [156] |
Ranjan D, Oakley J, Bonazza R (2011) Shock-bubble interactions. Annu Rev Fluid Mech 43: 117–140. https://doi.org/10.1146/annurev-fluid-122109-160744 doi: 10.1146/annurev-fluid-122109-160744
|
| [157] |
Mulla IA, Hardalupas Y (2022) Measurement of instantaneous fully 3d scalar dissipation rate in a turbulent swirling flow. Exp Fluids 63: 173. https://doi.org/10.1007/s00348-022-03518-2 doi: 10.1007/s00348-022-03518-2
|
Xu Han, Bin Yu, Hong Liu. Mixing mechanisms in the view of mixing indicators: from passive-scalar mixing to variable-density mixing[J]. Metascience in Aerospace, 2024, 1(1): 1-37. doi: 10.3934/mina.2024001
| Reference data sets | DEMTLS | DEMUAV | |||||||
| Name | Z (m) | Height (m) | SD (m) | Diff. (m) | Abs. Diff. (m) | Height (m) | SD (m) | Diff. (m) | Abs. Diff. (m) |
| Set-A_P01 | 459.97 | 459.93 | 0.02 | 0.04 | 0.04 | 459.87 | 0.03 | 0.10 | 0.10 |
| Set-A_P02 | 460.43 | 460.28 | 0.04 | 0.16 | 0.16 | 460.18 | 0.03 | 0.26 | 0.26 |
| Set-A_P03 | 460.89 | 460.88 | 0.02 | 0.01 | 0.01 | 460.94 | 0.02 | -0.05 | 0.05 |
| Set-A_P04 | 458.55 | 458.60 | 0.02 | -0.05 | 0.05 | 458.52 | 0.01 | 0.02 | 0.02 |
| Set-A_P05 | 458.62 | 458.66 | 0.04 | -0.04 | 0.04 | 458.42 | 0.02 | 0.20 | 0.20 |
| Set-A_P06 | 461.19 | 461.23 | 0.02 | -0.04 | 0.04 | 461.17 | 0.02 | 0.03 | 0.03 |
| Set-A_P07 | 459.75 | 459.77 | 0.02 | -0.02 | 0.02 | 459.74 | 0.01 | 0.02 | 0.02 |
| Set-A_P08 | 459.00 | 459.07 | 0.01 | -0.06 | 0.06 | 459.00 | 0.01 | 0.00 | 0.00 |
| Set-A_P09 | 458.45 | 458.48 | 0.01 | -0.03 | 0.03 | 458.33 | 0.02 | 0.12 | 0.12 |
| Set-A_P10 | 458.51 | 458.78 | 0.04 | -0.27 | 0.27 | 458.74 | 0.04 | -0.23 | 0.23 |
| Set-A_P11 | 458.67 | 458.82 | 0.01 | -0.15 | 0.15 | 458.28 | 0.02 | 0.38 | 0.38 |
| Set-A_P12 | 458.52 | 458.52 | 0.01 | -0.01 | 0.01 | 458.46 | 0.01 | 0.06 | 0.06 |
| Set-A_P13 | 458.57 | 458.57 | 0.02 | 0.00 | 0.00 | 458.60 | 0.01 | -0.03 | 0.03 |
| Set-A_P14 | 459.47 | 459.56 | 0.02 | -0.09 | 0.09 | 459.65 | 0.01 | -0.18 | 0.18 |
| Set-A_P15 | 458.62 | 458.66 | 0.02 | -0.04 | 0.04 | 458.58 | 0.02 | 0.04 | 0.04 |
| Set-A_P16 | 457.32 | 457.29 | 0.01 | 0.02 | 0.02 | 457.18 | 0.01 | 0.14 | 0.14 |
| Set-A_P17 | 458.25 | 458.27 | 0.01 | -0.02 | 0.02 | 458.32 | 0.01 | -0.08 | 0.08 |
| Set-A_P18 | 458.01 | 458.03 | 0.01 | -0.01 | 0.01 | 457.81 | 0.01 | 0.21 | 0.21 |
| Set-A_P19 | 457.83 | 457.84 | 0.01 | -0.01 | 0.01 | 457.51 | 0.02 | 0.33 | 0.33 |
| Set-A_P20 | 458.64 | 458.64 | 0.02 | 0.00 | 0.00 | 458.68 | 0.04 | -0.05 | 0.05 |
| Mean | 0.05 | 0.13 | |||||||
| SD | 0.07 | 0.11 | |||||||
| Set-B_P01 | 458.26 | 458.19 | 0.03 | 0.07 | 0.07 | 458.22 | 0.02 | 0.04 | 0.04 |
| Set-B_P02 | 458.12 | 458.13 | 0.01 | -0.01 | 0.01 | 458.13 | 0.02 | -0.01 | 0.01 |
| Set-B_P03 | 456.53 | 456.57 | 0.01 | -0.04 | 0.04 | 456.32 | 0.02 | 0.20 | 0.20 |
| Set-B_P04 | 458.01 | 458.01 | 0.01 | 0.00 | 0.00 | 457.81 | 0.01 | 0.20 | 0.20 |
| Set-B_P05 | 459.93 | 459.95 | 0.02 | -0.03 | 0.03 | 460.06 | 0.02 | -0.14 | 0.14 |
| Set-B_P06 | 459.92 | 459.95 | 0.03 | -0.03 | 0.03 | 459.86 | 0.03 | 0.06 | 0.06 |
| Set-B_P07 | 461.09 | 461.12 | 0.03 | -0.03 | 0.03 | 461.10 | 0.01 | -0.01 | 0.01 |
| Set-B_P08 | 459.13 | 459.12 | 0.02 | 0.00 | 0.00 | 458.81 | 0.02 | 0.32 | 0.32 |
| Set-B_P09 | 458.66 | 458.59 | 0.03 | 0.07 | 0.07 | 458.66 | 0.02 | 0.00 | 0.00 |
| Set-B_P10 | 458.58 | 458.61 | 0.01 | -0.04 | 0.04 | 458.38 | 0.03 | 0.20 | 0.20 |
| Set-B_P11 | 459.27 | 459.28 | 0.02 | -0.01 | 0.01 | 459.30 | 0.02 | -0.03 | 0.03 |
| Set-B_P12 | 458.75 | 458.77 | 0.02 | -0.02 | 0.02 | 458.80 | 0.01 | -0.05 | 0.05 |
| Set-B_P13 | 458.48 | 458.50 | 0.01 | -0.02 | 0.02 | 458.53 | 0.02 | -0.06 | 0.06 |
| Set-B_P14 | 457.23 | 457.24 | 0.01 | -0.02 | 0.02 | 457.07 | 0.01 | 0.16 | 0.16 |
| Set-B_P15 | 458.39 | 458.40 | 0.01 | -0.01 | 0.01 | 458.28 | 0.02 | 0.11 | 0.11 |
| Set-B_P16 | 458.46 | 458.47 | 0.01 | -0.01 | 0.01 | 458.34 | 0.03 | 0.11 | 0.11 |
| Set-B_P17 | 458.61 | 458.71 | 0.02 | -0.10 | 0.10 | 458.81 | 0.03 | -0.21 | 0.21 |
| Set-B_P18 | 459.38 | 459.45 | 0.01 | -0.07 | 0.07 | 459.39 | 0.02 | -0.01 | 0.01 |
| Mean | 0.03 | 0.11 | |||||||
| SD | 0.03 | 0.09 | |||||||
DownLoad: CSV| Reference data sets | DEMTLS | DEMUAV | |||||||
| Name | Z (m) | Height (m) | SD (m) | Diff. (m) | Abs. Diff. (m) | Height (m) | SD (m) | Diff. (m) | Abs. Diff. (m) |
| Set-A_P01 | 459.97 | 459.93 | 0.02 | 0.04 | 0.04 | 459.87 | 0.03 | 0.10 | 0.10 |
| Set-A_P02 | 460.43 | 460.28 | 0.04 | 0.16 | 0.16 | 460.18 | 0.03 | 0.26 | 0.26 |
| Set-A_P03 | 460.89 | 460.88 | 0.02 | 0.01 | 0.01 | 460.94 | 0.02 | -0.05 | 0.05 |
| Set-A_P04 | 458.55 | 458.60 | 0.02 | -0.05 | 0.05 | 458.52 | 0.01 | 0.02 | 0.02 |
| Set-A_P05 | 458.62 | 458.66 | 0.04 | -0.04 | 0.04 | 458.42 | 0.02 | 0.20 | 0.20 |
| Set-A_P06 | 461.19 | 461.23 | 0.02 | -0.04 | 0.04 | 461.17 | 0.02 | 0.03 | 0.03 |
| Set-A_P07 | 459.75 | 459.77 | 0.02 | -0.02 | 0.02 | 459.74 | 0.01 | 0.02 | 0.02 |
| Set-A_P08 | 459.00 | 459.07 | 0.01 | -0.06 | 0.06 | 459.00 | 0.01 | 0.00 | 0.00 |
| Set-A_P09 | 458.45 | 458.48 | 0.01 | -0.03 | 0.03 | 458.33 | 0.02 | 0.12 | 0.12 |
| Set-A_P10 | 458.51 | 458.78 | 0.04 | -0.27 | 0.27 | 458.74 | 0.04 | -0.23 | 0.23 |
| Set-A_P11 | 458.67 | 458.82 | 0.01 | -0.15 | 0.15 | 458.28 | 0.02 | 0.38 | 0.38 |
| Set-A_P12 | 458.52 | 458.52 | 0.01 | -0.01 | 0.01 | 458.46 | 0.01 | 0.06 | 0.06 |
| Set-A_P13 | 458.57 | 458.57 | 0.02 | 0.00 | 0.00 | 458.60 | 0.01 | -0.03 | 0.03 |
| Set-A_P14 | 459.47 | 459.56 | 0.02 | -0.09 | 0.09 | 459.65 | 0.01 | -0.18 | 0.18 |
| Set-A_P15 | 458.62 | 458.66 | 0.02 | -0.04 | 0.04 | 458.58 | 0.02 | 0.04 | 0.04 |
| Set-A_P16 | 457.32 | 457.29 | 0.01 | 0.02 | 0.02 | 457.18 | 0.01 | 0.14 | 0.14 |
| Set-A_P17 | 458.25 | 458.27 | 0.01 | -0.02 | 0.02 | 458.32 | 0.01 | -0.08 | 0.08 |
| Set-A_P18 | 458.01 | 458.03 | 0.01 | -0.01 | 0.01 | 457.81 | 0.01 | 0.21 | 0.21 |
| Set-A_P19 | 457.83 | 457.84 | 0.01 | -0.01 | 0.01 | 457.51 | 0.02 | 0.33 | 0.33 |
| Set-A_P20 | 458.64 | 458.64 | 0.02 | 0.00 | 0.00 | 458.68 | 0.04 | -0.05 | 0.05 |
| Mean | 0.05 | 0.13 | |||||||
| SD | 0.07 | 0.11 | |||||||
| Set-B_P01 | 458.26 | 458.19 | 0.03 | 0.07 | 0.07 | 458.22 | 0.02 | 0.04 | 0.04 |
| Set-B_P02 | 458.12 | 458.13 | 0.01 | -0.01 | 0.01 | 458.13 | 0.02 | -0.01 | 0.01 |
| Set-B_P03 | 456.53 | 456.57 | 0.01 | -0.04 | 0.04 | 456.32 | 0.02 | 0.20 | 0.20 |
| Set-B_P04 | 458.01 | 458.01 | 0.01 | 0.00 | 0.00 | 457.81 | 0.01 | 0.20 | 0.20 |
| Set-B_P05 | 459.93 | 459.95 | 0.02 | -0.03 | 0.03 | 460.06 | 0.02 | -0.14 | 0.14 |
| Set-B_P06 | 459.92 | 459.95 | 0.03 | -0.03 | 0.03 | 459.86 | 0.03 | 0.06 | 0.06 |
| Set-B_P07 | 461.09 | 461.12 | 0.03 | -0.03 | 0.03 | 461.10 | 0.01 | -0.01 | 0.01 |
| Set-B_P08 | 459.13 | 459.12 | 0.02 | 0.00 | 0.00 | 458.81 | 0.02 | 0.32 | 0.32 |
| Set-B_P09 | 458.66 | 458.59 | 0.03 | 0.07 | 0.07 | 458.66 | 0.02 | 0.00 | 0.00 |
| Set-B_P10 | 458.58 | 458.61 | 0.01 | -0.04 | 0.04 | 458.38 | 0.03 | 0.20 | 0.20 |
| Set-B_P11 | 459.27 | 459.28 | 0.02 | -0.01 | 0.01 | 459.30 | 0.02 | -0.03 | 0.03 |
| Set-B_P12 | 458.75 | 458.77 | 0.02 | -0.02 | 0.02 | 458.80 | 0.01 | -0.05 | 0.05 |
| Set-B_P13 | 458.48 | 458.50 | 0.01 | -0.02 | 0.02 | 458.53 | 0.02 | -0.06 | 0.06 |
| Set-B_P14 | 457.23 | 457.24 | 0.01 | -0.02 | 0.02 | 457.07 | 0.01 | 0.16 | 0.16 |
| Set-B_P15 | 458.39 | 458.40 | 0.01 | -0.01 | 0.01 | 458.28 | 0.02 | 0.11 | 0.11 |
| Set-B_P16 | 458.46 | 458.47 | 0.01 | -0.01 | 0.01 | 458.34 | 0.03 | 0.11 | 0.11 |
| Set-B_P17 | 458.61 | 458.71 | 0.02 | -0.10 | 0.10 | 458.81 | 0.03 | -0.21 | 0.21 |
| Set-B_P18 | 459.38 | 459.45 | 0.01 | -0.07 | 0.07 | 459.39 | 0.02 | -0.01 | 0.01 |
| Mean | 0.03 | 0.11 | |||||||
| SD | 0.03 | 0.09 | |||||||
