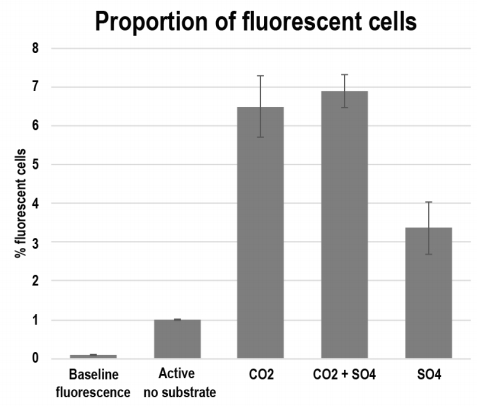
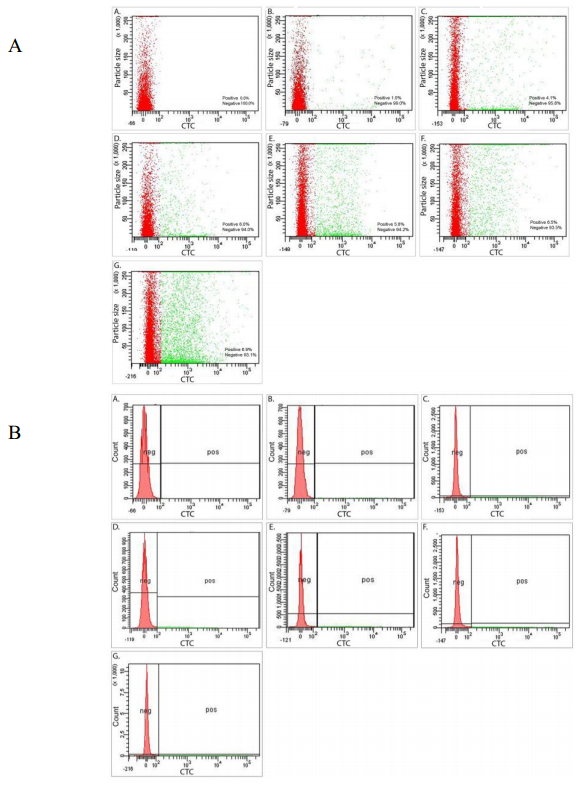
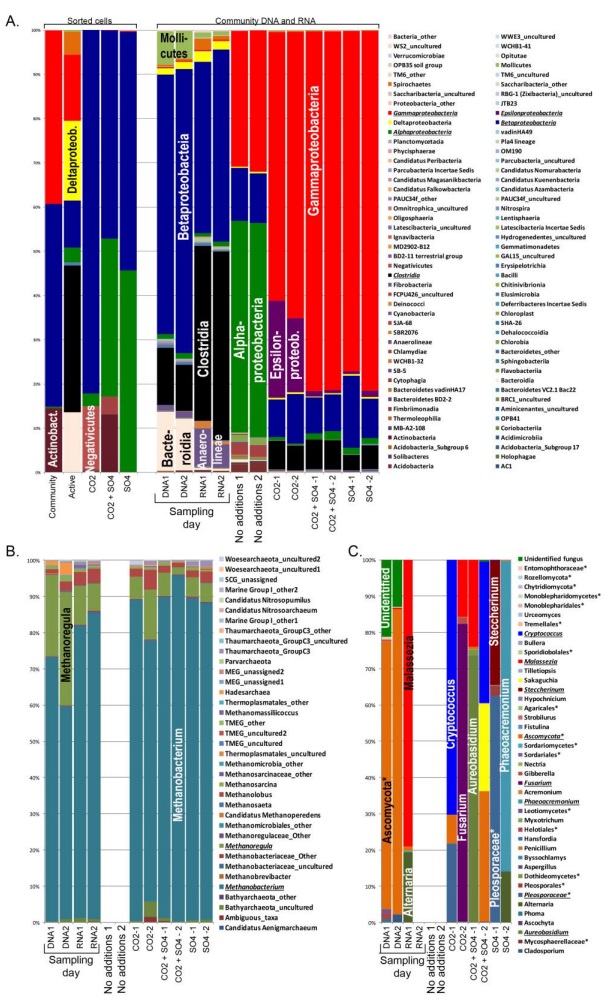
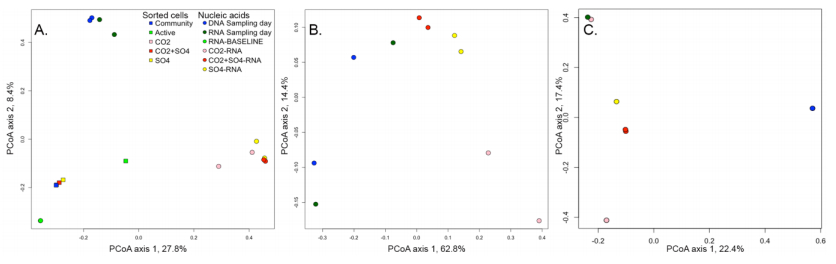
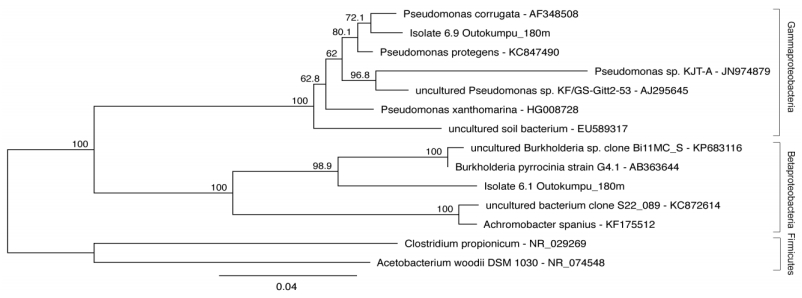
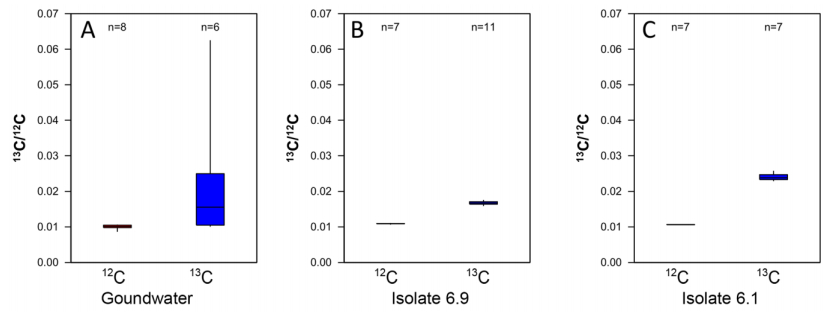
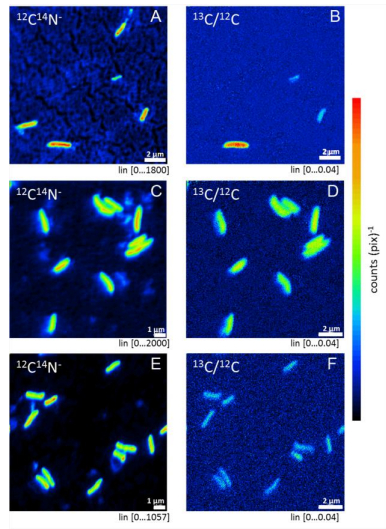
Microbial communities in deep subsurface environments comprise a large portion of Earth’s biomass, but the metabolic activities in these habitats are largely unknown. Here the effect of CO2 and carbonate on the microbial community of an isolated groundwater fracture zone at 180 m depth of the Outokumpu Deep Scientific Drill Hole (Finland) was tested. Outokumpu groundwater at 180 m depth contains approximately 0.45 L L−1 dissolved gas of which methane contributes 76%. CO2, on the other hand, is scarce. The number of microbial cells with intracellular activity in the groundwater was low when examined with redox staining. Fluorescence Assisted Cell Sorting (FACS) analyses indicated that only 1% of the microbial community stained active with the redox sensing dye in the untreated groundwater after 4 weeks of starvation. However, carbon substrate and sulfate addition increased the abundance of fluorescent cells up to 7%. CO2 and CO2 + sulfate activated the greatest number of microbes, especially increasing the abundance of Pseudomonas sp., which otherwise was present at only low abundance in Outokumpu. Over longer exposure time (2 months) up to 50% of the bacterial cells in the groundwater were shown to incorporate inorganic carbon from carbonate into biomass. Carbon recapture is an important feature in this ecosystem since it may decrease the rate of carbon loss in form of CO2 released from cellular processes.
1.
Introduction
Let A be an Abelian variety of dimension g, and let X⊂A be a smooth ample hypersurface in A such that the Chern class c1(X) of the divisor X is a polarization of type ¯d:=(d1,d2,…,dg), so that the vector space H0(A,OA(X)) has dimension equal to the Pfaffian d:=d1⋅⋯⋅dg of c1(X).
The classical results of Lefschetz [13] say that the rational map associated to H0(A,OA(X)) is a morphism if d1≥2, and is an embedding of A if d1≥3.
There have been several improvements in this direction, by work of several authors, for instance [15] showed that for d1≥2 we have an embedding except in a very special situation, and, for progress in the case d1=1, see for instance [14], [9].
Now, by adjunction, the canonical sheaf of X is the restriction OX(X), so a natural generalization of Lefschetz' theorems is to ask about the behaviour of the canonical systems of such hypersurfaces X. Such a question is important in birational geometry, but the results for the canonical maps can depend on the hypersurface X and not just on the polarization type only.
We succeed in this paper to find (respectively: conjecture) simple results for general such hypersurfaces.
Our work was motivated by a theorem obtained by the first author in a joint work with Schreyer [4] on canonical surfaces: if we have a polarization of type (1,1,2) then the image Σ of the canonical map ΦX is in general a surface of degree 12 in P3, birational to X, while for the special case where X is the pull-back of the Theta divisor of a curve of genus 3, then the canonical map has degree 2, and Σ has degree 6.
The connection of the above result with the Lefschetz theorems is, as we already said, provided by adjunction, we have the following folklore result, a proof of which can be found for instance in [6] (a referee pointed out that the proof in the case of a principal polarization appears in 2.10 of [12], and that of course Green's proof works in general)
Lemma 1.1. Let X be a smooth ample hypersurface of dimension n in an Abelian variety A, such that the class of X is a polarization of type ¯d:=(d1,d2,…,dn+1).
Let θ1,…,θd be a basis of H0(A,OA(X)) such that X={θ1=0}.
If z1,…,zg are linear coordinates on the complex vector space V such that A is the quotient of V by a lattice Λ, A=V/Λ, then the canonical map ΦX is given by
Hence first of all the canonical map is an embedding if H0(A,OA(X)) yields an embedding of A; secondly, since a projection of ΦX is the Gauss map of X, given by (∂θ1∂z1,…,∂θ1∂zg), by a theorem of Ziv Ran [18] it follows that the canonical system |KX| is base-point-free and ΦX a finite morphism.
This is our main result:
Theorem 1.2. Let (A,X) be a general pair, consisting of a hypersurface X of dimension n=g−1 in an Abelian variety A, such that the class of X is a polarization of type ¯d:=(d1,d2,…,dg) with Pfaffian d=d1…dg>1.
Then the canonical map ΦX of X is birational onto its image Σ.
The first observation is: the hypothesis that we take a general such pair, and not any pair, is necessary in view of the cited result of [4].
The second observation is that the above result extends to more general situations, using a result on openness of birationality (this will be pursued elsewhere). This allows another proof of the theorem, obtained studying pull-backs of Theta divisors of hyperelliptic curves (observe that for Jacobians the Gauss map of the Theta divisor is a rational map, see [7] for a study of its degree).
Here we use the following nice result by Olivier Debarre [8]:
Theorem 1.3. Let Θ⊂A′ be the Theta divisor of a general principally polarized Abelian variety A′: then the Gauss map of Θ, ψ:Θ→P:=Pg−1 factors through Y:=Θ/±1, and yields a generic covering Ψ:Y→P, meaning that
1. The branch divisor B⊂P of Ψ is irreducible and reduced;
2. The ramification divisor of Ψ, R⊂Y, maps birationally to B;
3. the local monodromies of the covering at the general points of B are transpositions;
4. the Galois group of Ψ (the global monodromy group of the covering Ψ) is the symmetric group SN, where N=(12g!).
The next question to which the previous result paves the way is: when is ΦX an embedding for (A,X) general?
An elementary application of the Severi double point formula [19] (see also [10], [2]) as an embedding obstruction, yields a necessary condition (observe that a similar argument was used by van de Ven in [20], in order to study the embeddings of Abelian varieties).
Theorem 1.4. Let X⊂A be a smooth ample hypersurface in an Abelian variety of dimension g, giving a polarization with Pfaffian d.
If the canonical map ΦX is an embedding of X, then necessarily
With some optimism (hoping for a simple result), but relying on the highly non-trivial positive result of the second author [6] concerning polarizations of type (1,2,2) (here g=3, d=4), and on the result by Debarre and others [9] that this holds true for polarizations of type (1,…,1,d) with d>2g, we pose the following conjecture:
Conjecture 1. Assume that (A,X) is a general pair of a smooth ample hypersurface X⊂A in an Abelian variety A, giving a polarization with Pfaffian d satisfying d≥g+1.
Then the canonical map ΦX is an embedding of X.
We end the paper discussing the conjecture.
2.
Proof of the main theorem 1.2
We give first a quick outline of the strategy of the proof.
The first step 2.1 reduces to the case where the Pfaffian d of the polarization type is a prime number p.
Step 2.2 considers the particular case where d=p and where X is the pull-back of the Theta divisor Θ of a principally polarized Abelian variety. In this case the Gauss map of X factors through Y:=Θ/±1.
Step 2.3 shows that if g=dim(A)=2, then Step 2.2 works and the theorem is proven.
Step 2.4, the Key Step, shows that if g≥3 and 2.2 does not work, then the image Σ of the canonical map lies birationally between X and Y, hence corresponds to a subgroup of the dihedral group Dp
Step 2.5 finishes the proof, showing that, in each of the two possible cases corresponding to the subgroups of Dp, the canonical map becomes birational onto its image for a general deformation of X.
2.1. Reduction to the case of a polarization of type (1,…,1,p), with p a prime number
We shall proceed by induction, basing on the following concept.
We shall say that a polarization type ¯d:=(d1,d2,…,dg) is divisible by ¯δ:=(δ1,δ2,…,δg) if, for all i=1,…,g, we have that δi divides di, di=riδi.
Lemma 2.1. Assume that the polarization type ¯d is divisible by ¯δ. Then, if the main Theorem 1.2 holds true for ¯δ, then it also holds true for ¯d.
Proof. We let (A′,X′) be a general pair giving a polarization of type ¯δ, so that ΦX′ is birational.
There exists an étale covering A→A′, with kernel ≅⊕i(Z/ri), such that the pull back of X′ is a polarization of type ¯d.
By induction, we may assume without loss of generality that all numbers ri=1, with one exception rj, which is a prime number p.
Then we have π:X→X′, which is an étale quotient with group Z/p. Moreover, since the canonical divisor KX is the pull-back of KX′, the composition ΦX′∘π factors through ΦX, and a morphism f:Σ→Σ′.
Since by assumption ΦX′ is birational, either ΦX is birational, and there is nothing to prove, or ΦX has degree p, f:Σ→Σ′ is birational, hence ΦX factors (birationally) through π.
To contradict the second alternative, it suffices to show that the canonical system H0(X,OX(KX)) separates the points of a general fibre of π. Since each fibre is an orbit for the group Z/p, it suffices to show that there are at least two different eigenspaces in the vector space H0(X,OX(KX)), with respective eigenvalues 1, ζ, where ζ is a primitive p-th root of unity.
Since then we would have as projection of the canonical map a rational map F:X⇢P1 such that, for g∈Z/p,
thereby separating the points of a general fibre.
Now, if there were only one non-zero eigenspace, the one for the eigenvalue 1, since we have an eigenspace decomposition
(here η is a nontrivial divisor of p-torsion), all eigenspaces would have dimension zero, except for the case i=p. In particular we would have that H0(X,OX(KX)) and H0(X′,OX′(KX′)) have the same dimension.
But this is a contradiction, since the dimension h0(X,OX(KX)) equals by lemma 1.1 the sum of the Pfaffian of X with g−1, and the Pfaffian of X is p-times the Pfaffian of X′.
2.2. The special case where X is a pull-back of a Theta divisor
Here, we shall consider a similar situation, assuming that X is a polarization of type (1,…,1,p), and that X is the pull back of a Theta divisor Θ⊂A′ via an isogeny A→A′ with kernel ≅Z/p.
We define Y:=Θ/±1 and use the cited result of Debarre [8].
We consider the Gauss map of X, f:X→P:=Pg−1, and observe that we have a factorization
The essential features are that:
(i) ϕ is a Galois quotient Y=X/G, where G is the dihedral group Dp.
(ii) Ψ is a generic map, in particular with monodromy group equal to SN, N=g!/2.
Either the theorem is true, or, by contradiction, we have a factorization of f through ΦX:X→Σ, whose degree m satisfies 2pN>m≥2.
2.3. Warm-up case: g=2, X defines a polarization of type (1,p) with p a prime number
In this case X is a Z/p étale covering of a genus 2 curve C=Θ, and X/G=P1.
That the canonical map of X is not birational means that X is hyperelliptic, and then f:X→P1 factors through the quotient of the hyperelliptic involution ι, which centralizes G. If we set Σ:=X/ι≅P1, we see that Σ corresponds to a subgroup of order two of G: since ι centralizes G, and is not contained in Z/p, follows that G is abelian, whence p=2.
We prove here a result which might be known (but we could not find it in [1]; a referee points out that, under the stronger assumption that A is also general, such a result is proven in [17] and in [16]).
Lemma 2.2. The general divisor in a linear system |X| defining a polarization of type (1,2) is not hyperelliptic.
Proof. In this case of a polarization of type (1,2), the linear system |X| on A is a pencil of genus 3 curves with 4 distinct base points, as we now show.
We consider, as before, the inverse image D of a Theta divisor for g=2, which will be here called C, so that A′=J(C).
The curve D is hyperelliptic, being a Galois covering of P1 with group G=(Z/2)2 (a so-called bidouble cover), fibre product of two coverings respectively branched on 2,4 points (hence D=E×P1P1, where E is an elliptic curve, and C is the quotient of D by the diagonal involution). The divisor cut by H0(A,OA(X)) on X is the ramification divisor of X→E, hence it consists of 4 distinct points.
The double covering D→E of an elliptic curve is also induced by the homomorphism J(D)→E, with kernel isogenous to A′. Therefore, moving X in the linear system |D|, all these curves are a double cover of some elliptic curve E′, such that J(X) is isogenous to A×E′.
Hence E′=X/σ, where σ is an involution.
Assume now that X is hyperelliptic and denote by ι the hyperelliptic involution: since ι is central, ι and σ generate a group G≅(Z/2)2, and we claim that the quotient of the involution ι∘σ yields a genus 2 curve C′ as quotient of X. In fact, the quotient X/G≅P1, hence we have a bidouble cover of P1 with branch loci of respective degrees 2,4 and the quotient C′ is a double covering of P1 branched in 6 points.
Hence the hyperelliptic curves in |D| are just the degree 2 étale coverings of genus 2 curves, and are only a finite number in |D| (since J(C′) is isogenous to A).
2.4. We proceed with the Key Step: Showing that birationally Σ must lie between X and Y
2.4.1. To achieve this we need to recall some basic facts about covering spaces
We shall use the Grauert-Remmert [11] extension of Riemann's theorem, stating that finite coverings X→Y between normal varieties correspond to covering spaces X0→Y0 between respective Zariski open subsets of X, resp. Y.
Remark 1. Given a connected unramified covering X→Y between good spaces, we let ˜X be the universal covering of X, and we write X=H∖˜X, Y=Γ∖˜X, hence x∈X as x=H ˜x, y∈Y as y=Γ ˜x, where both groups act on the left.
(1) Then the group of covering trasformations
where NH is the normalizer subgroup of H in Γ.
(2) The monodromy group Mon(X→Y), also called the Galois group of the covering in [8], is defined as Γ/core(H), where core(H) is the maximal normal subgroup of Γ contained in H,
which is also called the normal core of H in Γ.
(3) The two actions of the two above groups on the fibre over Γ˜x, namely H∖Γ≅{Hγ˜x|γ∈Γ}, commute, since G acts on the left, and Γ acts on the right (the two groups coincide exactly when H is a normal subgroup of Γ, and we have what is called a normal covering space, or a Galois covering).
We have in fact an antihomomorphism
with kernel core(H).
(4) Factorizations of the covering X→Y correspond to intermediate subgroups H′ lying in between, H⊂H′⊂Γ.
2.4.2. Our standard situation
We consider the composition of finite coverings X→Y→P.
To simplify our notation, we consider the corresponding composition of unramified covering spaces of Zariski open sets, and the corresponding fundamental groups
Then the monodromy group of the Gauss map of X is the quotient Γ1/core(K1).
We shall now divide all the above groups by the normal subgroup core(K1), and obtain
Since X→Y is Galois, and by Debarre's theorem Y→P is a generic covering, we have:
● we have a surjection of the monodromy group Γ→SN:=S(H∖Γ) with kernel core(H), where N=|H∖Γ|=g!2.
● H is the inverse image of a stabilizer, hence H maps onto SN−1,
● H is a maximal subgroup of Γ, since SN−1 is a maximal subgroup of SN;
● H/K≅G:=Dp,
● Γ acts on the fibre M:=K∖Γ
● K′:=K∩core(H) is normal in K, and K″:=K/K′ maps isomorphically to a normal subgroup of SN−1, which is a quotient of G, hence it has index at most 2p. Therefore there are only two possibilities:
(I) K″=SN−1, or
(II) K″=AN−1.
We consider now the case where there is a nontrivial factorization of the Gauss map f, X→Σ→P.
Define ˆH to be the subgroup of the monodromy group Γ associated to Σ, so that
and set:
Obviously we have K″⊂H″: hence
● in case (I), where K″=SN−1, we have either
(Ia) H″=SN−1 or
(Ib) H″=SN, while
● in case (II), where K″=AN−1, either
(IIa) H″=AN−1,
(IIb) H″=AN, or
(IIc) H″=SN
We first consider cases b) and c) where the index of H″ in SN is ≤2. Hence the index of ˆH in Γ is at most 2 times the index of H′ in core(H). Since K′⊂H′, and core(H)/K′ is a quotient of H/K, we see that the index of ˆH in Γ divides 2p (in fact, in case (IIb) K″=AN−1, hence in this case the cardinality of core(H)/K′ equals p).
Lemma 2.3. Cases (b) and (c), where the degree m of the covering Σ→P divides 2p, are not possible.
Proof. Observe in fact that m equals the index of ˆH in Γ. We have two factorizations of the Gauss map f:
hence we have that the degree of f equals
Consider now the respective ramification divisors Rf,R=RY,RΣ of the respective maps f:X→P, Ψ:Y→P, Σ→P.
Since X→Y is quasi-étale (unramified in codimension 1), Rf is the inverse image of R, hence Rf maps to the branch locus B with mapping degree 2p.
Since the branch locus is known to be irreducible, and reduced, and RΣ is non empty, it follows that X→Σ is quasi-étale, and Rf is the inverse image of RΣ, so that Rf maps to the branch locus B with mapping degree (N2pm)δ, where δ is the mapping degree of RΣ to B, which is at most p.
From the equality 2p=δN(2pm) and since N=g!/2, we see that g! divides 4p, which is absurd for g≥4. For g=3 it follows that p=3, and either δ=2, m=6, or δ=1, and m=3.
To show that these special cases cannot occur, we can use several arguments.
For the case m=3, then Σ is a nondegenerate surface of degree 3 in P4 (hence it is by the way the Segre variety P2×P1), and has a linear projection to P2 of degree 3: hence its branch locus is a curve of degree 6, contradicting that B has degree 12 (see [4], B is the dual curve of the plane quartic curve whose Jacobian is A′).
For the case m=6, we consider the normalization of the fibre product
so that there is a morphism of X into Z, which we claim to be birational. In fact, the degree of the map Z→P is 18, and each component Zi of Z is a covering of Σ; therefore, if Z is not irreducible, there is a component Zi mapping to P with degree 6: and the conclusion is that Σ→P factors through Y, which is what we wanted to happen, but assumed not to happen.
If Z is irreducible, then X is birational to Z, hence the group G acts on Z, and trivially on Y: follows that the fibres of X→Σ are G-orbits, whence Y=Σ, again a contradiction.
Remark 2. Indeed, we know ([4]) that the monodromy group of Θ→P is S4, and one could describe explicitly Γ in relation to the series of inclusions
where K1 is the subgroup associated to Θ.
At any rate, if m=3, we can take the normalization of the fibre product W:=Θ×PΣ, and argue as before that if W is reducible, then Θ dominates Σ, which is only possible if Σ=Y.
While, if W is irreducible, W=X and the fibres of X→Σ are made of Z/3-orbits, hence again Θ dominates Σ.
Excluded cases (b) and (c), we are left with case (a), where
equivalently Σ lies between X and Y, hence it corresponds to an intermediate subgroup of G=Dp, either Z/p and then Σ=Θ, or Z/2, and then Σ=X/±1 for a proper choice of the origin in the Abelian variety A.
2.5. In the case where Σ lies between X and Y, for a general deformation of X the canonical map becomes birational
Here, we can soon dispense of the case Σ=Θ: just using exactly the same argument we gave in lemma 2.1, that Z/p does not act on H0(X,OX(KX)) as the identity, so the fibres of X→Θ are separated.
For the case where Σ=X/(Z/2) we need to look at the vector space H0(X,OX(KX)), which is a p-dimensional representation of Dp, where we have a basis θ1,…,θp of eigenvectors for the different characters of Z/p. In other words, for a generator r of Z/p, we must have
If s is an element of order 2 in the dihedral group, then r∘s=s∘r−1, hence
hence we may assume without loss of generality that
It is then clear that s does not act as the identity unless we are in the special case p=2.
In the special case p=2, we proceed as in [4]. We have a basis θ1,θ2 of even functions, i.e., such that θi(−z)=θi(z), and Θ=X/(Z/2)2, where (Z/2)2 acts sending z↦±z+η, where η is a 2-torsion point on A. Since the partial derivatives of θ1 are invariant for z↦z+η, and since θ2(z+η)=−θ2(z), the canonical map ΦX factors through the involution ι:X→X such that
If for a general deformation of X as a symmetric divisor the canonical map would factor through ι, then X would be ι-invariant; being symmetric, it would be (Z/2)2-invariant, hence for all deformations X would remain the pull-back of a Theta divisor. This is a contradiction, since the Kuranishi family of X has higher dimension than the Kuranishi family of a Theta divisor Θ (see [4]).
3.
Embedding obstruction
Theorem 3.1. Let X be an ample smooth divisor in an Abelian variety A of dimension n+1.
Assume moreover that X is not a hyperelliptic curve of genus 3 yielding a polarization of type (1,2).
If X defines a polarization of type (m1,…,mn+1), then the canonical map ΦX of X is a morphism, and it can be an embedding only if pg(X):=h0(KX)≥2n+2, which means that the Pfaffian d:=m1⋅m2⋯⋅mn+1 satisfies the inequality
Proof. Assume the contrary, d≤n+1, so that X embeds in Pn+c, with codimension c≤n, c=d−1.
Observe that the pull back of the hyperplane class of Pn+c is the divisor class of X restricted to X, and that the degree m of X equals to the maximal self-intersection of X in A, namely m=Xn+1=d(n+1)!.
The Severi double point formula yields see ([10], also [5])
where Φ is the composition of ΦX with a linear embedding Pn+c↪P2n.
By virtue of the exact sequence
we obtain
To have a quick proof, let us also apply the double point formula to the section of X = \Phi (X) with a linear subspace of codimension (n-d+1) , which is a variety Y of dimension and codimension (d-1) inside {\mathbb{P}}^{2d-2} .
In view of the exact sequence
we obtain
equivalently,
Since, for d \leq n+1 , {n + d + 1 \choose d-1} \leq {2n+2 \choose n} , equality holding if and only if d = n+1 , we should have d = n+1 and moreover
We have equality for n = 1 , but then when we pass from n to n+1 the left hand side gets multiplied by (n+3) , the right hand side by \frac{(2n+4)(2n+3) }{ (n+2)^2} , which is a strictly smaller number since
We are done with showing the desired assertion since we must have n = 1 , and d = 2 , and in the case n = 1 , d = 2 we have a curve in {\mathbb{P}}^2 of degree 4 and genus 3 .
4.
Remarks on the conjecture
Recall Conjecture 1:
Conjecture 2. Assume that (A,X) is a general pair of a smooth ample hypersurface X\subset A in an Abelian variety A , giving a polarization with Pfaffian d satisfying d \geq g + 1.
Then the canonical map \Phi_X is an embedding of X .
The first observation is that we can assume g \geq 3 , since for a curve the canonical map is an embedding if and only if it is birational onto its image, hence we may apply here our main Theorem 1.2.
The second remark is that we have a partial result which is similar to lemma 2.1
Lemma 4.1. Assume that the polarization type \overline{d} is divisible by \overline{ \delta} . Then, if the embedding Conjecture 1 holds true for \overline{ \delta} , and the linear system |X'| is base point free for the general element X' yielding a polarization of type \overline{ \delta} , then the embedding conjecture also holds true for \overline{d} .
Proof. As in lemma 2.1 we reduce to the following situation: we have \pi : X {\rightarrow } X' , which is an étale quotient with group {\mathbb{Z}}/p . Moreover, since the canonical divisor K_X is the pull-back of K_{X'} , the composition \Phi_{X'} \circ \pi factors through \Phi_X , and a morphism f : \Sigma {\rightarrow } \Sigma' .
Since by assumption \Phi_{X'} is an embedding, \Phi_X is a local embedding at each point, and it suffices to show that \Phi_X separates all the fibres.
Recalling that
(here \eta is a nontrivial divisor of p -torsion), this follows immediately if we know that for each point p \in X' there are two distinct eigenspaces which do not have p as a base-point.
Under our strong assumption |K_{X'} + i \eta | contains the restriction of |X' + i \eta | to X' , but |X' + i \eta | is a translate of |X'| , so it is base-point free.
Already in the case of surfaces ( n = 2, g = 3 ) the result is not fully established, we want d \geq 4 , and the case of a polarization of type (1,1,4) is not yet written down ([6] treats the case of a polarization of type (1,2,2) , which is quite interesting for the theory of canonical surfaces in {\mathbb{P}}^5 ).
Were our conjecture too optimistic, then the question would arise about the exact range of validity for the statement of embedding of a general pair (X,A) .
Acknowledgments
the first author would like to thank Edoardo Sernesi and Michael Lönne for interesting conversations. Thanks to the second referee for useful suggestions on how to improve the exposition.













 DownLoad:
DownLoad: