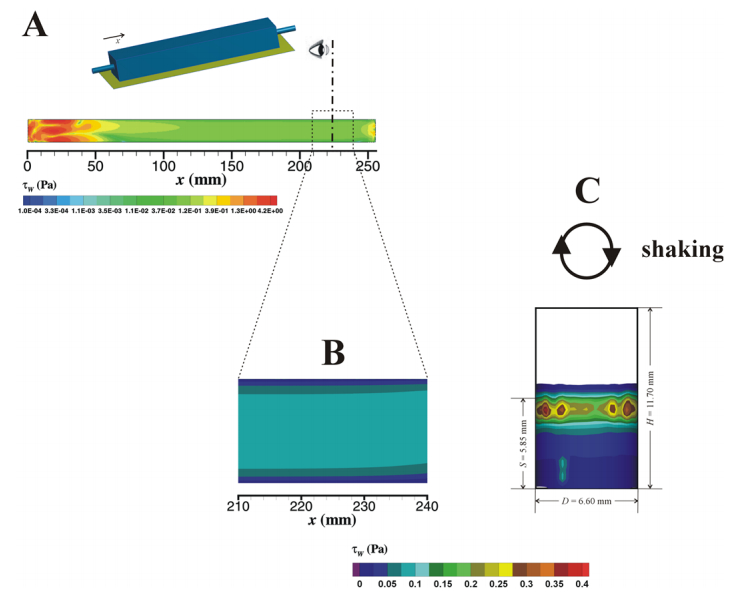
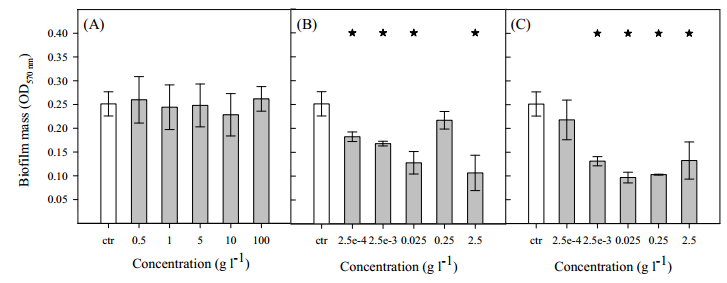
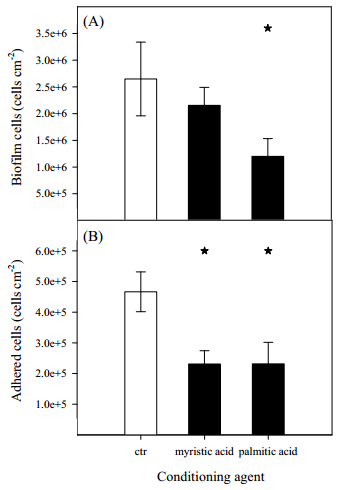
Bacterial adhesion and biofilm formation on food processing surfaces pose major risks to human health. Non-efficient cleaning of equipment surfaces and piping can act as a conditioning layer that affects the development of a new biofilm post-disinfection. We have previously shown that surface conditioning with cell extracts could reduce biofilm formation. In the present work, we hypothesized that E. coli cell wall components could be implicated in this phenomena and therefore mannose, myristic acid and palmitic acid were tested as conditioning agents. To evaluate the effect of surface conditioning and flow topology on biofilm formation, assays were performed in agitated 96-well microtiter plates and in a parallel plate flow chamber (PPFC), both operated at the same average wall shear stress (0.07 Pa) as determined by computational fluid dynamics (CFD). It was observed that when the 96-well microtiter plate and the PPFC were used to form biofilms at the same shear stress, similar results were obtained. This shows that the referred hydrodynamic feature may be a good scale-up parameter from high-throughput platforms to larger scale flow cell systems as the PPFC used in this study. Mannose did not have any effect on E. coli biofilm formation, but myristic and palmitic acid inhibited biofilm development by decreasing cell adhesion (in about 50%). These results support the idea that in food processing equipment where biofilm formation is not critical below a certain threshold, bacterial lysis and adsorption of cell components to the surface may reduce biofilm buildup and extend the operational time.
1.
Introduction
Groundnut (Arachis hypogaea L.) is a very important grain legume crop cultivated for home consumption and market in the semi-arid tropics of West and Central Africa (WCA). The region accounts for about 65 percent of Africa's groundnut area and more than 70 percent of the continent's groundnut production [1]. Nigeria, Senegal, Mali, Burkina Faso, Ghana, Chad, and Niger are the top producers, with smallholder farmers producing the majority of the crop. It is considered a women's crop in several countries, and women and youth play a key role in groundnut cultivation, processing, and marketing. The grain is used in a variety of ways, including boiled/roasted snacks, paste, sauce, cake and oil, and the haulm is a key source of animal feed. It is high in protein and other essential amino acids, and it is frequently used to prepare nutrient-dense foods like plumpynut to treat malnutrition in children and women [2]. Furthermore, it contributes to the long-term viability of agricultural systems by being utilized in crop rotation and fixing nitrogen that can be benefit to the following crop. Groundnut is also an important cash crop, accounting for over half of cash income in rural households [3].
Earthing up, a practice of covering the base and lower nodes of the plant with soil, is commonly practiced in groundnut cultivation. The practice is tedious, laborious, and time consuming for smallholder farmers because it is normally done manually or in some cases with an oxen-drawn cultivator. There is no consistent evidence about its benefit [4]. Some authors suggested that earthing up should not be used for groundnut as it reduces pod yield [5,6,7]. According to the authors, earthing up, especially in the early stage, influences plant development resulting in deformed plants with low or no production at the lower nodes, where flowers are unable to develop, and hence no pegs or pods form. Earthing up later in the season normally does not result in deformed plants, but it does result in poorer yields [6,7]. Another issue is that the practice can increase the risk of some diseases, such as white mould (Sclerotium rolfsii), causing a reduction in yield [7]. Earthing up during flowering may also affect peg formation due to damage to delicate flowers (hypanthium).
On the other hand, earthing up after final weeding and gypsum application to compact soil around the effective root zone could increase yield by allowing all pegs formed (geocarpic movement of pegs) to develop into pods. Thilini et al. [8] found that earthing up 37 days after planting was the best time for increasing yield in Sri Lanka. Earthing up has also been shown to boost yield for cultivars that produce aerial pegs [9,10], where many aerial pegs would otherwise remain unproductive in unearthed up plots because they do not enter the soil to develop into pods. The practice may also help late-formed pegs in entering the soil and forming pods. However, while waiting for the late-forming pods to develop, earlier-set pods of varieties with no seed dormancy may sprout or the peg attachment may weaken, resulting in their loss to the soil during harvest [4]. The developing pegs and pods may become exposed due to topsoil erosion in cases where the rainfall is torrential, making them vulnerable to pests and direct solar damage. Further, ridge planting is used for soil moisture management, and soil erosion may reveal the root system, pegs, and pods of those plants on ridges. Light earthing up may help to cover the exposed pegs and pods in such situations. Rather than earthing up, some farmers flatten the plants by stepping over them to bend the stems and branches and allow aerial and or late formed pegs to enter the soil.
In the semi-arid tropics of West Africa, there is no compelling evidence that earthing up or flattening helps to increase yield, while indications from elsewhere suggest that it might be beneficial if the timing is right. Furthermore, climate change and unpredictability affect crop selections and management methods in the region, necessitating a regular assessment of existing crop management practices such as earthing up. Therefore, this study was designed to evaluate the effects of earthing up and determine the best time to do so to increase groundnut yield, thus filling a knowledge gap in the Sudan agro-climatic conditions for groundnut cropping systems in the region.
2.
Materials and methods
2.1. Experimental site
The experiment was conducted at Samanko station, International Crops Research Institute for the Semi-Arid Tropics in Mali (ICRISAT-Mali) for three years, from 2016 to 2018. Samanko is 26 kilometers southwest of Bamako, 12~5'N, 8~54'W. The rainy season runs from June through October, and the station is located in the Sudan Savanah agroclimatic zone. The annual rainfall ranges from 800 to 1200 mm. The soil type is sandy-clay with a pH of 4.5, low fertility, and low organic matter content. The meteorological data collected during the experiment are shown in Table 1. The rainy seasons in 2016 and 2018 started in late June and lasted until the second week of October, as is typical. In 2017, rain began in late June and ended in early September. September and October are crucial in the groundnut grain filling process. The experiment site was plowed and disc harrowed by a tractor before planting, and Diammonium Phosphate fertilizer was applied at a rate of 100 kg/ha.
2.2. Treatments
The experiment was set up in split plot design with planting arrangement as main plot and time of earthing as subplot replicated three times. Two planting arrangements, row planting on ridges and row planting on flatbeds, were considered. The earthing up time was divided into ten treatments: control (no earthing up), earthing up at 14 days after planting, 21 days after planting, 28 days after planting, 35 days after planting, 42 days after planting, 49 days after planting, 56 days after planting, 63 days after planting, and 70 days after planting. The experiment utilized, ICGV 86124, which is a Spanish type improved groundnut variety with a bunch (erect) growth habit, early maturity (85–95 days) and drought tolerance. Apron Star 42WS (2.5g per kg) was used for seed treatment to protect seeds and seedlings from early season insect pests and soilborne diseases. The plot size was 4 meters long and 2.4 meters wide with 4 rows per plot in a spacing of 60 cm between rows and 10 cm between plants within a row.
2.3. Data collection and Analysis
Data were collected on the number of matured pods per plant (NMP) from an average of five random plants, Dry weight of pods per plot (dry pod yield–DPY, kg/plot), Dry weight of haulms per plot (dry haulm yield–DHY, kg/plot), Shelling percentage (%) from 200 random pods, and Dry weight of 100 seeds (100 seeds weight–100 SW, grams-g). For statistical analysis, the DPY and DHY were transformed to per hectare values by multiplying plot level value (in kg) by 10,000 (m2) and dividing by plot size (m2). The difference between treatments for DPY, DHY, NMP, 100 SW, and Shelling percentage was tested using an analysis of variance (ANOVA) using Genstat v.21. The F-test was employed to compare treatments to the ANOVA null hypothesis of equal means using Fisher's protected least significant difference (LSD) test.
3.
Results
The ANOVA results for DPY and DHY are presented in Table 2. The results revealed no statistically significant difference (P < 0.05) for DPY and DHY between flatbed and ridge planting in 2016, 2017 and 2018. Similarly, there was no statistically significant difference (P < 0.05) in DPY and DHY for the different times of earthing up except in 2017. In 2017, highly significant differences (P < 0.001) were observed between earthing times for both DPY and DHY. The DPY ranged from 1192 kg per hectare for earthing up at 63 days after planting to 1687 kg per hectare for earthing up at 28 days after planting. For DHY, the mean values ranged from 1256 kg per hectare for earthing up 70 days after planting to 1674 kg per hectare for earthing up 28 days after planting. The maximum DHY, 1674 kg per hectare was not statistically significantly different (P < 0.05) from 1619 kg per hectare for the control treatment. For both DPY and DHY, late earthing up at 63 days and 70 days after planting appeared to be detrimental.
Table 3 shows ANOVA results for NMP, 100 SW and shelling percent for each year. There was no statistically significant difference (P < 0.05) between the ridge and flatbed planting as main plots for both NMP, 100 SW and shelling percentage. In the case of the subplots (earthing up times), no statistically significant difference (P < 0.05) was observed for NMP in 2016, 2017 and 2018. For 100 SW, a highly significant difference (P < 0.001) was observed in 2018 but not in 2016 and 2017. In 2018, the 100 SW ranged from 23 g for the control treatment to 28.8 g for earthing up at 42 days after planting. The 28.8 g was not statistically significantly different from values obtained for earthing up at 28, 35, and 49 days after planting. In the case of shelling percentage, the treatments showed a highly significant difference (P < 0.001) in 2017 and 2018 but not in 2016. In 2017, the shelling percentage ranged from 61.3% for earthing up at 63 days after planting to 64.5% for earthing up at 28 days after planting. The maximum value, 64.5% was not statistically significantly different from 64.1% obtained for earthing up at 35 days after planting. In 2018, the shelling percentage ranged from 58% for the control treatment to 71.7% for earthing up at 42 days after planting. The control and late earthing up showed a lower values of shelling percentage both in 2017 and 2018.
Table 4 shows the results of ANOVA across years for DPY, DHY, NMP, 100 SW and shelling percent. A highly significant difference (P < 0.001) was observed between years for all the five traits considered. But there was no statistically significant difference (P < 0.05) between the main plots for all the five traits, and the subplots showed statistically significant differences (P < 0.001) only for the shelling percentage. The earthing up done at 21, 28, 35, 42 and 49 days appeared to have increased shelling percentage. The control treatment and the earthing up at 63 days and 70 days after planting showed lower values of shelling percentage. Highly significant earthing up x year interaction (P < 0.001) was observed for shelling percentage, but not for the other parameters considered.
4.
Discussion
The study revealed that planting on ridges was not better than planting on flatbeds for DPY, DHY, NMP, 100 SW and shelling percentage. The findings are consistent with those of Mvumi et al. [11], who found no significant differences between planting on flat ground (FG), earthing up after planting on flat ground (EFG), and planting on ridges (R) in pod yield, plant height and stem width but the number of pods and leaves. The present study revealed that earthing up during a typical rainfall season with appropriate planting time doesn*t increase DPY and DHY, which are the priority traits for groundnut producers. The individual years for 2016 and 2018 with typical rainfall seasons and the combined across years analyses showed no statistically significant differences (P < 0.05) between times of earthing up for DPY and DHY. In both 2016 and 2018, rain continued into the second week of October. The result corroborates with the recommendation that earthing up has no benefit and even may reduce yield [5,6], although no significant pod yield reduction was observed in the present study.
A highly significant difference was observed for the two traits in 2017. The earthing up at 28 and 35 days after planting gave statistically significantly higher DPY than the control treatment. The result for 2017 was in agreement with Thilini et al. [8] who found earthing up at 37 days after planting as the best time for increasing yield in Sri Lanka. However, the 2017 crop season was unusual in that crops, including groundnut, experienced terminal drought as a result of early rainfall cessation. After mid-September, there was no rain in the study area as a whole, with the experimental plots receiving the last rain on September 5. The statistically significant difference between treatments in 2017 suggests that earthing up at the right time can help maintain and increase DPY and DHY in a moisture stress scenario. This could be attributed to two advantages. One, the covering of the base and lower nodes may have reduced the amount of direct sunlight that the pods and roots were exposed to, as well as moisture loss due to evaporation. Second, earthing up as an inter-cultivation method helps in the removal of weeds and inhibits the late emergence of weeds [12], which might have reduced competition of groundnut and weeds for moisture and nutrients. Although the Sudan Savanah agroecology receives adequate rainfall in terms of quantity for groundnut cultivation, terminal drought remains a problem [13]. Rainfall distribution can be erratic, and given the region's current climate change and variability, this is expected to worsen resulting in some atypical rainfall seasons like the one in 2017. Furthermore, while early groundnut planting is encouraged, many farmers, particularly women, lack the requisite planting equipment, such as a plow, to do so. Planting priority is given to sorghum and pearl millet, which are the main staples. As a result, groundnut planting is often delayed, leaving the crop vulnerable to terminal drought. Drought tolerance and early maturity, in addition to pod yield, are among the most desired traits in groundnut varieties by farmers in the Sudan Savanah agroecology [13]. Accurate rainfall forecasts and making them available to groundnut farmers through climate services and national meteorological services would assist decision-making and management of cultural operations, such as whether or not to earth up. On the other hand, groundnut production in the Sahelian agroecology is seriously affected by terminal drought like many other crops [14,15].
For other traits, the NMP indicated no statistically significant differences (P < 0.05) for analyses at both the individual year and combined across years levels, unlike Ahmad et al. [9], who observed an increase in the number of pods per plant in Pakistan when earthing up was used. In the present study, although significant differences were observed between treatments for 1oo SW and shelling percentage in 2018, these variations did not transfer into an impact on DPY. Ahmad et al. [9] reported an increased 100 SW when earthing up was used.
5.
Conclusions
In the Sudan Savanah agro-climatic conditions of the semi-arid tropics of West Africa, earthing up is not economically beneficial during a typical rainfall season with appropriate planting time. Instead, it will increase the cost of production, lowering income. Hence, it shouldn*t be done. On the other hand, the findings from the present study, albeit only for one year, revealed that earthing up may be beneficial under a moisture stress scenario to increase yield by retaining soil moisture for extended periods. More research in representative sites for the Sahel agro-climatic zone, where moisture stress is one of the main groundnut production constraints, would be helpful to validate the benefits.
Acknowledgments
The research was funded by the Institutional Core Fund from ICRISAT. The authors are thankful to the team of the Groundnut Improvement Program, ICRISAT-Mali. The project "Climate Smart Agricultural Technologies for improving rural livelihoods and food security in Mali (CSAT-Mali)" is acknowledged for covering the article publishing charges (APC).
Conflict of interest
The authors have declared no conflict of interest.









 DownLoad:
DownLoad: