1. Introduction
Common bean (Phaseolus vulgaris L.) is cultivated worldwide, constituting a staple in developing countries in East Africa and South America, and also in some regions of Asia, where it is the main source of protein [1]. In some of them, common bean can account for up to 20% of the total daily protein intake per person [2,3]. In Europe, there has been a notable increase in common bean consumption in past years, due to a greater demand for healthy and functional food [4], and the current trend of vegetarian diets in Central Europe and the United Kingdom, in which beans and other pulses are included as meat substitutes. It is accepted that domestication of common bean from wild forms took place several thousand years ago in two main and independent centers of diversification, Mesoamerica (Mexico and Central America) and the Andes (Peru, Bolivia, and Northwest Argentina), resulting in two highly differentiated gene pools [5]. From these centers, the crop was spread all over the American continent, and, after the first voyages of Columbus (1492), common bean was brought to Europe. Both common bean gene pools spread widely in all parts of Europe with very complex pathways of dissemination that included several introductions from various regions of the Americas, combined with direct exchanges between European and other Mediterranean countries [6] and adaptation to European soils and climate conditions [3,7,8,9]. During the five centuries since the introduction of common beans into Europe, many varieties evolved under diverse environments and farmer preferences, to provide dry seeds or fresh pods [10], thus the loss of variation might have been less than previously suspected. What is more, hybridization that occurred in Europe between the Andean and Mesoamerican gene pools probably had a significant impact on the maintenance of the overall level of genotypic diversity [9].
Common bean can establish symbiotic interactions with both rhizobia (the Rhizobium-legume symbiosis, RL) and arbuscular mycorrhizal (AM) fungi, leading to the formation of nitrogen-fixing nodules and phosphate acquiring mycorrhiza [11]. Both symbiotic interactions play a vital role in ecosystems and sustainable crop production, and are central for efforts to decrease dependence on commercial fertilizers. The intensive application of N fertilizers over the last century has perturbed the N cycle, by leaching excess N fertilizers to watercourses and the emission of pollutant NOx gases to the atmosphere [12,13]. Common bean is generally known as a weak Nitrogen (N) fixer in comparison with other grain legumes [14,15]. Therefore, application of N fertilizers in bean fields is recommended to achieve higher yields. Selection in the 20th century based on common bean varieties with the best performance in highly mechanized monoculture systems is often reported to be the cause of the current relatively low Symbiotic Nitrogen Fixation (SNF) [16]. However, it has been reported that the climbing and indeterminate common bean varieties consistently have higher nodulation and SNF abilities, compared with most bush-type cultivars. These greater abilities are attributed to the relatively longer period of fixation during the growth cycle in climbing type cultivars [17,18,19,20]. Miranda and Bliss [21] reported that selection for high levels of SNF, especially when performed in low-fertility soils, might result in genetic gains in common bean breeding populations. Bliss [14] also discussed that the level of N fixation can vary significantly among common bean genotypes, and argued that reports of insufficient levels of N fixation were often based on observations with only a few genotypes, and were conducted with unsuitable N fixation measurement assays. Thus, proper characterization and evaluation of common bean germplasm collections as sources of adaptive alleles, and their utilization in breeding for enhanced SNF, are often limited or neglected. In addition to genetic background, several abiotic factors can greatly influence the SNF ability of common bean. Deficiencies of phosphorus (P), potassium (K), and sulfur (S) have been reported as environmental SNF-limiting factors, which may influence number and weight of nodules [22,23]. Direct impacts of P, K and (or) S deficiencies on nodules might be due to their influence on physiological and metabolic processes in nodules [23,24]. Other important environmental factors affecting SNF are salinity and different soil water conditions [25,26].
As a consequence, selection of best adapted common bean cultivars and most effective fixing rhizobial strains in each association is a must in order to maximize SNF [19]. Therefore, the study of rhizobia's natural diversity is a source of ecological information about symbioses, as it allows for the definition of host preferences and strain predominance, but, most importantly, since it provides the source for efficient strains to be used as inoculants in agricultural fields [18].
Breeding programs for improved SNF in common bean have been developed, resulting in the release of high N fixing Mesoamerican cultivars, promoting the development of cropping systems that are less dependent on N chemical fertilizers [27]. However, sustained success in developing Andean cultivars with enhanced SNF has been elusive. The availability of superior genotypes with higher N-fixation ability supports the idea that SNF in common bean may be improved through breeding efforts. In this sense, the advances in genetics and genomics resources of common bean and the high degree of synteny between this crop and its legume crops relatives can be exploited so as to understand complex traits associated with SNF, leading to the discovery of new genes or Quantitative Trait Loci (QTLs), as well as to improve genetic maps and develop molecular markers for Marker Assisted Selection (MAS). In this perspective, rhizobial biodiversity resources and the genes or QTLs of adaptive importance for RL interaction will be discussed, in order to accelerate the development of common bean cultivars with enhanced SNF.
2. Exploring the Natural Diversity of Rhizobia Nodulating Common Bean in Natural and Agricultural Soils
Diversity of the common bean nodule rhizobia has been extensively studied across many countries, showing that in the centers of origin, and in Latin America in general, where beans have been grown for several thousand years, a huge diversity of bean nodulating rhizobia is found. These native strains are very competitive for nodule occupancy, but, in general, they show a low N fixing efficiency [18]. Nevertheless, their efficiency can be increased with adequate selection processes and agronomical practices. Intensive selection programs of highly efficient rhizobial strains have been carried out in the last few years in Brazil, as one of the main dry bean-producing countries, in order to select elite inoculants [28,29].
The rhizobia classification has undergone major changes and revisions and several novel species have been described. The family Rhizobiaceae comprises seven main genera harboring plant-associated species, Rhizobium,
Neorhizobium, Allorhizobium, Agrobacterium, Ensifer (syn. Sinorhizobium), Shinella and the genus Ciceribacter. From 1996, the classification and molecular characterization of rhizobial species has been based mainly on the comparative analysis of gene sequences encoding for the 16S rRNA ribosomal subunit, a housekeeping gene [30]. However, events of recombination in these 16S rRNA genes have been reported [31] and genomes of rhizobia may lose or gain plasmids or genomic islands [32]. As a result, 16S rRNA sequencing may not be that informative for rhizobial taxonomy, and alternate phylogenies may be constructed using other housekeeping genes as well as the nod and nif genes, related to the symbiotic process [31]. In order to solve the taxonomic uncertainties concerning the plant-associated members of the Rhizobiaceae family, Mousavi et al. [32] performed Multilocus Sequence Analysis (MLSA) of 100 strains of the family Rhizobiaceae and 16 rhizobial strains from other rhizobial families, using four housekeeping genes namely 16S rRNA, atpD (ATP synthase F1, beta subunit), recA (recombinase A), and rpoB (RNA polymerase, beta subunit). The delineation of the new genus Pararhizobium and 13 new species combinations were proposed [32]. Rhizobium genus is a heterogeneous group accommodating two major sub-clusters: R. tropici and R. leguminosarum. The genus name Rhizobium encompasses 56 species; however, it is not a proper name for all, since some of them are phylogenetically interspersed among members of other genera in Rhizobiaceae. For instance, R. oryzae did not group with Rhizobium members according to several Multi Locus Sequence Analysis (MLSA) studies [33]. Another controversial group is the genus Ensifer; data obtained recently indicate that Ensifer adhaerens and "Sinorhizobium morelense" are not heterotypic synonyms, but represent separate species [34]. There are two main databases specialized in the phylogeny, taxonomy and diversity of the Rhizobiaceae family: http://edzna.ccg.unam.mx/rhizobial-taxonomy/ (CCG, UNAM, Cuernavaca, Mexico) [35], and http://www.rhizobia.co.nz/taxonomy/rhizobia [36], in which new rhizobial species are regularly added or reclassified.
Up to date, five genera and 19 species nodulating common bean have been described, including R. leguminosarum bv. phaseoli, R. etli bv. phaseoli, R. gallicum (bv. phaseoli and bv. gallicum), R. giardinii (bv. phaseoli and bv giardinii), R. lusitanum [37] and R. tropici [38,39,40,41], and, more recently, Pararhizobium giardinii [32]), R. ecuadorense [42], R. vallis, R. leucaneae
[43], R. mesoamericanum [44], R. mongolense, R. oryzae [45], R. freirei [46], R. rhizogenes, R. azibense [47], R. acidisoli [48], R. hidalgonense [49], as well as Ensifer meliloti [50,51], E. medicae [52], E. americanus [53], Bradyrhizobium spp. and the beta-proteobacteria Burkholderia [52,54,55]. Despite this high promiscuity, R. etli bv. phaseoli was found to be the predominant mycrosymbiont in both the Mesoamerican and the Andean common bean's centers of origin [1,3,40,56], and in many different areas across the whole world such as Southern and Central Europe [57,58], Tunisia [52], Central and West Africa [59,60], Ethiopia [55,61], Indonesia [59] and in Northeast China [62]. However, recent taxonomic studies reclassified some of the strains previously considered as R. etli into the R. phaseoli group or other species of common-bean rhizobia [63,64].
In the tropics or in areas with high temperatures and/or acidic soils, R. tropici replaces R. etli as the preferred symbiont for common bean. R. tropici shows a good tolerance to both constraints, even when beans from Mesoamerican cultivars are used as trap hosts [65,66]. In these areas, R. tropici has been proved to be far more competitive for nodulation than R. etli, blocking the nodulation of R. etli [67]. Two types of R. tropici, A and B have been clearly distinguished that seem to be diverging lineages sharing a common symbiotic plasmid [56,68], although there are some R. tropici strains with intermediate characteristics between A and B that do not belong to any of them [56,66,69]. Recently, accumulated phylogenetic data supported the reclassification of R. tropici strains belonging to type A into the new species R. leucaneae
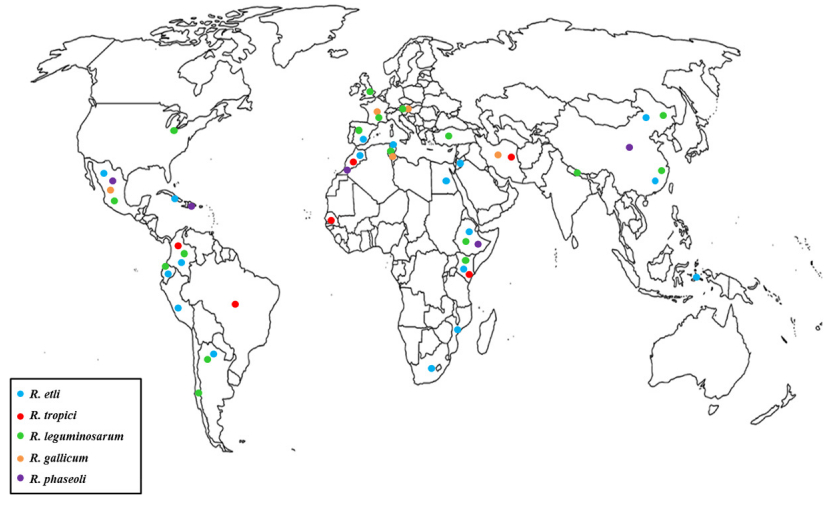
[43]. Recent genome analyses of R. tropici CIAT899 and two commercial strains of R. leucaneae revealed that these strains are well equipped to cope with low pH, high temperatures, and with oxidative and osmotic stress [70,71]. Figure 1 and Table 1 summarize the areas for several important rhizobia species, which are described below.
Table 1. Predominant rhizobium species isolated from common bean nodules in each country.
| Specie |
Country |
Method for classification |
References |
| R. etli |
Mexico, Colombia, Ecuador, Peru |
16S rRNA gene sequencing |
[39] |
| Argentina |
16S rRNA gene sequencing, RFLP of nodC gene |
[3] |
| Spain |
MLEE, RFLP and partial sequencing of the 16S rRNA genes, RFLP of symbiotic genes |
[57] |
| Austria |
RFLP of 16S rRNA and PCR of nifH genes |
[58] |
| Tunisia |
16S rRNA, RFPL of nifH and nodC genes |
[52] |
| Morocco |
RAPD fingerprinting of housekeeping and nodC genes |
[100] |
| Egypt |
16S rRNA gene sequencing |
[103] |
| Ethiopia |
AFLP fingerprinting and MLSA on 16S rRNA, nodC and nifH genes |
[55] |
| Kenya |
Sequencing of nif genes |
[105] |
| South Africa and Mozambique |
16S rRNA gene and other housekeeping genes, symbiotic genes |
[108] |
| Jordan |
nifH and nod genes |
[110] |
| Indonesia |
16S rRNA gene sequencing |
[59] |
| Northeastern China |
16S rRNA gene, and other housekeeping genes sequencing |
[62] |
| R. tropici |
Colombia |
16S rRNA gene sequencing |
[39] |
| Brazil |
16S rRNA gene sequencing |
[69] |
| Senegal and Gambia |
SDS-PAGE, RFLP of 16S rRNA gene |
[60] |
| Kenya |
Sequencing of nif genes |
[105] |
| Morocco |
16S rRNA gene sequencing |
[98,99] |
| R. leguminosarum |
Mexico |
MLSA of 16S rRNA, and other housekeeping genes nifH and nodC genes, |
[72,73] |
| Ecuador |
Phenotypic analysis and PCA of Box AIR-PCR banding patterns |
[74] |
| South-central Chile |
RFLP of 16S rRNA and nodC genes |
[87,88] |
| USA |
16S rRNA gene sequencing, biochemical and morphological characters |
[89] |
| England |
16S rRNA gene sequencing, biochemical and morphological characters |
[43] |
| Spain (Northwest) |
Analysis of ITS regions in housekeeping genes, sequencing of nodC genes; sequence analysis of housekeeping genes |
[95,96] |
| France |
16S rRNA gene sequencing |
[40] |
| Tunisia |
16S rRNA gene sequencing, RFPL of nifH and nodC genes |
[52] |
| Ethiopia |
AFLP fingerprinting and MLSA on 16S rRNA, nodC and nifH genes |
[55] |
| Kenya |
SDS-PAGE, RFLP of 16S rRNA gene |
[105] |
| Turkey |
16S rRNA and other housekeeping genes and, nif and nodA genes sequencing |
[109] |
|
Northeastern China |
Partial sequencing of 16S rRNA, and other housekeeping genes |
[62] |
| Nepal |
16S and 23S rRNA, nodC and nifH genes sequencing |
[118] |
| R. gallicum |
Mexico |
MLSA of 16S rRNA, and other housekeeping genes, nifH and nodC genes |
[72] |
| France |
16S rRNA gene sequencing |
[40] |
| Austria |
RFLP of 16S rRNA and PCR of nifH genes |
[58] |
| Tunisia |
16S rRNA gene sequencing, RFPL of nifH and nodC genes |
[52] |
| Iran |
RFLP of 16S rRNA gene |
[111] |
| R. giardinii |
France |
16S rRNA gene sequencing |
[40] |
| R. phaseoli |
Mexico |
MLSA of 16S rRNA, and other housekeeping genes nifH and nodC genes |
[63] |
| Morocco |
RAPD fingerprinting of housekeeping and nodC genes |
[100] |
| Ethiopia |
AFLP fingerprinting and MLSA on 16S rRNA, nodC and nifH genes |
[55] |
| Dominican Republic |
RAPD fingerprinting of housekeeping and nodC genes |
[85] |
2.1. American continent
In Mexico, other bacteria apart from R. etli bv. phaseoli have been isolated in bean nodules (R. leguminosarum bv. phaseoli [72]). Actually, the genetic diversity of rhizobial isolates in Mexico is so large that it could serve as the basis to propose new species [18,56], although most of the identified ones correspond to R. etli,
R. gallicum bv. phaseoli [73] or R. leguminosarum clusters [73]. According to the population genetic analyses performed by Silva et al. [72], there is a high genetic differentiation between the R. etli and R. gallicum strains isolated from common bean in Mexico, with no genetic exchange between them. In saline and/or alkaline soils, however, Ensifer
americanus was the predominant symbiont for common bean [73]. The isolates of E. americanus were classified in a subcluster different to the R. etli strains isolated in the same study [73]. Also, a novel rhizobium species, R. hidalgonense, has recently been isolated from nodules of common bean cultivated in acidic conditions in the Hidalgo state of Mexico [49], and classified attending to the sequences of housekeeping genes atpD, glnII and recA. This novel strain showed a high similarity (between 92 and 94%) with the type strains of related Rhizobium bean-nodulating species, including R. etli and R. phaseoli.
In Ecuador and Peru, rhizobia isolated from bean nodules have a high diversity, and may be divided into clusters different from the Mexican isolates [74], which suggests coevolution, or, at least, host selection [75]. It should be noted that in Ecuador, apart from R. etli, R. leguminosarum has been identified as another predominant strain in common bean nodules [74]. Common bean gene pool of Peru-Ecuador is unique, as it is originated in the borders between the two main centers of diversification [76], thus, studies of microsymbionts from this region are receiving increasing attention. As a result, Rhizobium ecuadorense sp. nov., an indigenous N-fixing symbiont of the Ecuadorian common bean, has recently been characterized, based on DNA-DNA hybridization, 16S rRNA gene sequence phylogeny and MLSA of three other housekeeping genes [42]. R. ecuadorense strains have been classified in the R. phaseoli/R. etli/R. leguminosarum phylogenetic clade, but showed unique biochemical and physiological properties, constituting a separate subclade.
Studies of common bean rhizobial diversity in other Mesoamerican countries are scarce. Nicaraguan common bean cultivars were reported to improve their productivity when inoculated with a commercial strain, highlighting the potential of these cultivars for N fixation efficiency [77], and the need for screening native rhizobial strains. In Guatemala, the R. leguminosarum strain CIAT632 was isolated from active nodules of wild and cultivated Mesoamerican common bean cultivars [78], although its predominance in common bean nodules in native Guatemalan soils has not yet been tested.
In Colombia, apart from R. etli, R. tropici is predominant; additionally, the reference strain CIAT899 was isolated in acid soils [38]. Later on, in 1995, a phylogenetic comparison of common bean isolates from Mexico and Colombia identified a genotypically diverse group of Colombian rhizobial strains strongly differentiated from the Mexican R. etli group, according to the Multilocus Enzyme Electrophoresis (MLEE) of the 16S rRNA gene sequence; all these 27 isolates were identified as Colombian native strains, although it is not clear if they belong to R. etli, R leguminosarum or R. tropici group [79].
In Northwest Argentina, in the Andean center of origin, R. etli was also found to be predominant in nodules of wild bean varieties [80], by using plasmid profile and DNA fingerprinting. In this study, 31 out of the 35 soil isolates presented the R. etli 16S rDNA allele, and phylogenetic similarity between pairs of isolates ranged from 71 to 99% [81]. Later, the diversity of rhizobial strains nodulating common bean in the same area was described using a collection of 400 isolates of rhizobia recovered from local soils and nodules [3]. The isolates were characterized by the analysis of 16S rRNA, nifH and nodC genes, and most isolates were identified as R. etli or R. leguminosarum, with a minor presence of Ensifer fredii, E. saheli, S. terangae and Mesorhizobium loti. Aguilar et al. [81] also analyzed the nodC genes in several R. etli strains from different countries (Mexico, Ecuador, Peru, Bolivia, Northwest Argentina and Colombia) belonging to the centers of common bean diversification. They found that the different nodC alleles from these American strains had varying predominance in each center of diversification, suggesting coevolution of common bean and rhizobia in the centers of host genetic diversification.
In Brazil, R. tropici and R. leucaneae are also the predominant species in common bean nodules, due to the good tolerance of these species to the acid soils of this country [1,66,67], even though R. etli is the most abundant in Brazilian soils [82]. In a phylogenetic study, the Brazilian R. etli strains were found to be closely similar in 16S rRNA sequences and in nodABC and nifH RFLP-PCR profiles to the Mexican CFN42 strain, and quite distinct from R. etli and R. leguminosarum strains from Europe [1], thus supporting the hypothesis that Brazilian common bean cultivars and their rhizobia are of Mesoamerican origin, and could have arrived in Brazil at pre-colonial times. In this study, R. tropici reference strains and Rhizobium sp. strains were clustered together in the same group at a level of similarity of 51%, and the 43 Brazilian R. etli strains constituted a large cluster along with the reference strain CFN42. R. tropici may have already been present in Brazilian soils, and, due to its tolerance to acidic soils and high temperature, it became the predominant microsymbiont of common bean. Supporting this hypothesis, R. tropici strains were recently isolated and characterized from wild common bean Brazilian varieties [83], with high genetic similarity to the reference strain CIAT899, and also with a similar symbiotic efficiency. R. leucaneae is abundant in the Brazilian Cerrados soil, and is frequently used as an inoculant due to its capacity to nodulate common bean and fix N under stressful environmental conditions [65]. Two other new species previously classified as R. tropici, R. freirei and R. paranaense, were isolated from common bean nodules in Brazil [46,84] and both proved to be very effective for N fixation, constituting an important source of commercial inoculants in the tropics, along with R. tropici and R. leucaneae. R. freirei was placed within the R. tropici phylogenetic group, based on the analysis of recA, atpD and rpoB gene sequences.
Caribbean islands, located along the trade routes between the Americas and Europe, played a crucial role in the exchange of common bean seeds and their endosymbionts, although only few studies are available about strains native of these islands. The Hispaniola Island, comprising the countries of Haiti and Dominican Republic, was the first stopover in the voyages of Columbus between America and Spain. The analysis of genomes of strains nodulating common bean in coastal and inner regions on this island showed that they were almost identical to American R. etli strains (recently reclassified as R. phaseoli) [85]. In Cuba, beans are widely cultivated all over the country and are at the core of the daily diet. Four Rhizobium species were isolated and identified from common bean nodules in Cuban soils: unclassified Rhizobium sp., R. etli, R. radiobacter and R. pisi bv. viciae (previously classified as R. leguminosarum). R. pisi was the most often isolated species, (20%) in addition to R. etli (10%) [86].
In Chile, the predominant species that nodulates common bean is R. leguminosarum [87], although the presence of three other species of rhizobia, R. leucaneae, R. tropici and R. etli, in common bean rhizosphere or nodules have recently been identified according to the nodC PCR-RFLP pattern in this South-Central region [88]. R. leguminosarum was also found to have the highest genetic diversity in both acidic and alkaline soils in central and South-Central locations.
In the United States of America (USA), common bean was rarely inoculated until recently, and, as a result, few studies regarding this issue have been found. In the state of Minnesota, rhizobia were recovered from bean nodules and characterized according to reference strains. Analysis of 16S rRNA gene sequences revealed that half the organisms tested were most similar to R. leguminosarum, with a small presence of R. etli-like strains [89].
2.2. European continent
In Europe, rhizobial species with high genomic similarity to those at the common bean centers of origin have also been isolated, suggesting that they were present in the surface of bean seeds when these where brought out from America [1,57,90]. However, promiscuity of common bean to nodulation with bacterial strains is much higher in introduced areas, where bean functions as a trap-host plant [91,92]. Segovia et al. [39] proposed that R. etli strains in the surface of the bean seeds could have transferred their symbiotic plasmid to R. leguminosarum strains present in European soils, allowing R. leguminosarum to recognize and nodulate common bean. Later, R. leguminosarum would have transferred the Sym plasmid with specific genes for common bean nodulation to R. gallicum and R. giardinii [40]. In most areas where common bean was introduced, cooccurrence of several strains is common, although with different symbiotic efficiencies.
In Portugal, a species named R. lusitanum was identified after isolation and molecular analysis of strains from several soils [37]. Afterwards, the diversity of 179 bean rhizobial isolates from Northwest Portugal was investigated. Five of the six phylogenetic groups were placed within R. lusitanum, and the remaining one was placed within R. tropici group, according to the RAPD analysis of housekeeping genes [93]. However, according to nodS gene sequencing, four R. lusitanum strains were placed within R. etli cluster, showing a similarity of 91–99% to the nodS sequence of the reference strain CFN42; the remaining strain was placed within the same cluster of R. tropici, and its nodS sequence was 100% identical to that of the CIAT899 reference strain. These classifications suggest that R. lusitanum was the recipient of the genes for symbiosis from both R. etli and R. tropici.
In Spain, five different rhizobial species, R. etli, R. leguminosarum, R. gallicum, R. giardinii and S. fredii (=Ensifer fredii) isolated from a single soil, were found to nodulate common bean [57]. Martínez-Romero and Caballero-Mellado [56] have also revealed the existence of one of the most genetically diverse collections of Rhizobium isolates from common bean nodules, being R. etli the predominant species. Later on, Velázquez et al. [94] identified the same five rhizobia species in bean nodule isolates from two different regions, Andalucía and León in the South and Northwest of Spain, respectively, using the staircase electrophoresis method for identification. However, García-Fraile et al. [95] found that common bean is nodulated preferentially by R. leguminosarum in a wide region in Northern Spain, the major dry bean producer region. Also, the inoculation of native R. leguminosarum strains from this area in common bean local varieties produced similar grain yield and number of pods than the N-fertilized control [96]. The genetic analysis showed that these R. leguminosarum isolates carry the same alleles for the nodC genes as the American strains of this species. These results suggest that R. etli could have had difficulty in persisting in the soils of Northern Spain when it was brought from America, probably because of the climatic conditions [95]. The symbiotic genes of this species might have been transferred, after the arrival of common bean, to strains of R. leguminosarum already present in Northern Spanish soils, and become better adapted. In the arid and saline soils of Lanzarote, on the Canary Islands, most of the isolates from common bean were identified as E. meliloti and E. fredii, according to the analysis of nodC sequences [51].
Other three Rhizobium species, R. leguminosarum, R. gallicum and R. giardinii, have also been isolated in France and Austria, and probably represent bacteria that pre-existed in European soils before common bean was introduced [40,58]. R. leguminosarum is also the predominant species in common bean nodules and soils in Croatia, although these data come only from five out of the twenty-three soil samples analyzed, since most soil samples in this study contained no indigenous common bean rhizobia [97]. The authors suggest cropping history and N fertilization for common bean as the possible origin of this absence of rhizobial presence in Croatian soils. Nevertheless, also in this case, inoculation of common bean with indigenous Croatian R. leguminosarum resulted in better nodulation and symbiotic efficiency than inoculation with the reference commercial strain.
2.3. African continent
Morocco is the main producer of green bean in Africa, and common bean was brought to Africa via Spain and Portugal after the colonization of the Americas. Therefore, American rhizobial strains harbored in these seeds were also distributed in Africa. In Morocco, R. tropici type B and other rhizobia (identified as R. leguminosarum and pseudo-Agrobacterium) were isolated from bean nodules; some of them were also highly salt-tolerant [98,99]. Salinity is an increasing problem in North Africa and in the Mediterranean, affecting RL symbioses and common bean productivity. In Morocco, common bean is cultivated in saline soils and its symbiosis depends on the presence or application of osmotolerant strains in these soils. Faghire et al. [100] identified 32 osmotolerant rhizobial strains from common bean collected in Moroccan soils, and classified them attending to the RAPD patterns of the housekeeping genes rrs, recA, atpD and the symbiotic gene nodC. The most abundant species were placed either within the R. etli or the R. phaseoli phylogenetic group, and a second group was identified as R. gallicum. The remaining strains belonged to the R. tropici phylogenetic group, with almost 100% identity to CIAT899 [100]. In another study, four Bulkholderia phymatum strains were also isolated from bean nodules grown in alkaline soils in Morocco [54]; all of them were able to fix N efficiently.
In Tunisia, the most abundant rhizobial species in bean nodules were R. gallicum, R. etli and R. leguminosarum, each of them representing between 20 and 29 % of the isolates [52], according to the RFLP analysis of 16S rRNA, nifH and nodC gene fragments. Four other minor groups of rhizobia were classified as R. giardinii and Ensifer spp. One of these isolated R. gallicum Tunisian strains, 23C2, was recently reclassified within the novel species R. azibense [47]. The 16S rRNA gene of this strain showed a 99% similarity with R. gallicum and R. mongolense reference strains, but phylogenetic analysis based on the sequences of housekeeping genes recA, atpD, dnaK and thrC showed that this strain represents a separate genomic group [47]
Also, in alkaline and/or saline Tunisian soils, Ensifer species as E. fredii, E. meliloti and E. americanum [101,102] were found to be the predominant symbionts of common bean, and they were phylogenetically related to the above-mentioned Ensifer strains isolated and identified in Spain [51] and Mexico [73] for these types of soil.
In Egypt, R. etli and R. gallicum were isolated from different soils, and were able to nodulate common bean, displaying cultivar-dependent symbiotic efficiency [103]. R etli represented about half of the isolates, characterized by the analysis of 16S rRNA sequences, whereas R. gallicum had a minor presence. Salinity and alkaline soils are also a major problem contributing to the low productivity of common bean in Egypt; the same authors identified new R. etli strains highly tolerant to these environmental stresses [104]. These results are consistent with the above-mentioned for bean nodule isolates from Tunisia [52].
In Sub-Saharian locations, the high acidic soils and high temperatures favor the prevalence of R. tropici in common bean nodules, as was reported in Kenya [105], Senegal and Gambia in West Africa [60]. In Kenya, several rhizobia were isolated from two soils with pHs of 4.5 and 6.8 and characterized on the basis of their host ranges and sequencing of nif genes. Most isolates were similar to R. etli and R. leguminosarum bv. phaseoli, while the predominant strain in acidic soils was likely to be R. tropici, although their characterization was presumptive, since little molecular evidence was gathered [105]. Later on, the symbiotic efficiency of native rhizobia nodulating common bean was assayed, showing a higher efficiency than the reference strain CIAT899 [106]. Commercial inoculants used in Western Kenya still contain exotic cultures from the USA [107], which may not be well adapted to local conditions; therefore, the identification of these strains is essential.
Ethiopian soils, as happens in neighboring Kenya, also harbor natural populations of rhizobia forming symbioses with common bean [61], although the diversity pattern is different from that reported in the latter. Based on Multilocus Enzyme Electrophoresis, the majority of the Ethiopian genotypes were genetically related to the type strain of R. leguminosarum. However, from analysis of 16S rRNA genes, most of them were placed in R. etli group. The possible reason for this might lie in the transfer and recombination of the 16S rRNA gene from the introduced R. etli to the local R. leguminosarum, as suggested for Europe rhizobial populations [39,40,93]. Additionally, a more extensive screening of native common bean rhizobial strains in Ethiopian soils revealed that the majority of the isolates belonged to the species R. etli, R. leguminosarum and R. phaseoli, with a minor presence of R. leucaneae and R. giardinii, based on the sequencing of symbiotic (nodC and nifH) and housekeeping genes (recA, glnII,
rpoB, and 16S rRNA) [55].
The diversity and phylogeny of root-nodule bacteria from common bean has also been studied recently in South Africa and Mozambique [108], using phylogenies of both symbiotic and housekeeping genes (16S rRNA and others). The analysis of nifH and nodC symbiotic genes allowed for the classification of most isolates into the R. etli group, with a small proportion of R. tropici-like genomes. Again, this classification was inconsistent with the phylogram of the housekeeping genes, which is an indication of lateral transfer among the Rhizobium isolates. R. leucaneae, belonging to the R. tropici group, was also isolated in Eastern Cape Province of South Africa, in very stressful acidic conditions, as in the Cerrados region in Brazil [65].
2.4. Asian continent
In Turkey, historical records indicate that cultivation of common bean started much later that in Europe, about 250–300 years ago [109]. In the Central Black Sea Region, 30 rhizobial isolates obtained from common bean have been classified according to the sequencing of housekeeping genes as 16S rRNA and the symbiotic genes nifH and nodA [109]. Half of the isolates were identified as R. leguminosarum, while the others were placed in either the group of R etli bv. phaseoli (8 out of 30 isolates) or R. phaseoli (6 out of 30). The phylogenetic analysis based on sequence data from nodA and nif genes showed that all rhizobial species in this study had the same haplotypes as the R. etli CFN42 reference strain, suggesting a further support for the lateral transfer of R. etli Sym plasmid amongst Turkish common bean nodulating isolates.
In Jordan, R. etli represented 80% of rhizobial species, in a collection of 30 isolates from common bean cultivated in 16 different locations, after analysis of nod and nif genes. A second group, comprising the remaining 20%, was identified as R. tropici [110]. R. etli was also the predominant strain in Egypt, and neighboring Jordan; taking into account the trade relationship between both countries, R. etli strains from both countries are likely to share a common origin [103].
Iran seems to constitute a separate biogeographical region from that of Turkey and Jordan, regarding common bean rhizobial diversity. Fifty-three isolates were sampled from common bean root nodules cultivated in different locations in Iran, and half of them were placed into either R. gallicum or R. tropici type B phylogenetic groups, according to the RFLP analysis of the 16S rRNA gene [111]. Despite the fact that an accurate identification of these strains is still pending, they seem to be native of Iran, and showed a good symbiotic effectiveness as well as some plant-growth promoting traits such as P solubilization and production of auxins and siderophores when inoculated in common bean [112].
As for East Asia, most of the studies about common bean rhizobia have been conducted in China, considered to be a secondary center of diversity for common bean [113]. Common bean was introduced from Latin America to China 600 years ago [114], and it has been widely cultivated throughout the country ever since. As a result, a huge diversity in common bean rhizobia can be encountered there, differing from one region to another. R. leguminosarum and R. etli were dominant in different ecoregions [62,115,116,117], with varied relative abundances. The analysis of the nodC and nifH genes in all the Rhizobium strains isolated in China, along with the predominance of R. etli, suggest that these species may have an American origin [117]. There was also a significant presence of Bradyrhizobium spp., R. phaseoli and Ensifer fredii in common bean nodules [115,117]. However,
Bradyrhizobium seems to be an opportunistic symbiont for common bean, since it formed ineffective nodules when inoculated separately [117]. In addition, two new rhizobial species were isolated from wild rice in China, R. mongolense and R. oryzae, which were also able to effectively nodulate common bean [45].
R. etli,
R. leguminosaum and R. phaseoli were also the most abundant species in common bean in Nepal, characterized by the partial sequencing of 16S and 23S rRNA, and nodC and nifH genes. The diversity in each of the seven sampled fields is strongly affected by soil pH and temperature; however, the predominant species in all soils was R. leguminosarum [118].
2.5. Oceania
Common bean has been grown in some Oceanian countries as Australia and New Zealand since the arrival of Europeans, and it is commonly cultivated in rich-N soils, fertilized with N or supplied with commercial inoculants [119,120]. However, symbiotic relationships between common bean and native rhizobia remain poorly characterized despite their importance [121]. In Australia, several strains of natural rhizobia have been isolated from native legumes or soil samples, and E. meliloti
[121], R. leguminosarum and R. tropici were identified [122].
3. Bacterial Molecular Determinants of Specificity in Rhizobia-common Bean Interactions
The large differences in symbiotic effectiveness within strains nodulating common bean were suggested to result from the coadaptation and coevolution of common bean cultivar and bacteria [4]. Some biogeographical analyses of common bean-rhizobia symbioses mentioned before, in which a parallel genetic variation has been reported, support this idea of coevolution in the centers of origin [18]. Coevolution has also been proposed as an explanation for the specificity of the interactions. However, rhizobia and common bean phylogenies are not parallel, because this is a weak and non-obligate symbiosis [123], and so the idea of coevolution is still to be proved.
The specificity of rhizobia-legume interaction is determined by both bacterial and host plant compounds, although common bean presents a high versatility for the association with different rhizobia sepecies and genera [92]. Several bacterial molecules are know to be involved in this specificity, including Nod factors, cell wall polysaccharides, and type Ⅰ and Ⅲ secreted proteins [124,125,126]
Cell wall polysaccharides include exopolysaccarides (EPS), lipopolysaccharides (LPS) and β-glucans [124,125]. The interactions between rhizobial surface polysaccharides and plant lectins (carbohydrate-binding receptors present in legume root hair surfaces) have long been considered to be determinant in host recognition by rhizobia [126]. EPS are released to the environment, and are the main surface polysaccharides related to symbiosis specificity, as alterations in rhizobial EPS can lead in some cases to impairment in symbiosis [125,127]. EPS are heteropolymers consisting in repeating units of monosaccharides substituted with non-carbohydrate residues, and a high diversity in their chemical structure has been described, which may be the cause of their involvement in symbiotic specificity [127]. Biosynthesis of EPS in rhizobia is a complex process regulated at both transcriptional and post-transcriptional levels and influenced by several environmental conditions, including hyperosmotic stress, temperature, oxygenation and pH, and also nutrients concentrations (nitrogen, sulfur, and phosphate) which may alter the recongition between symbionts [127,128]. LPS, composed by an oligosaccharide and a lipid that binds the molecule to the outer membrane, is another cell wall determinant of rhizobial identity. LPS acts as a suppressor of plant defense responses, key to allow the progression of bacteria inside the infection thread, and it has been proposed to be involved in the symbiosis specificity. However, the precise role of LPS in symbiosis remains unclear, and its effect in nodulation varies depending on the species [125,129].
However, most authors agree that the key components of host specificity in rhizobia are nod genes [124,125,126,130]. These genes are included in the Sym plasmids, which are specific for each biovar (a group of strains nodulating the same legume). Nod genes encode for the Nod factors (NF) released by rhizobia, as a response to plant flavonoids, chemical signals exudated by the legume that initiate the nodulation process [124,125,130]. Daidzein, coumestrol, naringenin, genistein, liquiritigenin, and isoliquiritigenin isoflavones were the major components of common bean cv. Rab39 extract, responsible for inducing expression of the nod genes of Rhizobium tropici, R. etli, and R. leguminosarum bv. phaseoli [131]. The NF synthesized by the rhizobia are perceived by legume plants and cause developmental responses such as the initiation of cell divisions in both cortex and pericycle as well as major deformations of root hair extension, leading to bacterial invasion. NF are lipochitooligosaccharides, complex molecules with a basic structure composed by an oligosaccharide, to which a fatty acid substitute is bond. The synthesis of this basic skeleton depends on nodA,
nodB and nodC genes [130,131]. NodC is the first enzyme in the pathway, and synthesizes a chitooligosaccharide using N-acetyl-glucosamine as substrate. NodB is the responsible of deacylate the non-reducing end of the oligosaccharide, which is subsequently N-acylated by NodA. To this basic structure several chemical groups can be added (including oligosaccharides, methyl, acetyl and sulphide groups, fatty acids, etc), originating a great variety of NF. The addition of these substitutions is encoded by other nod genes (nodH, nodPQ, nodL, etc), and depending on the rhizobial strain, different groups can be added [131]. This variety of NF constitutes the major determinant of host specificity in rhizobia, since, depending on their structure and substitute chains, they are perceived by different legume species [125,126,130,131,132]. Therefore, Sym plasmids, rather than core genomes of rhizobia, might have coevolved with the host plant [133]; this host selection of rhizobial genotypes seems to be a general phenomenon in most legume-rhizobia symbioses [134,135].
The presence of compatible rhizobia species and their corresponding NF is generally sufficient to trigger rhizobial infection and nodule development in common bean and other legumes [136]. Chemical structures of NF of most common bean-nodulating rhizobium strains have been characterized, revealing that they all have a common basic structure essential to nodulating common bean [137,138,139,140,141]. R. tropici CIAT899 strain has a broad host range, as it is able to synthesize the greatest diversity of NF found amongst the rhizobia species [141]. The explanation may be found in the complex regulatory mechanisms of NF production in this strain. Five nodD genes (regulators of NF production) have recently been sequenced and characterized in CIAT899, using nodD mutant strains; it was proposed that each one of the nodD genes perform different roles depending on the host plant and the environment [142]. Also in this study, almost 40 different NF were identified in R. tropici, and the synthesis of NF was enhanced under salt stress, suggesting that this diversity of NF might play a role in the tolerance of R. tropici to abiotic stresses [142]. In another study on R. tropici CIAT899, three different nodA genes were found in the Sym plasmid, which may also contribute to its broad host range [70].
Biotic and abiotic stresses strongly influence the selection of bacterial strains. Several abiotic stresses such as salinity and osmotic stress [142], drought [143], heavy metals [144], high temperature or low pH [145] have been found to affect either the production of NF or EPS by the bacterial partner or the perception of these compounds by the legume host. Plant pathogens often compete with rhizobia for colonization, and can inhibit their growth in the rhizosphere, their NF production, or their attachment to the legume root hairs [146]. Therefore, for each niche, common bean has chosen the best adapted strains. This is supported by the fact that diversity of rhizobial strains is much lower inside nodules of common bean than in the root surface [75]. In another recent population genomics study, the sequencing and comparison between genomes and Sym plasmids from rhizobial species, isolated from rhizosphere and common bean nodules, confirmed that all these strains coexist in both environments with very low genetic recombination across their core genomes [147]. On the other hand, Sym plasmids of rhizobial strains are extremely similar, with high rates of recombination, and do not appear to have coevolved with the chromosome or with other plasmids. In fact, a phylogenetic classification based on RFLP analysis of nodC and nifH genes revealed close relationships among common bean symbionts, regardless of their 16S-rRNA-based classification [148]. Lateral gene transfer of the Sym genes appears to be the most likely explanation for the phylogenetic incongruence between Sym and housekeeping genes such as 16S rRNA. This genetic transfer might have occurred across rhizobial species and, in some cases, also across Rhizobium and Ensifer genera, which may explain why some Ensifer strains are able to nodulate common bean in certain situations. Eventually, these transfer events have resulted in recombinant Sym plasmids, as is the case of a common bean nodulating E. fredii strain (isolated in Granada, Spain), which harbors a conjugative Sym plasmid assembled from two R. etli Sym plasmids and the core genome of E. fredii [149].
Thus, all the bacterial genes needed for SNF have been identified. Now, exciting progress is being made in elucidating the common bean plant's contribution to this mutually beneficial interaction, with the identification of crucial signal transduction genes early involved in the response to Rhizobium. In addition, the advent of current high-throughput technology provides valuable data that contribute to understanding the metabolic activity during bacterial N fixation. A genome-based study of the metabolic activity in N fixation, involving R. etli bacteroids located at the root nodules of common bean, revealed 415 proteins and 689 upregulated genes that orchestrate N fixation [150]. A change of metabolic activity in these enzymes, as a result of gene deletion, induced different effects in N fixation, which is in agreement with observations made in R. etli and other Rhizobiaceae. Also, a proteomic study on Rhizobium tropici PRF81 [151] allowed for the identification of proteins involved in the responses to heat stress, then revealing the diversity of adaptation mechanisms presented by this thermotolerant strain.
4. Genomic Common Bean Resources for Functional Analysis of the Rhizobia-common Bean Interaction
One way to discover adaptive alleles for SNF is to research large germplasm collections and to use association genetics so as to identify loci of interest. Both of these genetic approaches are based on the use of biodiversity and may eventually help in identifying the genes that plants use to respond to environmental challenges. In legumes, two wild species, Medicago truncatula and Lotus japonicus, as well as the cultivated soybean (Glycine max) have been adopted as models for genomic studies. The high degree of synteny among these model plants and their legume crops relatives, such as common bean, can be exploited to improve genetic maps and identify candidate genes for symbiotic genes [152]. In addition, research efforts have recently focused on developing the genomics resources, reference genome sequences and catalogues of mutant collections for nodulation efficiency, etc., required to carry out the identification of candidate genes within the common bean species.
4.1. Common bean genes involved in nodulation efficiency and comparison with relative legumes
Genomes of many legume species such as Lotus japonicus, [153], Medicago truncatula [154], soybean [155], chickpea [156] and common bean [157,158] have been entirely sequenced. Sequence conservation and genetic colinearity between common bean and soybean [159,160], which diverged from a common ancestor approximately 19 million years ago [155,161], allows for genomic information to be leveraged from one species to the other [162].
Comparative genomics has allowed for map-based cloning of genes required for nodulation in legumes; one example is the nodulation receptor kinase (NORK) gene that is required for both bacterial and fungal symbiosis [163].
NORK orthologs were located in the syntenic regions of four legume species (Medicago, alfalfa, Lotus and pea), and showed high conservation levels (similarity between 87 and 97%) [164]. Schmutz et al. [155] discovered 52 soybean nodulation genes, of which sixteen unigenes were seen to be expressed abundantly in common bean root tissues. Strong syntenic relationships between corresponding genomic regions were found for 20 SNF genes, where soybean and chickpea were the most closely related, followed by soybean and common bean; common bean and Medicago were, on the other hand, the most distantly related pair [165]. Other genomic analyses led to the characterization of 191, 92, 65 and 91 soybean, Medicago, Lotus and common bean orthologous and paralogous to functionally describe nodulation genes, respectively [166]. Common bean also controls the nodule number via an inbuilt signalling mechanism known as the Autoregulation of Nodulation (AON), which is mediated by novel peptide hormones called CLAVATA/ESR-related (CLE) [167]; hypernodulation is primarily controlled by the shoot [168] in both soybean and common bean species [169]. Hastwell et al. [170] identified 84 and 44 CLE peptide-encoding genes in soybean and common bean, respectively, and only three of the 44 genes identified in common bean did not have an apparent ortholog in soybean. Ferguson et al. [171] identified central components in the AON pathway of common bean, such as PvNARK which encodes a leucine-rich repeat receptor like protein kinase receptor (LRR-RLK). These kinases play an essential role in the signal transduction required in the early events of nodule formation. NF released by rhizobia are perceived by the LRR extracellular domain of the LRR-RLK in legume root cells, resulting in the initiation of the complex signaling cascade that ultimately leads to the formation of nodules [172]; in addition, it might also regulate root nodule numbers [171]. In soybean, AON involves long-distance signaling, requiring the interaction of RHIZOBIA-INDUCED CLE peptides (RIC1/RIC2), with NODULE AUTOREGULATION RECEPTOR KINASE (NARK) in the leaf and the subsequent inhibition of nodulation via the production of the nitrate-induced CLE peptide (NIC), which interacts with NARK in the root resulting in a nitrate-induced inhibitor [173]. In common bean, the homologous of RIC and NIC genes, PvRIC1,
PvRIC2 and PvNIC1, were identified [174], and as happened in soybean, PvRIC1 genes were expressed in inoculated common roots at early stages of rhizobial infection, while PvRIC2 was expressed at later time points in pre-fixing and mature nodules.
4.2. Transcriptome analysis of symbiosis
Through an examination of common bean mutants defective in nodulation and transcriptome dynamics, the root hair regulatory pathway activated in response to rhizobia inoculation or NF treatment was characterized.
Thus, the major advances originate from the discovery of plant genes that, if mutated, would affect the symbiotic function of the plant. By predominantly using mutagenesis with the chemical ethyl methyl sulfonate (EMS) followed by selection of the second mutant generation (M2), loss-of-function mutants were isolated for a large range of legumes (notably pea, soybean, Lotus and Medicago [175,176,177,178] including common bean (Table 2). Such mutants demonstrated that plant genes are essential for symbiotic success. Through the examination of this research in legumes, it was evidenced that NF-YC gene family has been involved in the development of determinate nodules, and that the NF-YC1 subunit is required for nodule organogenesis and rhizobial infection, as well as for the activation of cell cycle genes at early stages of the symbiotic interaction in common bean [179].
Table 2. Description of common bean mutants induced by EMS (Ethyl Methane Sulphonate) affected at different stages of nodule development.
| Cultivar |
Mutant name (gene) |
Main characteristics1 |
References |
| RIZ30 |
NOD238 (sym-2) |
Fix–, IN, small nodules, poor pod fertility |
[212,213] |
| NOD125 (sym-1) |
Nod– |
[214,215,216] |
| RIZ36 |
NOD109 (sym-2) |
Fix–, delayed nodulation, poor pod fertility |
[215,216] |
| R69 (nie) |
Ineffective nodulation, mr epistatic Park & Buttery, 1997; to nts, non allelic to sym-2 Ineffective nodulation, mr epistatic Park & Buttery, 1997; to nts, non allelic to sym-2 IN, MR epistatic to nts, non allelic to sym-2 |
[215,216] |
| R99 (nnd-2) |
nod–, MR, epistatic to nts and nie |
[215,216] |
| OAC Rico |
R699 (nie) |
nod+/fix–, Myc–, IN, MR |
[214,217,218] |
| R99 (nnd-2) |
nod–, Myc–, |
[168,219] |
| R32 (nts) |
NTSN, MR, delayed maturity, and slightly lower yield |
[168,218,219] |
| Swan Valley |
SV145 |
Nod–, IN, NTSN, MR |
[218] |
| 1nod–: no nodules; nod+: few nodules; fix–: no N fixation; myc–: resistant to mycorrhiza colonisation; IN: ineffective nodulation (non-functional nodules); NTSN: nitrate tolerant supernodulation; MR: monogenic trait and recessive gene. |
Transcriptomic datasets were released in order to perform a comprehensive analysis of the evolution of legume protein coding genes controlling the nodulation process. Ramírez et al. [180] sequenced 21,026 ESTs from various cDNA libraries (among other N-fixing root nodules and P-deficient roots) derived from the Negro Jamapa genotype. Approximately 10,000 ESTs were identified and at least 15 ESTs showed very high expression ratios in nodule-leaf and nodule-stem. These ESTs were identified as proteins for nodulation (leghemoglobin, nodulin 30 and early nodulin 55-2). In addition, a total of 41 independent common bean tentative consensus sequences (TCs) were differentially expressed in response to two R. etli strains of varying nodulation efficiency, of which nine were confirmed to differentially accumulate in efficient interactions [181]. Galeano et al. [182] developed a set of 313 intron-based markers for nodulation genes or genes expressed during nodulation. Quiceno-Rico et al. [183] cloned and characterized two cDNAs (PvuTRX1h and PvuASH1h) that encoded polypeptide homologs of trithorax group proteins, and demonstrated that PvuTRX1h is abundant at the early stages of nodule development, whereas PvuASH1h functions at the stages of highest N-fixing activity of the nodules. Montiel et al. [184] identified nine members of the Rboh gene family and found that PvRbohB accumulated abundantly in shoots, roots, and nodules. Islas-Flores et al. [185] found that the PvRACK1 increased during nodule development at 12–15 days post-inoculation. Barraza et al. [186] showed that trehalose accumulation in common bean is triggered by PvTRE1 downregulation, leading to an increased bacteroid number, nodule biomass, and nitrogenase activity and resulting in improved SNF. Dalla Via et al. [187] identified 2,606 genes from common bean that were differentially regulated at early stages of its interaction with Rhizobium etli. Formey et al. [136] identified new microRNAs and their corresponding targets in common bean that may function in the regulation of early nodulation events. The key regulatory role of miR172/AP2 during the rhizobia N-fixation symbiosis has been reported for soybean and common bean [173,188,189,190].
4.3. Mapping the genetic basis of symbiotic variation
Genetic variability for SNF and associated traits within common bean has been widely reported [119,191,192,193,194]. Rennie and Kemp [195] showed that cultivars with a longer vegetative growth period have a longer N fixation time and in consequence were high N fixers. Seventeen cultivars of common bean were investigated for symbiotic compatibility with 10 genetically diverse strains of bean rhizobia [196]; the strain USDA9001 was the most productive strain in terms of seed yield, and common bean varieties Italian Barlotti and BAT271 showed the highest values for both N fixation and plant weight. Rodi o et al. [197,198] characterized several genotypes of common bean for their ability to fix N with native R. leguminosarum and the reference strain R. tropici CIAT899. A correlation between shoot growth, N fixation rate and nodulation was observed, suggesting that growh performance and plant yield are dependent on SNF. Recently, Polania et al. [199] investigated the phenotypic variability in SNF ability of several common bean varieties under drought stress in a field harboring native Rhizobium strains. Four common bean cultivars showing both higher SNF efficiency and grain yield were selected, that could be used in common bean breeding programs for drought tolerance.
QTL analysis could be combined with a candidate gene approach to seek underlying genetic mechanisms for N use efficiency and SNF in common bean, and there are contrasting materials that can be used as sources of QTLs. Most bean breeding programs do not routinely select SNF because phenotyping is time-consuming, especially when large populations have to be screened. Furthermore, some of the main agronomic traits for breeding such as early flowering and determinate plant architecture are closely related to low N fixation efficiency [15,195]. Another handicap for the genetic improvement of SNF is its genetic complexity. SNF and nodulation related traits in common bean have a complex inheritance with the involvement of multiple genes [200,201,202,203,204,205]; additionally, their expression is significantly affected by environmental factors [206]. Several plant traits including nodulation, photosynthesis, biomass accumulation, and partitioning of photo-assimilates to the nodules are involved in SNF [207]. A non-additive genetic variation explains nodule number and shoot weight, while additive genetic variation was found for nodule weight in common bean [208]. Overall, all these factors limit the genetic enhancement of SNF, and therefore, the understanding of the genetic architecture of SNF in terms of genomic regions and/or genes involved is critical to expand knowledge of its genetic control.
The first QTL study on nodule number (NN) trait in common bean was performed by Nodari et al. [200], who reported four genomic regions for NN in a Recombinant Inbred Line (RIL) population derived from a cross between BAT93 and Jalo EEP558 varieties, and accounting for 50% of the phenotypic variation. Tsai et al. [201] and Souza et al. [202] screened the same RIL population under low and high N levels, finding new seven and five QTLs for NN under low and high N conditions, accounting for 34 and 28% of total phenotypic variation, respectively. DNA sequence comparison of markers closely linked to these QTLs allowed for the identification of some potential candidate genes. One of these genes encodes an auxin-responsive transcription factor, and might explain differences in N fixation ability between climbing and bushy cultivars [201]. One limitation of these studies is that NN is only an indirect measure of SNF, and in fact, it only gives an idea of nodulation efficiency, not of N fixation itself. Asfaw et al. [207] reported that QTLs for leaf chlorophyll content (SPAD) were the most consistent across environments. A RIL population derived from G2333 × G19839 was investigated for NN, nodule weight, SPAD, shoot dry weight, biomass N, and seed N under both field and greenhouse conditions, with QTLs for NN, nodule dry weight and Ndfa at harvest [203]. Overlapped QTLs for SPAD in the greenhouse and in the field were detected on Pv01 and Pv07. Two major QTLs for percent N fixed and total plant N fixed, contributed to 17 and 21% of phenotypic variation, respectively, and two candidate genes were detected underlying these QTLs: an auxin-responsive transcription factor, and AP2/ERF-domain-containing transcription factor. The former is associated with differences in growth, yield and N accumulation, while the latter with total amount of symbiotic N fixed. Farid [208] used single-nucleotide polymorphism (SNP) markers in a RIL population derived from a low × high-SNF navy bean population, and detected 42 QTLs for %Ndfa (Nitrogen derived from the atmosphere) on Pv01, Pv07 and Pv08. The QTL mapped in Pv08 accounted for up to 17% of the phenotypic variation; while other QTL located onin Pv07, accounting for 14% of the variation, was significantly associated with protein content. A correlation between %Ndfa and late flowering and maturity was detected, empowering the ability of plant to carry out N fixation [208]. Heilig et al. [209] identified 17 unique QTLs associated with SNF traits, most of them located in three large clusters on Pv01 (4 QTLs), Pv06 (6 QTLs), and Pv08 (6 QTLs), in a RIL from the cross of Puebla 152 × Zorro grown in the field and greenhouse under N-free conditions. Many of the QTLs were also associated with candidate genes expressed (transcription factors, transferases, and receptors involved in sensing rhizobacteria) in the nodules and roots.
A Genome Wide Association study (GWAs) focused on SNF traits in an Andean diversity panel of 259 common bean genotypes was carried out by Kamfwa et al. [205], and 11 significant SNPs were found closely linked to Ndfa in the shoot at flowering and in the seed. Several QTLs for Ndfa were confirmed on Pv03 and Pv07, and one SNP on Pv09 was associated with significant QTLs for Ndfa in the seed and shoot, SPAD, shoot biomass, and %N in shoot biomass. This close genetic association between N fixation and growth performance has to be taken into account in marker-assisted breeding programs in common bean for SNF. Three genes (Phvul.007G050500, Phvul.009G136200 and Phvul009G231000) were identified as candidate genes for Ndfa [205]. The Phvul.009G136200 gene on Chromosome (Chr) 09 codes for a LRR-RLK. The candidate gene Phvul.007G050500 on Chr07 also encodes for a LRR-RLK, with a role in nodule development [210]. The sequence of Phvul.009G23231000 showed a high correlation with that of genes coding for calmodulin, which are calcium transporting proteins, in Arabidopsis thaliana (TAIR) and Medicago (NCBI) [211]. Calmodulin transporters mediate the calcium spike following the Nod factor perception in the nodulation process. Calcium spiking, oscillations of the intracellular concentrations of Ca, is also an essential part of the signal transduction pathway required in nodule development [172], and therefore this gene is likely to play a significant role in nodule formation and subsequently, in N fixation efficiency.
5. Concluding Remarks
The natural diversity of rhizobia nodulating common bean has been widely studied, but, because of the promiscuity of this crop, novel symbionts of this legume should be expected and need to be screened. Information about rhizobia diversity in common bean serves to define host preferences and predominance of strains, to study the dynamics of exchange of genetic material, and provides a basis for the proposal of evolutionary trends. The diversity studies also reveal that each of the common bean-rhizobium associations coevolved independently after geographical separation, as did their genetic pools. Investigation about the structure of the indigenous rhizobial populations and their coevolution with the host plant could greatly contribute to better understanding and overcoming the frequent reports of nodulation failure. Molecular markers associated with nodulation genes are available in common bean, and QTL mapping studies showed that genes with varying effects seem to control N fixation. To date, few major QTLs and candidate genes have been reported in this legume. However, nodulating genes in model legumes have been cloned and several of their orthologs determined in common bean. Clearly, the evaluation of natural rhizobia diversity associated with common bean, making use of its well-characterized common bean biodiversity and feature-rich genomic tools, is becoming a powerful strategy of investigation, as are breeding cultivars for high symbiotic efficiency.
Acknowledgments
This work was financially supported by the Ministerio de Economía y Competitividad (RTC2016-4941-2 and AGL2014-51809R) and UE-FEDER Program.
Conflict of Interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: 



