Diabetes education—Cornerstone in management of diabetes mellitus in Jamaica

1.   Introduction

The interconnection between the dynamical behavior of discrete and continuous systems is referred to as a hybrid class. The concept of hybrid systems can be utilized to study the discrete dynamics of a model whenever the continuous form of the system has a suppressed effect. In networking, hybrid systems maximize the impact of new technology by integrating newly developed techniques with existing ones, thereby enhancing the efficiency of the constructed model. This type of system has gained remarkable attention in various evolving fields, such as networking and communications, industries, and circuit models ^[1,2,3]. The study of continuous-time models with switches at discrete time instants is referred to as switched systems. By abstracting away the discrete behavior and focusing on the possible switching patterns within a class, it is possible to derive switched systems from hybrid models. In the control design of systems with sub-modules, the switching mechanism plays a crucial role. This mechanism is categorized based on two criteria: time-dependent and state-dependent switches. In the case of switches which are dependent on the state, the space $\mathfrak{R}^{n}$ is divided into a set of operating regions by a family of switching sequence. Now each of these regions is interlinked with a sub-module which is continuous. When the trajectory of the system cuts through switching surface, the state response of the system suddenly undergoes a change and jumps to a new region by means of a reset map, whereas, if we consider a switching sequence which is time dependent the system consists of a piecewise constant switching signal $\mathtt{δ}:[0, \infty] \rightarrow \mathcal{P},$ where $\mathcal{P}$ is a finite positive set of integers. The discontinuities of a function $\mathtt{δ}$ at finite time instant is called switching time signals. Here, $\mathtt{δ}$ defines the active subsystem at each time instant. Existence of solution and its uniqueness for the uncertain class of the switched fractional model was presented in ^[4]. Positive solutions of switching models was established by ^[5]. Switching topologies of the multi-agent model was analyzed in ^[6].

The examination of system behavior in the presence of time delay is a crucial aspect while designing physiological and circuit systems. Moreover, analyzation of delay effect has gained even more attention while designing control models. Significant study time-delay control models can be found in ^[7,8,9]. Controllability is one of the most important and effective aspects of studying and manipulating the designed model according to specific requirements. This approach helps refine differential models. The impact of impulses on a system plays a vital role in designing the control input, as it requires formulating a piecewise control input for each interval. Few methods to study the impulsive control systems and their stability are found in ^{[10,11,12,13]}. When it comes to nonlinear controllability, the two vital techniques used are fixed point and differential geometry ^{[14,15,16,17]}. Switched system combined with impulsive effects is more efficient to model the discontinuous dynamics. Existing literature provides a great range of solution methods for hybrid systems. ^[18] et al. discussed the controllability of switch perturbed system with delays. The geometric method to analyze the reachability of the switched linear system was presented in ^[19]. Controllability of multi-delay switched models was presented in ^[20]. Some recent results on relative cotrollability of fractional order systems can be found in ^[21,22]. There are very few works pertaining to the analysis on stability and controllability of the switched fractional system. To mention a few, T. Kaczorek in ^[23] established the asymptotic behavior of the linear switched positive fractional system. Stability of impulsive switched fractional conformable system was discussed in ^[24]. Boundedness and stability of switched fractional models over finite time period was discussed in ^[25]. In ^[26], the authors discussed the controllability criteria for the Hilfer switched dynamical model. Relative controllability of the switched nonlinear fractional order system was established in ^[16]. Study on the control results of the nonlocal switching system can be found in ^[27]. Finite-time stability (FTS) refers to the study of whether a system's state remains within a predefined threshold over a fixed time interval. In other words, FTS ensures that the system's solution does not exceed a certain bound within a given time horizon, regardless of external disturbances or initial conditions. Unlike traditional asymptotic stability, which focuses on long-term behavior, FTS is particularly useful in scenarios where maintaining system constraints over a finite duration is critical, such as in control applications, robotics, and networked systems.

One of the key criteria for achieving FTS is ensuring that the system variables remain bounded within the specified time frame. This boundedness is essential in many real-world applications where transient behavior plays a crucial role, such as in aerospace systems, power grids, and biological models. Various techniques, including Lyapunov-based methods, comparison principles, and differential inequalities, are commonly employed to establish sufficient conditions for finite-time stability.

Due to its significance in practical applications, FTS has been a subject of extensive research in recent years. Numerous studies explore different approaches to analyze and enhance FTS, particularly in hybrid and switched systems, where impulsive effects and delays introduce additional complexities. Researchers continue to develop novel methodologies and theoretical frameworks to improve stability guarantees in such systems, making FTS an active and evolving area of study in control theory and applied mathematics. Work presented in ^[28] analyzes the FTS of neutral fractional system in-terms of fixed point results. Thresholds for impulsive singular systems to admit FTS was studied in ^[29]. Switching system stability was examined in ^[15,30]. A lot of informative results on FTS and how essentially it affects the analyzation of differential models are discussed in ^{[2,14,28,29,31,32,33,34]}. Comparative studies on stability and controllability of switching systems for various derivatives of fractional order are presented in ^{[15,26,35,36,37,38,39]}.

A careful examination of the aforementioned research works reveals that the general form of the solution is not easily deduced when the switched system is subject to time delays that occur at different time instants, particularly when coupled with nonlinear perturbations. This complexity presents a significant challenge in the analysis and control of such systems. In this context, this work investigates the finite-time stability and relative-type control criteria for fractional-order switched impulsive systems with delays occurring at distinct time instants. The aim is to develop effective control strategies that account for the interplay between time delays, nonlinearity, and fractional dynamics.

where the derivative order is $\mathtt{γ} \in(\frac{1}{2}\, ,1),$ the state response vector is $\mathcal{y}(\mathtt{τ})\in \mathfrak{R}^{n}$, and $\mathcal{w}(\mathtt{τ})\in \mathfrak{R}^{m}$. Then, $d > 0, \mathtt{ρ} > 0$ represents the time delay in the state and control input. $\mathtt{δ}(\mathtt{τ}):[0, \infty] \rightarrow \mathcal{S}_{1}^{\mathrm{K}} = {1, ..., \mathrm{K}}$ represents the switching function which is left continuous. At the instant $\mathtt{δ}(\mathtt{τ}) = j$ the $j^{th}$ subsystem $(\mathcal{H}_{j}, \mathcal{P}_{j}, \mathcal{Q}_{j})$ will be active. Jump at the instant $\mathtt{τ}_{l}$ is denoted by $\Delta{\mathcal{y}}(\mathtt{τ}_{l})+ \mathcal{y}(\mathtt{τ}_{l}^{-}) = \mathcal{y}(\mathtt{τ}_{l}^{+})$. The matrices are $\mathcal{H}_{j} \in \mathfrak{R}^{n\times n}, \mathcal{P}_{j}\in \mathfrak{R}^{n \times m}$ and $\mathcal{Q}_{j}\in \mathcal{C}([\mathtt{τ}_{0}, \mathtt{τ}_{l}]\times \mathfrak{R}^{n}\times \mathfrak{R}^{n}, \mathfrak{R}^{n}). \; \mathcal{E}_{\mathtt{δ}(\mathtt{τ})}:\mathfrak{R}^{n}\rightarrow \mathfrak{R}^{n},$ represents the impulsive function. Let $r_{l} = \mathtt{τ}_{l}-\mathtt{τ}_{l-1}$ represent the dwell time. At this point, it is important to note the switching signals and perturbations occur simultaneously and, therefore synchronize at $\mathtt{τ}_{l}.$ As a first step, we begin by deducing the solution of system (1.1) to analyze the stability and control results. Consider the following system

The authors in ^[40] proposed the solution of (1.2) as

where $\mathcal{Z}_{d}^{\mathcal{H}.^{\mathtt{γ}}}$ and $\mathcal{Z}_{d, \mathtt{γ}}^{\mathcal{H}.^{\mathtt{γ}}}$ will be described later. It is more complicated to evaluate the solution of (1.1) as in the form of (1.3); hence, we first establish improvised form of (1.3) to deduce the state response of (1.1).

While there is significant research on linear models and stability criteria for fractional-order differential equations, the nonlinear analytical methods specific to FTS systems remain less explored. Furthermore, there is a lack of generalization in the thresholds for FTS across different models. The study of generalized models and their identifiability or invertibility in the context of fractional delays has not been thoroughly established in previous works, especially concerning systems with nonlinear dynamics. The paper addresses identifiability and invertibility of generalized fractional models, which is not commonly explored in the literature. This contributes to the practical application of these models, particularly in fields involving parameter estimation and system identification. This integrated approach offers a more robust validation of the theoretical findings, providing a clear pathway from mathematical derivations to practical implementation. This was largely missing from earlier research where either theoretical or numerical methods were treated separately. We try to propose a piecewise continuous solution in the form of the delayed matrix Mittag Leffler function. Then, we deduce the require bound for (1.1) to admit finite time period stability. Further, analytical and fixed point techniques will be used to analyze the relative control results of (1.1). The framework of the article is outlined as follows:

In Section 2, we discuss the basic results, integral inequalities, and definitions which are required for theoretical study. The thresholds required for FTS are deduced in Section 3. In Section 4, we provide a nonlinear analytical study using theorems, such as the fixed point for (1.1), to be relatively controllable. In Section 5, we substantiate our study with concrete numerical simulations.

2.   Preliminaries

Let us take into account the vector space $\mathfrak{R}^{n}$ with $\| \mathcal{ H}\| = \sqrt{\lambda_{max}(\mathcal{H}^{T}\mathcal{H})}$ as the matrix norm, where $\lambda_{max}(\mathcal{H})$ is the largest eigenvalue of the matrix $\mathcal{H}$. Then, $\mathcal{J} = P.C. ([\mathtt{τ}_{0}-d, \mathtt{τ}_{N}], \mathfrak{R}^{n})$ denoted the piecewise continuous Banach space function. Let $\| \mathcal{y}\| = \sup\{\|\mathcal{y}(\mathtt{τ})\|, \mathtt{τ} \in \mathcal{J}\}.$ Moreover, let $\| \mathcal{y} \|_{L^{2}[\mathtt{τ}_{0}, \mathtt{τ}_{N}]} = \big(\int_{\mathtt{τ}_{0}}^{\mathtt{τ}_{N}} \| \mathcal{y}(\mathtt{ν}) \|^{2}d\mathtt{ν}\big)^{\frac{1}{2}}$ be the square functions which are integrable. The important assumption that we need to consider is $r_{l} > \max\{d, \mathtt{ρ}\}.$

Definition 2.1. ^[16] Let $\{\mathtt{τ}_{l}\}_{1}^{N}$ be a sequence of time periods. Then, $\mathtt{δ}:[\mathtt{τ}_{0}, \mathtt{τ}_{N}]\rightarrow \mathcal{S}_{1}^{K}$ is defined as an admissible switch if $\mathtt{δ}(\mathtt{τ}) = \mathtt{δ}(\mathtt{τ}_{l}^{+}) = \mathtt{δ}(\mathtt{τ}_{l+1}), \mathtt{τ} \in(\mathtt{τ}_{l-1}, \mathtt{τ}_{l}]$, and $\mathtt{δ}(\mathtt{τ}_{0}) = \mathtt{δ}(\mathtt{τ}_{0}^{+})$.

Definition 2.2. ^[16] For any given initial functions $\mathtt{ζ}_{1}(\mathtt{τ})$ and $\mathtt{ζ}_{2}(\mathtt{τ})$, the relative type controllability of (1.1) with respect to the $\{\mathtt{τ}_{l}\}_{l = 1}^{N}$ is guaranteed if for the admissible signal $\mathtt{δ}(\mathtt{τ})$ and the input $\mathcal{w}\in \mathcal{L}^{2}([\mathtt{τ}_{0}, \mathtt{τ}_{N}-\mathtt{ρ}], \mathfrak{R}^{m})$ in such a way that $\mathcal{y}(\mathtt{τ}_{N}) = \mathcal{y}_{f}.$

Definition 2.3. ^[7] The differential operator in the sense of Riemann-Liouville with order $\mathtt{γ}\in(0, 1)$ of a function $\mathcal{y}:[0, \infty)\rightarrow \mathfrak{R}$ is given as $(^{RL} {D}^{\mathtt{γ}} \mathcal{y})(\mathtt{τ}) = \dfrac{1}{\Gamma(1-\mathtt{γ})}\dfrac{d}{d\, \mathtt{τ}}\int_{0}^{\mathtt{τ}} \dfrac{\mathcal{y}(\mathtt{ν})}{(\mathtt{τ}-\mathtt{ν})^\mathtt{γ}} d\mathtt{ν}.$

Definition 2.4. ^[30] The differential operator in the sense of Caputo with order $\mathtt{γ}\in(0, 1)$ of a function $\mathcal{y}:[0, \infty)\rightarrow \mathfrak{R}$ is given as $(^{C} {D}^{\mathtt{γ}} \mathcal{y})(\mathtt{τ}) = (^{RL} {D}^{\mathtt{γ}} \mathcal{y})(\mathtt{τ})-\dfrac{\mathcal{y}(0)}{\Gamma(1-\mathtt{γ})}\mathtt{τ}^{-\mathtt{γ}}.$

Definition 2.5. ^[7] The Mittag-Leffler (ML) functions $\mathcal{E}_{\mathtt{γ}}$ and $\mathcal{E}_{\mathtt{γ}, \mathtt{ν}}$ are given as

Moreover, we have the integral identity

Definition 2.6. ^[16] The classical form of delayed type ML matrix is defined as $\mathcal{Z}_{d}^{\mathcal{H}\mathtt{τ}^{\mathtt{γ}}}:\mathfrak{R}\rightarrow \mathfrak{R}^{n \times n}$ with

where the notion $\Theta$ denoted the matrix with all entries zero and $\mathcal{I}$ is the identity matrix.

Definition 2.7. ^[16] The delayed type ML matrix of two parameters $\mathcal{Z}_{d, \mathtt{ν}}^{\mathcal{H}\mathtt{τ}^\mathtt{γ}}:\mathfrak{R}\rightarrow \mathfrak{R}^{n \times n}$ is of the type

Definition 2.8. ^[16] System (1.1) admits FTS with respect to $\{\mathcal{J}, \mathtt{δ}, \mathtt{ϵ}, \mathtt{µ}\}$, whenever $\max\{\| \mathtt{ζ}_{1}\|, \| \mathtt{ζ}_{2}\|\} < \mathtt{δ}$ and $\|\mathcal{w}\| < \mathtt{µ} \; \implies \; \| \mathcal{y}\| < \mathtt{ϵ},$ for all $\, \mathtt{τ} \in[\mathtt{τ}_{0}, \mathtt{τ}_{N}].$ Moreover $\mathtt{δ}, \mathtt{µ}, \mathtt{ϵ},$ are positive constants.

Lemma 2.1. ^[16] For $\mathtt{γ} > \dfrac{1}{2}, \mathtt{ν} > 0,$ then

Lemma 2.2. If $\mathtt{ζ}_{1} \in \mathcal{C}([\mathtt{τ}_{0}-d, \mathtt{τ}_{0}], \mathfrak{R}^{n})$, then the solution of (1.2) is formulated as

Proof. By following Theorem 3 ^[34], we get that

is a solution of $(^{c}D^{\mathtt{γ}}\mathcal{y})(\mathtt{τ}) = \mathcal{H}\mathcal{y}(\mathtt{τ}-d),$ with $\mathcal{y}(\mathtt{τ}) = \mathtt{ζ}_{1}(\mathtt{τ}), \mathtt{τ}_{0}-d \leq \mathtt{τ} \leq \mathtt{τ}_{0}$ as initial value.

Moreover, if $\mathtt{ζ}(0) = 0$, then $\mathcal{y}(\mathtt{τ}) = \int_{\mathtt{τ}_{0}}^{\mathtt{τ}} \mathcal{Z}_{d, \mathtt{γ}}^{\mathcal{H}(\mathtt{τ}-\mathtt{ν})^{\mathtt{γ}}}\mathcal{Q}(\mathtt{ν})d\mathtt{ν},$ as any solution of (1.2) has the form $\mathcal{y}(\mathtt{τ})+\mathcal{\tilde{y}}(\mathtt{τ}),$ and Eq (2.1) follows. □

As a direct consequence of the above lemma we present Lemma 2.3 without proof.

Lemma 2.3. Whenever $\mathtt{ζ}_{1}(\mathtt{τ}) \in \mathcal{C}([\mathtt{τ}_{0}-d, \mathtt{τ}_{0}], \mathfrak{R}^{n})$ and $\mathtt{ζ}_{2}(\mathtt{τ}) \in \mathcal{C}([\mathtt{τ}_{0}-\mathtt{ρ}, \mathtt{τ}_{0}], \mathfrak{R}^{n})$, for an admissible $\mathtt{δ}(\mathtt{τ})$, the state response of (1.1) can be formulated as

with $\mathtt{χ}_{n, l} = \prod\limits_{l = n}^{j+1} \mathcal{Z}_{d}^{\mathcal{H}_{\mathtt{δ}(\mathtt{τ}_{l})}(r_{l}-d)^{\mathtt{γ}}} = \mathcal{Z}_{d}^{\mathcal{H}_{\mathtt{δ}(\mathtt{τ}_{n})}(r_{n}-d)^{\mathtt{γ}}} \cdots \mathcal{Z}_{d}^{\mathcal{H}_{\mathtt{δ}(\mathtt{τ}_{j+1})}(r_{j+1}-d)^{\mathtt{γ}}}, n > j$ and $\mathtt{χ}_{n, n} = 1.$

H1: For the continuous function $\mathcal{Q}_{i}(.)$, there exists $\mathcal{F}_{i}, \mathcal{G}_{i}: \mathfrak{R}^{+} \rightarrow \mathfrak{R}^{+}$ so that

Therefore we get

where $\kappa_{i} = \mathcal{F}_{i}+\mathcal{G}_{i}\mathcal{b}_{i}, \mathcal{b}_{i} > 0.$

In order to make the paper in an easily readable manner, we consider the below given notions

where

3.   FTS result

The primary focus of this section is to avoid the Lyapnouv method and to reduce the conservative criterias to establish the stability over the bounded interval. Let

Then,

Theorem 3.1. FTS of system (1.1) is guarenteed if the following inequality holds:

where

Proof. Taking norm of Eq (2.2) on the interval $(\mathtt{τ}_{l-1}, \mathtt{τ}_{l}]$, we get

where $r = \max {r_{l}}, l = 1, 2..., N.$ Now, let $\Delta_{1} = \sum_{l = 1}^{n+1}\mathtt{ϕ}_{n+1, l}$ and $\Delta_{2} = \sum_{l = 2}^{n+1}\mathtt{ϕ}_{n+1, l}$, then we have

Then, while comparing the above inequality with the GI theorem ^[41], we formulate

□

4.   Relative controllability result

As an initial step to analyze the relatively controllable criteria of (1.1), we begin by formulating the following Grammian matrix.

where $\mathtt{δ}(\mathtt{τ})$ is a switching signal.

where

As a next step, we construct the operator $\sigma:\mathcal{J} \rightarrow \mathcal{J},$

The technique of the fixed point argument will be utilized for our theoretical analyzation.

Lemma 4.1. ^[42] If $\mathscr{D}$ is a closed convex subset of a banach space and if $\sigma : \mathscr{D} \rightarrow \mathscr{D}$ is an operator which is completely continuous, then there exists at least one fixed point for $\sigma$ in $\mathscr{D}.$

H2: Let $\mathtt{δ}(\mathtt{τ})$ be a switching signal which is admissible and satisfies the condition Rank $(\mathcal{M}) = n.$

Theorem 4.1. If the condition

holds then relative controllability of (1.1) is well-established.

Proof. We need to prove that $\sigma$ has a fixed point

To show $\tilde{\omega}\in \mathfrak{R}^{+}$ in such a way that $\sigma(\Gamma(\tilde{\omega}))\subset \Gamma(\tilde{\omega})$, we use the contradiction method to establish this result. Let there exist a possibility to find $\mathcal{y} \in \Gamma(\tilde{\omega})$ in such a way $\| \sigma \mathcal{y}\| > \frac{\omega}{2},$ then we have the following estimations.

When $\mathtt{τ} \in(\mathtt{τ}_{0}, \mathtt{τ}_{0}+\mathtt{ρ}],$

for $\mathtt{τ} \in (\mathtt{τ}_{0}+\mathtt{ρ}, \mathtt{τ}_{1}]$,

for $\mathtt{τ} \in (\mathtt{τ}_{n}, \mathtt{τ}_{n+1}]$,

where

As $U_{k}\geq 1,$ we have

where

Therefore, we obtain

which conflicts our assumed fact $\mathtt{θ} < 1,$ hence

Now we proceed to prove that $\sigma:\Gamma(\tilde{\omega})\rightarrow \Gamma(\tilde{\omega})$ is completely continuous.

$\mathcal{S}_{1}:$ The operator $\sigma$ is continuous.

If ${\mathcal{y}_{k}}$ converges to $\mathcal{y}$ in $\Gamma(\tilde{\omega})$, then continuity of $\mathcal{Q}_{l}$ follows from the fact

Therefore

where

Then, it is straightforward to view $\left\| \beta_{\mathcal{y}_{\, k}}-\beta_{\mathcal{y}}\right\| \rightarrow 0$ when $\left\|\mathcal{y_{\, k}} -\mathcal{y}\right\| \rightarrow 0,$ from which we get $\left\|\sigma \mathcal{y_{\, k}} -\sigma \mathcal{y}\right\| \rightarrow 0$ as $\left\|\mathcal{y_{\, k}} -\mathcal{y}\right\| \rightarrow 0$; hence, $\sigma$ is continuous.

$\mathcal{S_{2}}:\,$ The operator $\sigma$ is compact.

Consider $\Gamma_{0}$ to be a subset of $\Gamma(\tilde{\omega})$, which is bounded. Then, it is easy to view that $\sigma(\Gamma_{0}) \subset\Gamma(\tilde{\omega})$ is bounded uniformly on $[\mathtt{τ}_{0}-d, \mathtt{τ}_{N}]$.

Then, for $\mathtt{τ}_{0} < \mathtt{τ} < \mathtt{τ}+\mathtt{ϵ}\leq\mathtt{τ}_{1}$ and $\mathcal{y} \in \Gamma_{0}$, we get

where $\iota = \max\{\| \mathtt{ζ}_{1} \|, \|\mathcal{w_{y}}\|_{\mathtt{τ} \in [\mathtt{τ}_{0}, \mathtt{τ}_{1}-\mathtt{ρ}] }\}.$ As, we know that $\mathcal{Z}_{d}^{\mathcal{H}_{\mathtt{δ}(\mathtt{τ}_{1})} (\cdot)^{\mathtt{γ}}}$ and $\mathcal{Z}_{d, \mathtt{γ}}^{\mathcal{H}_{\mathtt{δ}(\mathtt{τ}_{1})} (\cdot)^{\mathtt{γ}}}$ are continuous functions and $\left\|(\sigma \mathcal{y})(\mathtt{τ}+\epsilon)-(\sigma \mathcal{y}(\mathtt{τ}))\right\|\rightarrow 0$ as $\mathtt{ϵ} \rightarrow 0$.

Further, for $\mathtt{τ}_{n-1} < \mathtt{τ} < \mathtt{τ}+\mathtt{ϵ}\leq\mathtt{τ}_{n}$ and $\mathcal{y} \in \Gamma_{0}$, we get

Analogous to the previous method, we get $\left\|(\sigma \mathcal{y})(\mathtt{τ}+\epsilon)-(\sigma \mathcal{y})(\mathtt{τ})\right\|\rightarrow 0,$ whenever $\mathtt{τ} \in (\mathtt{τ}_{n-1}, \mathtt{τ}_{n}].$ Moreover, we can conclude the equi-continuous of $\sigma(\Gamma_{0})$ on $(\mathtt{τ}_{0}-d, \mathtt{τ}_{N}]$. Then, $\sigma(\Gamma_{0})$ is relatively compact by the application Ascoli theorem. Then, from the above argument, we conclude that $\sigma$ is compact. Hence, $\tilde{\mathcal{y}} \in \sigma(\tilde{\omega})$ is relatively controllable. □

5.   Case in point

Example 5.1. Let us consider the system (1.1) with the below given choice of system parameters

Moreover, $\mathtt{τ}_{0} = 0, \mathtt{τ}_{1} = 0.2, \mathtt{τ}_{2} = 0.4, d = 0.1, \iota = 0.1.$ Let

It is straightforward to note that $\|\mathcal{Q}_{l}(\cdot)\|\leq \kappa_{l}(\omega), l = 1, 2.$

Now, let us fix

Then, on calculation we get $\| \mathcal{M}^{-1}\| \leq 7.153.$

Moreover, $G_{0} \leq 0.10, \quad G_{1}\leq 0.61, \quad G_{2} \leq 0.83, \quad L_{1}\leq 0.06, \quad L_{2}\leq 0.07, \quad V_{1}\leq 0.46, \quad V_{2} \leq 0.47,$ $P_{0}\leq 1.67, \quad R_{1} \leq 0.26, \quad R_{2} \leq 0.18, \quad \; P_{1} = 0.071.$

Then, by substituting the above values in (4.1), we get $\mathtt{θ} < 1.$ Thus, our considered form of switching system (1.1) is controllable relatively.

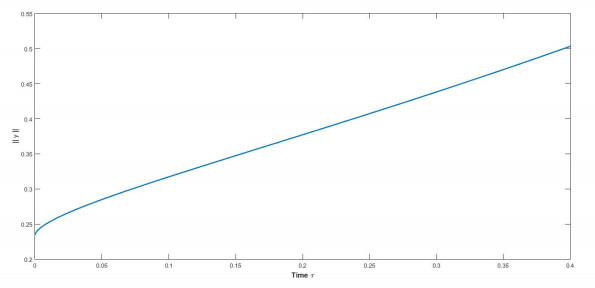
The FTS of (1.1) for the above choice of system parameters is shown in Table 1. Furthermore, the norm of the solution for the system in (1.1) is presented in Figure 1.

6.   Concluding remarks

In the presented work, we have considered a class of switching impulsive fractional control systems. An explicit form of the solution for (1.1) was derived using the delayed parameters ML function. Stability of the system was then analyzed by constructing appropriate thresholds with Gronwall's inequality. Furthermore, for an admissible switching signal we constructed an appropriate control input that is piecewise continuous over the given interval to determine the relatively controllable criteria of (1.1) with nonlinear arguments and impulses. Finally, a concrete numerical simulation is provided to substantiate the theoretical results. One of the challenging problems arising from this study is when the impulses are of the non-instantaneous type, which will be addressed in our future work. Moreover, the study of this problem will remain an interesting and active research field for future studies.

Author contributions

P. K. Lakshmi Priya, K. Kaliraj and Panumart Sawangtong: Conceptualization, methodology, formal analysis, software, writing – original draft and writing – review & editing. All authors of this article have been contributed equally. All authors have read and approved the final version of the manuscript for publication.

Use of Generative-AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research was funded by National Science, Research and Innovation Fund (NSRF), and King Mongkut's University of Technology North Bangkok with Contract no. KMUTNB-FF-68-B-33.

Conflict of interest

All authors declare no conflicts of interest in this paper