The relationship between facet tropism and lumbar disc herniation in patients with low back pain

1.   Introduction

Fluid flows in branching tubes are common in many biological and industrial applications such as physiological branching flows and flows through pipe and duct networks (see, for instance, ^{[1,2,3,4,5,6,7,8]}). This subject is extensively studied in both theoretical and practical points of views. A mathematical model of fluid flows in a network of thin tubes has been derived in ^[9] from the asymptotic expansion of Navier–Stokes equations. Consistent asymptotic analysis of Navier–Stokes equations in thin tube structures, by letting the diameter of the tubes tend to zero, has been recently studied in a series of papers, such as ^[10] and ^[11]. The Navier–Stokes equations with pressure boundary conditions in the junctions of thin pipes are considered in ^[12] and ^[13], where approximations based on Leray and Poiseuille problems are constructed therein.

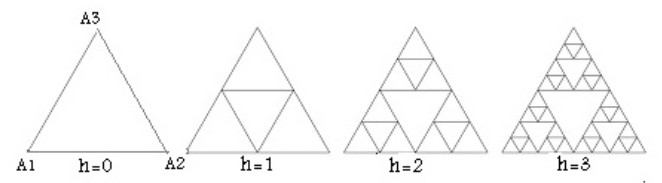
Let $ h $ be a positive integer. Let $ G_{h} $ be the pre-fractal polygonal curve obtained after $ h $-iterations of the contractive similarities of the Sierpinski gasket $ G $ (see Figure 1). We consider a network of circular cylindrical pipes whose axes are the sides of the polygon $ G_{h} $. We assume that these pipes are narrow axisymmetric tubes of radius $ \varepsilon _{h} $ very small with respect to the length $ 2^{-h} $ of each side of $ G_{h} $. We consider an incompressible fluid flow in the bounded domain $ \Omega ^{h} $ consisting of these pipes connected, after local adjustments near the bifurcation points, through smooth thin regions centered at the vertices of $ G_{h} $ (see Figure 4). We suppose that each pipe is split into two principal regions: junction zones of length $ \varepsilon _{h}\ln \left(1/\varepsilon _{h}\right) \ll $ $ 2^{-h} $ linked to the ends of the pipe and the rest of the pipe. We suppose that the fluid flow in $ \Omega ^{h} $ is driven by some volumic forces and governed by Stokes equations with boundary conditions for the velocity and the pressure on the external boundary of $ \Omega ^{h} $ and inner continuity conditions for the normal velocity on the interfaces between the junction zones and the rest of the pipes (see Section 2 for more details). We assume that the flow in the junction zones is controlled by a typical Reynolds number $ \text{Re}_{{\mathbf{j}}, h} $.

The main focus of this paper is to study the asymptotic behavior of the fluid flowing through the branching pipes as the radius of the tubes tends to zero and the sequence of pre-fractal curves converges in the Hausdorff metric to the Sierpinski gasket $ G $. Using $ \Gamma $-convergence methods (see, for instance, ^[14] and ^[15]), we prove that the effective potential energy of the fluid turns out to be of the form

where $ v $ is the fluid velocity, $ \mu $ is the fluid viscosity, $ \mathfrak{m} \left(\Theta \right) $ is the average value (see Eq. (6.10)) of the solution $ \Theta $ of boundary value problem (6.5), $ \dfrac{1}{ \mathfrak{m}\left(\Theta \right) \mathcal{H}^{d}\left(G\right) } $ is the permeability of the Sierpinski gasket $ G $, $ \mathcal{H}^{d} $ being the $ d $ -dimensional Hausdorff measure on $ G $ where

stands for the fractal dimension of $ G $, $ Z $ is a random matrix given in Section 4 (see Eq. (4.15)–(4.18)), $ {\boldsymbol{\nu}} $ is a singular measure with respect to the Hausdorff measure $ \mathcal{H} ^{d} $ on $ G $ called the Kusuoka measure (see Eq. (4.11)), which, according to ^[16], is a Gibbs measure of special kind, $ V^{\infty } $ is the admissible velocities space (see Definition 2$ _{3} $), and

Depending on the values of $ \sigma $, we obtain different asymptotic problems:

1. If $ \sigma \in \left(0, +\infty \right) $, then $ \text{Re}_{{\mathbf{j}}, h} = O\left(\varepsilon _{h}\right) $. In this case, the effective flow is described (see Theorem 3) by the following singular Brinkman equation in the Sierpinski gasket $ G $:

where $ u $ is the fluid velocity, $ p $ is the pressure, $ \Delta _{G} $ is the Laplace operator on the Sierpinski gasket (see Lemma 4), $ f $ is the effective source term, $ n = \left(1, 0\right) $ on the horizontal part of $ G $, $ n = \left(1/2, \sqrt{3}/2\right) $ on the part of $ G $ which is perpendicular to the unit vector $ \left(-\sqrt{3}/2, 1/2\right) $, and $ n = \left(1/2, -\sqrt{3}/2\right) $ on the part of $ G $ which is perpendicular to the unit vector $ \left(\sqrt{3}/2, 1/2\right) $. This equation includes the singular Brinkman viscous resistance term $ -\dfrac{2\mu \pi \mathfrak{m} \left(\Theta \right) \mathcal{H}^{d}}{3\sigma \mathcal{H}^{d}\left(G\right) }\Delta _{G}\left(u\right) $, which is due to the viscous behavior of the fluid flow at the junction zones, and the singular Darcy resistance term $ \dfrac{\mu \pi \mathcal{H}^{d}}{\mathfrak{m}\left(\Theta \right) \mathcal{H}^{d}\left(G\right) }u $.

2. If $ \sigma = +\infty $, then $ \text{Re}_{{\mathbf{j}}, h} $ $ = O\left(1\right) $ or $ \text{Re}_{{\mathbf{j}}, h}\longrightarrow \infty $ as $ h\longrightarrow \infty $. In this case, the term $ \dfrac{\mu \pi \mathfrak{m }\left(\Theta \right) }{3\sigma }\int_{G}\nabla v.Z \nabla v d{\boldsymbol{\nu}} $ in (1.1) disappears and the flow is governed by singular Darcy's law in the Sierpinski gasket $ G $.

3. If $ \sigma = 0 $, then $ \text{Re}_{{\mathbf{j}}, h} $ $ = O\left(\varepsilon _{h}^{\alpha }\right) $ with $ \alpha > 1 $. In this case, the energy $ F_{\infty }\left(v\right) $ is finite only if $ \int_{G}\nabla v.Z\nabla v d{\boldsymbol{\nu}} = 0 $, which implies that the velocity of the fluid flow is asymptotically constant in the Sierpinski gasket $ G $.

The study of asymptotic analysis of boundary value problems in domains with fractal boundaries or containing thin inclusions developing a fractal geometry has been recently addressed in a series of papers (see, for instance, ^{[17,18,19,20,21,22,23,24,25,26,27,28,29]}). The problems obtained at the limit generally consist of singular forms containing fractal terms. The problem considered in this work is quite different from the previous ones, as we deal here with the determination of the fluid motion through branching tubes having a fractal structure. The overall effect of the pre-fractal branching networks on the fluid flow appears in the singular effective equation (1.4), according to the characteristics of the flow, as the radius of the tubes tends to zero and the sequence of pre-fractal curves converges in the Hausdorff metric to the Sierpinski gasket $ G $. The asymptotic representation of the solution of the original singularly perturbed problem includes local perturbations representing the flow in the boundary layers in the junction zones. These local perturbations are solutions of Leray problems in semi-infinite cylinders representing the rescaled junctions. The main novelty of this paper lies in the construction of these local perturbations as well as the derivation of the effective flow described above by singular Brinkman and Darcy laws on the fractal $ G $ with divergence-free velocity in a fractal sense specified in Definition 2$ _{2} $ in Section 5.

The problem considered in this work has some implications for modeling the behavior of fluid flows in various complex geometrical configurations of branching tubes. An important field to which this model is closely related is the behavior of fluid flows in some physiological structures such as lung airways (see, for instance, ^[1] and ^[30]) the cardiovascular system and cerebral arteriovenous (see, for instance, ^[30], ^[31], and ^[32]). It has been shown that physiological branching networks exhibit fractal structures for minimal energy dissipation (see, for instance, ^[33] and ^[34]). In particular, blood vessels have self-similar structures with optimal transport property of their fractal networks (see, for instance, ^[35]). Blood has been treated in ^[31] as a homogeneous, incompressible, Newtonian viscous fluid, making the assumptions that the flow is steady and axisymmetric with sufficiently small Reynolds number so that the flow is laminar. The authors observed that the overall effect of the non-Newtonian characteristics would be small.

The present investigation on fractal branching flows provides some motivations in the haemodynamics. The blood vessels can be illustrated, under some simplifying assumptions, by the network $ \Omega ^{h} $ of narrow branching tubes with laminar flow far ahead of the bifurcations and boundary layer flow near the bifurcations, where the local Reynolds number is the most effective factor controlling the flow throughout the whole network.

This paper is organized as follows. The statement of the problem is presented in Section 2, with a subsection reserved for the nomenclature and another devoted to the position of the problem. In Section 3, we formulate the main results of this work. In Section 4, we introduce the energy forms, the Kusuoka measures, and gradients on the Sierpinski gasket. Section 5 is devoted to some a priori estimates and compactness results. Section 6 is consecrated to the proof of the main results. A final conclusion is made in Section 7.

2.   Statement of the problem

2.1.   Nomenclature

2.2.   Position of the problem

Let us consider the points of the plane $ xOy $: $ A_{1} = \left(0, 0\right) $, $ A_{2} = \left(1, 0\right) $, and $ A_{3} = \left(1/2, \sqrt{3}/2\right) $. Let us denote $ \left\{ \psi _{i}\right\} _{i = 1, 2, 3} $ as the family of contractive similitudes defined on $ \mathbb{R}^{2} $ by

Let $ \mathcal{V}_{0} = \left\{ A_{1}\text{, }A_{2}\text{, }A_{3}\right\} $ be the set of vertices of the equilateral triangle $ A_{1}A_{2}A_{3} $. We define inductively

for every $ h\in \mathbb{N} $, and set

The Sierpinski gasket, which is denoted here by $ G $, is defined as the closure of the set $ \mathcal{V}_{\infty } $

We consider the graph $ G_{h} = \left(\mathcal{V}_{h}, E_{h}\right) $, where $ E_{h} $ is the set of edges $ \left[a_{h}, b_{h}\right] $; $ a_{h}, b_{h}\in \mathcal{V}_{h} $, such that $ \left\vert a_{h}-b_{h}\right\vert = 2^{-h} $; $ \left\vert a_{h}-b_{h}\right\vert $ being the Euclidean distance between $ a_{h} $ and $ b_{h} $ (see Figure 2). The graph $ G_{h} $ is then the standard approximation of the Sierpinski gasket, which means that the sequence $ \left(G_{h}\right) _{h} $ converges, as $ h $ tends to $ \infty $, in the Hausdorff metric, to the Sierpinski gasket $ G $.

We denote $ Card\left(\mathcal{V}_{h}\right) $ as the number of vertices of $ \mathcal{V}_{h} $. We can easily check that

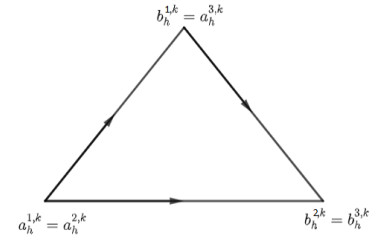
Let $ k\in \left\{ 1, 2, ..., 3^{h}\right\} $. We denote $ T_{h}^{k} $ as the $ k^{th} $ triangle of the graph $ G_{h} $ obtained at the step $ h $. Let $ n^{k} $ be the unit normal to $ T_{h}^{k} $. Then, $ n^{k} = \left(-\sqrt{3}/2, 1/2\right) $, $ n^{k} = \left(\sqrt{3}/2, 1/2\right) $, or $ n^{k} = \left(0, 1\right) $. We denote $ E_{h}^{1, k} = \left[a_{h}^{1, k}, b_{h}^{1, k}\right] $ as the edge of $ T_{h}^{k} $, which is normal to $ n^{k} = \left(0, 1\right) $, $ E_{h}^{2, k} = \left[a_{h}^{2, k}, b_{h}^{2, k}\right] $ as the edge of $ T_{h}^{k} $, which is normal to $ n^{k} = \left(-\sqrt{3}/2, 1/2\right) $, and $ E_{h}^{3, k} = \left[a_{h}^{3, k}, b_{h}^{3, k}\right] $ as the edge of $ T_{h}^{k} $ which is normal to $ n^{k} = \left(\sqrt{3}/2, 1/2\right) $ (see Figure 3).

Let us consider the following rotation matrices:

$ Id_{\mathbb{R}^{3}} $ being the $ 3\times 3 $ identity matrix. We also define the change of variables $ y_{h, 1}^{i, k} $, $ y_{h, 2}^{i, k} $, $ x_{3} $; $ i = 1, 2, 3 $, for every $ h\in \mathbb{N} $, every $ k\in \left\{ 1, 2, ..., 3^{h}\right\} $, and every $ x = \left(x_{1}, x_{2}, x_{3}\right) \in \left[a_{h}^{i, k}, b_{h}^{i, k}\right] \times \mathbb{R} $, by

Let $ S $ be the unit disk of $ \mathbb{R}^{2} $ centred at the origin. Let $ \left(\varepsilon _{h}\right) _{h\in \mathbb{N}} $ be a decreasing sequence of positive numbers, such that

We define, for $ h\in \mathbb{N} $, $ k\in \left\{ 1, 2, ..., 3^{h}\right\} $, and $ i = 1, 2, 3 $, the tube $ \Pi _{k}^{h, i} $ by

We define the interfaces

We then set

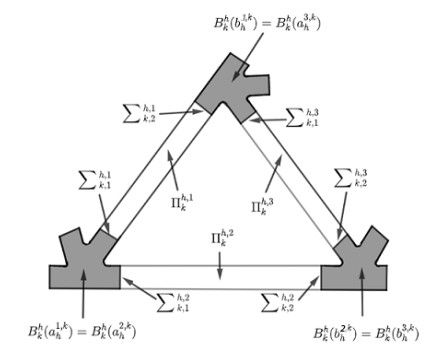
We now define thin, smooth regions which ensure the junctions between the tubes $ \Pi _{k}^{h, i} $. Let $ B_{k}^{h}\left(a_{h}^{i, k}\right) $ and $ B_{k}^{h}\left(b_{h}^{i, k}\right) $ be bounded open sets of thickness of order $ 2\varepsilon _{h} $ and centered at the points $ \left(a_{h, 1}^{i, k}, a_{h, 2}^{i, k}, 0\right) $ and $ \left(b_{h, 1}^{i, k}, b_{h, 2}^{i, k}, 0\right) $, respectively, such that $ \partial B_{k}^{h}\left(a_{h}^{i, k}\right) $ and $ \partial B_{k}^{h}\left(b_{h}^{i, k}\right) $ are $ C^{2} $-surfaces with

(see Figure 4).

We set

Let us define the pipe $ \Omega _{k}^{h, i} $; $ h\in \mathbb{N} $, $ k\in \left\{ 1, 2, ..., 3^{h}\right\} $, and $ i = 1, 2, 3 $, by

We consider the network $ \Omega ^{h} $ of interconnected pipes and its external boundary $ \Gamma ^{h} $ defined by

We consider a viscous incompressible fluid flow in $ \Omega ^{h} $. We suppose that this flow is essentially laminar except in the set $ \mathcal{ J}^{h} $ of the junction zones, where the main characteristics of the flow and their influence on the fluid motion will be analyzed. On the basis of works ^[12] and ^[13], we define the set $ \mathcal{J}^{h} $ as

where, for every $ k\in \left\{ 1, 2, ..., 3^{h}\right\} $ and $ i = 1, 2, 3 $,

Taking into account the typical scales in $ \Omega ^{h}\backslash \mathcal{J} ^{h} $, we suppose that the characteristic Reynolds number in these regions is of order $ \dfrac{2^{-h}}{\mu } $. The characteristic Reynolds number in $ \Omega ^{h} $ can be then defined as

where $ \text{Re}_{{\mathbf{j}}, h} $ is assumed to be a typical Reynolds number of the flow in the region $ \mathcal{J}^{h} $. According to ^[36], the product $ \mathrm{Eu}_{h}\text{Re}_{h} $ of the characteristic Euler number $ \mathrm{Eu}_{h} $ and the characteristic Reynolds number $ \text{Re}_{h} $ is the ratio between the caracteristic pressure and viscosity. Then, assuming that the characteristic pressure is the ratio between a constant normal force and the surface of the disk $ \varepsilon _{h}S $, we may write

According to the above equality, we suppose that the characteristic Euler number $ \mathrm{Eu}_{h} $ in the network $ \Omega ^{h} $ takes the form

On the other hand, as the diameter of any tube of the network $ \Omega ^{h} $ is $ 2\varepsilon _{h} $, we deduce, according to [37, page 98], that the ratio of the characteristic Froude number $ Fr_{h} $ to the characteristic Reynolds number $ \text{Re}_{h} $ is of order $ \varepsilon _{h}^{2} $. Accordingly, we suppose that the characteristic Froude number in $ \Omega ^{h} $ has the following scaling:

Since the characteristic Reynolds number is small in $ \Omega ^{h}\backslash \mathcal{J}^{h} $, we suppose that the inertia effects are negligible in the whole $ \Omega ^{h} $ and the flow is governed by the following Stokes equations:

where $ \dfrac{5^{h}}{3^{h+1}} $ is a scaling factor, which is associated to the ramification of the pre-fractal network $ \Omega ^{h} $ and determined by the decimation principle (see ^[38] for more details on scaling exponents governing some physical phenomena in fractal media), the source term $ f_{h} $ is the solution of the following problem posed in each tube $ \Omega _{k}^{h, i} $; $ k\in \left\{ 1, 2, ..., 3^{h}\right\} $ and $ i = 1, 2, 3 $,

where $ n $ is the outward unit normal on $ \partial \Omega _{k}^{h, i} $ and $ g_{h} $ is a $ L^{2}\left(\Omega ^{h}\right) $ function such that

$ \left\vert A\right\vert $ being the Lebesgue measure of the measurable and bounded subset $ A $ of $ \mathbb{R}^{3} $. The boundary conditions (2.25) are given, for every $ i = 1, 2, 3 $, by

where, in accordance with the divergence free of the velocity, the condition (2.25)$ _{2} $ ensures that the outward normal velocities are the same on the two interfaces $ \Sigma _{k, 1}^{h, i} $ and $ \Sigma _{k, 2}^{h, i} $, $ e_{1} = \left(1, 0, 0\right) $, and $ \dfrac{\partial p_{h}}{\partial n} $ is the normal derivative of the pressure on $ \Gamma ^{h} $; $ n $ being the outward unit normal on $ \Gamma ^{h} $.

Remark 1. The homogeneous Neumann boundary condition (2.25)$ _{3} $ on $ \Gamma ^{h} $ is justified as follows. According to [39, Chapter II], thin boundary layers are concentrated in the immediate neighborhood of the wall $ \Gamma ^{h} $ due to the homogeneous Dirichlet boundary condition for the velocity on $ \Gamma ^{h} $. The characteristic Reynolds number in these boundary layers, denoted here by $ \text{Re}_{w, h} $, is sufficiently large so that the viscous term $ \dfrac{1}{\text{Re}_{w, h}}\Delta u^{h} $ is negligible when one gets too close to the wall $ \Gamma ^{h} $. We deduce, according to [40, Remarks page 1119], that the boundary condition

obtained by taking into account equation (2.22)$ _{1} $ and the fact that $ f_{h}.n = 0 $ on $ \Gamma ^{h} $, can ostensibly be approximated by $ \mathrm{Eu} _{h}\dfrac{\partial p_{h}}{\partial n} = 0 $ on $ \Gamma ^{h} $, which implies that $ \dfrac{\partial p_{h}}{\partial n} = 0 $ on $ \Gamma ^{h} $.

Let us introduce the space $ V^{h} $ defined by

We state here a result of existence and uniqueness of a solution for problem (2.22) with boundary conditions (2.25).

Lemma 1. Problem (2.22)–(2.25) has a unique velocity solution $ u^{h}\in V^{h} $ and pressure solution $ p_{h}\in H^{1}\left(\Omega ^{h}\right) $, which is unique up to an additive constant.

Proof. Applying the divergence operator to the first equation of problem (2.22), using (2.23)–(2.24)$ _{1} $ and the boundary condition (2.25)$ _{3} $, we deduce that the pressure verifies the Neumann boundary value problem

This problem has a solution $ p_{h}\in H^{1}\left(\Omega ^{h}\right) $, which is unique up to an additive constant. On the other hand, as

for every $ v\in V^{h} $, the weak formulation of problem (2.22) can be written as, for every $ v\in V^{h} $,

Using the Poincaré inequality, we have

where $ C_{h} $ is a positive constant. Then, according to the Lax–Milgram theorem, we infer that problem (2.29) has a unique solution $ u^{h}\in V^{h} $.

Let us consider the functional $ F_{h} $ defined by

The velocity $ u^{h} $, solution of problem (2.29), is then the solution of the minimization problem

One of the main purposes of this paper is to prove the $ \Gamma $-convergence of the sequence of functionals $ \left(F_{h}\right) _{h} $ to the functional $ F_{\infty } $ defined in (1.1).

3.   The main result s

In this section we state our main results in this work. Let $ \mathcal{M}\left(\mathbb{R}^{3}\right) $ be the space of Borel regular measures on $ \mathbb{R}^{3} $. According to Proposition 8 in Section 5, we introduce the following topology $ \tau $:

Definition 1. We say that a sequence $ \left(v^{h}\right) _{h} $; $ v^{h}\in V^{h} $, $ \tau $-converges to $ \left(v, v^{\ast }, v^{\ast \ast }\right) $ if

where the symbol $ \overset{\ast }{\rightharpoonup } $ stands for the weak*-convergence of measures.

We formulate our result on the $ \Gamma $-convergence of the sequence of functionals $ \left(F_{h}\right) _{h} $ in the following

Theorem 2. We suppose that $ \sigma \in \left(0, +\infty \right) $. Then

1. ($ \lim \sup $ inequality) For every $ v\in V^{\infty } $, there exists a sequence $ \left(v^{h}\right) _{h} $, with $ v^{h}\in V^{h} $ and $ \left(v^{h}\right) _{h} $ $ \tau $-converges to $ \left(v, v^{\ast }, v^{\ast \ast }\right) $, where $ v^{\ast \ast } = 0 $, $ v^{\ast } = 0 $ on the part of $ G $ which is perpendicular to $ \left(0, 1\right) $, $ v^{\ast } = v\sqrt{3} $ on the part of $ G $ which is perpendicular to $ \left(-\sqrt{3}/2, 1/2\right) $, and $ v^{\ast } = -v\sqrt{3} $ on the part of $ G $ which is perpendicular to $ \left(\sqrt{3}/2, 1/2\right) $, such that

where $ V^{\infty } $ is defined in Definition 2$ _{3} $ of Section 5 and $ F_{\infty } $ is the functional energy defined in (1.1),

2. ($ \lim \inf $ inequality) For every sequence $ \left(v^{h}\right) _{h} $, such that $ v^{h}\in V^{h} $ and $ \left(v^{h}\right) _{h} $ $ \tau $ -converges to $ \left(v, v^{\ast }, v^{\ast \ast }\right) $, we have $ v\in V^{\infty } $, $ v^{\ast \ast } = 0 $ on $ G $, $ v^{\ast } = 0 $ on the part of $ G $ which is perpendicular to $ \left(0, 1\right) $, $ v^{\ast } = v\sqrt{3} $ on the part of $ G $ which is perpendicular to $ \left(-\sqrt{3}/2, 1/2\right) $, $ v^{\ast } = -v\sqrt{3} $ on the part of $ G $ which is perpendicular to $ \left(\sqrt{3}/2, 1/2\right) $, and

We are now in a position to formulate the asymptotic problem.

Theorem 3. Let $ \left(u^{h}, p_{h}\right) $ be the solution of problem (2.22) with boundary conditions (2.25). Under the hypothesis of Theorem 2, we have

1. The sequence $ \left(u^{h}\right) _{h} $ $ \tau $-converges to $ \left(u, u^{\ast }, 0\right) $, with $ u\in V^{\infty } $, $ u^{\ast } = 0 $ on the part of $ G $ which is perpendicular to $ \left(0, 1\right) $, $ u^{\ast } = u\sqrt{3} $ on the part of $ G $ which is perpendicular to $ \left(-\sqrt{3}/2, 1/2\right) $, and $ u^{\ast } = -u\sqrt{3} $ on the part of $ G $ which is perpendicular to $ \left(\sqrt{3}/2, 1/2\right) $. There exists $ p\in H_{Z}\left(G\right) $; $ H_{Z}\left(G\right) $ being the space defined in Definition 2 $ _{1} $ of Section 5, and $ f = \left(f_{1}, f_{2}, 0\right) \in L_{ \mathcal{H}^{d}}^{2}\left(G, \mathbb{R}^{3}\right) $, such that

where $ n = \left(1, 0\right) $ on the horizontal part $ G_{1} $ of $ G $, $ n = \left(1/2, \sqrt{3}/2\right) $ on the part $ G_{2} $ of $ G $ which is perpendicular to $ \left(-\sqrt{3}/2, 1/2\right) $, and $ n = \left(1/2, -\sqrt{3 }/2\right) $ on the part $ G_{3} $ of $ G $ which is perpendicular to $ \left(\sqrt{3}/2, 1/2\right) $,

2. The couple $ \left(u, p\right) $ is the solution of equation (1.4) stated in the Introduction.

4.   Energy forms on the Sierpinski gasket

4.1.   Standard Dirichlet forms

In this subsection we introduce the notion of Dirichlet forms on the Sierpinski gasket. For the definition and properties of Dirichlet forms, we refer to ^[41] and ^[42].

For any function $ w:\mathcal{V}_{\infty }\longrightarrow \mathbb{R} $, we define

We then define the energy $ \mathcal{E}_{G} $ on $ G $ by

with domain $ \mathcal{D}_{\infty } = \left\{ w:\mathcal{V}_{\infty }\longrightarrow \mathbb{R}:\mathcal{E}_{G}\left(w\right) < \infty \right\} $. According to [42, Theorem 2.2.6], every function $ w\in \mathcal{D} _{\infty } $ can be uniquely extended to be an element of $ C\left(G\right) $ still denoted by $ w $. Let us set

where $ \mathcal{E}_{G}\left(w\right) = \mathcal{E}_{G}\left(w\mid _{ \mathcal{V}_{\infty }}\right) $. Then, $ \mathcal{D\subset }C\left(G\right) \subset L_{\mathcal{H}^{d}}^{2}\left(G\right) $. We define the space $ \mathcal{D}_{\mathcal{E}} $ as

where $ \left\Vert.\right\Vert _{\mathcal{D}_{\mathcal{E}}} $ is the intrinsic norm

We denote $ \mathcal{E}_{G}\left(., .\right) $ as the bilinear form defined on $ \mathcal{D}_{\mathcal{E}}\times \mathcal{D}_{\mathcal{E}} $ by

from which we deduce, according to (4.2), that

where

The form $ \mathcal{E}_{G}\left(., .\right) $ is a closed Dirichlet form in the Hilbert space $ L_{\mathcal{H}^{d}}^{2}\left(G\right) $ and, according to [43, Theorem 4.1], $ \mathcal{E}_{G}\left(., .\right) $ is a local regular Dirichlet form in $ L_{\mathcal{H}^{d}}^{2}\left(G\right) $. This means that

1. (local property) $ w, z\in \mathcal{D}_{\mathcal{E}} $ with supp$ \left[ w\right] $ and supp$ \left[z\right] $ are disjoint compact sets $ \Longrightarrow $ $ \mathcal{E}_{G}\left(w, z\right) = 0 $,

2. (regularity) $ \mathcal{D}_{\mathcal{E}}\cap C_{0}\left(G\right) $ is dense both in $ C_{0}\left(G\right) $ (the space of functions of $ C\left(G\right) $ with compact support) with respect to the uniform norm and in $ \mathcal{D}_{\mathcal{E}} $ with respect to the intrinsic norm (4.5).

We deduce that $ \mathcal{D}_{\mathcal{E}} $ is injected in $ L_{\mathcal{H} ^{d}}^{2}\left(G\right) $ and is a Hilbert space with the scalar product associated to the norm (4.5). The second property implies that $ \mathcal{D}_{\mathcal{E}} $ is not trivial (that is, $ \mathcal{D}_{\mathcal{E} } $ is not made by only the constant functions). Moreover every function of $ \mathcal{D}_{\mathcal{E}} $ possesses a continuous representative. Indeed, according to [44, Theorem 6.3. and example 7$ _{1} $], the space $ \mathcal{D}_{\mathcal{E}} $ is continuously embedded in the space $ C^{\beta }\left(G\right) $ of Hölder continuous functions with $ \beta = \ln \dfrac{5}{3}/\ln 4 $.

Now, applying [45, Chap. 6], we have the following result:

Lemma 4. There exists a unique self-adjoint nonpositive operator $ \Delta _{G} $ on $ L_{\mathcal{H}^{d}}^{2}\left(G\right) $ with domain

dense in $ L_{\mathcal{H}^{d}}^{2}\left(G\right) $, such that, for every $ w\in \mathcal{D}_{\Delta _{G}} $ and $ z\in \mathcal{D}_{\mathcal{E}} $,

4.2.   Kusuoka measures and gradients

In this subsection we define the Kusuoka measure and the gradient on the Sierpinski gasket $ G $. For the definitions and properties of Kusuoka measures and gradients on fractals, we refer to ^{[46,47,48,49]}.

Let $ \varrho :\mathcal{V}_{\infty }\longrightarrow \mathbb{R} $. Then, according to [42, Proposition 3.2.1], there exists a unique $ \mathfrak{h}\in \mathcal{D}_{\infty } $ such that $ \mathfrak{h}|_{\mathcal{V} _{0}} = \varrho $ and

where $ \mathfrak{h} $ is called the harmonic function in $ G $ with boundary value $ \mathfrak{h}|_{\mathcal{V}_{0}} = \varrho $. On each $ \mathcal{V}_{h} $, $ h $ $ \in $ $ \mathbb{N}^{\ast } $, a harmonic function $ \mathfrak{h} $ verifies

(see [42, Proposition 3.2.1]), where $ \mathfrak{\psi } _{i_{1}...i_{h}} = \mathfrak{\psi }_{i_{_{1}}}\circ \cdots \circ \mathfrak{ \psi }_{i_{h}} $ and $ T_{i_{1}...i_{h}} = T_{i_{1}}...T_{i_{h}} $ with

Let $ M_{0} = \left\{ (x_{1}, x_{2}, x_{3})\in \mathbb{R}^{3}\text{; } x_{1}+x_{2}+x_{3} = 0\right\} $. Kigami ^[46] introduced the map $ \Phi :G\longrightarrow M_{0} $ defined by

with $ \mathfrak{h}_{i}\left(A_{j}\right) = \delta _{ij} $ for $ A_{j}\in \mathcal{V}_{0} $, where $ \delta _{ij} $ is, for $ i, j = 1, 2, 3 $, the Kronecker delta symbol. We have the following.

Proposition 5. [47, Proposition 4.4] If $ G_{H} = \Phi \left(G\right) $, then $ \Phi $ is a homeomorphism between $ G $ and $ G_{H} $. Moreover, define $ H_{i}:M_{0}\longrightarrow M_{0} $; $ i = 1, 2, 3 $, by

then $ G_{H} = \underset{i = 1, 2, 3}{\mathop{\cup }}H_{i}\left(G_{H}\right) $ and $ \Phi \circ \psi _{i} = H_{i}\circ \Phi $ for any $ i = 1, 2, 3 $.

$ G_{H} $ is called the harmonic Sierpinski gasket, which is the self-similar set associated with the collection of contractions $ \left\{ H_{1}, H_{2}, H_{3}\right\} $ on $ M_{0} $. Let $ P $ be the projection from $ \mathbb{R}^{3} $ into $ M_{0} $ defined, for every $ x = (x_{1}, x_{2}, x_{3})\in \mathbb{R}^{3} $, by

According to ^[48], the Kusuoka measure $ {\boldsymbol{\nu}} $ on $ G $ is the unique Borel probability measure defined by

where $ G_{i_{1}...i_{h}} = \mathfrak{\psi }_{i_{1}...i_{h}}\left(G\right) $. Let us define

and $ \pi :I\longrightarrow G $ such that $ \mathfrak{\psi }_{j}\circ \pi \left(\omega \right) = \pi \left(j\omega \right) $, for $ j = 1, 2, 3 $. For any $ \omega \in I $, there exists a unique $ x\in G $ such that

We now define, by abuse of notation, the Kusuoka measure $ {\boldsymbol{\nu}} $ on $ I $ (see, for instance, ^[49]) as the pullback of the Kusuoka measure $ {\boldsymbol{\nu}} $ on $ G $ under the projection map $ \pi $, that is

Let us set

Then, according to ^[48], for $ {\boldsymbol{\nu}} $-almost all $ \omega $, there exists a limit

Let $ Z\left(x\right) \equiv Z\left(\pi ^{-1}\left(x\right) \right) $. Then, $ Z\left(x\right) $ is well defined on $ \mathcal{V}_{\infty } $ (see for instance ^[47]). Indeed, according to [49, Theorem 3.6], for $ {\boldsymbol{\nu}}- $almost all $ x\in G $,

where

Let $ U $ be an open subset of $ M_{0} $ containing $ G_{H} $. Let us define

According to ^[47], if we fix an orthonormal basis of $ M_{0} $ and regard $ M_{0} $ as $ \mathbb{R}^{2} $, then, for any $ u\in C^{1}\left(G\right) $,

We have the following.

Theorem 6. [47, Theorem 4.8] $ C^{1}\left(G\right) $ is a dense subset of $ \mathcal{D}_{\mathcal{E}} $ under the norm

and, for any $ u, v\in C^{1}\left(G\right) $,

5.   A priori estimates and compactness results

In this section, we establish some a priori estimates and compactness results which will be useful for the proof of the main results.

Lemma 7. Let $ v^{h}\in V^{h} $, such that $ \sup_{h}F_{h}\left(v^{h}\right) < \infty $. If $ \sigma \in \left(0, +\infty \right) $ then

Proof. The proof follows from the Poincaré inequality in a bounded domain with the Dirichlet boundary condition on a part of the boundary and a scaling argument. Let us define, for every $ k\in \left\{ 1, 2, ..., 3^{h}\right\} $ and $ i = 1, 2, 3 $,

Let $ \varphi \in C^{1}\left(U_{k}^{h, i}\right) $, such that $ \varphi = 0 $ on $ \partial U_{k}^{h, i}\cap \partial S $. Using the Poincaré inequality, we infer that, for every $ y_{h, 1}^{i, k}\in \left(\varepsilon _{h}\ln \left(1/\varepsilon _{h}\right), 2^{-h}-\varepsilon _{h}\ln \left(1/\varepsilon _{h}\right) \right) $,

where $ C $ is a positive constant independent of $ h $ and

Now, introducing the scaling $ y_{h, 2}^{i, k} = \varepsilon _{h}y $, $ x_{3} = \varepsilon _{h}z $, and integrating with respect to $ y_{h, 1}^{i, k} $ between $ \varepsilon _{h}\ln \left(1/\varepsilon _{h}\right) $ and $ 2^{-h}-\varepsilon _{h}\ln \left(1/\varepsilon _{h}\right) $, we get

from which we deduce, using the change of variables (2.7), that, for every $ v^{h}\in V^{h} $,

We can use the same method in $ \mathcal{J}_{k}^{h, +, i}\cup \mathcal{J} _{k}^{h, -, i} $ to obtain

The combination of (5.1) and (5.2) implies that

Then, summing over $ i $ and $ k $ in (5.3), we obtain that

As $ \sigma \in \left(0, +\infty \right) $, we have that

from which we deduce that $ 2^{h}\leq C $ $ \dfrac{1}{\text{Re}_{{\mathbf{j}}, h}} $ in $ \mathcal{J}^{h} $. Thus, using (5.4),

Observing that $ 3^{h}\varepsilon _{h}^{2}2^{-h}\approx \dfrac{\left\vert \Omega ^{h}\right\vert }{\pi } $, we conclude that

We have the following result:

Proposition 8. Let $ \boldsymbol{1}_{\Omega ^{h}} $ be the characteristic function of the set $ \Omega ^{h} $. Let $ v^{h}\in V^{h} $, such that $ \sup_{h}F_{h}\left(v^{h}\right) < +\infty $. If $ \sigma \in \left(0, +\infty \right) $, then there exists a subsequence of $ \left(v^{h}\right) _{h} $, still denoted as $ \left(v^{h}\right) _{h} $, such that

where $ v = \left(v_{1}, v_{2}, v_{3}\right) \in L_{\mathcal{H}^{d}}^{2}\left(G, \mathbb{R}^{3}\right) $ with $ v_{3} = 0 $ on $ G $, $ v_{2} = 0 $ on the part of $ G $ which is perpendicular to $ \left(0, 1\right) $, $ v_{2} = v_{1}\sqrt{3} $ on the part of $ G $ which is perpendicular to $ \left(-\sqrt{3}/2, 1/2\right) $, and $ v_{2} = -v_{1}\sqrt{3} $ on the part of $ G $ which is perpendicular to $ \left(\sqrt{3}/2, 1/2\right) $.

Proof. Let us consider the sequence of measures $ \left(\vartheta _{h}\right) _{h} $ on $ \mathbb{R}^{3} $ defined by

Using an ergodicity argument (see, for instance, [50, Theorem 6.1]), we deduce that, for every $ \varphi \in C_{0}\left(\mathbb{R}^{3}\right) $,

from which we deduce that

Let $ v^{h}\in L^{2}\left(\Omega ^{h}, \mathbb{R}^{3}\right) $, such that $ \sup_{h}F_{h}\left(v^{h}\right) < +\infty $. If $ \sigma \in \left(0, +\infty \right) $ then, according to Lemma 7,

Observing that, for some positive constant $ C $ independent of $ h $,

and, by taking into account (5.7), we deduce that the sequence $ \left(\sqrt{ 5^{h}}v^{h}\vartheta _{h}\right) _{h} $ is uniformly bounded in variation, hence $ \ast $-weakly relatively compact. Possibly passing to a subsequence, we can suppose that the sequence $ \left(\sqrt{5^{h}}v^{h}\vartheta _{h}\right) _{h} $ $ \ast $-weakly converges to some $ \chi $. Let $ \varphi \in C_{0}\left(\mathbb{R}^{3}, \mathbb{R}^{3}\right) $. By using Fenchel's inequality, we have

As the left-hand side of this inequality is bounded, we deduce that

from which we deduce, according to Riesz' representation Theorem, that there exists $ v $ such that $ v\left(s, 0\right) \in L_{\mathcal{H}^{d}}^{2}\left(G, \mathbb{R}^{3}\right) $ and $ \chi = v\left(s, x_{3}\right) \vartheta $.

Let us introduce the function $ v^{h, i} $; $ i = 1, 2, 3 $, related to $ v^{h} $ by

where $ y_{h, 1}^{i, k}, y_{h, 2}^{i, k}, x_{3} $ are the variables defined in (2.7). We can easily prove, after some computations that for every $ i = 1, 2, 3 $,

where $ \text{div }_{y} $ is the divergence operator in the variables $ y_{h, 1}^{i, k}, y_{h, 2}^{i, k}, x_{3} $. On the other hand, as $ \Pi _{k}^{h, i} $ is a cylinder of revolution, we can introduce the cylindrical coordinates $ y_{h, 1}^{i, k}\equiv y_{h, 1}^{i, k} $, $ y_{h, 2}^{i, k} = r\cos \theta $, $ x_{3} = r\sin \theta $, and the polar components of $ v^{h, i} $ defined by

Let $ \widetilde{v}^{h, i} = \left(v_{1}^{h, i}, v_{r}^{h, i}, v_{\theta }^{h, i}\right) $. The divergence of $ \widetilde{v}^{h, i} $ in cylindrical coordinates is given by

Since $ \text{div }v^{h} = 0 $, we deduce from (5.9) and (5.11) that

Using the boundary condition (2.25)$ _{2} $, we have, for every $ h\in \mathbb{N} $,

from which we deduce, using Green's formula, that, for $ \psi \in C_{c}^{\infty }\left(0, 2\pi \right) $ and $ \varphi \left(\theta \right) = \int_{0}^{\theta }\psi \left(\xi \right) d\xi $ with $ \varphi \left(2\pi \right) = 0 $,

Since $ \text{div }_{r}\left(\widetilde{v}^{h, i}\right) = 0 $, we deduce from formula (5.11), according to (5.14), that

Using Green's formula, we deduce that

and

Combining with (5.15), we deduce that

Recalling that $ v_{\theta }^{h, i} = -v_{2}^{h, i}\sin \theta +v_{3}^{h, i}\cos \theta $ and $ v_{3}^{h, i} = v_{3}^{h} $, and using the first part of this Lemma, we obtain that

where

where $ G_{1} $ is the part of $ G $ which is perpendicular to $ \left(0, 1\right) $, $ G_{2} $ is the part of $ G $ which is perpendicular to $ \left(- \sqrt{3}/2, 1/2\right) $, and $ G_{3} $ is the part of $ G $ which is perpendicular to $ \left(\sqrt{3}/2, 1/2\right) $. We deduce from (5.19) that $ -w\left(s\right) \sin \theta +v_{3}\left(s\right) \cos \theta = 0 $ for every $ \theta \in \left(0, 2\pi \right) $, thus $ w = v_{3} = 0 $ on $ G $. Therefore, combining with (5.20), $ v_{2} = 0 $ on $ G_{1} $, $ v_{2} = v_{1} \sqrt{3} $ on $ G_{2} $, and $ v_{2} = -v_{1}\sqrt{3} $ on $ G_{3} $.

Proposition 9. We suppose that $ \sigma \in \left(0, +\infty \right) $. Let $ v^{h}\in V^{h}\cap H^{2}\left(\Omega ^{h}, \mathbb{R}^{3}\right) $, such that $ \sup_{h}F_{h}\left(v^{h}\right) < +\infty $. Then, for every sequence $ \left(\varphi _{h}\right) _{h} $, such that $ \varphi _{h}\in H^{1}\left(\Omega ^{h}\right) $ and

we have

1. $ \varphi \left(s, 0\right) \in \mathcal{D}_{\mathcal{E}} $ and $ \int_{G}\nabla \varphi.Z\nabla \varphi d{\boldsymbol{\nu}} < +\infty $,

2. there exists a subsequence of $ \left(v^{h}\right) _{h} $, still denoted as $ \left(v^{h}\right) _{h} $, and $ v\in L_{\mathcal{H}^{d}}^{2}\left(G\right) $, such that

where $ n = \left(1, 0\right) $ on the horizontal part of $ G $, $ n = \left(1/2, \sqrt{3}/2\right) $ on the part of $ G $ which is perpendicular to $ \left(- \sqrt{3}/2, 1/2\right) $, and $ n = \left(1/2, -\sqrt{3}/2\right) $ on the part of $ G $ which is perpendicular to $ \left(\sqrt{3}/2, 1/2\right) $.

Proof. 1. Let us define, for every $ k\in \left\{ 1, 2, ..., 3^{h}\right\} $ and $ i = 1, 2, 3 $,

and

where $ y_{h, 1}^{i, k}, y_{h, 2}^{i, k}, x_{3} $ are the change of variables defined in (2.7). Then

where $ \widetilde{\varphi }_{h}\left(x_{1}, x_{2}\right) = $ $ \widetilde{ \varphi }_{h}^{i}\left(y_{h, 1}^{i, k}\right) $ for $ \left(x_{1}, x_{2}\right) \in \left[a_{h}^{i, k}, b_{h}^{i, k}\right] $. We now introduce the harmonic extension of $ \widetilde{\varphi }_{h}\mid _{\mathcal{ V}_{h}} $ obtained by the so-called decimation procedure (see, for instance, [51, Corollary1]). We define the function $ H_{h+1} \widetilde{\varphi }_{h}:\mathcal{V}_{h+1}\longrightarrow \mathbb{R} $ as the unique minimizer of the problem

Then $ \mathcal{E}_{G}^{h+1}\left(H_{h+1}\widetilde{\varphi }_{h}\right) = \mathcal{E}_{G}^{h}\left(\widetilde{\varphi }_{h}\right) $. For $ m > h $, we define the function $ H_{m}\widetilde{\varphi }_{h} $ from $ \mathcal{V}_{m} $ into $ \mathbb{R}^{2} $ by

We have, for every $ m > h $, $ H_{m}\widetilde{\varphi }_{h}\mid _{\mathcal{V} _{h}} = \widetilde{\varphi }_{h}\mid _{\mathcal{V}_{h}} $ and

We define now, for fixed $ h\in \mathbb{N} $, the function $ H\widetilde{ \varphi }_{h} $ on $ \mathcal{V}_{\infty } $ as follows. For $ a\in \mathcal{V} _{\infty } $, we choose $ m\geq h $ such that $ a\in \mathcal{V}_{m} $ and set

As $ \sup_{h}\dfrac{5^{h}}{\left\vert \Omega ^{h}\right\vert }\int_{\Omega ^{h}}\left\vert \nabla \varphi _{h}\right\vert ^{2}dx < +\infty $, we have, according to (5.24), (5.26), and (5.27),

from which we deduce, using Section $ 4 $, that $ H\widetilde{\varphi }_{h} $ has a unique continuous extension on $ G $, still denoted as $ H\widetilde{ \varphi }_{h} $, and that the sequence $ \left(H\widetilde{\varphi } _{h}\right) _{h} $ is bounded in $ \mathcal{D}_{\mathcal{E}} $. Therefore, there exists a subsequence, still denoted as $ \left(H\widetilde{\varphi } _{h}\right) _{h} $, weakly converging in the Hilbert space $ \mathcal{D}_{ \mathcal{E}} $ to some $ \varphi ^{\ast }\in \mathcal{D}_{\mathcal{E}} $, such that

On the other hand, using the hypothesis (5.21)$ _{2} $, we have that

where $ T^{h} = \overset{3^{h}}{\underset{k = 1}{\mathop{\cup }}}T_{h}^{k} $; $ T_{h}^{k} $ being the $ k^{th} $ triangle obtained at the step $ k $ in the construction of the fractal $ G $. We deduce from this that, for every $ \psi \in C_{0}\left(G\right) $,

where $ \left(\upsilon _{h}\right) _{h} $ is the sequence of measures defined by

$ \delta _{a} $ being the Dirac measure at the point $ a $. Thus, $ \varphi ^{\ast }\left(s\right) = \varphi \left(s, 0\right) $, $ \varphi \left(s, 0\right) \in \mathcal{D}_{\mathcal{E}} $, and, according to (5.24) and (5.29),

from which we deduce, using Theorem 6, that

2. As $ \text{div }v^{h} = 0 $, we can write

where $ n^{i} = \mathcal{R}_{i}e_{1} $. Since $ \left\vert B^{h}\right\vert \longrightarrow 0 $ as $ h\rightarrow \infty $, using the proof of Lemma 7 and the hypothesis (5.21), we have that

Thus, passing to the limit in (5.35), we get

As $ \varphi \left(s, 0\right) \in \mathcal{D}_{\mathcal{E}} $, using some density argument, we may suppose that $ \varphi \left(s, 0\right) \in C^{1}\left(G\right) $. As $ v^{h} $ $ \in H^{2}\left(\Omega ^{h}, \mathbb{R} ^{3}\right) $, we may write

where $ \epsilon _{h}^{i} = \varepsilon _{h}\mathcal{R}_{i}^{t}e_{1} $. On the other hand, there exists a function $ r_{h}\in C^{1}\left(\Omega ^{h}\right) $ such that $ v^{h} = \nabla r_{h} $. Indeed, as $ \text{div }v^{h} = 0 $, $ r_{h} $ is a solution of the equation $ \Delta r_{h} = 0 $ in $ \Omega ^{h} $ with some boundary conditions on $ \partial \Omega ^{h} $. Using the smoothness of $ \varphi $, we infer that

Then, replacing in (5.37), taking into account the fact that $ \sup_{h}F_{h}\left(v^{h}\right) < +\infty $ and the estimates on $ v^{h} $ given in Lemma 7, we obtain that

As for the fractal $ G $, we can construct, according to Proposition 5, a graph approximation $ G_{H, h} $ of the harmonic Sierpinski gasket $ G_{H} $ and a sequence $ \left(\Omega _{H}^{h}\right) _{h} $ of thin branching tubes whose axes are iterated curves of the graph $ G_{H, h} $. As $ r_{h}\in C^{1}\left(\Omega ^{h}\right) $, there exists $ \mathfrak{r}_{h}\in C^{1}\left(\Omega _{H}^{h}\right) $, such that $ r_{h}\mid _{G_{h}} = \mathfrak{r}_{h}\mid _{G_{H, h}}\circ \Phi $. Similarly, there exists $ \mathfrak{\varsigma }\in C^{1}\left(U\right) $, $ U $ being an open subset of $ M_{0} $ containing $ G_{H} $, such that $ \varphi \mid _{G} = \varsigma \mathfrak{ \mid }_{G_{H}}\circ \Phi $. Let us set, for $ k_{1}, ..., k_{h}\in \left\{ 1, 2, 3\right\} $,

where $ \mathfrak{H}\left(A_{i}\right) = \left(\mathfrak{h}_{1}\left(A_{i}\right), \mathfrak{h}_{2}\left(A_{i}\right), \mathfrak{h}_{3}\left(A_{i}\right) \right) = \left(\delta _{1i}, \delta _{2i}, \delta _{3i}\right) $. Then, observing that, there exist $ k_{1}, ..., k_{h}\in \left\{ 1, 2, 3\right\} $ such that $ a_{h}^{i, k} = $ $ \mathfrak{\psi } _{k_{1}...k_{h}}\left(A_{i}\right) $, using (5.40), the fact that $ P^{t} = P $, $ T_{k_{1}...k_{h}}^{t}P = T_{k_{1}...k_{h}}^{t} $, and [46, Lemma 3.2], we deduce that

Using Lemma 8, there exists a subsequence of $ \left(v^{h}\right) _{h} $, still denoted as $ \left(v^{h}\right) _{h} $, and $ v\in L_{\mathcal{H} ^{d}}^{2}\left(G\right) $, such that

where $ v^{\ast } = 0 $ on the part of $ G $ which is perpendicular to $ \left(0, 1\right) $, $ v^{\ast } = v\sqrt{3} $ on the part of $ G $ which is perpendicular to $ \left(-\sqrt{3}/2, 1/2\right) $, and $ v^{\ast } = -v\sqrt{3} $ on the part of $ G $ which is perpendicular to $ \left(\sqrt{3}/2, 1/2\right) $. The corresponding subsequence of gradients $ \left(\nabla r_{h}\mid _{G_{h}} = \nabla \mathfrak{r}_{h}\mid _{G_{H}}\circ \Phi \right) _{h} $ converges to the same limit. Thus, using the limits (5.36)–(5.37), the relations (5.38)–(5.41), and the smoothness of $ \varphi $ and $ v^{h} $, we obtain that

where we have used the fact that $ \left(v, v^{\ast }\right).n = v $.

According to the above proposition, we introduce the following

Definition 2. 1. We define the space $ H_{Z}\left(G\right) $ by

2. Let $ n = \left(1, 0\right) $ on the horizontal part of $ G $, $ n = \left(1/2, \sqrt{3}/2\right) $ on the part of $ G $ which is perpendicular to $ \left(-\sqrt{3}/2, 1/2\right) $, and $ n = \left(1/2, -\sqrt{3}/2\right) $ on the part of $ G $ which is perpendicular to $ \left(\sqrt{3}/2, 1/2\right) $. Let $ v\in \mathcal{D}_{\mathcal{E}} $. We define the divergence of $ v $ on $ G $ by the relation

for every $ \varphi \in H_{Z}\left(G\right) $.

3. We define the space $ V^{\infty } $ by

We introduce the following useful result which is due to Bogovskiĭ ^[52]:

Lemma 10. Let $ D\subset \mathbb{R}^{3} $ be a bounded domain with Lipschitz continuous boundary $ \partial D $. There exists a linear operator $ \mathcal{B}:L^{2}\left(D\right) \rightarrow H_{0}^{1}\left(D; \mathbb{R} ^{3}\right) $, such that, for every $ \varpi \in L^{2}\left(D\right) $ satisfying $ \int_{D}\varpi dx = 0 $,

where $ C\left(D\right) $ is a constant which only depends on $ D $.

Let us define $ D = S\times \left(0, 1\right) $. As a consequence, we have the following result:

Lemma 11. Let $ D_{h} = \varepsilon _{h}S\times \left(0, 2^{-h}\right) $. There exists a linear operator $ \mathcal{B}_{h}:L^{2}\left(D_{h}\right) \rightarrow H_{0}^{1}\left(D_{h}; \mathbb{R}^{3}\right) $, such that, for every $ \varpi \in L^{2}\left(D_{h}\right) $ with $ \int_{D_{h}}\varpi dx = 0 $,

where $ C\left(D\right) $ is a constant which still only depends on $ D $.

Proof. For every $ \varpi \in L^{2}\left(D_{h}\right) $ satisfying $ \int_{D_{h}}\varpi dx = 0 $, we define

Then, since $ \int_{D_{h}}\varpi dy = 0 $, we can apply Lemma 10 in $ D $ to obtain

Let us define, for every $ x\in D_{h} $,

Then

On the other hand, observing that

where

we deduce that

Last, according to (5.45), we have

Therefore, combining (5.48) and (5.49), we infer that

Let $ \left(u^{h}, p_{h}\right) $ be the solution of problem (2.22) with boundary conditions (2.25). Let us define, for every $ h\in \mathbb{N} $, $ i = 1, 2, 3 $, and $ k\in \left\{ 1, 2, ..., 3^{h}\right\} $, the zero average-value pressure $ \widehat{p}_{k}^{h, i} $ by

and the pressure $ \widehat{p}_{h} $ by

The following estimates hold true:

Lemma 12. If $ \sigma \in \left(0, +\infty \right) $ then

1. $ \sup_{h}F_{h}\left(u^{h}\right) < +\infty $, $ \sup_{h}\dfrac{5^{h}}{ \left\vert \Omega ^{h}\right\vert }\int\nolimits_{\Omega ^{h}}\left\vert u^{h}\right\vert ^{2}dx < +\infty $,

2. $ \sup_{h}\dfrac{5^{h}}{\left\vert \Omega ^{h}\right\vert } \int\nolimits_{\Omega ^{h}}\left(\widehat{p}_{h}\right) ^{2}dx < +\infty $, $ \sup_{h}\dfrac{5^{h}}{\left\vert \Omega ^{h}\right\vert }\int\nolimits_{ \Omega ^{h}}\left\vert \nabla p_{h}\right\vert ^{2}dx < +\infty $.

Proof. 1. Applying Lemma 11 for the solution $ f_{h} $ of problem (2.23), we deduce that, for every $ k\in \left\{ 1, 2, ..., 3^{h}\right\} $ and $ i = 1, 2, 3 $,

Additionally, using the inequality (5.3), we have

We deduce from (5.53) and (5.54), that

then, using the hypothesis (2.24)$ _{2} $, we conclude that

Multiplying (2.22)$ _{1} $ by $ u^{h} $ and integrating by parts, we obtain that

from which we deduce, in virtue of the fact that $ \dfrac{1}{Fr_{h}}\dfrac{ 5^{h}}{3^{h+1}}\approx \dfrac{5^{h}}{\left\vert \Omega ^{h}\right\vert } $, by using inequality (5.6) and estimate (5.56),

and, as $ \sigma \in \left(0, +\infty \right) $, according to Lemma 7,

2. According to Lemma 11, there exists $ \phi _{k}^{h, i}\in H_{0}^{1}\left(\Omega _{k}^{h, i}, \mathbb{R}^{3}\right) $ such that

and

Let us define $ \phi ^{h} $ on $ \Omega ^{h} $ by $ \phi ^{h} = \phi _{k}^{h, i} $ on each $ \Omega _{k}^{h, i} $, for every $ k\in \left\{ 1, 2, ..., 3^{h}\right\} $ and $ i = 1, 2, 3 $. Then, according to inequality (5.61), we have that

Multiplying (2.22)$ _{1} $ by $ \phi ^{h} $ and integrating by parts, we deduce that

Using the fact that $ \mathrm{Eu}_{h} $ $ \dfrac{5^{h}}{3^{h+1}} = \dfrac{1}{ Fr_{h}}\dfrac{5^{h}}{3^{h+1}}\approx \dfrac{5^{h}}{\left\vert \Omega ^{h}\right\vert } $, inequality (5.62), and the uniform boundedness (5.56) and (5.58), we deduce that

which implies that

On the other hand, multiplying (2.27)$ _{1} $ by $ p_{h} $, integrating by parts, and, using the hypothesis (2.24)$ _{1} $, we get

from which we deduce by using (2.24)$ _{2} $ and the uniform boundedness (5.65):

6.   Proof of the main result

6.1.   Proof of Theorem 2

6.1.1.   Local problems

Let us define new orthonormal basis systems $ \left(e_{m}^{i}\right) _{m = 1, 2, 3} $; $ i = 1, 2, 3 $, by

where $ e_{m} = \left(\delta _{1m}, \delta _{2m}, \delta _{3m}\right) $. We define the rescaled junctions $ \mathcal{J}^{+, i} $ and $ \mathcal{J}^{-, i} $, for $ i = 1, 2, 3 $, by

We consider the following Leray problems:

and

where $ \Theta $ is the solution of the auxiliary problem

We define, for every $ k\in \left\{ 1, 2, ..., 3^{h}\right\} $ and $ i = 1, 2, 3 $, the sequence of functions $ \left(w^{h, \pm, i}\right) _{h} $ by

where the sets $ \mathcal{J}_{k}^{h, +, i} $ and $ \mathcal{J}_{k}^{h, -, i} $ are defined in (2.17) and the coordinates $ y_{h, 1}^{i, k} $, $ y_{h, 2}^{i, k} $, $ x_{3} $; $ i = 1, 2, 3 $, are related to the variable $ x $ through the relations (2.7). Let us define, for every $ k\in \left\{ 1, 2, ..., 3^{h}\right\} $ and $ i = 1, 2, 3 $, the intermediate tubes

and their upper and lower bases, respectively,

6.1.2.   Limit sup inequality

Let $ v\in C^{1}\left(G\right) $. Let $ x\in \Omega _{k}^{h, i} $. Then, $ \left(x_{1}, x_{2}\right) \in \left[a_{h}^{i, k}, b_{h}^{i, k}\right] $; $ i = 1, 2, 3 $, for every $ h\in \mathbb{N} $ and every $ k\in \left\{ 1, 2, ..., 3^{h}\right\} $. Let $ x_{h}^{i, k} = \dfrac{a_{h}^{i, k}+b_{h}^{i, k}}{2} $. We define the sequence of vector functions $ \left(v_{k}^{0, h, i}\right) _{h} $ by

where

and

with

We introduce the function $ \phi _{h}^{i, \pm, k} $ defined by

and the function $ \mathcal{\theta }_{k}^{h, \pm, 1} $ defined by

Let $ \eta _{k}^{h, i} $ be the solution of the problem

We define the sequence of test-functions $ \left(v_{k}^{h, i}\right) _{h} $; $ v_{k}^{h, i} = \left(v_{k, j}^{h, i}\right) _{j = 1, 2, 3} $, by

We then define the test function $ v^{h} $ in $ \Omega ^{h} $ by

We have the following results:

Proposition 13. We have

1. $ v^{h}\in V^{h} $ for $ \varepsilon _{h} $ small enough,

2. $ \left(v^{h}\right) _{h} $ $ \tau $-converges to $ \left(v, v^{\ast }, 0\right) $, where $ v^{\ast } = 0 $ on the part of $ G $ which is perpendicular to $ \left(0, 1\right) $, $ v^{\ast } = v\sqrt{3} $ on the part of $ G $ which is perpendicular to $ \left(-\sqrt{3}/2, 1/2\right) $, and $ v^{\ast } = -v\sqrt{3} $ on the part of $ G $ which is perpendicular to $ \left(\sqrt{3}/2, 1/2\right) $,

3. if $ \sigma \in \left(0, \infty \right) $, then

Proof. 1. Introducing the variables $ y_{2} = \dfrac{y_{h, 2}^{i, k}\left(x\right) }{ \varepsilon _{h}} $ and $ y_{3} = \dfrac{x_{3}}{\varepsilon _{h}} $, we have, for $ \varepsilon _{h} $ small enough, that

and

This implies that problem (6.15) is solvable. On the other hand, using [53, Theorem Ⅵ.1.2], there exists $ \tau > 0 $ such that, for any $ i = 1, 2, 3 $ and every $ y\in \mathcal{J}^{\pm, i} $,

from which we deduce that

which implies that

and, using [54, Lemma 9],

Since $ \text{div }\eta _{k}^{h, i} = 0 $, $ \text{div }_{y}w^{+, i} = \text{div } _{y}w^{-, i} = 0 $, for every $ i = 1, 2, 3 $, and $ \Theta $ is independent of $ y_{1} $, we have $ \ $

Therefore, for $ \varepsilon _{h} $ small enough, $ v^{h}\in V^{h} $.

2. Let $ \varphi \in C_{0}\left(\mathbb{R}^{3}\right) $. We have

and

Then, using the estimate (6.20) for $ w^{\pm, i}\left(y\right) $, the estimates (6.21)–(6.22) for $ \mathcal{\theta }_{k}^{h, \pm, i} $, the estimate (6.23) for $ \eta _{k}^{h, i} $, and the inequality (5.3) applied to $ \eta _{k}^{h, i} $, we deduce that

3. Let us suppose that $ \sigma \in \left(0, \infty \right) $. Then, in virtue of the estimates (6.20)–(6.23), we have that

where $ \mathcal{J}_{k}^{h, i} = \mathcal{J}_{k}^{h, +, i}\cup \mathcal{J} _{k}^{h, -, i} $. Then, as

and $ \int_{S}\left\vert \nabla \Theta \left(y_{2}, y_{3}\right) \right\vert ^{2}dy_{2}dy_{3} = \pi \mathfrak{m}\left(\Theta \right) $, we deduce that

After some computations, we infer that

and, for the last limit in (6.27),

Using once again the estimate (6.20), we deduce that

and

Now, combining (6.27)–(6.33), we get the result.

Proposition 14. If $ \sigma \in \left(0, +\infty \right) $, then for every $ v\in V^{\infty } $, there exists a sequence $ \left(v^{h}\right) _{h} $, with $ v^{h}\in V^{h} $ and $ \left(v^{h}\right) _{h} $ $ \tau $-converges to $ \left(v, v^{\ast }, v^{\ast \ast }\right) $, where $ v^{\ast \ast } = 0 $, $ v^{\ast } = 0 $ on the part of $ G $ which is perpendicular to $ \left(0, 1\right) $, $ v^{\ast } = v\sqrt{3} $ on the part of $ G $ which is perpendicular to $ \left(-\sqrt{3} /2, 1/2\right) $, and $ v^{\ast } = -v\sqrt{3} $ on the part of $ G $ which is perpendicular to $ \left(\sqrt{3}/2, 1/2\right) $, such that

Proof. Let $ v\in V^{\infty } $. Let $ \left(v_{m}\right) _{m} $ $ \subset C^{1}\left(G\right) $ such that $ v_{m}\underset{m\rightarrow \infty }{\longrightarrow } v $ with respect to the norm (4.5). We define the sequence $ \left(v^{m, h}\right) _{m, h} $ by replacing in (6.9), (6.16), and (6.17) $ v $ by $ v_{m} $. Then, according to Proposition 13, the sequence $ \left(v^{m, h}\right) _{m, h} $ $ \tau $-converges to $ \left(v_{m}, v_{m}^{\ast }, 0\right) $, where $ v_{m}^{\ast } = 0 $ on the part of $ G $ which is perpendicular to $ \left(0, 1\right) $, $ v_{m}^{\ast } = v_{m}\sqrt{3} $ on the part of $ G $ which is perpendicular to $ \left(-\sqrt{ 3}/2, 1/2\right) $, $ v_{m}^{\ast } = -v_{m}\sqrt{3} $ on the part of $ G $ which is perpendicular to $ \left(\sqrt{3}/2, 1/2\right) $, and

The continuity of $ F_{\infty } $ implies that $ \lim_{m\rightarrow \infty }\lim_{h\rightarrow \infty }F_{h}\left(v^{m, h}\right) = F_{\infty }\left(v\right) $. The topology $ \tau $ being metrizable, we deduce, using a diagonalization argument (see [14, Corollary 1.18]), that the sequence $ \left(v^{h}\right) _{h} = \left(v^{h, m\left(h\right) }\right) _{h} $; $ \underset{h\rightarrow \infty }{\lim }m\left(h\right) = +\infty $, $ \tau $ -converges to $ \left(v, v^{\ast }, 0\right) $, with $ v^{\ast } = 0 $ on the part of $ G $ which is perpendicular to $ \left(0, 1\right) $, $ v^{\ast } = v\sqrt{3} $ on the part of $ G $ which is perpendicular to $ \left(-\sqrt{3}/2, 1/2\right) $, $ v^{\ast } = -v\sqrt{3} $ on the part of $ G $ which is perpendicular to $ \left(\sqrt{3}/2, 1/2\right) $, and

6.1.3.   Limit inf inequality

Proposition 15. If $ \sigma \in \left(0, +\infty \right) $, then for every sequence $ \left(v^{h}\right) _{h} $, such that $ v^{h}\in V^{h} $ and $ \left(v^{h}\right) _{h} $ $ \tau $-converges to $ \left(v, v^{\ast }, v^{\ast \ast }\right) $, we have $ v\in V^{\infty } $, $ v^{\ast \ast } = 0 $ on $ G $, $ v^{\ast } = 0 $ on the part of $ G $ which is perpendicular to $ \left(0, 1\right) $, $ v^{\ast } = v\sqrt{3} $ on the part of $ G $ which is perpendicular to $ \left(-\sqrt{3}/2, 1/2\right) $, $ v^{\ast } = -v\sqrt{3} $ on the part of $ G $ which is perpendicular to $ \left(\sqrt{3}/2, 1/2\right) $, and

Proof. Observe that if $ \sup_{h}F_{h}\left(v^{h}\right) = +\infty $, then the lim inf inequality is trivial. We suppose that $ \sup_{h}F_{h}\left(v^{h}\right) < +\infty $ and, using some regularity argument, we may suppose that $ v^{h}\in V^{h}\cap H^{2}\left(\Omega ^{h}, \mathbb{R}^{3}\right) $. Then, according to Proposition 8, we have that $ v\in L_{\mathcal{H} ^{d}}^{2}\left(G\right) $, $ v^{\ast \ast } = 0 $ on $ G $, $ v^{\ast } = 0 $ on the part of $ G $ which is perpendicular to $ \left(0, 1\right) $, $ v^{\ast } = v \sqrt{3} $ on the part of $ G $ which is perpendicular to $ \left(-\sqrt{3} /2, 1/2\right) $, $ v^{\ast } = -v\sqrt{3} $ on the part of $ G $ which is perpendicular to $ \left(\sqrt{3}/2, 1/2\right) $, and, according to Proposition 5.9,

where $ H_{Z}\left(G\right) $ is the space defined in Definition 2$ _{1} $. Let $ \left(v_{m}\right) _{m} $ $ \subset C^{1}\left(G\right) $ such that $ v_{m}\underset{m\rightarrow \infty }{\longrightarrow } v $ with respect to the norm $ L_{\mathcal{H}^{d}}^{2}\left(G\right) $ -strong. We define the sequence $ \left(v^{m, h}\right) _{m, h} $ by replacing $ v $ by $ v_{m} $ in test-functions (6.9), (6.16), and (6.17). We deduce from the definition of the subdifferentiability of convex functionals that

We then compute

Using the estimate (6.23), we deduce that

from which we deduce that

On the other hand, using the fact that $ \varepsilon _{h}^{2}3^{h}\text{Re} _{h}\approx \dfrac{\left\vert \Omega ^{h}\right\vert }{\pi \mu } $ in $ \omega _{k}^{h, i} $ and according to the problem (6.5) of which $ \Theta $ is the solution, we deduce that

Using the limits (6.24) and (6.30), and the fact that

we deduce that

Analogously, using the estimate (6.20), the equations (6.5), the expression (6.12) of $ r_{k}^{h, i}\left(v\right) $, and the estimate (6.40), we get

and, similarly,

As $ \sup_{h}\dfrac{5^{h}}{3^{h+1}\text{Re}_{h}}\int\nolimits_{\Omega ^{h}}\left\vert \nabla \left(v^{h}-v^{m, h}\right) \right\vert ^{2}dx < +\infty $, we have

In addition, owing to Proposition 13, we have

Thus, combining (6.35)–(6.45), we deduce that

Then, letting $ m $ tend to $ \infty $, we obtain

and, as a consequence, $ \mathcal{E}_{G}\left(v\right) < +\infty $. Thus, $ v\in \mathcal{D}_{\mathcal{E}} $ and, taking into account (6.34), we have that $ v\in V^{\infty } $.

6.2.   Proof of Theorem 3

Proof. 1. Let $ \left(u^{h}, p_{h}\right) $ be a solution of problem (2.22) with boundary conditions (2.25). According to Lemma 12 and Proposition 8 there exists a subsequence of $ \left(u^{h}\right) _{h} $, still denoted as $ \left(u^{h}\right) _{h} $, such that

with $ u^{\ast } = 0 $ on the part of $ G $ which is perpendicular to $ \left(0, 1\right) $, $ u^{\ast } = u\sqrt{3} $ on the part of $ G $ which is perpendicular to $ \left(-\sqrt{3}/2, 1/2\right) $, and $ u^{\ast } = -u\sqrt{3} $ on the part of $ G $ which is perpendicular to $ \left(\sqrt{3}/2, 1/2\right) $. As the boundary $ \partial \Omega ^{h} $ is $ C^{2} $, the velocity $ u^{h} $ is at least in $ H^{2}\left(\Omega ^{h}\right) $. Thus, according to Proposition 5.9, we have that

On the other hand, since $ u^{h} $ is the unique velocity solution of problem (2.31), we deduce from Theorem 2 and [15, Theorem 7.8], that the whole sequence $ \left(u^{h}\right) _{h} $ verifies the convergence (6.47),

and, taking into account (6.48), we deduce that $ u\in V^{\infty } $. In addition, using Lemma 12 and the proof of Proposition 8, we have that

with $ p\in H_{Z}\left(G\right) $, and, using the uniform boundedness (5.56),

with $ f\in L_{\mathcal{H}^{d}}^{2}\left(G, \mathbb{R}^{3}\right) $. Using Proposition 5.9 and Lemma 12$ _{2} $, we deduce that, for every $ v\in V^{\infty } $,

where $ n = \left(1, 0\right) $ on the horizontal part of $ G $, $ n = \left(1/2, \sqrt{3}/2\right) $ on the part of $ G $ which is perpendicular to $ \left(- \sqrt{3}/2, 1/2\right) $, and $ n = \left(1/2, -\sqrt{3}/2\right) $ on the part of $ G $ which is perpendicular to $ \left(\sqrt{3}/2, 1/2\right) $.

2. According to Theorem 2 and [15, Theorem 7.8], $ u $ is the solution of the problem

Then, using Lemma 4 and the fact that $ \int_{G}vZ\nabla p.nd{\boldsymbol{\nu}} = 0 $ and $ \left(v, v^{\ast }\right) = v.n $, for every $ v\in V^{\infty } $, we deduce from (6.53) that, for every $ v\in V^{\infty } $,

where, by abuse of notation, $ f.n = \left(f_{1}, f_{2}\right).n $. Therefore, $ \left(u, p\right) $ is the solution (with $ p $ up to an additive constant) of the following problem:

which completes the proof of Theorem 3.

7.   Conclusion

In this paper, we considered the motion of a viscous incompressible fluid in a varying bounded domain consisting of branching cylindrical pipes whose axes are line segments that form a network of pre-fractal polygonal curves $ G_{h} $ obtained after $ h $-iterations of the contractive similarities of the standard Sierpinski gasket. We assumed that these pipes are narrow axisymmetric tubes of radius $ \varepsilon _{h} $ very small with respect to the length $ 2^{-h} $ of each side of $ G_{h} $. We supposed that the fluid flow is driven by some volumic forces and governed by Stokes equations with continuity of the velocity at the interfaces separating the junction zones from the rest of the pipes, homogeneous Dirichlet boundary condition for the velocity, and homogeneous Neumann boundary condition for the pressure on the wall of the tubes. The flow in each pipe is split into two streams: boundary layers flow in junction zones of length $ \varepsilon _{h}\ln \left(1/\varepsilon _{h}\right) \ll $ $ 2^{-h} $ and laminar flow in the rest of the pipe. We assumed that the flow in the junction zones is controlled by a typical Reynolds number $ \text{Re}_{{\mathbf{j}}, h} $. Using $ \Gamma $ -convergence methods, we studied the asymptotic behavior of the fluid flowing in the branching tubes as the radius of the tubes tends to zero and the sequence of the pre-fractal curves converges in the Hausdorff metric to the Sierpinski gasket. According to critical values taken by $ \text{Re}_{ {\mathbf{j}}, h} $, we derived three uncommon effective models of fluid flows in the Sierpinski gasket:

1. a singular Brinkman equation if $ \text{Re}_{{\mathbf{j}}, h} = O\left(\varepsilon _{h}\right) $,

2. a singular Darcy flow if $ \text{Re}_{{\mathbf{j}}, h} $ $ = O\left(1\right) $ or $ \text{Re}_{{\mathbf{j}}, h}\longrightarrow \infty $ as $ h\longrightarrow \infty $,

3. a flow with constant velocity if $ \text{Re}_{{\mathbf{j}}, h} $ $ = O\left(\varepsilon _{h}^{\alpha }\right) $ with $ \alpha > 1 $.

As far as the modeling is concerned, fractal branching pipe networks have to be considered to describe fluid flows in various complex geometrical configurations. An important field to which this model is closely related is the behavior of fluid flows in some physiological structures such as the blood circulation through arterial networks. Our model may serve as a starting point for further investigations in this area.

Author contributions

Haifa El Jarroudi: Writing-original draft, Writing-review and editing, Methodology, Formal Analysis; Mustapha El Jarroudi: Writing-original draft, Writing-review and editing, Methodology, Supervision.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors wish to express their gratitude to the anonymous referee for giving a number of valuable comments and helpful suggestions, which improve the presentation of sentation of the manuscript significantly.

Conflict of interest

The authors declare there is no conflict of interest.