Background: Caring for a child with cerebral palsy (CP) can be exhausting and stressful. There is paucity of information on the consequence of having a child with CP on mothers of these children. This study explored psychosocial problems encountered by mothers of children with CP receiving physiotherapy care in two selected tertiary health centres in Ogun State, Nigeria. Methods: A qualitative study was conducted through focus group discussion (FGD) utilizing 17 questions identified in the literature as a FGD guide. Participants were seven mothers of children with CP. The framework approach was used for thematic analysis of data. Results: The psychosocial challenges encountered by the mothers were associated with nine common sub-themes. These are: (i) stress of caring for over dependent child; (ii) mothers’ restricted participation in the society; (iii) financial constraint experienced by the mothers of children with CP; (iv) health problems experienced by mothers of children with CP; (v) feelings of uncertainty about the child’s future; (vi) society’s negative perception of child’s problems; (vii) support obtained by the caregivers from others; (viii) availability of support from healthcare facilities; and (ix) Personal belief about condition. Conclusion: Mothers of children with cerebral palsy experience substantial psychological and social problems that are often ignored by the general populace.
1.
Introduction
A competitive market will be introduced for all commodities, including electricity in the future. The monopoly electricity market has now been reorganized into three distinct entities: generation companies (GENCOs), transmission companies (TRANSCOs), and distribution companies (DISCOs) [1,2]. Competition will be introduced between GENCOs and DISCOs to increase the efficiency of generation and consumption. The grid is operated by a separate entity, the system operator.
A power grid is generally managed by one entity for economic reasons and for better control of the flow of power. Electricity demand is growing faster than the expansion of the grid. In addition, a large number of bilaterally or multilaterally agreed power contracts are increasing congestion on transmission lines [3]. Line congestion [4], can occur if all transactions are not properly controlled. It forces transmission capacity improvement or transmission network expansion. Congestion management is defined as the recommended measures to reduce line congestion. Land acquisition and installation costs are the most important limitations in the development of transmission networks. Additionally, depending on the deal, the increase in bandwidth may only be temporary during the duration of the deal, justifying capacity expansion as the best alternative to expansion.
Trade agreements that lead to increased currents lead to increased line losses, jeopardizing system stability and security. Therefore, it is required to make the best use of the transmission capacity already installed. This can be easily done by just installing the FACTS device [5,6,7]. There are two reasons for the increased use of these FACTS devices. First, recent advances in power electronic switching devices have made them cheaper and more efficient [8]. Identifying the location and size of these devices is critical for optimal performance and minimal cost. Various methods are available to select the optimal location and size of FACTS devices in the energy system [9,10,11]. Reference [12] recommends a sensitivity-based method for choosing the best location for TCSC and also examines the impact of line impedance on congestion mitigation. The TCSC location is optimized to reduce line congestion in the event of contingencies in [13]. Reference [14] deals with congestion mitigation and improved voltage stability in liberalized electricity markets using several FACTS devices. Minimizing the total congestion cost using FACTS devices is described in [15]. Differential evolution algorithms are applied to improve safety and reduce overload in power systems under conditions of single-line faults in [16]. Management of congestion using Bee colony optimization and cost minimization is also done in [17]. TCSC is placed at best locations for maximizing social benefit and reducing congestion in transmission lines in [18]. A genetic algorithm is used for finding the optimal location of TCSC to solve a transmission line congestion problem in [19].
In most of the studies on congestion management, the cause of congestion considered is the outage of transmission lines. The other equally important causes of line congestion like bilateral and multilateral transactions in deregulated power markets are not sufficiently addressed in the literature. The research gap of transmission congestion caused by increased load, bilateral transaction, and multilateral transaction in deregulated power networks is addressed in this work.
A new method based on whale optimization algorithm is proposed here to determine the optimal location and rating of TCSC and SVC devices.
The main contributions of this work are as follows: 1. The WOA, which is a recent optimization algorithm, is proposed. The algorithm exhibits better searching ability and convergence speed. 2. A comparison of the proposed WOA with some state-of the-art algorithms demonstrates the superior performance of the algorithm. The WOA tops the rank on the performance comparison with these algorithms. 3.Three different causes of congestion are taken in this study, viz, increase in load, bilateral transaction and multilateral transaction. 4. Experimental results of the CM task reveal that series and shunt connected combination of FACTS devices perform better than when they are used individually.
In Section 2 static power injection modeling of TCSC and SVC are presented. In Section 3 the objective function of minimizing congestion, loss, and voltage deviation is discussed. Searching behaviur and modelling of WOA algorithm are described in section 4. In section 5, the results and discussion are presented. Finally, in section 6, the work is concluded, and future scope is proposed.
2.
Modelling of FACTS devices
2.1. Static modeling of SVC device
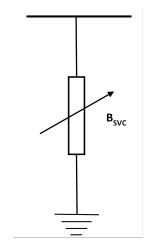
SVC devices can be operated as reactive power sources and sinks. This can be modeled as an ideal reactive power source/sink on bus $ i $ (2.1).
The main purpose of the SVC is usually to keep the weak bus voltage near its nominal value. It can be installed in the middle of the transmission line. The reactive power associated with SVC can be mathematically expressed as Equation (2.2) [20].
where, $ X_{sl} $ is the equivalent slope reactance denoted by p.u. $ V_{r} $ is the magnitude of the reference voltage. The SVC is modelled as a variable susceptance connected to bus $ i $ as shown in Figure 1.
2.2. Static modeling of TCSC device
A TCSC device is connected in series with a line and changes its reactance to change the power flow level [21]. It can act like a capacitor to generate reactive power, or it can act like an inductor to absorb reactive power. Its low cost compared to the cost of other FACTS devices makes it suitable for congestion management problems. Figure 2 shows the $ \pi $ model of a line between bus $ i $ and bus $ j $.
If $ V_{i}\angle\delta_{i} $ and $ V_{j}\angle\delta_{j} $ are the polar forms of voltages at buses $ i $ and $ j $. Active and reactive power flow from bus-i to bus-j can be given by Equations (2.3) and (2.4), respectively.
Power flows in the reverse direction, i.e, from bus $ j $ to bus $ i $ are given by Equations (2.5) and (2.6).
The TCSC insertion can be viewed as a variable reactance in series with the transmission line. Figure 3 shows a transmission line model with a TCSC. In steady state, TCSC can be modelled as a static capacitor/inductor with impedance $ jx_{TCSC} $.
The TCSC implementation modifies the power flow from bus $ i $ to bus $ j $ as given by Equations (2.7) and (2.8).
where, $ G_{ij}^{'} = \frac{r_{ij}}{r_{ij}^{2}+(x_{ij}-x_{TCSC})^{2}} $ $ B_{ij}^{'} = \frac{-(x_{ij}-x_{TCSC})}{(r_{ij}^{2}+(x_{ij}-x_{TCSC})^{2})} $
The congestion management problem is considered a static problem and uses the static model of FACTS devices that injects current at the ends of the line. According to this model, a TCSC device can be modelled as a PQ injection into a specific node. Figure 4 is the power injection model for the TCSC device.
The active and reactive power injections of bus $ i $ and bus $ j $ after inserting TCSC are given by Equations (2.9) to (2.12).
where, $ \Delta G_{ij} = \frac{(x_{TCSC} r_{ij} (x_{TCSC}-2x_{ij}))}{r_{ij}^{2 }+x_{ij}^{2}[r_{ij}^{2}+(x_{ij}-x_{TCSC})^{2}] } $ $ \Delta G_{ij} = \frac{-x_{TCSC} (r_{ij}^{2}-x_{ij}^{2} +x_{TCSC}x_{ij}}{r_{ij}^{2 }+x_{ij}^{2}[r_{ij}^{2}+(x_{ij}-x_{TCSC})^{2}]} $
3.
Formulation of congestion management problem
3.1. Congestion management
In a deregulated environment, TRANSCO, GENCO, and DISCO are different organizations. In all kinds of deregulated power system models there are grid operators to maintain coordination between them. This is usually an independent system operator (ISO). In a competitive electricity market, market participants are given sufficient freedom to interact with each other. Here, both buyers (DISCO) and sellers (GENCO) try to buy and sell power to maximize their profits. Transmission bottlenecks occur in deregulated electricity markets when transmission capacity is not sufficient to allow all transmissions simultaneously. Overloads should be mitigated as soon as possible because they cause tripping of the overloaded line and the possible cascaded trips of other lines, and possibly voltage stability problems. Therefore, removing bottlenecks quickly, systematically, and efficiently is critical in maintaining market efficiency. FACTS devices may be an alternative solution for reducing flow in heavily loaded lines.
3.2. Objectives
The main purpose of this work is to eliminate overloading of the lines by adjusting the design variables of generator bus voltage, transformer tap changes, and reactive power outputs of installed SVC and TCSC devices. Changes in the values of design variables affect the level of power system losses and voltage excursions. To explain these effects, three objectives are considered. i.e, minimize power flow violations, reduce power loss, and control voltage deviations.
Transmission lines are designed to transmit power within their thermal limits. Congestion management eliminates these overruns by minimizing active power over flows. This is our first objective here.
where $ P_{k} $ is the power flow at the $ k^{th} $ line, and $ P_{k rat} $ is the maximum power flow limit of the line.
For economical and efficient operations, the ISO should ensure minimum transmission loss, which is considered as the second objective.
where $ G_{k} $ is the conductance of the $ k^{th} $ line. $ V_{i} $ and $ V_{j} $ are the sending end and receiving end voltage magnitudes of the $ k^{th} $ line. $ \delta_{i} $ and $ \delta_{j} $ are the sending end and receiving end voltage angles of the $ k^{th} $ line.
The objective of power engineers is to ensure quality power at consumer end the voltage variations at load buses adversely affect the quality of power. This can be eliminated by considering voltage deviation as the third objective.
where $ V_{k} $ is the voltage of the $ k^{th} $ bus. $ V_{k ref} $ is the reference voltage at bus $ k $. It is taken as 1.0 p.u. in this work.
The congestion management problem is formulated as an optimization problem with multiple goals: minimizing power flow violation in transmission lines, reducing transmission losses, and minimizing voltage drift on load buses.
The weighted aggregated method is employed to convert the multi-objective modeling to single objective model as [22].
For determining the weight factors of multi-objective optimisation, since the power flow violation is the main concern, its corresponding weight factor is set as the highest value (0.6). The weights of other two objectives, i.e, loss and voltage deviation are set as 0.2.
i.e, C1 = 0.6, C2 = 0.2, C3 = 0.2.
3.3. Constraints
3.3.1. Equality constraints
The system must satisfy the real and reactive power flow constraints which are given by power flow equations as equality constraints.
where, $ P_{Gi} $, $ Q_{Gi} $ are the active and reactive power of $ i^{th} $ generator, and $ P_{Di} $, $ Q_{Di} $ are the active and reactive power of the $ i^{th} $ load bus.
3.3.2. Inequality constraints
Generator constraints:
Generator voltage and reactive power of $ i^{th} $ bus lies between their upper and lower limits as given below:
where, $ V_{i}^{min} $, $ V_{i}^{max} $ are the minimum and maximum voltages of the $ i^{th} $ generating unit, and $ Q_{Gi}^{min} $, $ Q_{Gi}^{max} $ are the minimum and maximum reactive power of the $ i^{th} $ generating unit.
Transmission line constraints:
Real power flow limit of a line is given as:
where, $ P_{i} $ is the apparent power flow of the $ i^{th} $ branch, and $ P_{i}^{max} $ is the maximum apparent power flow limit of the $ i^{th} $ branch.
Transformer taps constraints:
Transformer tap settings are bounded between upper and lower limit as given below:
where, $ T_{i}^{min} $, $ T_i^{max} $ are the minimum and maximum tap setting limits of the $ i^{th} $ transformer.
Shunt compensator constraints:
Shunt compensation is restricted by their limits as follows:
where, $ SVC_{i}^{min} $, $ SVC_{i}^{max} $ are the minimum and maximum VAR injection limits of the $ i^{th} $ shunt capacitor.
Series compensator constraints:
Series compensation is restricted by their limits as follows:
where, $ TCSC_{i}^{min} $, $ TCSC_{i}^{max} $ are the minimum and maximum reactance limits of the $ i^{th} $ series compensator of TCSC.
4.
Whale optimization algorithm
4.1. Overview
Whales rarely sleep because they need to breathe on the surface. Whales are always on alert to help them think, learn, judge, communicate, and even become emotional through their spindle cells [23]. Most whale species are able to live in families throughout their lives. Humpback whales are one of the largest animals with a specialized hunting behavior called bubble net feeding. Bubble net feeding is a specialized activity found only in humpback whales and is mathematically modelled in the next section to find the optimal solution in the search space. Algorithms inspired by nature are mimicked by organisms, such as foraging and survival mechanisms. The whale optimization algorithm was developed based on whale survival mechanisms in the deep sea.
4.2. Modelling of whale optimization algorithm
4.2.1. Encircling of prey
The WOA brings the current best candidate closer to the best solution. Once the best solution is found, other candidates will try to update their positions. This update action is represented by Equations (4.1) and (4.2).
where $ t $ is the current iteration number, $ A $ and $ C $ are the coefficients, $ X^{*} $ is the best solution so far, and $ X $ is the position vector. $ \lvert \rvert $ stands for size only, and the period (·) is the element-wise multiplication operator.
The $ A $ and $ C $ vectors are computed as follows:
The value of $ a $ is decreased linearly starting from 2 to 0 through the iterations and $ r $ is a random vector in (0, 1). The position (X, Y) of a whale is updated based on the position of the best history so far (X*, Y*). Positions around the current best position are obtained by adjusting the values of $ A $ and $ C $ vectors.
4.2.2. Bubble-net attacking (Exploitation phase)
There are two ways to model the behavior of a humpback's bubble web: the retracting enveloping mechanism and the spiral update position. We will use the former method here. This behavior is achieved by reducing the value of $ a $. Note that the range of variation of $ A $ is also reduced by $ a $. That is, $ A $ is a random value in the interval (–a, a), and $ a $ decreases from 1 to 0 with iteration. If the random values for $ A $ are set to (1, 1), the whale's new position can be defined between its original position and the current optimal agent's position.
4.2.3. Search for prey (Exploration phase)
Approaches using variations of the $ A $ vector are also used here to hunt for prey (reconnaissance). In fact, whales randomly seek each other's positions. Therefore, the value of $ A $ is chosen among values greater than 1 and less than -1 to prevent the search agent from straying too far from the reference whale. This notion and the $ |A| > 1 $ condition indicate search and allow the algorithm to perform a global search. The mathematical model is given by Equation (4.5).
where $ \overrightarrow{X_{rand}} $ is a random whale chosen from the current population.
The WOA algorithm begins with a set of randomly selected solutions. Each search agent is updated for its their position with respect to either a random search agent or the current best solution. A random search agent is chosen when $ |A| > 1 $, while the best solution is selected when $ |A| < 1 $ for updating the position of the search agents. The WOA algorithm starts with a set of randomly chosen solutions. Each search agent is updated with respect to its position relative to either the random search agent or the current best solution. If $ |A| > 1 $, a random search agent is chosen. The optimal solution is chosen for $ |A| < 1 $. Update the search agent location.
4.2.4. Application of WOA in congestion management problem
The implementation procedure for the WOA is explained below.
Step 1: Read the test system line and bus data and solve the system line flow problem using the NR load flow method for the current system state.
Step 2: Initialize the whales, and set the population size NP to 30 and the number of iterations to 300. Each whale is a set of control-variable values taken within the lower and upper bounds.
Step 3: Set as control variables such as generator bus voltage, transformer tap position, SVC, and TCSC device position and size.
Step 4: Randomly generate a population of whales and initialize an iteration counter.
Step 5: Run NR Power Flow to calculate objective values for each whale. Perform this procedure for all 30 whales to complete the iterations.
Step 6: Once the objective values for all whales have been computed, sort the whales in ascending order of objective function value. The first whale is the current best with the smallest objective function value.
Step 7: Update whales using Equations. (4.2)-(4.6).
Step 8: Run the NR tide analysis to calculate the updated whale population target.
Step 9: Identify the best current whales. Compare this best whale to the best whale ever saved. If this whale is better, keep this as the best solution or go back to step 7.
Step 10: When the stop is achieved, exit the program and return the result.
5.
Computational results and analysis
The proposed WOA-based congestion handling method is implemented in an IEEE 30 bus test system case. The system has 6 generators at nodes 1, 2, 5, 8, 11, and 13, 24 load nodes, and 41 branches [24]. Bus 1 is the reference bus, and the data is 100 MVA based. Three different transmission congestion cases are used in the simulation study: 35 % increased load, two-way transactions, and multilateral transactions. Table 1 shows the three congestion cases and the power trading volume for each case. The minimum and maximum values of the control variables of generator voltage magnitude and transformer tap change position are within 0.9 p.u. and 1.0 p.u. The SVC VAR output can be in the (0-10) MVAR range. TCSC reactance is measured between 20 % capacitive and 70 % inductance of the line. The proposed algorithm is run 50 times in the three different cases, and the best and worst results are compared with other algorithms. The time of execution in each case is also compared.
5.1. Case 1. 135 % load at all load buses
The total active power load of the system increases to 135%, resulting in increased MW flow through all lines. The most affected power flow is that of line 1, which carries a load of 131.2674 MW. The nominal power of this transmission line is 130 MW, but there is 1.2674 MW of surplus power. To ensure the security of a system that wires the Slack bus to the rest of the network, congestion must be mitigated. System control variables and TCSC and SVC parameters are controlled using the proposed congestion management algorithm. TCSC and SVC devices are optimally placed to provide maximum congestion relief. For comparison, Table 2 shows the power flow through various lines in the system during and after congestion handling. From the power flow, we can see that the overloaded lines are released, and the flow of all lines is adjusted so that the power is below capacity.
SVC and TCSC devices are deployed to optimize power flow patterns to alleviate congestion and minimize load node power loss and total voltage deviation. These benefits are shown in Table 3. The line loss during congestion was 15.2375 MW, but after congestion management the loss is reduced to 13.162 MW. A loss reduction of 2.0755 MW is achieved. To prove the strength of the proposed WOA-based method, the losses and voltage deviations reported by FFA and PSO are also presented in Table 3.
The best and worst values of objectives yielded by PSO, FFA, and WOA algorithms are given in Table 4. The values of reported by WOA are better than those of the other algorithms. The less execution time taken by WOA proves its speed of calculations. This indicates that the proposed method is less time expensive.
Design variables are adjusted during the optimization process to get the best values for line overload, loss and voltage difference objectives. The best set of control variables corresponding to the best global results is shown in Table 5. These values are recommended for operating the power system under healthy conditions.
As shown in Table 6, two SVCs and two TCSCs are proposed for different bus and line locations by the three algorithms. The location is ideal for case 1 congestion management.
The convergence quality of the proposed WOA algorithm is depicted in Figure 5 and it is clear from the Figure that the WOA algorithm is faster than the remaining two algorithms. Comparing the change in objective values over iterations, reported by the three algorithms, it is obvious that WOA better maintains the objective value.
5.2. Case 2- Bilateral transaction
In this case, bi-directional transactions are performed between buses 13 and 26. This transaction is done using bus 13 as the GENCO and bus 26 as his DISCO bus for power transactions. The contract provides for a power deal of 11.5 MW, resulting in 16 MW capacity line no. 34 getting overloaded. The power flow during this transaction is 16.1233 MW. The proposed WOA-based method is utilized to remove the congestion caused by line no. 34. The post-line flows obtained by the PSO, FFA, and WOA algorithms after line congestion are shown in Table 7.
Table 8 shows additional benefits of minimizing the loss levels and voltage deviations reported by the algorithm. The actual power loss achieved by the WOA during this bilateral transaction period was 6.193 MW, which is lower than the loss levels indicated by the two other algorithms. It is clear that the proposed method alleviates congestion and greatly minimizes line loss. The total voltage deviation under overload was 0.7370 and was reduced to 0.1678 by the WOA algorithm. Meanwhile, 0.2172 and 0.1747 are the voltage deviations obtained by the PSO and FFA algorithms.
The statistical analysis of objective values obtained by the different algorithms are shown in Table 9 for comparison. The best and worst values of WOA are better than those of PSO and FFA algorithms. The execution time taken by WOA is less than the time taken by PSO and FFA algorithms. This proves the fast convergence quality of WOA.
Generator voltage magnitude, transformer tap-changer settings, SVC and TCSC parameters are all optimized by the PSO, FFA, and WOA algorithms. Control variables are adjusted during the optimization process, taking into account upper and lower bounds. The well-matched control variables corresponding to the best results are shown in Table 10.
Table 11 shows the best bus and line locations identified for SVC and TCSCs in relieving congestion in this case that are different for different algorithms. when SVC and TCSC devices are located at the positions (bus and line numbers), the line overload, line loss and load bus voltages are optimized, and this helps the power system to be free from stressed conditions.
Figure 6 shows how the algorithm behaves in converging to the optimal goal value of the problem in this congestion managing problem caused by bilateral transaction. The proposed WOA method achieves the best results in fewer iterations and retains them throughout the optimization process.
5.3. Case 3- Multilateral transactions
In the multilateral transaction considered in this case, buses 8 and 11 use GENCO to sell 11 MW and 10 MW of electricity, respectively. DISCO is located on buses 21 and 29 with distributed power of 8 MW and 13 MW, respectively. This multilateral transaction causes congestion on branch 37, which has a capacity of 16 MW, but it is overloaded due to a power flow of 16.2977 MW. Table 12 compares line flows during and after congestion management.
Other goals for minimizing losses and voltage deviation are shown in Table 13. The total system loss is minimized by WOA from 6.9355 MW to 6.1216 MW. This loss reduction is an indicator of the effective congestion management achieved by the proposed WOA approach. As shown in Table 13, the deviation of the load bus voltage from the nominal value is minimal, confirming the suitability of the proposed approach for alleviating congestion on transmission lines.
Objective values of voltage deviation and loss produced by the algorithms used are given in Table 14 for comparison. The best and worst values of loss and voltage deviation reported by WOA are encouraging when compared to that of the values by PSO and FFA algorithms. The time taken by WOA for achieving the best results is less than the time required by PSO and FFA algorithms. This shows the speed of convergence of WOA.
Best control variable values, corresponding to congestion management in this case, are shown in Table 15. It is maintained that all the variables are taking values within the respective limits. It is recommended that these values are the highly suitable for relieving congestion and minimizing loss and voltage deviation.
From the information about the locations, identified by the three algorithms, for the FACTS devices for this case is as given in Table 16.
Figure 7 shows the convergence characteristics of WOA. It is clear that WOA outperforms the two other algorithms in this multilateral transaction case. The proposed algorithm further optimizes the desired value and prevents the algorithm from easily being trapped in local minima.
6.
Conclusions and future work
This work employs a novel biologically-inspired WOA to find the optimal location and size of SVC and TCSC controllers in the grid to alleviate congestion. Parallel-connected SVCs and series-connected TCSC compensators were used for congestion management. For SVC and TCSC allocation issues, appropriate location and size of the FACTS controllers that remove line flow violation, minimize loss, and minimize voltage excursions in the load bus are considered. The results show that WOA produces low ratings for SVC and TCSC controllers, ensuring low capital cost of the devices. Therefore, the WOA method can be used as an efficient technique to solve the optimal allocation of FACTS compensators in congestion management problems. Comparing the results obtained from other algorithms, the PSO and FFA algorithms, and their convergence properties, it is clear that the WOA-based method outperforms the others.
The work can be enhanced in the future by considering other FACTS devices like SSSC, STATCOM, UPFC or by using the multi objective optimization approaches.
Use of AI tools declaration
The authors declare they have not used artificial intelligence (AI) tools in the creation of this article.
Conflict of interest
The authors have no conflict of interest









 DownLoad:
DownLoad:









