Sedentary behaviour and physical activity patterns in adults with traumatic limb fracture

1.   Introduction

Protecting the privacy of electronic data is a major challenge for today's security researchers. A 2013 study by the Cloud Security Alliance revealed a worrying increase in the number of incidents in which cloud data was leaked as a result of negligence, malware, or insider attacks ^[39]. The problem is that the users lose control over potentially privacy sensitive data. Encrypting data before sending it to the cloud is a simple way of guaranteeing confidentiality. However, if one uses traditional encryption, it also becomes impossible for the cloud operators to carry out any kind of processing of that data, as they would have to decrypt it first. Solving this problem is an active area of research. A number of approaches have been studied, relying on different techniques to address the problem of cloud security without compromising the functionality. Here we focus on solutions that are purely based on homomorphic encryption (HE) for privacy preservation.

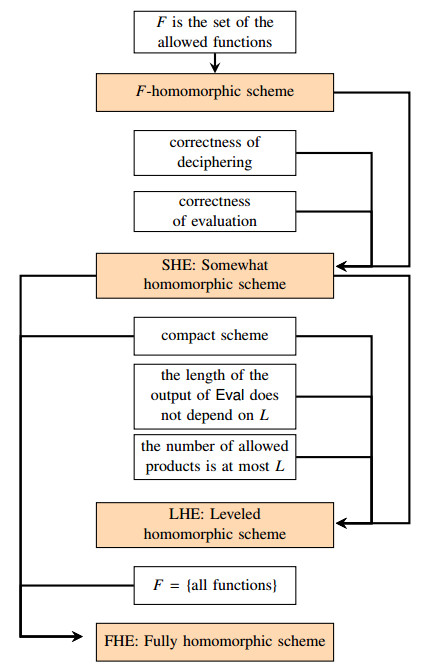
Homomorphic encryption schemes allow computations on the encrypted data. The result of those computations remains in encrypted form, and can thus only be recovered by the owner of the decryption key. Hence, homomorphic encryption offers privacy for both the client's and the server's data. For these reasons HE has shown great success in a variety of domains and applications, from the financial/business sector to the healthcare sector, the government sector, and even to neural networks ^[47]. The concept was imagined in the late seventies, but the first realization did not come until three decades later. HE schemes can be grouped into different categories, based on what operations they support and limitations they put on the circuit. Partially homomorphic encryption (PHE) schemes only support either addition or multiplication. Somewhat homomorphic encryption (SHE) supports both multiplication and addition on encrypted data. It cannot support arbitrarily deep circuits, making it unsuitable for some applications. Fully homomorphic encryption (FHE) schemes support both addition, multiplication, and circuits of arbitrary depth.

Research in the area exploded after 2009 when Craig Gentry presented the first FHE scheme. In HE schemes, for security reasons, the encryption adds noise to the data and the decryption process is the removal of that noise. Performing operations on ciphertexts increases the noise and too much noise prevents correct decryption. It is possible to circumvent this by using the bootstrapping technique ^[25]. Bootstrapping reduces the accumulated noise so that further computation can be done. This process can be repeated as many times as needed to evaluate any given circuit. However, bootstrapping is computationally expensive which is why in practice many solutions do not use it. These days, both the public and private sectors are embracing this new security paradigm and are actively working at making HE more practical and easier to use.

2.   Homomorphic encryption schemes

Let $ \mathcal{P} $ denote a plaintext space and let $ F $ be a family of functions defined on $ \mathcal{P}^n = \{ (m_1, \dots, m_n) \mid m_i \in \mathcal{P} \} $ that can be viewed as Boolean circuits $ C $. In most cases $ \mathcal{P} = \{0, 1\} $ is identifiable with the ring $ \mathbb{Z}_2 = \{ [0]_2, [1]_2\} $.

An encryption scheme $ \mathcal{E} $ is F-homomorphic (or an F-evaluation scheme) if it is given by the following four probabilistic algorithms in polynomial time:

where

● $\textsf{KeyGen}$ is the key generator; it takes as inputs a security parameter $ \lambda $ and an optional parameter $ \alpha $, representing for instance the number of homomorphic operations allowed, and outputs the secret key $ {\textsf{sk}} $, the public key $\textsf{pk}$, and the (public) evaluation key $\textsf{evk}$, needed to compute the homomorphic operations on the ciphertext. Writing $ \mathcal{A} $ for the auxiliary space and $ \mathcal{K}_s, \mathcal{K}_p $, and $ \mathcal{K}_e $ for the spaces of the secret, public, and evaluation keys, respectively, we obtain

In this paper we will usually denote the security parameter by $ \lambda $. In other works, sometimes the security parameter is denoted by $ 1^\lambda $ to keep track of its length.

● $\textsf{Enc}$ is the encryption algorithm; it takes as inputs the public key $\textsf{pk}$ and the message $ m $ and returns the ciphertext $ c $ as an element of the ciphertexts space $ \mathcal{X} $,

● $\textsf{Eval}$ is the evaluation algorithm; it takes as inputs the evaluation key $\textsf{evk}$, a function $ f \in F $, and a string $ (c_1, \dots, c_n) $ of either ciphertexts or previous evaluated texts and returns as output a ciphertext $ c_f $. Writing $ \mathcal{Y} $ for the space of the outputs of $ {\textsf{Eval}} $, with $ \mathcal{Z} $ the union of $ \mathcal{X} $ and $ \mathcal{Y} $ and with $ \mathcal{Z}^* $ the space of $ n $-strings in $ \mathcal{Z} $ for a generic $ n $, we get

● $\textsf{Dec}$ is the decryption algorithm; it takes as inputs the secret key $\textsf{sk}$ and a ciphertext $ c $ (or an output of the evaluation algorithm) and outputs the plaintext $ m' $,

Given a family $ F $ of functions, an $ F $-homomorphic scheme $ \mathcal{E} $ is called

● correct with respect to decrypting if for any plaintext $ m\in \mathcal{P} $, we have

● correct with respect to evaluation if for any function $ f\in F $, we have

for a negligible function $ \epsilon $ ^*.

^*A function $ \epsilon: \mathbb{N}\rightarrow \mathbb{R} $ is negligible if for any positive integer $ c $, there exists an integer $ N_c $ such that for every $ x > N_c $, one gets $ |\epsilon(x)| < x^{-c} $.

● a somewhat homomorphic encryption scheme (SHE) if it is correct with respect to both decrypting and evaluation.

● compact if there exists a polynomial $ p $ such that for every function $ f\in F $, every triplet of keys ($ {\textsf{sk}}, {\textsf{pk}}, {\textsf{evk}} $), and every ciphertext $ c_i \in \mathcal{X} $, the output of the evaluation algorithm $ {\textsf{Eval}}({\textsf{evk}}, f, (c_1, \dots, c_n)) $ consists of at most $ p(\lambda) $ bits, independent from the complexity of the function $ f $ (that is, from the length of the corresponding Boolean circuit $ C $). In other words, the length of the ciphertext does not grow too much when involved in homomorphic operations and the length of the final output depends on the length of the security parameter only.

● a leveled homomorphic encryption scheme (LHE) if it is a compact SHE scheme in which the length of the output of $\textsf{Eval}$ does not depend on the auxiliary parameter, usually denoted in this context by $ L $, that specifies the maximum number of consequent products allowed.

● a fully homomorphic encryption scheme (FHE) if it is a compact SHE scheme and $ F $ is the set of all functions (efficiently computable).

Figure 1.  Types of homomorphic schemes.

DownLoad: Full-Size Img PowerPoint

We remark that in a scheme that is correct with respect to evaluation, the cipheretexts

correspond to the same plaintext, but arise from distinct constructions (for instance, they could have different levels of noise).

In practice, the functions considered often correspond to sums (denoted by $ f_s $ or $ + $) and products (denoted by $ f_p $ or $ \times $) defined on a specific algebraic structure and the fact that the scheme is correct with respect to evaluation makes sure that, given two ciphertexts $ c_1 $ and $ c_2 $, we get

and

The origin of homomorphic encryption goes back to 1978 when, in ^[48], Rivest, Adleman and Dertouzos introduced the concept of privacy homomorphism and showed some examples of homomorphic schemes, one of which was RSA. Among other things, they posed the following question: For what algebraic systems does a useful privacy homomorphism exist? Later, various examples of homomorphic schemes based on a unique operation followed, such as the one by ElGamal ^[21] and Paillier ^[43]. In 2005, Boneh, Goh and Nissim (BGN) ^[7] described the first SHE scheme based on two operations: an arbitrary number of sums and a unique product, possibly followed by an arbitrary number of sums.

3.   The first FHE schemes

Craig Gentry was the first to describe a plausible construction of an FHE scheme in ^[25], marking a turning point in the theory. His strategy consisted of three steps: the construction of an SHE scheme based on evaluation of low-degree polynomials, the use of the technique of squashing to the encryption procedure in order to express it as a low-degree polynomial (supported by the scheme), and finally the application of the method of bootstrapping to obtain an FHE scheme. Gentry's SHE scheme is also the first to be built on ideal lattices: the secret key represents a good basis for the lattice, meaning that its vectors are pairwise orthogonal, while the public key is given by a bad basis of the same lattice, made by skew vectors. Indeed, the security of Gentry's scheme is based on the fact that the problem of finding an orthogonal basis of a lattice is hard. In order to make the scheme bootstrappable, Gentry suggested to reduce the length of the decrypting polynomial adding to the public key a large set of vectors, requiring for the secret key to be the sum of a very sparse subset of such a set (the security of the scheme is therefore based on the sparse subset sum problem (SSSP)).

The first implementation of Gentry's scheme was proposed in 2010 by Smart and Vercauteren (SV) in ^[51]. In that work, the authors used principal ideals with a prime determinant and expressed the secret key as a unique integer. However, given the complexity of the key generation (in order to obtain an ideal with a determinant that is prime, many candidates are required) such a scheme does not support parameters big enough to apply bootstrapping (it is not possible to generate keys with ideal lattices of dimension larger than 2048); it is therefore an SHE scheme that cannot be made into an FHE scheme.

Later, Gentry and Halevi (GH) ^[26] adopted the same approach of Smart and Vercauteren, working on the same ring $ R = \mathbb{Z}[x]/\langle x^N +1 \rangle $, for a positive integer $ N = 2^n $, but without requiring for the lattice to have a determinant that is a prime number. Moreover, they described a faster algorithm to generate the secret key (invoking Fourier's discrete transform and its inverse to compute the inverse of the polynomial that generates the principal ideal lattice in the case of a general integer $ N $ and an easier recursive procedure when $ N = 2^n $, as in the actual scheme described) and simplified the squashing, obtaining a decrypting polynomial of degree at most $ 15 $. In particular, the (GH) scheme is bootstrappable for every dimension of the lattice involved, even if its security is for low dimensions.

Figure 2.  SHE schemes defined on lattices.

DownLoad: Full-Size Img PowerPoint

The strength of the SHE schemes based on lattices lies on their theoretical feasibility and on the efficiency of the encrypting and decrypting algorithms obtained using the techniques of batching and squashing: the first allows one to cipher multiple messages in a unique ciphertext and the latter decreases the decrypting complexity. On the other hand, the fact that such schemes are constructed on complex mathematical structures induces high computational costs and requires a large amount of memory space, making it hard to implement them efficiently. Moreover, in ^[19], Cramer et al. highlighted the vulnerability of such schemes if attacked, for instance, by a quantum algorithm in polynomial time.

In 2010, van Dijk, Gentry, Halevi and Vaikuntanathan introduced in ^[52] a new family of SHE schemes working on the ring of integers $ \mathbb{Z} $ and basing the security on the SSSP and the approximate greatest common divisor problem (AGCD). The (DGHV) scheme is easier to treat with respect to Gentry's scheme (G) ^[25] since the operations involved are sums and products of integers in modular arithmetic. In ^[52], the authors applied Gentry's approach to show how to use the techniques of squashing and bootstrapping to build FHE schemes. The (DGHV) scheme is notably valued for its elegance and simplicity, but its high computational complexity and long bit-length of the public key make it less efficient in practical uses. Moreover, such a scheme is vulnerable to chosen-ciphertext attacks and noise flood attacks.

In what follows we give a detailed description of Gentry's scheme and of Smart and Vercauteren's scheme.

3.1.   Gentry's scheme (G)

Given a basis $ B = \{\vec{b}_1, \dots, \vec{b}_n\} $ of $ \mathbb {R}^n $, the corresponding lattice of dimension $ n $ is defined as

and the parallelepiped associated to $ B $ is

If $ \vec{u} \in \mathbb{R}^n $ is a vector, the expression

denotes the unique vector $ \vec{u}' \in \mathcal{P}(B) $ such that $ \vec{u} - \vec{u}' \in L $.

Let $ f(x) \in \mathbb{Z}[x] $ be a monic and irreducible polynomial of degree $ n $ (whose definition depends on the security parameter $ \lambda $) and consider the ring of integer polynomials modulo $ f $:

Every ideal of $ R $ is a lattice, and we will refer to such a structure as the ideal lattice. Note also that $ R $ can be viewed as a subset of $ \mathbb{Z}^n $, identifying any polynomial of $ R $ with the vector of their coefficients. Suppose that if $ B $ is a basis of the ideal lattice $ I $ of $ R $, then for every $ x \in R $ (corresponding to the vector $ \vec{x} $), the vector $ \vec{x} \mod B $ is unique and can be computed efficiently.

The plaintext space is $ \mathcal{P} = \{0, 1\} $, which can be embedded in $ R $ (and so in $ \mathbb{Z}^n $) setting $ \vec{m} = (0, \dots, 0) $ if $ m = 0 $ and $ \vec{m} = (0, \dots, 0, 1) $ if $ m = 1 $. Let $ J $ be an ideal lattice of $ R $ (again seen as a subset of $ \mathbb{Z}^n $).

● The keys are given by

where $ B_{ {\textsf{sk}}} $ and $ B_{ {\textsf{pk}}} $ are bases for $ J $, described as matrices, and the secret key is good (formed by pairwise orthogonal vectors) while the pubblic key is bad.

● Given the message $ m\in \{ 0, 1\} $ and the corresponding vector $ \vec{m} \in \mathbb{Z}^n $, the encryption algorithm is

where $ \vec{r} \in \mathbb{Z}^n $ is a random vector representing the noise. In other words, $ {\textsf{Enc}}({\textsf{pk}}, \vec{m}) $ is the unique vector of the parallelepiped $ \mathcal{P}(B_{ {\textsf{pk}}}) $ such that

and we can compute it as

● The decryption algorithm is

That is, we consider the congruence class modulo $ 2 $ of the unique vector $ \vec{c}' $ of the parallelepiped $ \mathcal{P}(B_{ {\textsf{sk}}}) $ such that $ \vec{c} - \vec{c}' \in J $, which can be computed as

● $ F $ is the family of sums (denoted by $ f_s $) and products (denoted by $ f_p $) in the ring $ R $ (so they are sums and products among real coefficients polynomials modulo $ f(x) $). The algorithm $ {\textsf{Eval}} $ outputs sums and products modulo $ {\textsf{evk}} = B_{ {\textsf{pk}}} $. If $ c_1 $ and $ c_2 $ are two ciphertexts, seen as elements of $ R $, then

With the notations $ \vec{(c_1 + c_2)} $ and $ \vec{(c_1 \cdot c_2)} $ we mean that we first compute the sum or the product of the polynomials $ c_1 $ and $ c_2 $ in $ R $ and then we express the result as a vector of coefficients in $ \mathbb{Z}^n $.

We remark that the scheme described by Gentry in ^[25] also allows for a larger plaintext space. More precisely, fixing an ideal lattice $ I $ of $ R $ and a basis $ B_I $, one can consider as a plaintext space any subset $ \mathcal{P} $ of $ R\!\mod B_I $. In this case, the output of the decryption algorithm will not be modulo $ 2 $ but modulo $ B_I $:

The scheme described above corresponds to taking $ I = \langle 2\rangle $, that is, the set of polynomials of degree at most $ n-1 $ with only even coefficients.

Gentry's scheme is correct with respect to decryption, as long as the noise vectors and the vectors of the public basis are small enough. Indeed, if $ \vec{m} \in \{0, 1\}^n $ is a plaintext (viewed as an element of $ R $), the corresponding ciphertext $ \vec{c} $ can be expressed as $ \vec{j} + (2\vec{r}+\vec{m}) $, for a vector $ \vec{j} \in J $. Hence

Since $ \vec{j} \in J $, the vector $ \vec{j} \cdot B_{ {\textsf{sk}}}^{-1} $ has integer coefficients and we deduce that

If the vectors forming the basis $ B_{ {\textsf{pk}}} $ and the vector $ 2\vec{r}+\vec{m} $ are small enough (for instance, if all coefficients of $ (2\vec{r}+\vec{m})\cdot B_{ {\textsf{sk}}}^{-1} $ have an absolute value less than $ 1/2 $), then

and so

The scheme is also correct with respect to the evaluation of sums. Let $ \vec{c}_1 = \vec{j}_1 + (2\vec{r}+\vec{m}_1) $ and $ \vec{c}_2 = \vec{j}_2 + (2\vec{r}+\vec{m}_2) $ be the ciphertexts associated with the plaintexts $ m_1 $ and $ m_2 $.

Then

Similarly, it is possible to verify that the scheme is correct with respect to the evaluation of the product. This proves that Gentry's scheme is an SHE scheme.

3.2.   Smart and Vercauteren's scheme (SV)

Let $ \lambda $ be the fixed security parameter, and let us consider

● an integer $ N = N(\lambda) = 2^n \in \mathbb{N} $, that defines the polynomial $ f(x) = x^N +1 $ and the ring

● an integer $ t = t(\lambda) \in N $.

Choose a polynomial $ v(x) = \sum_{i = 0}^{N-1} v_ix^i \in R $ such that $ v_0 $ is odd, and every coefficient has an absolute value less than $ 2^t $ (and at least one coefficient is an integer of bit-length $ t $). Given the matrix

its determinant $ d = \det(V) $ is a prime number.

Let us now consider the ideal lattice $ J = (v) $ generated by the polynomial $ v(x) $ and the unique number $ r \in [-d/2, d/2) $ that is a zero of both $ f(x) $ and $ v(x) $ modulo $ d $ (considering the reductions modulo $ d $ in the interval $ [-d/2, d/2) $). The uniqueness of $ r $ is proved in [50, Lemma 1] using algebraic number theory techniques. Note that the ideal $ J $ is completely determined by $ d $ and $ r $.

Finally, set $ r_i: = r^i \mod d $ and consider the normal Hermitian form of $ J $:

Note that the matrix $ V $ represents a good basis for $ J $, while $ B $ represents a bad basis. The plaintext space is $ \mathcal{P} = \mathbb{Z}_2 $. In this context, we can now present the algorithms of the scheme:

● The keys are given by

where $ w(x) $ is such that $ v(x) \cdot w(x) = d \mod f(x) $, so $ w(x) $ is an inverse of $ v(x) $ modulo $ f(x) $. The public key can also be defined as a matrix: $ {\textsf{pk}} = B $.

● Given the plaintext $ m\in \mathbb{Z}_2 $, the encryption algorithm is

where $ u = \sum_{i = 0}^{N-1} u_ix^i \in \mathbb{Z}[x] $ is a random polynomial with integer coefficients representing the noise and $ u(r) $ is the evaluation of the polynomial $ u $ in $ r $. If we write $ \vec{u} $ for the vector of the coefficients of $ u $ and $ \vec{m} $ for the vector corresponding to $ m $ (as in Gentry's scheme), encrypting $ m $ is equivalent to computing the first entry of the vector $ 2\vec{u} + \vec{m} \mod B $.

● The decryption algorithm is

where $ w_0 $ is the first coefficient of the polynomial $ w(x) $.

● The evaluation algorithm $ {\textsf{Eval}} $ outputs sums and products in the ring $ R $, computed modulo $ {\textsf{evk}} = d $.

By definition, the ciphertext $ c $ corresponding to the plaintext $ m $ is the first entry of the unique vector $ \vec{c'} $ of the parallelepiped $ \mathcal{P}(B) $ such that $ (2\vec{u} + m) - \vec{c'} \in J $. Using the polynomial notation and recalling that $ J $ is generated by $ v(x) $, we get

for a polynomial $ q(x) \in R $. Dividing by $ v(x) $, using the fact that $ v(x)^{-1} = w(x)d^{-1} $, and looking at the first coefficient of the polynomials, we obtain

If the error is small enough, that is, such that $ \left\lfloor \frac{(2u(r) + m)w_0}{d} \right\rceil = 0 $, then

and the decryption procedure is correct (as $ v_0 $ is odd by assumption):

It is not hard to prove that the evaluation is correct as well, and so this is an SHE scheme.

4.   FHE schemes from learning with errors

In 2011 Brakerski and Vaikuntanathan started a new reaserch direction introducing the first FHE schemes based on the learning with errors problem (LWE) ^[12] (extended version in ^[14]) and on the ring learning with errors problem (RLWE) ^[13]. Such schemes have a great relevance in modern cryptography. Indeed, they offer an optimal combination of security, functionality, and applicability. For $ n\geq 1 $ and $ q\geq 2 $, the (search-)LWE problem asks to recover $ s = (s_1, \ldots, s_n)\in \mathbb{Z}_q^n $ given any desired $ m = poly(n) $ independent linear equations such as the following,

where the matrix $ A = (a_{jk})\in \mathbb{Z}_q^{m\times n} $ is chosen uniformly, and each $ e_i $ is usually taken from a Gaussian distribution $ \chi $ and rounded to the nearest integer (modulo $ q $). The LWE problem is believed to be computationally hard, because of the Regev's reduction from the worst-case hardness of some lattice problems, such as GapSVP (the decision version of the Shortest Vector Problem, which consists in finding a non-zero vector $ v \in L $ that minimizes the Euclidean norm), to the search-LWE problem ^[46]. This reduction works for any modulus $ q\geq 2\sqrt n/\alpha $, with $ 0 < \alpha < 1 $, but it requires the use of quantum computation. In ^[45], Peikert proved that LWE is classically at least as hard as worst-case GapSVP on lattices for large modulus $ q\geq 2^{n/2} $. Since then, the LWE problem has become one of the most attractive and promising topics for post-quantum cryptography.

In Brakerski and Vaikuntanathan's scheme (BV), given a plaintext $ m\in \mathbb{Z}_2 $ and a secret key $ \vec{s} \in \mathbb{Z}_q^n $, the idea is to generate a ciphertext

where $ \vec{a} \in \mathbb{Z}_q^n $ is a vector chosen uniformly at random and $ e \in \mathbb{Z}_q $ is an error chosen with distribution $ \chi(\mathbb{Z}_q) $. In this way the message $ m $ is masked twice: by the scalar product $ \langle \vec{a}, \vec{s}\rangle $ and by the noise $ 2e $. These masks can be removed independently in the process of decrypting: the first is subtracted and the noise noise $ 2e $ is canceled considering the congruence class modulo $ 2 $ (as long as the error $ e $ is small enough, that is, such that $ 2e + m \mod q = 2e +m $). In ^[12] the authors also show how to make the scheme bootstrappable (and so into an FHE scheme), introducing the techniques of relinearization and modulus switching, in substitution of Gentry's squashing technique. The relinearization is used to control the growth of noise, in particular after operations of multiplication, while the modulus switching consists on considering an integer $ p $ smaller than $ q $ and, given a ciphertext $ c $ modulo $ q $, to multiply it by $ p/q $ and to approximate the result to the nearest integer, obtaining a new ciphertext $ c' $ modulo $ p $.

The scheme (BV-RLWE) described in ^[13] is a new version of (BV) whose security is based on the polynomial LWE problem, that is proved to be equivalent to the RLWE problem. The main difference is in the fact that plaintexts, keys and ciphertexts are built not working in $ \mathbb{Z}_q $, for an odd integer $ q $, but in the ring $ R_q = \mathbb{Z}_q[x]/\langle f(x) \rangle $, for a prime number $ q $ and a suitable polynomial $ f(x) \in \mathbb{Z}[x] $.

In 2012 Brakerski, Gentry and Vaikuntanathan (BGV) ^[10] (technical report in ^[9], extended version in ^[11]) proposed a procedure to build an LHE scheme (without invoking the bootstrapping) and a new bootstrapping technique used to obtain an FHE scheme. These innovations represented an important change in the field because they allow for the scheme to be truly applicable in various practical situations. The scheme (BGV) exists in two versions, based on the LWE and RLWE problems, respectively. The scheme (BGV-RLWE) is the most efficient and it was implemented in the open-source HElib library by IBM ^[35]. We point out that such a scheme has been improved in ^[27] (with optimized bootstrapping in ^[28]) and the library architecture is based on a variant of (BGV) proposed by Gentry, Halevi and Smart ^[29].

Again in 2012, Brakerski (B) ^[6] presented a variant of (BGV) based on the Scale-invariant technique, in substitution of modulus switching. In particular, in the encryption algorithm the plaintext $ \vec{m} $ is "scaled" multiplying it by the number $ \lfloor \frac{q}{2} \rfloor $ (and the decrypting algorithm is modified accordingly). In the scheme (B) the technique of key wwitching also appears, consisting of two algorithms: $ \texttt{SwitchKeyGen}_{q, \chi}(s, t) $ that, starting form a secret key $ s $ and a "target" key $ t $, outputs a matrix $ P_{s:t} $ and $ \texttt{SwitchKey}_{q}(P_{s:t}, c_s) $ that, using the matrix $ P_{s:t} $, allows it to express a ciphertext $ c_s $, encrypted using the key $ s $, as a ciphertext $ c_t $, encrypted using the key $ (1, t) $. As a consequence of this innovation, the dimension of the errors arising from the operations of multiplication grows linearly. Also, a classic reduction is used to show that its security is based on the hardness of (SVP) (in previous works the reductions were of quantum type only).

Fan and Vercauteren (FV) ^[24] implemented and optimized the RLWE version of Brakerski's scheme (B), introducing two ways of relinearizing the output of the product evaluation, in order to obtain a polynomial of degree 1 instead of 2. The scheme (FV) is one of the three schemes implemented in Microsoft's Simple Encrypted Arithmetic Library (SEAL) ^[49].

Figure 3.  First schemes based on the LWE and RLWE problems.

DownLoad: Full-Size Img PowerPoint

The next two subsections are devoted to the (BGV) scheme and to the (FV) scheme, respectively.

4.1.   Brakerski, Gentry and Vaikuntanathan's scheme (BGV)

We first present a base scheme (without evaluation) on which both the LWE and RLWE versions of the (BGV) scheme are built, as described in ^[10]. Choosing a security parameter $ \lambda $, we consider a ring $ R $ depending on $ \lambda $, setting for instance $ R = \mathbb{Z} $ in the LWE version and $ R = \mathbb{Z}[x]/\langle x^d + 1 \rangle $ in the RLWE version, for an integer $ d = d(\lambda) = 2^k \in \mathbb{N} $. For every positive integer $ t \in \mathbb{N} $, set

Hence, if $ R = \mathbb{Z} $ we get $ R_t = \mathbb{Z}_t $ and if $ R = \mathbb{Z}[x]/\langle x^d + 1 \rangle $ we obtain $ R_t = \mathbb{Z}_t[x]/\langle x^d + 1 \rangle $. The plaintext space is $ \mathcal{P} = R_2 $.

Let us consider the following further parameters:

● an integer $ \mu = \mu(\lambda) \in N $;

● an odd modulus $ q = q(\lambda)\in \mathbb{N} $ of $ \mu $-bit;

● two dimensions $ n = n(\lambda), N = N(\lambda) \in \mathbb{N} $;

● a distribution $ \chi = \chi(\lambda) $ on $ R $ (as small as possible).

The algorithms of the base scheme are defined as follows.

● The keys are given by

where $ \vec{s'} \in\chi(R_q^n) $ is a secret vector and, given a vector $ \vec{e} \in \chi(R_q^N) $ representing the error and a matrix $ A'\in \rm{Mat}_{N \times n}(R_q) $, the matrix $ A \in \rm{Mat}_{N \times (n+1)}(R_q) $ is defined as the matrix that has the vector $ \vec{b} = A'\cdot \vec{s'} + 2 \vec{e} \in R_q^N $ as the first column, followed by the $ n $ columns of the matrix $ -A' $. Note that $ A \cdot \vec{s} = 2\vec{e} $.

● Given a plaintext $ m \in R_2 $, set $ \vec{m} = (m, 0, \dots, 0) \in R_q^{n+1} $. The corresponding ciphertext is given by

where $ \vec{r}\in R_2^N $ is a vector representing the error.

We point out that in ^[10] the authors remark that the scheme (BGV-RLWE) is more efficient if one puts $ N = 1 $ (so that the matrix $ A $ can be thought of as a vector of length $ n+1 $) and introducing in the output of $ {\textsf{Enc}} $ a further small error $ \vec{e'} \in R_q^{n+1} $:

● The decryption algorithm is

Note that the base scheme is correct with respect to decryption if the error $ \vec{e} $ is small:

In [10, Section 3.4] the authors describe an LHE scheme, in which for every level $ l $, with $ 0 < l \leq L $, distinct keys and distinct moduli are defined. Instead of using bootstrapping to make it into an FHE scheme, they define an algorithm, called $\texttt{Refresh}$, that allows one to modify the level of the ciphertext, passing to keys and modulus of the previous level and decreasing the noise. The $\texttt{Refresh}$ algorithm uses an extra evaluation key $ {\textsf{evk}} $ (that can be viewed as an encryption of the secret key) and is formed by

● $\texttt{SwitchKey}$: Allows it to pass from a ciphertext $ \vec{c} $, encrypted using the secret key $ \vec{s}_l $ defined at the level $ l $, to a ciphertext $ \vec{c}_1 $, encrypted using the secret key $ \vec{s}_{l-1} $ defined at the level $ l-1 $, preserving the initial modulus $ q_{l} $;

● $\texttt{Scale}$: Starting from the ciphertext $ \vec{c}_1 $, it outputs a ciphertext $ \vec{c}_2 $ encrypted using the same secret key $ \vec{s}_{l-1} $ but with respect to the modulus $ q_{l-1} $.

The family $ F $ of homomorphic operations is formed by sums $ f_s $ and products $ f_p $ in the ring $ R_q^{n+1} $. Given two ciphertexts $ \vec{c}_1 $ and $ \vec{c}_2 $, encrypted using the same secret key (at the same level $ l $), the evaluation of the sum is

As for the product $ f_p $, we consider the following linear equation depending on the ciphertext $ \vec{c} $:

Note that decryption $ \vec{c} $ with the secret key $ \vec{s} $ corresponds to computing $ [[L_{\vec{c}}(\vec{s})]_q]_2 $. Given two ciphertexts $ \vec{c}_1 $ and $ \vec{c}_2 $, we can now consider a quadratic equation, that can be also viewed as a linear equation on tensor products:

We can now define the evaluation algorithm for the product:

We refer to ^[10] for the proof of the correctness of the evaluation.

4.2.   Fan and Vercauteren's scheme (FV)

In ^[24] Fan and Vercauteren applied the relinearization technique to decrease the length of products of ciphertexts and proposed two SHE schemes, which we are going to describe, referring to them as version $ 1 $ and version $ 2 $ of (FV).

Given a security parameter $ \lambda $, let us consider the polynomial rings

for a positive integer $ d = 2^k $ and a positive integer $ t = t(\lambda) $. The plaintext space is $ \mathcal{P} = R_t $.

Moreover, we fix the following parameters:

● an odd integer $ q = q(\lambda) \in \mathbb{N} $ (the modulus);

● an integer $ T\in \mathbb{N} $ (used for relinearization in version $ 1 $);

● an integer $ p\in \mathbb{N} $ (used for relinearization through modulo switching in version 2);

● two error distributions $ \chi = \chi(\lambda) $ and $ \chi' = \chi'(\lambda) $ defined on $ R $. The distribution $ \chi $ can be identify with the discrete Gaussian distribution. However, $ \chi' $ is used in version $ 2 $ and must differ from $ \chi $, otherwise the security of the scheme would be considerably weakened.

We remark that if $ x \in R_t $ and $ y\in R_2 = \mathbb{Z}_2[x]/ \langle x^d +1 \rangle $, then both $ x $ and $ y $ can be viewed as elements of $ R $ and as such can be multiplied. With the symbol $ \cdot $ we denote the operation of multiplication in $ R $.

The algorithms of (FV) are the following:

● the keys are generated by

where $ s \in R_2 $ and $ a \in R_q $ are chosen uniformly at random, $ e \in \chi(R) $ is an error and with $ {\textsf{evk}}_1 $ and $ {\textsf{evk}}_2 $ we denote the evaluation keys in versions $ 1 $ and $ 2 $ of the (FV) scheme, respectively.

In version $ 1 $, let $ \ell = \lfloor \log_T(q) \rfloor $, and for every $ i\in 0, \dots, \ell $ set $ a_i \in R_q $ (chosen uniformly at random), $ e_i \in \chi(R) $ and

In version $ 2 $, the relinearization consists of passing from computations modulo $ q $ to computations modulo $ pq $:

for $ a \in R_{p \cdot q} $ and $ e\in \chi'(R) $.

● Given a plaintext $ m \in \mathbb{R}_t $ and the public key

we get

for some $ u \in R_2 $ and errors $ e_1, e_2 \in \chi(R) $.

● Given a ciphertext $ \vec{c} = (\vec{c}[1], \vec{c}[2]) $, the decryption algorithm is

● The family $ F $ consists of sums $ f_s $ and products $ f_p $ in $ R $. Let $ \vec{c}_1 = (\vec{c}_1[1], \vec{c}_1[2]) $ and $ \vec{c}_2 = (\vec{c}_2[1], \vec{c}_2[2]) $ be two ciphertexts. The evaluation algorithm is defined among the sets

and, applied to the sum, is the natural evaluation:

As for the product, the relinearization technique is invoked and the output is different in the two versions of (FV). First, let us compute

and

In version $ 1 $, we express $ z $ as: $ z = \sum_{i = 0}^l z_i \cdot T^i $, for $ z_i \in R_T $, and we get

Instead, in version $ 2 $ the evaluation of the product is:

Both versions of (FV) are correct with respect to both decryption and evaluation, and so they are SHE schemes. Indeed, if the errors are small enough (that is, such that $ 0 $ is the nearest integer to the product $ \frac{t}{q} \cdot [ e \cdot u + e_1 + e_2 \cdot s \; ] $), it is easy to see that the decryption procedure is correct:

The proof of the correctness of the evaluation of sums and products can be read in detail in [24, Section 4]. Moreover, in [24, Sections 5 e 6] the authors show how to produce an LHE scheme and an FHE scheme.

5.   Other FHE schemes and recent developments

In 2013 Gentry, Sahai and Waters (GSW) ^[30] suggested a different approach for the computation of homomorphic operations, starting a research direction known as the third generation of FHE schemes. The (GSW) scheme does not invoke the modulus switching technique, but the approximate eigenvector method reduces the error arising from products to a small polynomial factor. On the other hand, the (GSW) scheme requires high communication costs (the ciphertext is larger with respect to the corresponding plaintext) and high computational complexity. To remedy such problems, various optimizations of such a scheme were later proposed. Alperin-Sheriff and Peikert (AP) ^[1] suggested a new bootstrapping algorithm considering the process of decrypting as an arithmetic function instead of a Boolean circuit, a procedure later improved by Hiromasa et al. ^[33] and extended to rings by Ducas and Micciancio (FHEW: Fastest Homomorphic Encryption in the West) ^[20]. We remark that the (FHEW) scheme is the first one to execute bootstrapping in a fraction of a second; in the literature, this innovative bootstrapping technique is known as AP/FHEW bootstrapping.

The (FHEW) scheme has been the starting point used by Chillotti et al. in 2020 ^[15] to define the (TFHE) scheme based on the torus that uses a new bootstrapping technique (known as GINX) first described by Gama et al. in ^[31]; see also ^[22] for an algebraic version of (TFHE) and ^[23] for an application. In a recent work, Lee and Micciancio et al. ^[41] described a bootstrapping technique combining the best aspects of AP/FHEW and GINX/TFHE.

In 2017, Cheon, A. Kim, M. Kim, and Song (CKKS) ^[17] started the so-called fourth generation of FHE schemes, suggesting a new method to construct an LHE scheme and including an open-source library (known as HEANN ^[34]) that implements it. The (CKKS) scheme was extended to an FHE scheme in ^[16] and constitutes the starting point for many further optimizations. For instance, in ^[37] Kim, Papadimitriou and Polyakov proposed a technique to decrease the propagation of errors, rescaling the ciphertexts before applying the homomorphic operations, and presented two RNS (residue number system) variants of (CKKS), both implemented in the PALISADE library ^[44].

One of the novelties of the fourth generation schemes is that they use approximate arithmetic, which makes the algorithms faster. In 2021, Li and Micciancio ^[40] proved that the (CKKS) scheme and its variants are vulnerable to attacks by adversaries knowing the encryption function.

Figure 4.  Third and fourth generation schemes based on the LWE and RLWE problems.

DownLoad: Full-Size Img PowerPoint

We conclude this survey on fully homomorphic encryption briefly describing recent results aimed at improving efficiency and security of FHE schemes.

5.1.   Chimera

In 2020, Boura, Gama, Georgieva and Jetchev introduced the scheme known as CHIMERA ^[8]: a hybrid scheme combining (TFHE), (FV) and (CKKS). In CHIMERA, the plaintext space is defined in such a way that the plaintext spaces of (TFHE), (FV) and (CKKS) could embed in it. Using bootstrapping, the authors describe a procedure that allows it to pass from ciphertexts encrypted using (TFHE) or (CKKS) to ciphertexts encrypted according to (FV), and vice versa. CHIMERA turned out to be very useful in many practical scenarios, in which the various natures of the operations involved caused the application of only one of the schemes (TFHE), (FV) or (CKKS) inadequate. Moreover, CHIMERA contributes the project of standardization of FHE schemes.

5.2.   HERA, RUBATO and HERMES

In 2021, Cho et al. ^[18] proposed a scheme, called (RtF) (real-to-finite-field), that combines (CKKS) and (FV) and exploits a new stream cipher, known as HERA, based on modular arithmetic. They showed how such strategies allow one to encrypt large real numbers without incurring in an excessive growth of the ciphertext's dimension or of the memory space needed to compute homomorphic operations. In 2022, Ha et al. ^[32] followed the approach of Cho et al. ^[18] and introduced a new stream cipher, called RUBATO, that further decreases the computational complexity of (RtF).

In 2023, Bae, Cheon, Kim, Park, and Stehlé ^[3] proposed two solutions to the ring packaging problem, that is, the problem of conversion of a scheme based on the LWE problem to one based on the RLWE problem. On one hand, they presented a strategy that speeds up the existing ring packaging technique through bootstrapping and ring switching; on the other, they introduced a completely new method, called HERMES, showing how to apply it to transform a symmetric cryptosystem based on LWE into a variant of (CKKS). In particular, the authors proved that HERMES is more efficient than both HERA and RUBATO.

5.3.   Variants of (BGV) and (FV)

In 2021, Kim, Polyakov and Zucca ^[38] described new schemes inspired by the (BGV) and (FV) schemes. The variant of (FV) contains various optimizations, including decreasing of noise growth and the definition of a novel algorithm for the evaluation of multiplication that reduces the computational complexity of the original one. As for (BGV), the authors describe a "pratical" variant that is more efficient than (FV) in certain real scenarios. Both variants have been implemented in the PALISADE library.

In 2023, Okada, Player and Pohmann ^[42] proposed a strategy to improve the evaluation of polynomials in the bootstrapping of (FV), using Galois automorphisms. Moreover, they showed how some of the bootstrapping techniques of (FHEW) and (TFHE) can be applied to (FV).

5.4.   ThFHE schemes

One of the strategies invoked to strengthen the security of public-key cryptosystems consists in dividing the secret key into $ n $ parts, delivered to $ n $ distinct clients, so that only their cooperation (or the cooperation of a certain number of them) could lead to decryption. Such a technique is known as threshold public key encryption and the expression $ t $-out-of-$ n $ means that at least $ t+1 $ of the $ n $ clients must cooperate to decipher the message. In ^[2] the authors showed that threshold public key encryption can be applied to FHE schemes, that are in this case denoted by ThFHE. In 2023, Boudgoust and Scholl ^[5] introduced a new ThFHE scheme of type $ t $-out-of-$ n $ based on the LWE problem that involves the use of a modulus given by a polynomial function of the security parameter (while previous works required a superpolynomial modulus, with consequent increase of computational costs).

We remark that the innovative bootstrapping procedure elaborated by Lee et al. in ^[41] is particularly efficient when applied to ThFHE schemes.

5.5.   Optimization in the choice of parameters

One of the major difficulties in applying FHE schemes to real scenarios lies in the determination of the best parameters to use in order to preserve security requiring low computational costs. In 2023, Bergerat et al. ^[4] formalized the problem of the parameters' choice as an optimization problem and suggested to encrypt a plaintext into more than one ciphertexts using novel algorithms. Their work focused on the (TFHE) scheme, but the strategy illustrated can also be applied to other FHE schemes.

5.6.   Optimization of rotation keys

Certain FHE schemes, such as (FV) and (CKKS), support rotation operations, that is, permutations of the ciphertexts components (e.g., the entries of the vector corresponding to the ciphertext). These operations are needed if the scheme contains homomorphic operations involving distinct components of the ciphertext and they require an evaluation key, called the rotation key. In 2023, Lee, Lee, Kim, and No ^[36] introduced a hierarchic system of rotation keys, which allows it to generate such keys starting from the public key and a small number of rotation keys, significantly decreasing the communication costs between client and server.

6.   Conclusions

Fully homomorphic encryption represents an important step forward in cryptography, offering unprecedented levels of privacy and data security. Its ability to perform computations on encrypted data without decryption has the potential to transform how we handle and use sensitive information in various domains, including healthcare, finance and national security. As FHE schemes continue to mature and practical applications emerge, this revolutionary technology is poised to play a critical role in defining the future of data security and privacy.

Gentry's work represented a breakthrough in the field of cryptography by presenting the first plausible scheme that supports arbitrary computations on encrypted data. This achievement has long been considered the Holy Grail of cryptography, due to its usefulness in multiple industries, from cloud computing to data mining. The original scheme was based on ideals and lacked efficient implementation. However, its central idea, i.e., the use of an SHE scheme capable of evaluating its own decryption circuit, was subsequently applied to other cryptographic systems, including LWE and AGCD, providing more efficient schemes. With the introduction of other important techniques, such as module and key switching, these systems have become increasingly efficient over time. The key advances in FHE cryptography can be summarized as follows:

● Development of FHE schemes based on cryptographic systems other than ideal ones: this has led to more efficient and practical schemes.

● Development of techniques to improve the efficiency of FHE schemes: such techniques include module and key switching and packing.

● Development of efficient implementations of FHE schemes: these implementations have made FHE schemes more accessible and usable.

Overall, advances in FHE have led to more efficient FHE schemes, which can be used in a wide range of applications, including:

● Healthcare data analytics: FHE can be used to perform complex analytics on sensitive healthcare data, such as medical images or genetic data, without compromising patient privacy.

● Financial data analysis: FHE can be used to perform complex financial analysis, such as risk assessment or price forecasting, without revealing sensitive customer or transaction information.

● Government data analysis: FHE can be used to perform analysis of sensitive government data, such as intelligence data or national security data, without compromising national security.

● Cloud computing: FHE can be used to allow cloud providers to process sensitive data securely, without having to decrypt it.

● Data mining: FHE can be used to perform data analysis on large datasets, without having to reveal sensitive information contained in the data.

Advances in the field have made FHE schemes a promising technology with significant potential to transform the way sensitive data is handled. As FHE schemes continue to improve, they are expected to have a significant impact on a wide range of scenarios.

Author contributions

Valentina Grazian: Investigation, Writing – original draft; Antonio Tortora and Maria Tota: Writing – review and editing.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors are members of the National Group for Algebraic and Geometric Structures, and their Applications. They would like to thank the referees for their useful comments, and Prof. Carlo Blundo for the inspiring conversations and meaningful suggestions that enabled them to improve this work.

Conflict of interest

The authors declare no conflict of interest in this paper.