1. Introduction
Several studies have confirmed that there are multiple rare genetic, environmental and even behavioral variants that collectively influence the expression and prevalence of traits and diseases known as multifactorial diseases in human populations.
The identification of multifactorial disease susceptibility factors has become foreboding for geneticists in the hope of predicting these diseases and discovering targeted remedies. There are several ways to identify these rare variants such as statistical methods and metaheuristics.
2. Multifactorial Diseases
Today, we can distinguish between two types of diseases: monogenic diseases and multifactorial diseases which are also called complex diseases.
For monogenic diseases, only one genetic factor is involved. Moreover, it is generally the main risk factor and the influence of the environment is often minimal. Thus, the share of genetic factors in the determination of the disease, called heritability, is often very important.
Unlike monogenic diseases, complex (multifactorial) genetic diseases are dependent on several polygenic factors where many markers at many genes are the multiple origins of the disease. Each individual effect of each of the environmental factors alone is insufficient to cause the disease.It is the common presence of these genetic factors in the same patient that leads to the onset of the disease. The susceptibility to these diseases results from the combined action (additive effects, multiplicative effects) of a large number of genes. Complex diseases also have an additive effect of genetic and environmental factors. The effects of interaction between these factors also determine the appearance of the disease. The environment has to be taken in the broad sense: what surrounds or has surrounded the patient as well as certain aspects of the patient's lifestyle.
This explains the ineffectiveness of the traditional methods used previously for Mendelian diseases, hence the use of more sophisticated methods such as statistical and metaheuristic methods.
3. Materials and Methods
In this paper, statistical and metaheuristic methods for the identification of complex traits of multifactorial diseases will be presented.
3.1. Statistical Methods for the Detection of Genetic Susceptibility Factors of Multifactorial Diseases
Two methods of identifying the genes involved in multifactorial diseases have been implemented such as linkage studies and association studies. Generally these two methods are used one after the other since they are complementary.
The aim of linkage study is to locate regions containing genes trait or disease genome through observations on related individuals. Then, in a second step, the association analysis seeks to identify that a particular allele, identical in all the population, increases the risk of a disease.
3.1.1. Linkage Studies
Linkage studies are based on the co-segregation of the disease in the family and alleles at a marker locus across generations [1] and location of the disease gene relative to the marker.
In other words, linkage studies refer to the fact that two alleles from two different genes tend to be transmitted together from an individual to his offspring.
This method applies to cases where combination is rare. The study of all informative families (or crosses) makes it possible to calculate the rate of recombination (and therefore the inter-gene distance) for two or more linked genes (carried by the same chromosome Linkage studies relies on the recombination fraction θ (the probability of recombination between two loci at meiosis) which is a function of the distance between the loci. This distance is expressed as a recombination unit or centiMorgan: 1 cM corresponds to a recombination frequency of 1% between the two loci. If θ = 0, the two loci are co-inherited in 100% of the cases (perfect link). The genetic distance between the two loci is then 0 cM. If θ = 0.5, the two loci are genetically independent in terms of segregation. There are two approaches to test the link: the parametric approach which corresponds to the probability that an important gene for a disease is linked to a genetic marker, it is studied by the LOD score and the non-parametric approach which studies the probability that an allele is identical to itself.
Hodge et al. [2] have developed a gene-gene interaction detection strategy based on conditioning family data on a known disease-causing allele or a disease-associated marker allele. They have applied the method to disease data and used computer simulation to exhaustively test the method for some epistatic models. They have computer-simulated multipoint linkage data for a disease caused by two interacting loci. They have removed family members who did not carry this allele. They have also used the lod scores for the data sets to prove the presence of interaction or no interaction was detectable. This new method was robust and reliable for a wide range of parameters and has worked well with the additive model except when allele frequencies at the two loci differ widely. All testing of this method have suggested that it have provided a reliable approach to detecting gene gene interaction.
In a genome-wide linkage study, Onouchi [3] has discovered that ITPKC and CASP3 are common susceptibility genes for Kawasaki disease. This prompted examination of the Ca2+/NFAT pathway and a subsequent continuous series of newly identified Kawasaki disease susceptibility genes. The recent identification of the FCGR2A, BLK, CD40, and HLA class Ⅱ gene regions in genome-wide association studies has brought new light on the pathogenesis of Kawasaki disease.
3.1.1.1. The Parametric Approach: The Logarithm of Odds Score (LOD Score)
The LOD score analysis has been proposed by Morton [4] to study genetic linkage between a trait locus and a marker locus. The method was intended to be applied to traits with known mode of inheritance and allele frequencies. It permitted the localisation of certain genes of diseases [5].
The LOD score is obtained by the decimal logarithm of the ratio between the link likelihood (the alternative hypothesis) between the marker (known position) and the disease gene (unknown position) for a given genetic distance, represented by the recombination rate θ (0 < θ < 0.5) and the hypothesis of genetic independence between this marker and the desired gene (null hypothesis, θ = 0.5).
For a family Fi the LOD score will be calculated as following:
For a set k of families the LOD score will be calculated as following:
Family likelihood is a measure of the plausibility of the observed data. Its value depends on the value of the recombination rate θ [6].
Let Y be the vector of phenotypes of the N individuals of the family F with n children and M the marker studied. The likelihood of θ is:
|
L(θ|F)∝L(F|θ)=P(Y,M|θ,α)=P(Yf,Mf,Ym,Mm,Y1,M1,...,Yn,Mn|θ,α)=P(Yf,Mf)P(Ym,Mm)P(Y1,M1,...,Yn,Mn|Yf,Mf,Ym,Mm,θ,α)=3∑K=1P(Yf|Gf,K)P(Gf,K)P(Mf)∗3∑K=1P(Ym|Gm,K)P(Gm,K)P(Mm)∗n∏o=13∑K=1P(Yo|Go,k,α)∗P(Go,k,Mo|Gf,k,Mf,Gm,k,Mm,θ)
|
(3)
|
With f = father and m = mother
For a family, the LOD score test is written as following:
|
Zi(θ1)=log10(Li(θ=θ1)Li(θ=0))
|
(4)
|
The LOD score of a sample of k families is the sum of the LOD scores of the k families:
In relation to the value of the LOD score, the following decision criteria can be determined:
If Z(θ1)≥3: There is a linkage.
If −2<Z(θ1)<3: The result is ambiguous and it is necessary to increase the number of meiosis analyzed and to repeat the calculation.
If Z(θ1)<−2: No linkage.
By applying parametric approaches, such as the LOD score, the parameters must be well stated in order to avoid any error. For complex diseases, hereditary mode of transmission of the disease is often too imprecise. The lack of information about these parameters generally leads to a problem of detection of the different links, hence the emergence of nonparametric methods.
3.1.1.2. The Nonparametric Approach: Method of affected sibling pairs
The Affected Sibling Pairs method is based on the fact that a non-random transfer of parental alleles was observed in children if there is a link. In this case, the affected children inherit the same alleles often. The common allele between two siblings from the same parental allele is said to be "identical by descent" (idendical by descent, IBD). This method evaluates, for a given marker, the proportion of the number of identical alleles per progeny within pairs of patients.
Thus, for a marker locus, the siblings can have in common 2, 1 or 0 alleles IBD inherited from their parents. The siblings who share two IBD alleles (IBD2) have inherited the same two alleles from their two parents. If they share an IBD allele (IBD1), they inherited the same allele from the same parent. Finally, they do not share any IBD allele (IBD0) if they inherit different alleles. In the case of Mendelian segregation (in the absence of binding), the siblings will inherit 2 IBD alleles from a given locus in 25% of cases, an IBD allele in 50% of cases, and 0 IBD alleles In the remaining 25%. One of the nonparametric methods proposed is that of Haseman and Elston[7] based on pairs of siblings.
For a quantitative trait, the model is a classical linear regression in the form:
With yi,1,yi,2 and πi are the phenotypes and the proportion of allele IBD (0, 1 or 2) in the siblings of the family i.
For a binary trait, the nonparametric method is classically based on the analysis of pairs of affected siblings. It consists in comparing the observed distribution of the proportion of IBD alleles in the sample with the distribution expected in siblings (¼, ½, ¼ for 0, 1, 2 alleles IBD). If the link exists, an excess of the pair of siblings where the IBD is equal to 2. Here the statistical test can be is a compliance χ2 test.
3.1.2. The Association Studies
The allelic association studies seek to demonstrate a difference in allelic frequency at such a locus between unrelated subjects, whether they are affected or not.
Costantino et al. [8] conducted a whole-genome high-density non-parametric linkage analysis to identify new genetic factors of susceptibility to Spondyloarthritis (SpA) which is a chronic inflammatory disorder with high heritability but with complex genetics. Multipoint non-parametric linkage was tested for all autosomal chromosomes which identified two regions significantly linked to SpA.
Hu et al. [9] have presented pedigree-VAAST (pVAAST), a disease-gene identification tool designed for high-throughput sequence data in pedigrees. pVAAST uses a sequence-based model to perform variant and gene-based linkage analysis. Linkage information is then combined with functional prediction and rare variant case-control association information in a unified statistical framework. pVAAST outperformed linkage and rare-variant association tests in simulations and have identified disease causing genes from whole-genome sequence data in three human pedigrees with dominant, recessive and de novo inheritance patterns. The approach was robust to incomplete penetrance and locus heterogeneity and was applicable to a wide variety of genetic traits. pVAAST have maintained high power across studies of monogenic, high-penetrance phenotypes in a single pedigree to highly polygenic, common phenotypes involving hundreds of pedigrees.
Toward understanding the complex genetic basis of schizophrenia, Greenwood et al. [10] have made a Linkage analyses of the 12 endophenotypes collectively which identified one region meeting genome-wide significance criteria, with a LOD (log of odds) score of 4.0 on chromosome 3p14 for the antisaccade task, and another region on 1p36 nearly meeting genome-wide significance, with a LOD score of 3.5 for emotion recognition. Twelve regions meeting genome-wide significant and suggestive criteria for previously identified heritable, schizophrenia-related endophenotypes were observed, and several genes of potential neurobiological interest were identified. Replication and further genomic studies are needed to assess the biological significance of these results.
3.1.2.1. Single-Marker Association Tests
Let an SNP has the alleles A and a.
Table 1. Genotypic contingency table.
|
AA |
Aa |
aa |
|
| Sick |
psx |
psy |
psz |
ps =Psick |
| Witness |
pwx |
pwy |
pwz |
Pw =Pwit |
|
px = PAA |
Py = PAa |
Pz = Paa |
P = P |
Table 2. Allelic contingency table.
|
A |
a |
|
| Sick |
qsx =2 × psx+ psy |
qsy = 2 × psz+ psy |
qs =2 × Psick |
| Witness |
qwx = 2 × pwx+ pwy |
qwy = 2 × pwz+ pwy |
qw =2 × Pwit |
|
qx =2 × PAA+ PAa |
qy =2 × Paa+ PAa |
q = 2P |
a. Odds Ratio (OR)
OR represents the variation in the proportion of sick people compared to healthy, between experimental and control groups. OR is a measure of the strength of the association between disease and SNP. It is equal to :
Confidence interval or p-value is used to determine whether a null hypothesis formulated before the performance of the study is to be accepted or rejected.
This interval of 95% can be estimated using Woolf and Miettinen method. The Woolf method consists in estimating the variance of the log (OR) following a normal distribution:
|
var(log(OR))=1qSX+1qSY+1qWX+1qWY
|
(8)
|
The 95% confidence interval is calculated as following :
|
IC95%=exp[log(OR)±1.96∗√var(log(OR))]
|
(9)
|
The Miettinen method is a simple method for calculating the confidence interval of the OR from the results of the χ2 association test between disease and SNP :
|
IC95%=exp[log(OR)±1.96∗√χ2]
|
(10)
|
b. Fisher's Exact Test
Is a statistical test used for the analysis of contingency tables. This test is generally used with low numbers but is valid for all sample sizes. The probability is equal to:
|
P(qsx)=(qsqsx)(qwqwx)(qqx)=qs!∗qw!∗q.x!∗qy!qsx!∗qsy!∗qwx!∗qwy!∗q!
|
(11)
|
The goal is to calculate all possible tables by fixing the marginals (qs, qw, qx and qy) and varying qsx as following:
|
max(0,qs+qx−q)≤qsx≤min(qs,qx)
|
(12)
|
c. The Cochran-Armitage Test
The Cochran-Armitage test (William Cochran and Peter Armitage [11,12]) can be seen as an improvement of the Pearson χ2 test taking into account the general tendency of the link between the variables tested. The Cochran-Armitage test is used in the analysis of categorical data when the objective is to evaluate the presence of an association between a variable with two categories and a variable with k categories.
The test is based on the genotypic contingency table (Table 1 Allelic genotypic table):
|
XT=p[p(psy+2psz)−ps(px+2py)]2pspw[p(px+4py)−(px+2py)2]∼χ2(1)
|
(13)
|
d. Logistic regression
Is a binomial regression model, it is considered as a particular case of the generalized linear model.
|
Logit(p)=ln(p1−p)=α+Xβ
|
(14)
|
With p=P(Y=1|X=x)=1−P(Y=0|X=x) and Y=1 for patients and 0 for witnesses.
e. Test of independence (χ2) : Allelic test
The test is based on the allelic contingency table (Table 2 Allelic contingency table)
The corresponding test is based on the Pearson statistics:
|
XA=∑i((qsi−qs∗qiq)2qs∗qiq+(qwi−qw∗qiq)2qw∗qiq)∼χ2(1degreeoffreedomdf)
|
(15)
|
With i = {x, y}
f. Test of independence (χ2) : Genotypic test
The test is based on the genotypic contingency table (Table 1 Allelic genotypic table).
The corresponding test is based on the Pearson statistics:
|
XG=∑i((psi−ps∗pip)2ps∗pip+(pwi−pw∗pip)2pw∗pip)∼χ2(2)
|
(16)
|
With i = {x, y, z}
g. Likelihood Ratio Test
In the case of the allelic test, the test is written as following:
|
LRTA=−2∑i∑jqijlog(qijqi∗qjq)∼χ2(1)
|
(17)
|
With i = {s, w} and j={x, y}
In the case of the genotypic test, the test is written as following :
|
LRTG=−2∑i∑jpijlog(pijpi∗pjp)∼χ2(2)
|
(18)
|
With i={s, w} and j={x, y}
h. Cochran-Mantel-Haenszel Test (CMH)
The Cohran-Mantel-Haenszel (MHC) test is used to test the independence hypothesis on a series of contingency tables corresponding to an experiment crossing two categorical variables, with a control variable taking several values. This test is used when patients are from different geographical origins.
Let o = 1, ..., O be the different geographic origins.
Table 3. Allelic contingency table of each geographical origin.
|
A |
a |
|
| Sick |
qosx |
qosy |
qos |
| Witnesses |
qowx |
qowy |
qow |
|
qox |
qoy |
qh |
The test statistic is written as following:
|
X2CMH=(∑Oo=1qosx−∑Oo=1kosx)2∑Oo=1Vosx
|
(19)
|
With
|
Vosx=qos∗qow∗qox∗qoyq3o(qo−1)∼χ2(O−1)
|
(20)
|
And
The overall OR is calculated as following:
|
ORCMH=∑oqosx∗qowyqo∑oqosy∗qowxqo
|
(22)
|
3.1.2.2. Multi-Marker Association Tests
a. Multivariate Regression
Let us take the model of logistic regression simple marker. In multivariate regression, the variable X is a matrix containing the p SNPs to be tested.
In this case, β is a vector of size p: β = (β1, ..., βp) The null hypothesis of absence of association is H0: β = β =... = βp. The density function is df is equal to p-1. Because of this number, which increases with the number p of SNPs tested, the multivariate regression test may lack power.
b. The haplotypic Test
The haplotype test is, as in the multivariate model, a test of χ2 to k-1 df. This approach takes into account the uncertainty in haplotype estimation. For a binary trait, the same model of the logistic regression simple marker is used.
3.1.3. Conclusion
Linkage Studies is a statistical analysis performedon data from people of the same family. It tests the independence of the marker alleles and the transmission of the disease in the families, and it can also locate the gene of the disease with respect to the marker.
Unlike Linkage Studies, association studies can be carried out on data from persons belonging to the same family or not.
The association studies aim to demonstrate a difference in the frequencies of the marker alleles between patients and controls.
Single marker association tests may be weak and do not allow the study of frequent low-effect genetic variants and the cost of large scale analysis of sequence data remains prohibitive for the study of complex diseases.
On the other hand, the use of multi-marker tests has better power compared to single-brand testing and can optimize the use of genetic variability and therefore increase the potency of studies.
Table 4. Different statistical methods table.
| Linkage Studies |
The Parametric Approach The LOD Score |
| The Non Parametric Approach : Method of Affected Sibling Pairs |
| Association Studies |
Single-marker association tests |
Odds Ratio (OR) |
| Fisher's Exact Test |
| Cochran-Armitage Test |
| Logistic Regression |
| Test of independence (χ2): Allelic test |
| Test of independence (χ2): Genotypic test |
| Likelihood Ratio Test |
| Cochran-Mantel-Haenszel Test (CMH) |
| Multi-marker association tests |
Multivariate regression |
| Haplotypic Test |
3.2. Metaheuristics for the Detection of Genetic Susceptibility Factors of Multifactorial Diseases
A metaheuristic is an optimization algorithm aiming to solve problems of difficult optimization for which no exact method is effective. Metaheuristics are generally iterative stochastic algorithms, which progress towards an overall optimum, ie, the global extremum of a function, by sampling an objective function. They behave like search algorithms, trying to learn the characteristics of a problem in order to find an approximation of the best solution (in a way close to the approximation algorithms). There are many different metaheuristics, ranging from simple local search to complex global search algorithms. These methods, however, use a high level of abstraction, allowing them to be adapted to a wide range of different problems.
Considering the non-deterministic polynomial-time hard characteristic of feature selection, meta-heuristics are introduced into feature selection in biomedicine; in our context for analyses of multifactorial diseases, on account of their excellent global search ability [13]. The metaheuristic approaches also allow to adjust the parameters of the classifiers and to select the optimal feature subsets which improves the classification results [13]. The metaheuristics were proposed as methods of feature selection in order to choose a subset of input variables by eliminating features with little or no predictive information [14,15,16]
In the following we will detail two types of metaheuristics known as iterated solution improvement (ISI) and iterative population lmprovement (IPI).
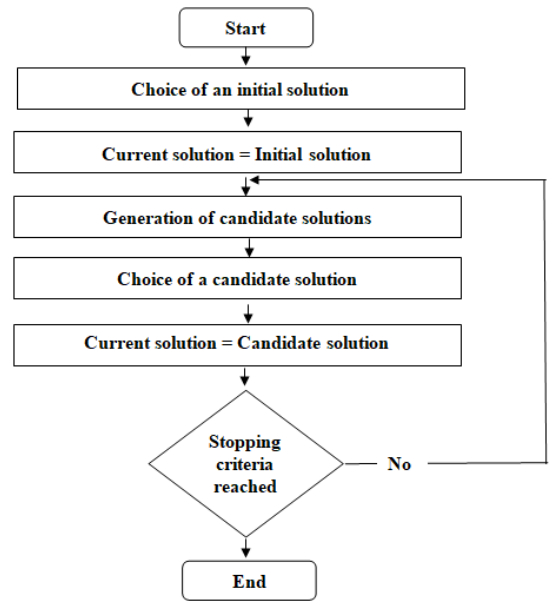
3.2.1. Iterated Solution Improvement (ISI)
The ISIs are all based on the same basic algorithm, called local or neighborhood search.
The Variable Neighborhood Search is a metaheuristic that sequentially moves through the feasible region by searching solutions in a neighborhood of the current best solution while, at the same time, systematically changes the size of the neighborhood to avoid getting trapped at local optima [17], it has been successfully applied to solve hard combinational optimization problems [18] in different fields such as microarray [19]. Belacet et al. [20] have used the variable neighborhood search metaheuristic for Fuzzy clustering of microarray gene expression data.
The neighborhood search begins with an arbitrary initial solution or with a solution obtained from another optimization algorithm, then improves it step by step by choosing, as a new current solution, a solution in its neighborhood [21].
This strategy is based on three facts [22]:
(1) A local optimum with respect to one neighborhood structure is not necessarily a local optimum in another one;
(2) A global optimum is a local optimum with respect to all possible neighborhood structures;
(3) For many problems local optima with respect to one or several neighborhood structures are relatively close to each other.
Several criteria have been defined to differentiate ISIs such as: (1) Memory; (2) The choice of the initial solution; (3) The generation of candidate solutions; (4) Selection of a candidate as a new current solution; and (5) The criterion for stopping the iterative process.
Now we will detail the different criteria for the ISI methods.
(1) Memory:
The memory contains all the data stored from one iteration to another. Metaheuristics use history to guide their search optimization for the following iterations. Some methods of metaheuristics are limited in their search to a given iteration to determine the next iteration, then we speak of methods without memory and this is the simplest case. Many metaheuristics use a more sophisticated memory, either by using solutions visited recently, or by memorizing a set of parameters describing the search.
(2) The choice of the initial solution:
The choice of the initial solution is generally made in a random manner, but it can also be generated by another heuristic which will obviously be of better quality than another solution produced randomly.
The GRASP (Greedy Random Adaptive Search Procedure) method [23] alternates between two different stages, the greedy method followed by a local search, using as the initial solution of the one the current solution of the end of the other. This idea brings together the advantages of several methods at once.
(3) The generation of candidate solutions:
The generation of the candidate solutions consists in finding the neighborhood which represents a subset of solutions reached by a series of given transformations.
The set of candidate solutions to retain may consist of all or part of the immediate neighborhood of the current solution. The number of successful candidates varies depending on the nature of the method used. If the neighborhood selection is very expensive, it is possible to select only a part of the immediate vicinity of the current solution. However, it is possible to choose candidates who do not belong to the nearest neighbors but also can choose faraway candidates based on memory elements.
(4) Selection of a candidate as a new current solution:
The step of selecting a candidate is to choose the next common solution among the candidates generated. Generally the best cost candidate is chosen; But at the same time, there are other selection criteria such as the simulated annealing method [24] where a candidate is chosen randomly and the tabu search method where the candidate is chosen according to the memory [25].
(5) The criterion for stopping the iterative process:
There are different stopping criteria. For example, an algorithm can stop when a maximum number of iterations previously defined is reached, this criterion which is the most used, it consists in introducing into the memory the number of iterations performed.
We can also meet other more complex shutdown criteria such as those for Tabu searches that take into account the evolution of the quality of the generated solutions and store the numberof iterations during which no quality improvement is produced by relation to the best solution found since the beginning of the research.
3.2.1.1. Hill Climbing
a. The principle of the Hill Climbing Algorithm
Hill Climbing is the oldest iterative optimization methods of the literature [26,27]. In these methods, memory is satisfied with only the current solution, which explains their ease and speed of execution. The principle of these methods consists in moving at each step towards a better quality solution called local optimum and stop when all neighboring solutions are worse compared to the current solution and cannot improve the objective function. There are several ways to choose the neighbor:
(1) The Steepest Descent Walk (SDW)
Only the best candidate can become the new common solution at every step. This method is used mainly when the number of candidates is high.
(2) The Stochastic Descent
The new current solution is selected in a random order. The candidates are visited in a random order and the first candidate of better quality than the current solution is chosen. This method is not deterministic; it makes it possible to obtain different results from the same initial solution.
(3) The Descent to the First Best
This method is similar to stochastic descent but is deterministic. The major difference is that here the order of the candidates visit is predetermined.
The major disadvantage of the descent methods that they remain stuck in the first local optimum encountered.
| Algorithm 1: Generic descent method |
Procedure: φ cost function
Local variable: S current solution
Choice of an initial solution So;
Current solution S←So;
(i) Generation of candidates;
Selection of the best candidate C;
if φ(C) < φ (S) then
S ← C;
Return to (i);
end if
Return S; |
b. Applications of the Hill Climbing Algorithm
Schlosberg et al. [28] have used Bayesian network structure learning (BNSL) to identify potential SNPs associated with the affected phenotype. The goal was to detect the true causal SNPs among the variants measured in these genes using Hill Climbing algorithm.
Nithya and Venkateswaran [29] have analyzed the various segmentation algorithms for glaucoma detection using color fundus images and spectral domain Optical Coherence Tomography (OCT) images of same subjects. In fundus images, the disc and the cup regions are segmented separately with four different segmentation algorithms namely Otsu method, Region growing, Hill climbing and Fuzzy C-means clustering algorithms. In OCT images, the cup and the disc diameter were measured by segmenting the retinal nerve fibre and retinal pigment epithelium layers. From both the analysis, the Cup to Disc Ratio (CDR) is calculated and compared with the clinical values. The experimental results show that the performance error in the OCT image analysis is less when compared to the fundus image analysis. Thus, it can be concluded that glaucoma detection can be done more effectively using OCT image analysis.
In order to predict accurately a seizure for the diagnosis of epilepsy, Bhardwaj et al. [30] have integrated local hill climbing search technique with the Genetic Programming (GP) because the destructive nature of crossover operator in GP decreases the accuracy of predicting the onset of a seizure.The new method proposed an hybrid crossover and mutation operator (CCM), which uses both the standard GP and CCM-GP, to choose high performing individuals in the least possible time. The results affirm the potential use of the method for accurately predicting epileptic seizures and hint on the possibility of building a real time automatic seizure detection system.
3.2.1.2. The Simulated Annealing (SA)
a. The Principle of the Simulated Annealing Algorithm
The simulated annealing is a method inspired by an algorithm known as the Metropolis algorithm used to simulate the cooling of materials by a process called annealing [31].
The simulated annealing method starts from an initial solution and searches in its neighborhood for another solution in a random way. Contrary to the method of descent, this method makes it possible to move towards a neighboring solution of less good quality with a non-zero probability. This allows to escape the local optima.
Thirty years later, the algorithm of Metropolis, from the domain of physics, has been translated into the domain of combinatorial optimization, hence the appearance of a new iterative metaheuristic called Simulated Annealing [24].
This method aims to find the extreme of a function by minimizing the objective function, close to the energy of a material, by introducing a fictitious temperature, which is controlled by a decreasing function which defines a scheme cooling.
The algorithm begins with an initial solution that can be generated randomly or by a heuristic. At each new iteration, a solution has been generated randomly in the neighborhood N(s) of the current solution s. The solution s' is retained if it is of better or equal performance compared to the current solution, i.e., f(s′)≤f(s). Otherwise, accepted with a probability e(−ΔfT).
This probability depends on two factors: On the one hand the importance of the degradationΔf=f(s′)−f(s), the lower degradations are more easily accepted. On the other hand, a temperature parameter T, a high temperature corresponds to a greater probability of accepting degradations.
At the beginning of the algorithm, the parameter T, associated with the temperature, is determined and decreases throughout the algorithm to tend towards 0. Depending on the value of T will result the probability of acceptance of the degradation solutions. The temperature T is high, the higher this probability).
The performance of the simulated annealing is dependent on several factors such as the cooling rule which represents the decrease of the parameter T. Cooling too fast would lead to a local optimum which may not be of good quality. Cooling too slowly would be expensive in terms of calculation time. The adjustment of these various parameters (initial temperature, number of iterations per temperature step, decrease in temperature, etc.) can be long and difficult.
| Algorithme 2: Simulated Annealing method |
Procedure: φ cost function, P← assignment according to a probability P
Local variable: S current solution, T current temperature, M best solution, K temperature plateau, Titemperature sequence
Choice of an initial solution S0;
Best solution M ← S;
Current temperature T ← T0;
while Next (T, Ti) < > NULL do
Iteration of bearing I ← 1;
while I ≤ K do
Generation of a candidate C by neighborhood operation
Δ←φ (C) - φ (S);
if Δ < 0 then
S ← C;
if φ (S) -φ (M) then
M ← S;
end if
else
Probability update P ← e−ΔKT;
SP←C;
end if
I ← I + 1;
T ← following (T, Ti);
end while
end while
Return S; |
b. Applications of the Simulated Annealing Algorithm
In order to identify the hereditary factors of susceptibility to the disease, Iossifov et al. [32] carried out epidemiological and genetic analyzes, in which they used the simulated annealing process in order to identify the optimum cluster of genes responsible.
Wirdefeldt et al. [33] have examined 12 families with familial Parkinson's disease for genetic linkage to a number of candidate loci. They have performed a multipoint link analysis that calculates both the parametric and nonparametric multipoint lod scores. The nonparametric approach cannot manipulate a large number of ascendants without subdividing them; it has been supplemented by a method that performs simulated annealing and random walk to calculate a location score that is comparable to the multipoint lod score.
In order to diagnosis the hepatitis disease, Sartakhti et al. [34] have proposed a novel machine learning method that hybridizes support vector machine (SVM) and simulated annealing (SA). They have taken the dataset used from the UCI machine learning database. The classification accuracy is obtained via 10-fold cross validation. The obtained classification accuracy of the new method was 96.25% and it was very promising with regard to the other classification methods in the literature for this problem.
According to Goya et al.[35] a robust and highly predictive group-based QSAR (GQSAR) model has been developed to select the optimal subset of variables (descriptors) which causeAlzheimer disease. They have combined simulated annealing (SA) with partial least square (PLS) regression to generate the GQSAR model.
3.2.1.3. Tabu Search (TS)
a. The Principle of the Tabu Search Algorithm
The Tabu search method was introduced in 1986 by Fred Glover [36] and can be applied to a large number of optimization problems [37].
The advantage of the Tabu search is that it has no stochastic character, it is based mainly on the notion of memory containing the set of digitized data from one iteration to another in other words on the history of its search called tabu list to avoid falling into a local optimum.
The memory of the Tabu search algorithm contains both the current solution, the best solution visited since the start of the search, a value that controls the progress of the search as well as the tabu list.
This method does not stop on its own but it must be determined a stop criterion according to the search time associated with it. This criterion can be, for example, the execution of a certain number of iterations or the non-improvement of the best solution during a certain number of iterations.
The principle of the Tabu Search algorithm is as following: at each iteration, a verification of the neighborhood (complete or neighborhood subset) of the current solution is done and the best solution will be selected.
By applying this principle, the method permits a shift towards solutions that appear to be of poorer quality but may have a better neighborhood.
The biggest disadvantage is that there is a risk of cycling between two solutions.
To avoid this phenomenon, the method inhibits the visit of a recently visited solution. To do this, a taboo list containing the attributes of the last solutions visited will be updated. Each new solution removes the oldest visited solution from this list.
Thus, the search for the following current solution is done in the neighborhood of the current solution without considering the solutions belonging to the tabu list.
| Algorithm 3: Generic method of Tabu Search |
Procedure:φ cost function
Local variable: S current solution, L list tabu, M best solution, K current iteration, N iteration number
Parameters: Size of the Tabu list, suction criterion
Choice of an initial solution S0;
Current solution S ← S0;
Best solution M ← S;
K ← 0;
while K < N do
K ← K + 1;
Updating L;
Generation of candidates E by neighborhood operation
C ← best (E);
if (φ (S) < φ (M)) OR C is not tabu verifies suction then
S ← C;
else
E ← E/ C;
end if
end while
Return S; |
b. Applications of the Tabu Search Algorithm
Shen et al. [38] have developed an hybrid Particle Swarm Optimization (PSO) and Tabu Search (HPSOTS) optimization method for selecting genes for tumor classification.The incorporation of the Tabu Search as a local improvement procedure allows the new method to superimpose the local optima and to present satisfactory performances. They have demonstrated that HPSOTS is a useful tool for gene selection and the exploitation of a large data.
Wang et al. [39] proposed a new hybrid algorithm HICATS incorporating Imperialist Competition Algorithm (ICA) which performs global search and tabu search (TS) that conducts fine-tuned search. They used this method in order to select informative genes playing an important role in classification platforms and disease diagnosis. In order to verify the performance of the proposed algorithm HICATS, they have tested it on 10 well-known benchmark gene expression classification datasets. The performance of the proposed method proved to be superior to other related works including the conventional version of binary optimization algorithm in terms of classification accuracy and the number of selected genes.
Nguyen et al. [40] have introduced an approach to classify EEG signals (The bioelectrical potentials generated by the cerebral cortex nerve cells of the brain) using wavelet transform and a fuzzy standard additive model (FSAM) with a tabu search learning mechanism. Classification performance is evaluated using accuracy, mutual information, Gini coefficient and F-measure. Widely-used classifiers, including feedforward neural network, support vector machine, k-nearest neighbours, ensemble learning Adaboost and adaptive neuro-fuzzy inference system, are also implemented for comparisons. The proposed tabu-FSAM method considerably dominates the competitive classifiers, and outperforms the best performance.
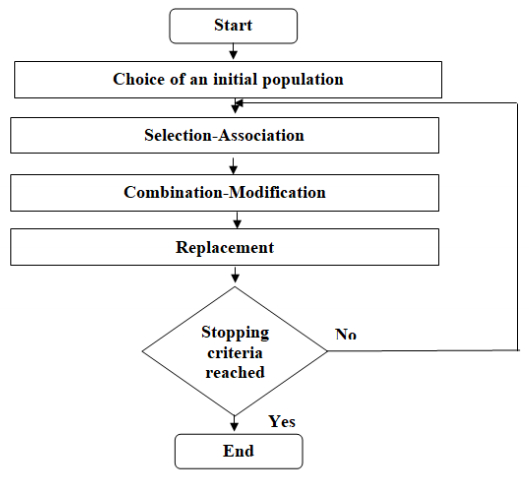
3.2.2. Iterative Population Lmprovement (IPI)
The general principle of IPI methods is to improve, iteratively after iteration, a population of solutions by combining these solutions to produce new solutions which are then re-injected into the population to replace other solutions.
An IPI heuristic begins with the choice of an initial population. Often, this population is randomly generated according to a uniform distribution or is produced by a method optimizing diversity. Indeed, the initial population must be well diversified so that it represents a good coverage of the research space. Thanks to this great diversity of the initial population, the IPI methods are naturally exploring. The size of the population, although it may vary, is very often fixed during the course of the IPI. It is a parameter of the method. The size of the population directly influences the time of execution of the method: the more solutions, the more treatments to be performed.
3.2.2.1. Genetic algorithm (GA)
a. The Principle of the Genetic Algorithm
Genetic algorithms belong to the Evolutionary Computation (EC) family of algorithms that are inspired by the theory of Darwinian evolution to solve various problems. According to the theory of the naturalist Charles Darwin, set out in 1859 [41], the evolution of species is the consequence of the combination of two phenomena: On the one hand natural selection that favors the individuals most adapted to their environment survive and reproduce, leaving a descent that will transmit their genes and, on the other hand, the presence of non-directed variations among the genetic traits of the species (mutations).
Genetic algorithms are the most widely used of evolutionary algorithms, they have emerged through John Holland and his students at the University of Michigan on adaptive systems [42].
GAs are based on the evolution mechanisms of populations of biological organisms and have been shown to be effective in solving dynamic problems and highly complex problems [43].
Goldberg [43] Studied Genetic Algorithms and enriched his theory with the following notions:
1) Chromosomes are the elements from which solutions (individuals) are developed;
2) An individual is bound to an environment by his DNA code;
3) A solution is linked to a problem by its quality index;
4) A good solution to a given problem can be seen as an individual likely to survive in a given environment;
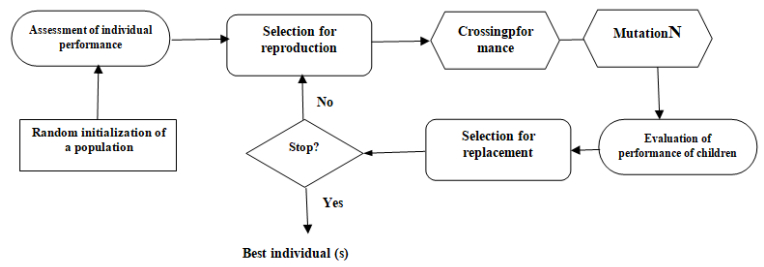
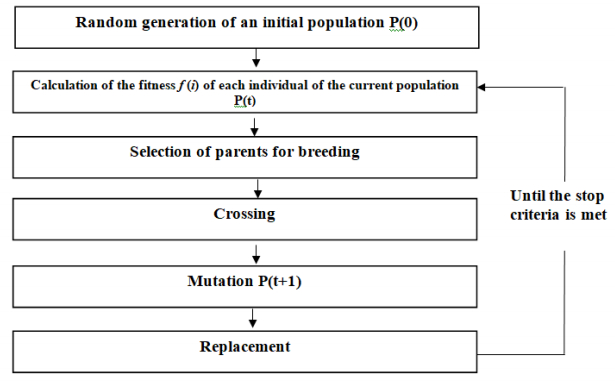
5) The operation of the GAs is easy. We start with a population of primitive solutions (chromosomes) randomly chosen.
Their corresponding performance (fitness) is measured. Based on these performances, a new population of potential solutions is created using diversification operators such as selection, crossing and mutation.This cycle is repeated until a satisfactory solution is found.
A genetic algorithm is defined by:
1) Chromosomes are the elements from which solutions (individuals) are developed.
2) The population is the set of chromosomes.
3) The fitness index, also known as the performance index, is an abstract measure for classifying chromosomes.
4) The evaluation function or cost function is the theoretical formula for calculating the quality index of a chromosome.Individuals are manipulated as following :
5) Selection: To determine which individuals are more likely to breed, a selection is made. There are several selection techniques, the main ones being roulette-wheel selection, tournament selection, ranking selection, etc [44,45].
6) Crossover: The crossover operator combines the characteristics of a set of previously selected parent (usually two) individuals, and generates new children. Again, there are many crossover operators, for example crossing at one point, crossing at n-points (n ≥ 2) and uniform crossing i.e. a multi-point crossing.
7) Mutation: The descendants are mutated, that is to say that a part of their genotype is randomly modified according to the mutation operator.
8) Replacement: Replacement (or survivor selection), as its name suggests, replaces some of the parents by some of the offspring. The simplest is to take the best individuals of thepopulation, according to their respective performances, in order to form a new population (typically of the same size as at the beginning of the iteration).
The use of genetic algorithms (GA) for the selection of attributes is justified and can compete with other methods in its effectiveness [46]. These methods are wrapper-methods, i.e., methods that use a learning algorithm to evaluate the different subsets of generated attributes.
b. Applications of the Genetic Algorithm
Underwood et al. [47] have developed a simulation optimization model that combines a simulation model with a genetic algorithm (GA) and a probabilistic classification and selection method to identify the best prostate-specific antigen (PSA). The results of the implementation of their GA demonstrate that the use of a classification and selection procedure can considerably reduce the time taken to implement the GA and patients should be screened more aggressively, but for a shorter duration than previously recommended to ensure better results.
Beheshti et al. [48] have developed a new computer-assisted diagnosis (CAD) system that uses feature ranking and a genetic algorithm to analyze structural magnetic resonance imaging data. Thanks to this system, they were able to predict the conversion of mild cognitive impairment (MCI) to Alzheimer's disease (AD) between one and three years before clinical diagnosis. The experimental results indicated that the system implemented is able to distinguishbetween stable MCI (sMCI) and progressive MCI (pMCI), and would be appropriate for practical use in clinical settings.
Singh and Kaur [49] have developed a new technique for the detection of heart disease and constructed an identification system based on genetic algorithm and fuzzy logic in order to extract features by applying the neural network classifier of heart disease. Thanks to this new technique, the advantages of GA and neural networks are combined to anticipate the risk of cardiovascular diseases. This method has proved its effectiveness and has given satisfactory results.
Paul et al. [50] have proposed a genetic algorithm based on a fuzzy decision making system to predict the risk level of heart disease. The proposed Fuzzy Decision Support System (FDSS) allows, firstly, a pre-processing of the data set, a selection of the actual attributes based on different methods, weighting of the fuzzy rules which are generated on the basis of a non-Attributes selected using GA, building the FDSS from the fuzzy knowledge base generated and finally predicting heart disease. Experiments with real data sets demonstrate the effectiveness of this proposed innovative approach.
Sachnev et al. [51] have developed a new balanced genetic algorithm combined with the extreme learning machine (SBGA-ELM) for the diagnosis of Parkinson's disease and the detection of bio-markers. The proposed approach includes two major steps: feature (genes) selection and classification. Feature selection procedure is based on proposed Samples Balanced Genetic Algorithm designed specifically for genes expression data and "classification" step begin from chosen set of genes used to train an Extreme Learning Machine (ELM) classifier for an accurate PD diagnosis. Both tested methods caused maximum generalization performance.
Paul et al. [52] have proposed a new feature selection strategy called GARF (Random Forest Genetic Algorithm) extracted from positron emission tomography (PET) images and clinical data. The most relevant characteristics, predictive of the therapeutic response or which are prognoses of patient survival 3 years after the end of treatment were selected using GARF on a cohort of 65 patients with cancer local advanced esophageal eligibility for chemotherapy. This method gave excellent performance with very good classification accuracy. These results wereconsolidated by comparison with the 4 other characteristics selection methods (Lasso, SFS, RFE, HFS), and the GARF method always shows more accurate results.
3.2.2.2. Scatter Search (SS)
a. The Principle of Scatter Search Algorithm
The Scatter Search method is part of the evolutionary algorithms, it has appeared thanks to Glover [37]. Scatter Search acts on a set of solutions called the reference set, combining them to create new ones.
The method starts with a population of solutions from which a moderate-sized set, the reference set (RefSet), is selected to evolve. The evolution is based on intensification and diversification strategies to take advantage of features associated with good solutions and to be able to escape from local optima. The solutions of the RefSet are combined to generate new ones and then a local search is applied to the resulting solutions. The RefSet is then updated to incorporate solutions taking into account quality and diversity. These steps are repeated until a stopping criterion is met [22]. Unlike other strategies of combination of existing rules like genetic algorithms, the search for a local optimum is a guided task [53].
In an SS, three operators are used: a dispersion operator, a recombination operator and an optimization operator.
The dispersion operator is used to generate an initial population well dispersed in the search space; it is used after a number of iterations, to counteract the convergence of the method by restoring a good level of diversity in the current population.
The purpose of the recombination operator is to group together the valorizing characteristics of the different solutions and to integrate a combination operator well adapted to the problem to be solved. Generally, Scatter Search uses, as a combination operator, the barycenter of solutions weighted by their quality.The optimization operator allows an optimization of the solutions obtained; the operator used is generally a fast ISI which can be a descent method for example.
b. Applications of the Scatter Search Algorithm
Nepomuceno et al. [54] have presented a scatter search approach based on linear correlations between genes to find biclusters that include both displacement and scale models and negatively correlated models. The performance of the proposed algorithm was compared to other reference biclustering algorithms, specifically a group of classical biclustering algorithms and two algorithms that use correlation-based merit functions. The proposed algorithm outperforms the reference algorithms and finds models based on negative correlations. Although these models contain an important relationship between genes, they are not found by most biclustering algorithms.
Lin and Chen [55] have developed a novel scatter search-based approach which combine Scatter Search and decision tree in order to acquire optimal parameter settings and to select the beneficial subset of features that result in better classification results. To evaluate the efficiency of the proposed approach, they used databases containing patients suffering from various diseases such as Breast cancer, Heart disease, Hepatitis and Pima Indians diabetes. Experimental results demonstrate that the parameter settings for the C4.5 algorithm obtained by the Scatter Search and decision tree approach are better than those obtained by other approaches. When feature selection is considered, classification accuracy rates on most datasets are increased. Therefore, the proposed approach can be utilized to identify effectively the best parameter settings for C4.5 algorithm and useful features.
Chen et al. [56] have proposed a Scatter Search approach to obtain the better parameters and select the beneficial subset of features to attain better classification results. Classification algorithms have their respective advantages and disadvantages, and suitability is influenced by the characteristics of the problem. This study adapts set of algorithms to function together in order to obtain better results. In order to evaluate the new method, it has been compared to others already existing on different databases some are related to multifactorial diseases such as heart disease and hepatitis. Results show that the proposed approach improved the classification accuracy rate in most datasets. Thus, the proposed approach can be useful to both practitioners and researchers.
López et al. [53] have proposed a Scatter Search metaheuristic for solving the Feature Subset Selection Problem. They have developed two combination methods: the Greedy Combination and the Reduced Greedy Combination, parallelization of the Scatter Search have been also proposed. The parallelization consists of running each combination method at a different processor.The results of this parallelization were satisfactory
García-Torres et al. [22] have applied the Scatter Search approach to detect relevant peakbins in Mass Spectrometry (MS) data. The Scatter Search has been embedded in two different filter and wrapper schemes coupled with Naive Bayes and SVM classifiers.
3.2.2.3. Genetic Programming (GP)
a. The principle of Genetic Programming Algorithm
Genetic programming is part of evolutionary algorithms. Koza [57] has introduced genetic programming. The paradigm of genetic programming continues the tendency to face the problem of representation in genetic algorithms by increasing the complexity of the structures being adapted. This paradigm of genetic programming begins with an initial population of computer programs randomly generated and composed of functions appropriate to the domain of the problem. Functions can be arithmetic standard operations, programming operations, mathematical functions, logical functions, or domain-specific functions. The genetic programming paradigm generates computer programs to solve problems by performing the following three steps:
(1) Generate an initial population of random compositions of the functions of the problem.
(2) Iteratively perform the following substeps until the termination criterion is satisfied:
Ⅰ. Run each program in the population and assign it a fitness value depending on how it solves the problem.
Ⅱ. Create a new population of computer programs by applying the following two main operations. These operations are applied to the computer program(s) in the selected population with a probability based on physical condition.
a) Copy the computer programs to the new existing population.
b) Create new computer programs by genetically recombining randomly selected parts of the two existing programs.
(3) The best computer program that has appeared throughout the generation is referred to as the result of genetic programming.
b. Applications of Genetic Programming Algorithm
Sohn et al. [58] have developed an open source pipeline optimization tool (TPOT-MDR) which uses GP to automate the study of complex diseases in GWAS. In TPOT-MDR, they have implemented Multifactor Dimensionality Reduction (MDR) as a feature construction method for modeling higher-order feature interactions, and have combined it with a new expert knowledge-guided feature selector for large biomedical data sets. They have demonstrated TPOT-MDR's capabilities using a combination of simulated and real world data sets from human genetics and find that TPOT-MDR significantly outperforms modern machine learning methods such as logistic regression and extreme Gradient Boosting (XGBoost). They have further analyzed the best pipeline discovered by TPOT-MDR for a real world problem and have highlighted TPOT-MDR's ability to produce a high-accuracy solution that is also easily interpretable.
Vyas et al. [59] have demonstrated the use of a new Genetic Programming (GP) based Symbolic Regression (SR) approach for predicting PPIs (Protein-protein interactions) related to a disease. In a case study, a dataset consisting of one hundred and thirty five PPI complexes related to cancer was used to construct a generic PPI predicting model with good PPI prediction accuracy and generalization ability.The GP model developed here serves a dual purpose: (a) a predictor of the binding energy of cancer related PPI complexes, and (b) a classifier for discriminating PPIcomplexes related to cancer from those of other diseases.
Hasan et al. [60] have developped a 10 fold cross validated mathematical model to detect breast cancer using symbolic regression of multigene genetic programming (MGGP). Data for MGGP is retrieved from UCI machine learning repository data set and is used for training and testing the 10 fold cross validated mathematical model. The developed model produces fast and accurate results for both training and testing data set. The error rate is very negligible for both benign and malignant type of breast cancer. The cross validated model shows the higher accuracy with respect to existing techniques.
3.2.2.4. The Ant Colony System Algorithm (ACS)
a. The principle of Ants System Algorithm
The Ant Colony SystemAlgorithm was introduced by Deneubourg et al. [61] Deneubourg and Goss [62]. The collective behavior of the ants appears from an intelligent and complex interaction of the members of a group called the colonies. The ants communicate with each other using a chemical called a pheromone, which is secreted by the glands in the ant abdomens.They are attracted by these substances, which they feel through receptors located in their antennae. The pheromone then creates a chemical track to guide the ants to their nests back and the other ants to the food source. They tend to choose the path with the highest concentration of pheromones. The cooperative behavior of ants seeking food was an inspiration to researchers who found that the ant system is an optimization method that determines the shortest path between the nest and food. The problem of ant colonies has been used with other problems like the problem of commercial travelers, etc.
b. Applications of Ant Colony System Algorithm
Husain et al. [63] have proposed an optimization method based on Improved Ant Colony Algorithm (IACA) in determining the optimal parameters of Least Squares Support Vector Machines (LSSVM) for diagnosing Hepatitis disease. IACA create a storage solution to keep the whole route of the ants. The solutions that have been stored were the value of the parameter LSSVM. There are three main stages in this study. Firstly, the dimension of Hepatitis dataset will be reduced by Local Fisher Discriminant Analysis (LFDA). Secondly, search the optimal parameter LSSVM with IACA optimization using the data training, and the last, classify the data testing using optimal parameters of LSSVM. Experimental have demonstrated good results.
Asad et al. [64] discussed the impact of two improvements to the baseline approach for automatic segmentation of retinal blood vessels which is a crucial stage in the diagnosis of many diseases based on the ant colony system. The first improvement is in features where the length of previous features vector used in segmentation is reduced to the half since four less significant features are replaced by a new more significant feature when applying the correlation based feature selection heuristic. The second improvement is in ant colony system where a new probability-based heuristic function is applied instead of the previous Euclidean distance based heuristic function. Experimental results showed the improved approach gives better performance than baseline approach.
3.2.2.5. Particle Swarm Optimiser (PSO)
a. The priciple of Particle Swarm Optimiser Algorithm
The particle swarm algorithm was introduced by Russell Eberhart and James Kennedy in 1995 [65]. It was inspired by the collective movements observed in certain social animals, such as fish and migratory birds, which tend to imitate the successful behaviors they observe in their surroundings, while bringing their personal variations.
The individuals of the algorithm are called particles and the population is called swarm. This method is based on the cooperation of different individuals, hence the similarity with the algorithm of ant colonies which is also based on the concept of self-organization.
At the start of the algorithm, each particle is thus positioned (arbitrarily or not) in the search space of the problem, each iteration moves the particles according to three components: its current velocity, the best solution Pi and the best solution obtained in its neighborhood Pg.
PSO algoithm focuses on cooperation rather than on competition between particles and there is no selection phase in the basic versions unlike the genetic algorithm, the idea being that a particle even currently mediocre deserves to be preserved, under pretext it will allow future success, especially because it comes out of the beaten path.
b. Applications of Particle Swarm Optimiser Algorithm
Sali et al. [66] focuses on cardiovascular disease diagnosis in an Iranian community by developing a Clinical Decision Support Systems (CDSS), based on Support Vector Machine (SVM) combined with Binary Particle Swarm Optimisation (BPSO). They used SVM as the classifier and benefited enormously from optimisation capabilities of BPSO in model development as well as feature selection in order to diagnose the disease in an early stage.
Shahsavari et al. [67] have proposed an Hybrid Particle Swarm Optimization (PSO) as an innovation to efficiently select the relevant feature elements used for classification of Parkinson's Disease (PD) (Patient people and healthy people). The main advantage of Hybrid PSO is locally improving of particles in order to jump over the local optimum solution and quickly converging to the global optimal solution. Evaluation of the proposed method on PD dataset proves the superiority of the propos method on the problem of PD classification, in comparison to the other learning methods.
Husain et al. [68] have predicted generalized anxiety disorders by using feature selection and classification approach for historical patient information stored in clinical databases especially because processing and extracting valuable information from huge data is a challenging and time-consuming task. Missing and incomplete data may easily cause the data to be ignored and not fully used in the prediction.
Kumar [69] have used an Optimized Particle Swarm Optimization (PSO) technique for disease dimension reduction. Filter based Artificial Neural Network is used for classifying the heart disease type as positive or negative based on the disease features. The performance of the proposed algorithm is analyzed by using the traditional approaches of Performance plot, Regression, ROC Value and Confusion Matrix. It is proved that the performance of the whole ANN network is optimized after the inclusion of proposed PSO for Feature Reduction.
Yang et al. [70] have proposed an effective algorithm named dynamic center particle swarm optimization k-nearest neighbors (DCPSO-KNN) to detect significant associations between mitochondrial displacement loops (D-loops) and chronic dialysis diseases. DCPSO-KNN uses dynamic center particle swarm optimization (DCPSO) to generate SNP combinations with a fitness function designed using the KNN method and statistical verification. Experimental results showed that DCPSO-KNN can improve the detection ability of SNP-SNP associations between mitochondrial D-loops and chronic dialysis diseases.
Gunasundari et al. [71] have proposed two new modified Boolean Particle Swarm Optimization algorithms namely Velocity Bounded BoPSO (VbBoPSO) and Improved Velocity Bounded BoPSO (IVbBoPSO) to solve feature selection problem. Compared to the basic Boolean PSO, these improved algorithms introduce Vmin parameter that makes it more effective in solving feature selection problem. The performance of VbBoPSO and IVbBoPSO are tested over 28 benchmark functions provided by CEC 2013 session. A comparative study of proposed algorithms with the recent modification of Binary Particle Swarm Optimization and Boolean PSO (BoPSO) is provided. The results prove that the proposed algorithms improve the performance of BoPSOsignificantly. In addition, the proposed algorithms are tested in the feature selection phase of intelligent disease diagnostic system.
Muthanantha Murugavel and Ramakrishnan [72] have proposed a novel scheme to detect epileptic seizures from electroencephalogram (EEG). This scheme is based on discrete wavelet packet transform and uses the transform coefficients to compute energy, entropy, kurtosis, skewness, mean, median and standard deviation to form feature vector for classification. Optimal features are selected and parameters are optimised using Particle Swarm Optimisation (PSO) with support vector machine as a classifier for creating objective function values for the PSO. Clinical EEG data from epileptic and normal subjects are used in the experiment. To evaluate the efficencity of the proposed scheme, a tenfold cross-validation is implemented, and the detection rate is found 100% accurate with 100% of sensitivity and specificity for the data under consideration.
3.2.2.6. Artificiel Immune Systems (AIS)
a. The principle of AIS
Artificial immune systems appeared in the late 1980s and early 1990s [73,74] and are considered as computing systems. They are inspired by the natural immune system of biological organisms.
Important actors entering an artificial immune system are antigens, antibodies and memory B cells.
b. Applications of AIS
Polat et al. [75] have conducted a diagnosis of heart disease with a machine learning system. In this system, a new weighting scheme based on k-nearest neighbour (k-nn) method was utilized as a preprocessing step before the main classifier. Artificial immune recognition system (AIRS) with fuzzy resource allocation mechanism was our used classifier. The obtained classification accuracy of the system was 87% and it was very promising with regard to the other classification applications in the literature for this problem.
Chikh et al.[76] have used a modified Artificial Immune Recognition System AIRS2 which is is a more efficient version of the AIRS algorithm, called MAIRS2 where they have replaced the k-nearest neighbors algorithm with the fuzzy k-nearest neighbors to improve the diagnostic accuracy of diabetes diseases. The diabetes disease dataset used was retrieved from UCI machine learning repository. The performances of the AIRS2 and MAIRS2 are evaluated regarding classification accuracy, sensitivity and specificity values.
Zhao and Davis [77] have introduced a modified artificial immune system (AIS)-based pattern recognition method to diagnosis breast cancer disease. They have integrated AIS with the radial basis function – partial least square regression (AIS-RBFPLS). This new method demonstrates its satisfactory effect on classification accuracy for clinical diagnosis, and also indicates its wide potential applications to other diagnosis and detection problems. Estimation of Distribution Algorithms (EDA).
3.2.2.7. The Estimation of Distribution Algorithm (EDA)
a. The principle of EDAs
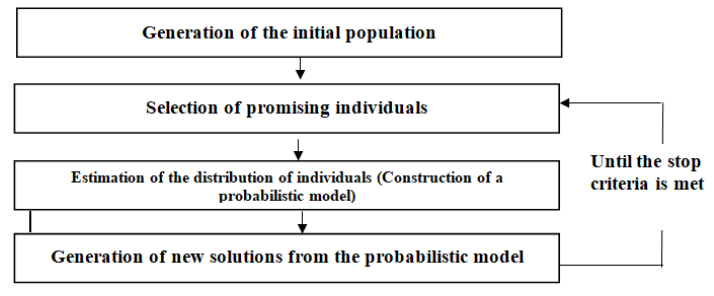
Estimation of Distribution Algorithms are algorithms that are inspired by genetic algorithms, were first proposed in 1994 [78] then in 1996 [79]. EDA belongs to the class of evolutionary algorithms. The main difference between EDAs and most conventional evolutionary algorithms is that evolutionary algorithms generate new candidate solutions using an implicit distribution defined by one or more variation operators, whereas EDAs use an explicit probability distribution encoded by one A Bayesian network, a normal multivariate distribution, or another model class. Like other evolutionary algorithms, EDAs can be used to solve optimization problems defined on a number of vector representations, and the quality of the candidate solutions is often evaluated using one or more purpose functions. EDAs can be applied to both a discrete domain and a continuous domain.
b. Applications of Estimation of Distribution Algorithms
Inza et al. [80] have developed a new randomized algorithm inspired on the new EDA (estimation of distribution algorithm) paradigm in order to predict the survival of cirrhotic patients treated with the transjugular intrahepatic portosystemic shun (TIPS) which is an interventional treatment for cirrhotic patients with portal hypertension. This new method has obtained the best average accuracy results for each classifier used such as FSS techniques, FSS–TREE.
Armananzas et al. [81] have introduced a consensus approach, built upon the classical EDA scheme, that improves stability and robustness of the final set of relevant biomarkers linked to complex diseases which are detected as signal regions called peaks.An entire data workflow is designed to yield unbiased results. Four publicly available MS data sets (two MALDI-TOF and another two SELDI-TOF) are analyzed. The results are compared to the original works, and a new plot (peak frequential plot) for graphically inspecting the relevant peaks is introduced.
In order to identify causative genes of Parkinson's disease, Funayama et al. [82] has did a genome-wide linkage analysis on eight affected and five unaffected individuals from a family with autosomal dominant Parkinson's disease (family A). Subsequently, they have done exomesequencing on three patients and whole genome sequencing on one patient in family A.
Variants were validated by Sanger sequencing in samples from patients with autosomal dominant Parkinson's disease, patients with sporadic Parkinson's disease, and controls. Participants were classified according to clinical information obtained by neurologists.
In order to detect possible link between epilepsy and bipolar disorder (BPD), Wotton and Goldacre [83] have used two large datasets of hospital admission data to determine whether epilepsy and BPD occur together in the same individuals more commonly than expected.They have undertook retrospective cohort studies using the Oxford Record Linkage Study (ORLS) and English national linked Hospital Episode Statistics. They have constructed a cohort of people in each dataset admitted with epilepsy (without prior admission for BPD), and a control cohort (without prior admission for BPD), and compared their subsequent admission rates for BPD. Conversely, they have constructed a cohort of people in each dataset admitted with BPD and a control cohort (both without prior admission for epilepsy), and compared their subsequent admission rates for epilepsy. Finaly, they have concluded that Epilepsy and BPD occur together in individuals more frequently than expected by chance.
3.2.3. Conclusion
For the selection of susceptibility factors for multifactorial diseases, Iterated Solution Improvement (ISI) and Iterative Population lmprovement (IPI) were distinguished. ISI envolve a single solution on the search space at each iteration, they are more focused on the exploitation of research space, so we are never sure of obtaining the optimal solution. HoweverIPI are rather exploratory and allow a better diversification of the research space hence better results.
Table 5. Different metaheuritics methods table.
| Iterated Solution Improvement (ISI) |
Iterative Population lmprovement (IPI) |
| Hill Climbing |
Genetic Algorithm (GA) |
| Simulated Annealing (SA) |
Scatter Search (SS) |
| Tabu Search (TS) |
Genetic Programming (GP) |
|
Ant Colony System Algorithm (ACS) |
|
Particle Swarm Optimiser (PSO) |
|
Artificial Immune Systems (AIS) |
4. Comparative Study of Metaheuristics and Statistical Methods for the Identification of Multifactorial Diseases
The major disadvantage of conventional statistical approaches is that any method that tests group summary measures can only find criteria that have a large gap between group means versus group variance.
The use of metaheuristics can improve the selection of the sample of markers of multifactorial diseases and spread the sample, this allows a better sensitivity and specificity in the classification of individuals in clinical groups compared to conventional statistical methods.Metaheuristics take into account the comparisons made for all possible pairs of individuals in all biological states, instead of simply grouping information for groups of individuals using a single collective median, while the statistical methods identify the entities individually.
Metaheuristics can complement standard statistical approaches to the discovery of genetic markers. The combination of these two methods can help refine the classifications of individuals reached using distinct sets of specific markers.
5. Conclusion
In this article, we have presented the different methods of identifying the factors responsible of multifactorial malaides. We presented statistical methods such as association studies as well as linkage studies and metaheuristics such as single-solution metaheuristics and those with a population of solution.
Thses two types of methods are promising for the feature selection task used in order to analyse multifactorial diseases and they have proved their effectiveness in many works which we have specified some of thempreviously.









 DownLoad:
DownLoad: