Impact of Physical Activity on Frailty Status and How to Start a Semiological Approach to Muscular System

1.   Introduction

Over the last 50 years, numerous experimental and numerical investigations have explored convective phenomena within closed domains. The majority of these studies focus on fluid motion resulting from temperature gradients alone. However, it is important to note that fluid motion can also be triggered by density variations caused by gradients in other scalar quantities. One example of such a scalar quantity is the concentration of pollutants within the fluid. The simultaneous influence of buoyancy forces from both temperature and concentration gradients is referred to as double-diffusive convection $ \left(DDC\right). $ This phenomenon has garnered substantial research attention recently due to its diverse applications across domains such as metal fabrication, drying techniques, oceanography, astrophysics, biology and chemical processes, geosciences, and other fields ^[1]. Across these application areas, many cavities with diverse shapes, encompassing rectangles, triangles, trapezoids, rhomboids, sinusoids, and ellipsoids, have been investigated to assess the impacts of heat and mass transmission. Gebhart and Pera ^[2] were among the pioneers in numerically examining double-diffusion, specifically in cases of vertical laminar fluid motions along surfaces or in plumes. Their study placed particular emphasis on scrutinizing the impact of non-dimensional parameters associated with double-diffusion. Additionally, they discussed the transition of heat and mass transport processes to turbulence. Bejan ^[3] conducted a comprehensive study involving scale analysis concerning heat and mass transport processes within cavities. The investigation considered pure thermal convection, pure solutal convection, as well as flows driven by heat transfer and mass transfer. Lee and Hyun ^[4] considered a rectangular enclosure to study $ DDC $. Their findings indicated a consistent decrease in the Nusselt number as the buoyancy ratio increases from low values. Ghorayeb and Mojtabi ^[5] examined the dynamics of $ DDC $ in an upright enclosure with varied aspect ratios and $ Le $. When examining the effects of buoyancy ratio on double-diffusive mixed convection, Mahapatra et al. ^[6] considered both uniform and non-uniform wall heating.

Modern industrial and engineering systems demand liquids with higher thermal conductivities, and the production of such fluids is hindered by the absence of low-conducting options. Researchers argue that conventional liquids like oil and ethylene glycol fall short in meeting the elevated requirements of efficient processes. Scientists are actively seeking liquids with enhanced thermal conductivities to address the industry's crucial needs, which are essential for the economic development of countries and the realization of sustainable energy growth. In this context, Maxwell's pioneering efforts in 1873 involved dispersing solid particles of millimetric and micrometric sizes in ordinary liquids. Unfortunately, this attempt faced challenges such as significant pressure drops, flow clogging, and erosion, rendering it unsuccessful. Subsequently, Choi and Eastman ^[7] proposed a novel class of particles with nanometric sizes ranging from 1–100 nm, exhibiting remarkable characteristics that contribute to the production of liquids with enhanced physical and chemical attributes. Recently, there has been growing interest among researchers in dispersing nanoparticles in base liquids to boost thermal conductivities. Nanoparticles commonly consist of metals/metal oxides, carbides, carbon nanotubes (CNTs), and graphene. The applications of nanomaterials found in various fields, including industrial cooling for electronic devices (such as cellphones and laptops), nuclear reactors, geothermal energy resource extraction, automotive systems (coolants), drug delivery (specifically in Cancer Therapy), microscale fluidic applications, and sensing and imaging ^{[8,9,10,11,12,13,14]}, among others. Researchers have addressed the enhancement of thermal properties in poorly conducting liquids, providing insights into the elevation of their thermal aspects. In this regards several interesting studies are performed like, Esfahani and Bordbar ^[15] conducted simulations to explore enhancing $ DDC $ heat transfer within a square-shaped enclosure using diverse nanofluids. Their study delved into how nanoparticle volume fraction and the $ Le $ influenced the Nusselt and Sherwood numbers. Parvin et al. ^[16] did numerical investigations on $ DDC $ of water-Al₂O₃ nanofluid within a partly heated enclosure. Their analysis demonstrated that the optimal heat transfer rate occurs at the highest $ Ra $. Nasrin and Alim ^[17] conducted a numerical study on laminar $ DDC $ within a solar collector, likely a prism utilizing a water-CuO nanofluid. Chen et al. ^[18] conducted a numerical investigation into entropy generation associated with $ DDC $ within a rectangular nanofluid enclosure. Alqahtani et al. ^[19] conducted a study investigating the influence of thermal radiation and viscous dissipation on the stagnation point flow of a copper-water nanofluid over a convective stretching/shrinking cylinder. The incorporation of copper into the water base fluid enhances the fluid ability to conduct heat by increasing its thermal conductivity. Puneeth et al. ^[20] analyzed the flow of Ree-Eyring nanofluid over a stretching sheet in the presence of an inclined magnetic field. The distribution of nanoparticles in the nanofluid is stabilized by the motion of motile microorganisms, contributing to a phenomenon known as bioconvection. Ali et al. ^[21] examines the significance of Lorentz and Coriolis forces in influencing the kinetics and gyratory Maxwell nanofluids flowing against a continually stretched surface. The incorporation of gyrotactic microbes serves the dual purpose of preventing the bioconvection of small particles and enhancing overall consistency. Ali et al. ^[22] conducted a theoretical investigation to ascertain the effects of nanoparticles aggregation (NPA) and thermal radiation on the radiant heat of nanofluids surrounding a vertical cylinder. In another article, Ali et al. ^[23] delved into the study of the flow characteristics of a magneto-hydrodynamic (MHD) bioconvective micro-polar nanofluid, which restrains microorganisms. The article presents the numerical solution for the 2-D laminar bioconvective boundary layer flow of micro-polar nanofluids. ^[24] investigated the impact of nanoparticle aggregation in conjunction with thermal radiation under prescribed heat flux conditions. The study utilized the Cattaneo- Christov heat flux (non-Fourier) and mass flux (non-Ficks) approaches within the optimized Buongiorno's model to analyze the magneto-transpose mechanisms of nanofluid over a surface influenced by the gyrotactic behavior of microbe dispersion.

Recently, researchers have been focusing on a novel category of nanofluids that involves hybrid combinations, achieved by diffusing two distinct types of nanoparticles within a base fluid ^[25]. Due to the synergistic effects that leverage the favorable properties of their components, these hybrid nanofluids hold potential applications across various domains of the heat transfer process. Composite nanoparticles incorporated within hybrid nanofluids lead to notable improvements in thermal conductivity and heat transfer coefficient. In their study, Kalidasan et al. ^[26] examined natural convection within a C-shaped open cavity. The cavity contained an isothermal block filled with a hybrid nanofluid consisting of copper $ \left(Cu\right) $-titanium dioxide (TiO)/water. The researchers observed that elevating the volume fraction of these hybrid nanoparticles led to enhanced heat transfer, notably when the Rayleigh number reached the value of $ {10}^{4} $. In addressing nanofluids, some researchers have explored scenarios involving thermosolutal convection. Specifically, the investigation of double-diffusive natural convection $ \left(DDNC\right) $ within a square enclosure encompassing a nanofluid comprised of a water-based fluid and one of the nanoparticles, such as Cu, Ag, Al₂O₃, and TiO₂, was undertaken by Chent et al. ^[27]. Their findings revealed that higher Rayleigh numbers and increased nanoparticle volume fractions led to heightened heat transfer rates while concurrently diminishing the mass transfer rate. Kadhim et al. ^[28] delved into the accessible convection attributes of a Cu-Al₂O₃ hybrid nanofluid within a cavity featuring wavy walls. They examined different volume fractions and inclination angles. The study highlighted the pivotal role of the cavity's angle of attack in influencing heat transfer behavior. The outcomes underscored the substantial enhancement in heat transfer performance achieved by utilizing the hybrid nanofluid. Goudarzi et al. ^[29] conducted a mathematical investigation on the free convection properties of an $ Ag–MgO $/water hybrid nanofluid. The study revealed that augmenting the volume fraction of $ Ag–MgO $ nanoparticles within the conventional fluid led to a notable heat transfer enhancement of up to 11% compared to the base water. Takabi and Salehi ^[30] analyzed Al₂O₃ water nanofluid and $ {Al}_{2}{O}_{3}–Cu-{H}_{2}O $ hybrid nanofluid to investigate the free convection behavior within an enclosure featuring undulating walls. Their study revealed that heightened volume fractions and increased Rayleigh numbers enhanced heat transfer within the cavity. Dogonchi et al. ^[31] as well as Moghadassi et al. ^[32], have unveiled the influence of both mono and hybrid nanofluids on free convection within a tube. They accomplished this by introducing Al₂O₃/water and Al₂O₃-

Cu/water hybrid nanofluids with a volume fraction of 0.1%. Their investigation demonstrated that the convective heat transfer characteristics increased as the Rayleigh number (Ra) was raised. Incorporating higher volume fractions led to amplified pressure drop and friction factor. Within the single-phase model, the hybrid nanofluid exhibited an average Nusselt enhancement of approximately 4.73% compared to water, whereas Al₂O₃/water demonstrated an increase of 13.46%. They added a small proportion of Cu nanoparticles translated to a 5% contribution toward heat transfer enhancement. Chu et al. ^[33] conducted a numerical investigation into the thermal performance of a hybrid nanofluid comprising four types of nanoparticles under the influence of a non-uniform heat source/sink and an inclined magnetic field. The study focused on the two-dimensional unsteady flow over a permeable stretched surface. The nanofluid consisted of four distinct types of nanoparticles copper, titanium dioxide, silver, and aluminum oxide suspended in a water-based fluid. Various studies have been conducted to augment heat transfer within cavities of varying geometries by employing nanofluids containing nanoparticles like $ Ag, Au, AgO, {Al}_{2}{O}_{3}, \mathrm{T}\mathrm{i}{O}_{2}–, Cu, CuO, $ and Carbon Nanotubes ($ CNTs) $ ^[34,35].

The impact of the magnetic field can be observed across a wide range of engineering applications, including geothermal energy harvesting, cavity flow dynamics, jet flow control, cooling systems for nuclear reactors, and beyond. The interplay between magnetohydrodynamics (MHD) and convective heat transfer has been extensively explored in various scenarios, such as within enclosed spaces. The goal is to evaluate how the presence of a magnetic field affects heat transfer, whether it occurs through conduction or convection mechanisms. A notable study conducted by Ghasemi et al. ^[36] delved into the realm of natural convection. Specifically, their research focused on an enclosure with a square configuration that was partially heated. This space was filled with an $ {\mathrm{A}\mathrm{l}}_{2}{\mathrm{O}}_{3} $-water nanofluid, and the influence of a magnetic field was taken into consideration. Their Top of Form findings indicated that the heat transmission rate escalates with increasing $ Re $while decreasing with increasing Hartmann numbers. Teamah ^[37] studied double-diffusive flow within a rectangular cavity, including a magnetic field and an internal heat source. Their findings indicated that the impact of the magnetic field led to a reduction in fluid circulation and the rates of heat and mass transfer within the enclosure. Teamah and Shehata ^[38] researched $ MHD $ involving $ DDNC $ within a trapezoidal inclusion at different inclination angles. Their investigation revealed that the heat and mass transfer rates declined as the inclination angle and $ Ha $ increased. Rahman et al. ^[39] explored magnetohydrodynamics $ DDNC $within a horizontal channel featuring an open cavity. On the other hand, Mahapatra et al. ^[40] conducted a numerical investigation focused on $ DDNC $ within a trapezoidal inclusion filled with nanofluid while considering the impact of a magnetic field.

Following a comprehensive review of existing literature, it is evident that researchers have extensively investigated the phenomenon of MHD natural convection within various enclosed cavities. They have considered MHD natural convection within a quadrant-shaped enclosure utilizing nanofluid, as well as the exploration of diverse enclosures filled with nanofluid. However, the investigation of MHD double-diffusive natural convection within a quadrant-shaped enclosure containing a hybrid nanofluid remains notably absent from the existing body of work. The motivation behind selecting this specific model is attributed to the relatively limited research conducted within this particular geometric configuration, specifically in the context of double-diffusive natural convection serving as the primary mode of heat and mass transfer. Moreover, the utilization of a hybrid nanofluid as the medium in this scenario adds to the novelty of this study. Remarkably, the incorporation of double diffusion transport mechanisms within the specified model represents a distinctive and novel aspect of the current research endeavor.

2.   Physical model

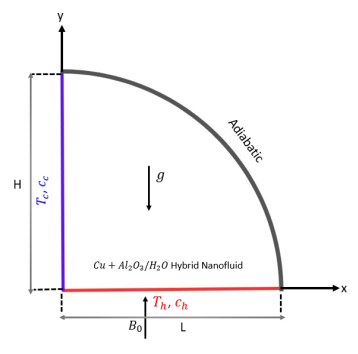
We have considered a quadrantal enclosure (1m in length and 1m in height) filled with Cu-Al2O3-water hybrid nanofluid, subjected to a continuous vertical magnetic field (Figure 1). A uniform concentration ($ {\mathrm{c}}_{\mathrm{h}}) $ and temperature ($ {\mathrm{T}}_{\mathrm{h}}) $ are kept at the lowermost wall, with the wall in an upright position kept at a consistently cold temperature $ {(\mathrm{T}}_{\mathrm{c}}) $ and constant concentration $ \left({\mathrm{c}}_{\mathrm{c}}\right) $. In contrast, the curvy wall is maintained in an adiabatic condition. The working hybrid nanofluid is prepared by dissolving equal quantities of copper and alumina nanoparticles in water, with each type constituting 50% of the mixture. The cavity flow is assumed to be steady, laminar, and incompressible, with the fluid considered Newtonian, all physical properties are treated as constant, except for density in the body force term, where the Boussinesq approximation is applied.

Figure 1.  Graphical visualization of the domain.

DownLoad: Full-Size Img PowerPoint

3.   Mathematical formulation

3.1.   Governing equations

The dimensional form of the conservation equations that govern the double-diffusive natural convection flow involving laminar and magnetohydrodynamic effects within a fluid domain is as follows: ^[27].

Continuity equation:

Momentum conservation equations:

Energy equation:

Concentration equation:

Here, $ u $ and $ v $ represent the velocities in the $ x $ and $ y $ directions, respectively. Moreover, $ p $ and $ T $ denote the fluid pressure and temperature. The parameters $ \beta $ and $ {\beta }_{0} $ correspond to the thermal expansion coefficient and the magnetic field strength density, respectively. Additionally, $ {\rho }_{hnf}, $ $ {\sigma }_{hnf}, $ $ {\alpha }_{hnf} $ and $ {\nu }_{hnf} $ are associated with the effective density, electrical conductivity, thermal diffusivity, and kinematic viscosity of the hybrid nanofluid.

3.2.   Thermo-physical properties of hybrid nanofluid

Table 1 presents the thermophysical characteristics of the host liquid (water), copper$ \left(Cu\right), $ and alumina $ \left(A{l}_{2}{O}_{3}\right) $. Numerous formulations for the thermophysical properties of hybrid nano liquid have been introduced in the existing literature. In this investigation, we employ the physical parameters of the hybrid nano liquid provided by Takabi and Salehi ^[30], detailed in Table 2.

Table 1.  Thermophysical properties of $ {H}_{2}O, Cu, \mathrm{a}\mathrm{n}\mathrm{d}\; A{l}_{2}{O}_{3} $ ^[34].

Physical properties	$ {H}_{2}O $	$ Cu $	$ A{l}_{2}{O}_{3} $
$ {C}_{p} $ $ \left({\raise0.5ex\hbox{$\scriptstyle J$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {kgK}$}}\right)$	4179	385	765
$ \rho $ $\left( {{\raise0.5ex\hbox{$\scriptstyle {kg}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{m^3}}$}}} \right)$	997.1	8933	3970
$ k $ $ \left( {{\raise0.5ex\hbox{$\scriptstyle W$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {mK}$}}} \right) $	0.613	401	40
$ \beta $ $\left( {{\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle K$}}} \right)$	$ 2.1\times {10}^{-4} $	$ 1.67\times {10}^{-5} $	$ 0.85\times {10}^{-5} $
$ \sigma $ $ {\left(\mathrm{\Omega }.\mathrm{m}\right)}^{-1} $	0.05	$ 5.96\times {10}^{7} $	$ {10}^{-10} $

---

 | Show Table

DownLoad: CSV

Table 2.  Thermo-physical characteristics of hybrid nanofluid ^[30].

	Properties of the hybrid nanofluid
Nanoparticles concentration	$ \phi ={\phi }_{C}+{\phi }_{A} $
Density	$ {\rho }_{hnf}=\left(1-\phi \right){\rho }_{f}+{\phi }_{A}{\rho }_{A}+{\phi }_{C}{\rho }_{C} $
Dynamic viscosity	$ {\mu }_{hnf}=\frac{{\mu }_{f}}{{(1-\phi)}^{2.5}} $
Thermal conductivity	$ \frac{{k}_{hnf}}{{k}_{nf}}=\frac{{k}_{C}+2{k}_{nf}-2{\phi }_{C}\left({k}_{nf}-{k}_{C}\right)}{{k}_{C}+2{k}_{nf}+{\phi }_{C}\left({k}_{nf}-{k}_{C}\right)} $ $ \frac{{k}_{nf}}{{k}_{f}}=\frac{{k}_{A}+2{k}_{f}-2{\phi }_{A}\left({k}_{f}-{k}_{A}\right)}{{k}_{A}+2{k}_{f}+{\phi }_{A}\left({k}_{f}-{k}_{A}\right)} $
Heat capacity	$ {\left(\rho {C}_{P}\right)}_{hnf}=\left(1-\phi \right){\left(\rho {C}_{P}\right)}_{f}+{\phi }_{A}{\left(\rho {C}_{P}\right)}_{A}+{\phi }_{C}{\left(\rho {C}_{P}\right)}_{C} $
Thermal expansion	$ {\left(\rho \beta \right)}_{hnf}=\left(1-\phi \right){\left(\rho \beta \right)}_{f}+{\phi }_{A}{\left(\rho \beta \right)}_{A}+{\phi }_{C}{\left(\rho \beta \right)}_{C} $
Thermal diffusivity	$ {\alpha }_{hnf}=\frac{{k}_{hnf}}{{\left(\rho {C}_{P}\right)}_{hnf}} $
Electrical conductivity	$ \left[\frac{{\sigma }_{hnf}}{{\sigma }_{nf}}=1+\frac{3\left(\frac{{\sigma }_{C}}{{\sigma }_{nf}}-1\right){\phi }_{C}}{\left(\frac{{\sigma }_{C}}{{\sigma }_{nf}}+2\right)-\left(\frac{{\sigma }_{C}}{{\sigma }_{nf}}-1\right){\phi }_{C}}\right] $ $ \frac{{\sigma }_{nf}}{{\sigma }_{f}}=\left[1+\frac{3\left(\frac{{\sigma }_{A}}{{\sigma }_{f}}-1\right){\phi }_{A}}{\left(\frac{{\sigma }_{A}}{{\sigma }_{f}}+2\right)-\left(\frac{{\sigma }_{A}}{{\sigma }_{f}}-1\right){\phi }_{A}}\right] $

---

 | Show Table

DownLoad: CSV

The boundary conditions for the problem under consideration are presented in dimensional form, as detailed in Table 3.

Table 3.  Dimensional boundary conditions of the present problem.

Boundary wall	Temperature	Concentration
Left	$ {T}_{c} $	$ {c}_{c} $
Bottom	$ {T}_{h} $	$ {c}_{h} $
Curved wall	$ \frac{\partial T}{\partial n}=0 $	$ \frac{\partial c}{\partial n}=0 $

---

 | Show Table

DownLoad: CSV

The system of Eqs (1)–(5) is converted into a non-dimensional form using the following variable transformations:

The resultant non-dimensional equations for continuity, momentum, energy, and concentration can be expressed as follows:

The boundary conditions in dimensionless form for the problem under consideration are provided in Table 4. The following definitions apply to physical parameters in Eqs (7)–(11).

Table 4.  Dimensionless boundary conditions of the present problem.

Boundary wall	Temperature	Concentration
Left	$ \theta =0 $	$ C=0 $
Bottom	$ \theta =1 $	$ C=1 $
Curved wall	$ \frac{\partial \theta }{\partial n}=0 $	$ \frac{\partial C}{\partial n}=0 $

---

 | Show Table

DownLoad: CSV

The Hartmann number $ \left(Ha\right) $ quantifies the influence of magnetic forces, while the Rayleigh number $ \left(Ra\right) $ characterizes the effects of buoyancy forces. The local Nusselt numbers, average Nusselt numbers, local Sherwood numbers, and average Sherwood numbers at the heated wall of the quadrantal enclosure can be described as follows, in sequence:

4.   Numerical technique

The governing Eqs (7)–(11), along with the boundary condition provided in Table 4, are solved using the commercial software COMSOL Multiphysics, version 5.6 ^[41], which employs the finite element method. The calculation domain is discretized into a small set of elements, and the variables (temperature, velocity, pressure, and concentration) are calculated by carefully choosing interpolation functions within these components. Subsequently, an iterative solver is applied to solve the principal equations until the convergence threshold of $ \left|\frac{{ϵ}^{n+1}-{ϵ}^{n}}{{ϵ}^{n}}\right| $ is reached, with $ ϵ $ representing the velocity components, pressure, temperature, and concentration. To balance numerical precision and the computational resources required, the ideal mesh type is chosen by evaluating a range of elements, ranging from very coarse ($ {\mathrm{L}}_{1} $) to extremely fine ($ {\mathrm{L}}_{9}) $, based on the average Nusselt and Sherwood numbers. Ultimately, a finely detailed mesh containing 14723 details is selected, as it has proven to be satisfactory, with a negligible impact on the average Nusselt and Sherwood numbers. This grid refinement analysis is summarized in Table 5.

Table 5.  Grid refinement checks with $ N{u}_{avg} $ and $ S{h}_{avg} $ at Pr = 6.2, N = 1, Ha = 25, $ {Ra = 10}^{4}, $ Le = 2.5 and $ \phi = 0.04 $.

Mesh	Elements number	Nodes number	$ N{u}_{avg} $	$ S{h}_{avg} $
$ {\mathrm{L}}_{1} $	166	28	5.3332	6.5132
$ {\mathrm{L}}_{2} $	296	42	5.6370	6.8940
$ {\mathrm{L}}_{3} $	440	54	5.7566	7.0251
$ {\mathrm{L}}_{4} $	833	81	6.0092	7.1892
$ {\mathrm{L}}_{5} $	1275	103	6.1712	7.3410
$ {\mathrm{L}}_{6} $	2056	128	6.3149	7.4723
$ {\mathrm{L}}_{7} $	5621	275	6.8264	7.8930
$ {\mathrm{L}}_{8} $	14723	535	7.2941	8.2941
$ {\mathrm{L}}_{9} $	21539	535	7.2932	8.2941

---

 | Show Table

DownLoad: CSV

The computational mesh that has been selected after the grid refinement test is depicted in Figure 2. Moreover, to validate the validity of the computational data, a numerical approach has been validated through a comparison between the current numerical outcomes and the previously published results of Dutta et al. ^[42] and depicted in terms of the average Nusselt number in Table 6. The agreement between the computed results in this study and the numerical findings indicates a high level of concurrence, further confirming the satisfactory accuracy of this present research.

Figure 2.  Mesh generation of the quadrantal enclosure.

DownLoad: Full-Size Img PowerPoint

Table 6.  Comparison of current and previous results for the average Nusselt number for different $ Ha $ values at $ Ra = {10}^{6} $ and $ \phi = 0.05 $.

$ Ha $	Dutta et al. [42]	Present work	Relative difference %
0	9.82	9.74	0.8
20	9.04	9.01	0.3
40	7.49	7.37	1.3
60	6.03	6.01	0.3
120	3.39	3.3	1.1

---

 | Show Table

DownLoad: CSV

5.   Results and discussion

In this segment, the outcomes obtained through numerical solutions are presented. These outcomes encompass visual depictions of streamlines, temperature distributions, and concentration gradients. Data representations are also included for critical parameters such as Nusselt and Sherwood numbers. These representations encompass a range of values, as outlined in Table 7.

Table 7.  Numerous ranges of considered parameters in the current study.

Parameters	Ranges
Rayleigh number $ \left(Ra\right) $	$ {10}^{3}\;\mathrm{t}\mathrm{o}\;{10}^{6} $
Hartmann number $ \left(Ha\right) $	$ 0\;to\;60 $
Buoyancy ratio$ \left(N\right) $	$ 1\;to\;10 $
The volume fraction of nanoparticles ($ \phi $)	$ 0\;to\;0.05 $
Lewis number $ \left(Le\right) $	$ 0.1 \;to \;10 $
Prandtl number $ \left(Pr\right) $	$ 6.2 \left(fixed\right) $

---

 | Show Table

DownLoad: CSV

Figure 3 displays the streamlines (left side), isotherms (center), and concentrations (right side) for $ Ra = {10}^{3}, {10}^{5}, \mathrm{ }\mathrm{a}\mathrm{n}\mathrm{d} {10}^{6} $ at $ Pr = 6.2, N = 1, Ha = 25, Le = 2.5 $ and $ \phi = 0.04. $ Since temperature discrepancies, the fluid moves upwards from the center of the wall at bottom. It descends within the vertical cold wall, resulting in the creation of counter-rotating vortices inside the inclusion. At low $ (Ra = {10}^{3}), $the stream function's intensity is limited due to heat transfer primarily occurring through conduction. As the Ra increases to $ {10}^{6} $, the buoyant force gains prominence, leading to a higher magnitude of the stream function $ {(\psi }_{max} = 9), $ evident from the streamlines in Figure 3. The validity of this observation is substantiated by a mathematical correlation utilizing dimensionless Rayleigh number coefficient, given by $ Ra = \frac{g{\beta }_{f}({T}_{h}-{T}_{c}{)L}^{3}}{{\alpha }_{f}{v}_{f}}. $ This relation signifies that with an increase in $ Ra, $ the viscosity of the fluid decreases, reflecting the inverse relationship between $ Ra $ and viscous forces. Nonetheless, the rise in the Rayleigh number does not modify the configuration of the circulating vortices. Instead, it causes a shift in the center of rotation from a circular to an oval shape. A notable transformation in isotherm and concentration patterns becomes apparent as the Rayleigh number $ \left(Ra\right) $ increases. At lower $ Ra = {10}^{3}, $ the contours of isotherms and concentrations appear as straight lines. In contrast, these lines become distorted at higher $ Ra = {10}^{5} $ due to intensified convection effects associated with elevated Ra. This distortion follows a similar trend in both cases, reflecting the parallel behavior dictated by comparable energy and mass equations. However, it is worth noting that the distortion in concentration lines is more pronounced than in isothermal lines. This discrepancy contributes to a heightened level of mass transfer.

Figure 3.  Streamlines, isotherms and isoconcentrations for different Rayliegh number $ \left(Ra\right) $ at $ Pr = 6.2, N = 1, Ha = 25, Le = 2.5 $and $ \phi = 0.04 $.

DownLoad: Full-Size Img PowerPoint

Figure 4 illustrates the influence of a magnetic field on streamlines, isotherms, and concentration contours while keeping other parameters constant. The involvement of the Hartmann number in the present study is significant due to the introduction of a magnetic field, which contributes to reducing the velocity profile and promoting laminar flow. In the absence of magnetic field ($ Ha = 0) $ the stream function value is measured $ {(\psi }_{max} = 6) $, indicating a more pronounced convection effect, in contrast, with the existence of a magnetic field $ (Ha = 40) $, the stream function value diminishes significantly to $ {(\psi }_{max} = 0.2) $. This phenomenon is attributed to the intensified magnetic field producing Lorentz forces that counteract motion, resulting in a deceleration of the flow. This observation is evident from the streamlines of Figure 4. The alteration in Ha has a notable impact on temperature and concentration distribution. The isotherm and concentration contour lines become distorted in a scenario with no magnetic field Ha = 0. This distortion serves as an indicator of heightened convection effects. As Ha increases to Ha = 60, the previously observed distortion gradually decreases and aligns more parallel. This trend indicates a reduction in convection effects due to the influence of Lorentz forces. Notably, a solid magnetic field intensifies the conductive mode of heat transfer rather than the convective mode, as observed.

Figure 4.  Streamlines, isotherms and isoconcentrations for different Hartmann number $ \left(Ha\right) $ at $ Pr = 6.2, N = 1, Ra = {10}^{4}, Le = 2.5 $and $ \phi = 0.04 $.

DownLoad: Full-Size Img PowerPoint

Figure 5 demonstrates the impact of varying nanoparticle volume fractions on streamlines, isotherms, and is concentrations while maintaining consistent values for other parameters. In a pure fluid $ (\phi = 0), $the fluid occupies the entire enclosure. However, introducing nanoparticles results in elevated fluid viscosity and thermal conductivity due to heightened effects of viscous forces and buoyancy forces. As the nanoparticle volume fraction $ \left(\phi \right) $ increases, the intensity of the flow field diminishes. This decrease occurs because the augmented viscous effects impede fluid motion, slowing the overall flow movement. At $ (\phi = 0) $, the maximum intensity of streamlines $ {(\psi }_{max}) $ is recorded as 9.23. However, as the $ \phi $ increases to 0.04 due to the addition of nanoparticles, the full power of streamlines decreases to 7.2. The incorporation of nanoparticles into the base fluid results in an improvement in conductive heat transfer. This enhancement is particularly prominent in isotherm and concentration contours, in contrast to the effects observed in streamlines. As $ \phi $ increases, the thermal and solutal boundary layer transforms at the heated surface. This alteration causes the isotherm and its concentration contours to adopt a linear configuration. This shift is attributed to the substantial thermal conductivity of the nanoparticles, leading to the prevalence of the conductive mode of heat transfer.

Figure 5.  Streamlines, isotherms and isoconcentrations for different volume fraction of nanoparticles $ \left(\phi \right) $ at $ Pr = 6.2, N = 1, Ra = {10}^{3}, Le = 2.5 $and $ Ha = 25 $.

DownLoad: Full-Size Img PowerPoint

In Figure 6, we have illustrated the numerical findings through streamlines, isotherms, and iso-concentration contours. These visual representations are based on different Lewis number (Le) values (1, 5, 10) while maintaining $ {Ra = 10}^{4} $, Pr = 6.2, N = 1, Ha = 25, and $ \phi = 0.04 $ as constants. The Lewis number serves as a parameter characterizing the ratio of thermal diffusivity to mass diffusivity within a fluid flow system. An escalating value of (Le) signifies the prevalence of thermal diffusivity, thereby constraining convective heat transport. The streamline patterns remain broadly consistent across the range of Lewis numbers, indicating minimal alteration. It is observed that the influence of Lewis numbers on the prevailing convection regimes is relatively subdued, suggesting a limited impact on the dominant convection characteristics. Convective distortion of the isotherms occurs within the enclosure due to the dominant effect of convective currents. The enhancement of the Lewis number results in a noticeable escalation in the temperature flow. As the Lewis number rises from $ 1to10 $, the contours of iso-concentrations exhibit undulations and distortions. This observation signifies an augmented mass transfer attributed to the diminishing effect of mass diffusivity.

Figure 6.  Streamlines, isotherms and isoconcentrations for different Lewis number $ \left(Le\right) $ at $ Pr = 6.2, N = 1, Ra = {10}^{3}, \phi = 0.04 $and $ Ha = 25 $.

DownLoad: Full-Size Img PowerPoint

Figure 7 presents the changes in average Nusselt $ {(Nu}_{avg}) $ and Sherwood number $ {(Sh}_{avg}) $for various considered parameters on the heated bottom wall of the quadrantal cavity. Figures 7 (A) and (B) illustrate the changes in the $ {Nu}_{avg} $ and $ {Sh}_{avg} $across different Rayleigh numbers $ \left(Ra\right) $ for pure fluid $ (\phi = 0) $, nanofluid $ (\phi = 0.02) $, and hybrid nanofluid $ (\phi = 0.04 $). At elevated $ Ra $ values, the intensity of free convection currents becomes more pronounced, leading to a heightened heat transfer rate. As $ Ra $ increases, the buoyancy force within the enclosure escalates, causing convection to take precedence as the primary mechanism for heat and mass transfer. Consequently, this amplifies both $ {Nu}_{avg} $ and $ {Sh}_{avg} $ values. Incorporating nanoparticles into a fluid can notably enhance the fluid's thermal conductivity and convective heat transfer properties. This augmentation becomes particularly evident at $ (\phi = 0.04 $), where a significant improvement in heat transfer performance is observed. Figure 7 (C) and (D) illustrate the changes in $ {Nu}_{avg} $ and $ {Sh}_{avg} $ concerning various $ Ha $values. The findings indicate that augmenting the magnetic field's impact leads to a reduction in both heat and mass transfer rates. This decrease is attributed to the influence of the Lorentz force, which lowers the fluid velocity and progressively emphasizes the conductive effect. Conversely, the introduction of nanoparticles amplifies the nanofluid's thermal conductivity, thereby enhancing heat transfer efficiency and causing a tendency towards higher $ {Nu}_{avg} $and $ {Sh}_{avg} $values.

Figure 7.  Influence of $ {Nu}_{avg} $ and $ {Sh}_{avg} $for various values of $ Ra $ (A) and (B), $ Ha $ (C) and (D), $ Le $ (E) and (F).

DownLoad: Full-Size Img PowerPoint

Figures 7 (E) and (F) present the variations of $ {Nu}_{avg} $ and $ {Sh}_{avg} $ across various Lewis numbers and nanoparticle volume fractions. Since the Lewis number signifies the ratio of thermal diffusivity to mass diffusivity, elevating the Le value leads to a proportional expansion of the mass boundary layer and a corresponding contraction of the thermal boundary layer around sources. Consequently, an escalation in Le prompts a rise in the mass transfer rate while simultaneously inducing a reduction in the heat transfer rate.

6.   Conclusions

We investigate MHD double-diffusive natural convection within a quadrantal-shaped enclosure filled with a Cu-Al₂O₃-water hybrid nanofluid. The finite element method was employed to solve the non-dimensional governing equations. The impacts of relevant parameters on fluid flow, temperature distribution, concentration distribution, and heat and mass transfer rate were examined through computational analysis. The significant findings and insights derived from the outcomes and subsequent discussions can be summarized as follows:

●  As Rayleigh number (Ra) values rise, fluid flow accelerates, but it slows down with increased magnetic field strength (Ha) and nanoparticle volume fraction ($ \phi $).

●  The average Nusselt number ($ {Nu}_{avg} $) and Sherwood number ($ {Sh}_{avg} $) increase with higher Rayleigh numbers and nanoparticle volume fractions. Conversely, when the Hartmann number rises, both $ {Nu}_{avg} $ and $ {Sh}_{avg} $decrease.

●  As the Lewis number rises, the heat transfer rate declines while the mass transfer rate escalates.

●   The characteristics of fluid streamlines, isotherms, and iso-concentrations within the enclosure show a significant reliance on the parameters under consideration.

●   Incorporating Cu-Al₂O₃ nanoparticles into base fluid reduces convective flow intensity, and this addition proves particularly effective in improving the rates of heat and mass transfer, surpassing the performance observed without particles.

●  The investigation demonstrates that augmenting the concentration of Cu-Al₂O₃ nanoparticles in the base fluid leads to a remarkable improvement in heat transfer efficiency, with potential enhancements of up to 11% in comparison to the base fluid.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare that they have no conflict of interest.