1.
Introduction
Throughout history, humans have extensively depended on plants both as a source of sustenance and for the mitigation of illnesses. Natural products have historically made substantial contributions to the advancement of modern medicine and continue to play a significant part in discovering new drugs. Medicinal plants are the primary sources of naturally occurring lead compounds that are utilized in the process of discovering and developing drugs to counteract the widespread occurrence of infectious diseases [1]. Their potent and therapeutic effects are attributed to their wide range of bioactive substances. The genus Eugenia is used in folk medicine to treat wounds, flu, fever, cough, gout, hypertension, digestive and liver diseases, rheumatism, tonsillitis, sore throat, hemorrhoids, and diarrhea [2]–[5].
Oxidative stress is a significant factor in the development of human diseases. The terms “free radicals” and “antioxidants” are often recognized among individuals who prioritize their health [6]. Oxidative stress, caused by the presence of active oxygen and free radicals, is responsible for tissue damage that can lead to a range of diseases, including cardiovascular disorders, aging, cancer, and neurological conditions [6]. Using entire plants and plant components to cure various ailments has been a longstanding practice worldwide, encompassing both developing and developed countries, through traditional medicinal systems [7]. Bioactive compounds present as natural constituents in plants provide health benefits beyond the basic nutritional value of the product.
Cancer is a major public health concern and the second leading cause of death globally [8]. According to estimates from the World Health Organization, this fatal health problem was responsible for 70% of deaths, especially in low- and middle-income countries [8]. The most prevalent kind of cancer and the second largest cause of cancer-related mortality for women worldwide is breast cancer (BC). According to the Cancer Statistics 2020 report, over 42,000 predicted fatalities and 276,480 new cases of cancer are expected in 2020, British Columbia accounts for 30% of all cancer diagnoses in women [9]. The existing chemotherapy treatment for breast cancer comes with a high cost, numerous side effects, and the potential to develop resistant cells. This emphasizes the importance of employing natural medicines to mitigate the detrimental effects of existing chemical treatments [10]. Several studies have evaluated the therapeutic efficacy of extracts derived from this plant through different extraction methods in several experimental models; however, this data from different varieties has never been analyzed altogether [11]–[13].
Computer-based strategies for incorporating pharmacokinetic factors into drug discovery programs are gaining popularity [14]. A potential lead compound can be described as a molecule that possesses both high potency and a favorable ADMET profile. Hence, compounds with unremarkable projected ADMET profiles can be promptly excluded from the roster of prospective therapeutic candidates, regardless of their high potency [15]. Computational techniques have been widely adopted in medical synthetic chemistry, but their utilization in studying natural substances has not been thoroughly investigated. Eugeni. uniflora L. (Myrtaceae), commonly referred to as the Brazilian cherry tree or pitangueira, is a globally distributed fruit-bearing tree [16]. It is utilized in traditional medicine for its diuretic, anti-rheumatic, anti-febrile, and anti-inflammatory properties, as well as its therapeutic effects on stomach ailments [16],[17]. Therefore, this work was conducted to investigate the in-vitro antioxidant activity of the crude extract coupled with some in-silico methods to forecast the drug-likeness, pharmacokinetic profiling, and binding effectiveness of the identified phytochemicals derived from the E. uniflora extract.
2.
Materials and methods
2.1. Plant identification
The species were identified and verified by a licensed botanist at the Department of Botany, Faculty of Science, Ahmadu Bello University. Subsequently, herbarium specimens of E. uniflora L. (vouchers ABU09634) were prepared and deposited. The species name was confirmed using the World Flora Online (WFO) at https://www.worldfloraonline.org/.
2.2. Sample extraction and percent yield determination
The leaves were cleaned with running water to eliminate any stains. A grinding machine was used to reduce the dehydrated samples to a fine powder. The powdered plant samples were measured by weighing 100 g of the sample. The Soxhlet technique was used to extract the components from the plant leaves with ethanol. The extraction results were filtered using Whitman No. 1 filter paper. The ethanol leaves were coarsely extracted with an E-Z-2-Elite evaporation equipment. The solvent pressure was set to 72 and the vacuum to 40 °C. The extracts were dried in a chilled vacuum oven at 40 °C until they attained a homogeneous mass, then concentrated using a rotary evaporator and weighed using an electronic balance [6]. The weight of crude yield was derived by the following simple calculation:
where, F1 = Mass of the crude extract, F2 = Mass of the sample [18].
2.3. Total phenolic content (TPC)
After adding 1.5 mL of Folin-Ciocalteu reagent to 200 µg of crude material, the mixture was subjected to a two-hour incubation period in a light-restricted environment. A spectrometer was used to measure the absorbance at a wavelength of 750 nm. Test samples were treated with gallic acid at doses ranging from 0 to 200 µg/mL. The results were quantified in milligrams of gallic acid equivalent [19] per gram of dry weight (DW) using the gallic acid standard curve equation, y = 0.0057x + 0.0025, where R2 = 0.9929 (Figure 1) [20].
2.4. Total flavonoid contents (TFC)
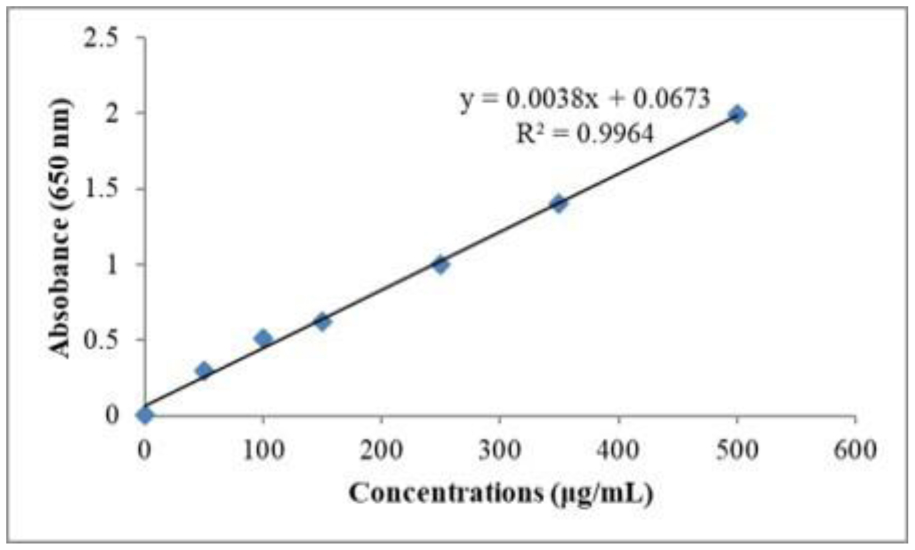
A total of 4 mL of filtered water, 0.3 mL of 5% sodium nitrate solution, and 1 mL of extract were mixed. After adding 2 mL of 1 M sodium hydroxide, 2.4 mL of water, and 0.3 mL of 10% aluminum chloride, the mixture was incubated for 15 minutes. Absorbance was measured with a spectrophotometer set to 510 nm in wavelength. Test samples contained 25 mg of standard quercetin at concentrations ranging from 0 to 100 µg/mL in 50 mL of ethanol. The results were expressed as mg of Quercetin Equivalent (QE) per g of dry weight (DW), and the measurements were fitted onto a standard curve of Quercetin using the equation y = 0.0002x + 0.0286, where R2 = 0.9985 (Figure 2) [21].
2.5. DPPH radical scavenging activity
A solution of DPPH (4 mg of DPPH dissolved in 100 mL of methanol) and a crude extract (1 mg dissolved in 1 mL of methanol) were made in a 96-well plate using the 2-fold dilution procedure. Ascorbic acid serves as the reference standard. The absorbance measurement was taken at a wavelength of 517 nm following a 30-minute incubation period in a dark environment at room temperature. The experiment was conducted in triplicate.
[7].
2.6. Ferric reducing antioxidant potential (FRAP) assay
Preparations were made for stock solutions consisting of 10 mL of acetate buffer with a pH of 3.6, 1 mL of TPTZ (2,4,6-tripyridyltriazine) solution in hydrochloric acid, and 1 mL of FeCl3 solution. A total of 100 µL of crude extracts and 300 µL of deionized water were combined with 3 mL of FRAP solution. The solution was combined and then placed in a water bath at 37 °C for 30 minutes. Ascorbic acid served as the positive control in this investigation. The spectrophotometer was used to measure the absorbance of the resulting solution at a wavelength of 593 nm, with acetate buffer serving as the blank. A standard curve was generated by utilizing various concentrations of FeSO4·7H2O. The equation for the curve is y = 0.0003x + 0.098, with an R2 value of 0.9961. The FRAP results were quantified in terms of milligram Ascorbic Acid Equivalent (AAE) per gram of dry weight (DW) [21].
2.7. Compound identification
The ethanolic crude extract was analyzed by means of gas chromatography linked to mass spectrometry (GC-MS, Shimadzu/QP2010) with an OV-5 bonded capillary column (30 m 0.25 mm 0.25 m film thickness). The propellant gas was helium, and the flow rate was 1.0 mL min. Temperatures of 220 and 240 °C were reached in the injector and detector, respectively. Injecting 1.0 µL at a split ratio of 1:20. The oven temperature was set to gradually increase from 60 °C to 240 °C at a rate of 3 °C/min. Collected pieces had velocities ranging from 40 to 650 m/z and an electron impact energy of 70 eV [22]. The chemical components were identified by cross-referencing them against a large database [18]. The spectrometers were run in electron-impact mode, with a 40–550 amu scan range, an ionization energy of 70 eV, and a 0.34 s scan rate. The temperatures of the quadrupole and ionization source were 150 and 280 °C, respectively. Differences in the composition of the volatile compounds extracted from E. uniflora leaves may also occur because of seasonal variations in the environment [23],[24].
2.8. In-silico studies
2.8.1. Drug-likeness and pharmacokinetic properties
The SMILES strings of the fifteen compounds found in the ethanolic leaves E. uniflora extract from our investigations were acquired from PubChem (http://pubchem.ncbi.nlm.nih.gov/). Subsequently, the drug-likeness parameters of the studied compounds were computed using the SwissADME online webserver (http://www.swissadme.ch/index.php), such as the molecular weight (MW), the number of hydrogen bond acceptors (nHBA), the number of hydrogen bond donors (nHBD), and the number of rotational bonds (nRB). The Lipinski's rule of five specifies that drug-like compounds must have a molecular weight (MW) of no more than 500 daltons, a maximum of 10 hydrogen bond acceptors (nHBA), a maximum of 5 hydrogen bond donors (nHBD), and a logarithm of the partition coefficient (clogP) not exceeding 5. Also, chemical substances that exhibit many violations of these defined criteria are not considered drug-like compounds [25]. Other in-silico pharmacokinetic properties that are predicted by SwissADME includes absorption, distribution, metabolism, and excretion (ADME) parameters such as cLogP (lipophilicity measured by the octanol-water partition coefficient), solubility, GIA (gastrointestinal absorption), BBB (blood-brain barrier) permeability, P-gp (p-glycoprotein) substrate, inhibition of CYP (cytochrome P450) isoforms, and Log Kp (skin permeability) among others [25].
2.8.2. In-silico bioactivity predictions
The Molinspiration Online tool (http://www.molinspiration.com) was used to assess the bioactivity scores of the compounds for different molecules, including G protein-coupled receptor (GPCR) ligands, ion channel modulators, kinase inhibitors, nuclear receptor ligands, and protease inhibitors. Before predicting the bioactivity score, the compounds' canonical SMILES strings were obtained from PubChem and inserted into the Molinspiration program [25].
2.8.3. Molecular docking protocol
The 3D crystal structure of human placental aromatase complexed with exemestane (PDB: 3S7S) was obtained from the Protein Data Bank (PDB). The 3S7S pdb structure was chosen based on various criteria, such as containing the full length of the sequence (503 aa), being crystallized with an inhibitor for comparison with docked ligands, having an acceptable resolution of less than 4 Å, and having no mutations. Chimera software [26] was utilized to remove the native ligand (Exemestane), which is a standard anti-breast cancer drug, hetero atoms, and water molecules from the PDB crystal structure. The 15 phytochemicals from E. uniflora leaves were investigated for the molecular docking studies. To facilitate the docking process, the smiles strings were converted into pdb files using the CORINA webserver [27]. Subsequently, the Chimaera software tools were employed to further prepare each ligand. This involved adding hydrogen, removing solvents, and establishing the charge. Three commercially available anti-cancer medications, Exemestane, Arimidex, and Femara were employed as controls for the docking experiments. The three medications were utilized as aromatase inhibitors in the treatment of hormone-dependent breast cancer. These drugs are successful in blocking estrogen production, showing notable effectiveness in decreasing the likelihood of breast cancer recurrence according to multiple research studies [28],[29]. The method and settings used for preparing the 15 phytochemicals mentioned above were also applied to the preparation of Exemestane, Arimidex, and Femara for docking. AutoDock suite-4.2.6.i86Windows and Mgltools_win32_1.5.6 optimized the protein molecule by performing several modifications. First, water molecules were removed, and then polar hydrogen was added. Additionally, non-polar hydrogen was combined, and Gasteiger charges were calculated. The docking grid box had a size of 40 × 40 × 40 and was positioned at the coordinates x: 86.08, y: 54.28, and z: 46.18. The docking process employed a genetic algorithm with specific parameters, including a population size of 150, a maximum of 27,000 generations, a mutation rate of 0.02, and a crossover rate of 0.80. To analyze the results, the chimaera software tools, and Discovery Studio 2021 Client were utilized to examine the conformations with the highest binding affinities.
2.8.4. Molecular dynamics (MD) simulation
For the molecular dynamics study, we aimed to examine the impact of the best ligand on protein flexibility. The chain A of aromatase without any ligands and the protein-ligand complex that was docked with the highest binding affinity were used for the molecular dynamics analysis. The MD simulation was conducted using MDWeb (https://mmb.irbbarcelona.org/MDWeb/) [30]. The parameters utilized in the simulation were as follows: simulation type = single structure, operation = coarse-grained MD: NMA (C-Alpha), time [31] = 100, Cutoff = 8.0 (Å), Linear Algorithm, force constant (kcal/mol*Å2) = 40. The resulting MD trajectories were analyzed using simulation analysis tools provided by MDweb to generate a plot of the root mean square fluctuation (RMSF) as atomic fluctuation values per residue.
2.9. Statistical analysis
All experiments were conducted in triplicate and all results were expressed as mean ± standard deviation of the measurements. Excel (Microsoft Co, Redmond, WA, USA) was used to calculate the standard deviation. The data obtained were also subjected to one-way ANOVA at 95% confidence interval.
3.
Results and discussion
3.1. In-vitro biological activity
The yield of ethanolic extract was 0.085%. Several aspects, such as the extraction method, temperature, length of extraction, phytochemical content, and solvent selection, affect the efficiency or optimization of crude yield [32]. Because alcohol is neutral and the compounds it extracts are compatible with other substances, polar solvents are very useful for extracting more active compounds from plants [33]. High-polarity solvents were shown to be more effective in most studies when it came to extracting chemicals from plants. This can be attributed to the plants' increased content of polar molecules, which are soluble in a variety of solvents, including ethanol, methanol, and water [32]. However, changes in the polarity of the solvent can affect the ability to extract bioactive compounds from plants. By means of photosynthesis, phenolic compounds are produced to provide defense against injury, infection, and UV radiation for plants [34]. Due to their high activity, phenolic and flavonoid chemicals have drawn attention. Demand for products with high phenolic and flavonoid content is rising [35]. The ethanol extract has an average total phenolic content of 8.72%, while the flavonoid content has an average content of 11. 3 % (Table 1). The ethanol leaves' extracts 25 µg/mL IC50 value demonstrated high scavenging activity as shown in (Figure 3). An electron-rich antioxidant plant extract containing free radicals can be transformed into a non-radical state using DPPH [7]. Brito et al. [36] also reported similar biological activity. The extract was found to convert Fe3+ to Fe2+ at 7.2 mmol/g (Table 1). The high phenolic and flavonoid content of the extract promoted the scavenging effect and iron reduction capacity. Antioxidants are a crucial factor in lowering the risk of chronic diseases because they shield cell tissues from oxidative damage by scavenging free radicals that have accumulated on them [37].
3.2. Chemical composition
The leaf ethanol extract was analyzed using GC-MS, a hybrid analytical technique that combines the separation characteristics of gas-liquid chromatography with the detection capabilities of mass spectrometry. This approach was used to determine the presence of compounds in the extract, as it has shown high activity. The data analysis revealed fifteen compounds [(1) 3-Undecene (2) Acetic acid (3) Benzofuran (4) Hydroquinone (5) alpha-L-Galactopyranose (6) Methyl hexofuranoside (7) n-Nonadecanoic acid (8) 10-Octadecenoic acid (9) 2-Nonen-1-ol (10) Z-8-Methyl-9-tetradecenoic (11) 10-Undecenal (12) 2-Octylcyclopropene-1-heptanol (13) 1,5-Cyclododecadiene (14) Allantoic acid (15) Stearic acid hydrazide] (Table 2). The extract's composition is significantly influenced by the polarity of the metabolites, the presence of chemicals, the extraction solvent, and the extraction technique [18]. Compounds in extracts are affected by temperature, geographical distribution, plant type, freshness, drying time, and extraction technique. The compounds were analyzed using molecular docking to determine their impact on the plant extract's overall biological activity. Evaluating binding behavior is crucial for rationally designing small compounds and understanding biological processes.
3.3. In-silico drug-likeness and pharmacokinetic properties
In appraising the drug-likeness of the 15 phytochemicals, the molecular weights and other Lipinski's parameters of the studied compounds are within the thresholds. In addition, drug-like compounds should contain a maximum of 10 hydrogen bond acceptors (nHBA) and a maximum of 5 hydrogen bond donors (nHBD) [38]. This implies that all the compounds may be easily absorbed, distributed, and transported [39]. Moreover, this suggests that when the compounds are supplied into the body, they can enter the gastrointestinal tract and be efficiently absorbed. The findings of each molecule's number of rotatable bonds are displayed in Table 2. With nRB = 17, compounds 7 and 15 had the highest number of rotatable bonds, followed by compound 12 (nRB = 16). All other compounds, on the other hand, have fifteen or fewer rotatable bonds. Compounds that exhibit favorable bioavailability possess a maximum of 15 rotatable bonds [40]. The table also displays the oral bioavailability results for the studied substances, the bioavailability of all the substances ranges from 0.55 to 0.85 (Table 2). The numbers indicate that the compounds conform to the Lipinski rule of five and have a high likelihood of being bioavailable. However, if a chemical is to be utilized for drug development because of its medicinal advantages but has low bioavailability, it should be changed to enhance its bioavailability [25].
All compounds, except for compounds 7, 12, and 15, demonstrated permeability and oral bioavailability potential as they fell within the acceptable range (nRB ≤ 15). Except for compound 6, which surpassed this limit with a clogP >5, all other compounds met the requirement of having a clogP ≤ 5. Lead compounds' solubility, selectivity, potency, permeability, and promiscuity are all strongly impacted by their lipophilicity [41]. The high lipophilicity compounds (clogP > 5) frequently show poor absorption, restricted solubility, and quick metabolic turnover. Moreover, an increase in lipophilicity (clogP > 5) increases the probability that drugs will bind to non-targeted hydrophobic protein targets, which might have detrimental effects on biological systems [25]. According to the Log S prediction model, the estimated aqueous solubility showed that all studied phyto-compounds are soluble except for compounds 7, 8, and 15 (Supplementary Table 1). Hence, these compounds must be soluble in water to pass through cell membranes and be absorbed. Furthermore, one of the factors influencing the distribution and absorption of drugs is solubility [42].
Except for compounds 5, 6, and 14, all the other compounds exhibited significant likelihoods of absorption in the gastrointestinal system (Supplementary Table 2). Consequently, these chemicals have the capacity to be assimilated in the gastrointestinal tract when taken orally [24]. The blood-brain barrier (BBB) is a layer of microvascular endothelial cells that acts as a barrier between the brain and the blood. Based on the acquired findings, some of the compounds demonstrate the ability to traverse the blood-brain barrier (BBB). Penetration of the blood-brain barrier (BBB) is necessary only for drugs that target the central nervous system (CNS) [43]. Compounds 2, 4, 5, 6, 8, 14, and 15 demonstrated no ability to penetrate the blood-brain barrier (BBB), as shown in Supplementary Table 2. Consequently, this lack of penetration can be advantageous since it reduces the probability of causing harmful effects in the central nervous system (CNS). Except for compound 6, all compounds were determined to be non-substrates for P-gp. This suggests that the compounds would be resistant to the efflux activity of P-gp, which aims to remove chemicals from cells. As a result, therapeutic efficacy may be compromised due to lower than anticipated concentrations. P-glycoproteins (P-gp) are membrane transporters that facilitate the movement of substances between the intracellular and extracellular environments [44]. The cytochrome P450 monooxygenase enzyme plays a crucial role in the metabolism and removal of drugs in living organisms. The lack of inhibitory action of the discovered compounds on these enzymes suggest that the compounds are likely to undergo transformation and become accessible when administered orally (Supplementary Table 2). The skin acts as a discerning barrier, permitting the penetration of various substances at varying rates based on their physicochemical characteristics. Skin permeability (LogKp) is a crucial measure used to evaluate substances that may need to be administered through the skin. All the compounds are anticipated to be impermeable due to their negative LogKp values. This suggests that the entire chemical could not be efficiently delivered via the skin. The assessment of the toxicity of compounds plays a vital role in the drug discovery process [24]. The ADME-Tox characteristics of the identified drugs were evaluated to be non-AMES which also determines suggest favorable pharmacokinetic qualities with good body's response upon their administration.
3.4. Molecular docking and dynamic simulation studies
The substantial level of antioxidants found in the plant extract, along with their notable ability to scavenge radicals, inspired us to conduct a more in-depth analysis of the isolated phytochemicals as potential anticancer agents through an in-silico study. To verify the docking protocol of the AutoDock software, the native ligand (exemestane) was isolated from the binding site of the aromatase structure (PDB: 3S7S). The AutoDock software successfully re-docked the isolated ligand back into the active site of the aromatase. The redocked ligand exhibited a close alignment with the corresponding co-crystallized exemestane, thus confirming the precision of the docking protocol. This validation of docking protocol was reported in our previous work [10]. The selection of the optimal docked ligand molecules was based on the criteria of the lowest binding energy and the lowest inhibitory constant (KI). It is crucial that the ultimate configuration is of low energy, as molecules in nature tend to exist in their lowest energy state. Understanding and incorporating these characteristics is vital for the effective design of potent inhibitors [45]. The results from the docking screening revealed that among the 15 compounds, Stearic acid hydrazide displayed the highest binding affinity with the targeted aromatase protein. This can be observed in Table 3, where the Stearic acid hydrazide compound exhibited the highest binding affinity of −7.86 (kcal/mol) in the active pocket of the receptor shown in Figure 4.
Stearic acid hydrazide formed atomic interactions with 17 specific amino acids, ARG115 ILE132 ILE133 PHE134 TRP141 ARG145 PHE221 TRP224 ALA306 ASP309 THR310 VAL370 ARG435 GLY436 CYS437 ALA438 LEU477 SER478 as shown in Figure 5. Four of the 17 interactions observed were hydrogen bonds, potentially elucidating the robust affinity between Stearic acid hydrazide and aromatase.
Postmenopausal women are more prone to developing breast cancer compared to younger women. Despite the fact that the ovaries cease to produce estrogen and progesterone after menopause, the production of estrogen in peripheral tissues increases [46]. Estrogen is the primary signal that is essential for the growth and progression of breast cancer cells [47]. Our research indicates that Stearic acid hydrazide may function as a potent inhibitor of aromatase, effectively blocking the production of Estrogen. In our docking study, we used three positive controls, Arimidex, and Femara, which are non-steroidal, and exemestane, which is steroidal. These controls exhibit a covalent interaction at the active site of aromatase. Stearic acid hydrazide also exhibited a significant interaction and Asp309 being identified as a crucial residue in the active site [48]. While a large number of synthetic drugs are effective and appropriately used, numerous medicines have been identified as causing severe adverse reactions [49]. Multiple research studies have indicated that Exemestane, Femara, and Arimidex exhibit various adverse effects when used as aromatase inhibitors [50]–[52]. Medications derived from natural products aim to minimize the various drawbacks linked to synthetic compounds and traditional chemotherapy approaches [53]. Several research studies have investigated the anti-cancer properties of Stearic acid hydrazide. The cytotoxicity of synthesized complexes derived from fatty acids, including Stearic acid hydrazide, was evaluated against two human cancer cell lines, MCF7 and A549. The complexes exhibited sensitivity to all the tested cell lines [54]. In a similar study, Jubie et al. [55] found that derivatives of fatty acids, particularly Stearic acid hydrazide, displayed notable suppression of human lung carcinoma A-549 cell lines.
The docked Stearic acid hydrazide-Aromatase complex showed a favorable agreement with the X-ray structure of DP4, as demonstrated by the molecular dynamics (MD) results indicating a good RMSF per Residue (Figure 6). The RMSF quantifies the angstrom distances between the native structure and the docked complex. The RMSF values for all atoms within each residue pair of the two proteins were found to be almost identical with a very slight and insignificant increase in the RMSF in some positions, not surpassing 2 angstroms. In regions 209 and 270, a minor increase in flexibility was observed; however, it does not impact the region since it is situated away from the active site. These findings indicate that the Stearic acid hydrazide-Aromatase complex remains stable, and the ligand does not impact the stability of aromatase. There are no previous studies on the interaction between Stearic acid hydrazide and Aromatase. The association between the usage of antioxidants as inhibitors of some cancer-related enzymes is seen to be noteworthy due to the conflicting findings in studies from proponents and opponents. Radical scavenging by antioxidants is crucial to preventing the harmful effects of free radicals in a variety of illnesses, such as cancer [56]. However, the correlation between anti-cancer properties and antioxidant effects is not yet fully understood and requires further in-depth investigation [57].
Researchers have been exploring the potential of natural products as aromatase inhibitors alongside the clinical achievements of various synthetic drugs in treating postmenopausal estrogen receptor-positive breast cancer. These natural products, which have traditionally been utilized for nutritional or medicinal purposes, could potentially offer aromatase inhibitors with reduced side effects. An increasing amount of evidence indicates that the intake of specific plants and their components, particularly flavonoids, could offer defense against certain forms of cancer [58]. Natural products that have been used for a significant period, like those derived from food or traditional medicines, and also possess the ability to inhibit aromatase, might be associated with reduced toxicity levels [59]. In our research, we endeavored to explore the feasibility of utilizing natural compounds found in E. uniflora as potential inhibitors of the aromatase enzyme.
4.
Conclusions
A total of 15 chemical compounds were extracted from the E. uniflora plant. The ethanol extract of the leaves exhibited potent antioxidant activity, as evidenced by its high total phenolic content 119.5 mg GAE/g, total flavonoid content 141.16 mg GAE/g, radical scavenging activity 25 µg/mL, and reducing power 7.2 mmol/g. A significant number of compounds were found to possess favorable physicochemical characteristics, along with several additional ADMET features. The drug-likeness property predictions indicated that all the compounds adhere to the Rule of Five (Ro5). Except for compound 8, all other compounds are considered safe for use. This determination is based on the fact that they did not exhibit any mutagenic or carcinogenic properties in the parameters that were examined. The prediction results must undergo validation by in vitro, in vivo, and clinical toxicity assessments. Stearic acid hydrazide exhibits the most significant interaction with aromatase compared to the other natural compounds investigated in this study. The finding highlights the potential of Stearic acid hydrazide as a promising natural inhibitor for aromatase, offering a potential avenue for the development of novel drugs for cancer treatment. Further in vitro and in vivo experiments are necessary to validate our in-silico findings, as well as clinical trials, this could be potential drug candidates for cancer.
Author contributions
A.M.D., A.A.M and M.A. performed in vitro analysis. A.A.A performed in silico analysis. A.M.D., A.A.M and M.A. managed resources A.M.D., A.A.M, M.A., H.D. A., S.W.B., S.W.H., A.A.L., and A.A.A. wrote and analysed the main manuscript text. A.M.D., A.A.M, M.A. and A.A.A. prepared figures and tables and reviewed the manuscript.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.









 DownLoad:
DownLoad:


 3-Undecene (CCCCCCCC=CCC)
3-Undecene (CCCCCCCC=CCC)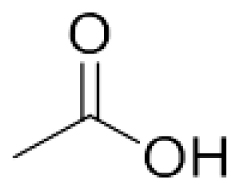 Acetic acid (CC(=O)O)
Acetic acid (CC(=O)O)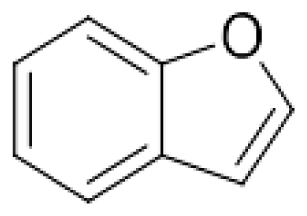 Benzofuran (C1=CC=C2C(=C1)C=CO2)
Benzofuran (C1=CC=C2C(=C1)C=CO2)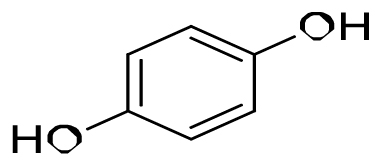 Hydroquinone (C1=CC(=CC=C1O)O)
Hydroquinone (C1=CC(=CC=C1O)O)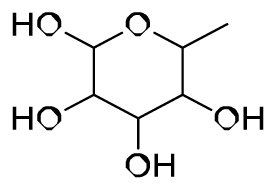 Alpha-L-Galactopyranose (CC1C(C(C(C(O1)O)O)O)O)
Alpha-L-Galactopyranose (CC1C(C(C(C(O1)O)O)O)O)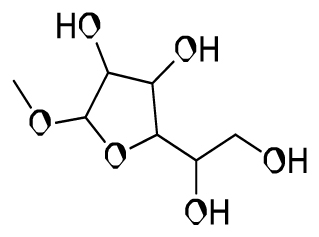 Methyl hexofuranoside (COC1C(C(C(O1)C(CO)O)O)O)
Methyl hexofuranoside (COC1C(C(C(O1)C(CO)O)O)O)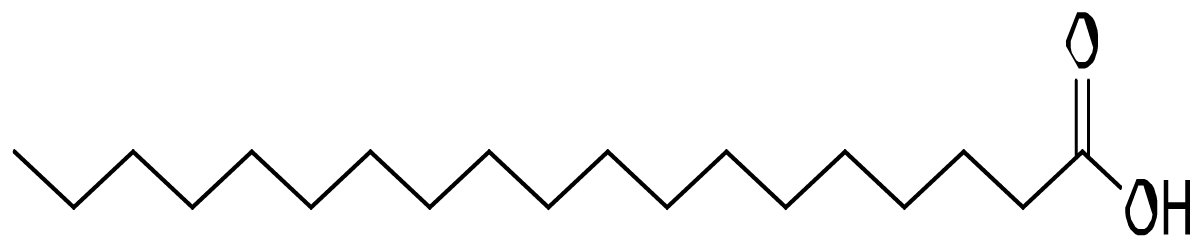 n-Nonadecanoic acid (CCCCCCCCCCCCCCCCCCC(=O) O)
n-Nonadecanoic acid (CCCCCCCCCCCCCCCCCCC(=O) O) 10-Octadecenoic acid (CCCCCCCCCCCCCCCC=CC(=O) O)
10-Octadecenoic acid (CCCCCCCCCCCCCCCC=CC(=O) O) 2-Nonen-1-ol (CCCCCCC=CCO)
2-Nonen-1-ol (CCCCCCC=CCO)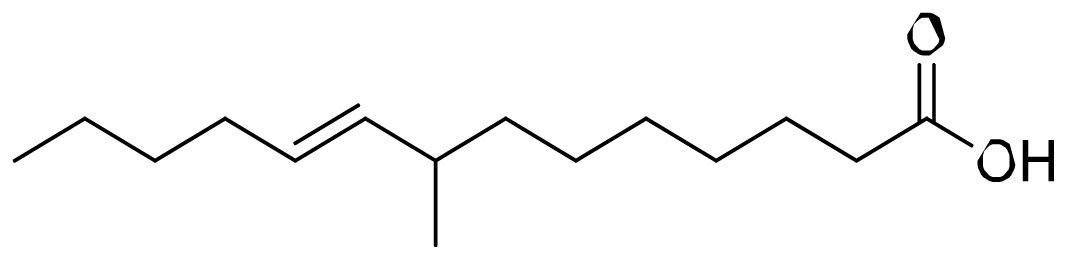 Z-8-Methyl-9-tetradecenoic acid (CCCCC=CC(C)CCCCCCC(=O) O)
Z-8-Methyl-9-tetradecenoic acid (CCCCC=CC(C)CCCCCCC(=O) O) 10-Undecenal (C=CCCCCCCCCC=O)
10-Undecenal (C=CCCCCCCCCC=O) 2-Octylcyclopropene-1-heptanol (CCCCCCCCC1=C(C1)CCCCCC CO)
2-Octylcyclopropene-1-heptanol (CCCCCCCCC1=C(C1)CCCCCC CO)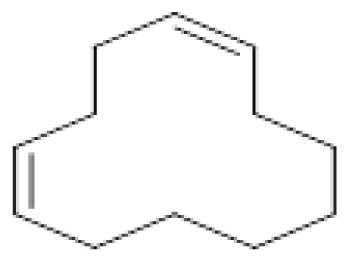 1,5-Cyclododecadiene (C1CCCC=CCCC=CCC1)
1,5-Cyclododecadiene (C1CCCC=CCCC=CCC1)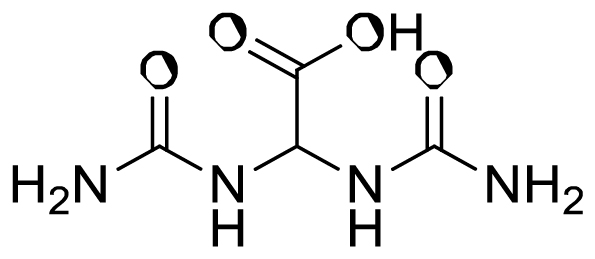 Allantoic acid (C(C(=O)O)(NC(=O)N)NC(=O)N)
Allantoic acid (C(C(=O)O)(NC(=O)N)NC(=O)N) Stearic acid hydrazide (CCCCCCCCCCCCCCCCCC(= O)NN)
Stearic acid hydrazide (CCCCCCCCCCCCCCCCCC(= O)NN)